SARS-COV-2: SIR Model Limitations and Predictive Constraints
Abstract
1. Introduction
2. Materials and Methods
2.1. Earth Seasons: From Stable Mean to Asymptotic Patterns of Susceptible, Infectious, or Recovered (SIR) Modeling Equation
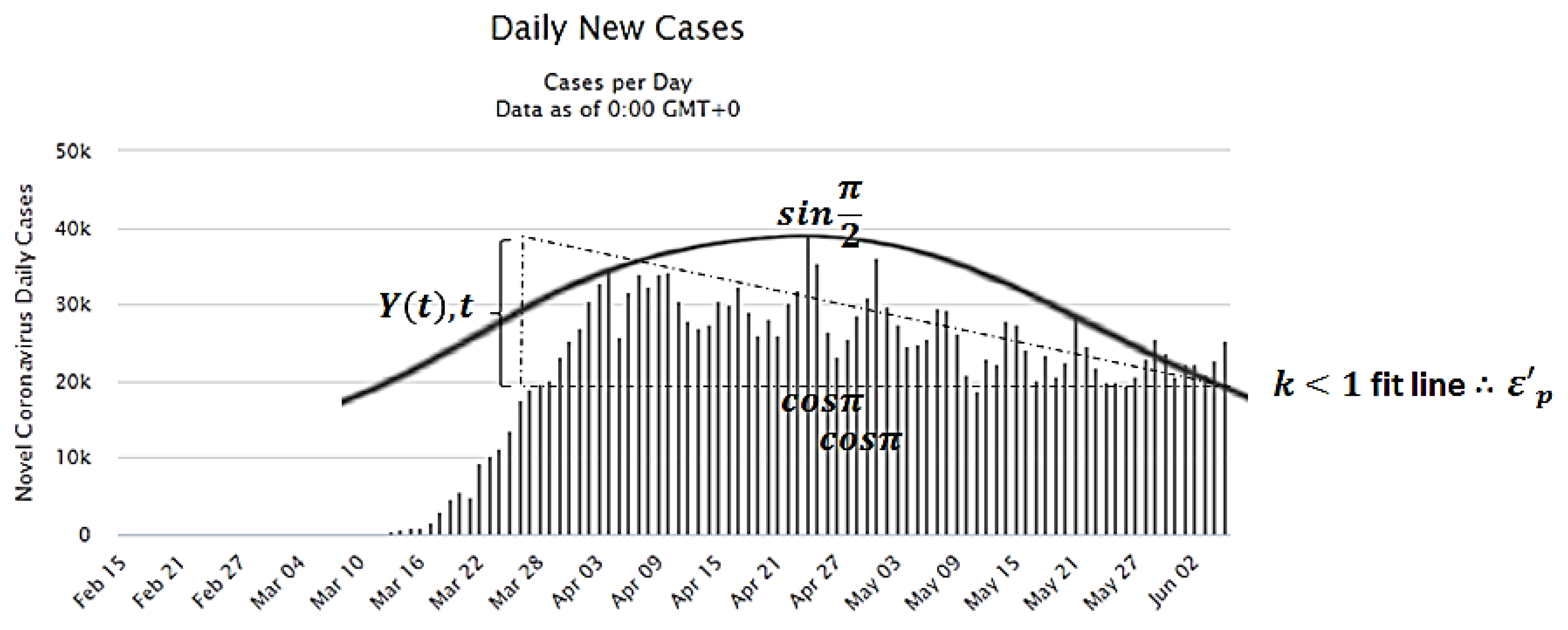
2.2. Skewness Validation and SIR Model Limitation
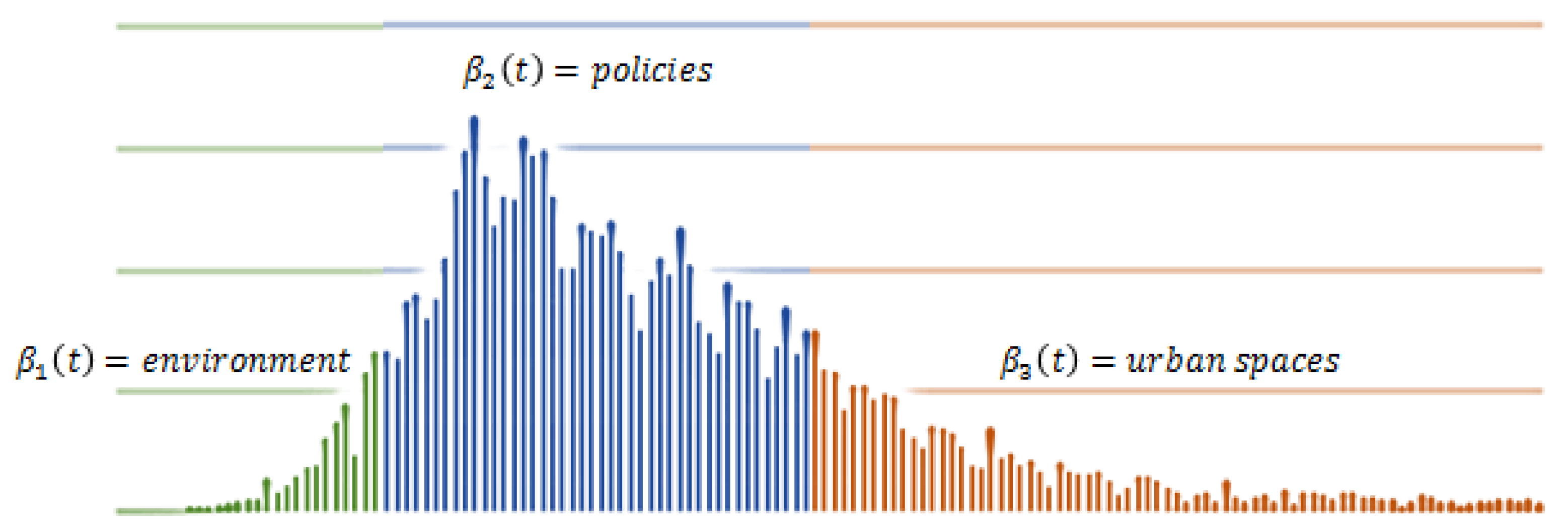
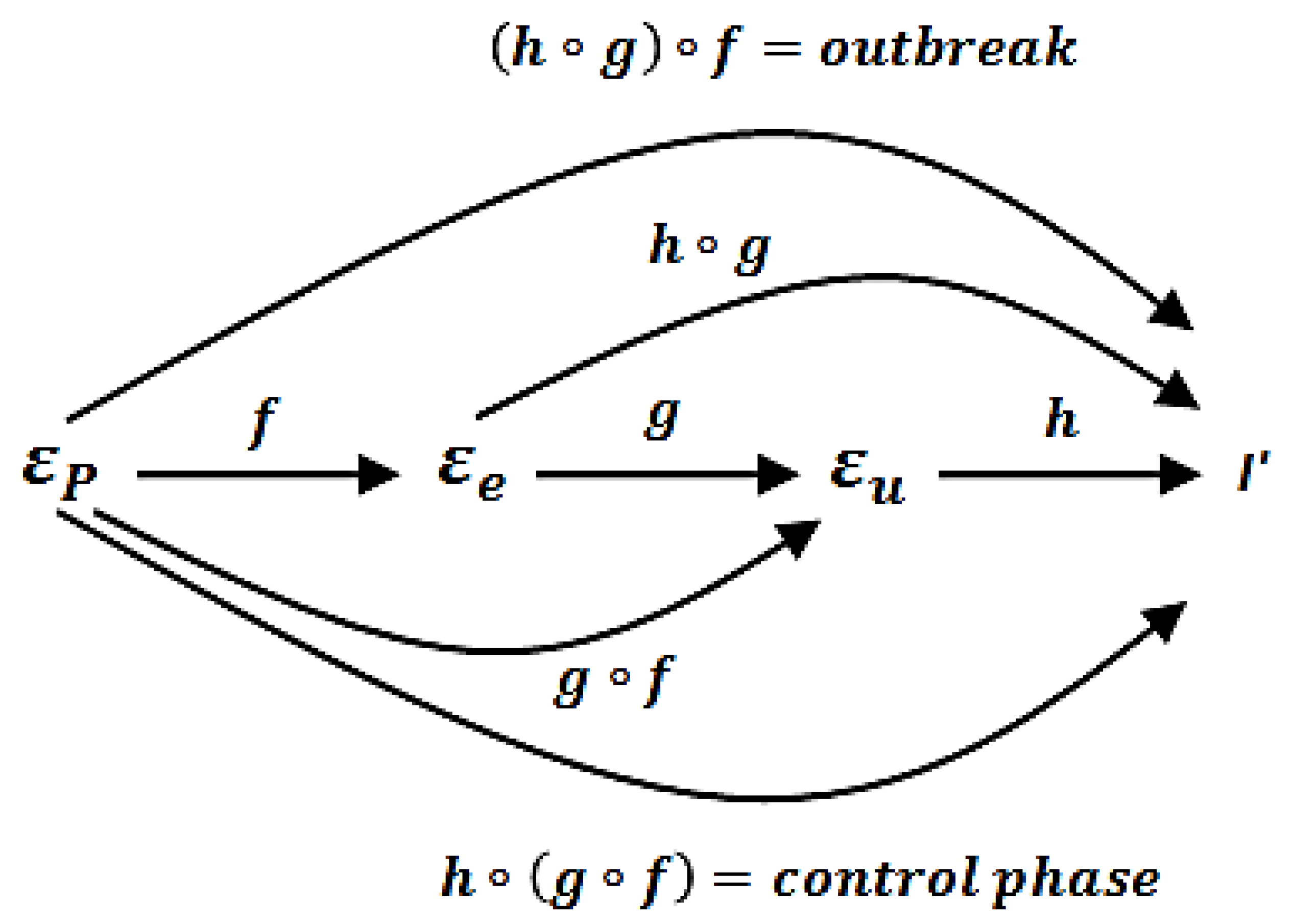
2.3. Mathematical Framework of Three Seasonality Forcing Behavior of Coronavirus Disease 2019 (COVID-19) Worldwide and SIR Model Variants Needed
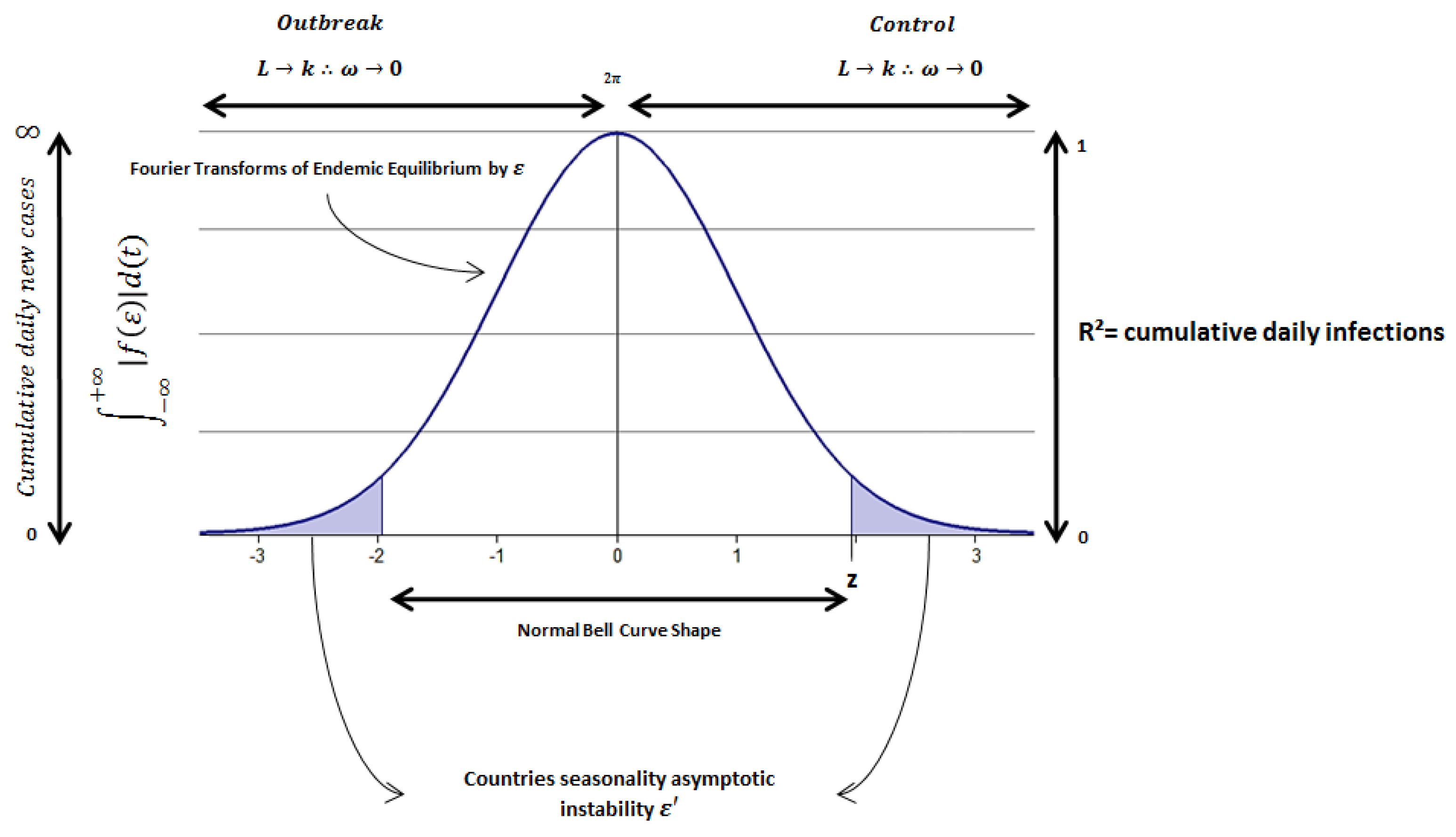
2.4. SIR Model Redefinition from the Original Equation to Skewness Patterns and Global Sensitivity
2.5. Birth and Death Persistence of COVID-19 Dissemination Patterns: From Positive to Negative Skew
3. Results
4. Discussion
5. Conclusions
6. Limitations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Grassly, N.C.; Fraser, C. Seasonal infectious disease epidemiology. Proc. R. Soc. B Biol. Sci. R. Soc. 2006, 273, 2541–2550. [Google Scholar] [CrossRef] [PubMed]
- Su, D.; Chen, Y.; He, K.; Zhang, T.; Tan, M.; Zhang, Y.; Zhang, X. Influence of Socio-Ecological Factors on COVID-19 Risk: A Cross-Sectional Study Based on 178 Countries/Regions Worldwide. SSRN Electron. J. 2020. [Google Scholar] [CrossRef]
- Telles, C.R.; Roy, A.; Ajmal, M.R.; Mustafa, S.K.; Ahmad, M.A.; de la Serna, J.M.; Frigo, E.P.; Rosales, M.H. Influence of countries adopted social distancing policy for COVID-19 reduction under the view of the airborne transmission framework (Preprint). JMIR Public Heal Surveill. 2020, 11. [Google Scholar] [CrossRef]
- Block, P.; Hoffman, M.; Raabe, I.J.; Dowd, J.B.; Rahal, C.; Kashyap, R.; Mills, M.C. Social network-based distancing strategies to flatten the COVID-19 curve in a post-lockdown world. Nat. Hum. Behav. 2020, 4, 588–596. [Google Scholar] [CrossRef] [PubMed]
- Ferguson, N.; Laydon, D.; Nedjati Gilani, G.; Imai, N.; Ainslie, K.; Baguelin, M.; Bhatia, S.; Boonyasiri, A.; Cucunuba Perez, Z.U.; Cuo-mo-Dannenburg, G.; et al. Report 9: Impact of Non-Pharmaceutical Interventions (NPIs) to Reduce COVID19 Mortality and Healthcare Demand; Imperial College London: London, UK, 2020. [Google Scholar] [CrossRef]
- Chu, D.K.; Akl, E.A.; Duda, S.; Solo, K.; Yaacoub, S.; Schünemann, H.J.; El-Harakeh, A.; Bognanni, A.; Lotfi, T.; Loeb, M.; et al. Physical distancing, face masks, and eye protection to prevent person-to-person transmission of SARS-CoV-2 and COVID-19: A systematic review and meta-analysis. Lancet 2020, 395, 1973–1987. [Google Scholar] [CrossRef]
- Lopes, H.; McKay, V. Adult learning and education as a tool to contain pandemics: The COVID-19 experience. Int. Rev. Educ. 2020, 66, 575–602. [Google Scholar] [CrossRef]
- Alberti, T.; Faranda, D. On the uncertainty of real-time predictions of epidemic growths: A COVID-19 case study for China and Italy. Commun. Nonlinear Sci. Numer. Simul. 2020, 90, 105372. [Google Scholar] [CrossRef] [PubMed]
- Roberts, M.; Andreasen, V.; Lloyd, A.; Pellis, L. Nine challenges for deterministic epidemic models. Epidemics 2015, 10, 49–53. [Google Scholar] [CrossRef] [PubMed]
- Dong, E.; Du, H.; Gardner, L. An interactive web-based dashboard to track COVID-19 in real time. Lancet Infect. Dis. 2020, 20, 533–534. [Google Scholar] [CrossRef]
- Altizer, S.; Dobson, A.; Hosseini, P.; Hudson, P.; Pascual, M.; Rohani, P. Seasonality and the dynamics of infectious diseases. Ecol. Lett. 2006, 9, 467–484. [Google Scholar] [CrossRef]
- Bacaër, N.; Dads, E.H.A. On the biological interpretation of a definition for the parameter R 0 in periodic population models. J. Math. Biol. 2011, 65, 601–621. [Google Scholar] [CrossRef] [PubMed]
- Siettos, C.I.; Russo, L. Mathematical modeling of infectious disease dynamics. Virulence 2013, 4, 295–306. [Google Scholar] [CrossRef] [PubMed]
- Mari, L.; Casagrandi, R.; Bertuzzo, E.; Rinaldo, A.; Gatto, M. Floquet theory for seasonal environmental forcing of spatially explicit waterborne epidemics. Theor. Ecol. 2014, 7, 351–365. [Google Scholar] [CrossRef]
- Zhang, Y.; You, C.; Cai, Z.; Sun, J.; Hu, W.; Zhou, X.H. Prediction of the COVID-19 outbreak based on a realistic stochastic model. medRxiv 2020. [Google Scholar] [CrossRef]
- Utsunomiya, Y.T.; Utsunomiya, A.T.H.; Torrecilha, R.B.P.; Paulan, S.D.C.; Milanesi, M.; Garcia, J.F. Growth Rate and Acceleration Analysis of the COVID-19 Pandemic Reveals the Effect of Public Health Measures in Real Time. Front. Med. 2020, 7, 247. [Google Scholar] [CrossRef] [PubMed]
- Stübinger, J.; Schneider, L. Epidemiology of Coronavirus COVID-19: Forecasting the Future Incidence in Different Countries. InHealthcare 2020, 8, 99. [Google Scholar] [CrossRef]
- Rock, K.; Brand, S.; Moir, J.; Keeling, M.J. Dynamics of infectious diseases. Rep. Prog. Phys. 2014, 77, 026602. [Google Scholar] [CrossRef]
- Billings, L.; Schwartz, I.B. Exciting chaos with noise: Unexpected dynamics in epidemic outbreaks. J. Math. Biol. 2002, 44, 31–48. [Google Scholar] [CrossRef] [PubMed]
- WHO. World Health Organization: Influenza Laboratory Surveillance Information by the Global Influenza Surveillance and Response System (GISRS). Available online: https://www.who.int/influenza/gisrs_laboratory/flunet/charts/en/ (accessed on 25 June 2020).
- Li, Y.; Wang, X.; Nair, H. Global Seasonality of Human Seasonal Coronaviruses: A Clue for Postpandemic Circulating Season of Severe Acute Respiratory Syndrome Coronavirus 2? J. Infect. Dis. 2020, 222, 1090–1097. [Google Scholar] [CrossRef] [PubMed]
- Smit, A.J.; Fitchett, J.M.; Engelbrecht, F.A.; Scholes, R.J.; Dzhivhuho, G.; Sweijd, N.A. Winter Is Coming: A Southern Hemisphere Perspective of the Environmental Drivers of SARS-CoV-2 and the Potential Seasonality of COVID-19. Int. J. Environ. Res. Public Health 2020, 17, 5634. [Google Scholar] [CrossRef]
- Engelbrecht, F.A.; Scholes, R.J. Test for Covid-19 seasonality and the risk of second waves. One Health 2021, 12, 100202. [Google Scholar] [CrossRef]
- Kanzawa, M.; Spindler, H.; Anglemyer, A.; Rutherford, G.W. Will Coronavirus Disease 2019 Become Seasonal? J. Infect. Dis. 2020, 222, 719–721. [Google Scholar] [CrossRef]
- Grenfell, B.; Kleczkowski, A.; Gilligan, C.; Bolker, B. Spatial heterogeneity, nonlinear dynamics and chaos in infectious diseases. Stat. Methods Med. Res. 1995, 4, 160–183. [Google Scholar] [CrossRef]
- Buonomo, B.; Chitnis, N.; D’Onofrio, A. Seasonality in epidemic models: A literature review. Ric. Mat. 2018, 67, 7–25. [Google Scholar] [CrossRef]
- Telles, C.R. Reducing SARS-CoV-2 infectious spreading patterns by removing S and R compartments from SIR model equa-tion. medRxiv 2020. [Google Scholar] [CrossRef]
- Carlson, C.J.; Gomez, A.C.R.; Bansal, S.; Ryan, S.J. Misconceptions about weather and seasonality must not misguide COVID-19 response. Nat. Commun. 2020, 11, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Manzo, G. Complex social networks are missing in the dominant covid-19 epidemic models. Sociologica 2020, 14, 31–49. [Google Scholar] [CrossRef]
- Merchant, H. CoViD-19 may not end as predicted by the SIR model. BMJ 2020, 369. Available online: https://www.bmj.com/content/369/bmj.m1567/rr (accessed on 30 April 2020).
- Adam, D. The simulations driving the world’s response to covid-19. How epidemiologists rushed to model the corona-virus pandemic. Nature 2020, 580, 316–318. [Google Scholar] [CrossRef]
- Luo, J. Predictive Monitoring of COVID-19; SUTD Data-Driven Innovation Lab.: Singapore, 2020. [Google Scholar]
- Best, R.; Boice, J. Where The Latest COVID-19 Models Think We’re Headed—And Why They Disagree. Abc News: FiveThir-tyEight. Available online: https://projects.fivethirtyeight.com/covid-forecasts/ (accessed on 11 June 2020).
- Koerth, M.; Bronner, L.; Mithani, J. Why It’s So Freaking Hard to Make a Good COVID-19 Model. Abc News: FiveThirtyEight. Available online: https://fivethirtyeight.com/features/why-its-so-freaking-hard-to-make-a-good-covid-19-model/ (accessed on 31 March 2020).
- Liu, Y.; Ning, Z.; Chen, Y.; Guo, M.; Liu, Y.; Gali, N.K.; Sun, L.; Duan, Y.; Cai, J.; Westerdahl, D.; et al. Aerodynamic analysis of SARS-CoV-2 in two Wuhan hospitals. Nat. Cell Biol. 2020, 582, 557–560. [Google Scholar] [CrossRef] [PubMed]
- Lin, K.; Marr, L.C. Humidity-Dependent Decay of Viruses, but Not Bacteria, in Aerosols and Droplets Follows Disinfection Kinetics. Environ. Sci. Technol. 2020, 54, 1024–1032. [Google Scholar] [CrossRef] [PubMed]
- Morawska, L.; Milton, D.K. It Is Time to Address Airborne Transmission of Coronavirus Disease 2019 (COVID-19). Clin. Infect. Dis. 2020. [Google Scholar] [CrossRef]
- Roda, W.C.; Varughese, M.B.; Han, D.; Li, M.Y. Why is it difficult to accurately predict the COVID-19 epidemic? Infect. Dis. Model. 2020, 5, 271–281. [Google Scholar] [CrossRef]
- Duarte, J.; Januário, C.; Martins, N.; Rogovchenko, S.; Rogovchenko, Y. Chaos analysis and explicit series solutions to the seasonally forced SIR epidemic model. J. Math. Biol. 2019, 78, 2235–2258. [Google Scholar] [CrossRef] [PubMed]
- Dietz, K. The Incidence of Infectious Diseases under the Influence of Seasonal Fluctuations. In Mathematical Models in Medicine; Springer: Berlin, Germany, 1976; pp. 1–15. [Google Scholar] [CrossRef]
- Telles, C.R. False asymptotic instability behavior at iterated functions with Lyapunov stability in nonlinear time series. In Science and Information Conference; Springer: Cham, Switzerland, 2020; pp. 673–693. [Google Scholar] [CrossRef]
- Jiang, R.; Murthy, D.N. A study of Weibull shape parameter: Properties and significance. Reliab. Eng. Syst. Saf. 2011, 96, 1619–1626. [Google Scholar] [CrossRef]
- Edelsbrunner, H.; Harer, J. Persistent homology-a survey. Contemp. Math. 2008, 453, 257–282. Available online: https://www.maths.ed.ac.uk/~v1ranick/papers/edelhare.pdf (accessed on 14 July 2020).
- Cohen-Steiner, D.; Edelsbrunner, H.; Harer, J. Stability of persistence diagrams. Discret. Comput. Geom. 2007, 37, 103–120. Available online: http://math.uchicago.edu/~shmuel/AAT-readings/Data%20Analysis%20/Edelsbrunner,%20Harer,%20Stability.pdf (accessed on 25 August 2020). [CrossRef]
- CDC. Centers for Disease Control and Prevention. CASES, DATA & SURVEILLANCE: Forecasts of Total Deaths July 2, 2020. Available online: https://www.cdc.gov/coronavirus/2019-ncov/covid-data/forecasting-us.html (accessed on 8 July 2020).
- Sajadi, M.M.; Habibzadeh, P.; Vintzileos, A.; Shokouhi, S.; Miralles-Wilhelm, F.; Amoroso, A. Temperature, Humidity, and Latitude Analysis to Estimate Potential Spread and Seasonality of Coronavirus Disease 2019 (COVID-19). JAMA Netw. Open 2020, 3, e2011834. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.; Huang, W.; Wen, M.; Li, D.; Ma, S.; Hua, J.; Hu, H.; Yin, S.; Qian, Y.; Chen, P.; et al. Containing the spread of coronavirus disease 2019 (COVID-19): Meteorological factors and control strategies. Sci. Total. Environ. 2020, 744, 140935. [Google Scholar] [CrossRef] [PubMed]
- Rucinski, S.L.; Binnicker, M.J.; Thomas, A.S.; Patel, R. Seasonality of Coronavirus 229E, HKU1, NL63, and OC43 from 2014 to 2020. In Mayo Clinic Proceedings; Elsevier BV: Amsterdam, The Netherlands, 2020; Volume 95, pp. 1701–1703. [Google Scholar]
- Mecenas, P.; Bastos, R.T.D.R.M.; Vallinoto, A.C.R.; Normando, D. Effects of temperature and humidity on the spread of COVID-19: A systematic review. PLoS ONE 2020, 15, e0238339. [Google Scholar] [CrossRef]
- Ghosh, S.; Bhattacharya, S. A data-driven understanding of COVID-19 dynamics using sequential genetic algo-rithm based probabilistic cellular automata. Appl. Soft Comput. 2020, 96, 106692. [Google Scholar] [CrossRef]
- Machado, J.A.T. An Evolutionary Perspective of Virus Propagation. Mathematics 2020, 8, 779. [Google Scholar] [CrossRef]
- Braun, P.; Haffner, S.; Woodcock, B.G. COVID-19 pandemic predictions using the modified Bateman SIZ model and observational data for Heidelberg, Germany: Effect of vaccination with a SARS-CoV-2 vaccine, coronavirus testing and application of the Corona-Warn-App. Int. J. Clin. Pharmacol. Ther. 2020, 58, 417–425. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roberto Telles, C.; Lopes, H.; Franco, D. SARS-COV-2: SIR Model Limitations and Predictive Constraints. Symmetry 2021, 13, 676. https://doi.org/10.3390/sym13040676
Roberto Telles C, Lopes H, Franco D. SARS-COV-2: SIR Model Limitations and Predictive Constraints. Symmetry. 2021; 13(4):676. https://doi.org/10.3390/sym13040676
Chicago/Turabian StyleRoberto Telles, Charles, Henrique Lopes, and Diogo Franco. 2021. "SARS-COV-2: SIR Model Limitations and Predictive Constraints" Symmetry 13, no. 4: 676. https://doi.org/10.3390/sym13040676
APA StyleRoberto Telles, C., Lopes, H., & Franco, D. (2021). SARS-COV-2: SIR Model Limitations and Predictive Constraints. Symmetry, 13(4), 676. https://doi.org/10.3390/sym13040676





