Next Article in Journal
Controllability of Semilinear Multi-Valued Differential Inclusions with Non-Instantaneous Impulses of Order α ∈ (1,2) without Compactness
Next Article in Special Issue
Magnetic Properties of Nickel-Titanium Alloy during Martensitic Transformations under Plastic and Elastic Deformation
Previous Article in Journal
A Weak Tripled Contraction for Solving a Fuzzy Global Optimization Problem in Fuzzy Metric Spaces
Previous Article in Special Issue
Self-Assembly of Hydrogen-Bonded Cage Tetramers of Phosphonic Acid
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Symmetry
Volume 13
Issue 4
10.3390/sym13040564
symmetry-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Structure-Property Relationship in Selected Naphtho- and Anthra-Quinone Derivatives on the Basis of Density Functional Theory and Car–Parrinello Molecular Dynamics

by
Beata Kizior
1,2,
Jarosław J. Panek
1,
Bartłomiej M. Szyja
2 and
Aneta Jezierska
1,*
1
Faculty of Chemistry, University of Wrocław, ul. F. Joliot-Curie 14, 50-383 Wrocław, Poland
2
Department of Fuels Chemistry and Technology, Wrocław University of Science and Technology, ul. Gdańska 7/9, 50-344 Wrocław, Poland
*
Author to whom correspondence should be addressed.
Symmetry 2021, 13(4), 564; https://doi.org/10.3390/sym13040564
Submission received: 8 March 2021 / Revised: 22 March 2021 / Accepted: 24 March 2021 / Published: 29 March 2021
(This article belongs to the Special Issue Exploring Inter- and Intramolecular Interactions as Building Blocks of Larger Systems)
Browse Figures
Versions Notes

Abstract

:
Intra- and inter-molecular interactions were studied in 2,3-dichloro-5,8-dihydroxy-1,4-naphthoquinone and 1,4-dihydroxy-anthraquinone to shed more light on the molecular assembly phenomena. The electronic ground and excited states features of the compounds were investigated to find structure-property dependencies. The theoretical study was carried out on the basis of Density Functional Theory (DFT), its Time-Dependent (TD-DFT) extension, and using Car–Parrinello Molecular Dynamics (CPMD). In order to show how the environmental effects modulate the physico-chemical properties, the simulations were performed in vacuo, with the solvent reaction field (Polarizable Continuum Model (PCM) and water as a solvent) and crystalline phase. The intramolecular hydrogen bonds and the bridged proton dynamics were analyzed in detail. The aromatic rings and electronic structure changes were estimated using the Harmonic Oscillator Model of Aromaticity (HOMA) and Atoms in Molecules (AIM) theory. The Symmetry-Adapted Perturbation Theory (SAPT) was employed for interaction energy decomposition in the studied dimers and trimers. It was found that the presence of a polar solvent decreased the energy barrier for the bridged proton transfer. However, it did not significantly affect the aromaticity and electronic structure. The SAPT results showed that the mutual polarization of the monomers in the dimer was weak and that the dispersion was responsible for most of the intermolecular attraction. The intermolecular hydrogen bonds seem to be much weaker than the intramolecular bridges. The TD-DFT results confirmed that the electronic excitations do not play any significant role in the intramolecular proton transfer. The CPMD results indicated that the protons are very labile in the hydrogen bridges. Short proton transfer and proton-sharing events were observed, and a correlation between them in the twin bridges was noticed, especially for the first investigated compound.

1. Introduction

Naphtho- and anthra-quinone are parent compounds for 2,3-dichloro-5,8-dihydroxy-1,4-naphthoquinone 1 [1] and 1,4-dihydroxy-anthraquinone 2 [2], which are the objects of the current study; see Figure 1. Naphtho- and anthra-quinone occur in many natural products, possessing diverse biological activity, being building blocks of many dyes; see for example [3,4,5,6,7,8,9,10,11,12,13]. They are also interesting classes of compounds from the materials science point of view. Their derivatives have been mentioned as, e.g., potential electrode-active material candidates in an acidic aqueous electrolyte [14]. They are able to improve the performance of flow batteries [15], and also, long-life lithium-organic batteries were developed based on the core structure of naphthoquinone [16]. The anthraquinone oligomers were reported as anode-active materials [17] in rechargeable nickel/oligomer batteries. In addition, naphthoquinone derivatives were found as colorimetric and fluorescence chemosensors for the selective recognition of Sn 2 + in an aqueous medium [18]. The examples mentioned above show how important and interesting from diverse points of view naphtho- and anthra-quinone derivatives are.
The main aim of the study covers theoretical investigations of intra- and inter-molecular interactions present in Compounds 1 [1] and 2 [2]. The detailed analysis of such interactions sheds more light onto molecular level processes involving the molecules, e.g., proton transfer phenomenon, aggregation processes, etc., which are important to design new molecules with desired properties. The crystal structure of Compound 1 is built up of stacked molecules, as shown in Figure 2 (see the CCDC Database Identifier DCDHNQ01, Deposition Number 1137406) [1]. The structure organization of the stacked dimers is as follows: due to the symmetry centers, the quinoid part of one molecule partially overlaps the benzenoid part of the neighboring molecules. According to the X-ray measurements, the distance between the overlapping planes of the dimers is 3.40(3) Å, and a charge-transfer complex with itself is formed in the solid-state [1]. Concerning Compound 2 (see Figure 3 for its unit cell), the X-ray measurements detected the presence of remarkably short intermolecular contacts with a O...O distance of 2.644 Å and 2.778 Å (see the CCDC Database Identifier DHXANT10, Deposition Number 1140045) [2]. This was explained by the fact that each O-H group is involved in the intra-, as well as the inter-molecular hydrogen bonding [2]; see Figure S4 of the Supplementary Materials. Both compounds possess strong, Resonance-Assisted Hydrogen Bonds (RAHBs) [19] forming quasi-rings and additionally stabilizing the structures. The presence of the intra- and inter-molecular hydrogen bonds made the compounds interesting and suitable for the discussion of the role of interactions as the building blocks of larger systems. The compounds are well-suited for our Density Functional Theory (DFT) study [20,21] to discuss the hydrogen bonds’ properties and the substituents’ influence on molecular features. Compounds 1 and 2 were investigated in the electronic ground and excited states. In order to study the Excited State Intramolecular Proton Transfer (ESIPT), the time-dependent extension of the classical DFT method was applied [22]. The electronic ground state computations were performed in vacuo, using the continuum solvation model (Polarizable Continuum Model (PCM)) [23] to reproduce the polar environment impact on the molecules, as well as in the crystalline phase. Special attention was paid to the theoretical description of intramolecular hydrogen bonds. We employed static and first principles molecular dynamics models to get a deeper insight into the hydrogen bridges’ dynamics and related phenomena—internal electronic and geometric parameters’ reorganization. The Harmonic Oscillator Model of Aromaticity (HOMA) [24] index was estimated to follow the aromaticity changes upon the O-H distance elongation in the hydrogen bridge. The Atoms In Molecules (AIM) theory [25] was applied to study the electronic structure evolution in the same manner. The intermolecular interactions and the energy decomposition in the dimers and trimers of the compounds were investigated using the Symmetry-Adapted Perturbation Theory (SAPT) method [26]. On the basis of the method, the stability of the formed complexes could be estimated and discussed in detail showing which energy components play the most important role. In order to reproduce the molecular properties of both hydrogen bridges, Car–Parrinello Molecular Dynamics (CPMD) [27] was employed. The isolated molecule simulations provided us with the details of the hydrogen bridges’ dynamics when the molecule exhibits degrees of freedom not limited by the presence of the neighboring molecules and the crystal field. However, the crystalline phase simulations gave us an unrelieved description of the intramolecular hydrogen bonds’ molecular features. The correlations of the bridged protons during the CPMD runs were analyzed to give a deeper insight into the bridged protons dynamics.

2. Computational Methodology

2.1. Static Models on the Basis of Density Functional Theory

The models for Density Functional Theory (DFT) [20,21] simulations were prepared based on the experimentally determined crystal structures of 2,3-dichloro-5,8-dihydroxy-1,4-naphthoquinone 1 and 1,4-dihydroxy-anthraquinone 2 [1,2]; see Figure 1. The dimers and trimers of the compounds were also extracted from the crystallographic data; see Figure 4 and Figure 5 for the dimers and Figures S3 and S4 of the Supplementary Materials for the trimers, respectively. The geometry optimization was performed in vacuo and with the solvent reaction field reproduced by the Polarizable Continuum Model (PCM) [23] (in its IEF-PCM formulation) using water as a solvent. The B3LYP [28], PBE [29,30], and ω B97XD [31] functionals were applied to calculate metric and electronic structure parameters. The Pople-style triple zeta split-valence 6-311+G(2d,2p) orbital basis set [32,33,34] was employed in the static DFT. Next, the harmonic frequencies were computed to check if the obtained geometries corresponded to the minimum on the Potential Energy Surface (PES). The proton reaction path in the intramolecular hydrogen bond was investigated by means of the scan with the optimization method (the OHO valence angle was fixed; the O-H distance was elongated by a 0.05 Å increment; while the remaining part of the molecules was optimized) using the ω B97XD functional. The same functional was applied to prepare wavefunctions for the calculations of aromaticity index and Atoms In Molecules (AIM) theory [25]. The geometry-based Harmonic Oscillator Model of Aromaticity (HOMA) [24] was used to estimate the aromaticity changes upon the O-H distance elongation in the hydrogen bridge. The HOMA index was computed in vacuo and in water. The initial geometries of the dimers and trimers for further Symmetry-Adapted Perturbation Theory (SAPT) analysis [26] were calculated at the B3LYP/6-311+G(2d,2p) level of theory. This part of the quantum-chemical simulations was performed with the Gaussian 16, Rev. C.01 program [35]. The aromaticity index was calculated with the Multiwfn program [36].

2.2. Atoms in Molecules Theory

Atoms In Molecules (AIM) [25] analysis was performed with the AIMAll package [37] in the gas phase. The analysis was carried out to investigate the electronic structure changes in the monomeric forms upon the intramolecular hydrogen bridge deformation by the O-H distance changes. The analysis was performed only for one hydrogen bridge due to the symmetry exhibited by the studied compounds. AIM theory served for the atomic charges’ calculations, as well as to estimate the changes of the molecular properties at the Bond Critical Points (BCPs): The electron density and its Laplacian. It is well known that the AIM formalism should be applied at the equilibrium geometry, and the standard method nomenclature related to the Bond and Ring Critical Points (BCPs and RCPs) could be used. Here, we investigated non-equilibrium structures obtained as a result of the O-H distance changes in the studied molecules. Therefore, the electronic structure and topological features cannot be strictly related to the nomenclature and terminology developed in the classical AIM theory. However, we labeled the located BCPs following the convention used in the literature in the studies of non-equilibrium structures where the AIM theory was applied [38,39].

2.3. Symmetry-Adapted Perturbation Theory

The energy decomposition of the dimers and trimers of 1 and 2 (see Figure 4 and Figure 5 and Figures S3 and S4) was carried out using Symmetry-Adapted Perturbation Theory (SAPT) [26]. The energy was decomposed for two sets of structures: (i) extracted from the experimental X-ray data [1,2] (ii) obtained as a result of quantum-chemical simulations at the B3LYP/6-311+G(2d,2p) level of theory. The SAPT analysis was done at the SAPT2 level of theory [40] for both sets of investigated dimers and trimers. The SAPT2 calculations for the DFT-optimized structures were performed with the aug-cc-pVDZ basis set [41] applied for the atomic orbital expansion. The interaction energy computation at the SAPT2/aug-cc-pVDZ level of theory involved also the counterpoise correction for the Basis Set Superposition Error (BSSE) [42], dividing the investigated dimers and trimers into “monomers”. The SAPT calculations were performed using the Psi4 1.2.1 [43] program.

2.4. Time-Dependent Density Functional Theory

The time-dependent DFT calculations were carried out using the ORCA program (Version 4.2.1) [44,45]. All equilibrium and non-equilibrium structures were investigated in order to evaluate the differences in the excitation energies with respect to the geometry. We used the hybrid, three-parameter B3LYP functional [28] and range-separated hybrid functional, with dispersion corrections: ω B97XD [31]. To maintain consistency with the static, ground state calculations, the Pople-style triple zeta split-valence 6-311+G(2d,2p) orbital basis set [32,33,34] was used.
The solvent effects were accounted for using the Conductor-like Polarizable Continuum Model (CPCM) as implemented in ORCA, with the dielectric constant of ϵ = 80.4 and refractive index of 1.33.

2.5. Car–Parrinello Molecular Dynamics In Vacuo and the Crystalline Phase

Car–Parrinello molecular dynamics simulations were performed in vacuo and in the crystalline phase for Compounds 1 and 2 [1,2]. The models used for CPMD in the gas phase are presented in Figure 1. The initial geometries were extracted from the X-ray data and placed into cubic boxes with a = 14 Å for Compound 1 and a = 16 Å for Compound 2. The models for CPMD in the crystalline phase are presented in Figure 2 and Figure 3, respectively. They were prepared on the basis of experimental monoclinic unit cells with a = 14.110 Å, b = 7.070 Å, c = 9.810 Å, and β = 102 . 09 ∘ with Z = 4 for 1 and a = 20.339 Å, b = 6.017 Å, c = 10.391 Å, and β = 125 . 46 ∘ with Z = 4 for 2. The exchange correlation functional by Perdew, Berke, and Ernzerhof (PBE) [29,30] and Troullier–Martins [46] pseudopotentials were applied. The fictitious Electron Mass (EMASS) was equal to 400 a.u. for both compounds and both phases’ simulations. The time-step was 3 a.u., and the kinetic energy cutoff for the plane-wave basis set was 80 Ry. The CPMD calculations were performed at 295 K controlled by a Nosé–Hoover thermostat [47,48]. Hockney’s scheme [49] was applied to remove interactions with periodic images of the cubic cell. The translational and rotational movements were removed from the CPMD data collection in the gas phase. The crystalline phase CPMD was performed with Γ point approximation [50] and Periodic Boundary Conditions (PBCs). The real-space electrostatic summations were set to TESR = 8 nearest neighbors in each direction. The initial part of the production run of the CPMD was taken as an equilibration (ca. 1.8 ps), and it was excluded during the post-processing procedures. The CPMD trajectories were collected further for 20 ps for both compounds in both phases. The data analysis focused mostly on the intramolecular hydrogen bonds dynamics. The CPMD simulations were carried out with the CPMD 3.17.1 program [51]. The graphics was prepared with the assistance of the VMD 1.9.3 [52] and Vesta (Version 3) [53] programs.

3. Results and Discussion

We focused on metric and electronic structure analyses of 2,3-dichloro-5,8-dihydroxy-1,4-naphthoquinone 1 [1] and 1,4-dihydroxy-anthraquinone 2 [2] in the electronic ground and excited states. We investigated the molecular features of the compounds using various theoretical approaches reproducing forces involved in the assembly of the compounds at the molecular level. We applied static DFT models, as well as first principles molecular dynamics using the Car–Parrinello formulation for the comprehensive theoretical description of molecular features in the studied naphtho- and anthra-quinone derivatives.

3.1. Geometric, Electronic Structure Parameters, and Intermolecular Forces Analysis in the Electronic Ground State

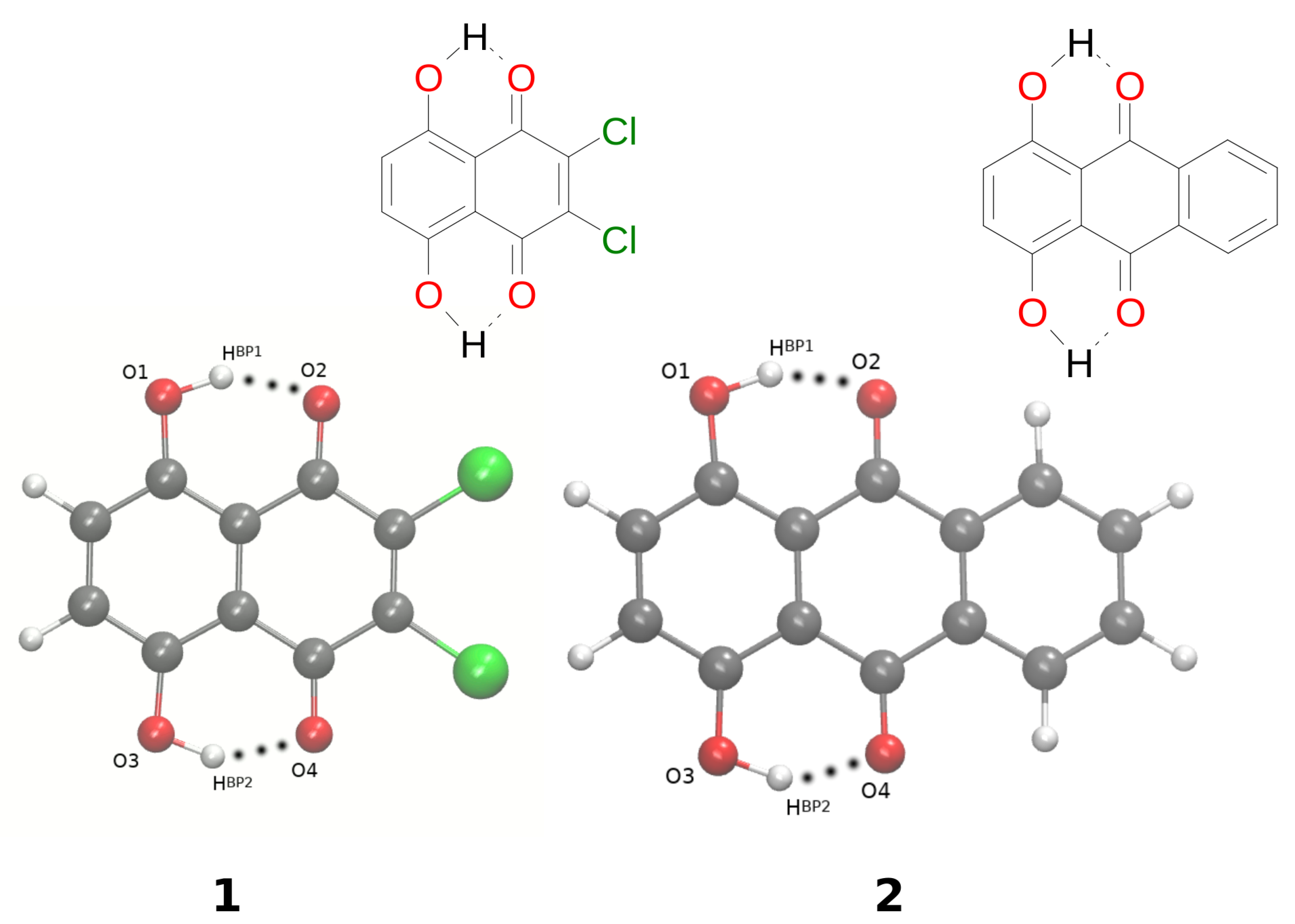
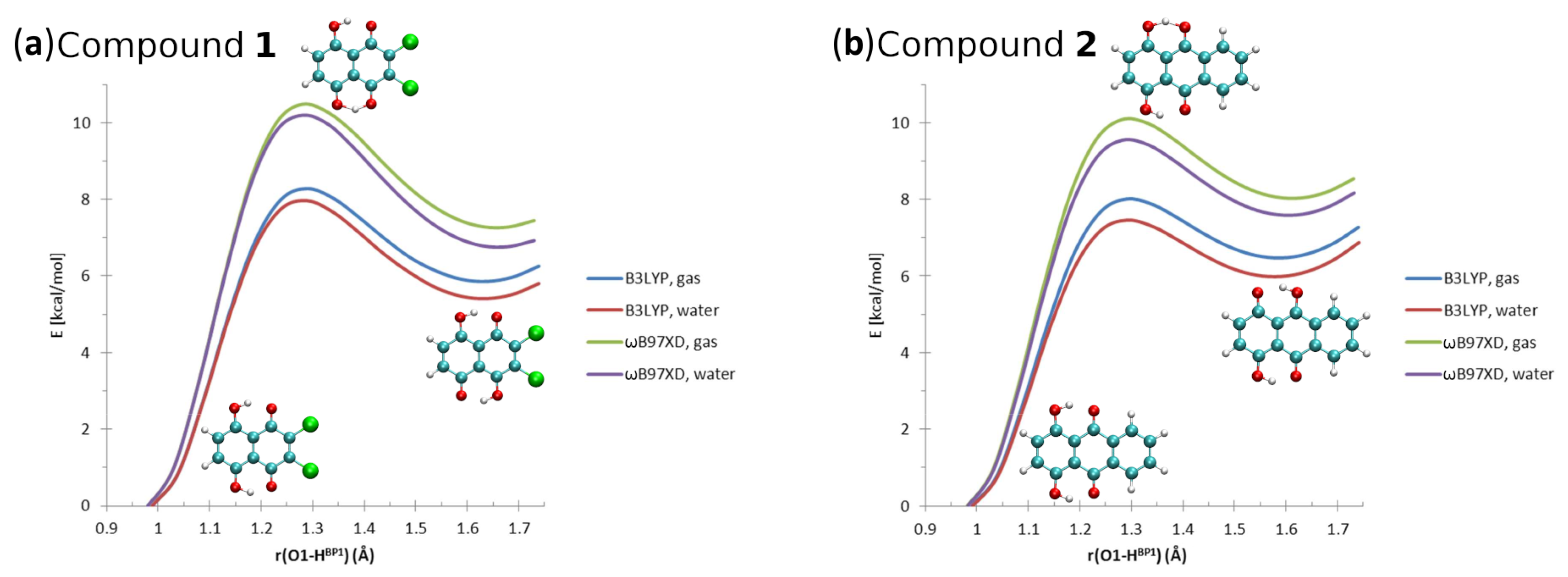
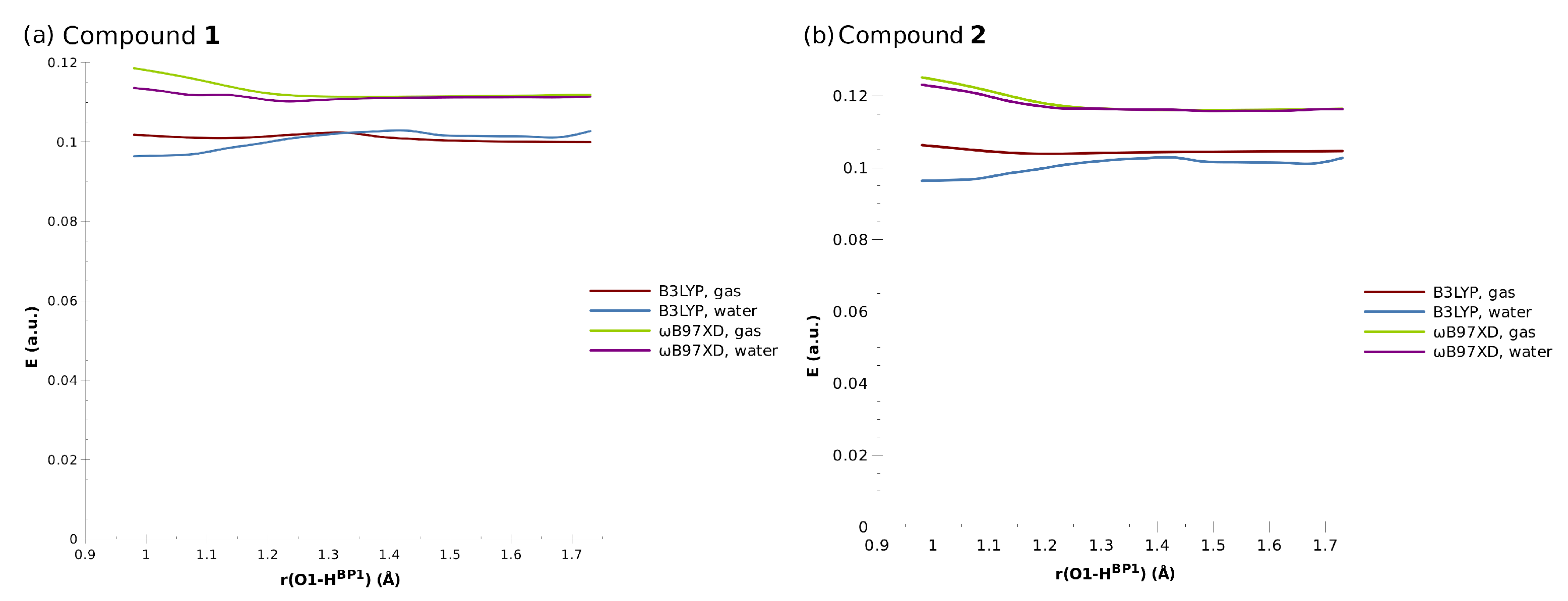
3.1.1. Geometric Parameters of the Intramolecular Hydrogen Bonding, Proton Potential Profiles, and Aromaticity of a Single Molecule

The calculated geometric parameters of intramolecular hydrogen bonds of Compounds 1 and 2 are presented in Tables S1 and S2, respectively. The molecular structures of the compounds with the atoms numbering scheme are shown in Figure 1 and Figure S1. The literature X-ray data for the intramolecular hydrogen bonds of both compounds [1,2] are presented in Figure S2. Concerning Compound 1, the comparison of experimental and computed metric parameters showed that the O1...O2 interatomic distances were reproduced correctly by the B3LYP and ω B97XD functionals, while the PBE functional shortened the distance ca. 0.06 Å in both phases (results of the gas phase simulations and with the PCM). The O 1 − H B P 1 bond length was reproduced correctly as well by the three applied functionals in both discussed phases. The computed values of intramolecular hydrogen bond differed from the experimental data. The biggest discrepancies compared to the X-ray structure were obtained for the PBE functional, as shown in Table S1. The computed values of the O 1 − H B P 1 − O 2 valence angle were larger compared to the experiment. The B3LYP and ω B97XD functionals were able to reproduce the geometric parameters of the intramolecular hydrogen bond more accurately than the PBE functional. The DFT simulations of the intramolecular hydrogen bond in Compound 2 provided us with a similar conclusion; see Table S2. The biggest discrepancies were noticed for the PBE functional compared to the X-ray data and the results obtained using the B3LYP and ω B97XD functionals. As we can see, the polar environment influence on the metric parameters is rather subtle concerning both compounds. This is valuable information while designing new naphtho- and anthra-quinone derivatives, similar to the discussed compounds, with specific molecular properties. The proton potential functions are presented in Figure 6. The proton reaction path was simulated in the gas phase and using the PCM (water as a solvent) with the assistance of the B3LYP and ω B97XD functionals. On the basis of the obtained results, we can draw the conclusion that the spontaneous proton-transfer phenomenon does not occur in Compound 1. However, the energy barriers to move the bridged proton to the proton-acceptor atom side are not extremely high. They are ca. 8.2 kcal/mol and ca. 10.5 kcal/mol according to the applied B3LYP and ω B97XD functionals and the basis set in the gas phase. The presence of the polar solvent slightly decreased the energy barriers up to 8 kcal/mol (B3LYP) and 10.2 kcal/mol ( ω B97XD). As is shown in Figure 6, the second shallow energy minimum is present. Similar results were obtained for Compound 2. The energy necessary to move the bridged proton to the proton-acceptor side is not very high, and it is ca. 8 kcal/mol and 10.1 kcal/mol depending on the functional for the gas phase simulations. The application of the continuum solvation model and water to reproduce the polar environment influence on the molecular properties provided us with slightly lower energy barriers, which were equal 7.5 kcal/mol and 9.5 kcal/mol, respectively. The second energy minimum was detected as well.
The changes of the aromaticity in both compounds were estimated based on HOMA index. The HOMA values were calculated as a function of the O 1 − H B P 1 distance changes in the gas phase and within the application of the PCM. The obtained results are summarized in Tables S3 and S4. In addition, they are presented in Figure S5 graphically to illustrate the observed dependencies. The structure in the equilibrium of Compound 1 consists of two rings, which are aromatic and anti-aromatic according to the HOMA index; see Table S3. While the bridged proton was moving to the proton-acceptor O2 atom, we noticed a consistent loss of aromaticity in the A ring; see Figures S1 and S2, respectively. Contrary results were obtained for the 1,4-benzoquinone ring (denoted as B). When the bridged proton was moving to the proton-acceptor O2 atom, the loss of anti-aromaticity was noticed. The aromaticity of the B ring increased, as shown in Figure S5. The introduction of the polar environment did not qualitatively affect the observed tendencies. This is in agreement with our geometric parameters’ analysis, which showed that the metric parameters did not change remarkably upon the polar solvent. Compound 2 consists of three fused rings: two aromatic and one anti-aromatic. The loss of aromaticity was noticed for the A ring when the bridged proton was moving to the acceptor atom side (in our case, the O2 atom) along the hydrogen bridge. In the B ring, the increased of aromaticity was observed. The aromaticity in the C ring was slightly affected due to the internal geometric and electronic structure reorganization; see Figure S5. The analysis of the HOMA index values in the polar solution provided us with the same dependencies as for the gas phase results. The aromaticity of the rings was only slightly affected quantitatively, as shown in Table S4.

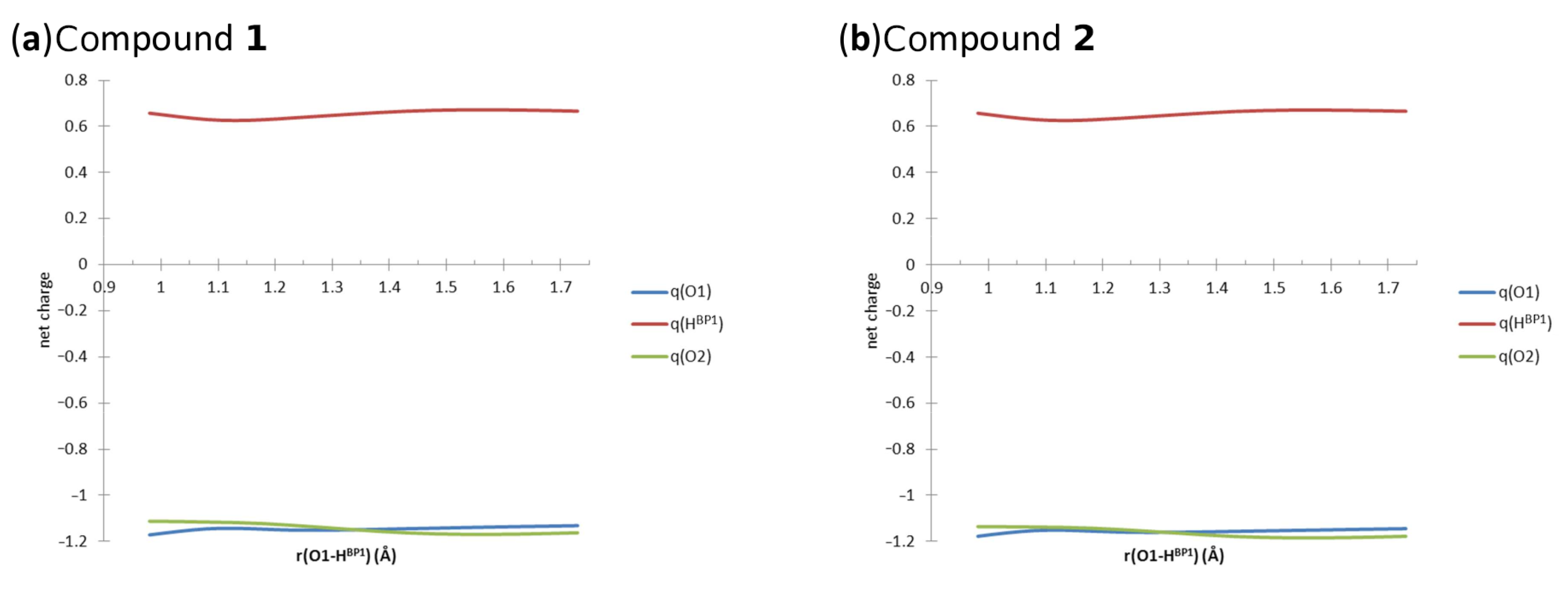
3.1.2. Electronic Structure and Topological Analysis of the Intramolecular Hydrogen Bonds Using Atoms in Molecules Theory

In Figure 7, the changes of the AIM net charges of atoms involved in the intramolecular hydrogen bond ( O 1 − H B P 1 ...O2) are presented. The values of the net atomic charges computed at the ω B97XD/6-311+G(2d,2p) level of theory are listed in Tables S5 and S6, respectively. The elongation of the O 1 − H B P 1 distance influenced the electronic structure of the studied Compounds 1 and 2, as discussed below. In Compound 1, the value of the net charge of the proton-donor O1 atom was increasing up to 1.1298 Å of the O-H distance, then the value decreased again, but at 1.3298 Å, it was constantly increasing, while the bridged proton was moving to the proton-acceptor side. The value of the net charge of H B P 1 was decreasing, while the O-H distance was elongated up to 1.1298 Å. Then, the net charge value was increasing, and finally, when the O-H distance was equal to 1.6298 Å, it was decreasing again. The value of the net charge of the proton-acceptor O2 atom was sharply decreasing, while the bridged proton was approaching the acceptor atom side. However, when the O-H distance was equal to 1.5798 Å, the increase of the net charge value was noticed. Other important AIM parameters of the covalent O 1 − H B P 1 bond, namely electron density and its Laplacian at the Bond Critical Points (BCPs), are provided in Figure S6. The electron density decreased, while the O-H distance elongated and the bridged proton was moving to the acceptor side. The electron density Laplacian values increased due to the O-H distance elongation. According to the AIM theory, the negative values of the electron density Laplacian indicate the covalent character of the interaction. The loss of the covalency was noticed while the bridged proton was moving closer to the proton-acceptor atom. In our case, the changes of the electron density Laplacian values indicate that the intramolecular hydrogen bond has a partially covalent character depending on the bridged proton position. In the case of Compound 2, the net atomic charge value changes of the atom O1 as a function of the O-H distance elongation showed similar dependencies compared to Compound 1. First, the net atomic charge value increased upon the O-H distance elongation to 1.1312 Å. The decrease of the net charge value was noticed for the O-H distance between 1.1812 Å and 1.2812 Å. When the bridged proton was moving closer to the proton-acceptor atom, the increase in the net charge value was noticed again. The changes in the net charge values of the bridged proton H B P 1 were as follows: The decrease of the values was noticed while the O-H distance was elongated up to 1.1812 Å. Then, the value increased, and when the O-H distance reached 1.5812 Å, it decreased again. Concerning the O2 proton-acceptor atom, the value of the net atomic charge decreased until the O-H distance was elongated up to 1.5812 Å. When the bridged proton was closer to the acceptor side, the value was increasing, as shown in Figure 7. The electron density and its Laplacian showed very similar dependencies compared to Compound 1; see Figure S6. The obtained results showed that for compounds with fused rings and strong, short intramolecular hydrogen bonds, we obtained very similar results. This kind of knowledge is valuable in the design of new molecules on the basis of naphtho- and anthra-quinone core parts. The substituents do not significantly affect the properties of the intramolecular hydrogen bond. Moreover, we can conclude that the influence of substituents on the AIM properties of the atoms involved in the hydrogen bridge is rather subtle. Compound 1 contains two electronegative chlorine substituents, while Compound 2 contains an additional benzene C ring extending the zone of aromaticity, but the overall picture of the changes during the proton scan is the same. The role of the C ring of Compound 2 as the aromaticity buffer was noted already in the HOMA study, where this ring kept a constant, very high HOMA value even when the A and B rings underwent significant aromaticity modifications.
An interesting point is the location of the transition point when the bridge proton is crossing from the donor to the acceptor side. The curves of the net atomic charges of the donor and acceptor oxygen atoms cross at ca. 1.35 Å for Compound 1 and 1.3 Å for Compound 2. The corresponding crossings between the electron densities at the O 1 − H B P 1 and H B P 1 − O 2 bond BCPs, as well as their Laplacians, occur however at a lower O 1 − H B P 1 distance, ca. 1.24 Å for both compounds. This inconsistency shows that there are other factors influencing the properties of the hydrogen bridge. Obviously, the hydrogen bridge is a part of a quasi-ring, and the A and B rings strongly influence the substituents. This inequality in a case that could be expected to exhibit more symmetry shows that the levels of aromaticity in the A and B rings strongly interact with the donor and acceptor atoms (resonance effect). Additionally, the second hydrogen bridge O 3 − H B P 2 − O 4 influences the studied bridge through the resonance.

3.1.3. The Intermolecular Interaction Energy Decomposition in the Dimers and Trimers on the Basis of Symmetry-Adapted Perturbation Theory Method

The dimers and trimers of Compounds 1 and 2 are presented in Figure 4 and Figure 5 and in Figures S3 and S4. The SAPT calculations were performed for the optimized gas phase structures, as well as for the dimers and trimers extracted from the crystal structure. The analysis of interactions was carried out to determine the relative importance of the factors responsible for the crystal structure integrity.
The network of intermolecular hydrogen bonds is shown in Figure S2, prepared on the basis of the source article [2]. The summary of the SAPT energy partitioning is shown in Table 1.
The comparison of the two levels of theory, the very fast SAPT0 and the more demanding SAPT2, shows a constant tendency of SAPT0 to bind the monomers stronger than SAPT2, with the only exception of the stacked dimer 5 of Compound 1, where the two SAPT levels are virtually identical. This structure is exceptional among the studied ones because of its domination by dispersion. The stacked monomers are aligned in an anti-parallel (centrosymmetric) arrangement; thus, their dipole moments are also aligned in the most advantageous manner. Indeed, among the electrostatic terms for Compound 1, the largest in magnitude is the one for the stacked dimer (−5.30 kcal/mol). The ratio of electrostatics and exchange terms is close to one in most cases, but again, in the stacked dimer, the strong dispersion contribution forces the monomers to become very close, while the Pauli exchange repulsion is exceptionally large.
The relatively low importance of the induction term indicates another feature of the studied naphtho- and anthra-quinone derivatives: They are molecules of low polarity (the symmetry of the -OH substituents’ arrangement is one of the factors responsible), and their polarizability (response to an electrostatic stimulus) cannot be used to the advantage of the dimer.
Finally, let us note that the intermolecular forces corresponding to the hydrogen bonds are rather weak, especially in comparison with the intramolecular contact. The external interactions compete rather unsuccessfully with the intramolecular resonance-assisted hydrogen bonds. Thus, the driving force for the arrangement of the molecules in the crystal is dispersion, but the electrostatics can determine the orientation of the dimer components. When the dimer is planar and cannot be stabilized by dispersion as strongly as the stacked dimer, the molecules reorient from the X-ray-determined positions to maximize the electrostatic attraction. This is true for Compound 1, but the planar dimer of Compound 2 minimizes the exchange contribution instead of maximizing the electrostatics term. All in all, the data for the dimer of Compound 2 are not very different from the dimers of Compound 1, even if the total interaction energy is lower (i.e., better) by ca. 1 kcal/mol. This lowering can be explained by stronger dispersion forces due to an additional benzene ring. Thus, the bifurcated hydrogen bond in the dimer of Compound 2, postulated on the basis of the experimental crystal structure [2] and mentioned in the Introduction, cannot be strong in its intermolecular part.
The SAPT partitioning of the interaction energy for the trimers is summarized in Table 2. Each trimer was divided into three dimers, AB, AC, and BC; these fragments were then treated separately. The trimer selected for Compound 1 was composed of three interactions of similar magnitude. Note that the optimized structures displayed an interesting relation between the interaction energy terms: electrostatics and exchange energies canceled out almost completely. This was already seen for the dimers; see above. The induction was small, and the stability of the trimers relied on dispersion. The structures taken directly from the crystal coordinates behaved in a similar way; however, the presence of an extended interaction network in the crystal forced the molecules closer, and the repulsive exchange term was not balanced by the electrostatics and induction. The triangular arrangement of the investigated trimer of Compound 1 was very different from that of Compound 2. In this case (see Figure S4), an infinite ladder of molecules was formed, and the molecules were aligned in an anti-parallel way along the ladder. The formation of such a ladder was facilitated, but not driven, by the interplay between intra- and inter-molecular hydrogen bonds, of which the intermolecular bridges were significantly weaker, as already discussed above. Please note also that the interaction of the two molecules set farthest apart (the dimers AC for Compound 2) was virtually non-existent. The molecules were too far away to interact strongly by dispersion forces, and their parallel arrangement made the electrostatics and induction terms equally negligible.

3.2. An Application of Time-Dependent Density Functional Theory

The TD-DFT results were in agreement with our intuitive expectations. The intramolecular proton transfer did not strongly influence the distribution of the electron density within the system, and as such, it did not lead to the significant differences in the excitation energies. The calculated values for the non-equilibrium geometries along the proton transfer are shown in Figure 8.
All investigated systems were characterized by the ability to absorb a photon within the UV-Vis range between 2.7 eV and 3.3 eV, which corresponds to the wavelengths of 460 nm and 375 nm, respectively. In all cases, the first excited state was determined to be the bright state, with an oscillator strength of approximately 0.2–0.4. The calculated wavelengths were blue-shifted with respect to the available experimental data on Compound 1: its UV-Vis absorption bands in chloroform solution were located at 570, 528, 496, and 468 nm [1]. A similar problem was noted for the parent compound, naphthazarin, which exhibited vibronic couplings in its first excited state (absorption maxima at 564, 547, 524, and 490 nm [54]). On the other hand, theoretical predictions placed the absorption of naphthazarin at 436 nm (CAM-B3LYP range-separated hybrid) and 490 nm (PBE0 hybrid functional). Such a discrepancy might be considered small, but it is believed that TD-DFT should be rather accurate in the case of organic dyes [55]. This issue is further discussed at the end of this section. At this point, it is important to stress that the results were similar for both Compounds 1 and 2, indicating that the substituent effects were rather limited.
Interestingly, taking into account the solvent effect did not bring significant differences in the excitation energies, and in all investigated cases, the curves for the gas phase and continuous solvent calculations overlapped for the most part. The biggest differences were observed for the optimized (equilibrium) geometries, with the presence of the water slightly decreasing the activation energies; however, the differences were still minor.
As far as the role of the functional used is concerned, the values obtained from the three-parameter B3LYP functional were smaller by approximately 0.02 a.u. (0.5 eV) compared to ω B97XD. A similar situation was found for naphthazarin, where the PBE0 hybrid gave better absolute agreement with the experiment, but the CAM-B3LYP functional was able to reproduce vibronic coupling pattern with the accuracy much improved over PBE0 [55]. In the case of Compound 1, the experimental bands were located at 570, 528, 496, and 468 nm, and the lowest energy value (570 nm) was still far away from the B3LYP estimate of ca. 460 nm. The explanation could be given in a manner similar to the case of naphthazarin: The symmetric double C=O stretching mode modulated the zwitterionic character of the enedione moiety (the quinoid ring), strongly affecting the HOMO–LUMO transition [55]. The visualization of the HOMO/LUMO orbitals (see Figure S7 in the SI) confirmed the π / π * character of these orbitals.
In general, despite the discrepancies between the exact values of the computational and experimental results, the trends still hold. There was a negligible effect of the substituent on the photoactive properties of the investigated compounds. In addition, the proton transfer did not significantly influence the electron configuration, and therefore, its role in the photoactivity was also negligible.

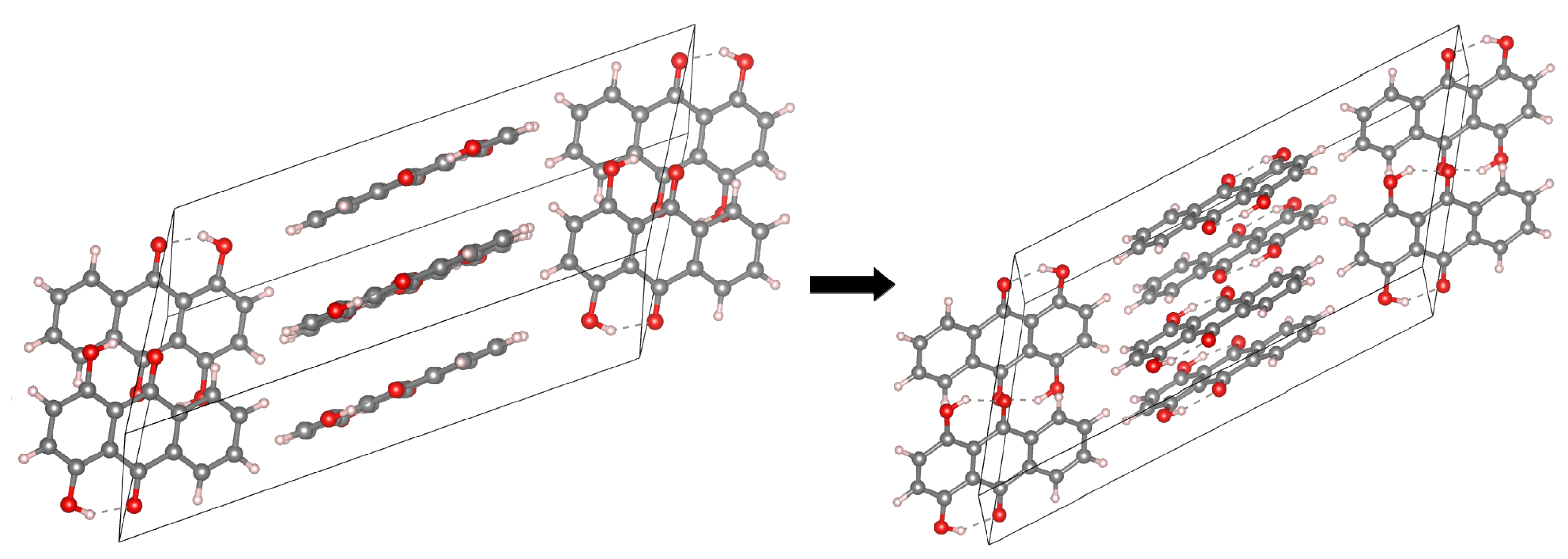
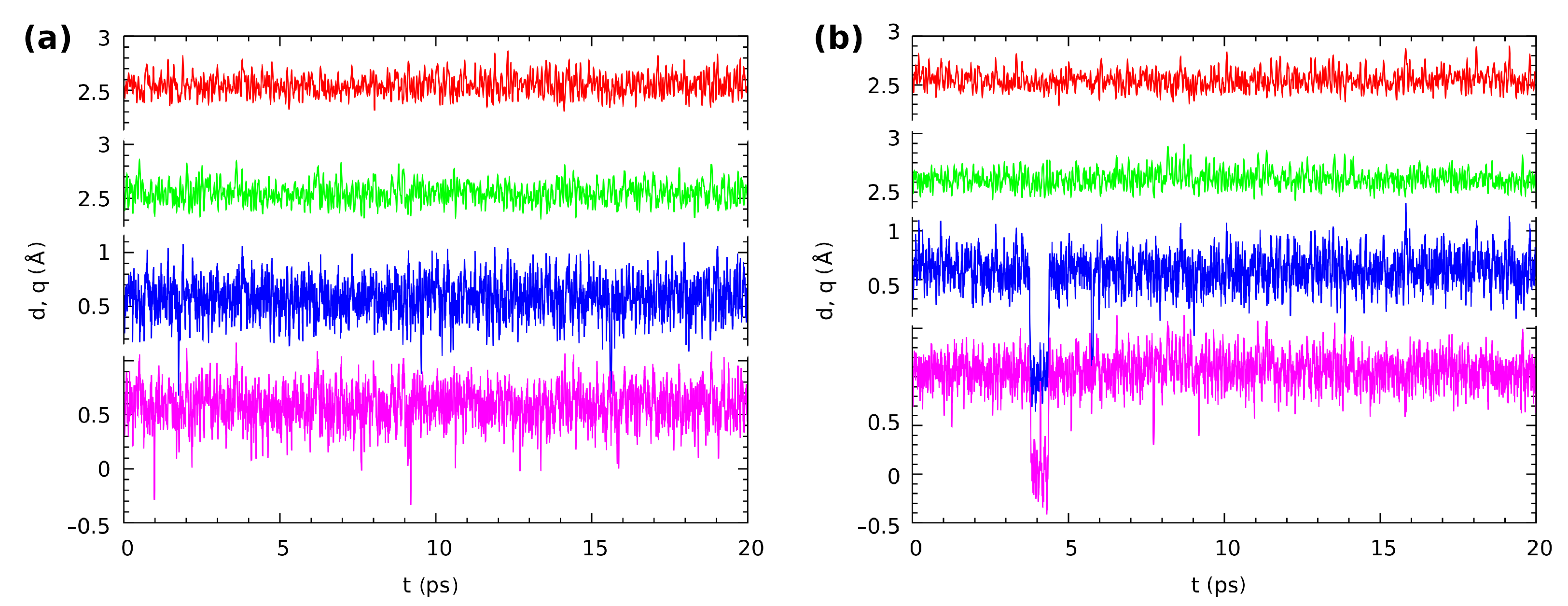
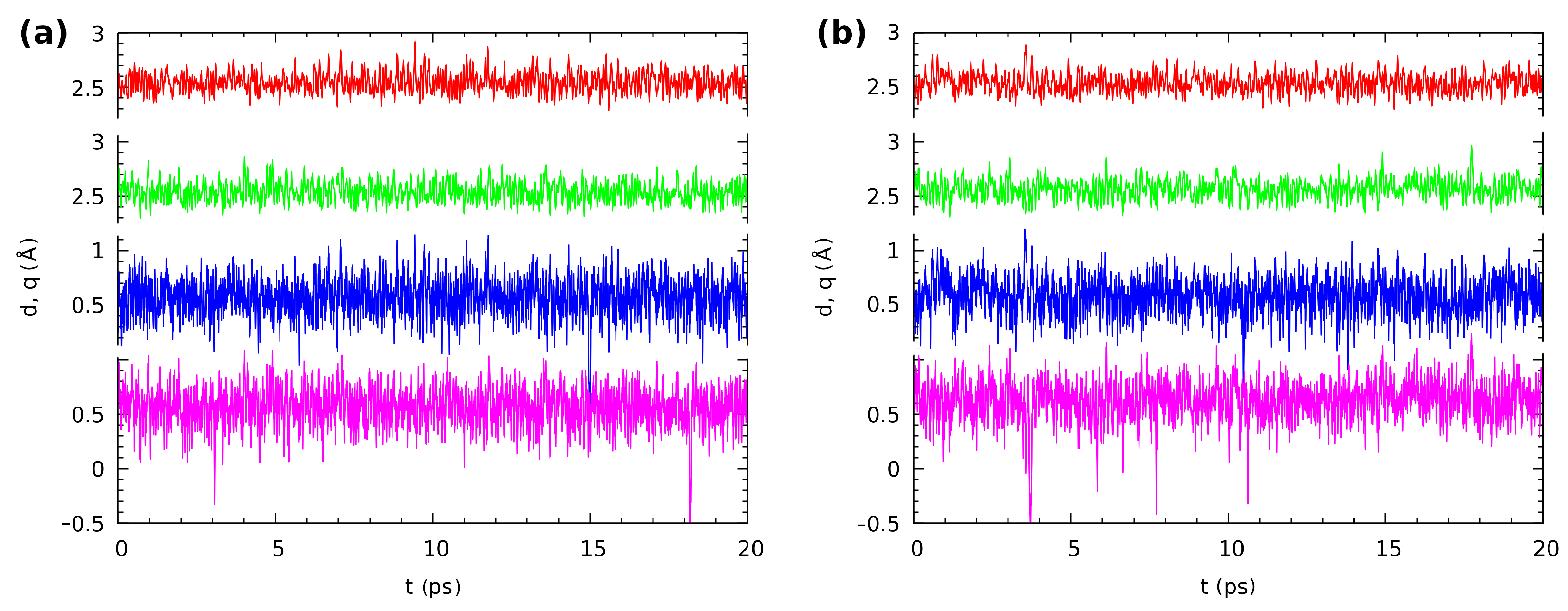
3.3. Car–Parrinello Molecular Dynamics Results in In Vacuo and in the Crystalline Phase—the Analysis of the Intra- and Intermolecular Hydrogen Bonds

Following our gas phase and solvent reaction field findings based on static DFT models, we applied Car–Parrinello molecular dynamics (CPMD) to study the proton dynamics in both intramolecular hydrogen bridges ( O 1 − H B P 1 . . . O 2 and O 3 − H B P 2 . . . O 4 ) in Compounds 1 and 2. The time-evolution of the metric parameters of atoms involved in the intramolecular hydrogen bonds in Compound 1 is presented in Figure 9. The q parameter is defined as the difference between the O-H and the hydrogen bond (H...O) distance in our case. When the q-parameter value oscillates around 0.5, the bridged proton is localized on the donor side. The q-parameter values around zero indicate that the proton is in the middle of the hydrogen bridge. Finally, the q-parameter value around −0.5 means that we observed proton transfer phenomena. The CPMD simulations of the isolated molecule showed that in both hydrogen bridges, the proton was labile, but localized on the donor side. However, as is shown in Figure 9a, there were very frequent events of the proton-sharing revealed by the CPMD simulation. The average interatomic distance of O...O in both hydrogen bridges was equal to 2.549 Å (due to the symmetry exhibited by the molecule). In the crystalline phase, the bridged proton dynamics was affected by several factors, e.g., crystal field and the presence of the neighboring molecules. The latter one provided additional intermolecular interactions, e.g., stacking type weak interactions induced by the arrangement of the aromatic rings in Compound 1. In Figure 9b, the results of bridged protons dynamics are presented. Similar to the gas phase results, the bridged protons were located on the donor side. However, the proton-sharing events and short proton transfer phenomena were noticed during the collection of the CPMD trajectory. The proton moved to the acceptor side and immediately returned to the donor side. This showed even larger proton mobility compared to the isolated molecule results. The average O...O interatomic distance was equal 2.543 Å, and it was shortened slightly by external forces associated with the crystalline phase. The hydrogen bridges’ correlation was examined as well. It was found that, similar to the gas phase, the cis arrangement of the bridged protons was preferable.
Compound 2 possessed strong, Resonance-Assisted Hydrogen Bonds (RAHBs). The CPMD results obtained for the isolated molecule indicated that the bridged proton was located mostly on the donor side. However, as is shown in Figure 10, the proton exhibited strong mobility. The proton-sharing events were noticed during the simulation time, as well as proton transfer phenomena were observed (very rare events). The bridged proton moved to the acceptor side for a very short period of time and returned again to the donor side. The average value of the O...O distance was 2.542 Å, and it was shorter compared to Compound 1. A very similar proton dynamics was obtained for the crystalline phase simulations. This could be related to the competition between the intra- and inter-molecular interactions. For the isolated molecule, only intramolecular interactions could be analyzed; therefore, it is a good reference to discuss the intermolecular interactions in the crystalline phase. Figure 10b presents results describing the intramolecular hydrogen bridges ’ dynamics. The bridged protons were located on the donor side, but they were strongly labile. The proton-sharing events were noticed, and even proton transfer phenomena occurred, but rare and very short. The bridged protons always returned to the proton-donor side. Interestingly, the average O...O interatomic distance was equal to 2.550 Å, and it was longer in the crystalline phase comparing to the gas phase results. This result could be explain by the arrangements of the molecules in the crystal unit cell. According to the experimental X-ray results [2] the 1,4-dihydroxy-anthraquinone molecules were connected by remarkably short contacts between oxygen atoms; see Figure S4. Therefore, in Compound 2, the external forces affected the intramolecular hydrogen bridge metric parameters, but did not significantly change the proton dynamics. This is in agreement with the SAPT discussion showing that the intermolecular contacts were much weaker than the intramolecular bridges.
The last, but very important point of the structural time evolution study is the question of the correlation between the motions of the protons in the twin hydrogen bridges. The investigated molecules exhibited C 2 v symmetry in their minima on the potential energy surface. The aromaticity analysis in the structural analysis section revealed that the quinoid ring did not become significantly more aromatic when a single proton transfer occurred; see Tables S3 and S4 and Figure S5 in the Supplementary Information. Even worse, when such a transfer occurred, there was also a large loss of aromaticity in the benzenoid ring. We can then expect that the proton-sharing events should be correlated between the twin bridges. This is indeed the case: most of the rare, short proton-sharing or transfer events of one proton were accompanied by a similar action of the other bridged proton. Figure 9 shows such events for Compound 1 in the gas phase at 1.7/1.9 ps (the convention we will use, t1/t2, is: t1—time for the first event at one of the protons, t2—the accompanying event for the other bridge proton), 9.1/9.6 ps, and 15.5/15.9 ps. There were however many cases where a short proton-sharing or transfer event of one proton was not accompanied by a respective motion in the other bridge, such as at 1.0 ps in the gas phase simulation of Compound 1. The solid state trajectory for this compound was more interesting, because it contained the sole observed instance of a longer sustained double-proton transfer lasting from 3.75 to 4.4 ps. Figure S8 in the Supplementary Materials shows the details of this event. The double-proton transfer was not ideally synchronous, but the response of one of the protons was delayed by just two–three periods of the bridge O-H stretching. The event happened because fortunately just before 3.75 ps of the simulation time, the respective donor-acceptor oxygen atom distances were very low, decreasing the instantaneous barrier. The protons after the transfer underwent motions of large amplitude in the potential well at the acceptor side, and one of them briefly returned to the donor side at 4.1 ps. When the amplitudes of the donor-acceptor motions rose again, the back-transfer to the donor side took place at 4.34–4.39 ps, and this was a synchronous motion in one continuous slide along the potential energy path. The remaining correlated proton-sharing events for the crystalline phase of Compound 1 (at 7.8/8.1 ps, 9.1/9.2 ps) were again of the rare and rapid type. The data for Compound 2 differed slightly from those reported above: The proton-sharing events were more frequent, but less correlated (more independent). Indeed, only the events at 18.1/18.7 ps in the gas phase and at 10.4/10.6 ps in the crystal can be considered as correlated. No sustained periods of proton transfer events were recorded for this compound.

4. Conclusions

The current study was designed to characterize the intra- and inter-molecular interactions in two selected derivatives of naphtho- and anthra-quinone. The theoretical investigations were performed in three phases: in vacuo, in polar solvent reproduced by the application of the PCM, and in the crystalline phase. The molecular properties of the two compounds were studied in the electronic ground and excited states. Concerning the intramolecular interactions, a detailed description of the hydrogen bond dynamics was provided on the basis of static DFT and CPMD models. The intermolecular forces were explored in dimers and trimers formed by the discussed compounds. Our theoretical findings were compared with experimental structural data [1,2]. Summarizing, the static DFT models provided us with a detailed description of the bridged proton reaction path. The second energy minimum was detected in both compounds; moreover, the energy barriers for the proton transfer to the acceptor side were found not to be very high. The introduction of the polar solvent did not significantly change the metric and electronic structure parameters. We observed that the polar solvent moderately decreased the energy barrier for the proton movement. The application of the HOMA index showed that the bridged proton position had an impact on the aromaticity changes in the rings. The decrease of aromaticity was noticed for the hydroxyquinone moiety ring, while its increase was observed in the 1,4-benzoquinone ring. The electronic structure and topological analysis indicated a partially covalent character of the intramolecular hydrogen bond showing a strong property dependence on the bridged proton position. The SAPT energy partitioning showed the decisive role of dispersion for the intermolecular attraction. The bifurcated hydrogen bonds in the dimers of Compound 2, postulated experimentally [2], were much weaker than the intramolecular contact.
TD-DFT calculations confirmed the assumption of a negligible effect of the proton transfer on the electronic excitation energies in the investigated compounds. As the proton transfer did not involve the change in the electron density and the distance covered during the transfer was too small to induce a change in the dipole moment of the molecule, it cannot lead to a significant change in the electron configuration of the systems. This was observed as flat excitation energy curves. The experimental excitation energies did not agree well with the calculated ones; however, this was most likely related to the incorrect description of the electron configuration of the parent compound, naphthazarin. However, the qualitative description of small influence of the substituents on the excitation energies was in good agreement with the experimental results.
The CPMD simulations revealed that in both compounds, the bridged protons were very labile, but localized on the donor side. However, proton-sharing events and rare, short proton transfer phenomena were noticed. Many of them were correlated between the bridges of Compound 1, much less so in the case of Compound 2. The only longer proton transfer period for both bridges in Compound 1 began with an almost synchronous movement of the two bridge protons: The delay of the response of the second proton was only a few O-H oscillations. The photochemical structure-property relationship makes the transmission of the input “signal” (a photonic-driven proton transfer at one of the bridges) to the output “gate” (the proton transfer in the other bridge will shortly follow) possible. This interesting feature along with the excited state properties of the studied compounds make Compound 1 a good candidate for further studies on molecular electronics building blocks.

Supplementary Materials

The following are available online at https://www.mdpi.com/article/10.3390/sym13040564/s1: Figure S1: Molecular structures of 2,3-dichloro-5,8-dihydroxy-1,4-naphthoquinone and 1,4-dihydroxy-anthraquinone with the atom numbering scheme, Figure S2: Experimental values (X-ray) of intramolecular hydrogen bonds present in 2,3-dichloro-5,8-dihydroxy-1,4-naphthoquinone and 1,4-dihydroxy-anthraquinone, Table S1: The intramolecular hydrogen bond metric parameters of 2,3-dichloro-5,8-dihydroxy-1,4-naphthoquinone, Table S4: The intramolecular hydrogen bond metric parameters of 1,4-dihydroxy-anthraquinone, Figure S3: The comparison of calculated at the B3LYP/6-311+G(2d,2p) level of theory and experimental X-ray data structures of the trimers of the 2,3-dichloro-5,8-dihydroxy-1,4-naphthoquinone, Figure S4: The comparison calculated at the B3LYP/6-311+G(2d,2p) level of theory and experimental X-ray data structures of the trimers of 1,4-dihydroxy-anthraquinone, Table S3: Computed values of the HOMA index for 2,3-dichloro-5,8-dihydroxy-1,4-naphthoquinone, Table S4: Computed values of the HOMA index for 1,4-dihydroxy-anthraquinone, Figure S5: The evolution of the HOMA index for the A, B, and C rings as a function of the O 1 − H B P 1 elongation, Table S5: The values of net atomic charges computed according to AIM at the ω B97XD/6-311+G(2d,2p) level of theory for 2,3-dichloro-5,8-dihydroxy-1,4-naphthoquinone, Table S6: The values of the net atomic charges computed according to AIM at the ω B97XD/6-311+G(2d,2p) level of theory for 1,4-dihydroxyanthraquinone, Figure S6: Dependence of the electron density and its Laplacian at selected BCPs on the donor O1—proton H B P 1 distance for the studied Compounds 1 and 2, Figure S7: The isosurfaces of the HOMO and LUMO orbitals of Compounds 1 and 2, Figure S8: A detailed view of the proton transfer event as shown by the time evolution of the distance parameters in the hydrogen bridges of Compound 1 in the crystal.

Author Contributions

Conceptualization, A.J., B.M.S., and J.J.P.; methodology, A.J., B.M.S., and J.J.P.; computations, B.K., A.J., B.M.S., and J.J.P.; data analysis, A.J., B.M.S., and J.J.P.; writing—original draft preparation, B.K., A.J., B.M.S., and J.J.P.; writing—review and editing, B.K., A.J., B.M.S., and J.J.P.; supervision, A.J.; funding acquisition, A.J. All authors read and agreed to the published version of the manuscript.

Funding

This research was funded by National Science Centre Grant Number UMO-2015/17/B/ ST4/03568.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available in the article and in the associated Supplementary Materials.

Acknowledgments

The authors thank the Wrocław Center for Networking and Supercomputing (WCSS) and the Academic Computer Centre Cyfronet AGH (PL-Grid infrastructure Prometheus) for CPU time and technical support. In addition, A.J. and J.J.P. thank the National Science Centre (Poland) for supporting this work under Grant No. UMO-2015/17/B/ST4/03568.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
AIMAtoms In Molecules theory of molecular structure
CPMDCar–Parrinello Molecular Dynamics
DFTDensity Functional Theory
HOMAHarmonic Oscillator Model of Aromaticity
PCMPolarizable Continuum Model—an implicit model of solvation
SAPTSymmetry-Adapted Perturbation Theory
TD-DFTTime-Dependent Density Functional Theory

References

  1. Rubio, P.; Florencio, F.; García-Blanco, S.; Rodriguez, J.G. Structure of 2, 3-dichloronaphthazarin. Acta Crystallogr. Sect. C Cryst. Struct. Commun. 1985, 41, 1797–1799. [Google Scholar] [CrossRef]
  2. Nigam, G.; Deppisch, B. Redetermination of the structure of 1, 4-dihydroxyanthraquinone (C14H8O4). Z. Kristallogr. Cryst. Mater. 1980, 151, 185–191. [Google Scholar] [CrossRef]
  3. Widhalm, J.R.; Rhodes, D. Biosynthesis and molecular actions of specialized 1, 4-naphthoquinone natural products produced by horticultural plants. Hortic. Res. 2016, 3. [Google Scholar] [CrossRef] [PubMed]
  4. Nematollahi, A.; Aminimoghadamfarouj, N.; Wiart, C. Reviews on 1, 4-naphthoquinones from Diospyros L. J. Asian Nat. Prod. Res. 2012, 14, 80–88. [Google Scholar] [CrossRef] [PubMed]
  5. Salas, C.O.; Faundez, M.; Morello, A.; Maya, J.D.; Tapia, R.A. Natural and Synthetic Naphthoquinones Active Against Trypanosoma Cruzi: An Initial Step Towards New Drugs for Chagas Disease. Curr. Med. Chem. 2011, 18, 144–161. [Google Scholar] [CrossRef]
  6. de Carvalho da Silva, F.; Ferreira, V.F. Natural Naphthoquinones with Great Importance in Medicinal Chemistry. Curr. Org. Synth. 2016, 13, 334–371. [Google Scholar] [CrossRef]
  7. Qiu, H.Y.; Wang, P.F.; Lin, H.Y.; Tang, C.Y.; Zhu, H.L.; Yang, Y.H. Naphthoquinones: A continuing source for discovery of therapeutic antineoplastic agents. Chem. Biol. Drug Des. 2017, 91, 681–690. [Google Scholar] [CrossRef]
  8. Pereyra, C.E.; Dantas, R.F.; Ferreira, S.B.; Gomes, L.P.; Silva, F.P., Jr. The diverse mechanisms and anticancer potential of naphthoquinones. Cancer Cell Int. 2019, 19. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  9. Yusuf, M.A.; Singh, B.N.; Sudheer, S.; Kharwar, R.N.; Siddiqui, S.; Abdel-Azeem, A.M.; Fraceto, L.F.; Dashora, K.; Gupta, V.K. Chrysophanol: A Natural Anthraquinone with Multifaceted Biotherapeutic Potential. Biomolecules 2019, 9, 68. [Google Scholar] [CrossRef] [Green Version]
  10. Zhuo, J.; Sun, G. Antimicrobial Functions on Cellulose Materials Introduced by Anthraquinone Vat Dyes. Appl. Mater. Interfaces 2013, 5, 10830–10835. [Google Scholar] [CrossRef]
  11. Iriarte-Velasco, U.; Chimeno-Alanís, N.; González-Marcos, M.; Álvarez Uriarte, J. Relationship between Thermodynamic Data and Adsorption/Desorption Performance of Acid and Basic Dyes onto Activated Carbons. J. Chem. Eng. Data 2011, 56, 2100–2109. [Google Scholar] [CrossRef]
  12. Campora, M.; Canale, C.; Gatta, E.; Tasso, B.; Laurini, E.; Relini, A.; Pricl, S.; Catto, M.; Tonelli, M. Multitarget Biological Profiling of New Naphthoquinone and Anthraquinone-Based Derivatives for the Treatment of Alzheimer’s Disease. Chem. Neurosci. 2021. [Google Scholar] [CrossRef]
  13. Fabian, J.; Nakazumi, H.; Matsuoka, M. Near-Infrared Absorbing Dyes. Chem. Rev. 1992, 92, 1197–1226. [Google Scholar] [CrossRef]
  14. Oka, K.; Murao, S.; Kobayashi, K.; Nishide, H.; Oyaizu, K. Charge- and Proton-Storage Capability of Naphthoquinone-Substituted Poly(allylamine) as Electrode-Active Material for Polymer–Air Secondary Batteries. Appl. Energy Mater. 2020, 3, 12019–12024. [Google Scholar] [CrossRef]
  15. Tong, L.; Goulet, M.A.; Tabor, D.P.; Kerr, E.F.; Porcellinis, D.D.; Fell, E.M.; Aspuru-Guzik, A.; Gordon, R.G.; Aziz, M.J. Molecular Engineering of an Alkaline Naphthoquinone Flow Battery. Energy Lett. 2019, 4, 1880–1887. [Google Scholar] [CrossRef]
  16. Joungphil, L.; Hoon, K.; Moon, J. Long-Life, High-Rate Lithium-Organic Batteries Based on Naphthoquinone Derivatives. Chem. Mater. 2016, 28, 2408–2416. [Google Scholar] [CrossRef]
  17. Clausen, C.; Dražević, E.; Andersen, A.; Henriksen, M.; Hinge, M.; Bentien, A. Anthraquinone Oligomers as Anode-Active Material in Rechargeable Nickel/Oligomer Batteries with Aqueous Electrolyte. Appl. Energy Mater. 2018, 1, 243–248. [Google Scholar] [CrossRef]
  18. Ravichandiran, P.; Prabakaran, D.S.; Bella, A.P.; Boguszewska-Czubara, A.; Masłyk, M.; Dineshkumar, K.; Johnson, P.M.; Park, B.H.; Han, M.K.; Kim, H.G.; et al. Naphthoquinone-Dopamine Linked Colorimetric and Fluorescence Chemosensor for Selective Detection of Sn2+ Ion in Aqueous Medium and Its Bio-Imaging Applications. Sustain. Chem. Eng. 2020. [Google Scholar] [CrossRef]
  19. Gilli, G.; Bellucci, F.; Ferretti, V.; Bertolasi, V. Evidence for resonance-assisted hydrogen bonding from crystal-structure correlations on the enol form of the .beta.-diketone fragment. J. Am. Chem. Soc. 1989, 111, 1023–1028. [Google Scholar] [CrossRef]
  20. Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef] [Green Version]
  21. Kohn, W.; Sham, L. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef] [Green Version]
  22. Runge, E.; Gross, E.K.U. Density-Functional Theory for Time-Dependent Systems. Phys. Rev. Lett. 1984, 52, 997–1000. [Google Scholar] [CrossRef]
  23. Barone, V.; Cossi, M. Quantum Calculation of Molecular Energies and Energy Gradients in Solution by a Conductor Solvent Model. J. Phys. Chem. A 1998, 102, 1995–2001. [Google Scholar] [CrossRef]
  24. Kruszewski, J.; Krygowski, T. Definition of aromaticity basing on the harmonic oscillator model. Tetrahedron Lett. 1972, 13, 3839–3842. [Google Scholar] [CrossRef]
  25. Bader, R. Atoms in Molecules: A Quantum Theory; International Series of Monographs on Chemistry; Clarendon Press: Oxford, UK, 1994. [Google Scholar]
  26. Jeziorski, B.; Moszynski, R.; Szalewicz, K. Perturbation Theory Approach to Intermolecular Potential Energy Surfaces of van der Waals Complexes. Chem. Rev. 1994, 94, 1887–1930. [Google Scholar] [CrossRef]
  27. Car, R.; Parrinello, M. Unified Approach for Molecular Dynamics and Density-Functional Theory. Phys. Rev. Lett. 1985, 55, 2471–2474. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  28. Becke, A. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef] [Green Version]
  29. Perdew, J.; Ernzerhof, M.; Burke, K. Rationale for mixing exact exchange with density functional approximations. J. Chem. Phys. 1996, 105, 9982–9985. [Google Scholar] [CrossRef]
  30. Perdew, J.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
  31. Chai, J.-D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  32. McLean, A.; Chandler, G. Contracted Gaussian basis sets for molecular calculations. I. Second row atoms, Z =11–18. J. Chem. Phys. 1980, 72, 5639–5648. [Google Scholar] [CrossRef]
  33. Clark, T.; Chandrasekhar, J.; Spitznagel, G.; Schleyer, P. Efficient diffuse function-augmented basis sets for anion calculations. III. The 3-21+G basis set for first-row elements, Li-F. J. Comput. Chem. 1983, 4, 294–301. [Google Scholar] [CrossRef]
  34. Frisch, M.; Pople, J.; Binkley, J. Self-consistent molecular orbital methods 25. Supplementary functions for Gaussian basis sets. J. Chem. Phys. 1984, 80, 3265–3269. [Google Scholar] [CrossRef]
  35. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Fox, D.J.; et al. Gaussian~16 Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
  36. Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
  37. Keith, T.A. AIMAll (Version 19.10.12), Software; AIMAll: Overland Park, KS, USA, 2019. [Google Scholar]
  38. Gálvez, O.; Gómez, P.; Pacios, L.F. Variation with the intermolecular distance of properties dependent on the electron density in hydrogen bond dimers. J. Chem. Phys. 2001, 115, 11166–11184. [Google Scholar] [CrossRef]
  39. Pacios, L. Change with the Intermolecular Distance of Electron Properties of Hydrogen Bond Dimers at Equilibrium and Non-equilibrium Geometries. Struct. Chem. 2005, 16, 223–241. [Google Scholar] [CrossRef]
  40. Hohenstein, E.; Sherrill, C. Density fitting of intramonomer correlation effects in symmetry-adapted perturbation theory. J. Chem. Phys. 2010, 133, 014101. [Google Scholar] [CrossRef] [Green Version]
  41. Kendall, R.; Dunning, T.; Harrison, R. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar] [CrossRef] [Green Version]
  42. Boys, S.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
  43. Parrish, R.M.; Burns, L.A.; Smith, D.G.A.; Simmonett, A.C.; DePrince, A.E.; Hohenstein, E.G.; Bozkaya, U.; Sokolov, A.Y.; Remigio, R.D.; Richard, R.M.; et al. Psi4 1.1: An Open-Source Electronic Structure Program Emphasizing Automation, Advanced Libraries, and Interoperability. J. Chem. Theory Comput. 2017, 13, 3185–3197. [Google Scholar] [CrossRef]
  44. Neese, F. Software update: The ORCA program system, version 4.0. Comput. Mol. Sci. 2017, 8. [Google Scholar] [CrossRef]
  45. Neese, F.; Wennmohs, F.; Becker, U.; Riplinger, C. The ORCA quantum chemistry program package. J. Chem. Phys. 2020, 152, 224108. [Google Scholar] [CrossRef] [PubMed]
  46. Troullier, N.; Martins, J.L. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B 1991, 43, 1993–2006. [Google Scholar] [CrossRef] [PubMed]
  47. Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef] [Green Version]
  48. Hoover, W. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef] [Green Version]
  49. Hockney, R. Potential Calculation and some applications. Methods Comput. Phys. 1970, 9, 135–211. [Google Scholar]
  50. Kittel, C. Introduction To Solid State Physics, 8th ed.; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
  51. CPMD 3.17.1. Copyright IBM Corp. (1990–2004) Copyright MPI für Festkoerperforschung Stuttgart (1997–2001). Available online: http://www.cpmd.org (accessed on 16 July 2014).
  52. Humphrey, W.; Dalke, A.; Schulten, K. VMD–Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
  53. Momma, K.; Izumi, F. VESTA 3for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
  54. Singh, I.; Ogata, R.; Moore, R.; Chang, C.; Scheuer, P. Electronic spectra of substituted naphthoquinones. Tetrahedron 1968, 24, 6053–6073. [Google Scholar] [CrossRef]
  55. Jacquemin, D.; Peltier, C.; Ciofini, I. Visible spectrum of naphthazarin investigated through Time-Dependent Density Functional Theory. Chem. Phys. Lett. 2010, 493, 67–71. [Google Scholar] [CrossRef]
Symmetry 13 00564 g001 550
Figure 1. Molecular structures of 2,3-dichloro-5,8-dihydroxy-1,4-naphthoquinone (1) and 1,4-dihydroxyanthraquinone (2) with the atoms of interest numbering scheme prepared especially for the study. Atoms’ coloring scheme: red—oxygen atom, grey—carbon atoms, green—chlorine atom, white—hydrogen atom. The dotted line indicates the presence of intramolecular hydrogen bonds.
Figure 1. Molecular structures of 2,3-dichloro-5,8-dihydroxy-1,4-naphthoquinone (1) and 1,4-dihydroxyanthraquinone (2) with the atoms of interest numbering scheme prepared especially for the study. Atoms’ coloring scheme: red—oxygen atom, grey—carbon atoms, green—chlorine atom, white—hydrogen atom. The dotted line indicates the presence of intramolecular hydrogen bonds.
Symmetry 13 00564 g001
Symmetry 13 00564 g002 550
Figure 2. The crystallographic unit cell for Compound 1. The molecules’ arrangement in the unit cell is shown at the left side, while the intramolecular hydrogen bonds at the right side. The dotted lines indicate the presence of intramolecular hydrogen bonds. The data were used to construct models for CPMD simulations in the crystalline phase [1].
Figure 2. The crystallographic unit cell for Compound 1. The molecules’ arrangement in the unit cell is shown at the left side, while the intramolecular hydrogen bonds at the right side. The dotted lines indicate the presence of intramolecular hydrogen bonds. The data were used to construct models for CPMD simulations in the crystalline phase [1].
Symmetry 13 00564 g002
Symmetry 13 00564 g003 550
Figure 3. The crystallographic unit cell for Compound 2. The molecules’ arrangement in the unit cell is shown at the left side, while the intramolecular hydrogen bonds at the right side. The dotted lines indicate the presence of intramolecular hydrogen bonds. The data were used to construct models for CPMD simulations in the crystalline phase [2].
Figure 3. The crystallographic unit cell for Compound 2. The molecules’ arrangement in the unit cell is shown at the left side, while the intramolecular hydrogen bonds at the right side. The dotted lines indicate the presence of intramolecular hydrogen bonds. The data were used to construct models for CPMD simulations in the crystalline phase [2].
Symmetry 13 00564 g003
Symmetry 13 00564 g004 550
Figure 4. Dimers of Compound 1. The comparison calculated at the B3LYP/6-311+G(2d,2p) level of theory (1,3) and experimental X-ray data (2,4,5) [1] of the dimers taken into account.
Figure 4. Dimers of Compound 1. The comparison calculated at the B3LYP/6-311+G(2d,2p) level of theory (1,3) and experimental X-ray data (2,4,5) [1] of the dimers taken into account.
Symmetry 13 00564 g004
Symmetry 13 00564 g005 550
Figure 5. Dimer of Compound 2. The comparison calculated at the B3LYP/6-311+G(2d,2p) level of theory (1) and experimental X-ray data (2) [2] of the dimers taken into account. The dotted lines indicate the presence of the shortest intermolecular contact distances between heavy atoms.
Figure 5. Dimer of Compound 2. The comparison calculated at the B3LYP/6-311+G(2d,2p) level of theory (1) and experimental X-ray data (2) [2] of the dimers taken into account. The dotted lines indicate the presence of the shortest intermolecular contact distances between heavy atoms.
Symmetry 13 00564 g005
Symmetry 13 00564 g006 550
Figure 6. The potential energy scans for the proton motion in the hydrogen bridges of Compounds 1 and 2. X axis: donor-proton ( O 1 − H B P 1 ) distance.
Figure 6. The potential energy scans for the proton motion in the hydrogen bridges of Compounds 1 and 2. X axis: donor-proton ( O 1 − H B P 1 ) distance.
Symmetry 13 00564 g006
Symmetry 13 00564 g007 550
Figure 7. The net atomic charges on the atoms of one of the hydrogen bridges; results of the AIM analysis for Compounds 1 and 2 in the gas phase.
Figure 7. The net atomic charges on the atoms of one of the hydrogen bridges; results of the AIM analysis for Compounds 1 and 2 in the gas phase.
Symmetry 13 00564 g007
Symmetry 13 00564 g008 550
Figure 8. The energies of the first electronic excited states for the investigated compounds.
Figure 8. The energies of the first electronic excited states for the investigated compounds.
Symmetry 13 00564 g008
Symmetry 13 00564 g009 550
Figure 9. The time evolution of the distance parameters in the hydrogen bridges of Compound 1, (a) in vacuo and (b) in the crystal. Two upper lines: donor-acceptor distances r; two lower lines: The corresponding proton position parameters q (defined as rH B P ...O – rO-H B P ). Color coding is as follows: red—r(O1...O2), green—r(O3...O4), blue—q(O1-H B P 1 -O2), violet—q(O3-H B P 2 -O4).
Figure 9. The time evolution of the distance parameters in the hydrogen bridges of Compound 1, (a) in vacuo and (b) in the crystal. Two upper lines: donor-acceptor distances r; two lower lines: The corresponding proton position parameters q (defined as rH B P ...O – rO-H B P ). Color coding is as follows: red—r(O1...O2), green—r(O3...O4), blue—q(O1-H B P 1 -O2), violet—q(O3-H B P 2 -O4).
Symmetry 13 00564 g009
Symmetry 13 00564 g010 550
Figure 10. The time evolution of the distance parameters in the hydrogen bridges of Compound 2, (a) in vacuo and (b) in the crystal. Two upper lines: donor-acceptor distances r; two lower lines: The corresponding proton position parameters q (defined as r H B P . . . O − r O H B P ). Color coding is as follows: red—r(O1...O2), green—r(O3...O4), blue—q(O1- H B P 1 -O2), violet—q(O3- H B P 2 -O4).
Figure 10. The time evolution of the distance parameters in the hydrogen bridges of Compound 2, (a) in vacuo and (b) in the crystal. Two upper lines: donor-acceptor distances r; two lower lines: The corresponding proton position parameters q (defined as r H B P . . . O − r O H B P ). Color coding is as follows: red—r(O1...O2), green—r(O3...O4), blue—q(O1- H B P 1 -O2), violet—q(O3- H B P 2 -O4).
Symmetry 13 00564 g010
Table
Table 1. The SAPT energy partitioning for the indicated dimers, with the structures either taken from the X-ray experiments (X-ray) or optimized at the B3LYP/6-311+G(2d,2p) level of theory (opt). Dimers are labeled according to Figure 4 and Figure 5. All energies in kcal/mol.
Table 1. The SAPT energy partitioning for the indicated dimers, with the structures either taken from the X-ray experiments (X-ray) or optimized at the B3LYP/6-311+G(2d,2p) level of theory (opt). Dimers are labeled according to Figure 4 and Figure 5. All energies in kcal/mol.
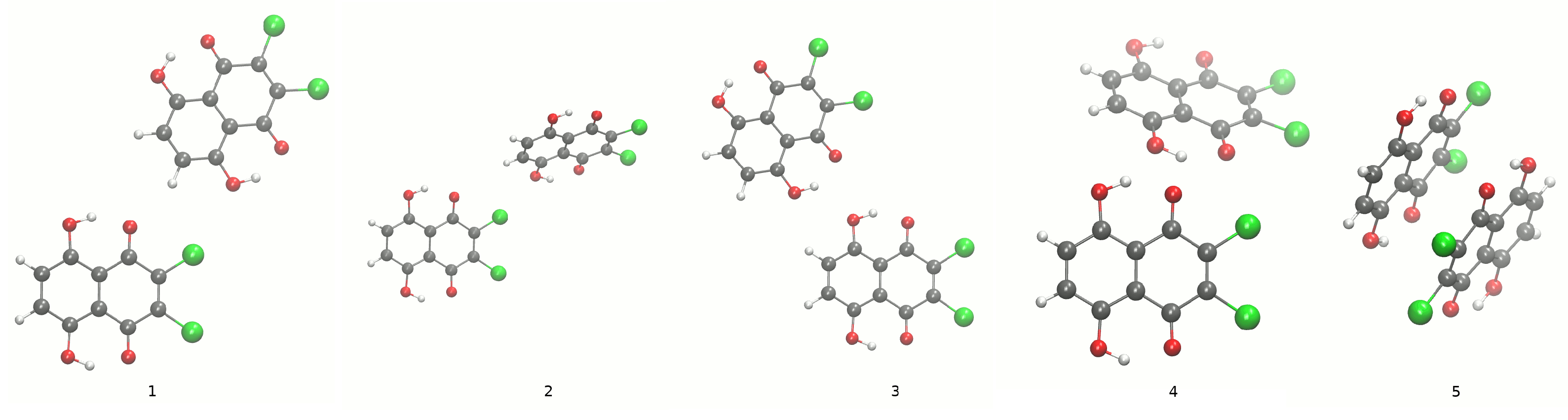
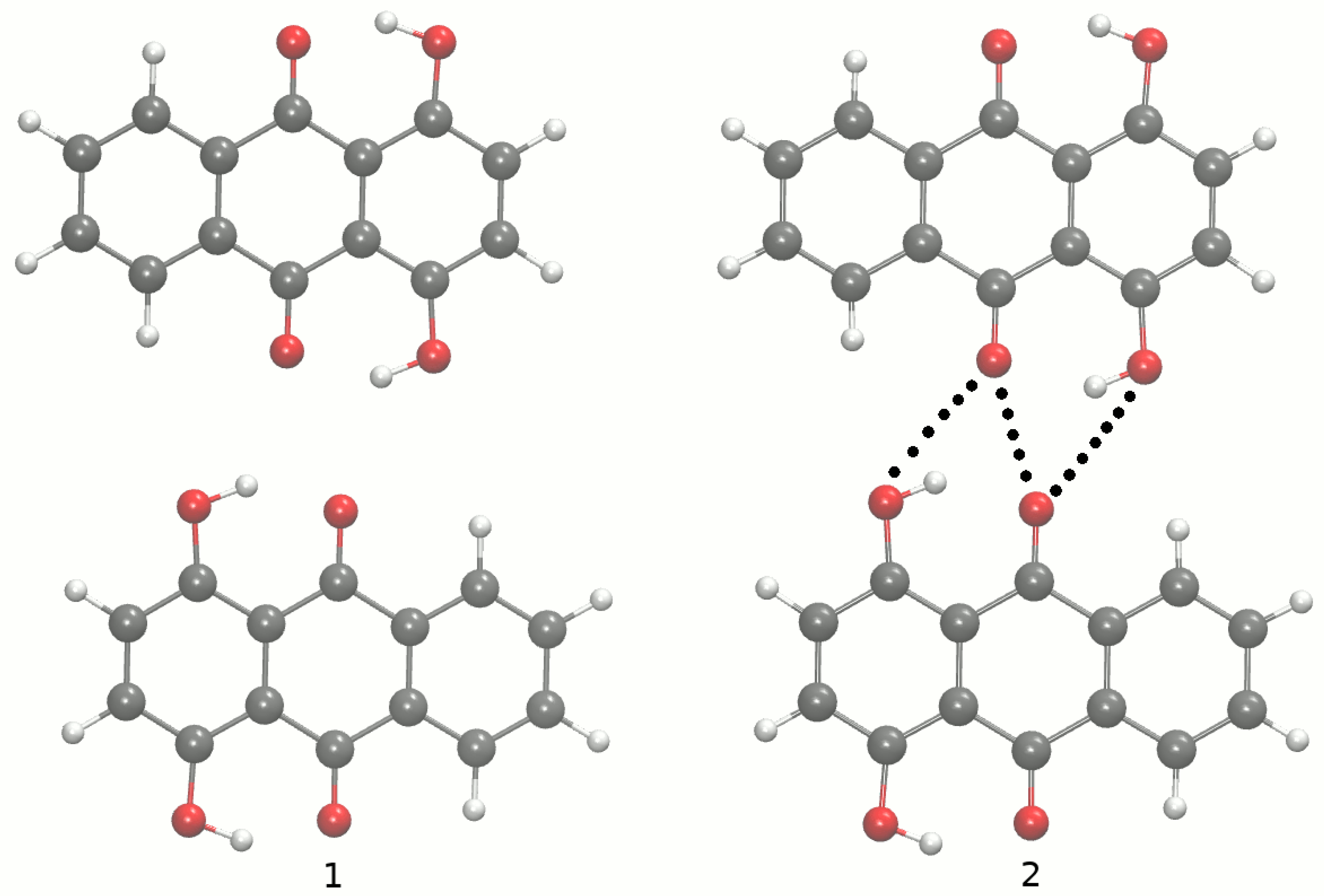
Compound, StructureElstExchIndDispSAPT0SAPT2
Comp. 1, dimer 1, opt−2.682.81−0.71−3.27−4.56−3.84
Comp. 1, dimer 2, X-ray−2.022.57−0.44−2.88−3.21−2.78
Comp. 1, dimer 3, opt−3.213.34−0.54−3.30−4.18−3.71
Comp. 1, dimer 4, X-ray−2.724.09−0.48−4.33−3.89−3.44
Comp. 1, dimer 5, X-ray−5.3014.24−1.82−22.79−15.69−15.67
Comp. 2, dimer 1, opt−3.663.92−0.61−4.55−5.54−4.90
Comp. 2, dimer 2, X-ray−5.848.71−1.14−6.19−5.41−4.46
Table
Table 2. The SAPT energy partitioning for the indicated trimers (decomposed into dimers AB, BC, and AC), with the structures either taken from the X-ray experiments (X-ray) or optimized at the B3LYP/6-311+G(2d,2p) level of theory (opt). Trimers are labeled according to Figures S3 and S4. All energies in kcal/mol.
Table 2. The SAPT energy partitioning for the indicated trimers (decomposed into dimers AB, BC, and AC), with the structures either taken from the X-ray experiments (X-ray) or optimized at the B3LYP/6-311+G(2d,2p) level of theory (opt). Trimers are labeled according to Figures S3 and S4. All energies in kcal/mol.
Compound, StructureElstExchIndDispSAPT0SAPT2
Comp. 1, fragment AB, opt−3.063.17−0.52−3.20−4.06−3.62
Comp. 1, fragment AC, opt−2.692.95−0.75−3.31−3.31−3.80
Comp. 1, fragment BC, opt−1.871.84−0.38−2.33−3.18−2.74
Comp. 1, fragment AB, X-ray−2.724.09−0.48−4.33−3.89−3.44
Comp. 1, fragment AC, X-ray−2.022.57−0.44−2.88−3.21−2.78
Comp. 1, fragment BC, X-ray−0.892.04−0.38−2.92−2.23−2.15
Comp. 2, fragment AB, opt−5.863.95−0.61−4.56−5.55−4.90
Comp. 2, fragment AC, opt0.060.00−0.00−0.020.050.02
Comp. 2, fragment BC, opt−5.873.96−0.62−4.57−5.56−4.91
Comp. 2, fragment AB, X-ray−3.685.73−0.78−5.22−5.10−4.47
Comp. 2, fragment AC, X-ray0.050.00−0.00−0.010.060.03
Comp. 2, fragment BC, X-ray−3.698.71−1.14−6.19−5.41−4.46
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Kizior, B.; Panek, J.J.; Szyja, B.M.; Jezierska, A. Structure-Property Relationship in Selected Naphtho- and Anthra-Quinone Derivatives on the Basis of Density Functional Theory and Car–Parrinello Molecular Dynamics. Symmetry 2021, 13, 564. https://doi.org/10.3390/sym13040564

AMA Style

Kizior B, Panek JJ, Szyja BM, Jezierska A. Structure-Property Relationship in Selected Naphtho- and Anthra-Quinone Derivatives on the Basis of Density Functional Theory and Car–Parrinello Molecular Dynamics. Symmetry. 2021; 13(4):564. https://doi.org/10.3390/sym13040564

Chicago/Turabian Style

Kizior, Beata, Jarosław J. Panek, Bartłomiej M. Szyja, and Aneta Jezierska. 2021. "Structure-Property Relationship in Selected Naphtho- and Anthra-Quinone Derivatives on the Basis of Density Functional Theory and Car–Parrinello Molecular Dynamics" Symmetry 13, no. 4: 564. https://doi.org/10.3390/sym13040564

APA Style

Kizior, B., Panek, J. J., Szyja, B. M., & Jezierska, A. (2021). Structure-Property Relationship in Selected Naphtho- and Anthra-Quinone Derivatives on the Basis of Density Functional Theory and Car–Parrinello Molecular Dynamics. Symmetry, 13(4), 564. https://doi.org/10.3390/sym13040564

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop