Novel Approach for EKG Signals Analysis Based on Markovian and Non-Markovian Fractalization Type in Scale Relativity Theory
Abstract
1. Introduction
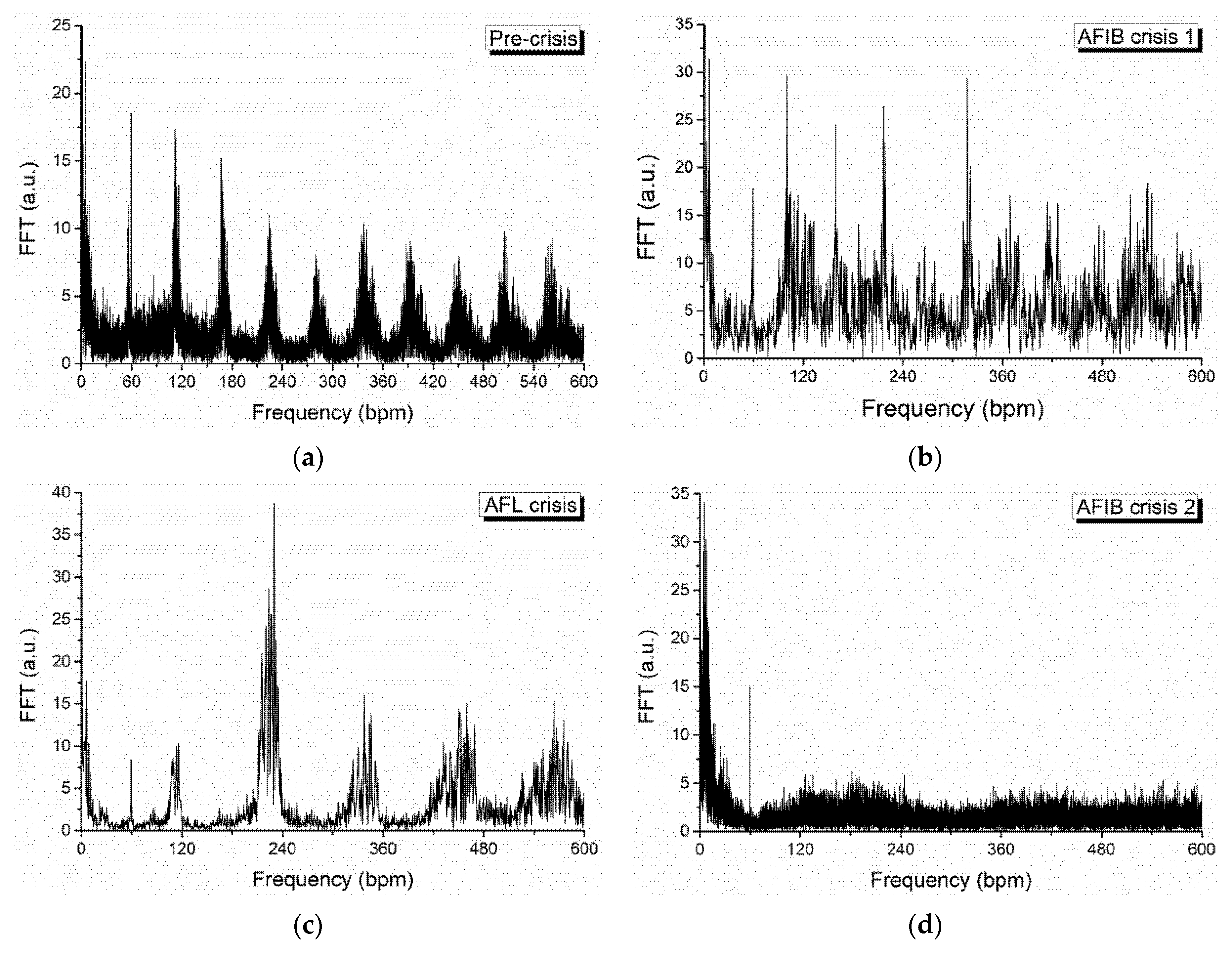
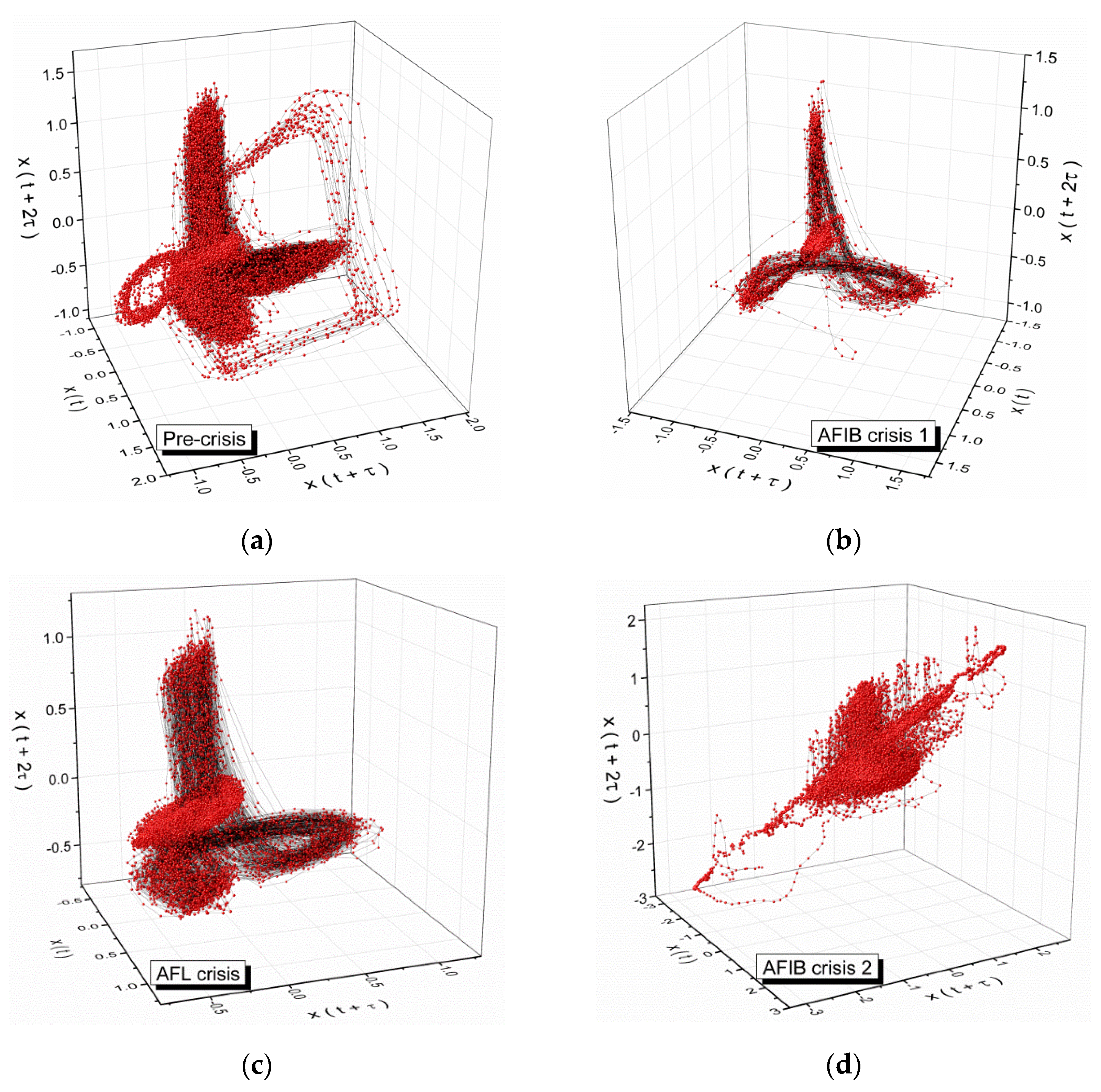
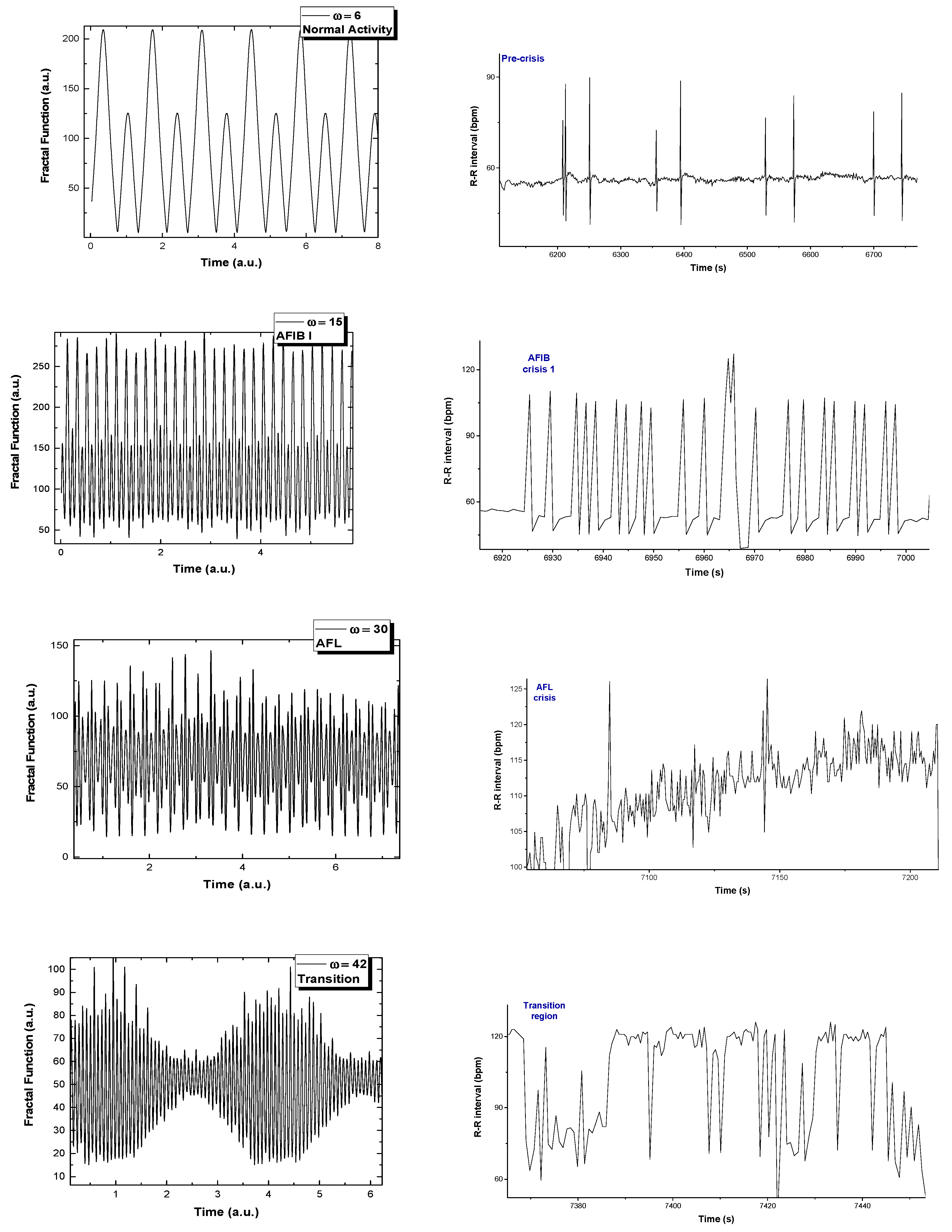
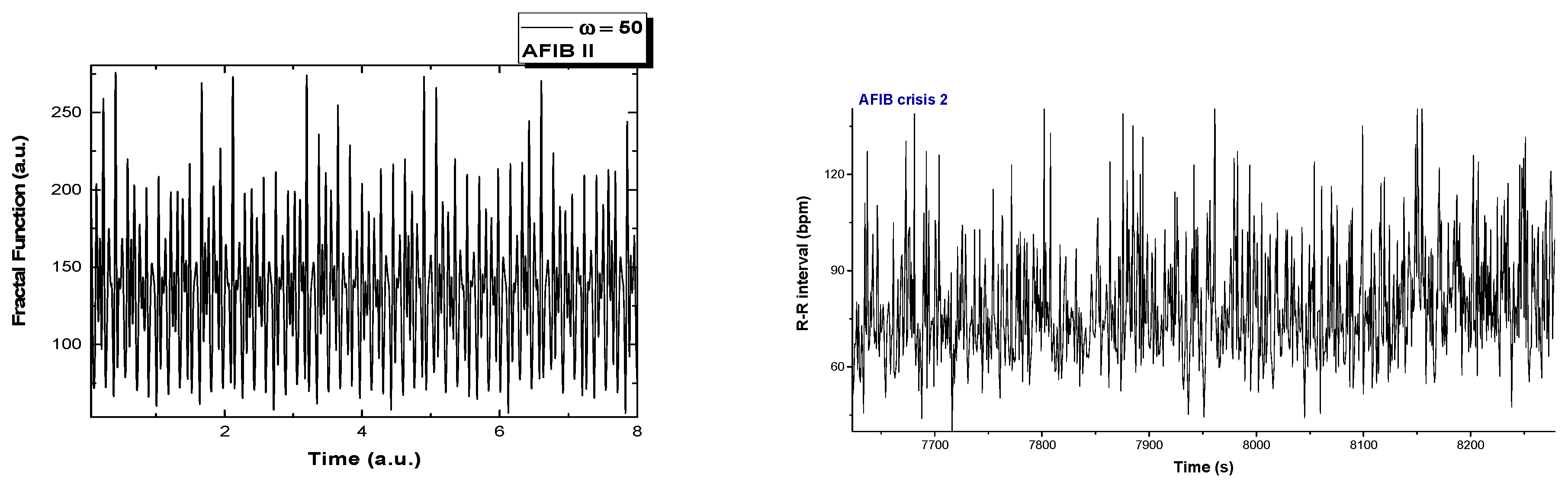
2. Analysis of Atrial Fibrillation by Applying Non-Linear Dynamics Methods
Results of Signal Analysis
3. The Reconstruction of EKG Signals through Scale Relativity Theory
3.1. Dynamics through Markovian and Non-Markovian Fractalization Types at Various Scale Resolutions
- (i)
- (ii)
- During the zoom operation of , any dynamics are related to the behaviors of a set of functions through the substitution principle .
- (iii)
- Any dynamics are described by multifractal functions. Then, two derivatives can be defined:The sign “” specifies the forward dynamics. The sign “” specifies the backward ones.
- (iv)
- The differential of the spatial coordinate has the form:The differentiable part does not depend on the scale resolution, while the non-differentiable part is scale resolution dependent.
- (v)
- The quantities satisfy the relation:where are constant coefficients associated to differential-non-differential transition, is the singularity spectrum of order α, α is the singularity index and DF is the fractal dimension of the “motion curves.”There are many modes of defining the fractal dimension. Thus, several fractal dimensions may be employed, but the fractal dimension in the sense of Hausdorff–Besikovitch [26] or the fractal dimension in the sense of Kolmogorov, are the most commonly used ones. In the case of many models, selecting one of these definitions and operating it in the context of any biological system dynamics implies that the value of the fractal dimension must be constant and arbitrary for the entirety of the dynamical analysis: for example, it is regularly found that DF < 2 for correlative processes in the dynamics of any biological system, DF > 2 for non-correlative processes. In the description of biological system dynamics we operate with (i.e., simultaneously operating with several fractal dimensions, on multifractal manifolds, as in the multifractal theory of motion) instead of operating with DF (i.e., with a single fractal dimension, on monofractal manifolds, as in the case of Nottale’s model). This leads to a series of advantages [13], such as the possibility to identify the areas of biological system dynamics that are characterized by a certain fractal dimension (for example, cell dynamics from either normal or tumoral tissues) or to identify the number of areas in the biological system dynamics for which the fractal dimensions are situated in an interval of values (for example, cell dynamics from tissue with various metastasis degrees). Finally, one of the biggest advantages of the method is the ability to identify classes of universality in the biological system dynamics, even when regular or strange attractors have various aspects (for example, the diagnosis of diseases from regular or strange attractor dynamics, as shown here).
- (vi)
- The differential time reflection invariance is recovered by means of the operator:In such context, applying this operator to , yields the complex velocity:withIn this relation the differential velocity is scale resolution independent, while the non–differentiable one is scale resolution dependent.
- (vii)
- Since the multi-fractalization describing biological structures dynamics implies stochasticization, the whole statistic “arsenal” (averages, variances, covariances, etc.) are operational. Thus, for example, let us select the subsequent functionality:with
- (viii)
- The biological structures dynamics, with previous functionality, can be described through the scale covariant derivative given by the operatorwhereNow, accepting the scale covariant principle in the describing of any biological structure dynamics, the conservation law of the specific momentum (i.e., geodesic equations on a multifractal manifold) takes the form:The explicit form of depends on the type of multi-fractalization used. It can be admitted that the multi-fractalization process can take place through various stochastic processes. Stochastic dynamics can be Markovian (thus, memoryless) biological processes. This is the case of scale relativity theory in Nottale’s sense, referring to biological dynamics on monofractal manifolds (with fractal dimension ). For non-Markovian biological processes, memory-like qualities are expected. Since biological processes usually display some sort of memory-related traits, it is then necessary to operate with mathematical procedures vastly different than the ones previously mentioned. In this case, wherein it is possible to generalize many of the previous results [21,23], the following constraints are admitted:where and are two constant coefficients associated to the differential-nondifferential scale transition, and is Kronecker’s pseudotensor. In such context, the conservation laws on multifractal and Euclidian manifolds are given in Appendix B, while in Appendix C nonlinear behaviors at non-differentiable scale are presented.
3.2. Dynamics Generated by Differential Geometry of Riemann Type in Scale Space
4. Conclusions
- (i)
- Diagnostics and evolution of atrial fibrillation by applying non-linear dynamics method skewness and kurtosis values are in accordance with pulse rate distributions from the histograms of the analyzed ECG signal. The Lyapunov exponent has positive values, close to zero for normal heart rhythm, and with values over one order of magnitude higher in the case of fibrillation crises, highlighting a chaotic behavior for cardiac muscle dynamics. Additionally, in the case of atrial flutter, a pattern of alternating 2:1, 3:1, 4:1, and 5:1 conduction ratio can be observed. Some abnormal heart rhythms were analyzed through strange attractors dynamics in the reconstructed phase space. For each stage of a crisis, a specific strange attractor was associated, proving that the specific attractors dynamics can constitute a valid method for evaluating various cardiac afflictions. The obtained results encourage us to further pursue this line of research.
- (ii)
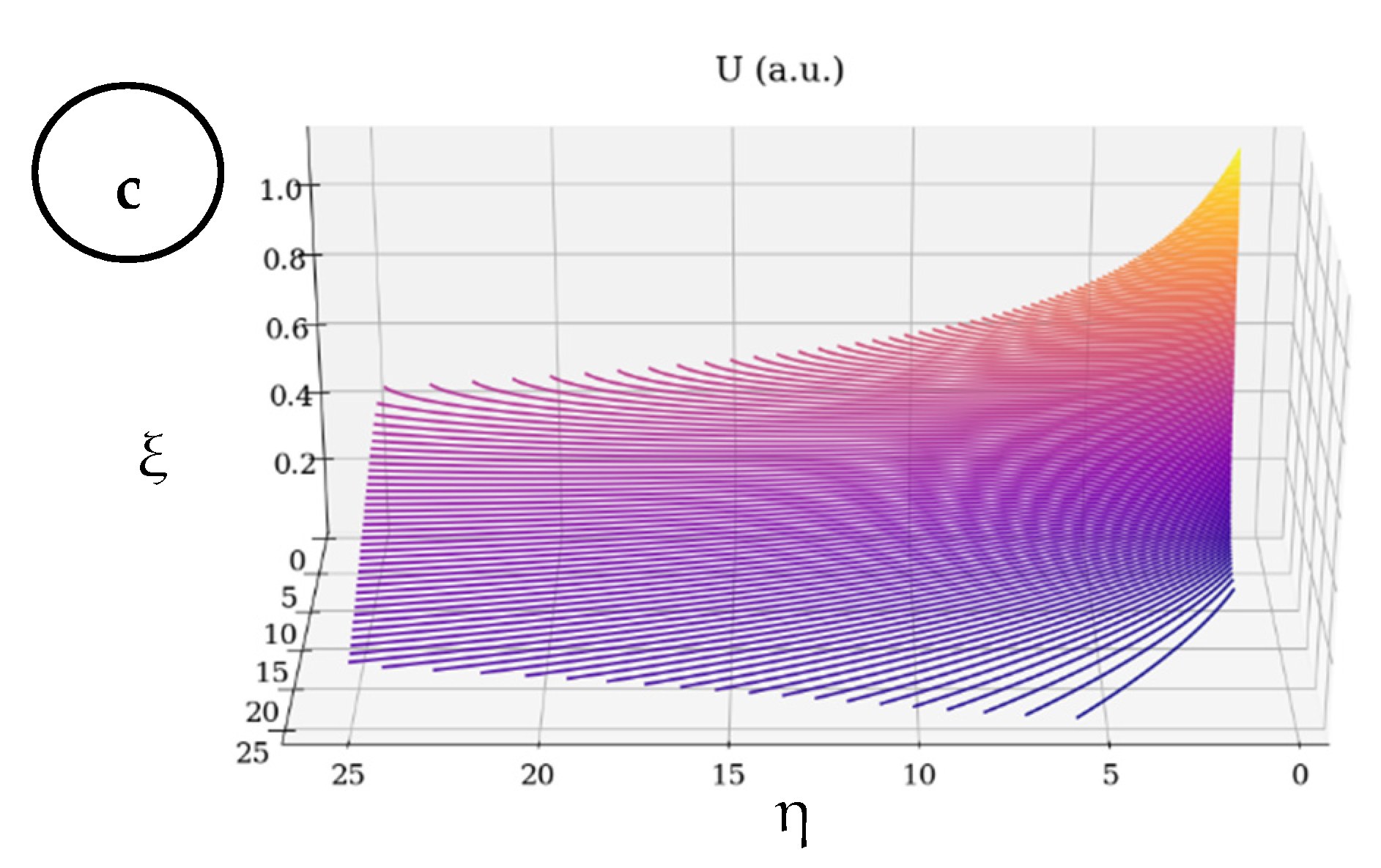
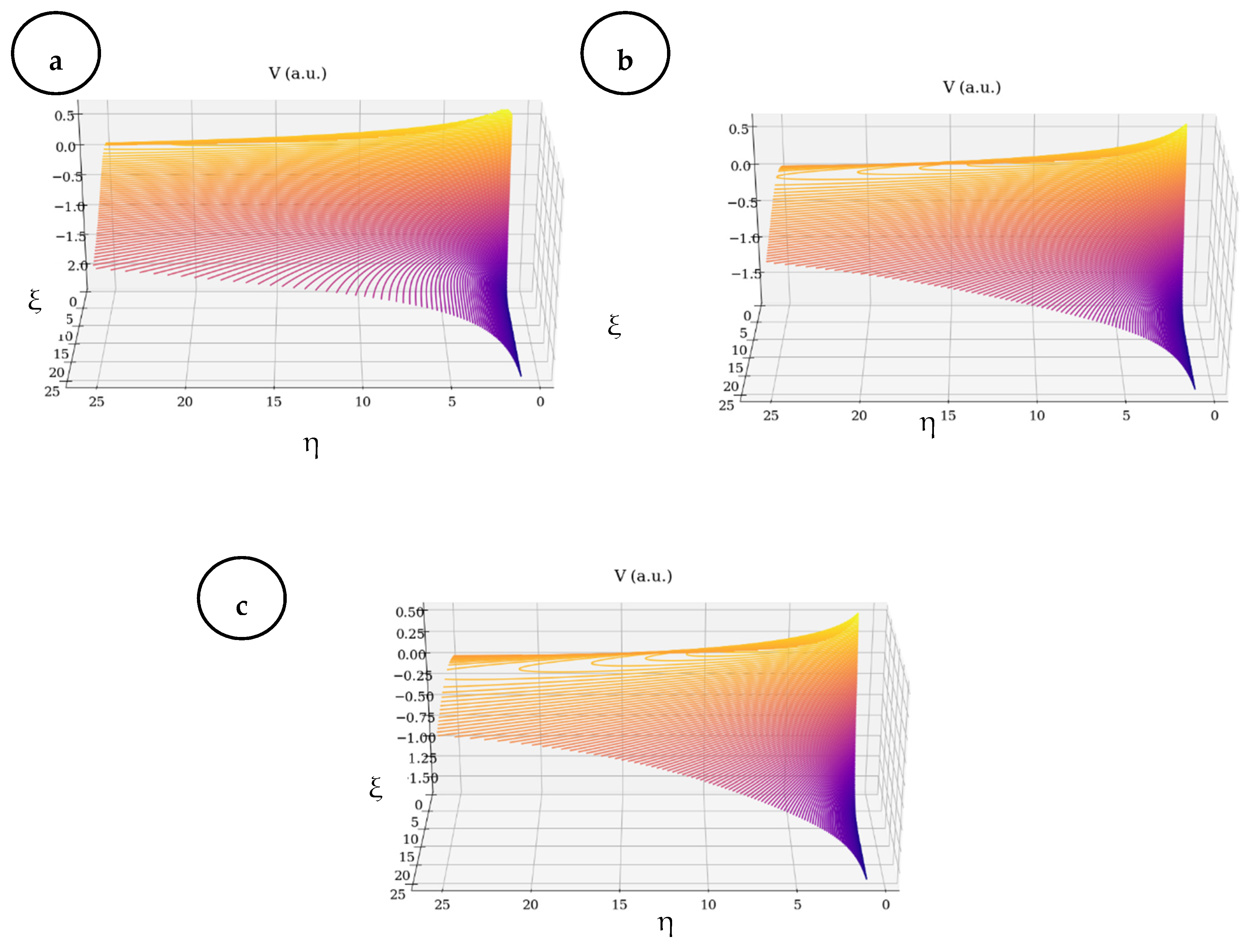
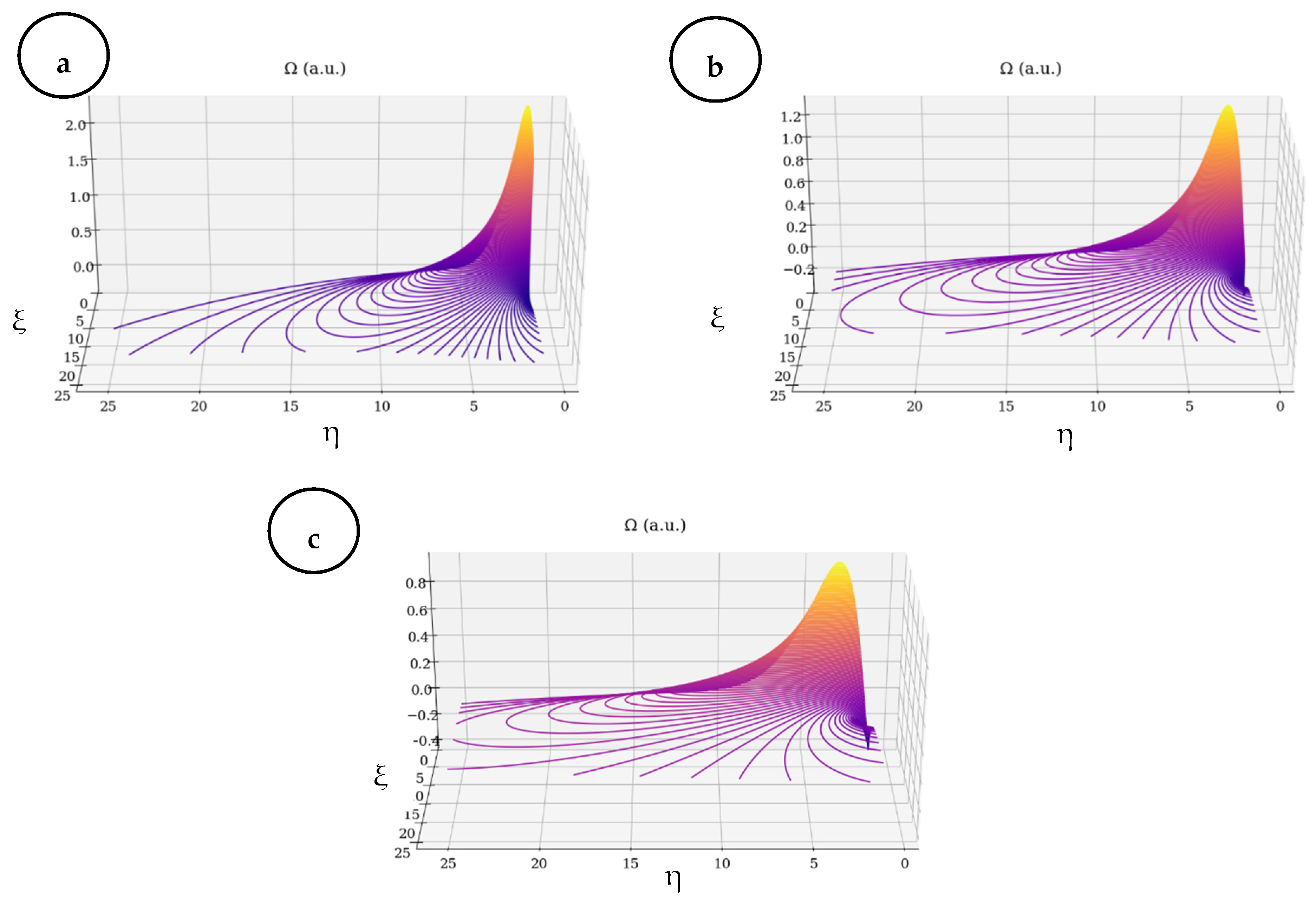
- Based on multi-fractalization through Markovian and non-Markovian-type stochasticizations in the framework of the scale relativity theory, any type of EKG signal can be reconstructed by means of harmonic mappings from the usual space to the hyperbolic one. These mappings mime various scale transitions by differential geometries, with parallel transport of direction in Levi–Civita sense, in Riemann-type spaces. The aforementioned spaces are associated to families of cubics, with symmetries of SL(2R)-type (i.e., invariances with respect to SL(2R)-type transformations).
- (iii)
- Then, the two operational procedures are not mutually exclusive, but rather become complementary, through their finality regarding the obtainment of valuable information concerning fibrillation crises. As such, the author’s proposed method could be used for developing new models for medical diagnosis and evolution tracking of heart diseases (both through attractors dynamics and signal reconstruction).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. A Breakdown of ECG Fragments

Appendix B. Dynamics on Multifractal and Euclidean and Multifractal Manifolds
Appendix C. Nonlinear—Type Behaviors at Non-Differentiable Scale Resolution

References
- Noble, D. A modification of the Hodgkin-Huxley equations applicable to Purkinje fibre action and pace-maker potentials. J. Physiol. 1960, 160, 317–352. [Google Scholar] [CrossRef] [PubMed]
- Fink, M.; Niederer, S.A.; Cherry, E.M.; Fenton, F.H.; Koivumäki, J.T.; Seemann, G.; Thul, R.; Zhang, H.; Sachse, F.B.; Beard, D.; et al. Cardiac cell modelling: Observation from the heart of the cardiac physiome project. Prog. Biophys. Mol. Biol. 2011, 104, 2–21. [Google Scholar] [CrossRef] [PubMed]
- Guevara, M.R.; Glass, L.; Shrier, A. Phase locking, period-doubling bifurcations, and irregular dynamics in periodically stimulated cardiac cells. Science 1981, 214, 1350–1353. [Google Scholar] [CrossRef] [PubMed]
- Ritzenberg, A.L.; Adam, D.R.; Cohen, R.J. Period multupling-evidence for nonlinear behaviour of the canine heart. Nature 1984, 307, 159–161. [Google Scholar] [CrossRef] [PubMed]
- Glass, L.; Mackey, M.C. From Clock to Chaos. The Rhythms of Life; Princeton University Press: Princeton, NJ, USA, 1988. [Google Scholar]
- Acharia, U.R.; Paul, J.K.; Kannathal, N.; Lim, C.M.; Suri, J.S. Heart Rate Variability. In Advances in Cardiac Signal Processing; Acharia, U.R., Suri, J.S., Spaan, J.A.E., Krishnan, S.M., Eds.; Springer: Berlin, Germany, 2007; pp. 121–165. [Google Scholar]
- Krogh-Madsen, T.; Christini, D.J. Nonlinear dynamics in cardiology. Annu. Rev. Biomed. Eng. 2012, 14, 179–203. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Nayak, S.K.; Bit, A.; Dey, A.; Mohapatra, B.; Pal, K. A review of the nonlinear dynamical system analysis of electrocardiogram signal. J. Healthc. Eng. 2018, 2018, 6920420. [Google Scholar] [CrossRef] [PubMed]
- Henriques, T.; Ribeiro, M.; Teixeira, A.; Castro, L.; Antunes, L.; Costa-Santos, C. Nonlinear methods most applied to heart-rate time series: A review. Entropy 2020, 22, 309. [Google Scholar] [CrossRef] [PubMed]
- Task Force of the European Society of Cardiology, North American Society of Pacing Electrophysiology—Heart rate variability: Standards of measurement, physiological interpretation, and clinical use. Circulation 1996, 93, 1043–1065. [CrossRef]
- Su, Z.-Y.; Wu, T.; Yang, P.-H.; Wang, Y.-T. Dynamic analysis of heartbeat rate signals of epileptics using multidimensional phase space reconstruction approach. Phys. A 2008, 387, 2293–2305. [Google Scholar] [CrossRef]
- Young, H.; Benton, D. We should be using nonlinear indices when relating heart-rate dynamics to cognition and mood. Sci. Rep. 2015, 5, 16619. [Google Scholar] [CrossRef] [PubMed]
- West Bruce, J. Fractal Physiology and Chaos in Medicine, 2nd ed.; World Scientific: Singapore, 2013. [Google Scholar]
- Bar-Yam, Y. Dynamics of Complex Systems, the Advanced Book Program; Addison-Wesley: Reading, MA, USA, 1997. [Google Scholar]
- Mitchell, M. Complexity: A Guided Tour; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Badii, R. Complexity: Hierarchical Structures and Scaling in Physics; Cambridge University Press: Cambridge, MA, USA, 1997. [Google Scholar]
- Flake, G.W. The Computational Beauty of Nature; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Shang, Y. Modeling epidemic spread with awareness and heterogeneous transmission rates in networks. J. Biol. Phys. 2013, 39, 489–500. [Google Scholar] [CrossRef] [PubMed]
- Liao, C.-M.; Chang, C.-F.; Liang, H.-M. A Probabilistic Transmission Dynamic Model to Assess Indoor Airborne Infection Risks. Risk Anal. 2005, 25, 1097–1107. [Google Scholar] [CrossRef] [PubMed]
- Băceanu, D.; Diethelm, K.; Scalas, E.; Trujillo, H. Fractional Calculus, Models and Numerical Methods; World Scientific: Singapore, 2016. [Google Scholar]
- Ortigueria, M.D. Fractional Calculus for Scientists and Engineers; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Nottale, L. Scale Relativity and Fractal Space-Time: A New Approach to Unifying Relativity and Quantum Mechanics; Imperial College Press: London, UK, 2011. [Google Scholar]
- Merches, I.; Agop, M. Differentiability and Fractality in Dynamics of Physical Systems; World Scientific: Hackensack, NJ, USA, 2016. [Google Scholar]
- Jackson, E.A. Perspectives of Nonlinear Dynamics; Cambridge University Press: New York, NY, USA, 1993; Volumes 1 and 2. [Google Scholar]
- Cristescu, C.P. Nonlinear Dynamics and Chaos. In Theoretical Fundaments and Applications; Romanian Academy Publishing House: Bucharest, Romania, 2008. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W.H. Freeman and Co.: San Fracisco, CA, USA, 1982. [Google Scholar]
- Mazilu, N.; Agop, M. Skyrmions: A Great Finishing Touch to Classical Newtonian Philosophy; Nova Science Publisher: New York, NY, USA, 2014. [Google Scholar]
- Fels, M.; Olver, P.J. Moving Coframes I. Acta Appl. Math. 1998, 51, 161–213. [Google Scholar] [CrossRef]
- Fels, M.; Olver, P.J. Moving Coframes II. Acta Appl. Math. 1999, 55, 127–208. [Google Scholar] [CrossRef]
- Flanders, H. Differential Forms with Applications to the Physical Sciences; Dover Publications: New York, NY, USA, 1989. [Google Scholar]
- Rogers, C.; Schief, W.K. Bäcklund and Darboux Transformations; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Burnside, W.S.; Panton, A.W. The Theory of Equations; Dover Publications: New York, NY, USA, 1960. [Google Scholar]
- Barbilian, D. Apolare und Überapolare Simplexe. Mathematica (Cluj) 1935, 11, 1–24. [Google Scholar]
- Atiyah, M.F.; Manton, N.S. Skyrmions from Instantons. Phy. Lett. B 1989, 222, 438–442. [Google Scholar] [CrossRef]
- Shang, Y. On the Structural Balance Dynamics under Perceived Sentiment. Bull. Iran. Math. Soc. 2019, 46, 717–724. [Google Scholar] [CrossRef]
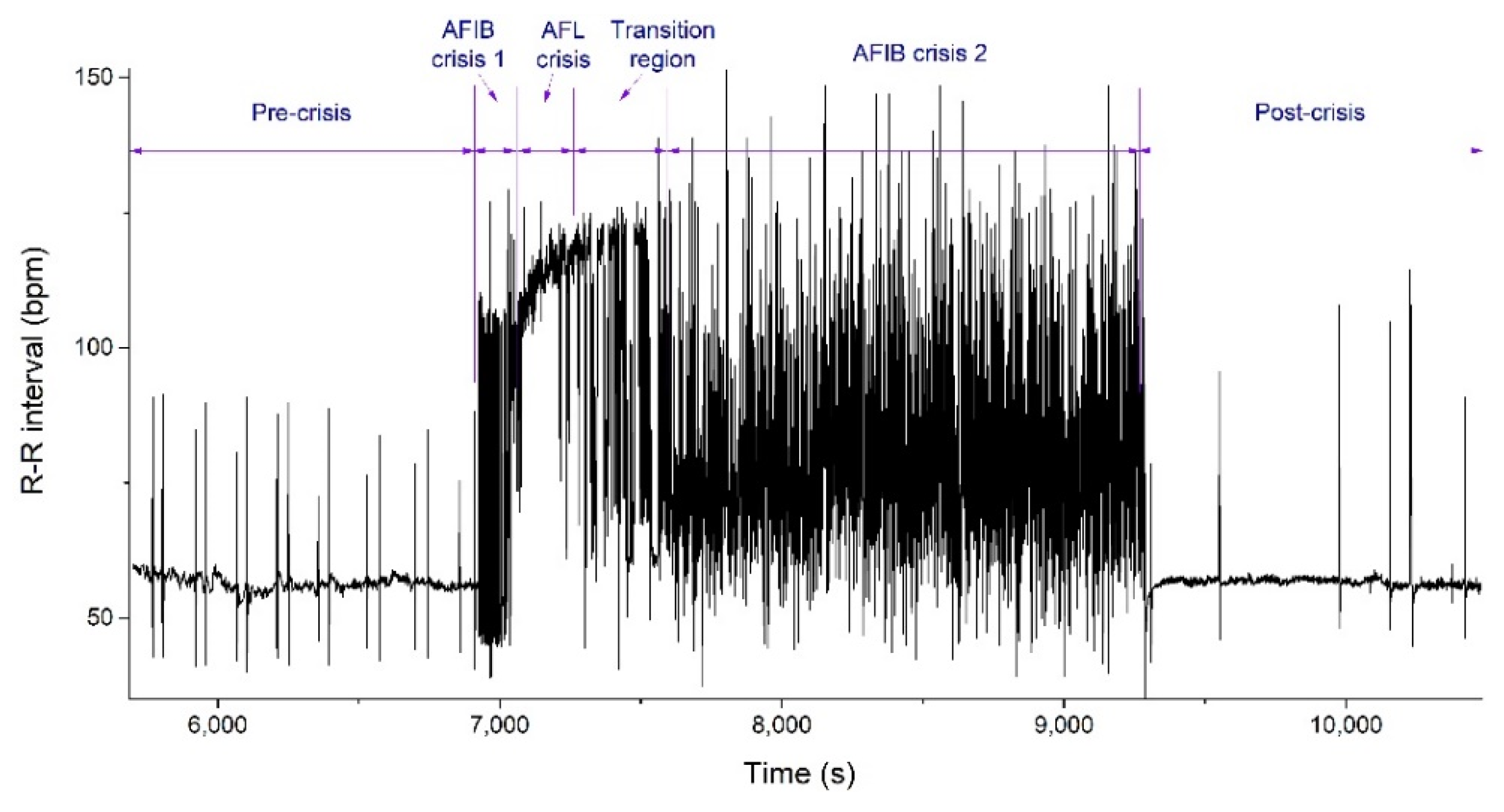

| Signal | 1/R-R Interval Median (bpm) | Variance | Geometric Standard Deviation | Skewness | Kurtosis | Largest Lyapunov Exponent |
|---|---|---|---|---|---|---|
| Pre-crisis | 56.3909 | 16.858 | 1.0673 | 4.4938 | 37.6779 | 0.013981 |
| AFIB 1 | 53.3807 | 718.649 | 1.4309 | 0.7814 | −1.098 | 0.211145 |
| AFL | 115.3846 | 17.9911 | 1.2105 | −0.0359 | 0.462 | 0.082811 |
| AFIB 2 | 76.9231 | 391.197 | 1.2662 | 0.7047 | 0.0456 | 0.138646 |
| Post-crisis | 56.6037 | 22.871 | 1.0684 | 8.2509 | 82.8455 | 0.014529 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agop, M.; Irimiciuc, S.; Dimitriu, D.; Rusu, C.M.; Zala, A.; Dobreci, L.; Valentin Cotîrleț, A.; Petrescu, T.-C.; Ghizdovat, V.; Eva, L.; et al. Novel Approach for EKG Signals Analysis Based on Markovian and Non-Markovian Fractalization Type in Scale Relativity Theory. Symmetry 2021, 13, 456. https://doi.org/10.3390/sym13030456
Agop M, Irimiciuc S, Dimitriu D, Rusu CM, Zala A, Dobreci L, Valentin Cotîrleț A, Petrescu T-C, Ghizdovat V, Eva L, et al. Novel Approach for EKG Signals Analysis Based on Markovian and Non-Markovian Fractalization Type in Scale Relativity Theory. Symmetry. 2021; 13(3):456. https://doi.org/10.3390/sym13030456
Chicago/Turabian StyleAgop, Maricel, Stefan Irimiciuc, Dan Dimitriu, Cristina Marcela Rusu, Andrei Zala, Lucian Dobreci, Adrian Valentin Cotîrleț, Tudor-Cristian Petrescu, Vlad Ghizdovat, Lucian Eva, and et al. 2021. "Novel Approach for EKG Signals Analysis Based on Markovian and Non-Markovian Fractalization Type in Scale Relativity Theory" Symmetry 13, no. 3: 456. https://doi.org/10.3390/sym13030456
APA StyleAgop, M., Irimiciuc, S., Dimitriu, D., Rusu, C. M., Zala, A., Dobreci, L., Valentin Cotîrleț, A., Petrescu, T.-C., Ghizdovat, V., Eva, L., & Vasincu, D. (2021). Novel Approach for EKG Signals Analysis Based on Markovian and Non-Markovian Fractalization Type in Scale Relativity Theory. Symmetry, 13(3), 456. https://doi.org/10.3390/sym13030456







