Reference Frame Induced Symmetry Breaking on Holographic Screens

Abstract

Any interaction between finite quantum systems in a separable joint state can be viewed as encoding classical information on an induced holographic screen. Here we show that when such an interaction is represented as a measurement, the quantum reference frames (QRFs) deployed to identify systems and pick out their pointer states induce decoherence, breaking the symmetry of the holographic encoding in an observer-relative way. Observable entanglement, contextuality, and classical memory are, in this representation, logical and temporal relations between QRFs. Sharing entanglement as a resource requires a priori shared QRFs.

1. Introduction

The holographic principle (HP) states, in its covariant formulation, that for any finite spacelike boundary $\mathcal{B}$, open or closed, the classical, thermodynamic entropy $S\left(L\right(\mathcal{B}\left)\right)$ of any light-sheet $L\left(\mathcal{B}\right)$ of $\mathcal{B}$ satisfies:

$$S\left(L\right(\mathcal{B}\left)\right)\le A\left(\mathcal{B}\right)/4,$$

(1)

where $A\left(\mathcal{B}\right)$ is the area of $\mathcal{B}$ in Planck units [1]. The HP was motivated by the Bekenstein bound on the thermodynamic entropy of a black hole (BH), and has traditionally been interpreted as a bound on the thermodynamic entropy of, and hence the classical information encodable on, an independently-defined surface $\mathcal{B}$, e.g., the stretched horizon of a BH [2,3]; see [1,4] for reviews.

We can, however, also view (1) from a more general perspective, as a fundamental principle of information geometry that associates a (finite) minimal surface $\mathcal{B}$ with any bit string of (finite) entropy S, and hence with any classical channel of width S bits. Such a channel can be constructed, without loss of generality, as follows: Let $U=AB$ be a finite, closed quantum system, assume separability, $|AB\rangle =|A\rangle |B\rangle$ over any time interval of interest, and write the interaction:

$$H_{AB}={\beta }^k{k}_B{T}^k\sum _i^N{\alpha }_i^k{M}_i^k,$$

(2)

where $k=A$ or B, the $M_i^k$ are N Hermitian operators with eigenvalues in $\{-1,1\}$, the ${\alpha }_i^k\in [0,1]$ are such that ${\sum }_i^N{\alpha }_i^k=1$, $k_B$ is Boltzmann’s constant, $T^k$ is k’s temperature, and ${\beta }^k\ge$ ln 2 is an inverse measure of k’s thermodynamic efficiency that depends on the internal dynamics $H_k$. At each time step, A obtains exactly N bits of information about B from this channel and vice versa, entirely independently of the internal dynamics $H_A$ and $H_B$. With this construction, we can state the following generalized holographic principle (cf. [5] Thm. 1):

GHP: If but only if a pair of finite quantum systems A and B have a separable joint state $|AB\rangle =|A\rangle |B\rangle$, there is a finite spacelike surface $\mathcal{B}$, with area $A\left(\mathcal{B}\right)\ge A{\left(\mathcal{B}\right)}_{min}=4\ln 2N{l}_P^2$, N the dimension of $H_{AB}$ and $l_P$ the Planck length, that implements $H_{AB}$ as a classical channel.

This GHP is a purely information-theoretic principle that makes no reference to any spatial embedding of A or B. We show in [5] that it holds for any spatial embedding of A and B allowed by special relativity. As $\mathcal{B}$ is ancillary to the interaction $H_{AB}$, we will be unconcerned with the spatial scale of $\mathcal{B}$; in systems with low energy densities, we can expect $A\left(\mathcal{B}\right)\gg A{\left(\mathcal{B}\right)}_{min}$.

The form of the Hamiltonian (2) has two immediately-apparent symmetries. First, the number N of transferred bits is fixed; hence Equation (2) is symmetric as a channel. The holographic screen $\mathcal{B}$ “looks the same” and encodes the same information, N bits, from either A’s or B’s perspective. Second, the terms ${\alpha }_i^k{M}_i^k$ of Equation (2) can be re-arranged in any order. If we view $\mathcal{B}$ as implemented by an ancillary array of non-interacting qubits as in [5,6], these qubits can be permuted arbitrarily; hence the state of $\mathcal{B}$ is invariant under the symmetric group $S_N$.

Here we consider the system A to be an “observer” of B, and study apparent, observer-relative symmetry breaking on $\mathcal{B}$ induced by the implementation of one or more quantum reference frames (QRFs) by the internal Hamiltonian $H_A$. The role of reference frames in physical theory is to allow observations made at different times and/or places to be compared. While in classical physics reference frames are often treated in abstracto, in quantum theory they must be considered to be physically implemented, and hence as QRFs; meter sticks, clocks, and gyroscopes are canonical examples [7]. Sharing an external QRF, e.g., a Cartesian frame, across either space or time requires the observers involved to implement an equivalent internal QRF [8]; hence all QRFs deployed by A can, without loss of generality, be considered to be implemented by $H_A$ (cf. [9,10]).

We begin in Section 2 below by briefly reviewing some consequences of separating systems A and B by a holographic screen $\mathcal{B}$; such separation prevents, in particular, measurements by A of the entanglement entropy of B. We then introduce in Section 3 an explicit, fully general, and semantically-rich category-theoretic formalism with which to specify the QRFs deployed by any observer, focussing first on QRFs employed for system identification (Section 3.1) and then considering QRFs employed for pointer measurements (Section 3.2). We show that sequential pointer measurements break the $S_N$ symmetry of the screen $\mathcal{B}$, inducing decoherence (Section 3.3). For illustration, we turn to the particular case of measuring Hawking quanta from a BH, showing explicitly that no experiment can demonstrate entanglement between a BH and a distant free quantum of radiation (Section 3.4). We close this section by showing that the free-energy costs of deploying a QRF induce coarse-graining (Section 3.5). These results provide the background required to prove, in Section 4, that sharing entanglement as a resource requires a priori shared, entangled QRFs, and then to prove, in Section 5, that whether two observers share QRFs is finite Turing undecidable. We close in Section 6 by showing that writing classical memories to a screen $\mathcal{B}$ creates phase correlations that further disrupt the $S_N$ symmetry of the screen. These results together suggest that, far from being “an apparent law of physics that stands by itself” [1], the HP in its generalized GHP form is central to quantum information theory.

2. Instantaneous Interactions across $\mathcal{B}$

To write the Hamiltonian (2), we require the joint state $|AB\rangle$ to be separable; it is this separability that makes $\mathcal{B}$ a classical channel. Distinguishing the classical entropy (S) from the entanglement entropy ($\mathcal{S}$), we can restate the GHP in summary form as:

Lemma 1.

If systems A and B are separated by a finite holographic screen $\mathcal{B}$, the entanglement entropy of the joint state $\mathcal{S}\left(\right|AB\rangle )=0$.

Proof. 

By the definition of $\mathcal{B}$; see [5], Thm. 1 showing that any finite-bandwidth classical communication channel can be represented as a finite holographic screen for details. □

Lemma 1 immediately rules out transfers of quantum information across $\mathcal{B}$; hence A has access to neither the internal Hamiltonian $H_B$ or the entanglement entropy $\mathcal{S}\left(B\right){=}_{def}max\left(\mathcal{S}\left(\right|B_1{B}_2\rangle \right))$ over tensor-product decompositions $B_1{B}_2=B$. It is clear, moreover, that Equation (2) can hold only if the Hilbert space dimensions $dim\left({\mathcal{H}}_A\right),dim\left({\mathcal{H}}_B\right)\ge N$, where equality holds only if A and B contain no “hidden” degrees of freedom that do not, over any time interval under consideration, contribute to $H_{AB}$. Hence A cannot place upper limits on either the dimension $dim\left({\mathcal{H}}_B\right)$ or the entanglement entropy $\mathcal{S}\left(B\right)$ of B. We will assume in what follows that B is “large,” $dim\left({\mathcal{H}}_B\right)\gg N$, and has near-maximal entanglement entropy $\mathcal{S}\left(B\right)\approx dim\left({\mathcal{H}}_B\right)/2$; this is effectively the assumption that $H_{AB}$ only minimally perturbs $|B\rangle$. As with this assumption the full state $|B\rangle$ is not observable by A, we will use the notation ${|B\rangle }^A$ to indicate the “observed” (by A) partial state of B that is encoded on $\mathcal{B}$. By (2), this observed state ${|B\rangle }^A$ is an eigenstate of $H_{AB}$ with dimension N.

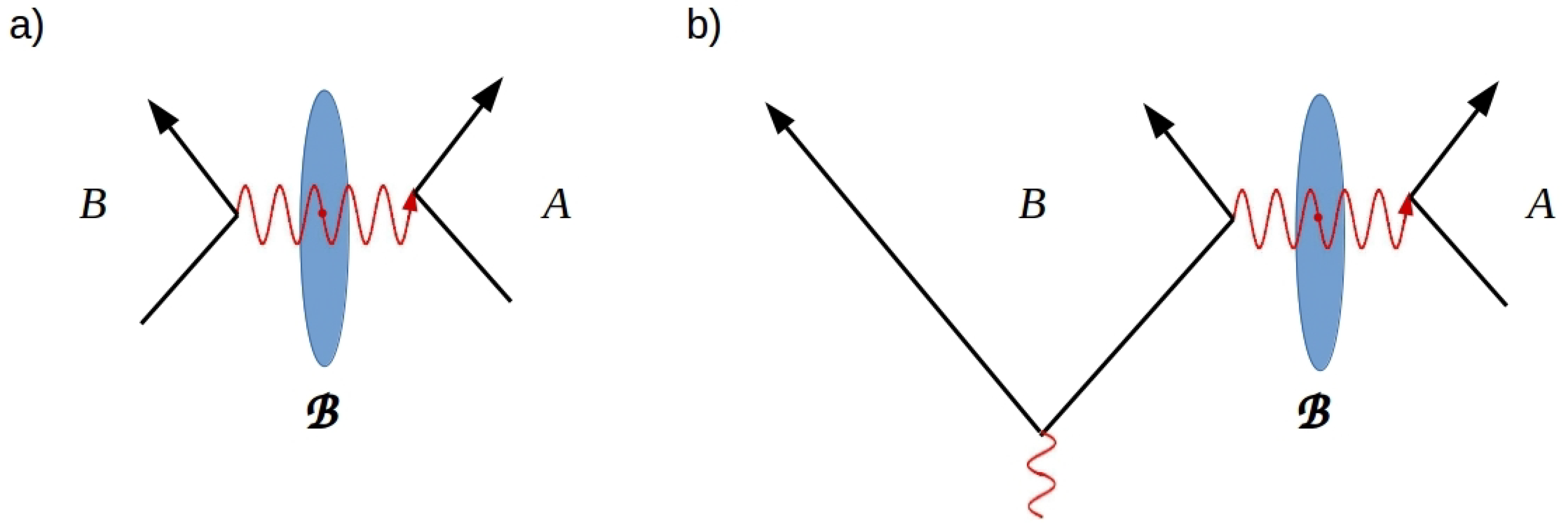
2.1. Example: Scattering

Consider a scattering process mediated by a gauge boson, as shown in Figure 1a. Both incoming and outgoing joint states are asymptotically separable, so the exchanged information is encoded on a holographic screen $\mathcal{B}$. Ignoring charge and spin, the encoded information specifies a classical momentum transfer $\Delta \overrightarrow{p}$. No quantum information is transferred across $\mathcal{B}$; in particular, the scattering processes transfers no information about the entanglement entropy $\mathcal{S}\left(B\right)$ to A (Figure 1b).

Writing the Hamiltonian as in (2) requires the dimension N of the observed state ${|B\rangle }^A$ to be finite and hence the momentum transfer $\Delta \overrightarrow{p}$ to be discrete. Discrete values of $\Delta \overrightarrow{p}$ reflect the discrete cost of information in units of ℏ. In a experimental setting in which $\Delta \overrightarrow{p}$ is measured at some asymptotically-distant location, the dimension N, and hence the number of (ancillary) qubits required to represent $\mathcal{B}$ as a channel, is set operationally by the resolution of the detector. In this case $\Delta \overrightarrow{p}$ is the measured pointer value, and a full description of the interaction requires specification of the QRF employed for system identification as discussed in Section 3 below.

2.2. Example: Hawking Radiation

For an asymptotic observer A, coupled pair annihilation and production near a holographic screen $\mathcal{B}$, with one positive- and one negative-energy mode transiting the screen (Figure 2a) is indistinguishable from a scattering event at $\mathcal{B}$ (Figure 2b). Hence far from a black hole (BH), Hawking radiation from the BH is indistinguishable from scattering from the stretched horizon of the BH. Lemma 1 forbids any modes detectable by A from carrying information about the entanglement entropy $\mathcal{S}\left(B\right)$ as discussed above; hence the only observable entropy of B is the classical, thermodynamic entropy $S\left(L\right(\mathcal{B}\left)\right)$ given by Equation (1).

The distinction between the thermodynamic entropy $S\left(L\right(\mathcal{B}\left)\right)$ and the entanglement entropy $\mathcal{S}\left(B\right)$ for B a BH, and hence $\mathcal{B}$ the stretched horizon, has been recently clarified from a number of perspectives [11,12,13,14], showing in particular that preserving unitarity does not require a firewall [15] to prevent detection of excess entanglement. Considering the outgoing states to be measured by some observer requires specifying a QRF as noted above; we consider this issue in the particular case of Hawking quanta further in Section 3.4 below.

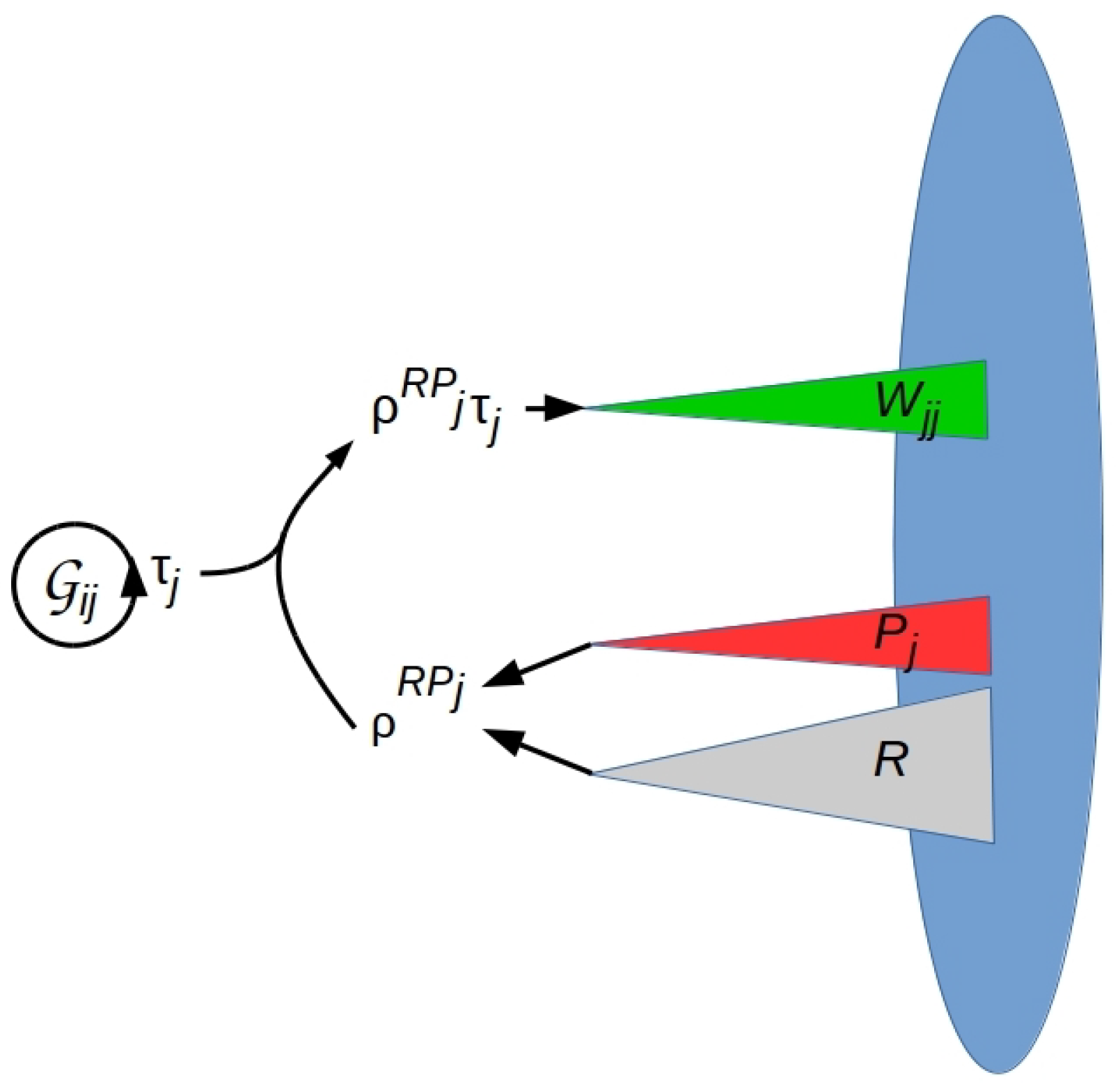
2.3. Symmetry across $\mathcal{B}$ Corresponds to “Free Choice” of QRFs

A QRF deployed by A, i.e., implemented by $H_A$, corresponds to a set of observables held fixed while other observables are allowed to vary [6,8] as discussed more explicitly in Section 3 below. It thus corresponds to a subset of the $M_i^A$. Associative groupings of the $M_i^A$ in Equation (2) are clearly independent of associative groupings of the $M_i^B$; hence choices of QRF by A have no bearing on choices of QRF by B or vice versa. Equivalently, swapping the labels A and B has no effect on Equation (2).

This “free choice” of QRFs corresponds to a the absence of superdeterminist correlations between A and B. Such correlations implement entanglement [16,17] so are forbidden if $|AB\rangle =|A\rangle |B\rangle$. We discuss the effects of locally breaking this free-choice symmetry in Section 4 below.

3. Reference Frame Induced Decoherence

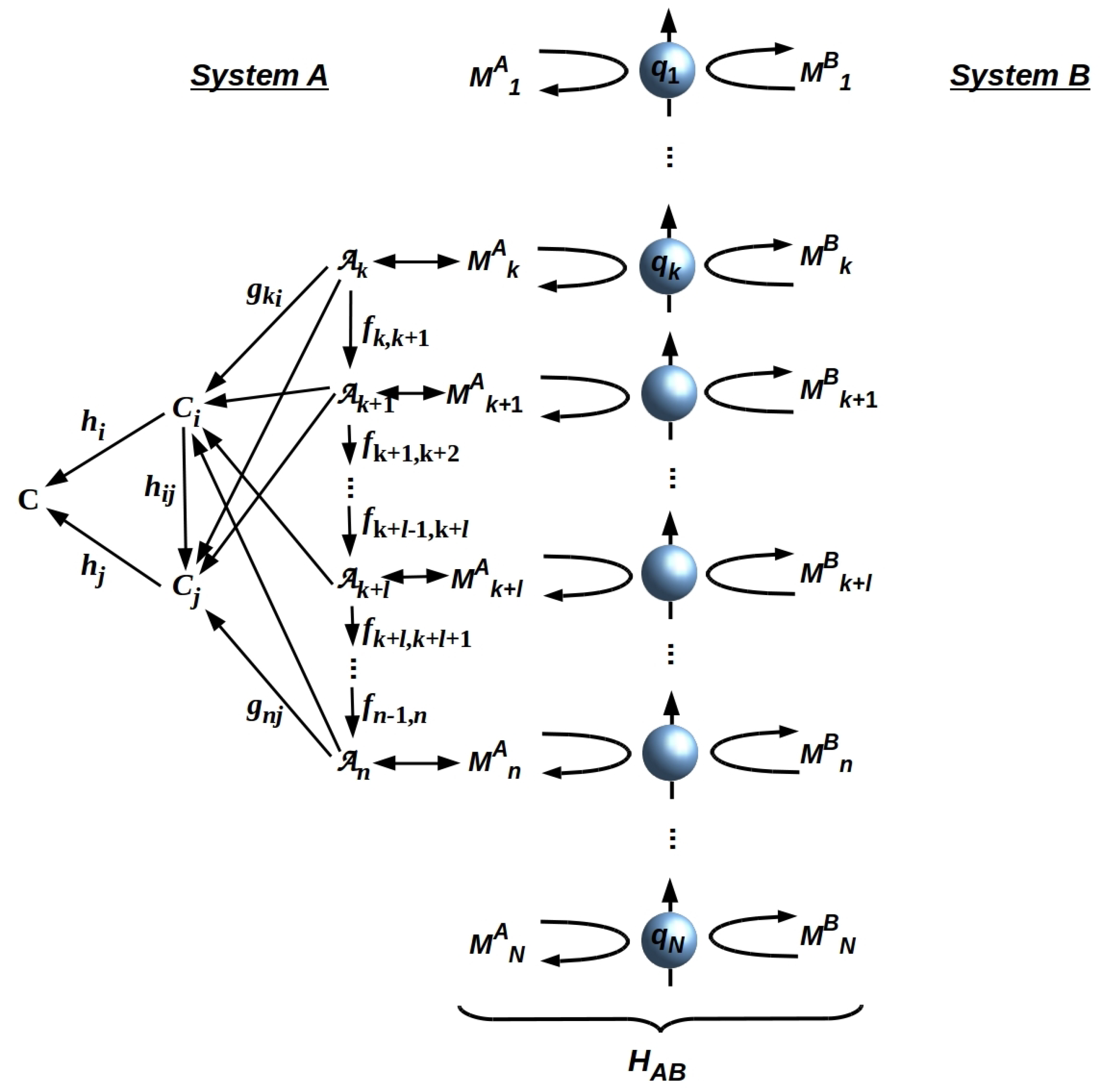
3.1. QRFs for System Identification

From A’s perspective, the partial state ${|B\rangle }^A$ encoded on $\mathcal{B}$ is pure: it encodes all of the information about B that is accessible, even in principle, to A. Mixed or decoherent states (we will use these terms interchangeably), in contrast, always indicate a lack of access to information that is in principle accessible: a state ${\rho }^S$ of S is decoherent if there is some non-null system E such that ${\rho }^S={\mathrm{Tr}}_E{\rho }^{SE}={\mathrm{Tr}}_E|SE\rangle \langle SE|$. In this case, E is the purifier or “environment” of the S and $|SE\rangle$ is the purification of ${\rho }^S$ by E (see [18,19,20] for extended discussions). That such a purifying E exists physically, not just formally, for any mixed ${\rho }^S$ is a fundamental assumption of quantum theory [21,22], sometimes stated as an explicit axiom [23]. From an operation perspective, E comprises degrees of freedom that interact with those of S but that cannot be, or at least are not observed when ${\rho }^S$ is measured. If ${\rho }^S$ is, for example, the state of a particle beam, E would include the degrees of freedom of the ion source, the magnetic fields, the ambient vacuum in the beam lines, etc.

The minimal setting employed here avoids the circularity that arises when a system-environment decomposition $B=SE$ is stipulated a priori [24,25,26,27] by forcing S to be identified by some QRF implemented by A. As shown in [6], any QRF can be specified by a cocone diagram (CCD), a category-theoretic construction comprising a hierarchical arrangement of Barwise-Seligman Information Flow binary classifiers/classifications ${\mathcal{A}}_{\alpha }$ [28] as depicted in Figure 3. These classifiers represent observables in context; namely, each classifier is a conceptual representation ${\mathcal{A}}_{\alpha }=\langle even{t}_{\alpha },{(condition,context)}_{\alpha },valuatio{n}_{\alpha }\rangle$ (essential details of the concepts and constructions are recalled in Appendix A, and in particular Appendix A.1 for the latter concept) (More generally, these classifiers can be seen as a triad of: (i) events (atomic, observed or experienced, imposition of boundaries, etc.); (ii) conditions/contents/influences as paired with contexts/measurements/detectors; and (iii) valuation. Again see Appendix A.1 for the formal details). Each classifier ${\mathcal{A}}_{\alpha }$ is valued in $\{-1,1\}$ in accordance with its associated operator $M_{\alpha }^A$ implementing “yes/no questions” as intrinsic to Equation (2) ([6], Section 3.2). In this sense, ${\mathcal{A}}_{\alpha }$ may be alternatively regarded as an eigen-classifier for $M_{\alpha }^A$.

To construct the CCD, we select a subset $\{M_k^A,\dots M_n^A\}$ of measurement operators and assign to each a binary classifier ${\mathcal{A}}_k,\dots ,{\mathcal{A}}_n$, respectively, with each requiring a fixed value, $+1$ or $-1$, from the corresponding operator; the ${\mathcal{A}}_k\dots {\mathcal{A}}_n$ thus specify a fixed bit string as input to the CCD. Further binary classifiers, each of which can be thought of as a classical logic gate, are added to form “hidden layers” $\mathcal{C}$; the maps between classifiers are “infomorphisms” as defined in [28] that satisfy the diagram-commutativity requirements for a cocone (see [29,30] for general category-theoretic definitions, Reference [31] for discussion of the cocone as a general representation of complex conditionals, Reference [32] for applications, examples, and discussion of the obvious analogy with artificial neural networks, and [6] for summaries of the relevant definitions as they apply in the current context). As shown in [6], a CCD exists over a subset ${\mathcal{A}}_k\dots {\mathcal{A}}_n$ of classifiers if and only if the corresponding subset $\{M_k^A,\dots M_n^A\}$ of binary-valued operators all mutually commute (see [33] for a formal proof). The colimit $\mathbf{C}$ of the CCD encodes the classical “output” of the QRF as a bit string. As formulated in [33], the CCD then becomes manifestly a scale-free context-dependent architecture. Operationally, it can be thought of as a “deep” neural network with re-entrant connections [32]. In the general case these connections are implemented by quantum processes (i.e., by $H_A$); the intermediate classifiers at each layer $\mathcal{C}$ then implement measurements, with the general form of (2), of the outcomes of these processes.

The channel implemented by the qubits $q_1\dots q_N$ is free of classical noise by definition: there is no external system to provide a noise source [6,8]. It is evident in Figure 3, however, that this channel transmits a fixed classical bit string, e.g., (1, 1, 1, …, 1) from B to A if but only if A and B share a z axis. Hence we have:

Lemma 2.

The channel implemented by a holographic screen between A and B is free of quantum noise if and only if A and B share QRFs.

Proof. 

If A and B share QRFs, each channel qubit is prepared and then measured in the same basis. As the preparation—measurement cycle is effectively instantaneous, prepared and measured outcomes must be the same up to measurement resolution. If A and B do not share QRFs, the preparation and measurement bases for each channel qubit may be arbitrarily different, introducing arbitrary phase rotations, i.e., quantum noise, between B’s preparation and A’s measurement. □

Shared QRFs correspond to einselection of a preferred basis for decoherence [18,22] at $\mathcal{B}$. We show in Section 4 below that Lemma 2 strongly restricts classical communication, and hence execution of local operations, classical communication (LOCC) protocols [7,34] by spacelike separated observers.

3.2. Reference and Pointer Measurements

The CCD in Figure 3 has a natural physical interpretation: it specifies the hierarchy of logical constraints that must be satisfied to identify the outcome values produced by the operators $M_k^A\dots M_n^A$, and hence the components $k\dots n$ of the pure state ${|B\rangle }^A$, as the observed (effective or virtual) state ${\rho }^S$ of an observed (effective or virtual) system S. The state ${\rho }^S$ of any such S has by convention two components, a time-varying pointer state ${\rho }^P$ that is of interest as a measurement outcome, and the remaining reference state ${\rho }^R$ that by remaining fixed over the macroscopic time required for multiple cycles of pointer measurements enables the re-identification of the single, fixed system S with pointer state ${\rho }^P$. The pointer state ${\rho }^P$ here includes not just the traditional “pointer(s)” of S, but also any adjustable “settings” of S that may vary during a sequence of measurements. The reference state ${\rho }^R$, in contrast, specifies the fixed properties of the system S that fix its identity and hence allow re-identification over time. If S is a macroscopic item of apparatus, for example, these include both the exterior size, shape, color, brand name, and location required to pick the apparatus out, e.g., by visual search, from the cluttered background of the laboratory as a whole, as well as the internal structural and functional properties that enable it to serve as a measurement device, i.e., as a QRF [10].

Following the notation of [6], we indicate by $\left\{M_i^P\right\}$ and $\{M_j^R\}$ the disjoint subsets of $M_k^A\dots M_n^A$ that measure ${\rho }^P$ and ${\rho }^R$, respectively. Call the dimensions of these components $N^P+N^R=N^S$. As ${\rho }^R$ serves as a fixed reference, clearly $\forall i,j,[M_i^P,M_j^R]=0$. Pointer state measurements, however, generically do not commute; adjustable apparatus settings, in particular, are useful only to the extent that they do not commute with pointer readings. Hence generically, $\exists i,j,[M_i^P,M_j^P]\ne 0$. Call the set of mutually-commuting subsets of $\left\{M_i^P\right\}$, and hence of classifiers ${\mathcal{A}}_i^P$, $\left\{P_i\right\}$; in this case a state ${\rho }_i^S$ is computed by a CCD over $R{P}_i$. This decomposition is shown in a simplified notation in Figure 4. Clearly under these conditions the joint state ${\rho }^S$ must be separable as ${\rho }^R{\rho }^{P_i}$, i.e., the system components R and P must be mutually decoherent.

3.3. Sequential Pointer Measurements Induce Decoherence

State transitions ${\mathcal{G}}_{ij}:{\rho }_i^S\left(t\right)\to {\rho }_j^S(t+\Delta t)$, although associative and invertible, in general do not commute, and have a set of multiple identities; hence they can be represented as elements of a groupoid [35,36] $(\left\{{\mathcal{G}}_{ij}\right\},\circ )$ such that ${\mathcal{G}}_{ij}\circ {\mathcal{G}}_{ji}\ne {\mathcal{G}}_{ji}\circ {\mathcal{G}}_{ij}$ if and only if $[M_i^P,M_j^P]\ne 0$ [6]. The action of $(\left\{{\mathcal{G}}_{ij}\right\},\circ )$ on this set of system states, indexed by a macroscopic discrete time $\tau$, is illustrated in Figure 5 (for the formal definition of the action of a groupoid on a set, see, e.g., ([36], Section 10.4)).

A reference state ${\rho }^R$ computed by a CCD R from the outcome values of a set of operators $M_j^R$ is, effectively, a logical constraint on the identities of the qubits $q_j$ that the $M_j^R$ measure. Hence we have:

Lemma 3.

In any system $AB$ characterized by (2), fixing a reference state ${\rho }^R$ over a macroscopic time interval τ locally breaks the $S_N$ symmetry of the holographic screen $\mathcal{B}$ encoding the eigenvalues of $H_{AB}$.

Proof. 

Suppose the $M_j^R$ measure the states of $N^R=n-k$ qubits as shown in Figure 3; we can neglect P and assume that the other qubits constitute the environment and are swap-symmetric. Holding ${\rho }^R$ fixed for $\tau$ is holding the $N^R$ outcomes of the $M_j^R$ fixed for $\tau$; $\forall j,M_j^R|q_j\left(t\right)\rangle =|1\rangle$ or $|-1\rangle$ for t within $\tau$. This cannot be guaranteed if $q_j$ is swapped for some environmental $q_i$ with an unconstrained state; hence any such swap must be forbidden by a “selection rule.” This breaks the $S_N$ symmetry on $\mathcal{B}$. □

Lemma 3 is in fact obvious: the CCD R assigns each of the physical degrees of freedom $q_j$ a specific role in the computation of ${\rho }^R$, one that an arbitrary qubit in an arbitrary state cannot satisfy. The qubits $q_j$ are classically phase-locked by R, while the phases of the environmental qubits can vary freely, preserving their swap symmetry. The CCD R effectively divides $\mathcal{B}$ into two (not necessarily simply connected) regions, one in which the qubits are classically phase-correlated and the other in which they are not. Any such division induces decoherence between non-swap-symmetric and swap-symmetric qubits. These conditions equally hold for any CCD measuring a pointer state ${\rho }^{P_i}$.

Lemma 3 associates decoherence with system identification as a necessary prerequisite of pointer-state measurement. As Zurek emphasized ([22] p. 1794),

[T]he formulation of the measurement problem and its resolution through the appeal to decoherence require a universe split into systems. Yet, it is far from clear how one can define systems given an overall Hilbert space ‘of everything’ and the total Hamiltonian.

Subsequent work demonstrated that no preferred decomposition of an overall Hilbert space or its Hamiltonian could legitimately be assumed a priori [37,38], rendering all formulations of decoherence that assumed an a priori $B=SE$ decomposition circular (see [24,25,26,27] for relevant discussion). By characterizing all observations as mediated by a holographic screen $\mathcal{B}$, the GHP localizes the $B=SE$ decomposition to the observer’s QRFs [5,6]. All systems S and states ${\rho }^S$ are, therefore, virtual in the precise sense of computational processes implemented on underlying, observationally inaccessible hardware [39]: the observer A itself with its Hamiltonian $H_A$.

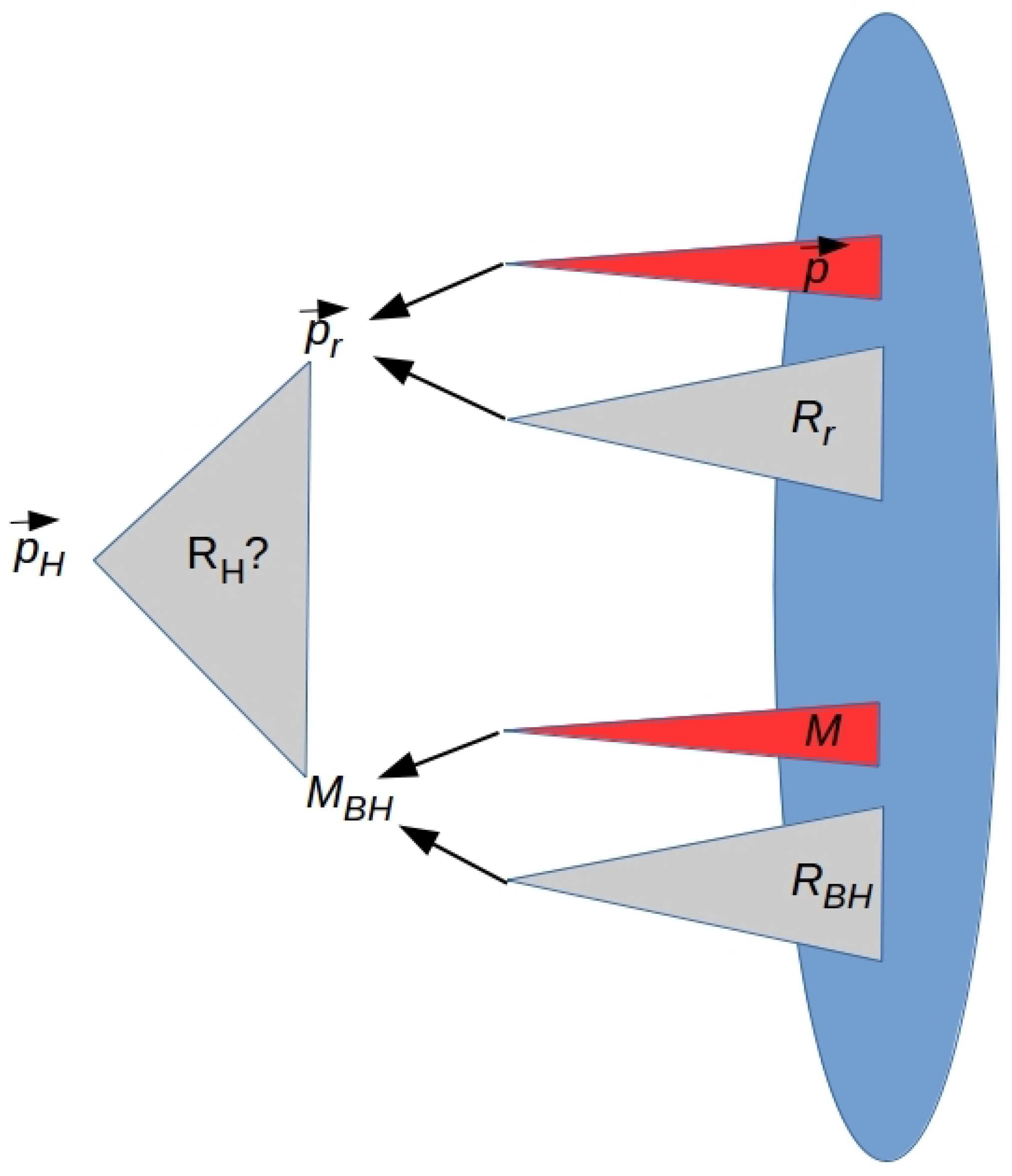
3.4. Example: Mass and Hawking Radiation QRFs for a BH

Suppose A employs a local QRF $R_{BH}$ (e.g., a local sample of the ambient photon field) to measure both the position x and the mass M of a distant BH B and a particle detector $R_r$ to measure the momentum $\overrightarrow{p}$ of one or more quanta of radiation. Her task, familiar from discussions of horizon complementarity [40] and the firewall paradox [15], is to determine whether her local quantum r is a Hawking quantum $r_H$ from B (see [11,12,13,14] for relevant discussion). As illustrated in Figure 6, answering this question requires a QRF $R_H$ that associates $\overrightarrow{p}$ with an identified Hawking quantum.

Lemma 3 shows that the required $R_H$ cannot be implemented, even in principle: determining that the BH has lost information requires observation over macroscopic time, inducing decoherence on $\mathcal{B}$. Hence not only is A prevented by $\mathcal{B}$ from obtaining information about the BH entanglement entropy $\mathcal{S}\left(B\right)$ (Lemma 1); she cannot obtain entanglement information about identified systems if distinct QRFs are required for their identification. The entanglement entropy $\mathcal{S}\left(\right|B>|r>)$ is, in particular, experimentally inaccessible even in principle. Horizon complementarity is, therefore, not required to prevent observations of no-cloning violations by Hawking quanta; such observations cannot be made because the QRF needed to identify an observable BH as the source of the quanta is unavailable. Thought experiments in which observers measure entanglement entropies before and after falling into a BH, as employed in, e.g., [15], are unrealizable even in principle.

The limitation imposed by Lemma 3 generalizes, via the ER = EPR hypothesis, to any system with a spatially-distributed purifier, e.g., an “octopus” BH topologically connected to its entangled Hawking quanta by ER bridges [11,41]. The complete system state is pure but unobservable in principle, as the QRFs required to localize the spatially-distributed components would induce decoherence separately on each component. This problem of QRF-induced decoherence in spatially-distributed purifiers is similarly relevant to treatments of potential entanglement effects surviving the inflationary epoch, e.g., [42,43,44,45]. Bell-type communication protocols, e.g., [46,47,48,49], circumvent this problem by employing classical communication, treated as an a priori preferred QRF, to provide localization information as discussed in Section 4 below.

3.5. Computation and Memory Costs Induce Coarse-Graining

Provided their intermediate states are not recorded to a persistent, classical memory, logically reversible computations can in principle be performed without net energetic cost; logically irreversible computations, in contrast, cost at least ln2 $k_{B}T$ per bit [50,51]. What is of interest in practice, however, is the incremental cost of computation, including the cost of writing intermediate states to a classical memory, even if the computational step is to be reversed later. An observation can only be considered to have been “made” if the result is written to a classical memory from which it can later reported, e.g., classically communicated to another observer [52]. A system S can, in particular, only be regarded as “observed” at a time t if its reference state ${\rho }^R\left(t\right)$ is written to a classical memory from which it can be reported. System identification over macroscopic $\tau$ clearly requires writing to and reading from such a memory as discussed further in Section 6 below.

The free energy required to fund the incremental cost of computing and recording must be supplied by what Landauer [50] called the “non-information-bearing degrees of freedom” of the computer and/or its environment, even if this free energy is repaid in part later. Viewed on the output side, i.e., in terms of A’s action on B, these non-information-bearing degrees of freedom exhaust the waste heat generated by the computing and recording processes. This distinction between information-bearing and non-information-bearing degrees of freedom breaks $S_N$ symmetry as discussed above. As shown in [6], this symmetry breaking can be expressed thermodynamically as the requirement that ${\beta }^R,{\beta }^P>{\beta }^E\ge$ ln 2, where ${\beta }^E$ is the efficiency of the operators $M_k^E$ acting on E. The environment E provides, in other words, the incremental free energy required to irreversibly identify R and measure P. The fuel value ${\beta }^E{k}_{B}T$ is independent of the bit value (+1 or −1) of the outcome; hence these outcomes are “non-information-bearing” for the computation implemented by $H_A$. They therefore retain full permutation symmetry, justifying the trace over their joint state.

Any classical computation can be performed reversibly, e.g., with Toffoli gates, and any reversible computation can be performed with some unitary operator [46]. The only obligate classical steps in computing either ${\rho }^R$ or ${\rho }^{P_j}$ are, therefore, the initial step of writing the “input” outcomes of the $M_j^R$ and the selected $M_i^P$ onto the relevant classifiers and the final step of writing the time-stamped joint state specification ${\rho }^{R{P}_j}$ on a classical memory. The criterion of classicality for the memory is operational: the time-stamped state specification must be reportable at any later time without disturbing other processes. For a perfectly efficient system, the free energy required to write each (Reference, Pointer) outcome ${\rho }^{R{P}_j}$ to memory is, therefore:

$$\Delta H_j\ge \ln 2(N^R+N^P+N^{\rho }+N^{\tau })k_{B}T,$$

(3)

where $N^R+N^P$ is the number of bits required to record the inputs, $N^{\rho }$ is the number of bits required to record ${\rho }^{R{P}_j}$, $N^{\tau }$ is the number of bits required to record the timestamp. This incremental $\Delta H_j$ must be supplied by E during each interval ${\tau }_j$, so (3) places a lower limit $N^E\ge N^R+N^P+N^{\rho }+N^{\tau }$ on the number of qubits of E and therefore on the total area $A\left(\mathcal{B}\right)$ of the holographic screen $\mathcal{B}$. In any realistic system thermodynamic efficiency is less than ideal; hence ${\beta }^E>$ ln2 and $A\left(\mathcal{B}\right)$ is correspondingly larger.

As $N^R+N^P$ remains fixed, $\Delta H_j$ is minimized as $N^{\rho }+N^{\tau }\to 0$, i.e., as classical memory is coarse-grained relative to $\mathcal{B}$. We can, therefore, generically expect QRFs to encode high redundancy over states ${|B\rangle }^A$ mapped to the same ${\rho }^{R{P}_j}$, i.e., we can expect any CCD implementing a QRF to include logical OR gates and hence to lose information. Optimal coarse-graining jointly minimizes the cost of memory and the cost of redundancy. Furthermore, any QRF that is coarse-grained engenders redundancy and can be considered as a quantum error correcting code (QECC) [46]. This is relevant to the discussion in Section 3.4 above: a QEEC can be used to reconstruct local effective field theory observables, which as pointed out in [53], are applicable to BH states whose entanglement entropy falls short of saturating the Bekenstein-Hawking bound. Such local observables are designed to protect coherence in the Hilbert space of codes by correcting errors due to the emission of Hawking quanta, by entangling radiation within other regions of Hilbert space and inducing entanglement swaps that increase the entanglement entropy of the BH interior over time. As discussed in Section 3.4 above, such postulated entanglement swaps are unobservable even in principle.

4. Reference Frame Induced Entanglement

Communication protocols that employ shared entanglement depend on shared QRFs, e.g., shared z-axis QRFs for $s_z$ measurements [8]. This suggests that the shared entanglement is in fact induced by the shared QRFs, a suggestion consistent with the general observer-dependence of entanglement [37,38].

Consider a Bell protocol described in the lab frame, as shown in Figure 7. An entangled state is distributed from a source to Alice and Bob, who remain spacelike-separated throughout the protocol’s operation. They are free to adjust their detector settings during the interval $\Delta t_{set}$. Following data processing (the interval $\Delta t_{proc}$), Bob sends his classically-encoded measurement outcomes to Alice via a classical channel. Alice can then compute the joint statistics, obtaining a Bell-inequality violation and hence an observation of entanglement at $t_{meas}$. Alice’s ability to compute the joint statistics, and hence to observe entanglement, critically depends on two assumptions. First, Alice must know the code that Bob employs to encode his results; effectively, they must “speak the same language”. Second, the communication from Bob to Alice must be classical, i.e., must not involve a quantum measurement [7]. If the communication is not considered classical, i.e., if Bob sends Alice a QRF with which he is entangled, Alice must identify the transmitted QRF in order to measure its state, inducing decoherence as discussed in Section 3.4 above. These two assumptions are operationally equivalent: Alice scrambling Bob’s message by decohering a transmitted quantum state has the same effect as Alice scrambling Bob’s classical coding scheme by employing, e.g., an obsolete one-time pad. In either case, Alice does not “understand” Bob’s encoded results and her subsequent statistical analysis is meaningless [33].

The assumption of classical communication is, effectively, the assumption of a preferred pointer measurement that returns the content of the communicated message without requiring prior identification, via a separate measurement, of the physical medium, i.e., the QRF, via which the message has been transmitted. Alice, in other words, does not have to identify Bob to receive his message, just as Wigner does not, in his famous thought experiment, have to identify his friend to receive his friend’s observational outcomes [54]. Hence assuming classical communication is assuming an a priori shared QRF [8]. This breaks the free-choice symmetry across $\mathcal{B}$ as discussed in Section 2.3 above; if $\mathcal{B}$ is considered a qubit array as in Figure 3, the assumption of classical communication is the assumption that A and B use identical z-axis QRFs on a subset of qubits as confirmed by Lemma 2 above. Call this subset of qubits $message$; the observed states ${|message\rangle }^A$ and ${|message\rangle }^B$ are superdeterministically correlated. Choosing a decomposition that identifies the shared QRFs shows that $|message\rangle ={|message\rangle }^{AB}$ is a single pure state. That such a pure state exists is the operational meaning of the requirement that Alice and Bob “share a language” for classical communication.

Redescribing the Bell protocol in the frame of the entangled state, as illustrated in Figure 8, makes both the shared QRF and its entangled state manifest. Hence we have:

Theorem 1.

Sharing entanglement requires shared entanglement.

Proof. 

Spacelike-separated Alice and Bob can observe entanglement only if they can compare their observational outcomes. By Lemma 2, this requires an a priori shared QRF. Classical transfer of a QRF also requires an a priori shared QRF [8]; hence the shared QRF can only be shared as an entangled state. □

Superdeterminist correlations, i.e., absence of free choice of QRFs, is a general feature of LOCC communication protocols. In the Bell protocol, Alice’s response to the bit string received from Bob is predetermined by the requirement of a shared QRF. Other protocols superdetermine the “choices” made during $\Delta t_{set}$, and hence the outcomes observed. Entanglement-enabled secure communication protocols, for example, require Alice and Bob to deploy QRFs and execute measurement on an otherwise-uncharacterized qubit in the order specified by the protocol. These protocols avoid decoherence, and hence enable quantum communication, by rendering Alice’s and Bob’s QRFs effectively entangled for the duration of the protocol. Here again, avoiding decoherence is equivalent, operationally, to sharing a language in which, e.g., protocol instructions are classically communicated.

The special role played by classical communication in LOCC protocols has been investigated previously in extended Wigner’s friend experiments in which the outcomes of classical communication between pairs of “observers” and “friends” are contrasted with the outcomes of quantum measurements of “friends” by “observers” [55,56]. These experiments have been interpreted as showing, subject to an assumption of no superdeterminism, that observed events cannot be regarded as observer-independent. By treating all observed events as relative to observer-implemented QRFs, we show here that the assumption of classical communication between observers, widely regarded as physically inconsequential prior to [55,56], is to enforce local superdeterminism.

5. Reference Frame Induced Contextuality

Contextuality and entanglement are conceptually equivalent [57]. For a fixed P, switching between QRFs over $M_j^R$ and $M_k^T$, where $[M_j^R,M_k^T]\ne 0$ for at least one pair $j,k$ induces contextuality, i.e., no non-contextual probability distribution consistent with the Kolmogorov axioms and hence with Dutch-book coherence can be defined over the combined set of outcomes [6,33].

Consistent with the findings of [55,56], no Kolmogorov-consistent, non-contextual probability distribution can be defined over the combined outcomes of Alice’s and Bob’s observations unless it can be demonstrated, for the relevant P, and for R and T the QRFs deployed by Alice and Bob, respectively, that $\forall j,k,[M_j^R,M_k^T]=0$. This cannot, however, be demonstrated by any observer of Alice and Bob, as no such observer has, by Lemma 1, access to the internal Hamiltonians $H_{\mathrm{Alice}}$ or $H_{\mathrm{Bob}}$.

This result can be stated in more formal terms of undecidability.

Theorem 2.

Whether arbitrarily-chosen QRFs R and T compute the same function f is finite Turing undecidable.

Proof. 

Let f designate the function computed by R, i.e., the function computed by the CCD representing R; we then ask whether T computes this same f. Whether an arbitrarily chosen computer computes any non-trivial function f cannot, however, be decided by any finite Turing machine [58]. Hence whether T computes f is finite Turing undecidable. □

As shown in [33], contextuality induced by non-commuting QRFs renders the Frame problem, the problem of circumscribing the degrees of freedom that do not change their values as the result of an action, e.g., a measurement [59] unsolvable even in domains with small numbers of degrees of freedom (cf. [60]).

Theorems 1 and 2 have as an obvious corollary:

Corollary 1.

Whether two observers share an entangled state is finite Turing undecidable.

Hence whether Alice and Bob have successfully completed a quantum communication protocol is finite Turing undecidable.

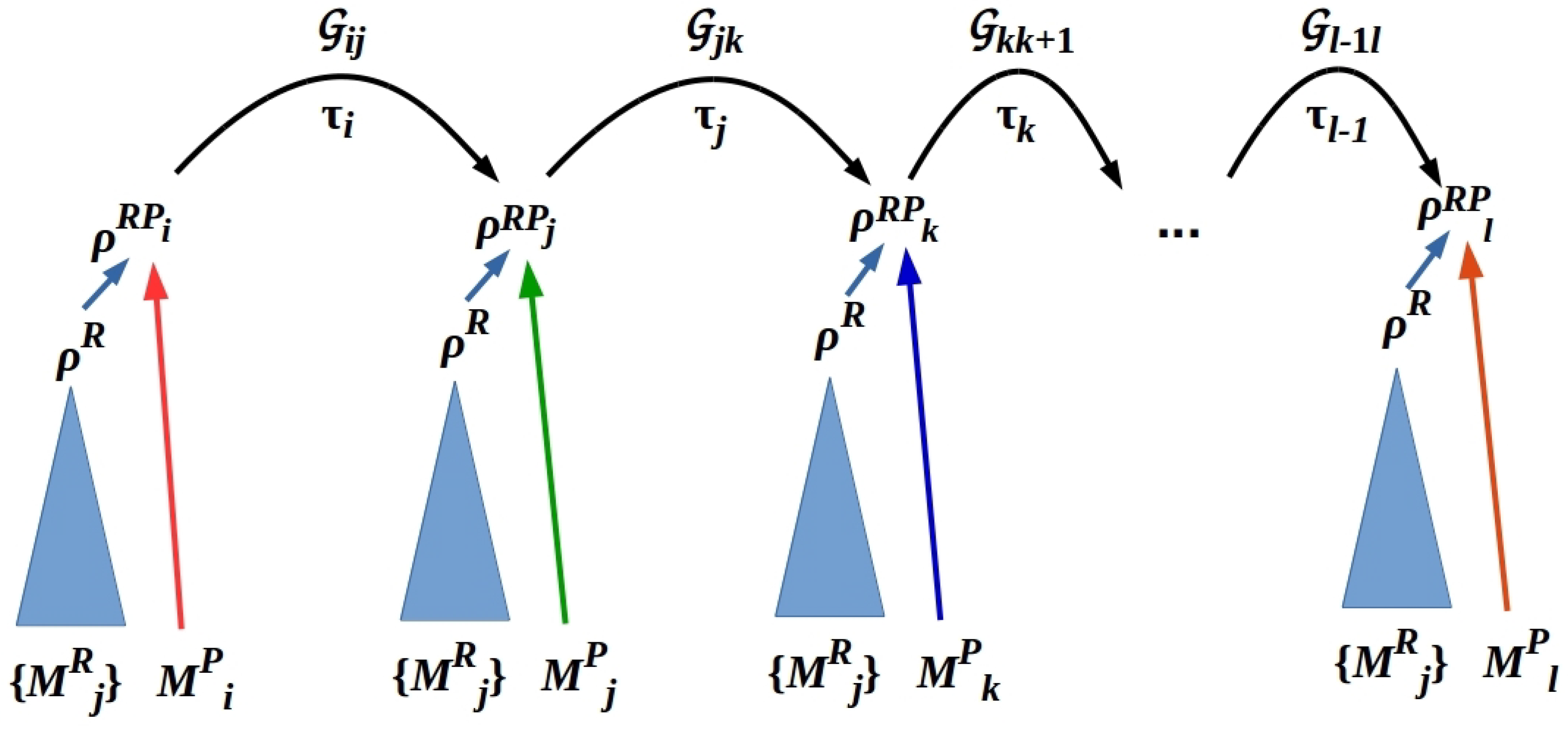
6. Writing and Reading Classical Memories

As noted earlier, a sequence of observations made over macroscopic time is only reportable at some later time if the observations have been recorded on a classical memory. Distinguishing measurements made at different times requires, moreover, some method of distinguishing the memories. We therefore assume that the bit string composing each memory record includes a substring encoding a time stamp ${\tau }_j$, which we take to be generated by the groupoid action of the ${\mathcal{G}}_{ij}$. Considering this classical memory to be implemented by $H_A$ would prima facie require internal decoherence, i.e., disrupt the purity of $|A\rangle$. This can be avoided if A is regarded as writing all classical memories on $\mathcal{B}$. As the result to be written to memory is coarse-grained compared to the input from which it was generated (Section 3.5), only a relatively small number of qubits on $\mathcal{B}$ need be devoted to memory.

Reversing the arrows in a CCD yields the dual construction, a cone diagram (CD) with the single source classifier the limit over the bottom-level classifiers [32]. A CD can be constructed to encode any finite bit string on an underlying bit array, i.e., to write any finite bit string to memory. Regarding each memory bit as a preparation instruction for a corresponding qubit on $\mathcal{B}$, we can represent a memory-write operation to $\mathcal{B}$ as in Figure 9.

Reading the memory reverses the arrows on the memory-write CD $W_{jj}$ to a CCD, i.e., a QRF for retrieving the time-stamped value $({\rho }^{R{P}_j},{\tau }_j)$. Writing readable memory records on $\mathcal{B}$ imposes phase correlations across time on $\mathcal{B}$; such correlations obviously further disrupt the $S_N$ symmetry of $\mathcal{B}$. Reading and rewriting memory records also imposes an energetic cost as in Section 3.

7. Conclusions

We have investigated, in this paper, a generalization of the HP in which interactions $H_{AB}$ between finite quantum systems A and B that maintain a separable joint state are represented as exchanges of information across a holographic screen $\mathcal{B}$. While the role of $\mathcal{B}$ is ancillary to the action of $H_{AB}$, the permutation symmetry of $\mathcal{B}$ is broken when the internal Hamiltonian $H_A$ is considered to implement QRFs that identify “systems” and measure their states. This symmetry breaking induces decoherence of identified systems by forcing the “environment” that remains to serve as both free energy source and waste heat sink. Observable entanglement, contextuality, and classical memory are, in this representation, logical and temporal relations between QRFs implemented by $H_A$.

It is natural to interpret the holographic screen $\mathcal{B}$ not merely as ancillary, but as a “physical” space, i.e., a stretched horizon, separating A from B. In this context, broken permutation symmetries on $\mathcal{B}$ become broken exchange symmetries between points in the $2+1$ spacetime defined by $(\mathcal{B},\tau )$, $\tau$ a characteristic “macroscopic” time scale for $H_{AB}$ as above (see [61] for details). From A’s observational perspective, exchange-inequivalent regions of $(\mathcal{B},\tau )$ correspond to coarse-grained, decoherent “systems” while exchange-symmetric regions are “empty space” that supplies free energy and exhausts waste heat. That the GHP itself forces these virtual decoherent systems to obey gauge symmetries is shown in [61].

It is tempting to speculate that a third spatial dimension is induced when, but only when, A implements QRFs capable of identifying single systems across time while varying pointer observables such as size, shape, and color, and that inertial mass is a QRF representing the observable response of an identified system to actions by A. Whether the fundamental symmetries of space, time, and matter, or even all of physics can be completely reconstructed “within” an observer A, and hence viewed as a computation implemented by $H_A$, remains to be determined. The fact that physics is done by physicists, systems that appear to interact with their environments via a Hamiltonian of the form (2), suggests that such a reconstruction is possible; possible routes forward are discussed in [62,63,64].

It is, finally, increasingly being suggested that the entropic structure of a BH may be more than a phenomenological correlate of its mass, possibly providing a route toward defining mass [65], specifying nontrivial internal topological structure [11], or even generating the phenomenology of dark energy or dark matter [66]. Theoretical investigation of the QRFs implemented by a BH may, therefore, offer exciting future developments.