Abstract
Aerial images are large-scale and susceptible to light. Traditional image feature point matching algorithms cannot achieve satisfactory matching accuracy for aerial images. This paper proposes a recursive diffusion algorithm, which is scale-invariant and can be used to extract symmetrical areas of different images. This narrows the matching range of feature points by extracting high-density areas of the image and improving the matching accuracy through correlation analysis of high-density areas. Through experimental comparison, it can be found that the recursive diffusion algorithm has more advantages compared to the correlation coefficient method and the mean shift algorithm when matching accuracy of aerial images, especially when the light of aerial images changes greatly.
1. Introduction
In aerial surveying and mapping, scattered aerial images can be spliced into a whole area image through the positioning of the connection points, providing support for the solution of aerial triangulation. In the early days, connection points were manually placed on the ground. The development of image processing technology makes it possible to use the feature points of an aerial image itself as connection points, which will greatly improve the automation rate of aerial surveying and mapping. However, aerial images have a large scale and are susceptible to changes in airflow and light, which requires the feature point matching algorithm to have strong spatial scale invariance and robustness. In order to meet the above conditions, we presented a recursive diffusion algorithm which is suitable for the extraction of symmetrical areas to promote the matching accuracy of the feature points for aerial images.
Many research studies on the matching of image feature points have been conducted [1,2]. Lowe [3,4,5] proposed the Scale Invariant Feature Transform (SIFT), which converts an image into many local feature vectors. Based on this, many pieces of research on the application and improvement of the SIFT method have been carried out [6,7,8,9,10]. In addition to the SIFT method, the Mean Shift, which is a general non-parametric technique, was introduced in 1975 [11]. Meer et al. [12,13,14] adopted the Mean Shift to analyze complex multimodal feature space and depict clusters of arbitrary shapes. Hu et al. [15] used the Mean Shift to extract the road centerline from images of complex urban areas based on multiple features. Feng et al. [16] detected moving objects in the visual perception network by introducing the Gaussian Mixture Model and Mean Shift algorithm. Yue et al. [17] applied the Mean Shift for multi-level clustering to extract the low-level texture area from distorted building images.
Additionally, Duraisamy et al. [18] proposed a strategy to register 3D LiDAR data with 2D images. Jeong et al. [19,20] developed a matching algorithm suitable for deformable objects. Ma et al. [21,22,23] proposed a variety of feature matching methods to seek reliable correspondences and eliminate the mismatching of feature sets. Abdel-Basset et al. [24] designed a two-level clustering strategy to discover the copy movement forgery in digital images.
Deep learning technology has provided more research points for image processing. The Convolutional Neural Networks (CNNs) were used by Simo-Serra et al. [25] as an alternative to SIFT for the learning and training of a Siamese network. Liu et al. [26] proposed a trained local feature generation method named Deeply Learned Feature Transform (DELFT), which was used to describe image patches through triple convolutional networks and showed good distinctiveness and robustness. Krizhevsky et al. [27] designed a large-scale deep convolutional neural network to handle the classification problem of 1.2 million images with high resolution, obtaining better results than previous studies. Wang et al. [28] adopted the cross-graph convolution for supervised graph correspondence learning. Kluger et al. [29] presented a strong estimator suitable for the fitting of multi-parameter models, and a neural network was introduced to determine the probability of hypothesis selection.
Many researchers have made efforts to improve image feature point matching, but the proposed matching methods have certain limitations, and the matching results are not ideal when used in aerial images. This research aims to develop a scale-invariant and robust method called recursive diffusion algorithm for feature point matching in aerial images, which is unaffected by changes in light and rotation of shooting angles. The rest of this paper is organized as follows: In Section 2, the methodology of the recursive diffusion algorithm is introduced, including the division of density nodes, the marking of high-density nodes, the extraction of high-density areas, and the matching of feature points. The results and discussion of the aerial image feature point matching experiments are demonstrated in Section 3. Section 4 is the main conclusion of this paper.
2. Methodology
The core idea of the recursive diffusion algorithm is to first extract high-density areas with dense feature points in aerial images so as to reduce the feature point matching area from the entire image to a small local area. Then, correlation analysis is performed to restrict the matching range of feature points, which will effectively improve the matching accuracy and greatly reduce algorithm complexity. The recursive diffusion algorithm for image feature point matching includes four main steps: dividing feature point density nodes, marking high-density nodes, extracting high-density areas, and matching feature points, as shown in Figure 1.

Figure 1.
Process of the recursive diffusion algorithm.
2.1. Dividing of Density Nodes
In order to facilitate computer processing, the aerial image needed to be divided into small square units through a grid, as shown in Figure 2. Each grid cell was defined as a feature point density node.

Figure 2.
The division of the feature point density nodes.
The size of the feature point density node is related to the algorithm’s accuracy. The smaller the density node, the more accurate the matching area obtained, and the larger the density node, the rougher the matching area obtained. In actual image processing, too-large or too-small density nodes are not ideal. The appropriate size of the density node was determined according to the size of the Harris operator feature point detection window. When the detection window was a 7 × 7 pixel matrix, multiple experiments were conducted by selecting 10, 20, 40, and 80 pixels as the side length of the density node. Figure 3 shows that when the density node was divided into 10 × 10 pixels or 20 × 20 pixels, the number of feature points in a single density node was too scarce. When the density node was divided into 80 × 80 pixels, the area with low feature point density would also be regarded as a high-density area. Through the comparison of experimental results, selecting 40 × 40 pixels as the density node division standard best reflected the distribution of feature points.


Figure 3.
Division results of different sizes of the feature point density nodes: (a) 10 × 10 pixels; (b) 20 × 20 pixels; (c) 40 × 40 pixels; (d) 80 × 80 pixels.
2.2. Marking of High-Density Nodes
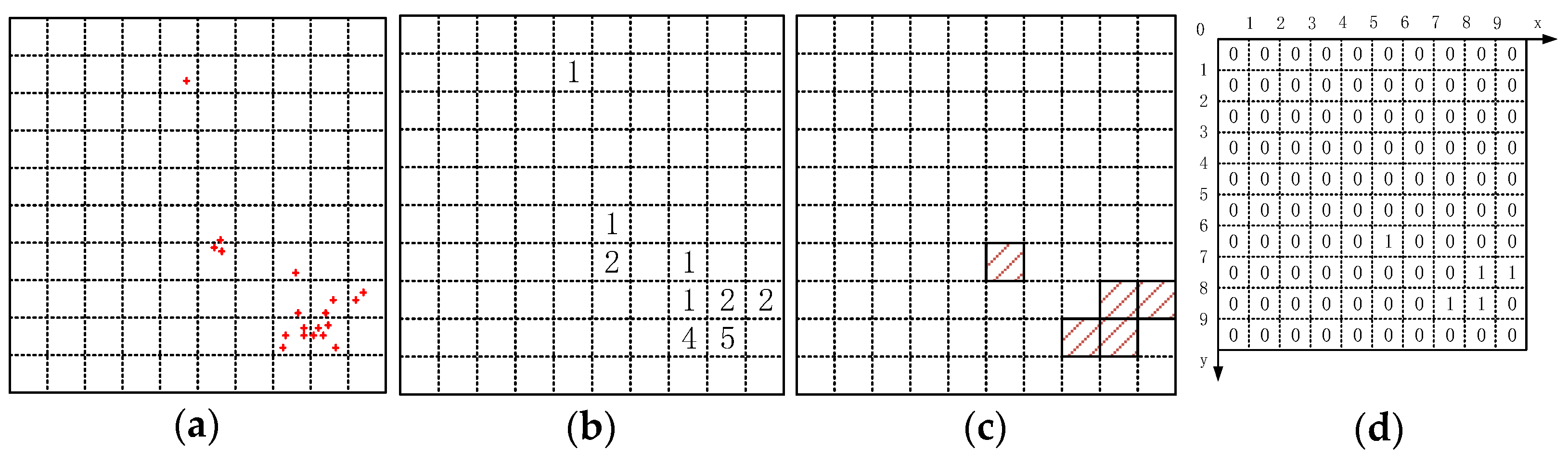
Traverse all the feature point density nodes on the image to count the number of feature points, n, in each density node and set a threshold, t. When n ≥ t, this density node is marked as a high-density node. Otherwise, it was marked as a low-density node. Using t = 1 as an example to mark the high-density nodes, Figure 4a,b can be obtained. The squares represented by diagonal lines in Figure 4c were high-density nodes. For the subsequent algorithm calculation, the high-density node was represented by 1 and the low-density node was represented by 0. The coordinate system as shown in Figure 4d was established with the upper-left corner of the image as the origin of the coordinate system, with the horizontal and vertical axis as the x-axis and y-axis, respectively.
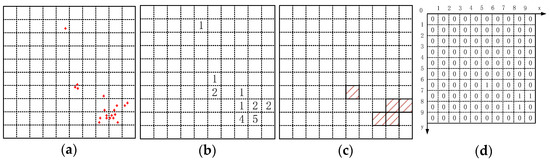
Figure 4.
Marking of high-density nodes: (a) Feature points traversal; (b) The number of feature points in each density node; (c) The high-density nodes; (d) The coordinate system.
2.3. Extracting of High-Density Areas
2.3.1. Data Structure
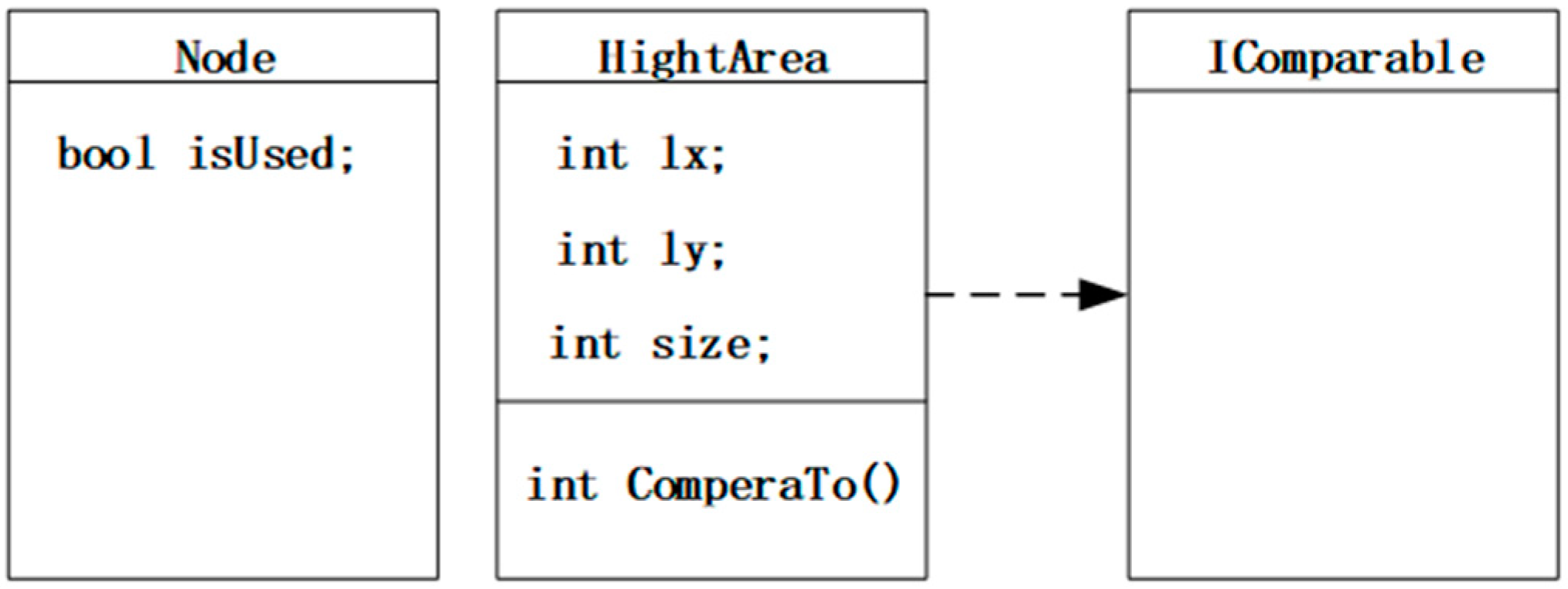
The appropriate data structures should be determined in advance to store the high-density node and high-density area for the recursive diffusion algorithm development. The data structure of the high-density node was represented by a data class called “Node”, in which only a bool variable named “isUsed” was needed to mark whether the node had been used. The high-density area was composed of multiple connected high-density nodes. A data class called “HightArea”, which contained three integer variables and a comparator, was used to represent the data structure of the high-density area. The three integer variables were represented by 1x, 1y, and size. 1x and 1y are used to record the x-axis value and the y-axis value in the upper left corner of the high-density area, respectively. The integer variable size was used to record the number of high-density nodes contained in the high-density area. Additionally, a comparator was needed to compare the size of the high-density areas, which was sorted by the value of the integer variable size from largest to smallest. The algorithm data structures are shown in Figure 5.
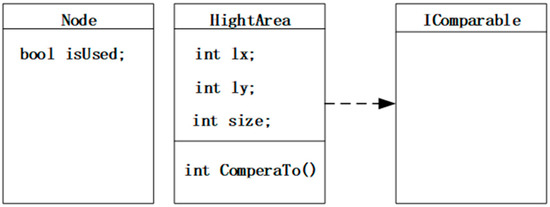
Figure 5.
The algorithm data structures.
2.3.2. Logical Design
Recursion is a process of simplifying a big problem into smaller problems with the same structure. The big problem that needs to be solved is defined as a parent problem, and the simplified small problems are defined as sub-problems. The high-density area extraction in this paper was regarded as the parent problem, and whether the four adjacent nodes of a high-density node are high-density was the sub-problem decomposed from the parent problem. The end condition of the recursion is that there are no unmarked high-density nodes around a high-density node.
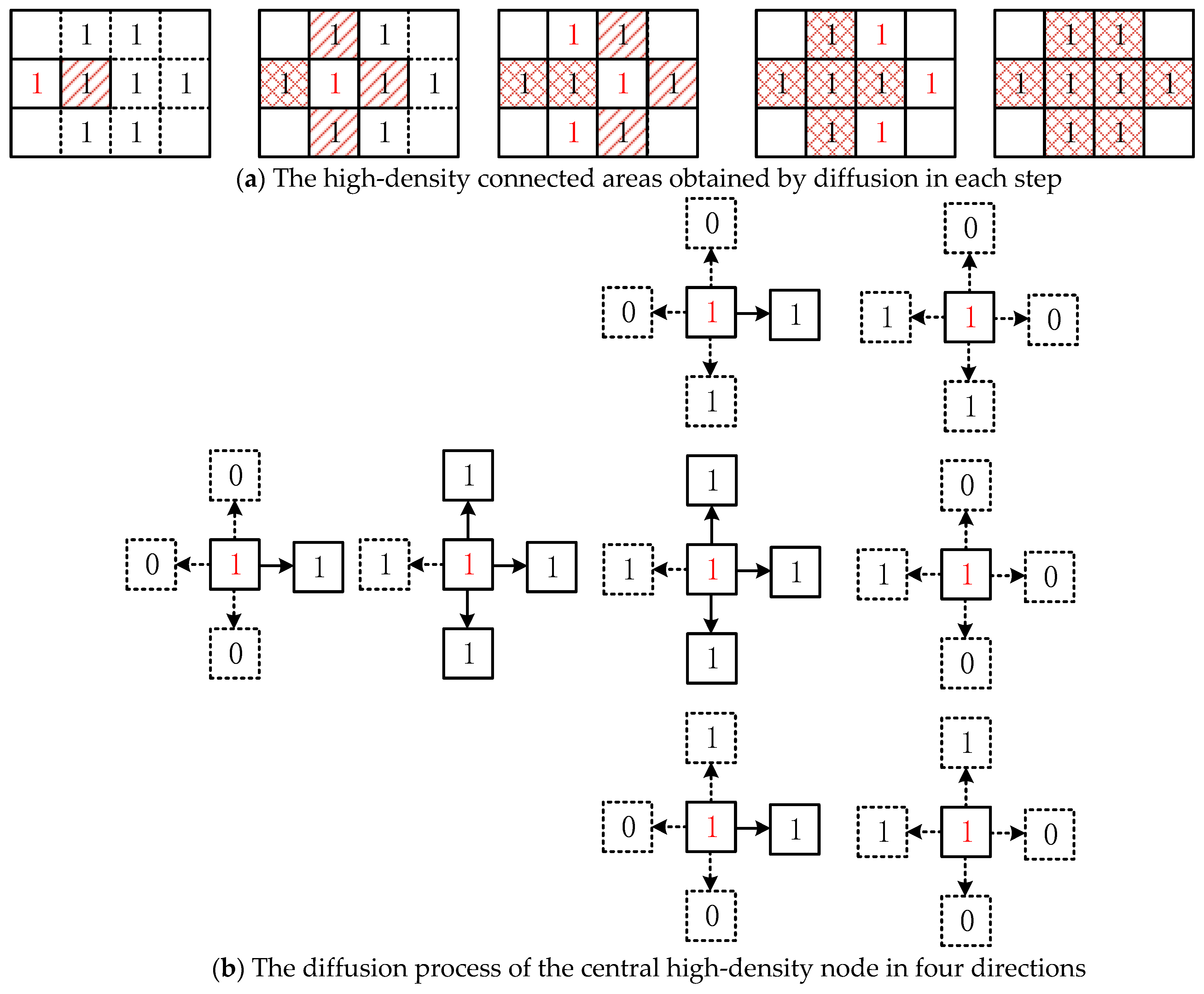
Take the high-density node diffusion process shown in Figure 6 as an example. In Figure 6a, the red 1 represents the current high-density node recursively, and the single slash shading 1 represents the high-density node that has been diffused. Figure 6b describes the diffusion process of the central high-density node in four directions. The 0 in the dashed box represents the low-density node that cannot be diffused, and the 1 in the solid box represents the high-density node that could be diffused. In the same way, the high-density nodes diffused in the previous stage were used as the new central high-density node in the later stage to diffuse in four directions (the diffused high-density node will no longer be diffused twice). When no new central high-density nodes were produced, the entire diffusion process ended and the high-density connected areas were obtained.
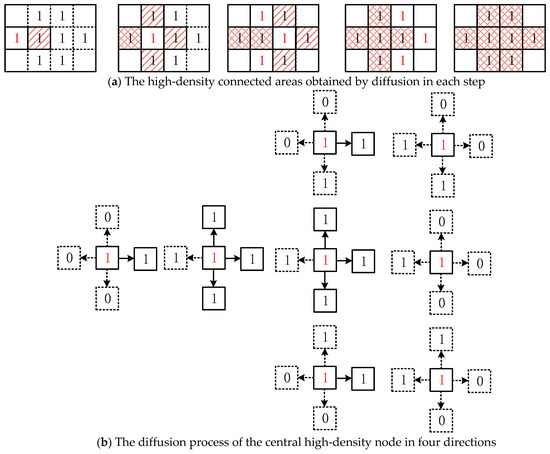
Figure 6.
Process of the high-density node diffusion: (a) The high-density connected areas obtained by diffusion in each step; (b) The diffusion process of the central high-density node in four directions.
2.3.3. Model Construction
Construction of a recursive diffusion function is shown in Equation (1):
where the function represents the diffusion recursive sub-function in which the high-density node moves up, down, left, and right by one step. This movement is expressed using the trinocular equation:
where is the judgment condition of the high-density node, and means that the density node has not been used. If the result of the function is true, continue to recurse with (x,y) as the diffusion center. Otherwise, exit the recursion.
2.3.4. Coordinate Position Update
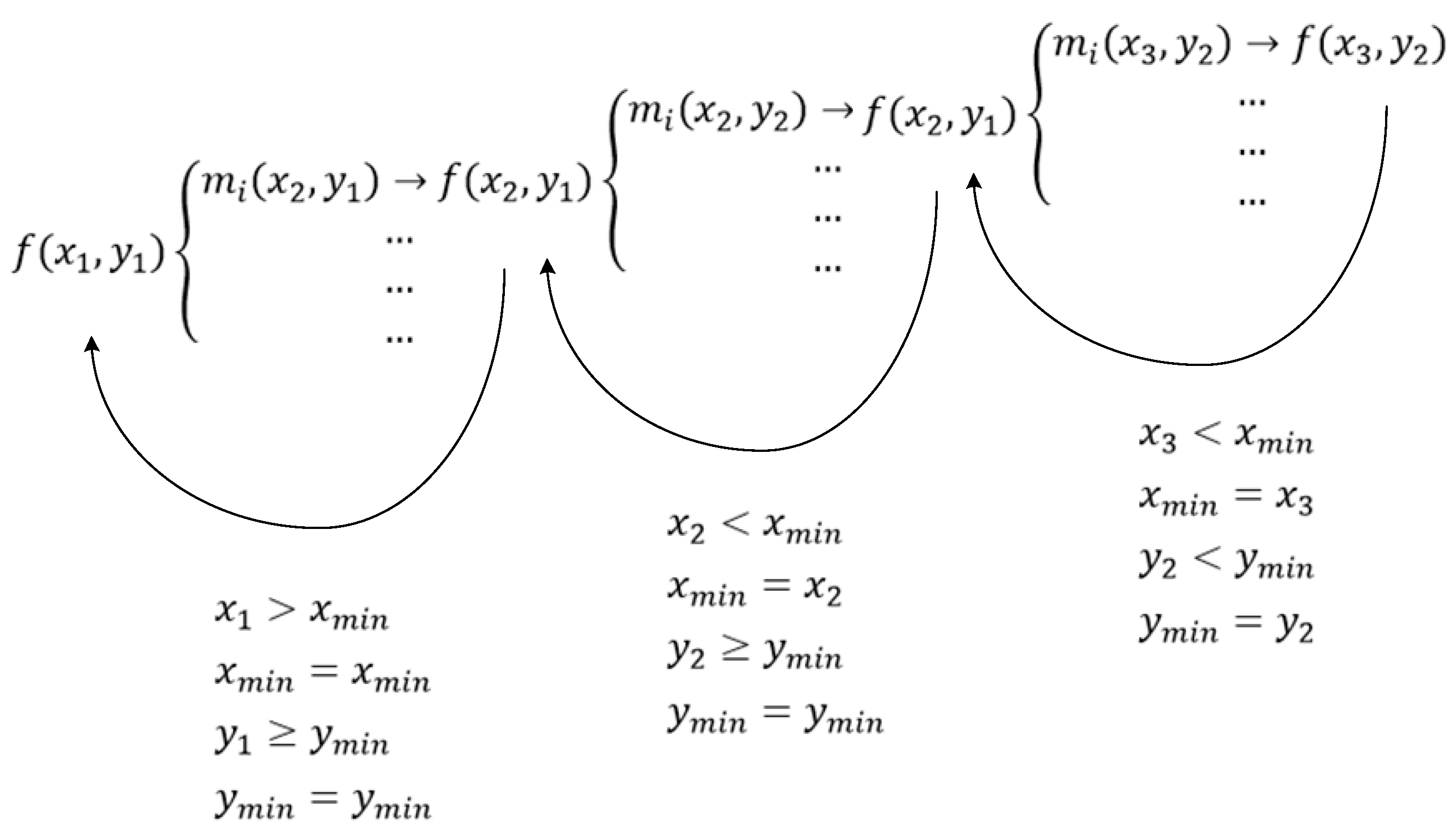
To facilitate the subsequent feature points matching of the high-density area, the coordinates of the upper left corner of the area, namely the smallest x-value component and the smallest y-value component, were selected to represent the distribution position of the area. Taking a branch of the entire recursive diffusion algorithm as an example, the high-density area extraction process is shown in Figure 7. From to is a recursive stacking process. When the function is called for the first time, its sub-process in a certain direction looks for the high-density node that can be diffused. This new high-density node will serve as the diffusion center of the next recursion, and its distribution position will be passed into as an input parameter for a new recursive call. When the recursion proceeds to , no suitable diffusible high-density node can be found anymore, and then the recursion end condition is triggered. In accordance with the order of the arc arrows, the sub-process takes the return value and compares it with step-by-step to update the position coordinates of the high-density area.
Figure 7.
Position coordinates update of the high-density area.
2.4. Matching of Feature Points
The extracted high-density areas contained two pieces of information: position (x, y coordinates) and the number of high-density nodes (size). The high-density areas of the two images that needed to be matched (represented by the left image and the right image) were arranged in their respective queues according to the number of high-density nodes from large to small. Select the first largest high-density area in the queue of the left image to compare with the high-density areas in the queue of the right image. The specific matching steps are as follows:
Step 1: Compare the distribution positions (x,y) of the high-density areas of the left and right images. If the x or y difference between the two areas exceeds half of the side length of the image, exclude them. Otherwise, go to step 2.
Step 2: If the difference in the number of high-density nodes contained in the left and right high-density areas is greater than 2, exclude them. Otherwise, go to step 3.
Step 3: Perform correlation analysis.
With the high-density area distribution positions of the left and right images as the center, spread 40 × 40 pixels around to obtain two corresponding pixel matrices, denoted by X and Y respectively. Calculate the correlation coefficient of X and Y by Equation (3):
where cov(X,Y) is the covariance of the pixel matrices X and Y, and is the standard deviation product of the pixel matrices X and Y.
Step 4: Select a group of high-density areas with the largest correlation coefficient to match the left and right images. The distribution positions difference is the calibration parameter of the left and right images and the calculation equation is as follows:
where and are the x components. and are the y components. is the allowable matching error, and the value set in this paper is 25 pixels.
3. Results and Discussion
3.1. Matching Results of the Diffusion Recursive Algorithm
A group of aerial images over a mine in northwestern China were collected as the experimental object. Before the feature point matching, the image block preprocessing was performed, and the feature points were extracted by the Harris operator. Considering that the light of the collected aerial images changes greatly, the diffusion recursive algorithm proposed in this paper was used to match the feature points of the images by C# language programming.
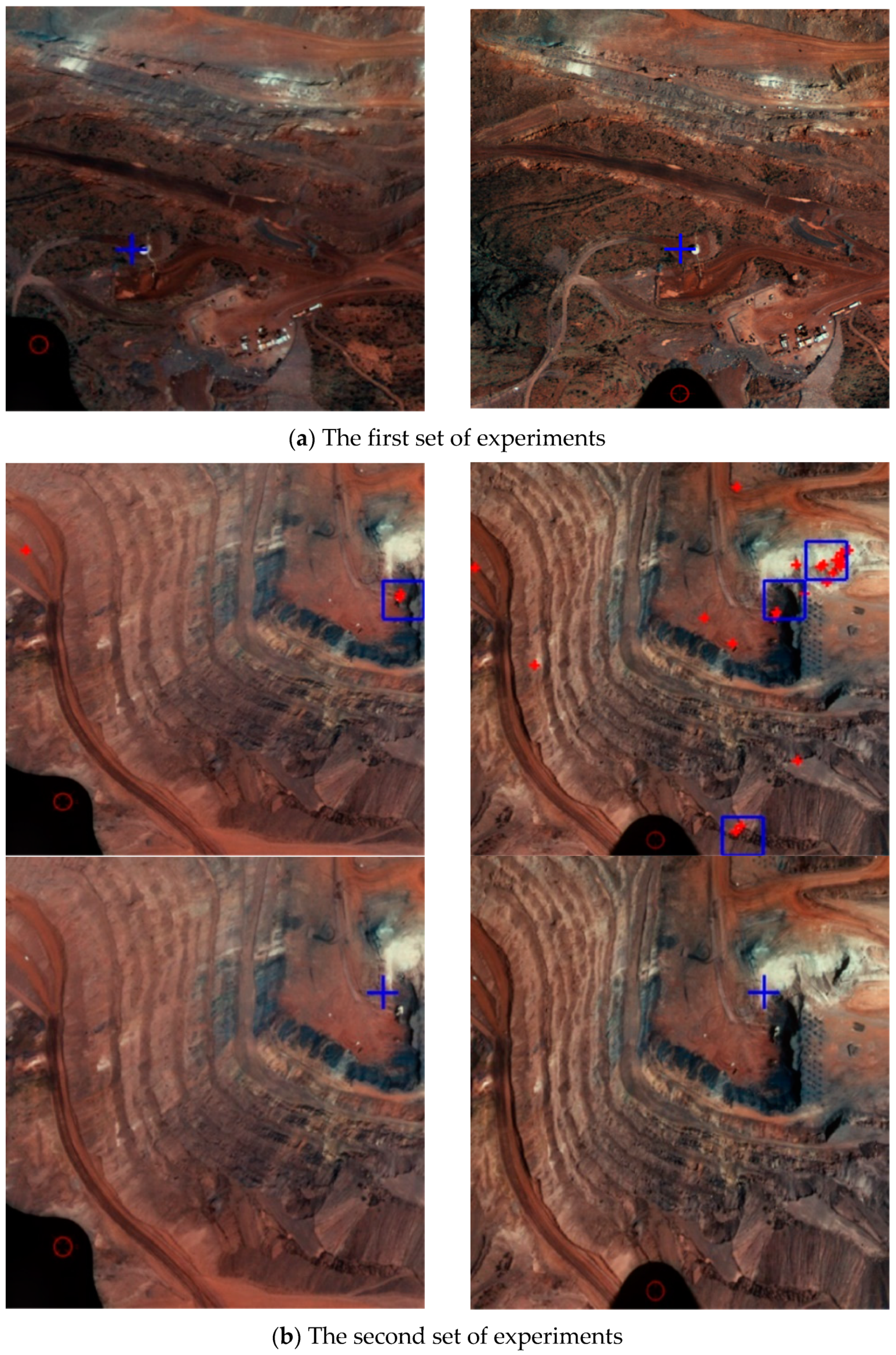
Three sets of representative experimental results are shown in Figure 8, where the red crosshairs represent the feature points of the image, the blue boxes represent the extracted high-density areas, and the blue crosshairs are the matching reference points. It can be found that the recursive diffusion algorithm can deal with the problem of image light changes well, especially in the third set of experiments. The brightness difference in this experiment is obvious, which leads to the different extraction results of high-density areas. However, due to the increase of the correlation analysis of high-density areas, a good matching result is obtained in the end.


Figure 8.
Matching results of the diffusion recursive algorithm: (a) The first set of experiments; (b) The second set of experiments; (c) The third set of experiments.
3.2. Comparison with the Mean Shift Algorithm
The mean shift algorithm was also applied to match the feature points in the third set of experiments, and the results are shown in Figure 9. Through comparison, it can be found that when the light of the image changes significantly, the matching accuracy obtained by the mean shift algorithm is not as good as the recursive diffusion algorithm. The recursive diffusion algorithm has good stability to the light changes of aerial images.

Figure 9.
Matching results of the mean shift algorithm.
3.3. Comparison with the Correlation Coefficient Matching Algorithm
Three sets of comparative experiments with traditional correlation coefficient matching algorithms were carried out, and the results can be seen from Figure 10, Figure 11 and Figure 12. In Figure 10, the correlation coefficient method matches the two feature points with the largest correlation coefficient, but the matching results have obvious errors. The diffusion recursive algorithm can avoid this kind of false matching through the restriction of spatial location. Figure 11 shows the matching results when the correlation coefficient method and the diffusion recursive algorithm are applied to natural environment images with fewer man-made objects. Due to the high similarity between the feature points of natural environment images, the matching effect of the correlation coefficient method is not ideal, but the diffusion recursive algorithm can obtain good matching results. Similarly, when the light changes significantly, the diffusion recursive algorithm has a better matching accuracy than the correlation coefficient method, which can be seen in Figure 12.

Figure 10.
The first set of experiments: (a) Results of the correlation coefficient matching algorithm; (b) Results of the diffusion recursive algorithm.

Figure 11.
The second set of experiments: (a) Results of the correlation coefficient matching algorithm; (b) Results of the diffusion recursive algorithm.


Figure 12.
The third set of experiments: (a) Results of the correlation coefficient matching algorithm; (b) Results of the diffusion recursive algorithm.
3.4. Analysis of Matching Accuracy and Timing Performance
A total of 18 sets of experimental images were selected, and the correlation coefficient method, the mean shift algorithm, and the diffusion recursive algorithm were used respectively to match the feature points of these experimental images. The matching accuracy and timing performance of the three different methods were compared and analyzed. The results are shown in Table 1. Among the 18 sets of experimental images, the number of successful matches using the correlation coefficient method was four sets, and the successful matching rate was only 22.2%. The number of successful matches using the mean shift algorithm was 15 sets, and the successful matching rate was 83.3%. The number of successful matches using the diffusion recursive algorithm was 17 sets, and the successful matching rate was 94.4%. The time-consumption of the correlation coefficient method, the mean shift algorithm, and the diffusion recursive algorithm are 7434 ms, 12,587 ms, and 16,648 ms, respectively, with the Intel Core i7-4720HQ processor. Compared with the other two methods, the diffusion recursive algorithm has no advantage in timing performance. However, when there are high requirements for image matching accuracy, the diffusion recursive algorithm can obtain satisfactory matching results.

Table 1.
The matching accuracy and timing performance of the three different methods.
4. Conclusions
A new feature point matching method named diffusion recursive algorithm has been presented to deal with the problems of large scale and susceptibility to light interference of aerial images. The method mainly includes four steps: dividing of density nodes, marking of high-density nodes, extracting of high-density areas, and matching of feature points. Through the extraction of high-density areas of the image, the feature point matching area is reduced from the entire image to the extracted area. The correlation analysis of high-density areas further restricts the matching range of feature points. The experimental analysis of the collected aerial images shows that the diffusion recursive algorithm is suitable for the feature point matching of aerial images, and it can still obtain good matching accuracy even when the light changes greatly. Compared with the correlation coefficient method and the mean shift algorithm, although the diffusion recursive algorithm has no advantage in timing performance, it has the best matching accuracy and can meet the requirements of high-precision matching.
However, this research still has some limitations. First, the determination of the density node division standard still requires manual calibration, which limits the real-time performance of the diffusion recursive algorithm. In follow-up research, an improvement is needed to expand the applicability of the proposed algorithm. Second, the algorithm is currently suitable for 2D image matching. The feasibility of the algorithm in 3D image matching should be further studied by adding auxiliary technologies such as LiDAR. In addition, when there are higher requirements for image matching accuracy, sub-pixel positioning technology can be introduced to further improve the algorithm.
Author Contributions
Conceptualization, J.S. and X.G.; methodology, J.S.; software, J.S.; validation, W.Z., Y.Z. and J.L.; formal analysis, W.Z.; investigation, Y.Z.; resources, X.G.; data curation, J.L.; writing—original draft preparation, J.S.; writing—review and editing, X.G.; visualization, W.Z.; supervision, Y.Z.; project administration, J.S.; funding acquisition, J.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Major Science and Technology Special Project of the Transportation Department of Jiangsu Province, grant number Z02.
Acknowledgments
The authors acknowledge the financial support from the Major Science and Technology Special Project of the Transportation Department of Jiangsu Province, and the laboratory equipment support from the School of Transportation of Southeast University.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hassaballah, M.; Abdelmgeid, A.A.; Alshazly, H.A. Image Features Detection, Description and Matching. In Image Feature Detectors and Descriptors; Awad, A., Hassaballah, M., Eds.; Springer: Cham, Switzerland, 2016; Volume 630, pp. 11–45. [Google Scholar]
- Chen, L.; Rottensteiner, F.; Heipke, C. Feature detection and description for image matching: From hand-crafted design to deep learning. Geo-Spat. Inf. Sci. 2020. [Google Scholar] [CrossRef]
- Lowe, D.G. Object Recognition from Local Scale-Invariant Features. In Proceedings of the IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; pp. 1150–1157. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Brown, M.; Lowe, D.G. Automatic panoramic image stitching using invariant features. Int. J. Comput. Vis. 2007, 74, 59–73. [Google Scholar] [CrossRef]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the IEEE International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar]
- Dellinger, F.; Delon, J.; Gousseau, Y.; Michel, J.; Tupin, F. SAR-SIFT: A SIFT-Like Algorithm for SAR Images. IEEE Trans. Geosci. Remote Sens. 2015, 53, 453–466. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, S.P.; Wang, Z.F. Multi-focus image fusion with dense SIFT. Inf. Fusion 2015, 23, 139–155. [Google Scholar] [CrossRef]
- Shi, H.T.; Guo, L.; Tan, S.; Li, G.; Sun, J. Improved Parallax Image Stitching Algorithm Based on Feature Block. Symmetry 2019, 11, 348. [Google Scholar] [CrossRef]
- Yang, J.R.; Huang, J.W.; Jiang, Z.Y.; Dong, S.B.; Tang, L.Q.; Liu, Y.P.; Liu, Z.J.; Zhou, L.C. 3D SIFT aided path independent digital volume correlation and its GPU acceleration. Opt. Lasers Eng. 2021, 136, 106323. [Google Scholar] [CrossRef]
- Fukunaga, K.; Hostetler, L.D. The Estimation of the Gradient of a Density Function, with Applications in Pattern Recognition. IEEE Trans. Inf. Theory 1975, 21, 32–40. [Google Scholar] [CrossRef]
- Comaniciu, D.; Meer, P. Mean shift: A robust approach toward feature space analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 603–619. [Google Scholar] [CrossRef]
- Subbarao, R.; Meer, P. Nonlinear Mean shift over Riemannian Manifolds. Int. J. Comput. Vis. 2009, 84, 1–20. [Google Scholar] [CrossRef]
- Anand, S.; Mittal, S.; Tuzel, O.; Meer, P. Semi-Supervised Kernel Mean Shift Clustering. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 1201–1215. [Google Scholar] [CrossRef]
- Hu, X.Y.; Li, Y.J.; Shan, J.; Zhang, J.Q.; Zhang, Y.J. Road Centerline Extraction in Complex Urban Scenes From LiDAR Data Based on Multiple Features. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7448–7456. [Google Scholar]
- Feng, Q.; Wang, T.J.; Liu, F.; Lin, H.F. Research on multi-camera information fusion method for intelligent perception. Multimed. Tools Appl. 2018, 77, 15003–15026. [Google Scholar]
- Yue, L.W.; Li, H.J.; Zheng, X.W. Distorted Building Image Matching with Automatic Viewpoint Rectification and Fusion. Sensors 2019, 19, 5205. [Google Scholar] [CrossRef]
- Duraisamy, P.; Jackson, S. Orthogonal Detection and Registration for Microstructures Images. In Proceedings of the IEEE International Conference on Communication and Computer Vision, Coimbatore, India, 20–21 December 2013; pp. 1–6. [Google Scholar]
- Won, I.; Jeong, J.; Yang, H.; Kwon, J.; Jeong, D. Adaptive Image Matching Using Discrimination of Deformable Object. Symmetry 2016, 8, 68. [Google Scholar] [CrossRef]
- Jeong, J.; Won, I.; Yang, H.; Lee, B.; Jeong, D. Deformable Object Matching Algorithm Using Fast Agglomerative Binary Search Tree Clustering. Symmetry 2017, 9, 25. [Google Scholar] [CrossRef]
- Ma, J.Y.; Zhou, H.B.; Zhao, J.; Gao, Y.; Jiang, J.J.; Tian, J.W. Robust Feature Matching for Remote Sensing Image Registration via Locally Linear Transforming. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6469–6481. [Google Scholar] [CrossRef]
- Ma, J.Y.; Jiang, J.J.; Zhou, H.B.; Zhao, J.; Guo, X.J. Guided Locality Preserving Feature Matching for Remote Sensing Image Registration. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4435–4447. [Google Scholar] [CrossRef]
- Ma, J.Y.; Zhao, J.; Jiang, J.J.; Zhou, H.B.; Guo, X.J. Locality Preserving Matching. Int. J. Comput. Vis. 2019, 127, 512–531. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Manogaran, G.; Fakhry, A.E.; El-Henawy, I. 2-Levels of clustering strategy to detect and locate copy-move forgery in digital images. Multimed. Tools Appl. 2020, 79, 5419–5437. [Google Scholar] [CrossRef]
- Simo-Serra, E.; Trulls, E.; Ferraz, L.; Kokkinos, I.; Fua, P.; Moreno-Noguer, F. Discriminative Learning of Deep Convolutional Feature Point Descriptors. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 11–18 December 2015; pp. 118–126. [Google Scholar]
- Liu, Z.S.; Li, Z.X.; Zhang, J.Y.; Liu, L.G. Euclidean and Hamming Embedding for Image Patch Description with Convolutional Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 1145–1151. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Wang, R.Z.; Yan, J.C.; Yang, X.K. Learning Combinatorial Embedding Networks for Deep Graph Matching. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 3056–3065. [Google Scholar]
- Kluger, F.; Brachmann, E.; Ackermann, H.; Rother, C.; Yang, M.Y.; Rosenhahn, B. CONSAC: Robust Multi-Model Fitting by Conditional Sample Consensus. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 4633–4642. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).