A Note on Effects of Generalized and Extended Uncertainty Principles on Jüttner Gas
Abstract
1. Introduction
2. The Maxwell–Boltzmann and Jüttner Distribution Functions
2.1. Non-Relativistic Gas
2.2. Relativistic Gas
3. Generalized Uncertainty Principle, Partition and Distribution Functions
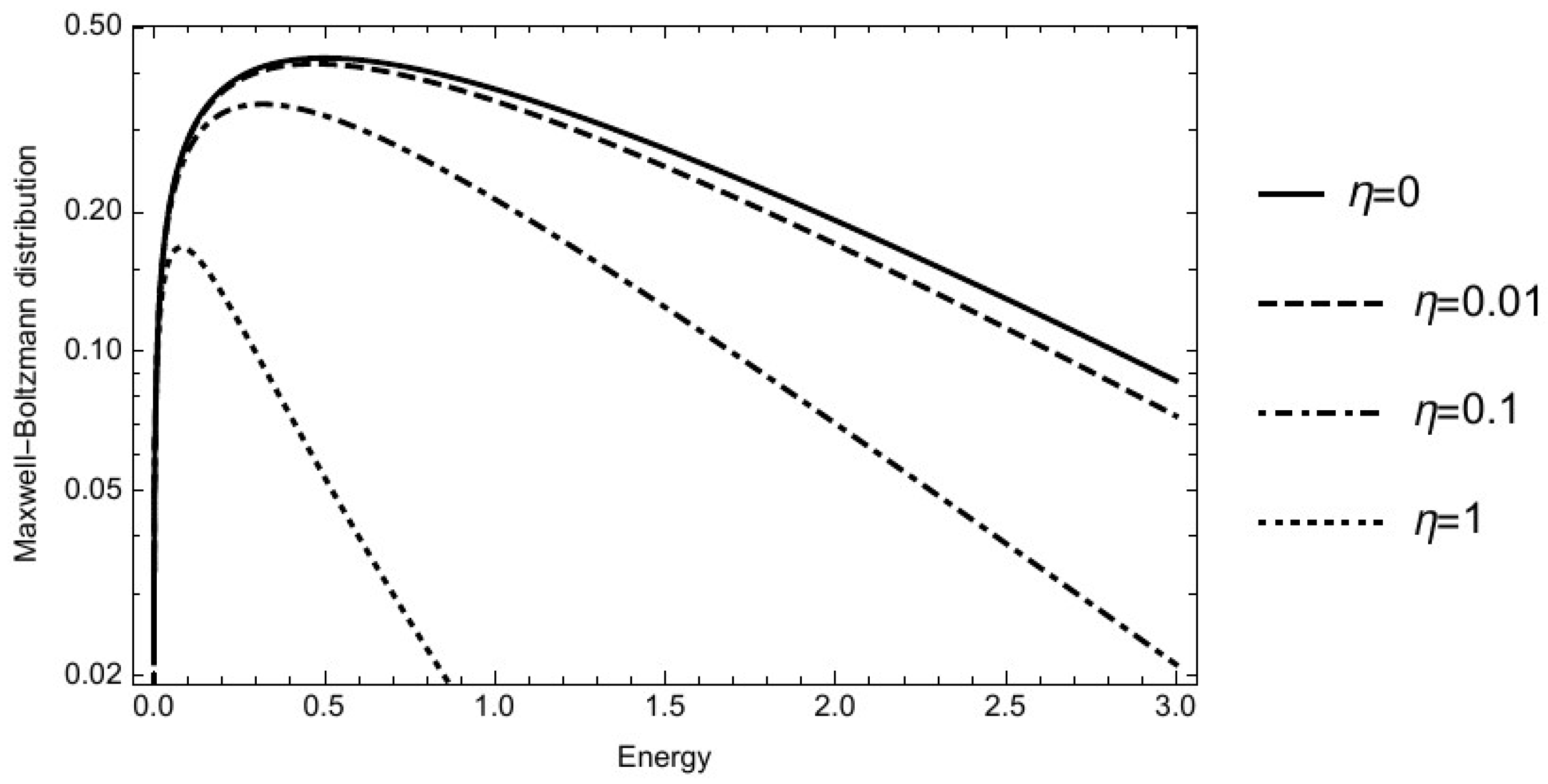
3.1. Maxwell–Boltzmann Statistics
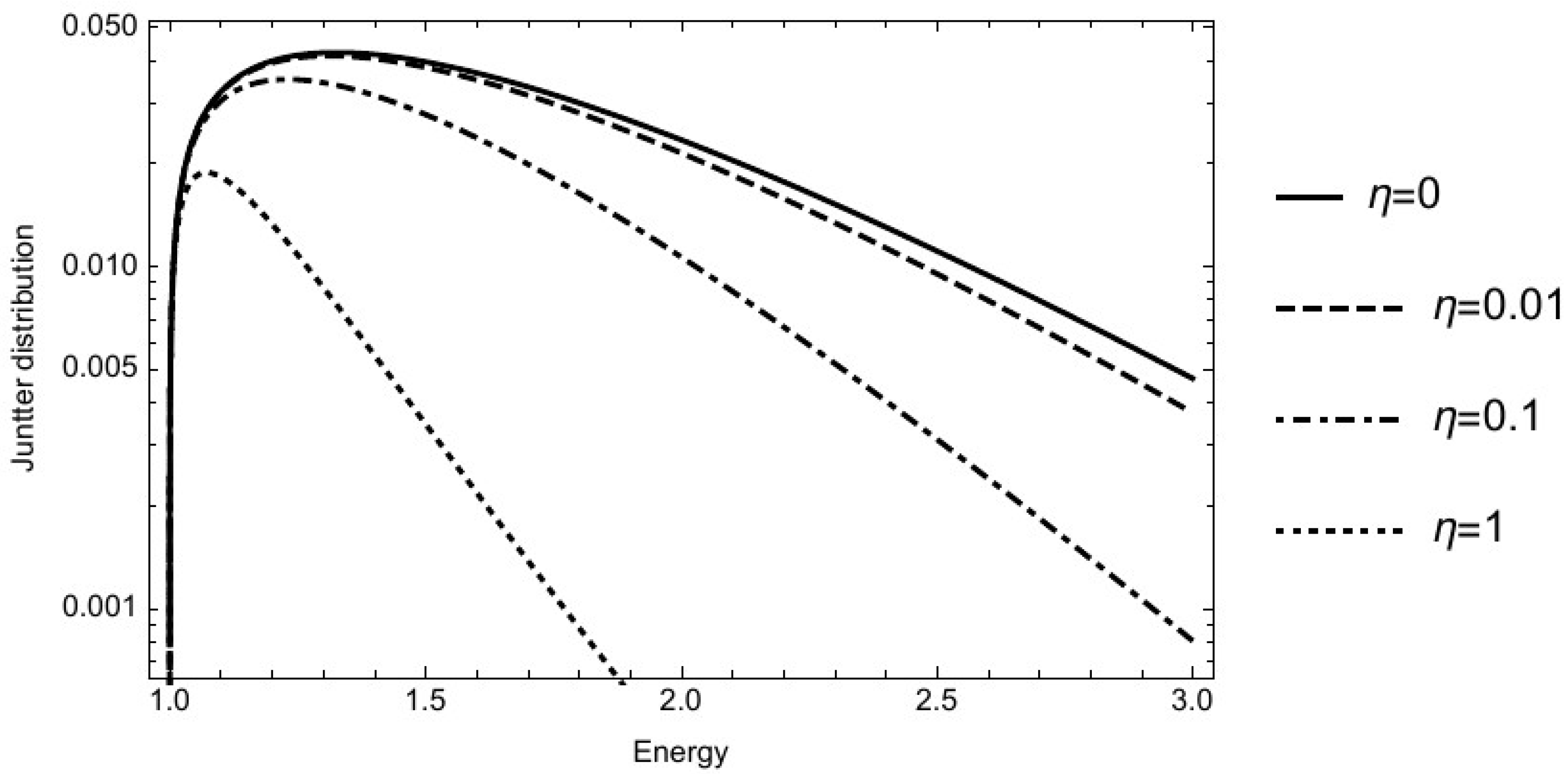
3.2. Jüttner Statistics
4. Extended Uncertainty Principle, Partition and Distribution Functions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Maggiore, M. Quantum groups, gravity, and the generalized uncertainty principle. Phys. Rev. D 1994, 49, 5182–5187. [Google Scholar] [CrossRef]
- Konishi, K.; Paffuti, G.; Provero, P. Minimum physical length and the generalized uncertainty principle in string theory. Phys. Lett. B 1990, 234, 276–284. [Google Scholar] [CrossRef]
- Scardigli, F. Generalized uncertainty principle in quantum gravity from micro-black hole gedanken experiment. Phys. Lett. B 1999, 452, 39–44. [Google Scholar] [CrossRef]
- Maggiore, M. The algebraic structure of the generalized uncertainty principle. Phys. Lett. B 1993, 319, 83–86. [Google Scholar] [CrossRef]
- Casadio, R.; Scardigli, F. Generalized Uncertainty Principle, Classical Mechanics, and General Relativity. Phys. Lett. B 2020, 807, 135558. [Google Scholar] [CrossRef]
- Vagenas, E.C.; Ali, A.F.; Hemeda, M.; Alshal, H. Linear and quadratic GUP, Liouville theorem, cosmological constant, and Brick Wall entropy. Eur. Phys. J. C 2019, 79, 398. [Google Scholar] [CrossRef]
- Shababi, H.; Chung, W.S. On the two new types of the higher order GUP with minimal length uncertainty and maximal momentum. Phys. Lett. B 2017, 770, 445–450. [Google Scholar] [CrossRef]
- Shababi, H.; Pedram, P.; Chung, W.S. On the quantum mechanical solutions with minimal length uncertainty. Int. J. Mod. Phys. A 2016, 31, 1650101. [Google Scholar] [CrossRef]
- Pedram, P. Generalized uncertainty principle and the conformally coupled scalar field quantum cosmology. Phys. Rev. D 2015, 91, 063517. [Google Scholar] [CrossRef]
- Snyder, H.S. Quantized Space-Time. Phys. Rev. 1947, 71, 38–41. [Google Scholar] [CrossRef]
- Yang, C.N. On Quantized Space-Time. Phys. Rev. 1947, 72, 874. [Google Scholar] [CrossRef]
- Feng, Z.; Li, H.L.; Zu, X.T.; Yang, S.Z. Quantum corrections to the thermodynamics of Schwarzschild–Tangherlini black hole and the generalized uncertainty principle. Eur. Phys. J. C 2016, 76, 1–9. [Google Scholar] [CrossRef]
- Tawfik, A.M.; Diab, A.M. A review of the generalized uncertainty principle. Rep. Prog. Phys. 2015, 78, 126001. [Google Scholar] [CrossRef] [PubMed]
- Khalil, M.M. Some Implications of Two Forms of the Generalized Uncertainty Principle. Adv. High Energy Phys. 2014, 2014, 1–8. [Google Scholar] [CrossRef]
- Miraboutalebi, S.; Matin, L.F. Thermodynamics of canonical ensemble of an ideal gas in presence of Planck-scale effects. Can. J. Phys. 2015, 93, 574–579. [Google Scholar] [CrossRef]
- Ali, A.F.; Moussa, M. Towards Thermodynamics with Generalized Uncertainty Principle. Adv. High Energy Phys. 2014, 2014, 1–7. [Google Scholar] [CrossRef]
- Abbasiyan-Motlaq, M.; Pedram, P. The minimal length and quantum partition functions. J. Stat. Mech. Theory Exp. 2014, 2014, P08002. [Google Scholar] [CrossRef]
- Das, S.; Vagenas, E.C. Universality of Quantum Gravity Corrections. Phys. Rev. Lett. 2008, 101, 221301. [Google Scholar] [CrossRef]
- Rama, S.K. Some consequences of the generalised uncertainty principle: Statistical mechanical, cosmological, and varying speed of light. Phys. Lett. B 2001, 519, 103–110. [Google Scholar] [CrossRef]
- Kempf, A. Non-pointlike particles in harmonic oscillators. J. Phys. A Math. Gen. 1997, 30, 2093–2101. [Google Scholar] [CrossRef]
- Park, D. Generalized uncertainty principle and d -dimensional quantum mechanics. Phys. Rev. D 2020, 101, 106013. [Google Scholar] [CrossRef]
- Bosso, P.; Das, S.; Pikovski, I.; Vanner, M.R. Amplified transduction of Planck-scale effects using quantum optics. Phys. Rev. A 2017, 96, 023849. [Google Scholar] [CrossRef]
- Pikovski, I.; Vanner, M.R.; Aspelmeyer, M.; Kim, M.; Brukner, Č. Probing Planck-scale physics with quantum optics. Nat. Phys. 2012, 8, 393–397. [Google Scholar] [CrossRef]
- Das, S.; Mann, R.B. Planck scale effects on some low energy quantum phenomena. Phys. Lett. B 2011, 704, 596–599. [Google Scholar] [CrossRef]
- Luciano, G.G.; Petruzziello, L. GUP parameter from maximal acceleration. Eur. Phys. J. C 2019, 79, 283. [Google Scholar] [CrossRef]
- Gecim, G.; Sucu, Y. The GUP effect on Hawking radiation of the 2 + 1 dimensional black hole. Phys. Lett. B 2017, 773, 391–394. [Google Scholar] [CrossRef]
- Husain, V.; Seahra, S.S.; Webster, E.J. High energy modifications of blackbody radiation and dimensional reduction. Phys. Rev. D 2013, 88, 024014. [Google Scholar] [CrossRef]
- Chemissany, W.; Das, S.; Ali, A.F.; Vagenas, E.C. Effect of the Generalized Uncertainty Principle on post-inflation preheating. J. Cosmol. Astropart. Phys. 2011, 2011, 017. [Google Scholar] [CrossRef]
- Sprenger, M.; Nicolini, P.; Bleicher, M. Neutrino oscillations as a novel probe for a minimal length. Class. Quantum Gravity 2011, 28, 235019. [Google Scholar] [CrossRef]
- Zhu, T.; Ren, J.-R.; Li, M.-F. Influence of generalized and extended uncertainty principle on thermodynamics of FRW universe. Phys. Lett. B 2009, 674, 204–209. [Google Scholar] [CrossRef]
- Mureika, J. Extended Uncertainty Principle black holes. Phys. Lett. B 2019, 789, 88–92. [Google Scholar] [CrossRef]
- Chung, W.S.; Hassanabadi, H. Quantum mechanics on (anti)-de Sitter background. Mod. Phys. Lett. A 2017, 32, 1850150. [Google Scholar] [CrossRef]
- Mignemi, S. Extended Uncertainty Principle and the Geometry of (anti)-de sitter space. Mod. Phys. Lett. A 2010, 25, 1697–1703. [Google Scholar] [CrossRef]
- Bambi, C.; Urban, F.R. Natural extension of the generalized uncertainty principle. Class. Quantum Gravity 2008, 25, 095006. [Google Scholar] [CrossRef]
- Hinrichsen, H.; Kempf, A. Maximal localization in the presence of minimal uncertainties in positions and in momenta. J. Math. Phys. 1996, 37, 2121–2137. [Google Scholar] [CrossRef]
- Kempf, A. On quantum field theory with nonzero minimal uncertainties in positions and momenta. J. Math. Phys. 1997, 38, 1347–1372. [Google Scholar] [CrossRef]
- Da̧browski, M.P.; Wagner, F. Extended uncertainty principle for rindler and cosmological horizons. Eur. Phys. J. C 2019, 79, 716. [Google Scholar] [CrossRef]
- Lambiase, G.; Scardigli, F. Lorentz violation and generalized uncertainty principle. Phys. Rev. D 2018, 97, 075003. [Google Scholar] [CrossRef]
- Walker, D.; Fremlin, J.H. Acceleration of Heavy Ions to High Energies. Nat. Cell Biol. 1953, 171, 189–191. [Google Scholar] [CrossRef]
- Kalaydzhyan, T. Testing general relativity on accelerators. Phys. Lett. B 2015, 750, 112–116. [Google Scholar] [CrossRef]
- Camelia, G.A. Quantum-Spacetime Phenomenology. Living Rev. Relativ. 2013, 16, 5. [Google Scholar] [CrossRef] [PubMed]
- Chang, L.N.; Minic, D.; Okamura, N.; Takeuchi, T. Effect of the minimal length uncertainty relation on the density of states and the cosmological constant problem. Phys. Rev. D 2002, 65, 125028. [Google Scholar] [CrossRef]
- Fityo, T. Statistical physics in deformed spaces with minimal length. Phys. Lett. A 2008, 372, 5872–5877. [Google Scholar] [CrossRef]
- Wang, P.; Yang, H.; Zhang, X. Quantum gravity effects on statistics and compact star configurations. J. High Energy Phys. 2010, 2010, 1–17. [Google Scholar] [CrossRef]
- Hossenfelder, S. Minimal Length Scale Scenarios for Quantum Gravity. Living Rev. Relativ. 2013, 16, 1–90. [Google Scholar] [CrossRef]
- Shalyt-Margolin, A.E.; Tregubovich, A.Y. Deformed density matrix and generalized uncertainty relation in thermodynamics. Mod. Phys. Lett. A 2004, 19, 71–81. [Google Scholar] [CrossRef]
- Shalyt-Margolin, A.E.; Suarez, J.G. Quantum mechanics at planck’s scale and density matrix. Int. J. Mod. Phys. D 2003, 12, 1265–1278. [Google Scholar] [CrossRef]
- Vakili, B.; Gorji, M.A. Thermostatistics with minimal length uncertainty relation. J. Stat. Mech. Theory Exp. 2012, 2012, P10013. [Google Scholar] [CrossRef]
- Mirtorabi, M.; Miraboutalebi, S.; Masoudi, A.; Matin, L.F. Quantum gravity modifications of the relativistic ideal gas thermodynamics. Phys. A Stat. Mech. Appl. 2018, 506, 602–612. [Google Scholar] [CrossRef]
- Chung, W.S.; Hassanabadi, H. Extended uncertainty principle and thermodynamics. Int. J. Mod. Phys. A 2019, 34, 1950041. [Google Scholar] [CrossRef]
- Nozari, K.; Etemadi, A. Minimal length, maximal momentum, and Hilbert space representation of quantum mechanics. Phys. Rev. D 2012, 85, 104029. [Google Scholar] [CrossRef]
- Jüttner, F. Das Maxwellsche Gesetz der Geschwindigkeitsverteilung in der Relativtheorie. Ann. Phys. 1911, 34, 856. [Google Scholar] [CrossRef]
- Pathria, R.K.; Beale, P.D. Statistical Mechanics, 3rd ed.; Elsevier: Burlington, MA, USA, 2011. [Google Scholar]
- Pauli, W. The Theory of Relativity; Pergamon Press: London, UK, 1958. [Google Scholar]
- Horwitz, L.; Schieve, W.; Piron, C. Gibbs ensembles in relativistic classical and quantum mechanics. Ann. Phys. 1981, 137, 306–340. [Google Scholar] [CrossRef]
- de Groot, S.R.; van Leeuwen, W.A.; van Weert, C.G. Relativistic Kinetic Theory—Principles and Applications; North-Holland: Amsterdam, The Netherlands, 1980. [Google Scholar]
- Livadiotis, G. Modeling anisotropic Maxwell–Jüttner distributions: Derivation and properties. Ann. Geophys. 2016, 34, 1145–1158. [Google Scholar] [CrossRef]
- Cubero, D.; Casado-Pascual, J.; Dunkel, J.; Talkner, P.; Hänggi, P. Thermal Equilibrium and Statistical Thermometers in Special Relativity. Phys. Rev. Lett. 2007, 99, 170601. [Google Scholar] [CrossRef] [PubMed]
- Montakhab, A.; Ghodrat, M.; Barati, M. Statistical thermodynamics of a two-dimensional relativistic gas. Phys. Rev. E 2009, 79, 031124. [Google Scholar] [CrossRef] [PubMed]
- Ghodrat, M.; Montakhab, A. Time parametrization and stationary distributions in a relativistic gas. Phys. Rev. E 2010, 82, 011110. [Google Scholar] [CrossRef]
- Dunkel, J.; Talkner, P.; Hänggi, P. Relative entropy, Haar measures and relativistic canonical velocity distributions. N. J. Phys. 2007, 9, 144. [Google Scholar] [CrossRef]
- Kempf, A.; Mangano, G.; Mann, R.B. Hilbert space representation of the minimal length uncertainty relation. Phys. Rev. D 1995, 52, 1108–1118. [Google Scholar] [CrossRef]
- Rastegin, A.E. Entropic Uncertainty Relations for Successive Measurements in the Presence of a Minimal Length. Entropy 2018, 20, 354. [Google Scholar] [CrossRef]
- Tawfik, A.N.; Diab, A.M. Generalized uncertainty principle: Approaches and applications. Int. J. Mod. Phys. D 2014, 23, 1430025. [Google Scholar] [CrossRef]
- O’ Luanaigh, C. Cern. Available online: https://home.cern/news/news/accelerators/first-successful-beam-record-energy-65-tev (accessed on 10 April 2015).
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Zhao, K.; Zhang, Q.; Chini, M.; Wu, Y.; Wang, X.; Chang, Z. Tailoring a 67 attosecond pulse through advantageous phase-mismatch. Opt. Lett. 2012, 37, 3891–3893. [Google Scholar] [CrossRef] [PubMed]
- Walton, D.B.; Rafelski, J. Equilibrium Distribution of Heavy Quarks in Fokker-Planck Dynamics. Phys. Rev. Lett. 2000, 84, 31–34. [Google Scholar] [CrossRef] [PubMed]
- Tirnakli, U.; Borges, E.P. The standard map: From Boltzmann-Gibbs statistics to Tsallis statistics. Sci. Rep. 2016, 6, 23644. [Google Scholar] [CrossRef]
- Parvan, A.S. Equivalence of the phenomenological Tsallis distribution to the transverse momentum distribution of q-dual statistics. Eur. Phys. J. A 2020, 56, 1–5. [Google Scholar] [CrossRef]
- Liu, F.-H.; Gao, Y.-Q.; Li, B.-C. Comparing two-Boltzmann distribution and Tsallis statistics of particle transverse momentums in collisions at LHC energies. Eur. Phys. J. A 2014, 50, 123. [Google Scholar] [CrossRef]
- Si, R.-F.; Li, H.-L.; Liu, F.-H. Comparing Standard Distribution and Its Tsallis Form of Transverse Momenta in High Energy Collisions. Adv. High Energy Phys. 2018, 2018, 1–12. [Google Scholar] [CrossRef]
- Zheng, H.; Zhu, L.; Bonasera, A. Systematic analysis of hadron spectra inp+pcollisions using Tsallis distributions. Phys. Rev. D 2015, 92, 074009. [Google Scholar] [CrossRef]
| HUP | GUP | EUP | |
|---|---|---|---|
| The volume of phase space element | 1 | ||
| Density of States | |||
| Single Partition Function |
| HUP | GUP | EUP | |
|---|---|---|---|
| The volume of phase space element | 1 | ||
| Density of States | |||
| Single Partition Function | when |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moradpour, H.; Aghababaei, S.; Ziaie, A.H. A Note on Effects of Generalized and Extended Uncertainty Principles on Jüttner Gas. Symmetry 2021, 13, 213. https://doi.org/10.3390/sym13020213
Moradpour H, Aghababaei S, Ziaie AH. A Note on Effects of Generalized and Extended Uncertainty Principles on Jüttner Gas. Symmetry. 2021; 13(2):213. https://doi.org/10.3390/sym13020213
Chicago/Turabian StyleMoradpour, Hooman, Sarah Aghababaei, and Amir Hadi Ziaie. 2021. "A Note on Effects of Generalized and Extended Uncertainty Principles on Jüttner Gas" Symmetry 13, no. 2: 213. https://doi.org/10.3390/sym13020213
APA StyleMoradpour, H., Aghababaei, S., & Ziaie, A. H. (2021). A Note on Effects of Generalized and Extended Uncertainty Principles on Jüttner Gas. Symmetry, 13(2), 213. https://doi.org/10.3390/sym13020213






