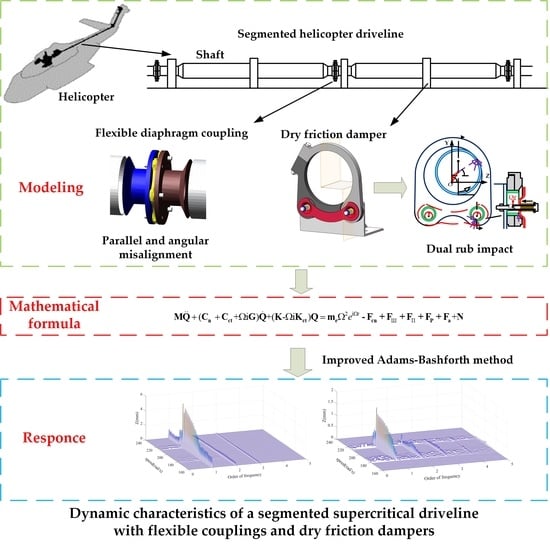
Dynamic Characteristics of a Segmented Supercritical Driveline with Flexible Couplings and Dry Friction Dampers
Abstract
1. Introduction
2. The Mathematical Formulation for Segmented Helicopter Driveline with Flexible Coupling
2.1. Slender Flexible Shaft with Viscous Internal Damping
2.2. Flexible Diaphragm Couplings Subject to Misalignment
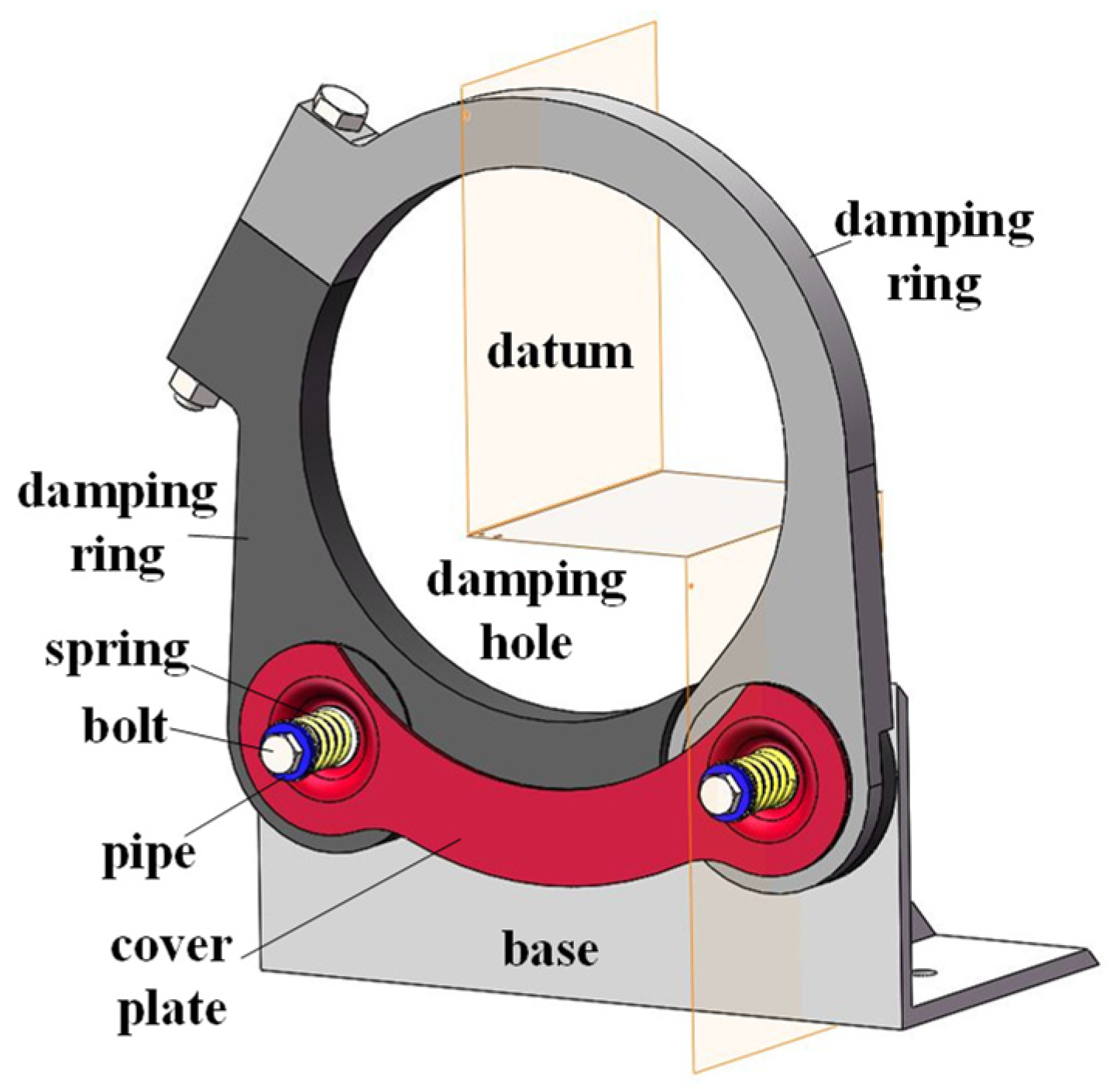
3. Vibration Suppression of the Dry Friction Damper and Equations of Motion
3.1. Multiple Stages
3.2. Dual Rub-Impact Model
3.2.1. The First Rub-Impact with Variable DOFs
3.2.2. Radical Impact Stiffness of the First Rub Impact
- Linearization of the local surface stiffness
- 2.
- Impact stiffness of the damping ring
3.2.3. The Second Rub-Impact with Nonlinear Restricted Stiffness
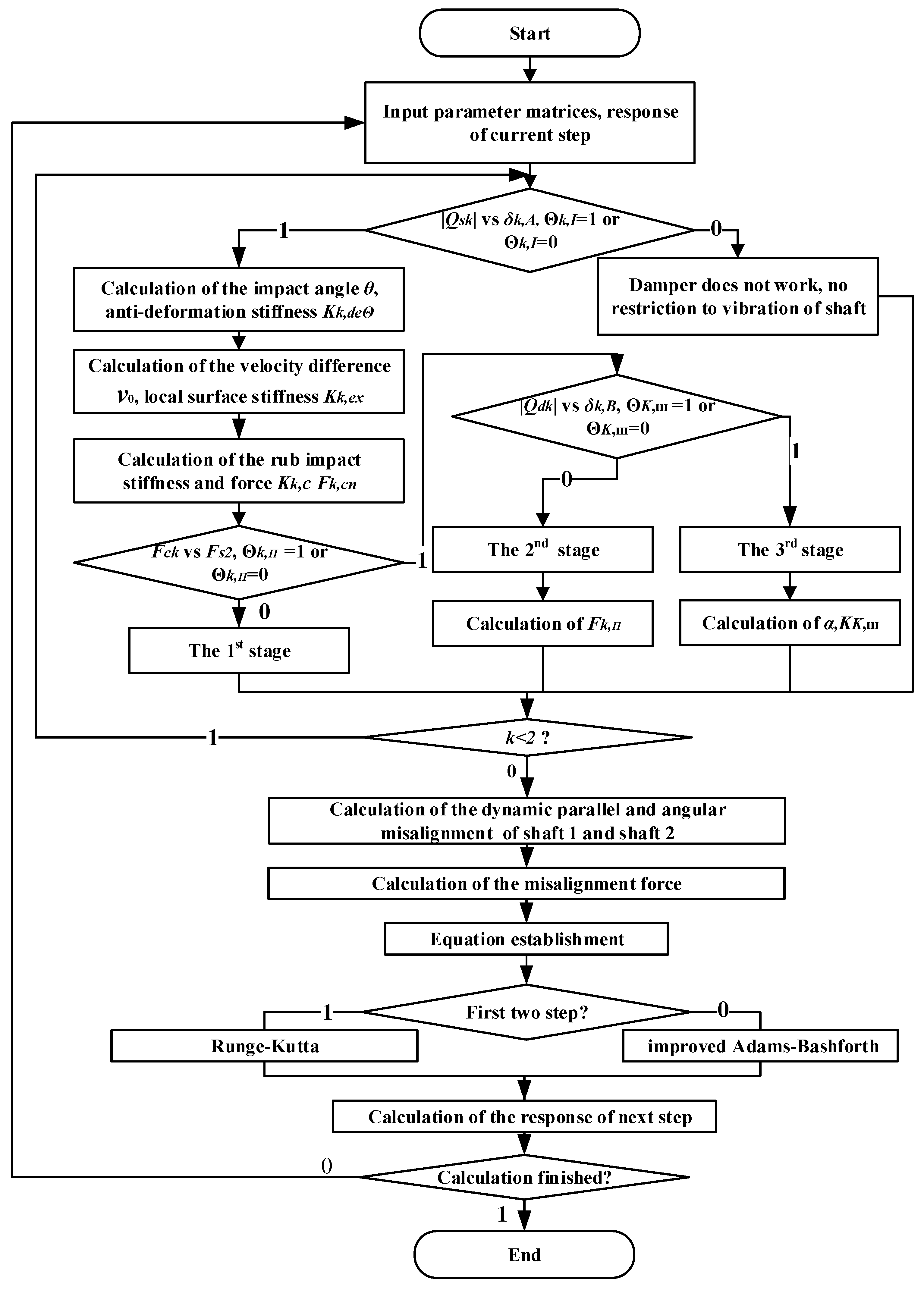
3.3. Equations of Motion
4. Simulations and Results
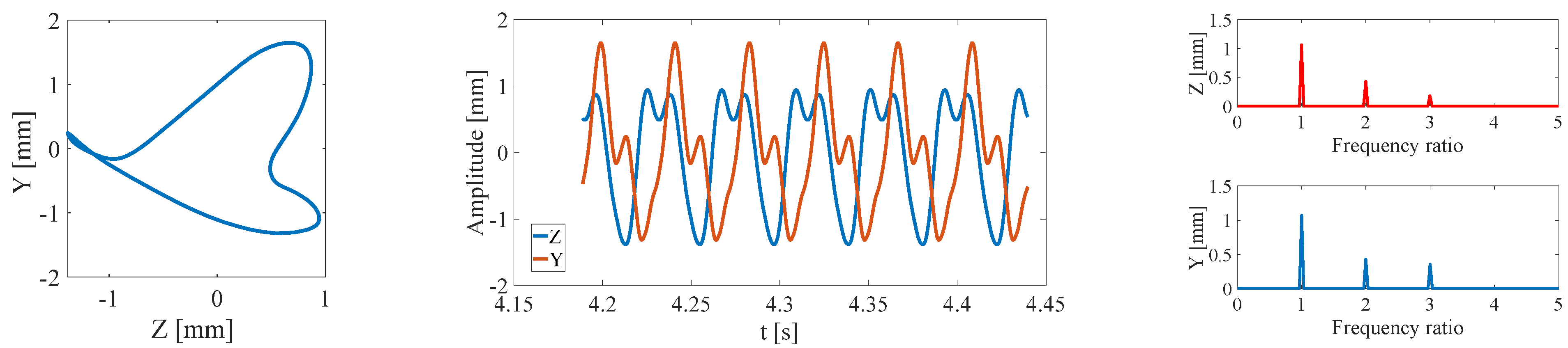
4.1. Dynamics of Multiple Vibration Suppression
4.2. Misalignment Effect of Flexible Diaphragm Coupling
4.2.1. Angular and Parallel Misalignment
4.2.2. Static Misalignment
4.3. Coeffect of Misalignment and Vibration Suppression
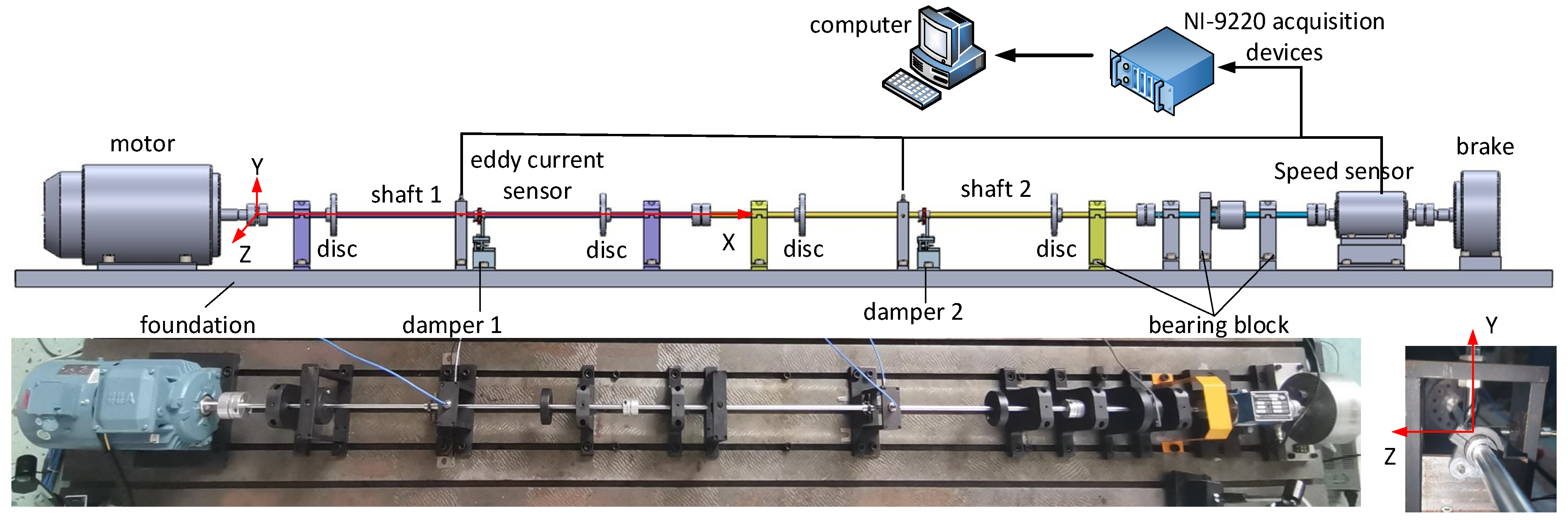
5. Experimental Verification
6. Conclusions
- (1)
- The vibration response in every vibration suppression stage is analyzed. The vibration suppression of the two dampers is not synchronized for the same parameter settings. Single rub impact occurs in the 1st and 2nd stage, dual rub-impact with interaction occurs in the 3rd stage. The amplitudes of shaft 1, shaft 2, damper 1, and damper 2 have step increases and step decreases. Full annual rub between the sleeve and damping ring occurs in the 1st and 3rd stages, while partial rub occurs in the 2nd stage. The amplitude bifurcation spanning the critical speed indicates that the transformation conditions are consistent with the theoretical analysis. The analytical model developed in this work can reflect the practical system. Even if the damper is more greatly affected by rub impact than the shaft, the degree of chaos is mild due to the low friction coefficient on its surface.
- (2)
- Parallel misalignment and angular misalignment result in 2nd and 3rd harmonic frequencies, respectively. In addition, they are not intercoupled with each other. Resonances also appear at the first critical speed due to misalignment. The vibration energy in the case of only static misalignment is smaller than that coexisting of static and dynamic misalignment, but the characteristics are similar.
- (3)
- In the case of the coexistence of rub impact and misalignment, both of them can stimulate each other and increase their components relative to the eccentricity. However, misalignment still accounts for most of the frequency spectrum of the shaft. In addition, more severe instability and more serious rub impact can be demonstrated from more high-frequency components appearing in the damper.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Nomenclature | |||
| density, elastic modulus | clearance | ||
| I | cross-sectional transverse moment of inertia | kinetic, dissipation, and strain energy | |
| stiffness | J | lumped inertia | |
| length | unit pulse function | ||
| vibration displacement in X Y Z | force, vector | ||
| force, scalar | amplitude vector of deflection | ||
| N | torque | poisson’s ratio | |
| damping coefficient | angular misalignment | ||
| rotating speed and rotation angle of the shaft | the angle between the tangent of contact point A in the fillet on the plate and the vertical line | ||
| the rotation angle of rotating coordinate | the ratio of static friction to dynamic friction coefficient on the surface of the ring | ||
| center | modal function | ||
| R | radius | the angle around Z-axis | |
| eccentricity | Heaviside function, | ||
| quality | whirling angular velocity of the shaft | ||
| the friction coefficient between the damping hole and sleeve | the distance from pipe to contact point A and arc radius of the fillet on the plate. | ||
| static friction coefficients between the ring and plate, the ring and base | friction coefficients between bushing and plate, bushing and base, pipe and plate, respectively. | ||
| Subscript | |||
| 1 or 2 | shaft 1 or shaft 2 | I, II, III | the 1st, 2nd,3rd stage |
| st | static misalignment | cp | coupling |
| X Z Y | in X, Z, Y direction | r | modal number of the shaft |
| vi | viscous internal damping | n | bearing block |
| h | sleeve | rt | in the rotating coordinate frame |
| s | shaft | d | damper |
| N0 | pre-tightening | sp | spring |
| torsion around X-axis | cn | contact | |
| N | normal direction | T | tangential direction |
| a | angular misalignment | p | parallel misalignment |
Appendix A

References
- Hamann, J.; Kpken, H.G.; Stoiber, D. Drive of a Tail Rotor of a Helicopter. U.S. Patent 9,631,516, 25 April 2017. [Google Scholar]
- Shaik, K.; Dutta, B.K. Tuning Criteria of Nonlinear Flexible Rotor Mounted on Squeeze Film Damper Using Analytical Approach. J. Vib. Eng. Technol. 2021, 9, 325–339. [Google Scholar] [CrossRef]
- Bui, Q.-D.; Nguyen, Q.H.; Tien, N.T.; Mai, D.-D.; Nguyen, T.T. Development of a Magnetorheological Damper with Self-Powered Ability for Washing Machines. Appl. Sci. 2020, 10, 4099. [Google Scholar] [CrossRef]
- Mingfu, L.; Mingbo, S.; Siji, W. Active Elastic Support/Dry Friction Damper with Piezoelectric Ceramic Actuator. Shock Vib. 2014, 2014, 712426. [Google Scholar] [CrossRef]
- Khanlo, H.; Ghayour, M.; Ziaei-Rad, S. The effects of lateral–torsional coupling on the nonlinear dynamic behavior of a rotating continuous flexible shaft–disk system with rub–impact. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 1524–1538. [Google Scholar] [CrossRef]
- Wang, Y.; He, Z.; Zi, Y. A Comparative Study on the Local Mean Decomposition and Empirical Mode Decomposition and Their Applications to Rotating Machinery Health Diagnosis. J. Vib. Acoust. 2010, 132, 021010. [Google Scholar] [CrossRef]
- Wang, Y.; Markert, R.; Xiang, J.; Zheng, W. Research on variational mode decomposition and its application in detecting rub-impact fault of the rotor system. Mech. Syst. Signal Process. 2015, 60–61, 243–251. [Google Scholar] [CrossRef]
- Wang, S.; Yang, L.; Chen, X.; Tong, C.; Ding, B.; Xiang, J. Nonlinear Squeezing Time-Frequency Transform and Application in Rotor Rub-Impact Fault Diagnosis. J. Manuf. Sci. Eng. 2017, 139. [Google Scholar] [CrossRef]
- Hu, A.; Xiang, L.; Zhang, Y. Experimental study on the intrawave frequency modulation characteristic of rotor rub and crack fault. Mech. Syst. Signal Process. 2019, 118, 209–225. [Google Scholar] [CrossRef]
- Tao, Z.; Yian, D.; Fan, H.; Xiangqi, Z.; Yaoyao, W.; Tianlin, L.; Bolchover, P.; Tao, Y.; Guishui, Z.; Rongbing, C.; et al. Reducing Vibration of a Rotating Machine with Deep Reinforcement Learning. In Proceedings of the 2020 IEEE International Conference on Mechatronics and Automation, Beijing, China, 2–5 August 2020; pp. 932–937. [Google Scholar] [CrossRef]
- Dai, W.; Mo, Z.; Luo, C.; Jiang, J.; Zhang, H.; Miao, Q. Fault Diagnosis of Rotating Machinery Based on Deep Reinforcement Learning and Reciprocal of Smoothness Index. IEEE Sens. J. 2020, 20, 8307–8315. [Google Scholar] [CrossRef]
- Wang, N.; Jiang, D.; Xu, H. Effects of Rub-Impact on Vibration Response of a Dual-Rotor System-Theoretical and Experimental Investigation. EXP Tech. 2019, 44, 299–311. [Google Scholar] [CrossRef]
- Yang, Y.; Cao, D.; Wang, D.; Jiang, G. Response analysis of a dual-disc rotor system with multi-unbalances–multi-fixed-point rubbing faults. Nonlinear Dyn. 2017, 87, 109–125. [Google Scholar] [CrossRef]
- Han, Q.; Zhang, Z.; Wen, B. Periodic motions of a dual-disc rotor system with rub-impact at fixed limiter. Arch. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2008, 222, 1935–1946. [Google Scholar] [CrossRef]
- Ma, H.; Shi, C.; Han, Q.; Wen, B. Fixed-point rubbing fault characteristic analysis of a rotor system based on contact theory. Mech. Syst. Signal Process. 2013, 38, 137–153. [Google Scholar] [CrossRef]
- Al-Shudeifat, M.A. Stability analysis and backward whirl investigation of cracked rotors with time-varying stiffness. J. Sound Vib. 2015, 348, 365–380. [Google Scholar] [CrossRef]
- AL-Shudeifat, M.A. On the finite element modeling of the asymmetric cracked rotor. J. Sound Vib. 2013, 332, 2795–2807. [Google Scholar] [CrossRef]
- Wang, J.; Ma, L.; Zhang, J.; Lu, X.; Yu, Y. Mitigation of nonlinear rub-impact of a rotor system with magnetorheological damper. J. Intell. Mater. Syst. Struct. 2019, 31, 321–338. [Google Scholar] [CrossRef]
- Xiao, S.; Liu, S.; Wang, H.; Lin, Y.; Song, M.; Zhang, H. Nonlinear dynamics of coupling rub-impact of double translational joints with subsidence considering the flexibility of piston rod. Nonlinear Dyn. 2020, 100, 1203–1229. [Google Scholar] [CrossRef]
- Chen, L.; Qin, Z.; Chu, F. Dynamic characteristics of rub-impact on rotor system with cylindrical shell. Int. J. Mech. Sci. 2017, 133, 51–64. [Google Scholar] [CrossRef]
- Hua, C.; Rao, Z.; Ta, N.; Zhu, Z. Nonlinear dynamics of rub-impact on a rotor-rubber bearing system with the Stribeck friction model. J. Mech. Sci. Technol. 2015, 29, 3109–3119. [Google Scholar] [CrossRef]
- Zhang, W.-M.; Meng, G.; Chen, D.; Zhou, J.-B.; Chen, J.-Y. Nonlinear dynamics of a rub-impact micro-rotor system with scale-dependent friction model. J. Sound Vib. 2008, 309, 756–777. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, Y.; Gao, Z. Nonlinear analysis of a rub-impact rotor with random stiffness under random excitation. Adv. Mech. Eng. 2016, 8. [Google Scholar] [CrossRef]
- Zhang, G.F.; Xu, W.N.; Xu, B.; Zhang, W. Analytical study of nonlinear synchronous full annular rub motion of flexible rotor–stator system and its dynamic stability. Nonlinear Dyn. 2009, 57, 579–592. [Google Scholar] [CrossRef]
- Verma, A.K.; Sarangi, S.; Kolekar, M.H. Experimental Investigation of Misalignment Effects on Rotor Shaft Vibration and on Stator Current Signature. J. Fail. Anal. Prev. 2014, 14, 125–138. [Google Scholar] [CrossRef]
- Browne, M.; Palazzolo, A. Super harmonic nonlinear lateral vibrations of a segmented driveline incorporating a tuned damper excited by non-constant velocity joints. J. Sound Vib. 2009, 323, 334–351. [Google Scholar] [CrossRef]
- Lu, X.; Lu, T.; Zhang, J. Optimization of Geometric Parameters and Stiffness of Multi-Universal-Joint Drive Shaft Considering the Dynamics of Driveline. In Advances in Evolutionary and Deterministic Methods for Design, Optimization and Control in Engineering and Science; Springer: Cham, Switzerland, 2019; pp. 445–453. [Google Scholar]
- Kang, Y.; Shen, Y.; Zhang, W.; Yang, J. Stability region of floating intermediate support in a shaft system with multiple universal joints. J. Mech. Sci. Technol. 2014, 28, 2733–2742. [Google Scholar] [CrossRef]
- DeSmidt, H.; Wang, K.W.; Smith, E. Stability of a segmented supercritical driveline with non-constant velocity couplings subjected to misalignment and torque. J. Sound Vib. 2004, 277, 895–918. [Google Scholar] [CrossRef]
- Al-Hussain, K. Dynamic stability of two rigid rotors connected by a flexible coupling with angular misalignment. J. Sound Vib. 2003, 266, 217–234. [Google Scholar] [CrossRef]
- Xia, Y.; Pang, J.; Yang, L.; Zhao, Q.; Yang, X. Study on vibration response and orbits of misaligned rigid rotors connected by hexangular flexible coupling. Appl. Acoust. 2019, 155, 286–296. [Google Scholar] [CrossRef]
- Avendano, R.D.; Childs, D.W. One Explanation for Two-Times Running Speed Response Due to Misalignment in Rotors Connected by Flexible Couplings. J. Eng. Gas Turbines Power 2013, 135, 062501. [Google Scholar] [CrossRef]
- Jiang, J.; Ulbrich, H.; Chavez, A. Improvement of rotor performance under rubbing conditions through active auxiliary bearings. Int. J. Non-Linear Mech. 2006, 41, 949–957. [Google Scholar] [CrossRef]






















| 0 | 90 | 180 | 270 | |
|---|---|---|---|---|
| 1.9 | 1 | 1.95 | 4.6 |
| Parameter | Value/Unit | Parameter | Value/Unit |
|---|---|---|---|
| 3653, 3514 mm | 1965, 1757 mm | ||
| 3642, 11 mm | 76, 76 mm | ||
| 72 GPa | 747 mm2 | ||
| 0.0001 N s/m | 1.633 × 106 mm4 | ||
| 7850 kg/M3 | 2700 kg/m3 | ||
| 0.05%, 0.04% | 7.47 × 10−4 m2 | ||
| 2 mm | 1.44 mm | ||
| 160 N s/m | 0.06705 m | ||
| 150 kN/m | 0.4925 kg | ||
| 23.17 kN/m | 0.3033 kg | ||
| 0 | 0 | ||
| 0.8 | 2.055 × 10−3 m4 m2 | ||
| 1.7 × 1011 Pa | 0.3 | ||
| 70 mm | 9 × 108 Pa | ||
| 0.4 | 72 mm | ||
| 1 × 104 kN/m | 1.1 × 104 kN m/rad | ||
| 0.19, 0.19, 0.25, 0.2, 0.2, 0.15 | |||
| Components | Material Composition | Value |
|---|---|---|
| Shaft 1 and shaft 2 | steel | Φ10 × 700 mm, Φ10 × 1000 mm, elastic modulus 211 GPa, Poisson’s ratio 0.31, and internal damping 0.001 N s/m |
| Disc and sleeve | steel | Φ78 × 34 mm, Φ16 × 20 mm, |
| Hexagon diaphragm coupling | steel | 8 × 104 N/m 6 × 104 N m/rad |
| damping ring | graphite, POB and PTFE | R 16.2 × T 3.6 × W 5.2 mm |
| Bearing | Left and right: stiffness 40 kN/m, damping 25 N s/m | |
| Unbalance in the disc | Left and right: 2.5 g, eccentricity distance 35 mm | |
| motor and control | constant acceleration from 10 to 2000 rpm in 20 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Z.; Tan, J.; Liu, C.; Lu, X. Dynamic Characteristics of a Segmented Supercritical Driveline with Flexible Couplings and Dry Friction Dampers. Symmetry 2021, 13, 281. https://doi.org/10.3390/sym13020281
Huang Z, Tan J, Liu C, Lu X. Dynamic Characteristics of a Segmented Supercritical Driveline with Flexible Couplings and Dry Friction Dampers. Symmetry. 2021; 13(2):281. https://doi.org/10.3390/sym13020281
Chicago/Turabian StyleHuang, Zhonghe, Jianping Tan, Chuliang Liu, and Xiong Lu. 2021. "Dynamic Characteristics of a Segmented Supercritical Driveline with Flexible Couplings and Dry Friction Dampers" Symmetry 13, no. 2: 281. https://doi.org/10.3390/sym13020281
APA StyleHuang, Z., Tan, J., Liu, C., & Lu, X. (2021). Dynamic Characteristics of a Segmented Supercritical Driveline with Flexible Couplings and Dry Friction Dampers. Symmetry, 13(2), 281. https://doi.org/10.3390/sym13020281