Figure 1.
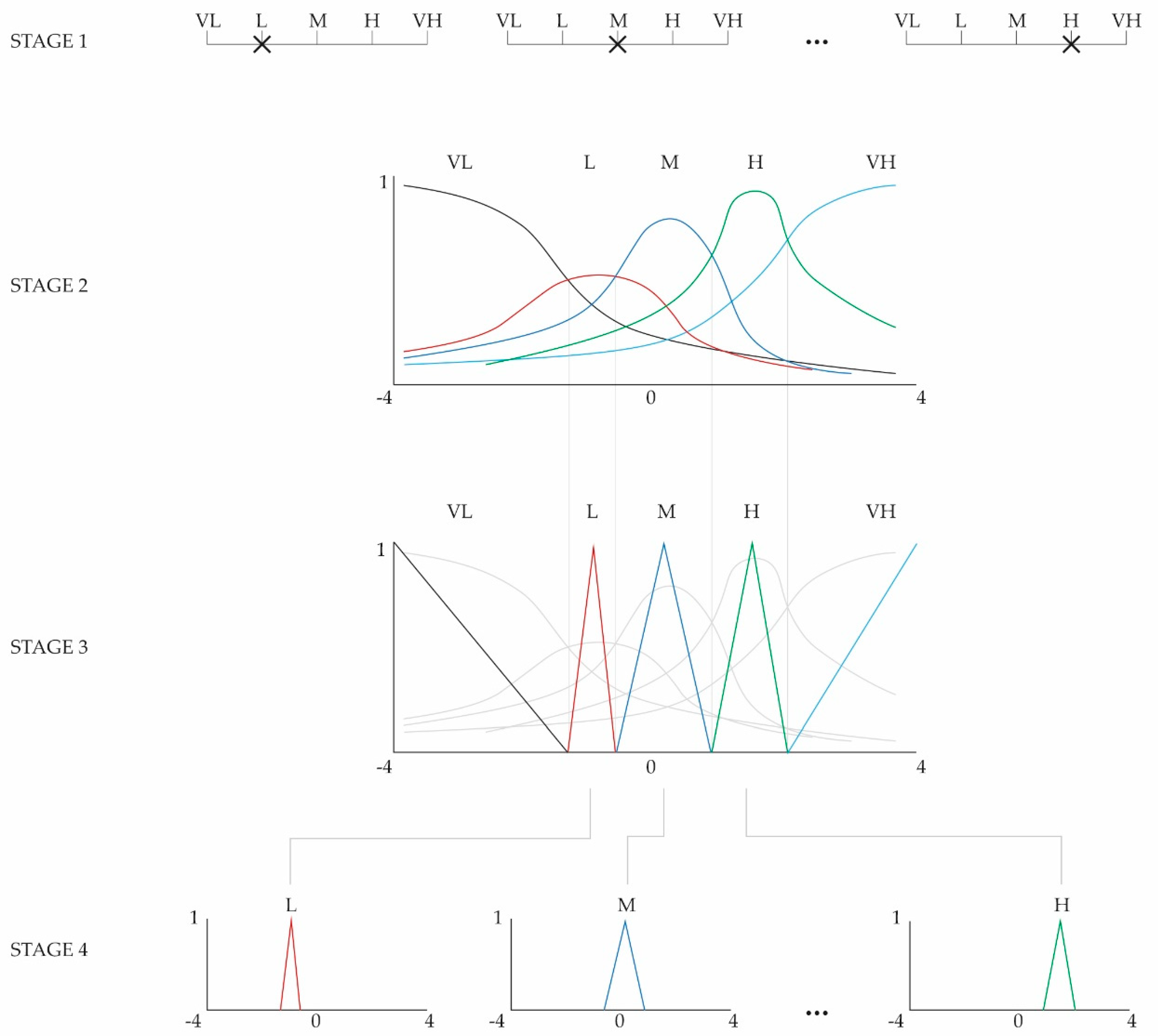
Scheme of transformation of ordinal scales to fuzzy conversion scales.
Figure 1.
Scheme of transformation of ordinal scales to fuzzy conversion scales.
Figure 2.
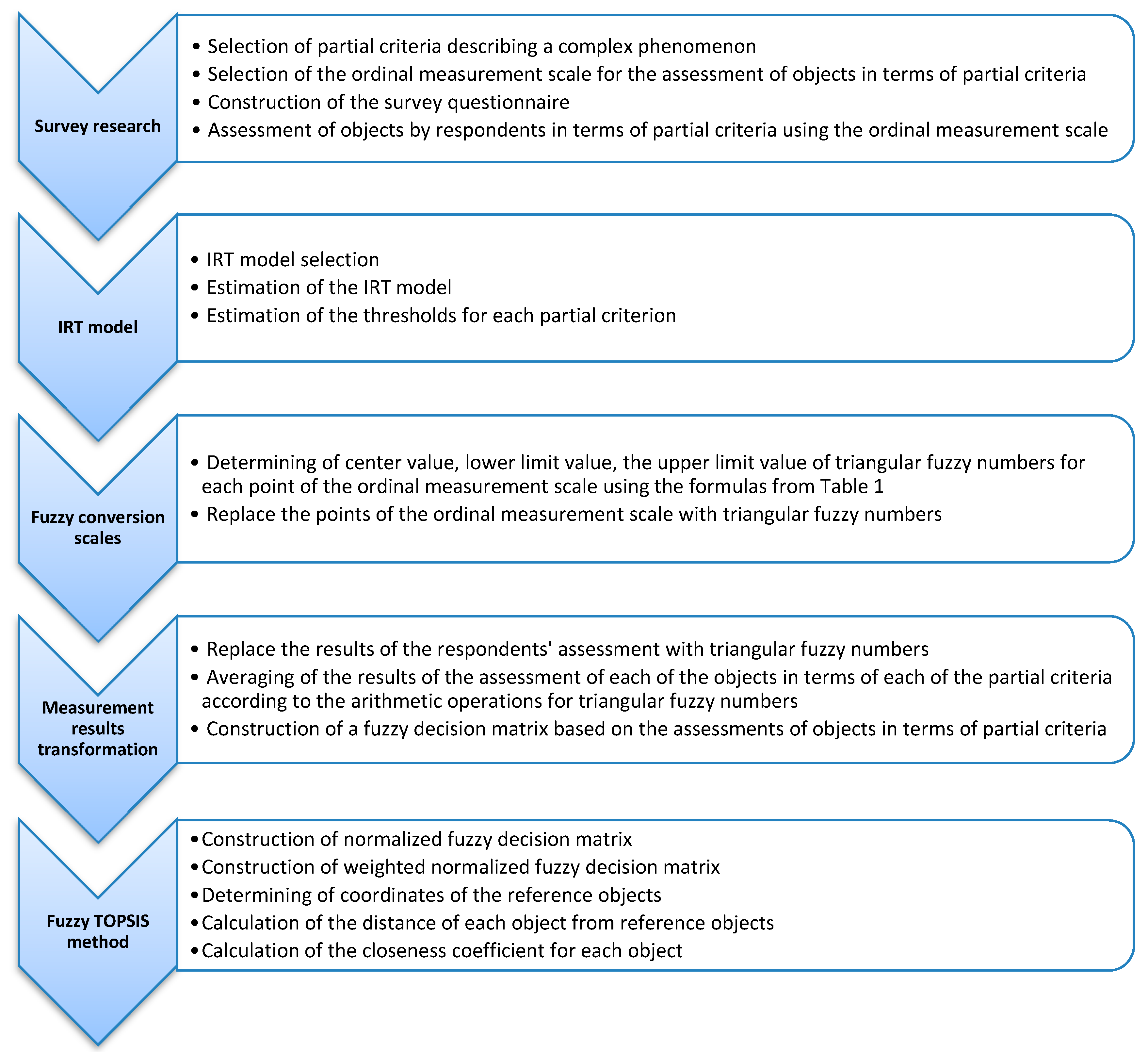
Total research flow chart.
Figure 2.
Total research flow chart.
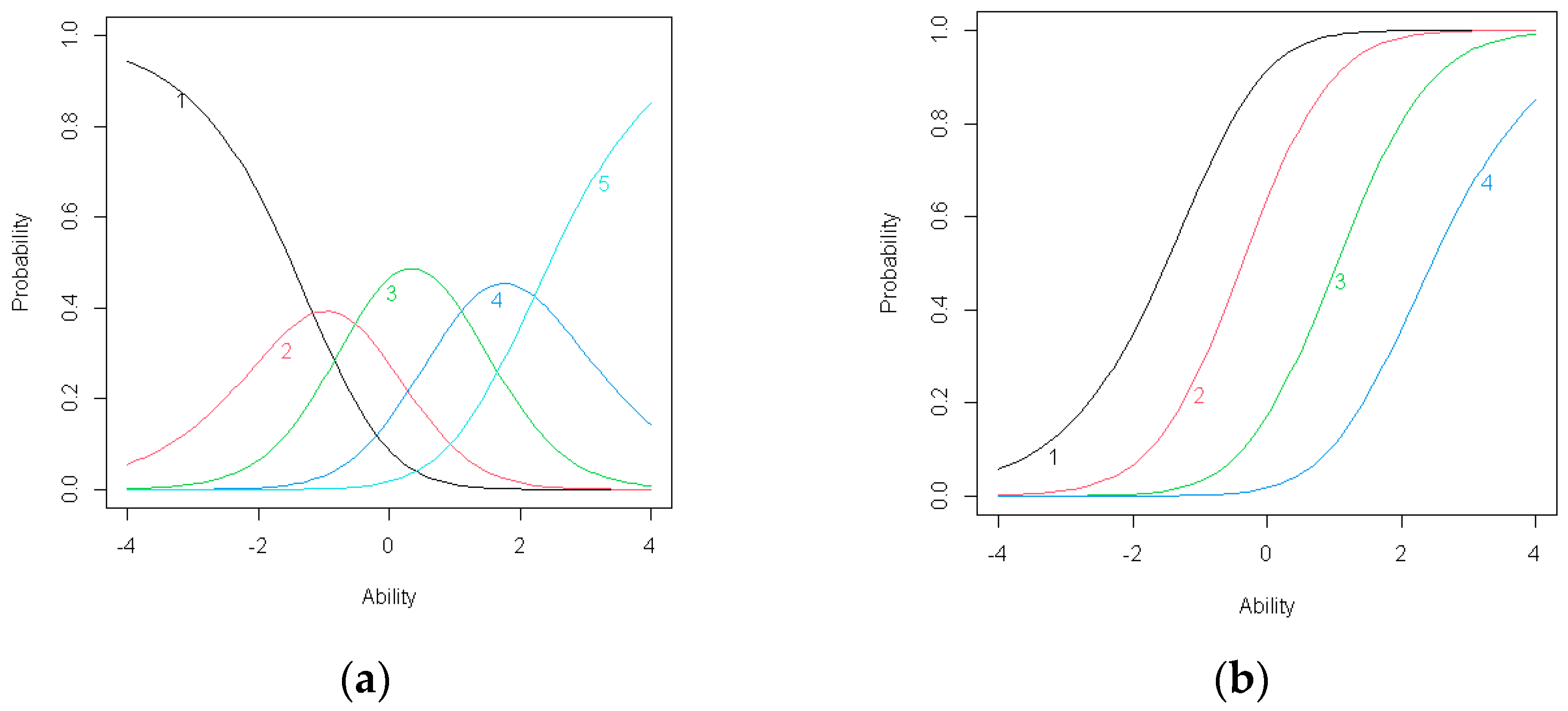
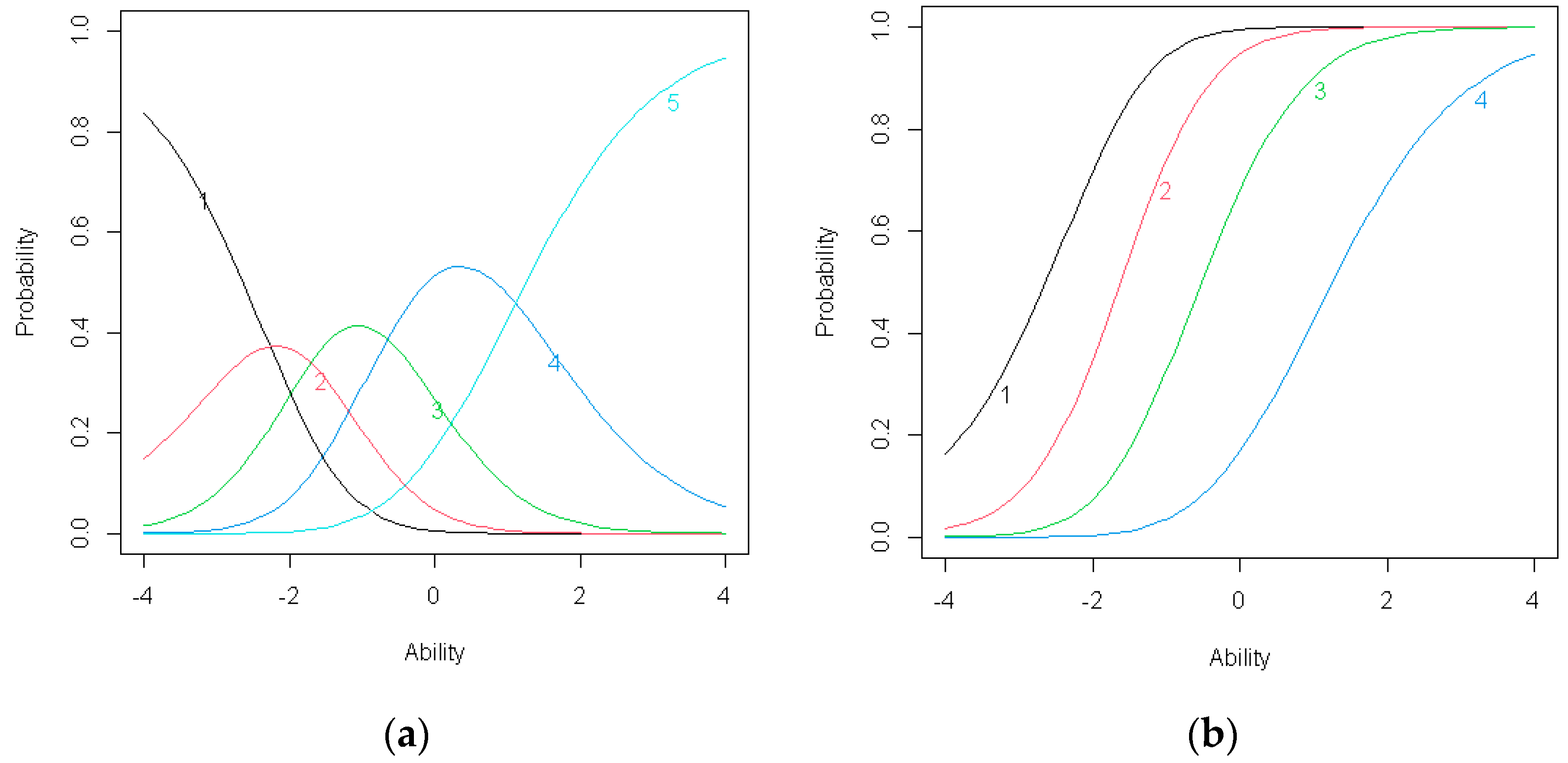
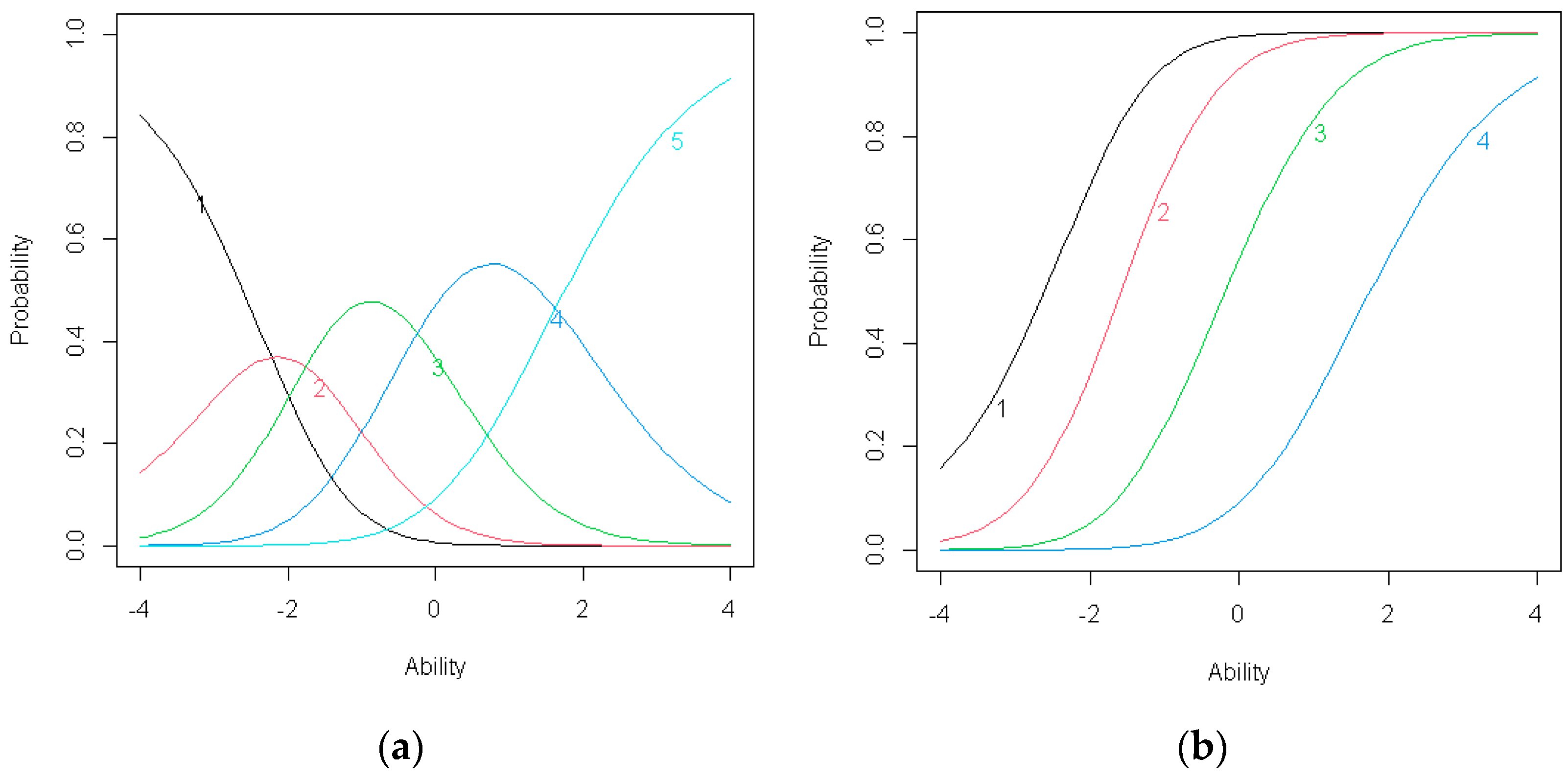
Figure 3.
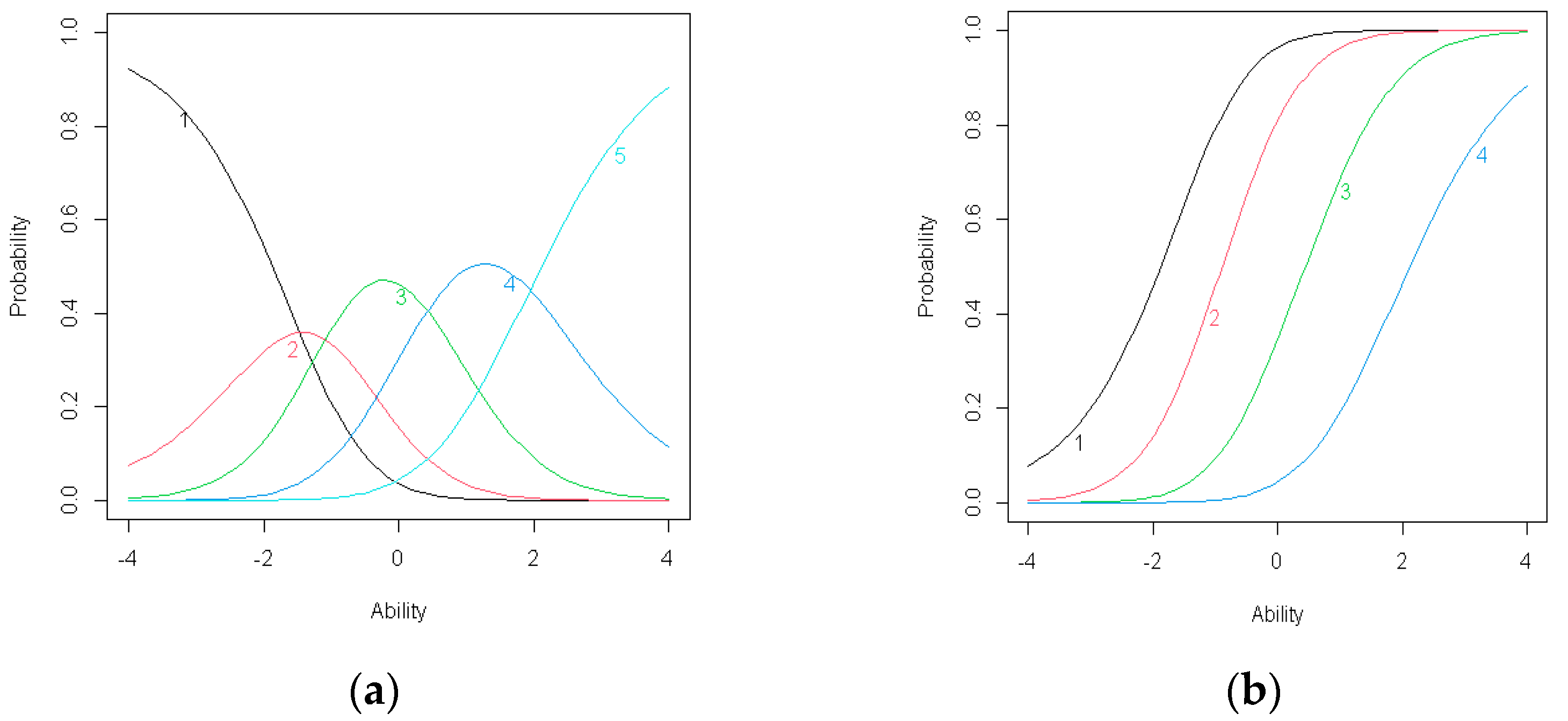
(a) Item response category characteristic curves for C1; (b) Item operation characteristic curves for C1.
Figure 3.
(a) Item response category characteristic curves for C1; (b) Item operation characteristic curves for C1.
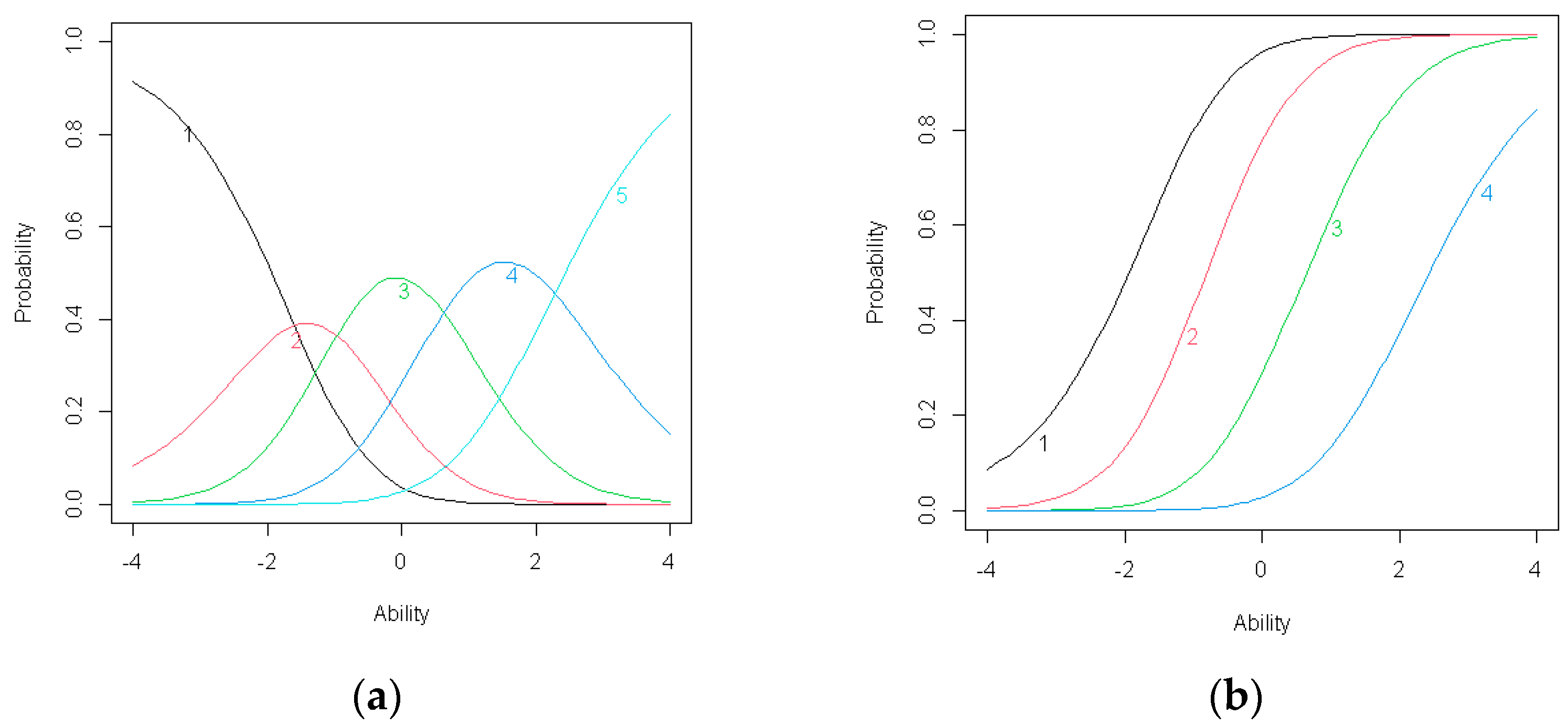
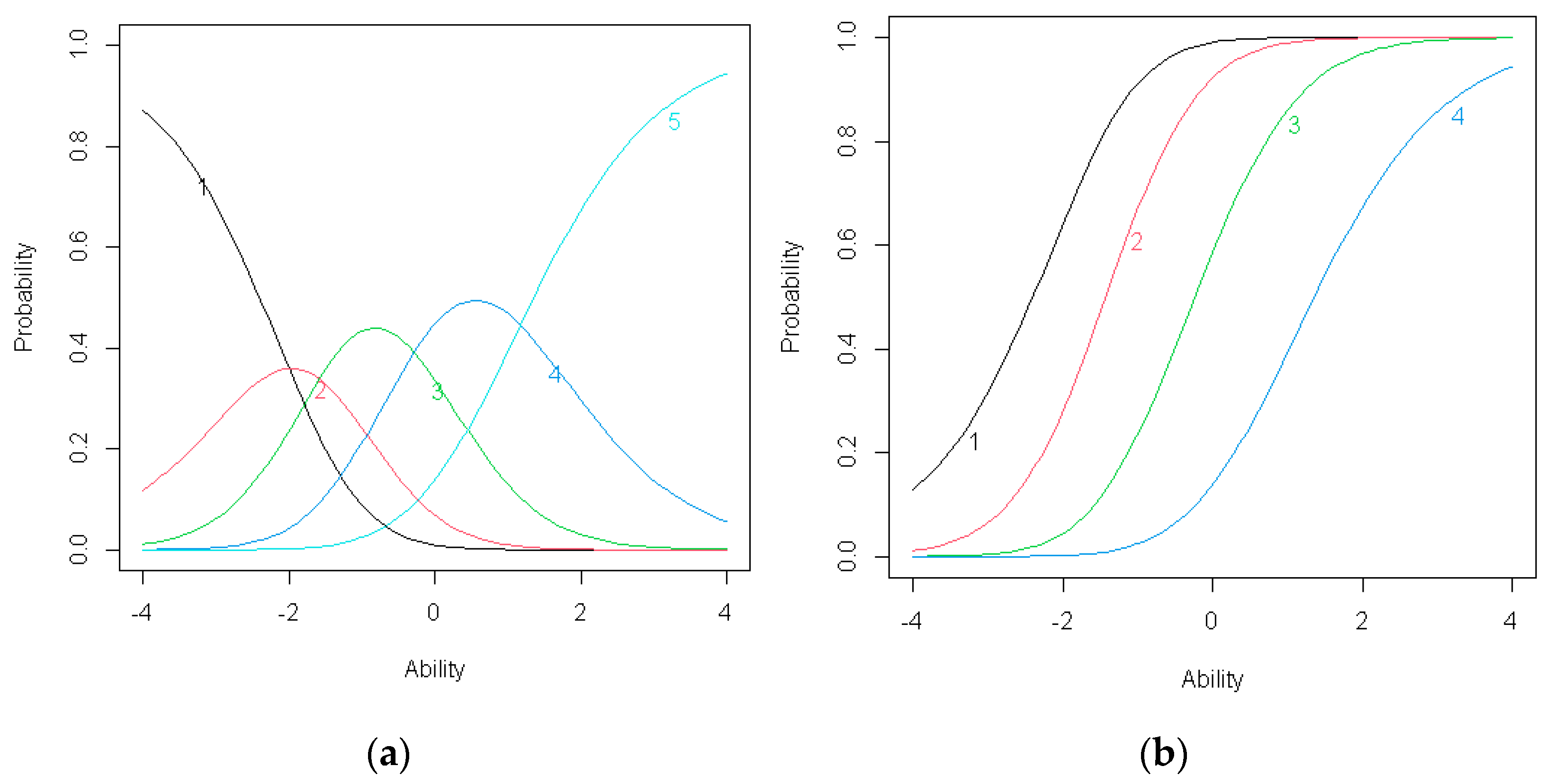
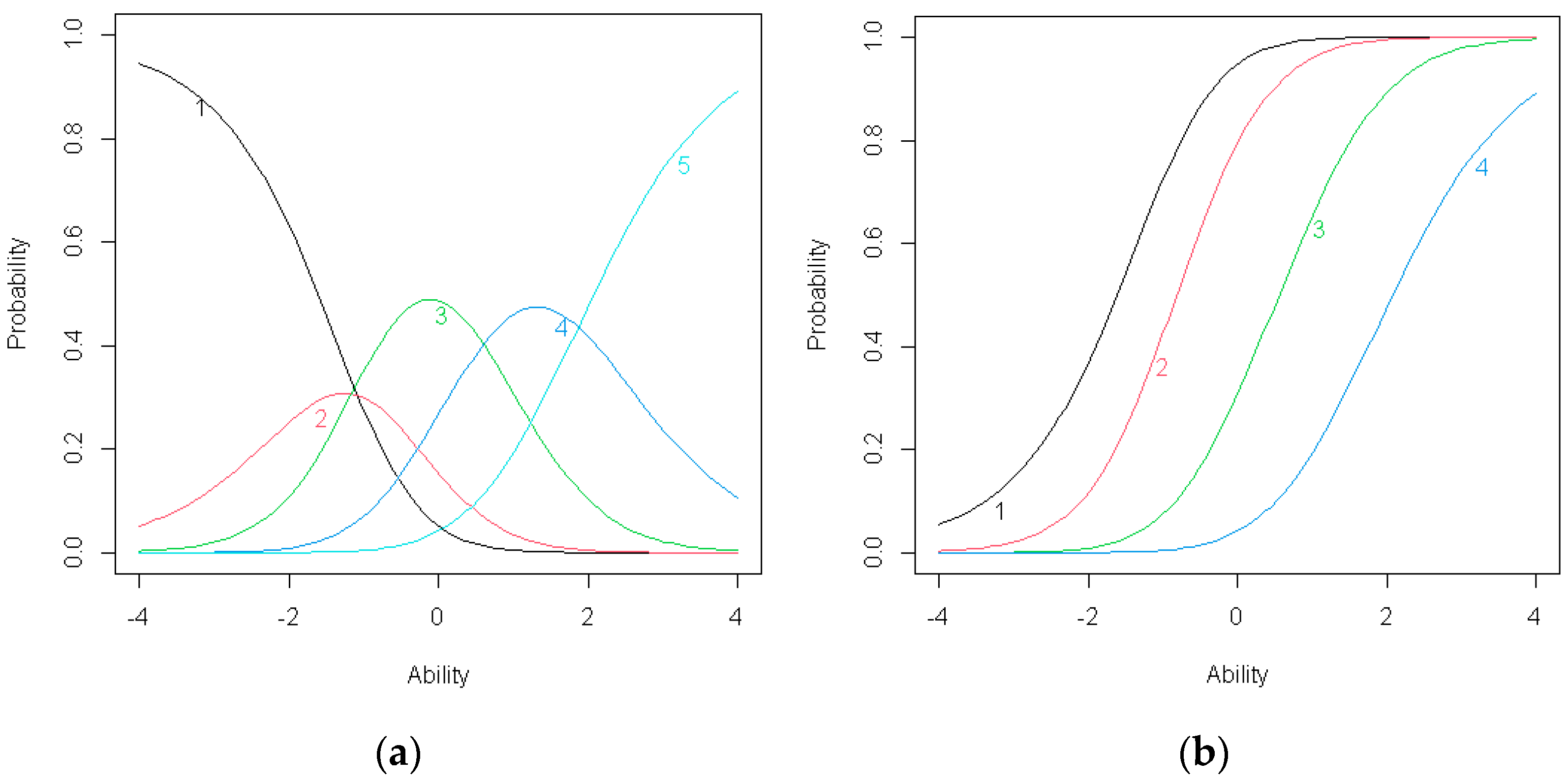
Figure 4.
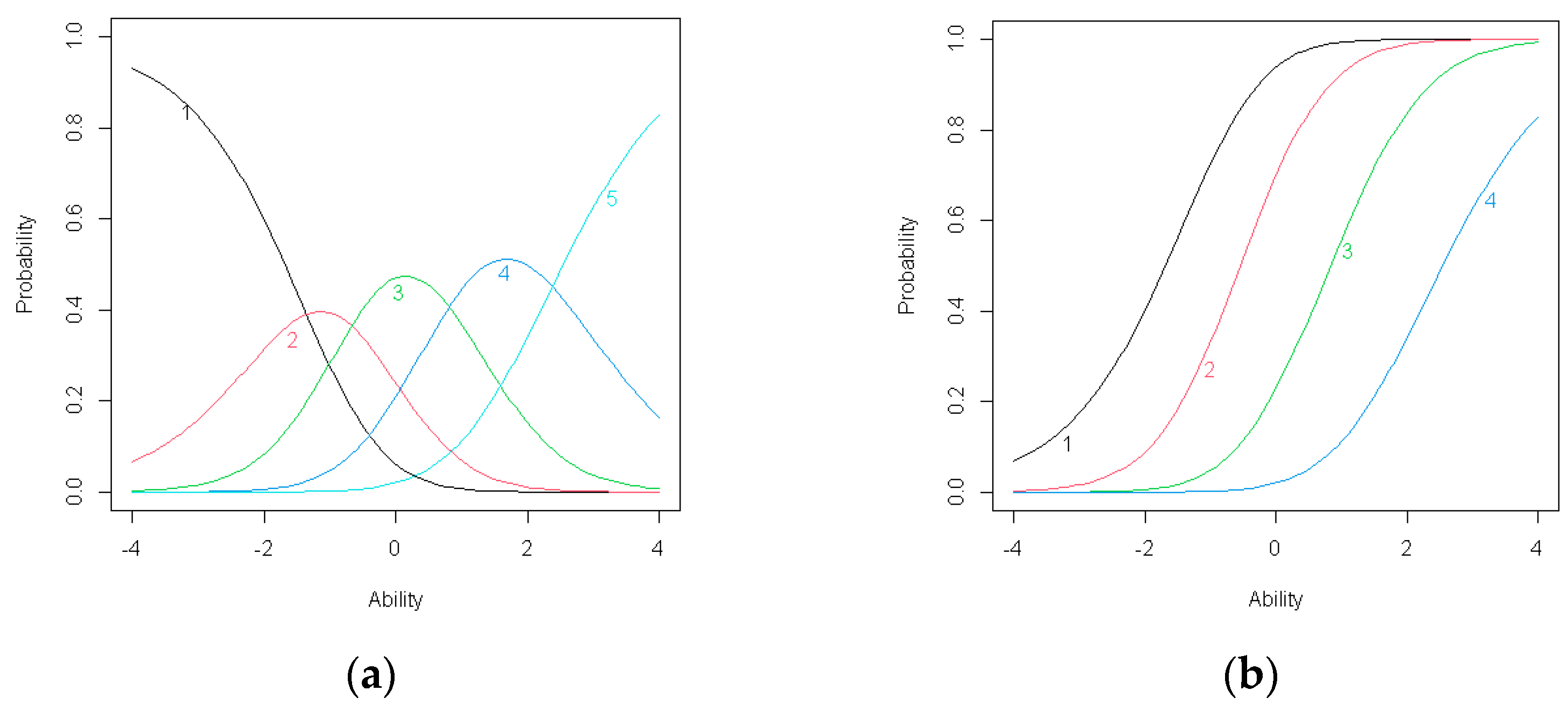
(a) Item response category characteristic curves for C2; (b) Item operation characteristic curves for C2.
Figure 4.
(a) Item response category characteristic curves for C2; (b) Item operation characteristic curves for C2.
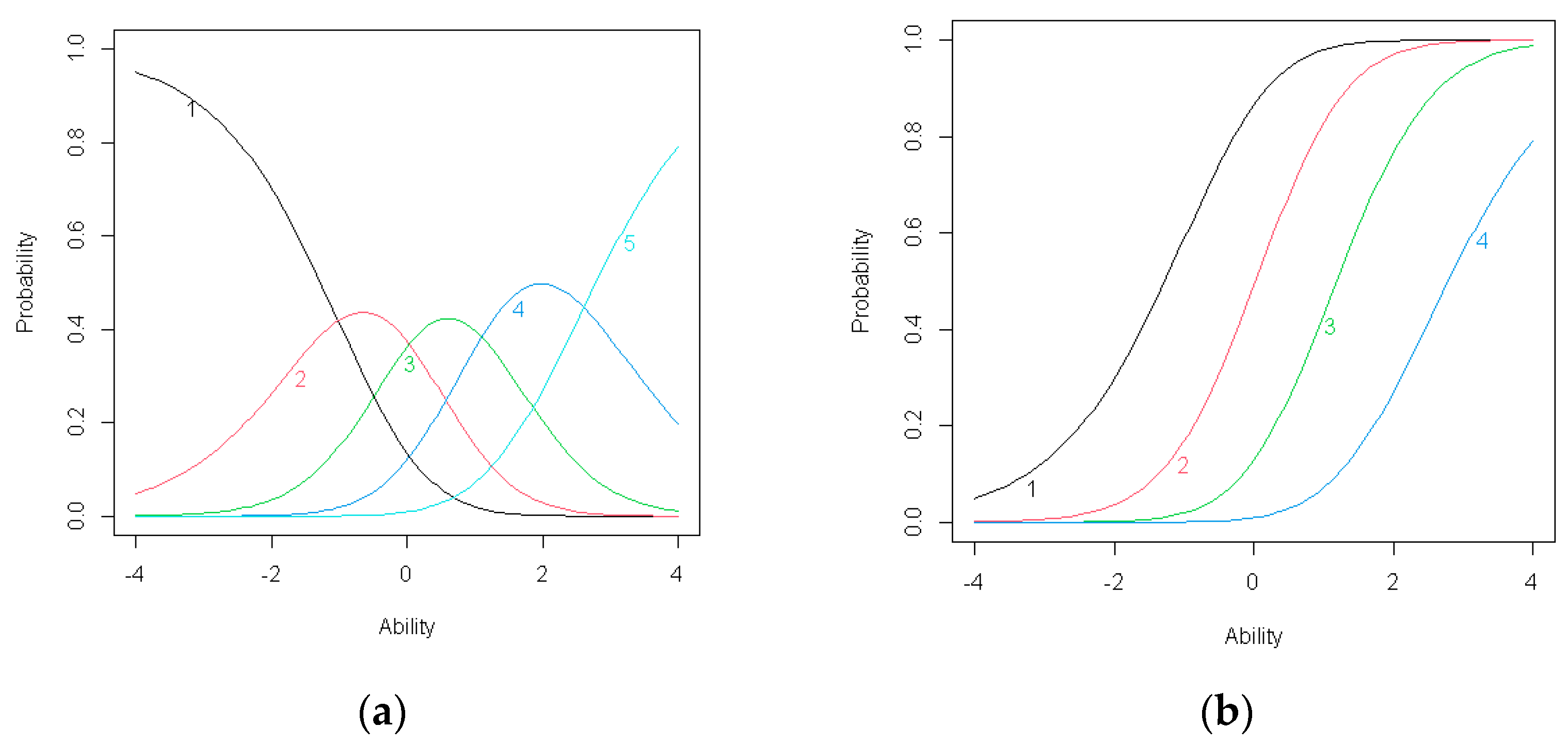
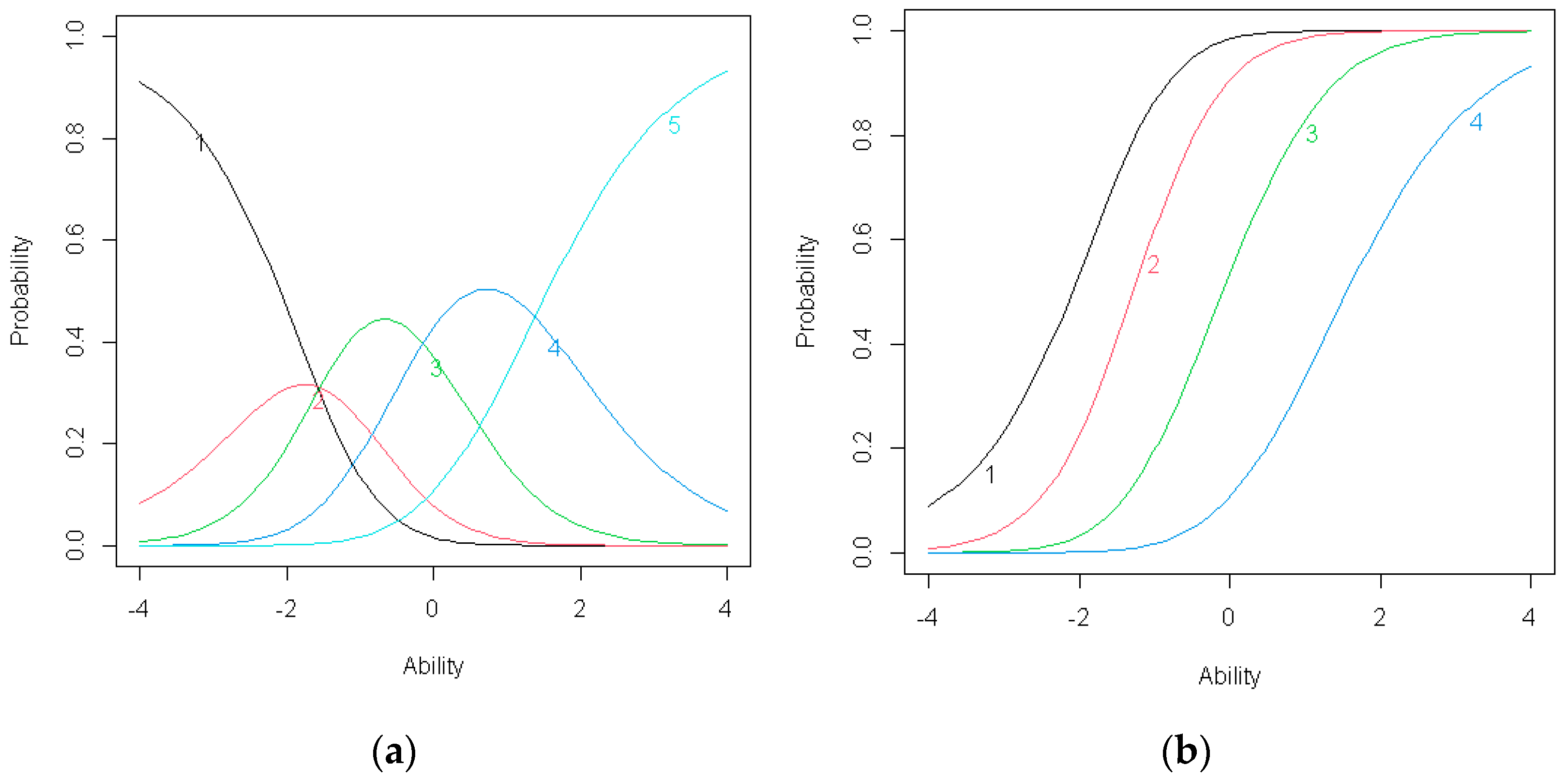
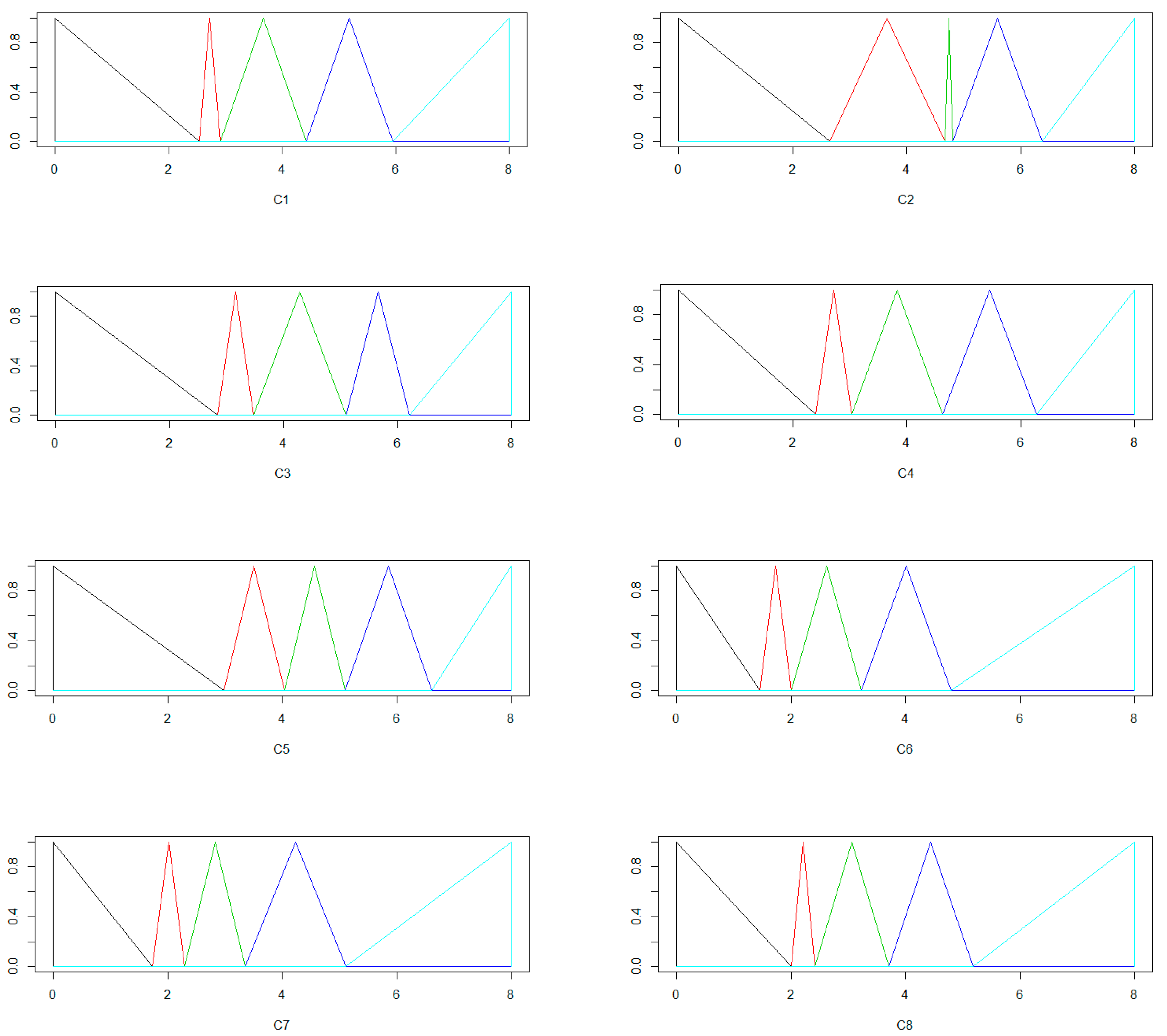
Figure 5.
(a) Item response category characteristic curves for C3; (b) Item operation characteristic curves for item C3.
Figure 5.
(a) Item response category characteristic curves for C3; (b) Item operation characteristic curves for item C3.
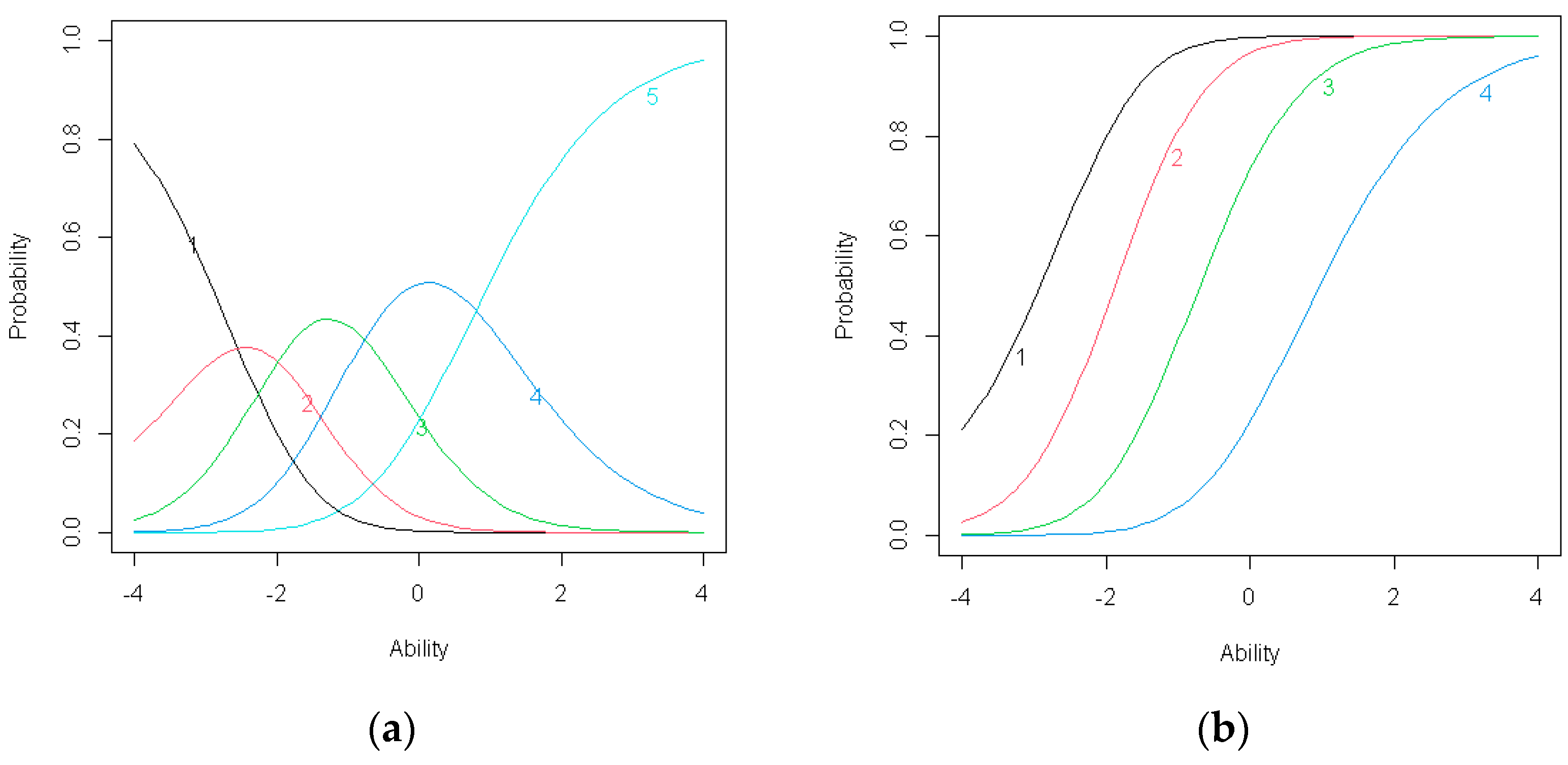
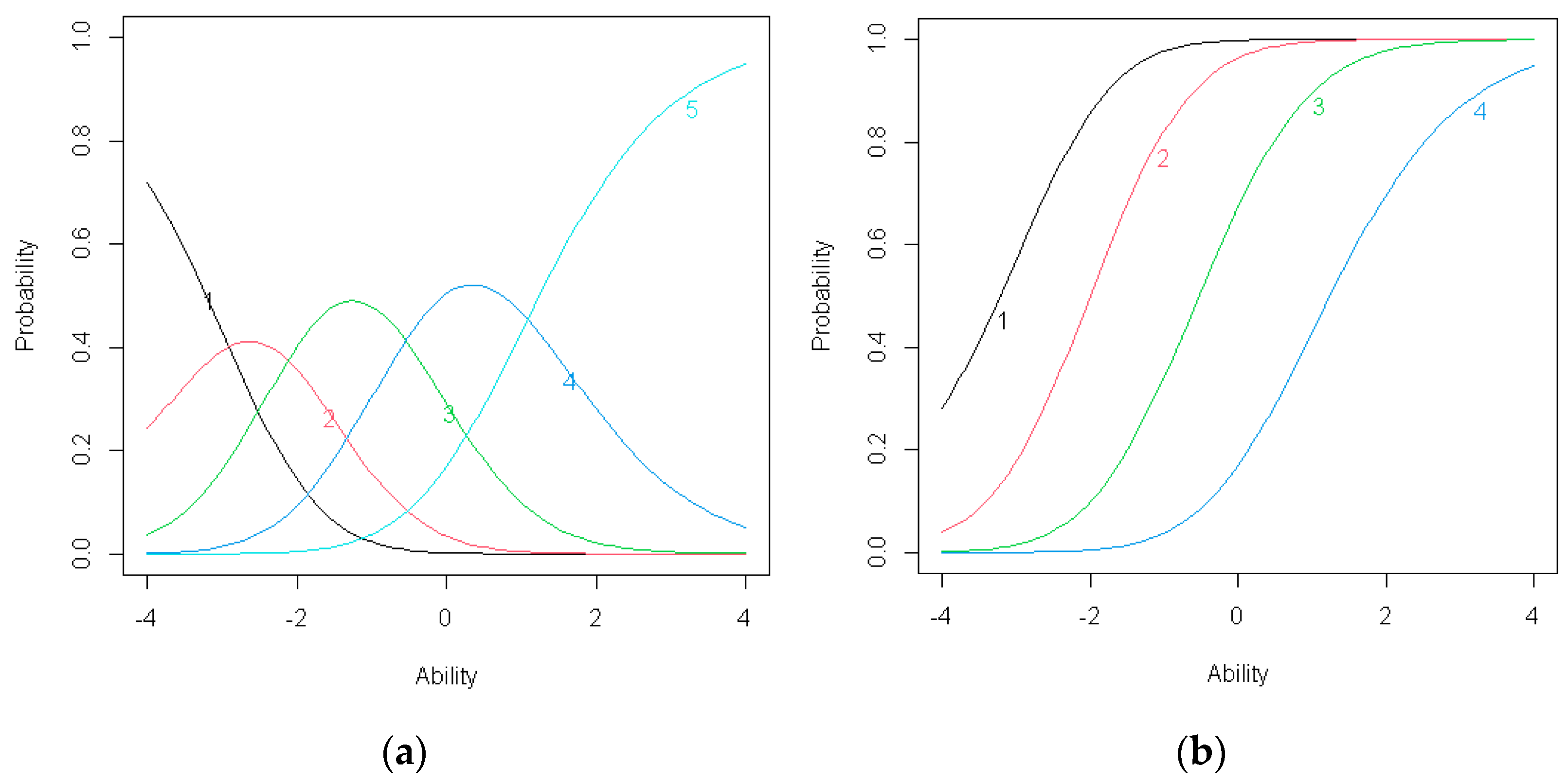
Figure 6.
(a) Item response category characteristic curves for C4; (b) Item operation characteristic curves for C4.
Figure 6.
(a) Item response category characteristic curves for C4; (b) Item operation characteristic curves for C4.
Figure 7.
(a) Item response category characteristic curves for C5; (b) Item operation characteristic curves for C5.
Figure 7.
(a) Item response category characteristic curves for C5; (b) Item operation characteristic curves for C5.
Figure 8.
(a) Item response category characteristic curves for C6; (b) Item operation characteristic curves for C6.
Figure 8.
(a) Item response category characteristic curves for C6; (b) Item operation characteristic curves for C6.
Figure 9.
(a) Item response category characteristic curves for C7; (b) Item operation characteristic curves for C7.
Figure 9.
(a) Item response category characteristic curves for C7; (b) Item operation characteristic curves for C7.
Figure 10.
(a) Item response category characteristic curves for C8; (b) Item operation characteristic curves for C8.
Figure 10.
(a) Item response category characteristic curves for C8; (b) Item operation characteristic curves for C8.
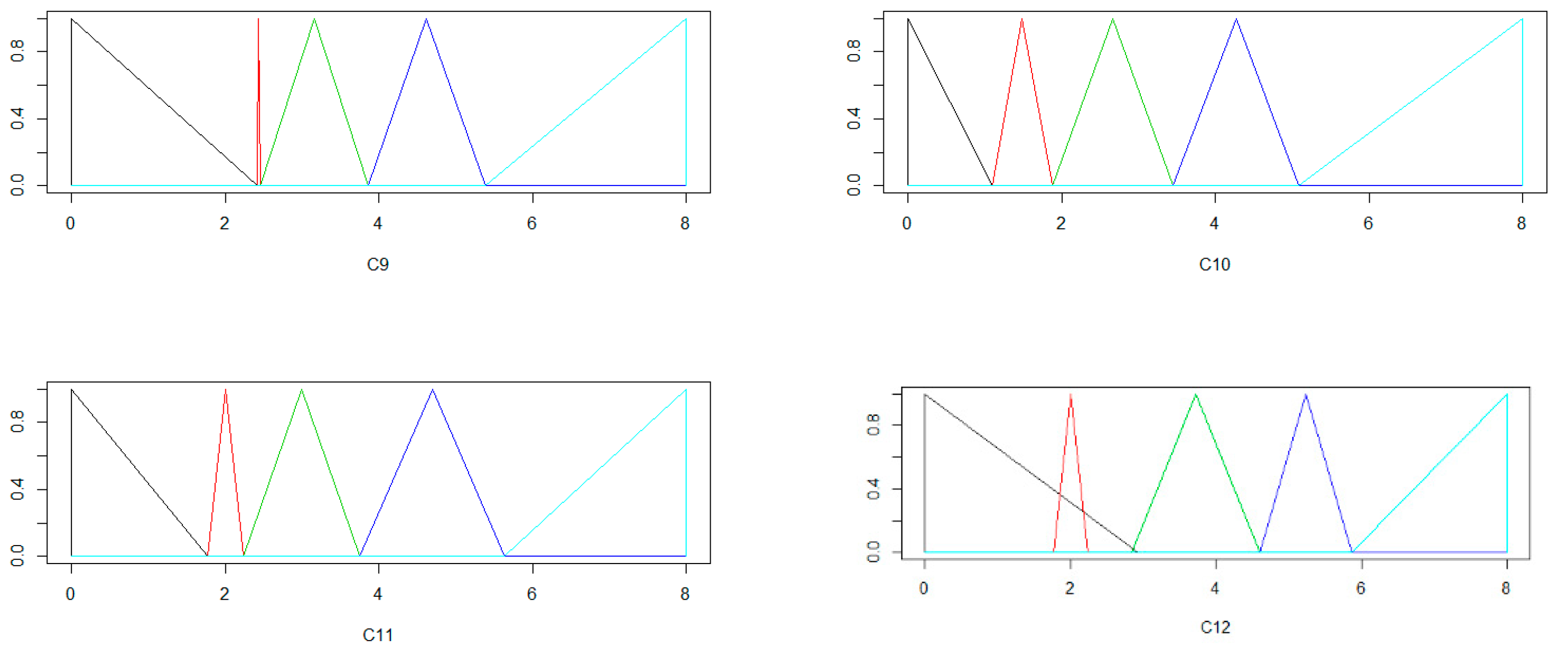
Figure 11.
T(a) Item response category characteristic curves for C9; (b) Item operation characteristic curves for C9.
Figure 11.
T(a) Item response category characteristic curves for C9; (b) Item operation characteristic curves for C9.
Figure 12.
(a) Item response category characteristic curves for C10; (b) Item operation characteristic curves for C10.
Figure 12.
(a) Item response category characteristic curves for C10; (b) Item operation characteristic curves for C10.
Figure 13.
(a) Item response category characteristic curves for C11; (b) Item operation characteristic curves for C11.
Figure 13.
(a) Item response category characteristic curves for C11; (b) Item operation characteristic curves for C11.
Figure 14.
(a) Item response category characteristic curves for C12; (b) Item operation characteristic curves for C12.
Figure 14.
(a) Item response category characteristic curves for C12; (b) Item operation characteristic curves for C12.
Figure 15.
Triangular fuzzy numbers for criteria C1–C12.
Figure 15.
Triangular fuzzy numbers for criteria C1–C12.
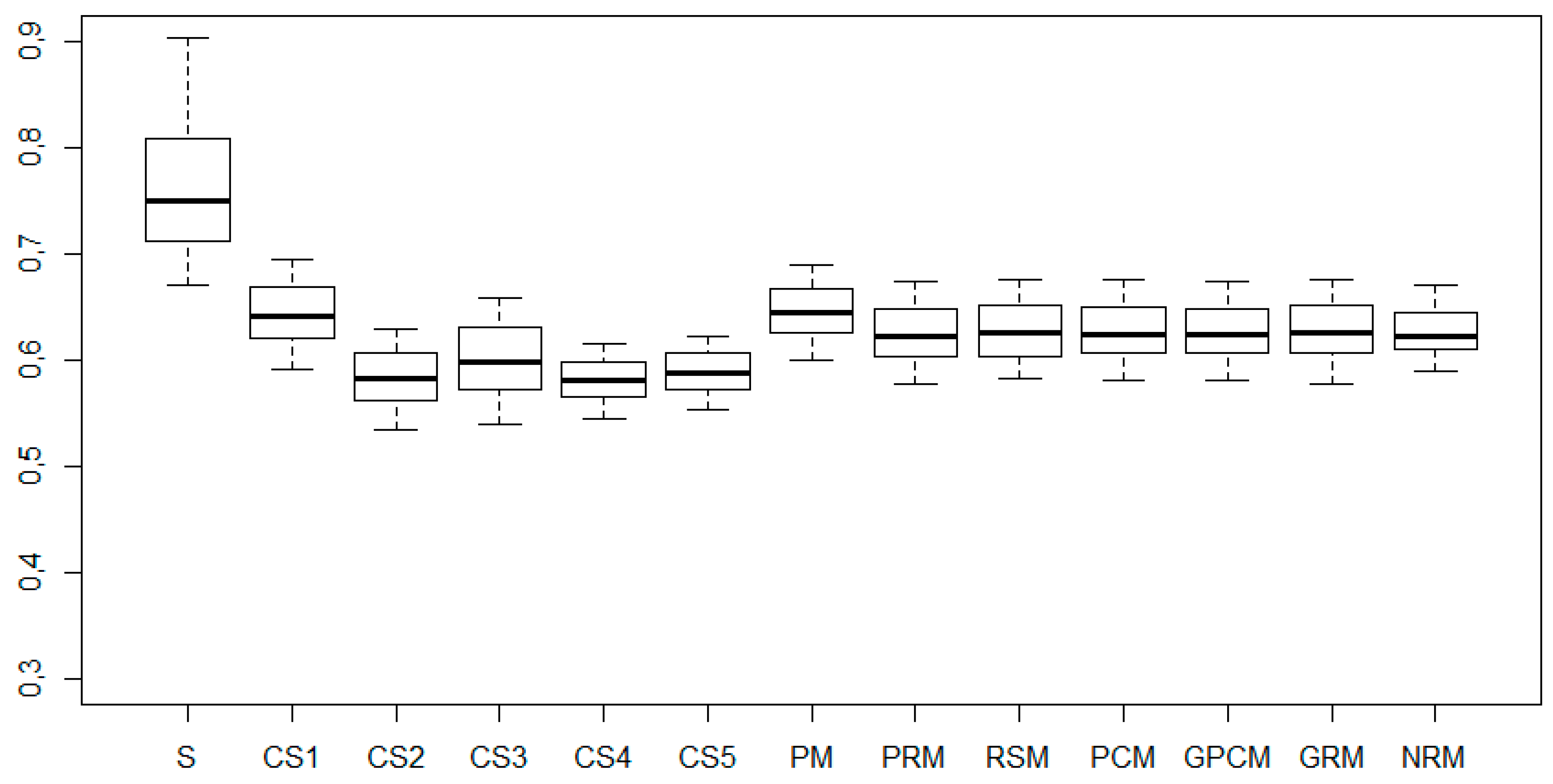
Figure 16.
Box-plots for values of the fuzzy TOPSIS for (the first case).
Figure 16.
Box-plots for values of the fuzzy TOPSIS for (the first case).
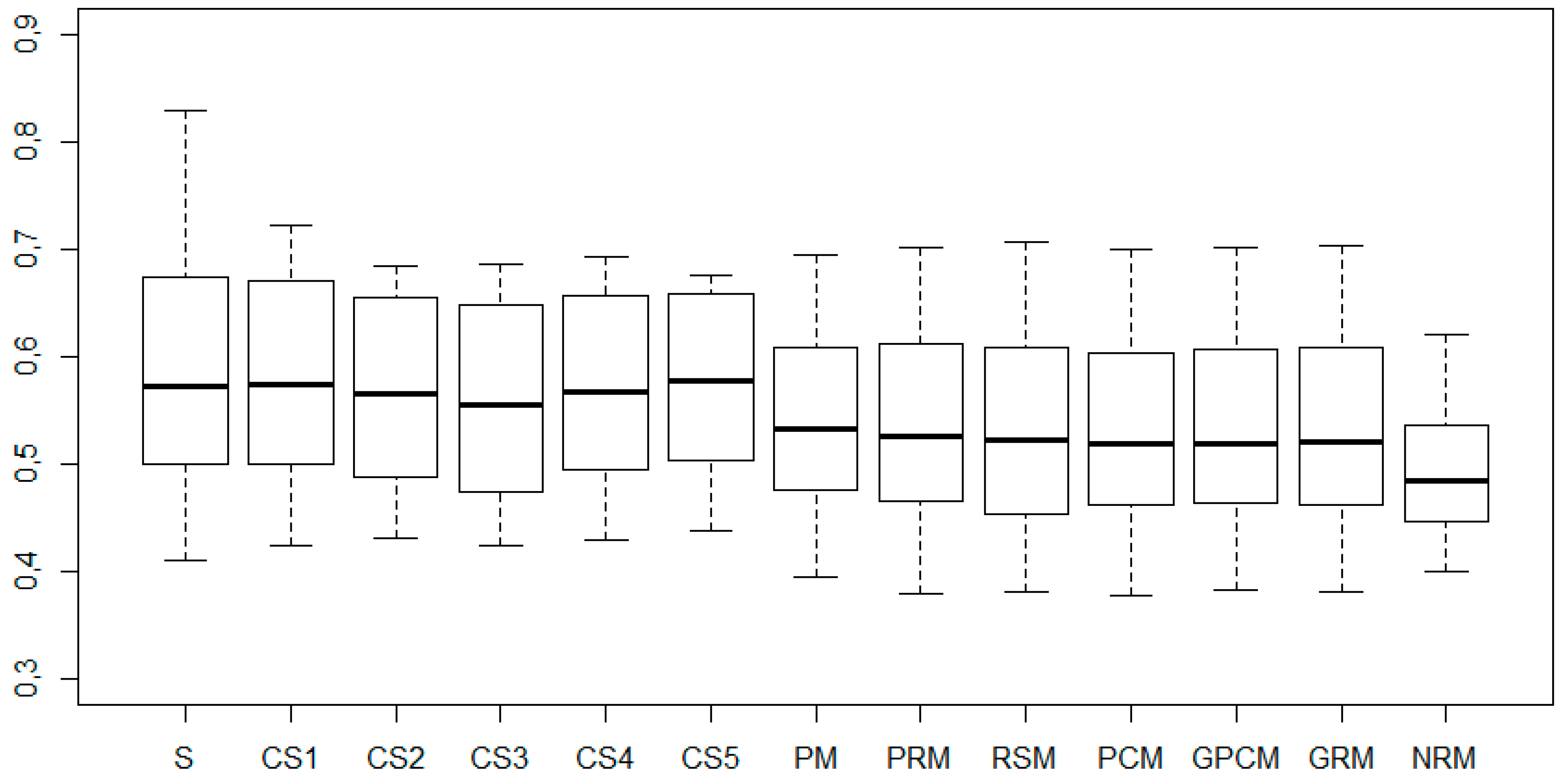
Figure 17.
Box-plots for values of the fuzzy TOPSIS for (the second case).
Figure 17.
Box-plots for values of the fuzzy TOPSIS for (the second case).
Table 1.
Formulas for determining the parameters of triangular fuzzy numbers.
Table 1.
Formulas for determining the parameters of triangular fuzzy numbers.
| Category | Parameters of Triangular Fuzzy Numbers |
|---|
| | |
|---|
| VL | −4 | −4 | |
| L | | | |
| M | | | |
| H | | | |
| VH | | 4 | 4 |
Table 2.
The distribution of the research sample by place of residence.
Table 2.
The distribution of the research sample by place of residence.
| | Planned Sample Size | Realized Sample Size |
|---|
| | Maximum Sampling Error Assumed = 3% | Maximum Sampling Error Obtained = 3% |
|---|
| Total | 1047 | 1054 |
| Commune A | 97 | 95 |
| Commune B | 107 | 110 |
| Commune C | 97 | 98 |
| Commune D | 242 | 283 |
| Commune E | 504 | 468 |
Table 3.
Thresholds for the Polychoric Correlation Model (PM) (for criteria C1–C6).
Table 3.
Thresholds for the Polychoric Correlation Model (PM) (for criteria C1–C6).
| Thresholds | C1 | C2 | C3 | C4 | C5 | C6 |
|---|
| 1→2 | −1.270 | −1.110 | −0.980 | −1.280 | −0.820 | −1.970 |
| 2→3 | −0.597 | −0.352 | −0.231 | −0.529 | 0.032 | −1.291 |
| 3→4 | 0.323 | 0.574 | 0.714 | 0.445 | 0.830 | −0.430 |
| 4→5 | 1.310 | 1.560 | 1.560 | 1.480 | 1.730 | 0.620 |
Table 4.
Thresholds for the PM (for criteria C7–C12).
Table 4.
Thresholds for the PM (for criteria C7–C12).
| Thresholds | C7 | C8 | C9 | C10 | C11 | C12 |
|---|
| 1→2 | −1.790 | −1.640 | −1.460 | −2.100 | −1.750 | −1.120 |
| 2→3 | −1.125 | −0.985 | −0.894 | −1.317 | −1.059 | −0.552 |
| 3→4 | −0.311 | −0.126 | −0.029 | −0.314 | 0.087 | 0.397 |
| 4→5 | 0.780 | 0.860 | 0.980 | 0.770 | 1.060 | 1.310 |
Table 5.
Thresholds for the Polytomous Rasch Model (PRM) (for criteria C1–C6).
Table 5.
Thresholds for the Polytomous Rasch Model (PRM) (for criteria C1–C6).
| Thresholds | C1 | C2 | C3 | C4 | C5 | C6 |
|---|
| 1→2 | −1.468 | −1.356 | −1.16 | −1.599 | −1.018 | −2.549 |
| 2→3 | −1.09 | 0.675 | −0.523 | −0.968 | 0.033 | −1.991 |
| 3→4 | 0.424 | 0.808 | 1.102 | 0.625 | 1.103 | −0.771 |
| 4→5 | 1.946 | 2.380 | 2.215 | 2.284 | 2.610 | 0.800 |
Table 6.
Thresholds for the PRM (for criteria C7–C12).
Table 6.
Thresholds for the PRM (for criteria C7–C12).
| Thresholds | C7 | C8 | C9 | C10 | C11 | C12 |
|---|
| 1→2 | −2.268 | −2.000 | −1.589 | −2.911 | −2.225 | −1.081 |
| 2→3 | −1.707 | −1.584 | −1.545 | −2.121 | −1.764 | −1.157 |
| 3→4 | −0.651 | −0.287 | −0.145 | −0.549 | −0.244 | 0.598 |
| 4→5 | 1.114 | 1.175 | 1.384 | 1.088 | 1.632 | 1.868 |
Table 7.
Thresholds for the Rating Scale Model (RSM) (for criteria C1–C6).
Table 7.
Thresholds for the Rating Scale Model (RSM) (for criteria C1–C6).
| Thresholds | C1 | C2 | C3 | C4 | C5 | C6 |
|---|
| 1→2 | −1.463 | −1.142 | −0.986 | −1.342 | −0.724 | −2.503 |
| 2→3 | −0.927 | −0.606 | −0.450 | −0.806 | −0.188 | −1.967 |
| 3→4 | 0.386 | 0.707 | 0.864 | 0.508 | 1.125 | −0.653 |
| 4→5 | 1.839 | 2.160 | 2.316 | 1.960 | 2.578 | 0.799 |
Table 8.
Thresholds for the RSM (for criteria C7–C12).
Table 8.
Thresholds for the RSM (for criteria C7–C12).
| Thresholds | C7 | C8 | C9 | C10 | C11 | C12 |
|---|
| 1→2 | −2.284 | −2.073 | −1.911 | −2.375 | −2.020 | −1.368 |
| 2→3 | −1.748 | −1.537 | −1.376 | −1.839 | −1.484 | −0.832 |
| 3→4 | −0.435 | −0.224 | −0.062 | −0.525 | −0.171 | 0.481 |
| 4→5 | 1.018 | 1.229 | 1.391 | 0.927 | 1.282 | 1.934 |
Table 9.
Thresholds for the Partial Credit Model (PCM) model (for criteria C1–C6).
Table 9.
Thresholds for the Partial Credit Model (PCM) model (for criteria C1–C6).
| Thresholds | C1 | C2 | C3 | C4 | C5 | C6 |
|---|
| 1→2 | −1.365 | −1.258 | −1.075 | −1.484 | −0.941 | −2.377 |
| 2→3 | −0.997 | −0.613 | −0.471 | −0.883 | 0.041 | −1.838 |
| 3→4 | 0.405 | 0.763 | 1.035 | 0.592 | 1.041 | −0.702 |
| 4→5 | 1.830 | 2.239 | 2.091 | 2.147 | 2.461 | 0.761 |
Table 10.
Thresholds for the PCM model (for criteria C7–C12).
Table 10.
Thresholds for the PCM model (for criteria C7–C12).
| Thresholds | C7 | C8 | C9 | C10 | C11 | C12 |
|---|
| 1→2 | −2.113 | −1.863 | −1.483 | −2.711 | −2.072 | −1.009 |
| 2→3 | −1.573 | −1.458 | −1.419 | −1.955 | −1.622 | −1.056 |
| 3→4 | −0.589 | −0.254 | −0.122 | −0.498 | −0.213 | 0.566 |
| 4→5 | 1.051 | 1.110 | 1.305 | 1.027 | 1.532 | 1.761 |
Table 11.
Thresholds for the Generalized Partial Credit Model (GPCM) model (for criteria C1–C6).
Table 11.
Thresholds for the Generalized Partial Credit Model (GPCM) model (for criteria C1–C6).
| Thresholds | C1 | C2 | C3 | C4 | C5 | C6 |
|---|
| 1→2 | −1.366 | −1.283 | −1.107 | −1.583 | −1.076 | −2.317 |
| 2→3 | −1.026 | −0.661 | −0.542 | −1.045 | 0.084 | −1.788 |
| 3→4 | 0.408 | 0.800 | 1.144 | 0.673 | 1.306 | −0.686 |
| 4→5 | 1.865 | 2.351 | 2.238 | 2.434 | 3.086 | 0.747 |
Table 12.
Thresholds for the GPCM model (for criteria C7–C12).
Table 12.
Thresholds for the GPCM model (for criteria C7–C12).
| Thresholds | C7 | C8 | C9 | C10 | C11 | C12 |
|---|
| 1→2 | −1.916 | −1.747 | −1.455 | −2.560 | −2.026 | −0.960 |
| 2→3 | −1.320 | −1.253 | −1.120 | −1.815 | −1.577 | −1.456 |
| 3→4 | −0.444 | −0.212 | −0.086 | −0.467 | −0.210 | 0.730 |
| 4→5 | 0.887 | 0.996 | 1.108 | 0.970 | 1.495 | 2.131 |
Table 13.
Thresholds for the Graded Response Model (GRM) model (for criteria C1–C6).
Table 13.
Thresholds for the Graded Response Model (GRM) model (for criteria C1–C6).
| Thresholds | C1 | C2 | C3 | C4 | C5 | C6 |
|---|
| 1→2 | −1.739 | −1.648 | −1.506 | −2.036 | −1.462 | −2.798 |
| 2→3 | −0.795 | −0.523 | −0.365 | −0.820 | 0.049 | −1.777 |
| 3→4 | 0.450 | 0.826 | 1.040 | 0.676 | 1.448 | −0.575 |
| 4→5 | 1.842 | 2.380 | 2.435 | 2.410 | 3.247 | 0.838 |
Table 14.
Thresholds for the GRM model (for criteria C7–C12).
Table 14.
Thresholds for the GRM model (for criteria C7–C12).
| Thresholds | C7 | C8 | C9 | C10 | C11 | C12 |
|---|
| 1→2 | −2.139 | −2.000 | −1.701 | −2.916 | −2.457 | −1.839 |
| 2→3 | −1.308 | −1.168 | −1.030 | −1.766 | −1.439 | −0.942 |
| 3→4 | −0.335 | −0.129 | −0.037 | −0.422 | −0.111 | 0.545 |
| 4→5 | 0.897 | 1.021 | 1.109 | 1.021 | 1.454 | 2.088 |
Table 15.
Thresholds for the Nominal Response Model (NRM) model (for criteria C1–C6).
Table 15.
Thresholds for the Nominal Response Model (NRM) model (for criteria C1–C6).
| Thresholds | C1 | C2 | C3 | C4 | C5 | C6 |
|---|
| 1→2 | −1.371 | −1.559 | −1.280 | −1.533 | −1.130 | −2.374 |
| 2→3 | −1.203 | −0.973 | −0.791 | −1.416 | −0.454 | −2.505 |
| 3→4 | −0.598 | −0.318 | −0.158 | −0.635 | 0.038 | −1.518 |
| 4→5 | −0.096 | 0.389 | 0.539 | 0.197 | 0.891 | −0.924 |
Table 16.
Thresholds for the NRM model (for criteria C7–C12).
Table 16.
Thresholds for the NRM model (for criteria C7–C12).
| Thresholds | C7 | C8 | C9 | C10 | C11 | C12 |
|---|
| 1→2 | −2.053 | −1.855 | −1.541 | −2.707 | −2.788 | 0.692 |
| 2→3 | −1.628 | −1.504 | −1.370 | −2.577 | −2.059 | −1.898 |
| 3→4 | −1.136 | −0.993 | −0.779 | −1.622 | −1.220 | −0.455 |
| 4→5 | −0.732 | −0.608 | −0.357 | −0.859 | −0.472 | 0.438 |
Table 17.
Parameters of triangular fuzzy numbers estimated on the basis of the PM (for criteria C1–C6).
Table 17.
Parameters of triangular fuzzy numbers estimated on the basis of the PM (for criteria C1–C6).
| Category | Fuzzy Number Parameters | Criteria |
|---|
| C1 | C2 | C3 | C4 | C5 | C6 |
|---|
| 1—VL | a | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| b | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| c | 2.730 | 2.890 | 3.020 | 2.720 | 3.180 | 2.030 |
| 2—L | a | 2.730 | 2.890 | 3.020 | 2.720 | 3.180 | 2.030 |
| b | 3.067 | 3.269 | 3.395 | 3.096 | 3.606 | 2.370 |
| c | 3.403 | 3.648 | 3.769 | 3.471 | 4.032 | 2.709 |
| 3—M | a | 3.403 | 3.648 | 3.769 | 3.471 | 4.032 | 2.709 |
| b | 3.863 | 4.111 | 4.242 | 3.958 | 4.431 | 3.140 |
| c | 4.323 | 4.574 | 4.714 | 4.445 | 4.830 | 3.570 |
| 4—H | a | 4.323 | 4.574 | 4.714 | 4.445 | 4.830 | 3.570 |
| b | 4.817 | 5.067 | 5.137 | 4.963 | 5.280 | 4.095 |
| c | 5.310 | 5.560 | 5.560 | 5.480 | 5.730 | 4.620 |
| 5—VH | a | 5.310 | 5.560 | 5.560 | 5.480 | 5.730 | 4.620 |
| b | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 |
| c | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 |
Table 18.
Parameters of triangular fuzzy numbers estimated on the basis of the PM (for criteria C7–C12).
Table 18.
Parameters of triangular fuzzy numbers estimated on the basis of the PM (for criteria C7–C12).
| Category | Fuzzy Number Parameters | Criteria |
|---|
| C7 | C8 | C9 | C10 | C11 | C12 |
|---|
| 1—VL | a | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| b | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| c | 2.210 | 2.360 | 2.540 | 1.900 | 2.250 | 2.880 |
| 2—L | a | 2.210 | 2.360 | 2.540 | 1.900 | 2.250 | 2.880 |
| b | 2.543 | 2.688 | 2.823 | 2.292 | 2.596 | 3.164 |
| c | 2.875 | 3.015 | 3.106 | 2.683 | 2.941 | 3.448 |
| 3—M | a | 2.875 | 3.015 | 3.106 | 2.683 | 2.941 | 3.448 |
| b | 3.282 | 3.445 | 3.539 | 3.185 | 3.514 | 3.923 |
| c | 3.689 | 3.874 | 3.971 | 3.686 | 4.087 | 4.397 |
| 4—H | a | 3.689 | 3.874 | 3.971 | 3.686 | 4.087 | 4.397 |
| b | 4.235 | 4.367 | 4.476 | 4.228 | 4.574 | 4.854 |
| c | 4.780 | 4.860 | 4.980 | 4.770 | 5.060 | 5.310 |
| 5—VH | a | 4.780 | 4.860 | 4.980 | 4.770 | 5.060 | 5.310 |
| b | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 |
| c | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 |
Table 19.
Parameters of triangular fuzzy numbers estimated on the basis of the PRM (for criteria C1–C6).
Table 19.
Parameters of triangular fuzzy numbers estimated on the basis of the PRM (for criteria C1–C6).
| Category | Fuzzy Number Parameters | Criteria |
|---|
| C1 | C2 | C3 | C4 | C5 | C6 |
|---|
| 1—VL | a | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| b | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| c | 2.532 | 2.644 | 2.840 | 2.401 | 2.982 | 1.451 |
| 2—L | a | 2.532 | 2.644 | 2.840 | 2.401 | 2.982 | 1.451 |
| b | 2.721 | 3.660 | 3.159 | 2.717 | 3.508 | 1.730 |
| c | 2.910 | 4.675 | 3.477 | 3.032 | 4.033 | 2.009 |
| 3—M | a | 2.910 | 4.675 | 3.477 | 3.032 | 4.033 | 2.009 |
| b | 3.667 | 4.742 | 4.290 | 3.829 | 4.568 | 2.619 |
| c | 4.424 | 4.808 | 5.102 | 4.625 | 5.103 | 3.229 |
| 4—H | a | 4.424 | 4.808 | 5.102 | 4.625 | 5.103 | 3.229 |
| b | 5.185 | 5.594 | 5.659 | 5.455 | 5.857 | 4.015 |
| c | 5.946 | 6.380 | 6.215 | 6.284 | 6.610 | 4.800 |
| 5—VH | a | 5.946 | 6.380 | 6.215 | 6.284 | 6.610 | 4.800 |
| b | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 |
| c | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 |
Table 20.
Parameters of triangular fuzzy numbers estimated on the basis of the PRM (for criteria C7–C12).
Table 20.
Parameters of triangular fuzzy numbers estimated on the basis of the PRM (for criteria C7–C12).
| Category | Fuzzy Number Parameters | Criteria |
|---|
| C7 | C8 | C9 | C10 | C11 | C12 |
|---|
| 1—VL | a | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| b | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| c | 1.732 | 2.00 | 2.411 | 1.089 | 1.775 | 2.919 |
| 2—L | a | 1.732 | 2.00 | 2.411 | 1.089 | 1.775 | 2.919 |
| b | 2.013 | 2.208 | 2.433 | 1.484 | 2.006 | 2.881 |
| c | 2.293 | 2.416 | 2.455 | 1.879 | 2.236 | 2.843 |
| 3—M | a | 2.293 | 2.416 | 2.455 | 1.879 | 2.236 | 2.843 |
| b | 2.821 | 3.065 | 3.155 | 2.665 | 2.996 | 3.721 |
| c | 3.349 | 3.713 | 3.855 | 3.451 | 3.756 | 4.598 |
| 4—H | a | 3.349 | 3.713 | 3.855 | 3.451 | 3.756 | 4.598 |
| b | 4.232 | 4.444 | 4.620 | 4.270 | 4.694 | 5.233 |
| c | 5.114 | 5.175 | 5.384 | 5.088 | 5.632 | 5.868 |
| 5—VH | a | 5.114 | 5.175 | 5.384 | 5.088 | 5.632 | 5.868 |
| b | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 |
| c | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 |
Table 21.
Parameters of triangular fuzzy numbers estimated on the basis of the RSM (for criteria C1–C6).
Table 21.
Parameters of triangular fuzzy numbers estimated on the basis of the RSM (for criteria C1–C6).
| Category | Fuzzy Number Parameters | Criteria |
|---|
| C1 | C2 | C3 | C4 | C5 | C6 |
|---|
| 1—VL | a | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| b | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| c | 2.537 | 2.858 | 3.014 | 2.658 | 3.276 | 1.497 |
| 2—L | a | 2.537 | 2.858 | 3.014 | 2.658 | 3.276 | 1.497 |
| b | 2.805 | 3.126 | 3.282 | 2.926 | 3.544 | 1.765 |
| c | 3.073 | 3.394 | 3.550 | 3.194 | 3.812 | 2.033 |
| 3—M | a | 3.073 | 3.394 | 3.550 | 3.194 | 3.812 | 2.033 |
| b | 3.730 | 4.050 | 4.207 | 3.851 | 4.469 | 2.690 |
| c | 4.386 | 4.707 | 4.864 | 4.508 | 5.125 | 3.347 |
| 4—H | a | 4.386 | 4.707 | 4.864 | 4.508 | 5.125 | 3.347 |
| b | 5.113 | 5.433 | 5.590 | 5.234 | 5.852 | 4.073 |
| c | 5.839 | 6.160 | 6.316 | 5.960 | 6.578 | 4.799 |
| 5—VH | a | 5.839 | 6.160 | 6.316 | 5.960 | 6.578 | 4.799 |
| b | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 |
| c | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 |
Table 22.
Parameters of triangular fuzzy numbers estimated on the basis of the RSM (for criteria C7–C12).
Table 22.
Parameters of triangular fuzzy numbers estimated on the basis of the RSM (for criteria C7–C12).
| Category | Fuzzy Number Parameters | Criteria |
|---|
| C7 | C8 | C9 | C10 | C11 | C12 |
|---|
| 1—VL | a | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| b | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| c | 1.716 | 1.927 | 2.089 | 1.625 | 1.980 | 2.632 |
| 2—L | a | 1.716 | 1.927 | 2.089 | 1.625 | 1.980 | 2.632 |
| b | 1.984 | 2.195 | 2.357 | 1.893 | 2.248 | 2.900 |
| c | 2.252 | 2.463 | 2.624 | 2.161 | 2.516 | 3.168 |
| 3—M | a | 2.252 | 2.463 | 2.624 | 2.161 | 2.516 | 3.168 |
| b | 2.908 | 3.119 | 3.281 | 2.818 | 3.172 | 3.825 |
| c | 3.565 | 3.776 | 3.938 | 3.475 | 3.829 | 4.481 |
| 4—H | a | 3.565 | 3.776 | 3.938 | 3.475 | 3.829 | 4.481 |
| b | 4.291 | 4.502 | 4.664 | 4.201 | 4.555 | 5.208 |
| c | 5.018 | 5.229 | 5.391 | 4.927 | 5.282 | 5.934 |
| 5—VH | a | 5.018 | 5.229 | 5.391 | 4.927 | 5.282 | 5.934 |
| b | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 |
| c | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 |
Table 23.
Parameters of triangular fuzzy numbers estimated on the basis of the PCM (for criteria C1–C6).
Table 23.
Parameters of triangular fuzzy numbers estimated on the basis of the PCM (for criteria C1–C6).
| Category | Fuzzy Number Parameters | Criteria |
|---|
| C1 | C2 | C3 | C4 | C5 | C6 |
|---|
| 1—VL | a | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| b | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| c | 2.635 | 2.742 | 2.925 | 2.516 | 3.059 | 1.623 |
| 2—L | a | 2.635 | 2.742 | 2.925 | 2.516 | 3.059 | 1.623 |
| b | 2.819 | 3.065 | 3.227 | 2.816 | 3.550 | 1.893 |
| c | 3.003 | 3.387 | 3.529 | 3.117 | 4.041 | 2.162 |
| 3—M | a | 3.003 | 3.387 | 3.529 | 3.117 | 4.041 | 2.162 |
| b | 3.704 | 4.075 | 4.282 | 3.854 | 4.541 | 2.730 |
| c | 4.405 | 4.763 | 5.035 | 4.592 | 5.041 | 3.298 |
| 4—H | a | 4.405 | 4.763 | 5.035 | 4.592 | 5.041 | 3.298 |
| b | 5.118 | 5.501 | 5.563 | 5.369 | 5.751 | 4.029 |
| c | 5.830 | 6.239 | 6.091 | 6.147 | 6.461 | 4.761 |
| 5—VH | a | 5.830 | 6.239 | 6.091 | 6.147 | 6.461 | 4.761 |
| b | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 |
| c | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 |
Table 24.
Parameters of triangular fuzzy numbers estimated on the basis of the PCM (for criteria C7–C12).
Table 24.
Parameters of triangular fuzzy numbers estimated on the basis of the PCM (for criteria C7–C12).
| Category | Fuzzy Number Parameters | Criteria |
|---|
| C7 | C8 | C9 | C10 | C11 | C12 |
|---|
| 1—VL | a | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| b | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| c | 1.887 | 2.137 | 2.517 | 1.289 | 1.928 | 2.991 |
| 2—L | a | 1.887 | 2.137 | 2.517 | 1.289 | 1.928 | 2.991 |
| b | 2.157 | 2.340 | 2.549 | 1.667 | 2.153 | 2.968 |
| c | 2.427 | 2.542 | 2.581 | 2.045 | 2.378 | 2.944 |
| 3—M | a | 2.427 | 2.542 | 2.581 | 2.045 | 2.378 | 2.944 |
| b | 2.919 | 3.144 | 3.230 | 2.774 | 3.082 | 3.755 |
| c | 3.411 | 3.746 | 3.878 | 3.502 | 3.787 | 4.566 |
| 4—H | a | 3.411 | 3.746 | 3.878 | 3.502 | 3.787 | 4.566 |
| b | 4.231 | 4.428 | 4.592 | 4.265 | 4.660 | 5.163 |
| c | 5.051 | 5.110 | 5.305 | 5.027 | 5.532 | 5.761 |
| 5—VH | a | 5.051 | 5.110 | 5.305 | 5.027 | 5.532 | 5.761 |
| b | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 |
| c | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 |
Table 25.
Parameters of triangular fuzzy numbers estimated on the basis of the GPCM (for criteria C1–C6).
Table 25.
Parameters of triangular fuzzy numbers estimated on the basis of the GPCM (for criteria C1–C6).
| Category | Fuzzy Number Parameters | Criteria |
|---|
| C1 | C2 | C3 | C4 | C5 | C6 |
|---|
| 1—VL | a | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| b | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| c | 2.634 | 2.717 | 2.893 | 2.417 | 2.924 | 1.683 |
| 2—L | a | 2.634 | 2.717 | 2.893 | 2.417 | 2.924 | 1.683 |
| b | 2.804 | 3.028 | 3.176 | 2.686 | 3.504 | 1.948 |
| c | 2.974 | 3.339 | 3.458 | 2.955 | 4.084 | 2.212 |
| 3—M | a | 2.974 | 3.339 | 3.458 | 2.955 | 4.084 | 2.212 |
| b | 3.691 | 4.070 | 4.301 | 3.814 | 4.695 | 2.763 |
| c | 4.408 | 4.800 | 5.144 | 4.673 | 5.306 | 3.314 |
| 4—H | a | 4.408 | 4.800 | 5.144 | 4.673 | 5.306 | 3.314 |
| b | 5.137 | 5.576 | 5.691 | 5.553 | 6.196 | 4.030 |
| c | 5.865 | 6.351 | 6.238 | 6.434 | 7.086 | 4.747 |
| 5—VH | a | 5.865 | 6.351 | 6.238 | 6.434 | 7.086 | 4.747 |
| b | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 |
| c | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 |
Table 26.
Parameters of triangular fuzzy numbers estimated on the basis of the GPCM (for criteria C7–C12).
Table 26.
Parameters of triangular fuzzy numbers estimated on the basis of the GPCM (for criteria C7–C12).
| Category | Fuzzy Number Parameters | Criteria |
|---|
| C7 | C8 | C9 | C10 | C11 | C12 |
|---|
| 1—VL | a | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| b | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| c | 2.084 | 2.253 | 2.545 | 1.440 | 1.974 | 3.040 |
| 2—L | a | 2.084 | 2.253 | 2.545 | 1.440 | 1.974 | 3.040 |
| b | 2.382 | 2.500 | 2.713 | 1.812 | 2.198 | 2.792 |
| c | 2.680 | 2.747 | 2.880 | 2.185 | 2.423 | 2.544 |
| 3—M | a | 2.680 | 2.747 | 2.880 | 2.185 | 2.423 | 2.544 |
| b | 3.118 | 3.268 | 3.397 | 2.859 | 3.107 | 3.637 |
| c | 3.556 | 3.788 | 3.914 | 3.533 | 3.790 | 4.730 |
| 4—H | a | 3.556 | 3.788 | 3.914 | 3.533 | 3.790 | 4.730 |
| b | 4.221 | 4.392 | 4.511 | 4.251 | 4.643 | 5.430 |
| c | 4.887 | 4.996 | 5.108 | 4.970 | 5.495 | 6.131 |
| 5—VH | a | 4.887 | 4.996 | 5.108 | 4.970 | 5.495 | 6.131 |
| b | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 |
| c | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 |
Table 27.
Parameters of triangular fuzzy numbers estimated on the basis of the NRM (for criteria C1–C6).
Table 27.
Parameters of triangular fuzzy numbers estimated on the basis of the NRM (for criteria C1–C6).
| Category | Fuzzy Number Parameters | Criteria |
|---|
| C1 | C2 | C3 | C4 | C5 | C6 |
|---|
| 1—VL | a | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| b | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| c | 2.629 | 2.441 | 2.720 | 2.467 | 2.870 | 1.626 |
| 2—L | a | 2.629 | 2.441 | 2.720 | 2.467 | 2.870 | 1.626 |
| b | 2.713 | 2.734 | 2.964 | 2.526 | 3.208 | 1.560 |
| c | 2.797 | 3.027 | 3.209 | 2.584 | 3.546 | 1.495 |
| 3—M | a | 2.797 | 3.027 | 3.209 | 2.584 | 3.546 | 1.495 |
| b | 3.099 | 3.355 | 3.526 | 2.975 | 3.792 | 1.988 |
| c | 3.402 | 3.682 | 3.842 | 3.365 | 4.038 | 2.482 |
| 4—H | a | 3.402 | 3.682 | 3.842 | 3.365 | 4.038 | 2.482 |
| b | 3.653 | 4.035 | 4.191 | 3.781 | 4.465 | 2.779 |
| c | 3.904 | 4.389 | 4.539 | 4.197 | 4.891 | 3.076 |
| 5—VH | a | 3.904 | 4.389 | 4.539 | 4.197 | 4.891 | 3.076 |
| b | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 |
| c | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 |
Table 28.
Parameters of triangular fuzzy numbers estimated on the basis of the NRM (for criteria C7–C12).
Table 28.
Parameters of triangular fuzzy numbers estimated on the basis of the NRM (for criteria C7–C12).
| Category | Fuzzy Number Parameters | Criteria |
|---|
| C7 | C8 | C9 | C10 | C11 | C12 |
|---|
| 1—VL | a | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| b | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| c | 1.947 | 2.145 | 2.459 | 1.293 | 1.212 | 4.692 |
| 2—L | a | 1.947 | 2.145 | 2.459 | 1.293 | 1.212 | 4.692 |
| b | 2.160 | 2.321 | 2.545 | 1.358 | 1.576 | 3.397 |
| c | 2.372 | 2.496 | 2.630 | 1.423 | 1.941 | 2.102 |
| 3—M | a | 2.372 | 2.496 | 2.630 | 1.423 | 1.941 | 2.102 |
| b | 2.618 | 2.751 | 2.926 | 1.900 | 2.360 | 2.824 |
| c | 2.864 | 3.007 | 3.221 | 2.378 | 2.780 | 3.545 |
| 4—H | a | 2.864 | 3.007 | 3.221 | 2.378 | 2.780 | 3.545 |
| b | 3.066 | 3.199 | 3.432 | 2.760 | 3.154 | 3.992 |
| c | 3.268 | 3.392 | 3.643 | 3.141 | 3.528 | 4.438 |
| 5—VH | a | 3.268 | 3.392 | 3.643 | 3.141 | 3.528 | 4.438 |
| b | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 |
| c | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 |
Table 29.
Parameters of triangular fuzzy numbers estimated on the basis of the GRM (for criteria C1–C6).
Table 29.
Parameters of triangular fuzzy numbers estimated on the basis of the GRM (for criteria C1–C6).
| Category | Fuzzy Number Parameters | Criteria |
|---|
| C1 | C2 | C3 | C4 | C5 | C6 |
|---|
| 1—VL | a | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| b | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| c | 2.261 | 2.352 | 2.494 | 1.964 | 2.538 | 1.202 |
| 2—L | a | 2.261 | 2.352 | 2.494 | 1.964 | 2.538 | 1.202 |
| b | 2.733 | 2.914 | 3.065 | 2.572 | 3.293 | 1.713 |
| c | 3.205 | 3.477 | 3.635 | 3.180 | 4.049 | 2.223 |
| 3—M | a | 3.205 | 3.477 | 3.635 | 3.180 | 4.049 | 2.223 |
| b | 3.827 | 4.151 | 4.338 | 3.928 | 4.749 | 2.824 |
| c | 4.450 | 4.826 | 5.040 | 4.676 | 5.448 | 3.425 |
| 4—H | a | 4.450 | 4.826 | 5.040 | 4.676 | 5.448 | 3.425 |
| b | 5.146 | 5.603 | 5.737 | 5.543 | 6.348 | 4.132 |
| c | 5.842 | 6.380 | 6.435 | 6.410 | 7.247 | 4.838 |
| 5—VH | a | 5.842 | 6.380 | 6.435 | 6.410 | 7.247 | 4.838 |
| b | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 |
| c | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 |
Table 30.
Parameters of triangular fuzzy numbers estimated on the basis of the GRM (for criteria C7–C12).
Table 30.
Parameters of triangular fuzzy numbers estimated on the basis of the GRM (for criteria C7–C12).
| Category | Fuzzy Number Parameters | Criteria |
|---|
| C7 | C8 | C9 | C10 | C11 | C12 |
|---|
| 1—VL | a | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| b | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| c | 1.861 | 2.000 | 2.299 | 1.084 | 1.543 | 2.161 |
| 2—L | a | 1.861 | 2.000 | 2.299 | 1.084 | 1.543 | 2.161 |
| b | 2.277 | 2.416 | 2.634 | 1.659 | 2.052 | 2.609 |
| c | 2.692 | 2.832 | 2.970 | 2.234 | 2.561 | 3.058 |
| 3—M | a | 2.692 | 2.832 | 2.970 | 2.234 | 2.561 | 3.058 |
| b | 3.179 | 3.352 | 3.467 | 2.906 | 3.225 | 3.801 |
| c | 3.665 | 3.871 | 3.963 | 3.578 | 3.889 | 4.545 |
| 4—H | a | 3.665 | 3.871 | 3.963 | 3.578 | 3.889 | 4.545 |
| b | 4.281 | 4.446 | 4.536 | 4.300 | 4.671 | 5.316 |
| c | 4.897 | 5.021 | 5.109 | 5.021 | 5.454 | 6.088 |
| 5—VH | a | 4.897 | 5.021 | 5.109 | 5.021 | 5.454 | 6.088 |
| b | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 |
| c | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 | 8.000 |
Table 31.
The values of the fuzzy Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS).
Table 31.
The values of the fuzzy Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS).
| Communes | Fuzzy TOPSIS | | Rating |
|---|
| PM | PRM | RSM | PCM | GPCM | GRM | NRM |
|---|
| A | 0.626 | 0.604 | 0.604 | 0.607 | 0.607 | 0.606 | 0.611 | 4 |
| B | 0.644 | 0.623 | 0.625 | 0.624 | 0.624 | 0.625 | 0.623 | 3 |
| C | 0.667 | 0.648 | 0.651 | 0.650 | 0.649 | 0.651 | 0.645 | 2 |
| D | 0.689 | 0.674 | 0.676 | 0.675 | 0.674 | 0.676 | 0.670 | 1 |
| E | 0.600 | 0.578 | 0.582 | 0.581 | 0.580 | 0.578 | 0.589 | 5 |
Table 32.
Fuzzy conversion scales for comparative analysis.
Table 32.
Fuzzy conversion scales for comparative analysis.
| Fuzzy Conversion Scale CS1 [12] | Fuzzy Conversion Scale CS2 [10] |
| | Triangular fuzzy number | | Triangular fuzzy number |
| Category | a | b | c | Category | a | b | c |
| Terrible | 0.1 | 0.1 | 0.2 | Very low | 0 | 0 | 0.2 |
| Bad | 0.2 | 0.3 | 0.4 | Low | 0 | 0.2 | 0.4 |
| Normal | 0.4 | 0.5 | 0.6 | Fair | 0.3 | 0.5 | 0.7 |
| Good | 0.6 | 0.7 | 0.8 | High | 0.6 | 0.8 | 1 |
| Superb | 0.8 | 0.9 | 0.9 | Very high | 0.8 | 1 | 1 |
| Fuzzy conversion scale CS3 [14] | Fuzzy conversion scale CS4 [16] |
| Category | a | b | c | Category | a | b | c |
| Very poor | 0 | 0 | 1 | Very poor | 0 | 1 | 3 |
| Poor | 0 | 1 | 3 | Poor | 1 | 3 | 5 |
| Fair | 3 | 5 | 7 | Fair | 3 | 5 | 7 |
| Good | 7 | 9 | 10 | Good | 5 | 7 | 9 |
| Very good | 9 | 10 | 10 | Very good | 7 | 9 | 10 |
| Fuzzy conversion scale CS5 [17] | | | | |
| Category | a | b | c | | | | |
| Very low | 1 | 1 | 3 | | | | |
| Low | 1 | 3 | 5 | | | | |
| Medium | 3 | 5 | 7 | | | | |
| High | 5 | 7 | 9 | | | | |
| Very high | 7 | 9 | 9 | | | | |