Lie Group Method for Solving the Negative-Order Kadomtsev–Petviashvili Equation (nKP)

Abstract

A comprehensive study of the negative-order Kadomtsev–Petviashvili (nKP) partial differential equation by Lie group method has been presented. Initially the infinitesimal generators and symmetry reduction, which were obtained by applying the Lie group method on the negative-order Kadomtsev–Petviashvili equation, have been used for constructing the reduced equations. In particular, the traveling wave solutions for the negative-order KP equation have been derived from the reduced equations as an invariant solution. Finally, the extended improved $\left(G^{\prime }/G\right)$ method and the extended tanh method are described and applied in constructing new explicit expressions for the traveling wave solutions. Many new and more general exact solutions are obtained.

1. Introduction

It is known that all physical phenomena can be described through nonlinear partial differential equations, so finding exact solutions to these equations and studying them represents the cornerstone through which we can better understand the mechanisms of the complex physical phenomena that these equations represent. They enable us also to clearly understand the dynamic processes these equations accompaniment. Moreover, those exact solutions can also help to investigate the stability of these solutions and to test numerical analysis for these nonlinear partial differential equations. In recent years, the reduction of partial differential equations (PDEs) into ordinary differential equations (ODEs) has proven a successful idea for constructing interesting exact solutions of the nonlinear differential equations. The Lie Group method is a basic and powerful tool for obtaining symmetries for differential equations, which used for reducing the differential equations and obtaining the exact solutions [1,2,3,4,5,6]. The mathematical method in the present study is the one-parameter group transformation. In the Lie group method, the infinitesimal functions which consist of independent and dependent variables have been presented for expressing the infinitesimals. Finding the infinitesimal functions is the first and basic step in the Lie group method, through these functions the auxiliary equation can be constructed and thus we get the invariant symmetries. The infinitesimal functions are calculated by solving a system of linear partial differential equations called the determining equations that arise by applying the invariance conditions to the partial differential equations and their auxiliary conditions. Therefore, the Lie group method can be used easily to solve different types of nonlinear problems. The major characteristic of Lie group method is decreasing the number of independent variables for the partial differential equations by one. Thus, the obtained symmetries were used to reduce the negative-order Kadomtsev–Petviashvili equation to an ordinary differential equation [7]. Consequently, the travelling wave solutions are obtained as invariant solutions.

Travelling waves arise naturally in many physics phenomena, typically expresses as partial differential equations. Special classes of travelling waves that have specific properties are solitary and soliton waves [8,9]. Solitary waves, as their name implies, commonly consist of one single disturbance or a train of solitary waves at the same time and in close proximity that spread over time. So, the solitary waves may be different shapes and sizes. The most important main feature of the soliton solutions is that they propagate in the shape of pulses without any change in their identity, shape, and speed, during their travel through a nonlinear dispersive domain. There are approaches for obtaining the exact travelling wave solutions, such as, the $\left(G^{\prime }/G\right)$ expansion method [10,11], Exp-function method [12,13,14], Extended tanh method [15,16], Jacobi elliptic function expansion methods [17,18], and F—expansion methods [19].

The KdV equation has a significant role in characterization motions of long waves in a density-stratified ocean, acoustic waves on a crystal lattice, quantum mechanics, fluid mechanics, optics and plasma physics. It is also used as a model in soliton wave theory that gives rise to soliton solutions. The KdV equation is written as

$$u_t+6 u_x{u}_{xx}+u_{xxx}=0.$$

(1)

Here $u(x,t)$ the dependent variable, $x$ and $t$ are the independent variables. Equation (1) describes how waves emerge under the effects of weak nonlinearity term $u_x u_{xx}$ and weak dispersion term $u_{xxx}$. It is also extensively used for the explanation of weakly nonlinear long waves in many branches of physics and engineering [8,20,21,22,23]. Kadomtsov and Petviashivili obtained the Kadomtsev–Petviashvili equation as an extension of the KdV equation from (1 + 1) dimensions to (2 + 1) dimensions. The KP [24,25] equation is written as

$${\left(u_t+6 u_x{u}_{xx}+u_{xxx}\right)}_x+\gamma u_{yy}=0$$

(2)

with $\gamma =\pm 1$, the choice of $\gamma$ depends on the relevant magnitude of gravity and surface tension. The KP equation was used to describe the wave propagation along two spatial dimensions, $x$ and $y$, and one temporal coordinate $t$. One of the popular uses of the KP equation is as a classic model for developing and testing new mathematical techniques, e.g., in studying the dynamical system methods for water waves and in studying the problems of well-posedness in non-classical function spaces.

It is important to point out that the KdV and the KP equations both are completely integrable equations. There are different techniques for constructing the nonlinear integrable system [26,27], like bi-Hamiltonian formulation, Lax pairs and hereditary symmetry operators. The main and important properties of integrable equations are that they have an infinite number of symmetries, an infinite number of conservations laws, and they have the ability to have also the multiple soliton solutions in certain directions. The KP equation can generally be used as a model for two-dimensional shallow water waves and ion sound waves in plasma physics. The recursion operator [28,29,30,31,32,33,34,35,36] plays a significant role in the study of the integrable systems; it was presented and developed firstly by Olver [31]. The recursion operator is an integrodifferential operator which can create a new symmetry generator from a known symmetry generator for the evolution equation. The hereditary symmetry $\Phi (u)$ is a recursion operator [32] of the following hierarchy of evolution equations

$$u_t = {\Phi }^n u_x, n=0, 1, 2,\dots$$

(3)

Equation (3) gives rise to a variety of (1+1)-dimensional equations. Hence, the recursion operator $\Phi (u)$ for the KdV equation in (1) is given by [4,7]

$$\Phi (u)=-{\partial }_x^2+4u+2u_x{\partial }_x^{-1},$$

(4)

where ${\partial }_x$ denotes the total derivative with respect to $x$, and ${\partial }_x^{-1}$ is its integration operator.The inverse operator ${\partial }_x^{-1}$ is defined as

$$\left({\partial }_x^{-1}f\right) (x)=\underset{-\infty }{\overset{x}{\int }}f(t)dt.$$

(5)

As an extension of Oliver’s work which admitted the use of negative direction, which obtained in a sequence of equations of increasingly negative orders were presented by Verosky [35]. Therefore, from Equation (3) we have

$$u_t = \Phi u_x.$$

(6)

Equation (6) can be used in the negative order hierarchy as follows

$$u_t = {\Phi }^{-1} u_x,$$

(7)

which mean that the powers of $\Phi$ goes to the opposite direction [34,35,36]. Hence, the negative order equation is given by

$$\Phi u_t = u_x.$$

(8)

By substituting Equation (8) in Equation (4), we get

$$\begin{array}{l}{v}_t=w_x,\\ w_{xxx}+4 v w_x+2 v_x w=0\end{array}\}.$$

(9)

The first equation of Equation (9), yields that

$$w={\partial }_x^{-1}{v}_t.$$

(10)

By substituting Equation (10) in the second equation of (9), we obtain

$$v_{xxt}+4 v v_t+2 v_x {\partial }_x^{-1}{v}_t=0.$$

(11)

Since the negative-order Kadomtsev–Petviashvili equation also extended to the negative-order KdV equation from (1+1) dimensions to (2+1) dimensions [7], hence

$${\left(v_{xxt}+4 v v_t+2 v_x {\partial }_x^{-1}{v}_t\right)}_x+\gamma v_{yy}=0.$$

(12)

By using the potential

$$v=u_x,$$

(13)

From Equation (10), we also have

$$w=u_t.$$

(14)

Equation (13) will carry out Equation (12) to the negative order KP (nKP) equation

$${\left(u_{xxxt}+4 u_x u_{xx}+ 2u_{xx} u_t\right)}_x+\gamma u_{xyy}=0.$$

(15)

In 2017, Wazwaz [7] introduced the specific constraints that are necessary to guarantee the existence of the multiple soliton solutions for the negative-order Kadomtsev–Petviashvili equation (nKP). These soliton solutions are the only solutions presented so far.

In our work, the Lie group method is applied to study the negative-order Kadomtsev–Petviashvili equation (nKP). Basically, the Lie group analysis relies on reducing the number of independent variables by one; consequently the traveling wave solution is the only invariant solution which obtained by reducing the partial differential equation to nonlinear ordinary differential equation. The importance of this work is, to construct new exact solutions including Hyperbolic function, periodic function and rational function solutions for the negative-order Kadomtsev–Petviashvili equation by applying the extended improved $\left(G^{\prime }/G\right)$ method and the extended tanh method.

2. Lie Symmetry Group Method

Consider the negative- order Kadomtsev–Petviashvili equation (nKP) as follows [7]:

$$u_{xxxxt}+4u_{xx}^2+4u_x{u}_{xxx}+2 u_{xxx} u_t+2 u_{xx} u_{tx}+\gamma u_{xyy}=0.$$

(16)

We start by determining the Lie point symmetry generators admitted by Equation (16) so that we can reduce it to ordinary differential equation [2,3,4]. Equation (16), invariant under the one—parameter Lie group of transformations generated by (${\Gamma }_{\epsilon }=\exp (\epsilon X)$), where $\epsilon$ is the infinitesimal parameter and $X$ is the infinitesimal generator defined as

$$X\equiv {\xi }^1\frac{\partial }{\partial x}+{\xi }^2\frac{\partial }{\partial y}+{\xi }^3\frac{\partial }{\partial t}+\eta \frac{\partial }{\partial u},$$

(17)

where ${\xi }^1, {\xi }^2,{\xi }^3$ and $\eta$ are functions in $\left(x, y, t, u\right)$. The corresponding one-parameter group of infinitesimal transformations reads as

$$\begin{array}{l}{x}^{*} = x + \epsilon {\xi }^1\left( x, y,t, u \right)+O({\epsilon }^2), y^{*}=y+\epsilon {\xi }^2\left( x, y,t, u \right)+O({\epsilon }^2),\\ t^{*} = t+\epsilon {\xi }^3\left( x, y,t, u \right)+O({\epsilon }^2), u^{*} =u+\epsilon \eta \left( x, y,t, u \right)+O({\epsilon }^2)\end{array}\},$$

(18)

where $\epsilon$ is the Lie group parameter, ${\xi }^1={\frac{\partial x^{{}_{*}}}{\partial \epsilon }|}_{\epsilon =0}$, ${\xi }^2={\frac{\partial y^{{}_{*}}}{\partial \epsilon }|}_{\epsilon =0}$, ${\xi }^3={\frac{\partial t^{{}_{*}}}{\partial \epsilon }|}_{\epsilon =0}$ and $\eta ={\frac{\partial u^{{}_{*}}}{\partial \epsilon }|}_{\epsilon =0}$. The infinitesimal generator $X$ is said to be a Lie point symmetry generator for the negative-order KP equation if

$${\mathrm{Pr}}^{\left(n\right)}\left( \left\{ 16 \right\} \right)\equiv 0,$$

(19)

where $n$ represents prolongation order for each equation according to the highest derivative. Since the negative-order KP equation has at most fifth—order derivatives, therefore, the fifth prolongation of the generator must be considered in the form

$$\begin{array}{l}{\mathrm{Pr}}^{\left(5\right)}X\equiv {\xi }^1\frac{\partial }{\partial x}+{\xi }^2\frac{\partial }{\partial y}+{\xi }^3\frac{\partial }{\partial t}+\eta \frac{\partial }{\partial u}+{\eta }^x\frac{\partial }{\partial u_x}+{\eta }^t\frac{\partial }{\partial u_t}+{\eta }^{xx}\frac{\partial }{\partial u_{xx}}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\eta }^{xt}\frac{\partial }{\partial u_{xt}}+{\eta }^{xxx}\frac{\partial }{\partial u_{xxx}}+{\eta }^{xyy}\frac{\partial }{\partial u_{xyy}}+{\eta }^{xxxxt}\frac{\partial }{\partial u_{xxxxt}}\end{array}$$

(20)

where

$$\begin{array}{l}{\eta }^x=D_x\left(\eta \right)-u_x D_x\left({\xi }^1\right)-u_y D_x\left({\xi }^2\right)-u_t D_x\left({\xi }^3\right),\\ {\eta }^t=D_t\left(\eta \right)-u_x D_t\left({\xi }^1\right)-u_y D_t\left({\xi }^2\right)-u_t D_t\left({\xi }^3\right),\\ {\eta }^{xx}=D_x\left({\eta }^x\right)-u_{xx} D_x\left({\xi }^1\right)-u_{xy} D_x\left({\xi }^2\right)-u_{xt} D_x\left({\xi }^3\right),\\ {\eta }^{xt}=D_t\left({\eta }^x\right)-u_{xx} D_t\left({\xi }^1\right)-u_{xy} D_t\left({\xi }^2\right)-u_{xt} D_t\left({\xi }^3\right),\\ {\eta }^{xxx}=D_x\left({\eta }^{xx}\right)-u_{xxx} D_x\left({\xi }^1\right)-u_{xxy} D_x\left({\xi }^2\right)-u_{xxt} D_x\left({\xi }^3\right),\\ {\eta }^{xxxxt}=D_t\left({\eta }^{xxxx}\right)-u_{xxxxx} D_t\left({\xi }^1\right)-u_{xxxxy} D_t\left({\xi }^2\right)-u_{xxxxt} D_t\left({\xi }^3\right).\end{array}\}.$$

(21)

The infinitesimal generator $X$ given by Equation (17) is said to be a Lie point symmetry vector field for Equation (16) if

$${\mathrm{Pr}}^{\left(5\right)}X\left\{ \left( 16 \right) \right\}=0.$$

(22)

The infinitesimals obtained by solving the determining equations resulted from Equation (22), hence we get

$$\begin{array}{l}{\xi }^1=- c_3 x+c_4,\hspace{1em} {\xi }^2=-2 c_3 y+c_5,\hspace{1em}{\xi }^2=- c_3 t+c_6,\\ \eta =F_1(y)+\frac{1}{2}\left(2 t y-x y\right) c_1+\frac{1}{2}\left(2 t-x\right) c_2+c_3 u\end{array}\}.$$

(23)

Hence, the negative-order Kadomtsev–Petviashvili Equation (16) admits the infinite dimensional Lie symmetry algebra ${\beta }_0^{\infty }$, the basis generators of ${\beta }_0^{\infty }$ are

$$\begin{array}{l}{X}_0\equiv F_1(y)\frac{\partial }{\partial u},\hspace{1em}{X}_1\equiv x\frac{\partial }{\partial x}+2 y\frac{\partial }{\partial y}+t\frac{\partial }{\partial t}-u\frac{\partial }{\partial u}, \\ X_2\equiv \frac{\partial }{\partial x} , \hspace{1em}\hspace{1em}{X}_3\equiv \frac{\partial }{\partial y} ,\hspace{1em}{X}_4\equiv \frac{\partial }{\partial t} ,\\ X_5\equiv y \left(2 t -x\right)\frac{\partial }{\partial u} , X_6\equiv \left(2 t-x\right)\frac{\partial }{\partial u}\end{array}\}.$$

(24)

It is convenient to present the commutators of Lie algebra through its commutator table in Table 1, where the entry in the i-th row and j-the column is defined as [4]:

$$[ X_i,X_j]=X_i X_j-X_j X_i.$$

(25)

Table 1. Table of commutators of the basis operators.

	$X_1$	$X_2$	$X_3$	$X_4$	$X_5$	$X_6$	$X_7$	$X_8$
$X_1$	0	$-X_2$	$-2X_3$	$-X_4$	$4X_5$	$2X_6$	$3X_7$	$X_8$
$X_2$	$X_2$	0	0	0	$-X_7$	$-X_8$	0	0
$X_3$	$2X_3$	0	0	0	$X_6$	0	$X_8$	0
$X_4$	$X_4$	0	0	0	$2X_7$	$2 X_8$	0	0
$X_5$	$-4X_5$	$X_7$	$-X_6$	$-2X_7$	0	0	0	0
$X_6$	$-2X_6$	$X_8$	0	$-2X_8$	0	0	0	0
$X_7$	$-3X_7$	0	$-X_8$	0	0	0	0	0
$X_8$	$-X_8$	0	0	0	0	0	0	0

The commutator table is antisymmetric with its diagonal elements all zero as we have $[ X_i,X_j]=-[ X_j,X_i]$ [4,5]. Since the commuatator must table closed under its operations, since, $[ X_3,X_5]=y\frac{\partial }{\partial u}$ and $[ X_3,X_4]=2 \frac{\partial }{\partial u}$. So we must add two generator namely, $X_7\equiv y \frac{\partial }{\partial u}$ and $X_8\equiv \frac{\partial }{\partial u}$ to Equation (24) after removing $X_0$.

The adjoint action on Lie algebras is defined by the adjoint operator given by

$$A{d}_{\exp (\epsilon X_i)}⟨ X_j ⟩=e^{- \epsilon X_i} X_j e^{ \epsilon X_i}.$$

(26)

In terms of Lie brackets using Campbell–Baker–Hausdorff theorem [4,5], this operator can be rewritten as

$$A{d}_{\exp (\epsilon X_i)}⟨ X_j ⟩=X_j-\epsilon \left[ X_i,X_j\right]+\frac{{\epsilon }^2}{2!}\left[ X_i,\left[X_i,X_j\right] \right]-\cdots$$

(27)

The calculations of the adjoint action are summarized in Table 2.

Table 2. Table of adjoint representations.

Ad	$X_1$	$X_2$	$X_3$	$X_4$	$X_5$	$X_6$	$X_7$	$X_8$
$X_1$	$X_1$	$X_2 e^{ \epsilon }$	$X_3 e^{2 \epsilon }$	$X_4 e^{\epsilon }$	$X_5 e^{ - 4 \epsilon }$	$X_6 e^{- 2 \epsilon }$	$X_3 e^{- 3 \epsilon }$	$X_8 e^{-\epsilon }$
$X_2$	$X_1-\epsilon X_2$	$X_2$	$X_3$	$X_4$	$X_5+\epsilon X_7$	$X_6+\epsilon X_8$	$X_7$	$X_8$
$X_3$	$X_1-2\epsilon X_3$	$X_2$	$X_3$	$X_4$	$X_5-\epsilon X_6$	$X_6$	$X_7-\epsilon X_8$	$X_8$
$X_4$	$X_1-\epsilon X_4$	$X_2$	$X_3$	$X_4$	$X_5-2\epsilon X_7$	$X_6-2\epsilon X_8$	$X_7$	$X_8$
$X_5$	$X_1+4\epsilon X_5$	$X_2-\epsilon X_7$	$X_3+\epsilon X_6$	$X_4+2\epsilon X_7$	$X_5$	$X_6$	$X_7$	$X_8$
..	$X_1+2\epsilon X_6$	$X_2-\epsilon X_8$	$X_3$	$X_4+2\epsilon X_8$	$X_5$	$X_6$	$X_7$	$X_8$
$X_7$	$X_1+3\epsilon X_7$	$X_2$	$X_3+\epsilon X_8$	$X_4$	$X_5$	$X_6$	$X_7$	$X_8$
$X_8$	$X_1+\epsilon X_8$	$X_2$	$X_3$	$X_4$	$X_5$	$X_6$	$X_7$	$X_8$

Therefore, a symmetry generator represented by Equation (17) is a linear combination of Equation (24).

The auxiliary equation can be expressed as

$$\begin{array}{ll}\frac{dx}{- c_3 x+c_4}& =\frac{dy}{ -2 c_3 y+c_5}=\frac{dt}{- c_3 t+c_6}\\ & =\frac{du}{ F_1(y)+\frac{1}{2}\left(2 t y-x y\right) c_1+\frac{1}{2}\left(2 t-x\right) c_2+c_3 u}\end{array}$$

(28)

Invariant Solution Generated by $X_1$

Under the invariant condition of the Lie group method, the auxiliary equation will be

$$\frac{dx}{- x}=\frac{dy}{-2 y}=\frac{dt}{- t}=\frac{du}{ u}.$$

(29)

Hence the general solution is

$$u(x,y,t)=\frac{1}{t}\phi (\xi ,\delta ),$$

(30)

where $\xi =\frac{x}{t}$ and $\delta =\frac{y}{t^2}$, Substitution of Equation (30) into Equation (16), we get

$$\begin{array}{l}-5{\phi }_{\xi \xi \xi \xi }-2\delta {\phi }_{\delta \xi \xi \xi \xi }-\xi {\phi }_{\xi \xi \xi \xi \xi }+4{\phi }_{\xi \xi }^2+4{\phi }_{\xi }{\phi }_{\xi \xi \xi }-2\phi {\phi }_{\xi \xi \xi }\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-4{\phi }_{\delta }{\phi }_{\xi \xi \xi }-2\xi {\phi }_{\xi }{\phi }_{\xi \xi \xi }-4{\phi }_{\xi }{\phi }_{\xi \xi }-4_{\delta }{\phi }_{\delta \xi }{\phi }_{\xi \xi }-2\xi {\phi }_{\xi \xi }^2+\gamma {\phi }_{\delta \delta \xi }=0\end{array}$$

(31)

Apply Lie group method again on Equation (31) and the infinitesimal generator will be:

$$X\equiv {\xi }^{11}\frac{\partial }{\partial \xi }+{\xi }^2\frac{\partial }{\partial \delta }+{\eta }^{11}\frac{\partial }{\partial \phi },$$

(32)

Repeating as procedure Equations (18)–(23), we get

$${\xi }^{11}=0, {\xi }^2=0 \mathrm{and} {\eta }^{11}=\frac{C_{11}}{\sqrt{\delta }}.$$

(33)

Unfortunately, the investigation of the reduced partial differential Equation (31) again by the means of Lie symmetry techniques will not add any symmetry can be used for reducing it to ordinary differential equation. Hence, the scaling symmetry generator does not seem to be very useful.

3. Travelling Wave Solution

The travelling wave solution obtained as an invariant solution generated by linear combination of ${\mathrm{X}}_2, {\mathrm{X}}_3$, and ${\mathrm{X}}_4$. Hence, the auxiliary equation will be

$$\frac{dx}{c_4 }=\frac{dy}{ c_5 }=\frac{dt}{c_6 }=\frac{du}{0}.$$

(34)

Solving Equation (34), leads to

$$\begin{array}{l}u(x,y,t)=\phi (\xi ),\\ \xi =\alpha x+\beta y-C t.\end{array}\}$$

(35)

where $\alpha$, $\beta$ and $C$ are arbitrary constants.

To construct the travelling wave solutions, we assume the system dynamics in an infinite space with $\phi (+\infty )={\phi }_l$ and $\phi (-\infty )={\phi }_r$ thus ${\phi }_l$ and ${\phi }_r$ are arbitrary constants.

By substituting Equation (35) in Equation (16), we get

$$-C {\alpha }^4 {\phi }^{(v)}+2 {\alpha }^3\left(2 \alpha -C\right) {{\phi }^{″}}^2+2 {\alpha }^3\left(2 \alpha -C\right) {\phi }^{\prime } {\phi }^{‴}+\gamma \alpha {\beta }^2 {\phi }^{‴}=0.$$

(36)

Integrating Equation (36) twice and setting the constant of first integration to zero yields

$$-C {\alpha }^4 {\phi }^{‴}+{\alpha }^3\left(2 \alpha -C\right) {{\phi }^{\prime }}^2+\gamma \alpha {\beta }^2 {\phi }^{\prime }+M=0,$$

(37)

where $M$ is the constant of the second integration. Clearly, Equation (37) can be solved with respect to different values of $C$. The solutions arise if $C=2 \alpha$ and if $C\ne 2 \alpha$.

If $C=2 \alpha$, the general solutions of Equation (37) will be

$$u(\xi )=\{\begin{array}{l}{c}_{11}-\frac{2M}{\gamma C {\beta }^2} \xi +c_{12} \sin \left(\frac{2 \sqrt{-2 \gamma } \beta \xi }{C^2}\right)+c_{13} \cos \left(\frac{2 \sqrt{-2 \gamma } \beta \xi }{C^2}\right), \gamma <0,\\ c_{11}-\frac{2M}{\gamma C {\beta }^2} \xi +c_{12} e^{\frac{2\sqrt{2 \gamma } \beta \xi }{C^2}}+c_{13} e^{- \frac{2\sqrt{2 \gamma } \beta \xi }{C^2}},\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \gamma >0\end{array},$$

(38)

where $c_{11}$, $c_{12}$, $c_{13}$ are arbitrary constants and $\xi =\alpha x+\beta y-C t$.

In the rest of our paper, we look for the solutions of Equation (37) for $C \ne 2 \alpha$.

3.1. The Extended Improved $\left(G^{\prime }/G\right)$ Method

In this section, the extended $\left(G^{\prime }/G\right)$- method is used to obtain more general exact solutions for the negative order KP equation (nKP).The first appearance of the method of expansion $\left(G^{\prime }/G\right)$ was in 2008 when it was presented by Wang et al. [37], to search for traveling wave solutions of nonlinear partial differential equations in mathematical physics. In this method, the traveling wave solutions are expressed as a polynomial in $\left(G^{\prime }/G\right)$, where $G=G\left(\xi \right)$ is a solution to $G^{″}(\xi )+\lambda G^{\prime }(\xi )+\mu G(\xi )=0$. In 2009, Zhang et al. presented the extended improved $\left(G^{\prime }/G\right)$ method as an extension of Wang et al.’s work. The traveling wave solutions in this case are also expressed as polynomial $\left(G^{\prime }/G\right)$ but with positive and negative powers [38].

Now, our main goal is to derive exact solutions for the nonlinear Equation (37) by using the improved $\left(G^{\prime }/G\right)$- expansion method [39].Suppose that the solution of Equation (37) can be expressed by a polynomial in $\left(G^{\prime }/G\right)$ as follows:

$$U(\xi )={\displaystyle \sum _{i = 0}^N a_i {\left(\frac{G^{\prime }(\xi )}{G(\xi )}\right)}^i}+{\displaystyle \sum _{i = 1}^N b_i {\left(\frac{G^{\prime }(\xi )}{G(\xi )}\right)}^{-i}},$$

(39)

where $a_i$ and $b_i$ are unknown real constants to be determined. Expansion (39) reduces to the standard $\left(G^{\prime }/G\right)$-expansion method by setting $b_i=0$. The positive integer $N$ determined by balancing the highest order derivatives appearing in Equation (37) ${\phi }^{‴}$ with the highest order nonlinear terms ${{\phi }^{\prime }}^2$. From which, we find $N=1$.

By substituting $N=1$ in Equation (39), we get

$$U(\xi )=a_0 + a_1\frac{G^{\prime }(\xi )}{G(\xi )}+b_1 {\left(\frac{G^{\prime }(\xi )}{G(\xi )}\right)}^{-1}.$$

(40)

The function $G(\xi )$ is the general solution of the auxiliary linear ordinary differential equation

$$G^{″}(\xi )+\lambda G^{\prime }(\xi )+\mu G(\xi )=0,$$

(41)

where $\lambda$ and $\mu$ are real constants to be determined. Hence, depending on the sign of ${\lambda }^2-4\mu$, whether it is positive, negative, or equal to zero, the solutions of Equation (41) change from a hyperbolic function solutions, trigonometric periodic wave function solutions, or rational function solutions respectively. Then, the rational function $\left(G^{\prime }/G\right)$ given as follows:

$$\frac{G^{\prime }(\xi )}{G(\xi )}=\{\begin{array}{l}\frac{\sqrt{{\lambda }^2-4\mu }}{2} \tanh \left(\frac{\sqrt{{\lambda }^2-4\mu }}{2} \xi +{\xi }_0\right)-\frac{\lambda }{2},\hspace{1em}\hspace{1em}{\lambda }^2-4\mu >0, \tanh ({\xi }_0)=\frac{B}{A},\left|\frac{B}{A}\right|<1,\\ \frac{\sqrt{4\mu -{\lambda }^2}}{2}\frac{-A \sin \left(\frac{\sqrt{4\mu -{\lambda }^2}}{2} \xi \right)+B \cos \left(\frac{\sqrt{4\mu -{\lambda }^2}}{2} \xi \right)}{A \cos \left(\frac{\sqrt{4\mu -{\lambda }^2}}{2} \xi \right)+B \sin \left(\frac{\sqrt{4\mu -{\lambda }^2}}{2} \xi \right)}-\frac{\lambda }{2},\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\lambda }^2-4\mu <0,\\ \frac{A}{A \xi +B }-\frac{\lambda }{2},\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\lambda }^2-4\mu =0\end{array}$$

(42)

where $A$ and $B$ are arbitrary constants. These results can be further be written in some more easy forms depending upon the conditions on the ratio of $A$ and $B$ as

$$\frac{G^{\prime }(\xi )}{G(\xi )}=\{\begin{array}{l}\frac{\sqrt{{\lambda }^2-4\mu }}{2} \tanh \left(\frac{\sqrt{{\lambda }^2-4\mu }}{2} \xi +{\xi }_0\right)-\frac{\lambda }{2},\hspace{1em}\hspace{1em}{\lambda }^2-4\mu >0, \tanh ({\xi }_0)=\frac{B}{A},\left|\frac{B}{A}\right|<1,\\ \frac{\sqrt{{\lambda }^2-4\mu }}{2} \coth \left(\frac{\sqrt{{\lambda }^2-4\mu }}{2} \xi +{\xi }_0\right)-\frac{\lambda }{2},\hspace{1em}\hspace{1em}{\lambda }^2-4\mu >0, \coth ({\xi }_0)=\frac{B}{A},\left|\frac{B}{A}\right|>1,\\ \frac{\sqrt{4\mu -{\lambda }^2}}{2}\cot \left(\frac{\sqrt{4\mu -{\lambda }^2}}{2} \xi +{\xi }_0\right)-\frac{\lambda }{2},\hspace{1em}\hspace{1em}\hspace{1em}{\lambda }^2-4\mu <0, \cot ({\xi }_0)=\frac{B}{A},\\ \frac{A}{A \xi +B }-\frac{\lambda }{2},\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\lambda }^2-4\mu =0\end{array}.$$

(43)

By substituting Equations (40) and (41) in Equation (37) yields polynomials in ${\left(G^{\prime }/G\right)}^m$ and ${\left(G^{\prime }/G\right)}^{-m}$, ($m=0, 1,\dots , 4$). By summing together the coefficients of polynomials which have the same degree and then setting those coefficients to zero, we obtain a set of algebraic equations for $a_1$, $b_1$, $\mu$, $\lambda$ and $C$. By solving these algebraic equations, we obtain four sets of constraints:

3.1.1. Case

$$a_1=\frac{6 \alpha C}{C-2 \alpha }, b_1=0, M=0 \mathrm{and} \mu =\frac{{\lambda }^2}{4}-\frac{\gamma {\beta }^2}{4 C {\alpha }^3},$$

(44)

where $\gamma$, $C$, $\alpha$, $\beta$ and $\lambda$ are free parameters. Hence, ${\lambda }^2-4\mu =\frac{\gamma {\beta }^2}{C {\alpha }^3}$.

By substituting Equation (44) in Equation (40), we get

$$U(\xi )=a_0 + \frac{6 \alpha C}{C-2 \alpha } \frac{G^{\prime }(\xi )}{G(\xi )}.$$

(45)

Hyperbolic function solutions: When $\frac{\gamma {\beta }^2}{C {\alpha }^3}>0$, we obtain

$$U(\xi )= a_0 + \frac{6 \alpha C}{C-2 \alpha } \left(\frac{1}{2} \sqrt{\frac{\gamma {\beta }^2}{C {\alpha }^3}}\frac{A \sinh \left(\frac{1}{2} \sqrt{\frac{\gamma {\beta }^2}{C {\alpha }^3}} \xi \right)+B \cosh \left(\frac{1}{2} \sqrt{\frac{\gamma {\beta }^2}{C {\alpha }^3}} \xi \right)}{A \cosh \left(\frac{1}{2} \sqrt{\frac{\gamma {\beta }^2}{C {\alpha }^3}} \xi \right)+B \sinh \left(\frac{1}{2} \sqrt{\frac{\gamma {\beta }^2}{C {\alpha }^3}} \xi \right)}-\frac{\lambda }{2}\right).$$

(46)

where $\xi =\alpha x+\beta y-C t$.

Trigonometric function solutions: When $\frac{\gamma {\beta }^2}{C {\alpha }^3}<0$, we obtain

$$U(\xi )= a_0 + \frac{6 \alpha C}{C-2 \alpha } \left(\frac{1}{2}\sqrt{-\frac{\gamma {\beta }^2}{C {\alpha }^3}}\frac{-A \sin \left(\frac{1}{2}\sqrt{-\frac{\gamma {\beta }^2}{C {\alpha }^3}} \xi \right)+B \cos \left(\frac{1}{2}\sqrt{-\frac{\gamma {\beta }^2}{C {\alpha }^3}} \xi \right)}{A \cos \left(\frac{1}{2}\sqrt{-\frac{\gamma {\beta }^2}{C {\alpha }^3}} \xi \right)+B \sin \left(\frac{1}{2}\sqrt{-\frac{\gamma {\beta }^2}{C {\alpha }^3}} \xi \right)}-\frac{\lambda }{2}\right).$$

(47)

where $\xi =\alpha x+\beta y-C t$.

Rational function solutions: When $\frac{\gamma {\beta }^2}{C {\alpha }^3}=0$, we obtain

$$U(\xi )= a_0 + \frac{6 \alpha C}{C-2 \alpha } \left(\frac{A}{A \xi +B }-\frac{\lambda }{2}\right).$$

(48)

where $\xi =\alpha x-C t$.

3.1.2. Case

$$a_1=\frac{6 \alpha C}{C-2 \alpha }, b_1=\frac{1}{2{\alpha }^2}\frac{\gamma {\beta }^2 }{C-2 \alpha }, M=-\frac{1}{4\alpha }\frac{ {\gamma }^2 {\beta }^4 }{C-2 \alpha }, \mu =0 \mathrm{and} \lambda =0,$$

(49)

where $\gamma$, $C$, $\alpha$ and $\beta$ are free parameters. From Equation (49) ${\lambda }^2-4 \mu =0$, hence, the rational function solution is the only solution exists in this case. By substituting Equation (49) in Equation (40), we get

$$U(\xi )=a_0 + \frac{6 \alpha C}{C-2 \alpha } \frac{A}{A \xi +B }+\frac{1}{2 {\alpha }^2}\frac{\gamma {\beta }^2 }{C-2 \alpha } {\left(\frac{A}{A \xi +B }\right)}^{-1}.$$

(50)

where $\xi =\alpha x+\beta y-C t$.

3.1.3. Case

$$a_1=0, b_1=\frac{3}{2{\alpha }^2}\frac{\gamma {\beta }^2-{\lambda }^2 {\alpha }^3 C }{C-2 \alpha }, M=0 \mathrm{and} \mu =\frac{{\lambda }^2}{4}-\frac{\gamma {\beta }^2}{4 C {\alpha }^3}$$

(51)

where $\gamma$, $C$, $\alpha$, $\beta$ and $\lambda$ are free parameters. Hence, ${\lambda }^2-4 \mu =\frac{\gamma {\beta }^2}{C {\alpha }^3}$.

By substituting Equation (51) in Equation (40), we get

$$U(\xi )=a_0 +\frac{3}{2{\alpha }^2}\frac{\gamma {\beta }^2 }{C-2 \alpha } {\left(\frac{G^{\prime }(\xi )}{G(\xi )}\right)}^{-1}.$$

(52)

Hyperbolic function solutions: When $\frac{\gamma {\beta }^2}{C {\alpha }^3}>0$, we obtain

$$U(\xi )= a_0 + \frac{3}{2{\alpha }^2}\frac{\gamma {\beta }^2-{\lambda }^2 {\alpha }^3 C }{C-2 \alpha } {\left(\frac{1}{2} \sqrt{\frac{\gamma {\beta }^2}{C {\alpha }^3}}\frac{A \sinh \left(\frac{1}{2} \sqrt{\frac{\gamma {\beta }^2}{C {\alpha }^3}} \xi \right)+B \cosh \left(\frac{1}{2} \sqrt{\frac{\gamma {\beta }^2}{C {\alpha }^3}} \xi \right)}{A \cosh \left(\frac{1}{2} \sqrt{\frac{\gamma {\beta }^2}{C {\alpha }^3}} \xi \right)+B \sinh \left(\frac{1}{2} \sqrt{\frac{\gamma {\beta }^2}{C {\alpha }^3}} \xi \right)}-\frac{\lambda }{2}\right)}^{-1}$$

(53)

where $\eta =\alpha x+\beta y-C t$.

Trigonometric function solutions: When $\frac{\gamma {\beta }^2}{C {\alpha }^3}<0$, we obtain

$$U(\xi )= a_0 +\frac{3}{2{\alpha }^2}\frac{\gamma {\beta }^2-{\lambda }^2 {\alpha }^3 C }{C-2 \alpha } {\left(\frac{1}{2} \sqrt{-\frac{\gamma {\beta }^2}{C {\alpha }^3}}\frac{-A \sin \left(\frac{1}{2} \sqrt{-\frac{\gamma {\beta }^2}{C {\alpha }^3}} \xi \right)+B \cos \left(\frac{1}{2} \sqrt{-\frac{\gamma {\beta }^2}{C {\alpha }^3}} \xi \right)}{A \cos \left(\frac{1}{2} \sqrt{-\frac{\gamma {\beta }^2}{C {\alpha }^3}} \xi \right)+B \sin \left(\frac{1}{2} \sqrt{-\frac{\gamma {\beta }^2}{C {\alpha }^3}} \xi \right)}-\frac{\lambda }{2}\right)}^{-1}$$

(54)

where $\eta =\alpha x+\beta y-C t$.

Rational function solutions: When $\frac{\gamma {\beta }^2}{C {\alpha }^3}=0$, yields $\beta =0$, we obtain

$$U(\xi )= a_0 -\frac{3}{2{\alpha }^2}\frac{{\lambda }^2 {\alpha }^3 C }{C-2 \alpha } {\left(\frac{A}{A \xi +B }-\frac{\lambda }{2}\right)}^{-1}$$

(55)

where $\xi =\alpha x-C t$.

3.1.4. Case

$$a_1=\frac{6 \alpha C}{C-2 \alpha }, b_1=\frac{3}{8 {\alpha }^2}\frac{\gamma {\beta }^2 }{C-2 \alpha }, M=0, \lambda =0 \mathrm{and} \mu =-\frac{\gamma {\beta }^2}{16 C {\alpha }^3},$$

(56)

where $\gamma$, $C$, $\alpha$ and $\beta$ are free parameters. Hence, ${\lambda }^2-4 \mu =\frac{\gamma {\beta }^2}{4 C {\alpha }^3}$.

By substituting Equation (56) in Equation (40), we get

$$U(\xi )=a_0 + \frac{6 \alpha C}{C-2 \alpha }\frac{G^{\prime }(\xi )}{G(\xi )}+\frac{3}{8 {\alpha }^2}\frac{\gamma {\beta }^2 }{C-2 \alpha } {\left(\frac{G^{\prime }(\xi )}{G(\xi )}\right)}^{-1}.$$

(57)

Hyperbolic function solutions: When $\frac{\gamma {\beta }^2}{4 C {\alpha }^3}>0$, we obtain

$$\begin{array}{l}U(\xi )= a_0 + \frac{6 \alpha C}{C-2 \alpha } \left(\frac{1}{2} \sqrt{\frac{\gamma {\beta }^2}{4 c {\alpha }^3}} \frac{A \sinh \left(\frac{1}{2} \sqrt{\frac{\gamma {\beta }^2}{4 c {\alpha }^3}} \xi \right)+B \cosh \left(\frac{1}{2} \sqrt{\frac{\gamma {\beta }^2}{4 c {\alpha }^3}} \xi \right)}{A \cosh \left(\frac{1}{2} \sqrt{\frac{\gamma {\beta }^2}{4 c {\alpha }^3}} \xi \right)+B \sinh \left(\frac{1}{2} \sqrt{\frac{\gamma {\beta }^2}{4 c {\alpha }^3}} \xi \right)}\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\frac{3}{8 {\alpha }^2}\frac{\gamma {\beta }^2 }{c-2 \alpha } {\left(\frac{1}{2} \sqrt{\frac{\gamma {\beta }^2}{4 c {\alpha }^3}} \frac{A \sinh \left(\frac{1}{2} \sqrt{\frac{\gamma {\beta }^2}{4 c {\alpha }^3}} \xi \right)+B \cosh \left(\frac{1}{2} \sqrt{\frac{\gamma {\beta }^2}{4 c {\alpha }^3}} \xi \right)}{A \cosh \left(\frac{1}{2} \sqrt{\frac{\gamma {\beta }^2}{4 c {\alpha }^3}} \xi \right)+B \sinh \left(\frac{1}{2} \sqrt{\frac{\gamma {\beta }^2}{4 c {\alpha }^3}} \xi \right)}\right)}^{-1}\end{array}$$

(58)

where $\xi =\alpha x+\beta y-C t$.

Trigonometric function solutions: When $\frac{\gamma {\beta }^2}{4 C {\alpha }^3}<0$, we obtain

$$\begin{array}{l}U(\xi )= a_0 + \frac{6 \alpha c}{C-2 \alpha } \left(\frac{1}{2} \sqrt{-\frac{\gamma {\beta }^2}{4 C {\alpha }^3}}\frac{-A \sin \left(\frac{1}{2} \sqrt{-\frac{\gamma {\beta }^2}{4 C {\alpha }^3}} \xi \right)+B \cos \left(\frac{1}{2} \sqrt{-\frac{\gamma {\beta }^2}{4 C {\alpha }^3}} \xi \right)}{A \cos \left(\frac{1}{2} \sqrt{-\frac{\gamma {\beta }^2}{4 C {\alpha }^3}} \xi \right)+B \sin \left(\frac{1}{2} \sqrt{-\frac{\gamma {\beta }^2}{4 C {\alpha }^3}} \xi \right)}\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\frac{3}{8 {\alpha }^2}\frac{\gamma {\beta }^2 }{C-2 \alpha } {\left(\frac{1}{2} \sqrt{-\frac{A {\beta }^2}{4 C {\alpha }^3}}\frac{-A \sin \left(\frac{1}{2} \sqrt{-\frac{\gamma {\beta }^2}{4 C {\alpha }^3}} \xi \right)+B \cos \left(\frac{1}{2} \sqrt{-\frac{\gamma {\beta }^2}{4 C {\alpha }^3}} \xi \right)}{A \cos \left(\frac{1}{2} \sqrt{-\frac{\gamma {\beta }^2}{4 C {\alpha }^3}} \xi \right)+B \sin \left(\frac{1}{2} \sqrt{-\frac{\gamma {\beta }^2}{4 C {\alpha }^3}} \xi \right)}\right)}^{-1}\end{array}$$

(59)

where $\xi =\alpha x+ \beta y-C t$.

Rational function solutions: When $\frac{\gamma {\beta }^2}{4 C {\alpha }^3}=0$, yields $\beta =0$, we get

$$U(\xi )= a_0 + \frac{6 \alpha C}{C-2 \alpha } \left(\frac{A}{A \xi +B }\right)$$

(60)

where $\xi =\alpha x-C t$.

3.2. The Modified Extended Tanh Method with Riccati Equation

In this section, we applied the modified extended tanh method for constructing the exact solutions for the nonlinear Equation (37). The extended modified tanh method with Riccati equation mainly depends on converting non-linear ordinary differential equations into a system of algebraic equations as pervious in the extended improved $\left(G^{\prime }/G\right)$ method. Hence, the exact solutions are obtained by solving this algebraic system. Details can be found in [15].

In this method, we suppose that Equation (37) admits a solution of the infinite expansion

$$U(\xi )={\displaystyle \sum _{i = 0}^N A_i {\left(\Phi (\xi )\right)}^i}+{\displaystyle \sum _{i = 1}^N B_i {\left(\Phi (\xi )\right)}^{-i}},$$

(61)

where $N$ is a positive integer. The positive integer $N$ determined by balancing the highest order derivatives with the highest order nonlinear terms in Equation (37). As we did before. Hence, $N=1$ and Equation (61) becomes

$$U(\xi )=A_0+A_1 \Phi (\xi )+B_1 {\left(\Phi (\xi )\right)}^{-1},$$

(62)

The function $\Phi (\xi )$ is the general solution of the linear ordinary differential equation.

$${\Phi }^{\prime }(\xi )=K+{\Phi }^2(\xi ),$$

(63)

where $K$ is real constant to be determined. The Riccati Equation (63) has general solutions

$$\Phi (\xi )=\{\begin{array}{l}\begin{array}{l}-\sqrt{-K}\tanh \left(\sqrt{-K} \left(\xi +{\xi }_0\right)\right)\\ -\sqrt{-K}\coth \left(\sqrt{-K} \left(\xi +{\xi }_0\right)\right)\end{array}\},\hspace{1em}\hspace{1em}K<0,\\ \begin{array}{l}\sqrt{K}\tan \left(\sqrt{K} \left(\xi +{\xi }_0\right)\right)\\ -\sqrt{K}\cot \left(\sqrt{K} \left(\xi +{\xi }_0\right)\right)\end{array}\},\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}K>0,\\ -\frac{1}{ \xi +{\xi }_0 },\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \hspace{1em}\hspace{1em}K=0.\end{array}$$

(64)

where ${\xi }_0$ is arbitrary constant. Therefore, the shape of the exact solution will be related to $K$ sign.

By substituting Equations (18) and (19) in Equation (20) yields polynomials in ${\left(\Phi \left(\xi \right)\right)}^m$, ($m=0, 1, 2, \dots$). By summing together the coefficients of polynomials which have the same degree and then setting those coefficients to zero, we obtain a set of algebraic equations for $A_1$, $B_1$ and $K$. By solving these algebraic equations, we obtain four groups of constants:

3.2.1. Case

$$A_1=-\frac{6 \alpha C}{C-2 \alpha }, B_1=0, K=-\frac{\gamma {\beta }^2}{4 {\alpha }^3 C} \mathrm{and} M=0,$$

(65)

where $\gamma$, $C$, $\alpha$ and $\beta$ are free parameters. By substituting Equation (65) in Equations (62) and (64), we get

$$U(\xi )=\{\begin{array}{l}{A}_0+\frac{6 \alpha C}{C-2 \alpha } \sqrt{-K}\tanh \left(\sqrt{-K} \left(\xi +{\xi }_0\right)\right),\hspace{1em}\hspace{1em} K<0,\\ A_0-\frac{6 \alpha C}{C-2 \alpha }\sqrt{K}\tan \left(\sqrt{K} \left(\xi +{\xi }_0\right)\right),\hspace{1em} \hspace{1em} K>0,\\ A_0+\frac{6 \alpha C}{C-2 \alpha }\frac{1}{ \left(\xi +{\xi }_0\right) },\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \hspace{1em}\hspace{1em}K=0.\end{array}$$

(66)

where $\xi =\alpha x+\beta y-C t.$

3.2.2. Case

$$A_1=-\frac{6 \alpha C}{C-2 \alpha }, B_1=-\frac{1}{2{\alpha }^2}\frac{\gamma {\beta }^2 }{C-2 \alpha }, K=0 \mathrm{and} M=-\frac{1}{4\alpha }\frac{ {\gamma }^2 {\beta }^4 }{C-2 \alpha } \mathrm{or} M=0,$$

(67)

where $\gamma$, $C$, $\alpha$ and $\beta$ are free parameters. By substituting Equation (67) in Equations (62) and (64), we get

$$U(\xi )=A_0 + \frac{6 \alpha C}{C-2 \alpha } \frac{1}{\left(\xi +{\xi }_0\right) }+\frac{1}{2 {\alpha }^2}\frac{\gamma {\beta }^2 }{C-2 \alpha } {\left(\frac{1}{\xi +{\xi }_0 }\right)}^{-1}.$$

(68)

where $\xi =\alpha x+\beta y-C t.$

3.2.3. Case

$$A_1=0, B_1=-\frac{3}{2 {\alpha }^2}\frac{\gamma {\beta }^2 }{C-2 \alpha }, K=-\frac{\gamma {\beta }^2}{4 {\alpha }^3 C} \mathrm{and} M=0,$$

(69)

where $\gamma$, $C$, $\alpha$ and $\beta$ are free parameters. By substituting Equation (69) in Equations (62) and (64), we get

$$U(\xi )=\{\begin{array}{l}{A}_0+\frac{3}{2 {\alpha }^2}\frac{A {\beta }^2 }{C-2 \alpha }{\left(\sqrt{-K}\tanh \left(\sqrt{-K} \left(\xi +{\xi }_0\right)\right)\right)}^{-1},\hspace{1em} K<0,\\ A_0-\frac{3}{2 {\alpha }^2}\frac{A {\beta }^2 }{C-2 \alpha }{\left(\sqrt{K}\tan \left(\sqrt{K} \left(\xi +{\xi }_0\right)\right)\right)}^{-1},\hspace{1em} \hspace{1em}K>0,\\ A_0,\hspace{1em} \hspace{1em}K=\beta =0.\end{array}$$

(70)

where $\xi =\alpha x+\beta y-C t.$

3.2.4. Case

$$A_1=-\frac{6 \alpha C}{C-2 \alpha }, B_1=-\frac{3}{8 {\alpha }^2}\frac{A {\beta }^2 }{C-2 \alpha }, K=-\frac{A{\beta }^2}{16 {\alpha }^3 C} \mathrm{and} M=0,$$

(71)

where $\gamma$, $C$, $\alpha$ and $\beta$ are free parameters. By substituting Equation (71) in Equations (62) and (64), we get

$$U(\xi )=\{\begin{array}{l}{A}_0+\frac{6 \alpha C}{C-2 \alpha } \sqrt{-K}\tanh \left(\sqrt{-K} \left(\xi +{\xi }_0\right)\right)+\frac{3}{8 {\alpha }^2}\frac{A {\beta }^2 }{C-2 \alpha }{\left(\sqrt{-K}\tanh \left(\sqrt{-K} \left(\xi +{\xi }_0\right)\right)\right)}^{-1},\hspace{1em}K<0,\\ A_0-\frac{6 \alpha C}{C-2 \alpha } \sqrt{K}\tan \left(\sqrt{K} \left(\xi +{\xi }_0\right)\right)-\frac{3}{8 {\alpha }^2}\frac{A {\beta }^2 }{C-2 \alpha }{\left(\sqrt{K}\tan \left(\sqrt{K} \left(\xi +{\xi }_0\right)\right)\right)}^{-1},\hspace{1em} \hspace{1em}\hspace{1em}\hspace{1em}K>0,\\ A_0+\frac{6 \alpha C}{C-2 \alpha }\frac{1}{ \left(\xi +{\xi }_0\right) },\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}K=\beta =0\end{array}$$

(72)

where $\xi =\alpha x+\beta y-C t.$

3.3. Connection between the Extended Tanh Method and Extended Improved $\left(G^{\prime }/G\right)$ Method

All solutions obtained by the extended improved $\left(G^{\prime }/G\right)$ can be obtained by the extended tanh method with Riccati equation using the following relations:

$$U(\xi )={\displaystyle \sum _{i = 0}^N a_i {\left(\frac{G^{\prime }(\xi )}{G(\xi )}\right)}^i}+{\displaystyle \sum _{i = 1}^N b_i {\left(\frac{G^{\prime }(\xi )}{G(\xi )}\right)}^{-i}=}{\displaystyle \sum _{i = 0}^N A_i {\left(\Phi (\xi )\right)}^i}+{\displaystyle \sum _{i = 1}^N B_i {\left(\Phi (\xi )\right)}^{-i}}.$$

(73)

where $A_i$ and $B_i$ are unknown real constants to be determined in term of $a_i$ and $b_i$.

To proof Equation (73), first divide Equation (41) by $G(\xi )$ and after some simplification, we get

$${\left(\frac{G^{\prime }(\xi )}{G(\xi )}\right)}^{\prime }+ {\left(\frac{G^{\prime }(\xi )}{G(\xi )}\right)}^2+\lambda \frac{G^{\prime }(\xi )}{G(\xi )}+\mu =0,$$

(74)

Equation (74) can be written as follows:

$${\left(\frac{G^{\prime }(\xi )}{G(\xi )}\right)}^{\prime }+ {\left(\frac{G^{\prime }(\xi )}{G(\xi )}+\frac{\lambda }{2}\right)}^2+\frac{4\mu -\lambda { }^2}{4}=0,$$

(75)

Equation (75) is completely equal to Equation (63) by considering

$$\begin{array}{l}K=\frac{4\mu -\lambda { }^2}{4},\\ \Phi (\xi )=- \frac{G^{\prime }(\xi )}{G(\xi )}- \frac{\lambda }{2}.\end{array}\}$$

(76)

By substituting Equation (76) in Equation (73), yields

$$U(\xi )={\displaystyle \sum _{i = 0}^N a_i {\left(-\Phi (\xi )-\frac{\lambda }{2}\right)}^i}+{\displaystyle \sum _{i = 1}^N b_i {\left(-\Phi (\xi )-\frac{\lambda }{2}\right)}^{-i}=}{\displaystyle \sum _{i = 0}^N A_i {\left(\Phi (\xi )\right)}^i}+{\displaystyle \sum _{i = 1}^N B_i {\left(\Phi (\xi )\right)}^{-i}}.$$

(77)

Hence $A_i$ and $B_i$ can easily determined by comparing the coefficients.

For example, in Section 3.1.1, in the extended improved $\left(G^{\prime }/G\right)$ method: We have $\frac{4\mu -{\lambda }^2}{4}=-\frac{\gamma {\beta }^2}{4 C {\alpha }^3}$ and $M=0$ by using Equations (76) and (77), yields $K=-\frac{\gamma {\beta }^2}{4 C {\alpha }^3}$, $A_1=-a_i$ and $B_1=- b_i=0$ which are identical to the obtained in Equation (65).

4. Results and Discussion

The graphical representation is an essential tool to introduce the problems and clarify properly the solutions of phenomena. So, in this section, the physical explanations and graphical representations for the obtained traveling wave solutions in Section 3.1.1 are presented in Figure 1, Figure 2 and Figure 3. While the graphical representations for the other cases that presented in Section 3 are omitted for convenience. Also, we have checked all the obtained solutions in Section 3 by substituting back into the original Equation (16) and found correct.

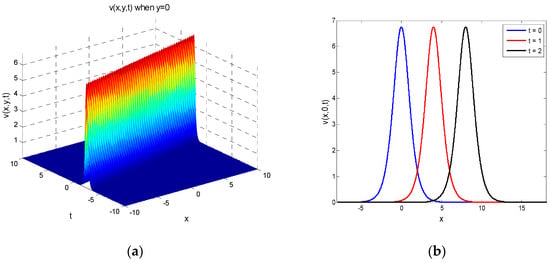
Figure 1. (a) Represents $v(x,0,t)$ in (80) for $\gamma =1$, $\beta =3$, $C=4$ and $\alpha =1$, and (b) represents $v(x,0,t)$ in Equation (80) for $\gamma =1$, $\beta =3$, $C=4$ and $\alpha =1$ and $t=0, 1, 2.$

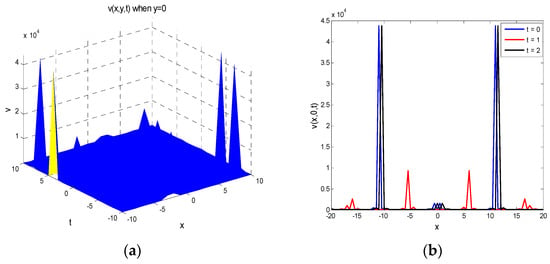
Figure 2. (a) Represents $v(x,0,t)$ in Equation (84) for $\gamma =-1$, $\beta =3$, $C=0.25$ and $\alpha =1$, and (b) represents $v(x,0,t)$ in Equation (84) for $\gamma =-1$, $\beta =3$, $C=0.25$, $\alpha =1$, and $t=0, 1, 2.$

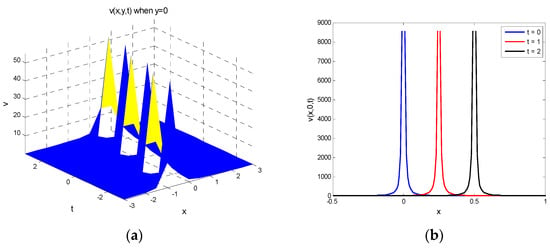
Figure 3. (a) Represents $v(x,0,t)$ in Equation (86) for $\beta =0$, $C=0.25$, $\alpha =1$, and (b) represents $v(x,0,t)$ in Equation (86) for $\gamma =-1$, $\beta =3$, $C=0.25$, $\alpha =1$ and $t=0, 1, 2.$

When $\frac{\gamma {\beta }^2}{{\alpha }^3 C}>0$, for simplicity, consider $\lambda =0$ in Equation (46) yields the following traveling wave solution:

$$u(x,y,t)= a_0 + \frac{3 \alpha C}{C-2 \alpha } \sqrt{\frac{\gamma {\beta }^2}{C {\alpha }^3}}\frac{A \sinh \left(\frac{1}{2} \sqrt{\frac{\gamma {\beta }^2}{C {\alpha }^3}} \left(\alpha x+\beta y-C t\right)\right)+B \cosh \left(\frac{1}{2} \sqrt{\frac{\gamma {\beta }^2}{C {\alpha }^3}} \left(\alpha x+\beta y-C t \right)\right)}{A \cosh \left(\frac{1}{2} \sqrt{\frac{\gamma {\beta }^2}{C {\alpha }^3}} \left(\alpha x+\beta y-C t \right)\right)+B \sinh \left(\frac{1}{2} \sqrt{\frac{\gamma {\beta }^2}{C {\alpha }^3}} \left(\alpha x+\beta y-C t \right)\right)} .$$

(78)

If we set specific values of $A$ and $B$, various known solutions can be rediscovered.

Soliton solutions: Setting $A\ne 0$ but $B=0$ in Equation (78), we obtain

$$u(x,y,t)=a_0+\frac{1}{2}\frac{6 \alpha C}{C-2 \alpha } \sqrt{\frac{\gamma {\beta }^2}{{\alpha }^3 C}}\tanh \left(\frac{1}{2}\sqrt{\frac{\gamma {\beta }^2}{{\alpha }^3 C}} \left(\alpha x+\beta y-C t\right)\right),$$

(79)

Substituting by Equation (79) in Equation (13) yield the potential

$$v(x,y,t)=u_x=\frac{3 \gamma {\beta }^2}{2 \alpha }\frac{ 1 }{C-2 \alpha } \sec h^2\left(\frac{1}{2}\sqrt{\frac{\gamma {\beta }^2}{{\alpha }^3 C}} \left(\alpha x+\beta y-C t\right)\right).$$

(80)

Solution in Equation (80) represents the exact bell-shaped soliton solutions, which appeared also as a soliton solution for the KdV, KP, and Kdv–KP equations [19]. Hence, our exact solution agrees with the physical phenomenon.

Singular soliton solutions: Setting $A=0$ but $B\ne 0$ in Equation (78), we obtain

$$v(x,y,t)=u_x=\frac{3 \gamma {\beta }^2}{2 \alpha }\frac{ 1 }{C-2 \alpha } \cos ec{h}^2\left(\frac{1}{2}\sqrt{\frac{\gamma {\beta }^2}{{\alpha }^3 C}} \left(\alpha x+\beta y-C t\right)\right).$$

(81)

Solution (81) is the singular soliton solution. Singular soliton solutions are another kind of solitary waves that appear with a singularity, usually infinite discontinuity. This solution has spike and therefore it can probably provide an explanation to the formation of Rogue waves.

Periodic solutions

When $\frac{\gamma {\beta }^2}{{\alpha }^3 C}<0$, for simplicity, consider $\lambda =0$ in Equation (47) yields the following traveling wave solution:

$$u(x,y,t)= a_0 + \frac{3 \alpha C}{C-2 \alpha } \sqrt{-\frac{\gamma {\beta }^2}{C {\alpha }^3}} \frac{-A \sin \left(\frac{1}{2}\sqrt{-\frac{\gamma {\beta }^2}{C {\alpha }^3}} \left(\alpha x+\beta y-C t\right)\right)+B \cos \left(\frac{1}{2}\sqrt{-\frac{\gamma {\beta }^2}{C {\alpha }^3}} \left(\alpha x+\beta y-C t\right)\right)}{A \cos \left(\frac{1}{2}\sqrt{-\frac{\gamma {\beta }^2}{C {\alpha }^3}} \left(\alpha x+\beta y-C t\right)\right)+B \sin \left(\frac{1}{2}\sqrt{-\frac{\gamma {\beta }^2}{C {\alpha }^3}} \left(\alpha x+\beta y-C t\right)\right)}.$$

(82)

Setting $A\ne 0$ but $B=0$ in Equation (82), we obtain

$$u(x,y,t)=a_0-\frac{ 3 \alpha C}{C-2 \alpha } \sqrt{-\frac{\gamma {\beta }^2}{{\alpha }^3 C}}\tan \left(\frac{1}{2}\sqrt{-\frac{\gamma {\beta }^2}{{\alpha }^3 C}} \left(\alpha x+\beta y-C t\right)\right),$$

(83)

Substituting by Equation (83) in Equation (13) yield the potential

$$v(x,y,t)=u_x=-\frac{1}{4} \left|\frac{ \gamma {\beta }^2}{ {\alpha }^{3}C}\right| \frac{6 \alpha C }{C-2 \alpha } {\sec }^2\left(\frac{1}{2}\sqrt{-\frac{\gamma {\beta }^2}{{\alpha }^3 C}} \left(\alpha x+\beta y-C t\right)\right).$$

(84)

Periodic traveling waves play an important role in numerous physical phenomena, including reaction–diffusion–advection systems, and self-reinforcing systems. Mathematical modeling of many intricate physical events, for instance biology, chemistry, physics, mathematical physics, and many more phenomena look like periodic traveling wave solutions.

Singular rational soliton: When $\frac{\gamma {\beta }^2}{{\alpha }^3 C}=0$, for simplicity, consider $\lambda =0$ in Equation (48) yields the following traveling wave solution:

$$u(x,y,t)=a_0+\frac{6 \alpha C}{C-2 \alpha } \frac{1}{x- C t}.$$

(85)

Substituting by Equation (85) in Equation (13) yield the potential

$$v(x,y,t)=u_x=-\frac{6 \alpha C}{C-2 \alpha } \frac{1}{{\left(x- C t\right)}^2}.$$

(86)

Many partial differential equations do not have exact solutions, and thus require the use of numerical methods to solve for approximate solutions. Since the Lie group method failed to reduce Equation (31) into an ordinary differential equation. As an extension to this work, we may investigate Equation (31) by any suitable numerical method, Such as finite element method.

5. Conclusions

The negative-order Kadomtsev–Petviashvili (nKP) equation investigated. By Lie group method, first, we analyze the symmetry of (nKP) equation including its point Lie symmetries and its Lie algebra. Consequently, the obtained symmetries have been used for reducing the (nKP) equation to an ordinary differential equation; the new exact traveling solutions were obtained via the extended improved $\left(G^{\prime }/G\right)$ method and the extended tanh method. The soliton, singular soliton, periodic singular soliton and singular solutions are obtained as special cases from our traveling wave solutions. Moreover, we proved that the extended improved $\left(G^{\prime }/G\right)$ method is completely equivalent to the extended tanh and both methods are reliable and effective and they give new exact solutions. It is important to point out that the obtained solutions in Section 3 are new exact solutions and not considered before. All the obtained solutions were verified that they satisfy the negative-order Kadomtsev–Petviashvili.