Implications of Gauge-Free Extended Electrodynamics
Abstract
1. Introduction
2. Physical Significance of the Magnetic Vector Potential
3. Road to Re-Structure: Independence of Non-Gauged Potentials
4. Derivation of the Form for the Scalar Field
5. EED and the Scalar Lonitudinal Wave
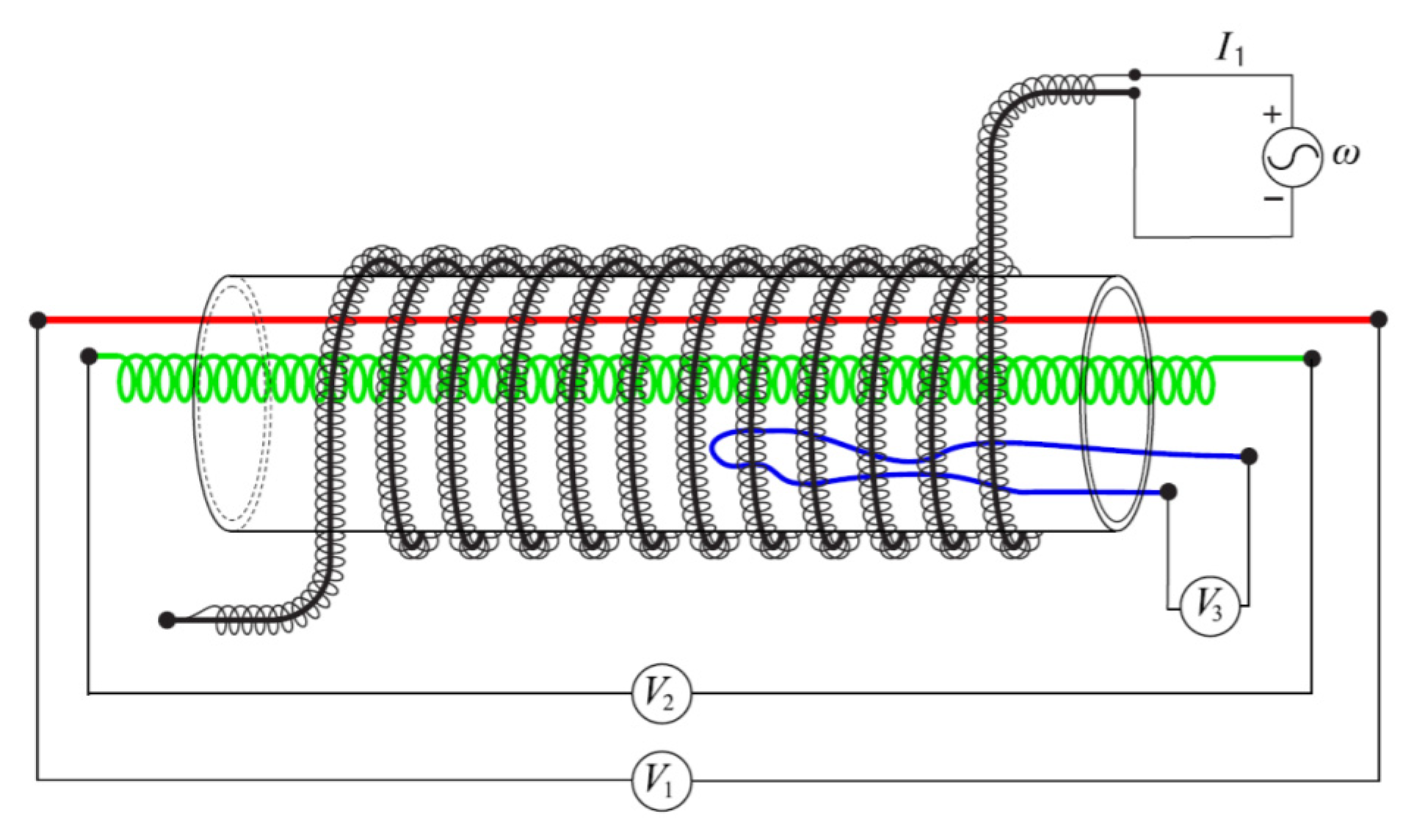
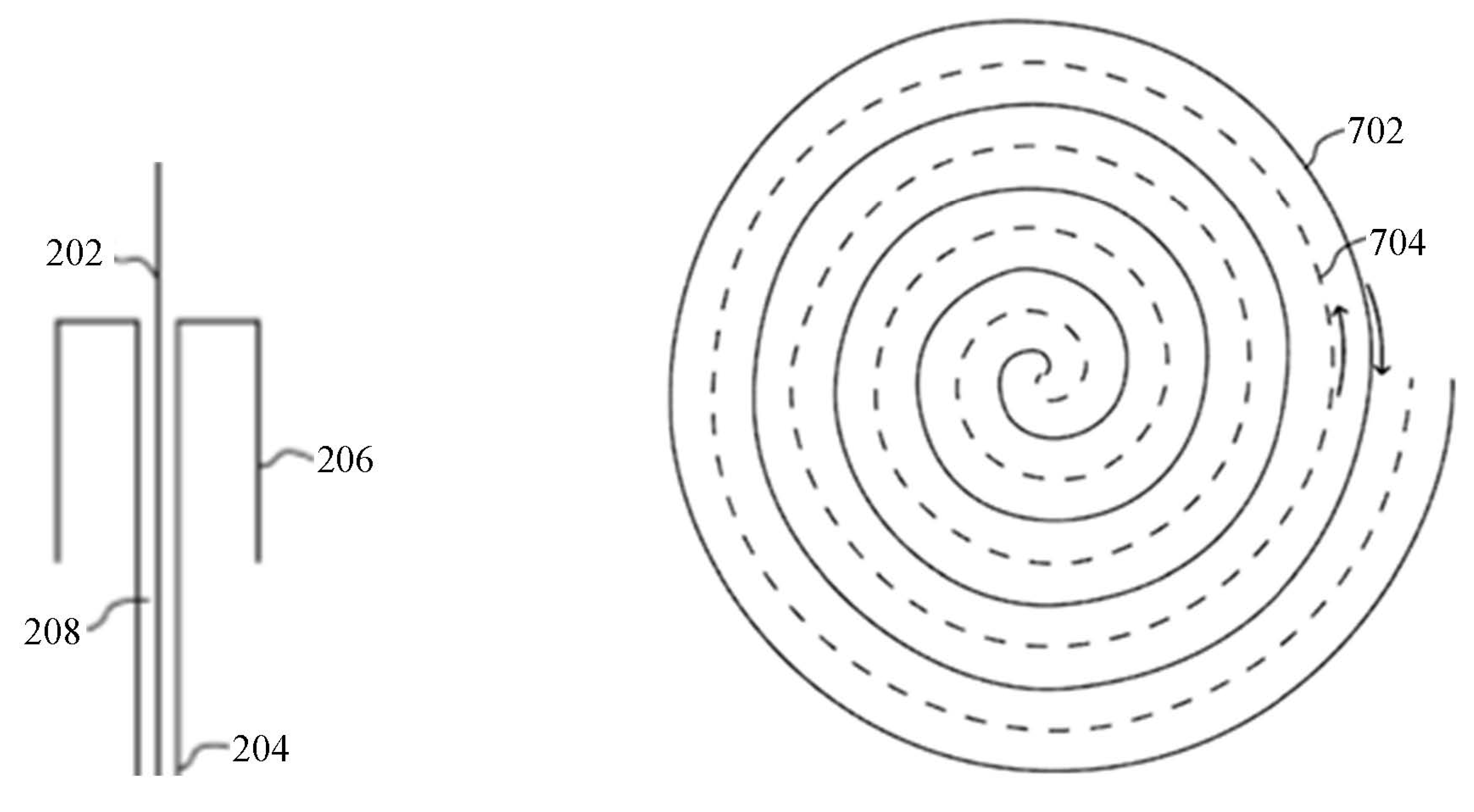
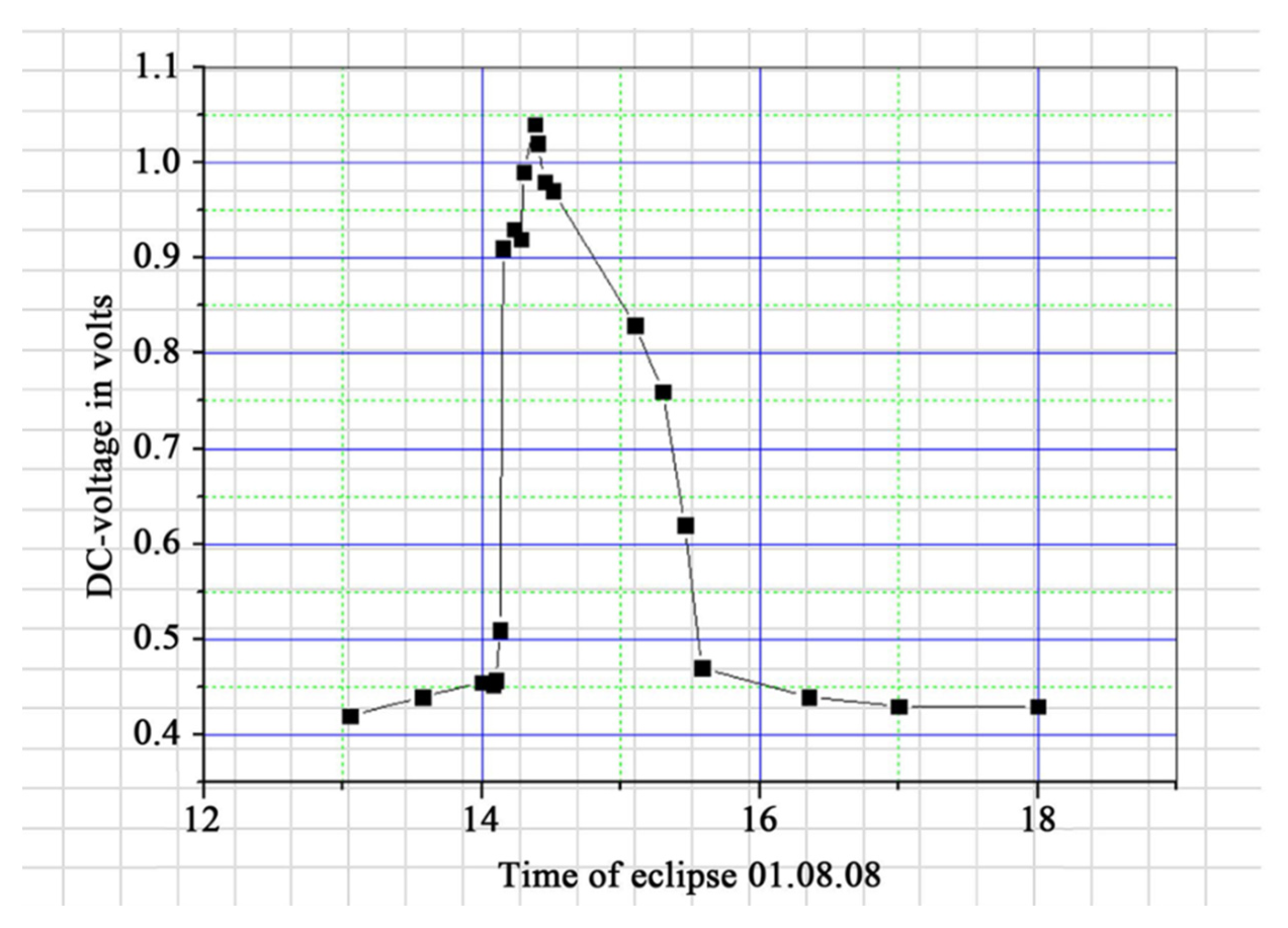
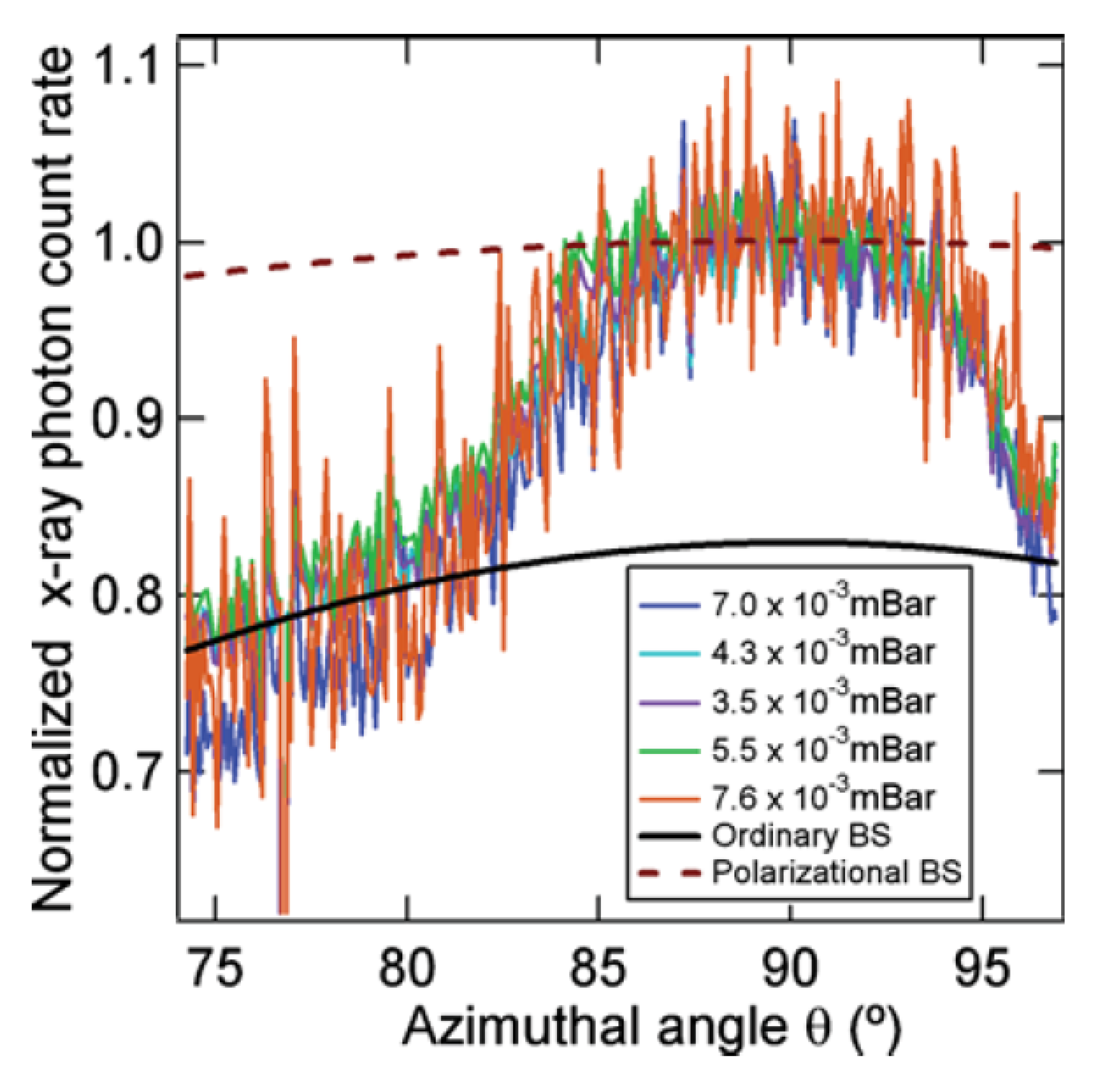
6. Evidence for the SLW: Both Inanimate and Biological
7. EED Implications for Quantum Mechanics and General Relativity
8. Conclusions and Prospects
Author Contributions
Funding
Conflicts of Interest
References
- Dyson, F.J. Feynman’s proof of the Maxwell equations. Am. J. Phys. 1990, 58, 209–211. [Google Scholar] [CrossRef]
- Woodside, D.A. Three-vector and scalar field identities and uniqueness theorems in Euclidean and Minkowski spaces. Am. J. Phys. 2009, 77, 438–446. [Google Scholar] [CrossRef]
- Hively, L.M.; Loebl, A.S. Classical and Extended Electrodynamics. Phys. Essays 2019, 32, 112–126. [Google Scholar] [CrossRef]
- Giuliani, G. Vector potential, electromagnetic induction and ‘physical meaning’. arXiv 2010, arXiv:1005.2350v1. [Google Scholar] [CrossRef]
- Barbieri, S.; Cavinato, M.; Giliberti, M. An educational path for the vector potential and it physical implications. arXiv 2013, arXiv:1303.5619v1. [Google Scholar]
- Bork, A.M. Maxwell and the vector potential. Isis 1967, 58, 210–222. [Google Scholar] [CrossRef]
- Griffiths, D.J. Introduction to Electrodynamics; Prentice-Hall: New Delhi, India, 2007. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics; John Wiley & Sons, Inc.: New York, NY, USA, 1962. [Google Scholar]
- Majumdar, P.; Ray, A. Maxwell Electrodynamics in terms of Physical Potentials. Symmetry 2019, 11, 915. [Google Scholar] [CrossRef]
- Majumdar, P.; Battacharjee, S. Gauge-free electrodynamics. arXiv 2018, arXiv:0903.4340v4. [Google Scholar]
- Nikolova, N.K.; Zimmerman, R.K. Detection of the Time-Dependent Electromagnetic Potential at 1.3 GHz, CEM-R-46; Department of Electrical and Computer Engineering, McMaster University: Hamilton, ON, Canada, 2007. [Google Scholar]
- Konopinski, E.J. What the electromagnetic vector potential describes. Am. J. Phys. 1978, 46, 499–500. [Google Scholar] [CrossRef]
- Faraday, M. Experimental Researches in Electricity; Martin, T., Ed.; London 1839–1855; Creative Media Partners LLC: New York, NY, USA, 1839; Volume 1, para. 60–71. [Google Scholar]
- Martin, T. (Ed.) Faraday’s Diary (1820–1862); G. Bells & Sons: London, UK, 1932; Volumes 1–7. [Google Scholar]
- Jones, H.B. The Life and Letters of Faraday; Cambridge University Press: London, UK, 1870; Volume 2, p. 9. [Google Scholar]
- Faraday, M. Experimental researches in electricity. Phil. Trans. R. Soc. London 1852, 142, 25–56. [Google Scholar]
- Faraday, M. On the physical character of the lines of magnetic force. Phil. Mag. 1852, 3, 401–428. [Google Scholar] [CrossRef]
- Ehrenberg, W.; Siday, R.E. The refractive index in electron optics and the principles of dynamics. Proc. Phys. Soc. 1949, B62, 8–21. [Google Scholar] [CrossRef]
- Aharonov, Y.; Bohm, D. Significance of electromagnetic potentials in the quantum theory. Phys. Rev. 1959, 115, 485–491. [Google Scholar] [CrossRef]
- Tonomura, A.; Osakabe, N.; Matsuda, T.; Kawasaki, T.; Endo, J.; Yano, S.; Yamada, H. Evidence for the Aharonov-Bohm effect with magnetic field completely shielded from electron wave. Phys. Rev. Lett. 1986, 56, 792–795. [Google Scholar] [CrossRef] [PubMed]
- Osakabe, N.; Matsuda, T.; Kawasaki, T.; Endo, J.; Tonomura, A.; Yano, S.; Yamada, H. Experimental confirmation of Aharonov-Bohm effect using a toroidal magnetic field confined by a superconductor. Phys. Rev. A 1986, 34, 815–822. [Google Scholar] [CrossRef] [PubMed]
- Webb, R.A.; Washburn, S.; Umbach, C.P.; Laibowitz, R.B. Observation of h/e Aharonov-Bohm oscillations in normal-metal rings. Phys. Rev. Lett. 1985, 54, 2696–2699. [Google Scholar] [CrossRef]
- Chandrasekhar, V.; Rooks, M.J.; Wind, S.; Prober, D.E. Observation of Aharonov-Bohm electron interference effects with periods h/e and h/2e in individual micron-size, normal-metal rings. Phys. Rev. Lett. 1985, 55, 1610–1613. [Google Scholar] [CrossRef]
- Datta, S.; Melloch, M.R.; Bandyopadhyay, S.; Noren, R.; Vaziri, M.; Miller, M.; Reifenberger, R. Novel Interference Effects between Parallel Quantum Wells. Phys. Rev. Lett. 1985, 55, 2344–2347. [Google Scholar] [CrossRef]
- Wu, T.T.; Yang, C.N. Concept of nonintegrable phase factors and global formulation of gauge fields. Phys. Rev. D 1975, 12, 3845–3857. [Google Scholar] [CrossRef]
- Olofson, A.E.S.; Squire, R.H. Is “4n + 2” a general quantum electromagnetic topological invariant? Int. J. Quantum Chem. 1995, 29, 313–330. [Google Scholar] [CrossRef]
- Van Oudenaarden, A.; Devoret, M.H.; Nazarov, Y.V.; Mooij, J.E. Magneto-electric Aharonov–Bohm effect in metal rings. Nature 1998, 391, 768–770. [Google Scholar] [CrossRef]
- Varma, R.K. Curl-free vector potential observation on the macroscale for charged particles in a magnetic field compared with that on the micro-scale: The Aharonov-Bohm effect. Phys. Scr. 2012, 86, 045009. [Google Scholar] [CrossRef]
- Varma, R.K. Observability of the effects of curl-free magnetic vector potential on the macroscale and the nature of the ‘transition amplitude wave’. Pramana J. Phys. 2010, 74, 491–511. [Google Scholar] [CrossRef]
- Varma, R.K. From hunches to surprises—Discovering macro-scale quantum phenomena in charged particle dynamics. Curr. Sci. 2012, 103, 497–511. [Google Scholar]
- Varma, R.K. Quantum manifestation of systems on the macroscale—The concept of transition state and transition amplitude wave. Pramana J. Phys. 2007, 68, 901–911. [Google Scholar] [CrossRef]
- Varma, R.K.; Puntihavelu, A.M.; Banerjee, S.B. Observation of matter wave beat phenomena in the macrodomain for electrons moving along a magnetic field. Phys. Rev. E 2002, 65, 026503. [Google Scholar] [CrossRef]
- Shukla, P.K. Curl-free vector potential observed at the macroscale. Phys. Scr. 2012, 86, 048201. [Google Scholar] [CrossRef]
- Rousseaux, G.; Kofman, R.; Minazzoli, O. The Maxwell-Lodge effect: Significance of electromagnetic potentials in the classical theory. Eur. Phys. J. D. 2008, 49, 249–256. [Google Scholar] [CrossRef]
- Blondel, A. Sur l’énoncé le plus general des lois de l’induction. C. R. Acad. Sci. 1914, 159, 674–679. [Google Scholar]
- Daibo, M.; Oshima, S.; Sasaki, Y.; Sugiyama, K. Vector Potential Coil and Transformer. IEEE Trans. Magn. 2013, 51, 100604. [Google Scholar]
- Daibo, M.; Oshima, S. Vector Potential Generation Device, Vector Potential Transformer, Shield Permeation Device, Non-Contact Space Electric Field Generation Device, Null Circuit, and Structure for Vector Potential Generation Device. U.S. Patent 10,037,840, 31 July 2018. [Google Scholar]
- Maxwell, J.C. Electromagnetic field theory. Trans. Camb. Phil. Soc. 1856, 10, 27–109. [Google Scholar]
- Maxwell, J.C. On physical lines of force Parts I-II. Phil. Mag. 1861, 21, 161–346. [Google Scholar] [CrossRef]
- Maxwell, J.C. A Dynamical Theory of the Electromagnetic Field, Part III. Phil. Trans. R. Soc. Lond. 1865, 155, 459–512. [Google Scholar]
- Einstein, A. Zur Elektrodynamik bewegter Korper. Ann. Phys. 1905, 17, 891–921. [Google Scholar] [CrossRef]
- Woodside, D.A. Uniqueness Theorems for classical four-vector fields in Euclidean and Minkowski spaces. J. Math. Phys. 1999, 40, 4911–4943. [Google Scholar] [CrossRef][Green Version]
- Woodside, D.A. Classical four-vector fields in the longitudinal gauge. J. Math. Phys. 2000, 41, 4622–4653. [Google Scholar] [CrossRef]
- Stueckelberg, E.C.G. Die Wechselwirkungskräfte in der Elektrodynamik und in der Feldtheorie der Kräfte. Helv. Phys. Acta 1938, 11, 225–244. [Google Scholar]
- Liu, L.-X.; Shao, C.-G. Re-estimatation of the upper limit on the photon mass with the solar wind method. Chin. Phys. Lett. 2012, 29, 111401. [Google Scholar] [CrossRef]
- Jack, P.M. Physical space as a quaternion structure, I.; Maxwell’s equations. A brief note. arXiv 2003, arXiv:math-ph/0307038v1. [Google Scholar]
- Saa, D. An Alternative to Classical Electromagnetic Theory; 2015 ResearchGate Preprint. Available online: https://d1wqtxts1xzle7.cloudfront.net/37878536/AnAlternativeToClassicalElectromagnetism.pdf?1433987946=&response-content-disposition=inline%3B+filename%3DAn_Alternative_to_Classical_Electromagne.pdf&Expires=1608276532&Signature=As~mC-f71v2-dlaUfmHPyp~nQ0LSZfFOcDasPZMevUK3LMM6vHIDrCgwUVtonrsLpW-CslZyp29n8aWX9VhZnpubcXWnlUCruAO2QsEjzj9yF8SeiKHu3jSy2NmFhsz9uL0Q0mo7AEo3pGBBgvARg2K1Z9ENyhzkLGwcUp7e8urymbfxbUMuYqK1tVFKXRpO3yvBbnJAHJ1~9UDbT~8H3iVM76h3G~DNe-7AAXNQ1lu644Dws~3Q5n6-NXa6HJZzvVb2R9JOw7Ln1bYzbmwlsLrdhTKvD4uLWNTntGziDjfmfh6ZIGELOx0jCL9waEYKtLNnXUC26R0BjRqdpRAPCQ__&Key-Pair-Id=APKAJLOHF5GGSLRBV4ZA (accessed on 15 December 2020).
- Saa, D. A Reformulation of Electromagnetism and Relativity Theory; 2019 ResearchGate Preprint. Available online: https://d1wqtxts1xzle7.cloudfront.net/58933563/A_Reformulation_of_Relativity_Theory20190417-23859-1hnqo2j.pdf?1555516270=&response-content-disposition=inline%3B+filename%3DA_REFORMULATION_OF_ELECTROMAGNETISM_AND.pdf&Expires=1608276592&Signature=a7NLk0dFNWZ2QgP6YpxWF-QCS~TzMVJrRuOK51pNelw6F78CjOtDftNj0yfiBV4aXyfQSBWQOxdIZoFSjB6NT2ZZLebAmkwUePFPInyNy7QWqp8B5udaqzP9aPHK-55yaeBHyZxFMVsH7OBEJhnToP2tnrtMe0PkJ5gzk7GZrta6o6rXpIeIUzWCuA8zMIR~YLSqsH4JiVELlqwE7WabLnwC~ck5z88vA7RQr3ouRsf0nuXj7rXiXnhQ2Ofa9pJ0STs8p9zL94-T0t-KelCeIPcbBKOpD1BAMFL3PP6qB71m2Le~H6PoYyTfKUi5z84szQntzEA~KPB4N6cIP399Hw__&Key-Pair-Id=APKAJLOHF5GGSLRBV4ZA (accessed on 15 December 2020).
- Williamson, J.G. A new linear theory of light and matter. IOP Conf. Ser. J. Phys. Conf. Ser. 2019, 1251, 012050. [Google Scholar] [CrossRef]
- Williamson, J.G. Fermions from bosons and the origin of the exclusion principle. Proc. MENDEL 2012. 2012. Available online: https://www.researchgate.net/profile/John_Williamson5/publication/286708466_Fermions_from_bosons_and_the_origin_of_the_exclusion_principle/links/5e9301f74585150839d69b0b/Fermions-from-bosons-and-the-origin-of-the-exclusion-principle.pdf (accessed on 15 December 2020).
- Williamson, J.G. The nature of the photon and electron. In The Nature of Light: What are Photons VI; Roychoudhuri, C., Kracklauer, A., Raedt, H.D., Eds.; SPIE: Bellingham, WA, USA, 2015. [Google Scholar]
- Williamson, J.G.; Van der Mark, M.B. Is the electron a photon with toroidal topology? Ann. Foundation L. Broglie 1997, 22, 133–160. [Google Scholar]
- Fock, V.; Podolsky, E. On the quantization of electro-magnetic waves and the interaction of charges. In Dirac Theory; Faddeev, L.D., Khalfin, L.A., Komarov, I.V., Eds.; 1932. Reprinted in Fock, V.A. Selected Work—Quantum Mechanics and Quantum Field Theory; Chapman & Hall/CRC: New York, NY, USA, 2004; pp. 225–241. [Google Scholar]
- Dirac, P.A.M.; Fock, V.A.; Podolsky, B. On Quantum Electrodynamics; Faddeev, L.D., Khalfin, L.A., Komarov, I.V., Eds.; 1932. Reprinted in Fock, V.A. Selected Work—Quantum Mechanics and Quantum Field Theory; Chapman & Hall/CRC: New York, NY, USA, 2004; pp. 243–255. [Google Scholar]
- Ohmura, T. A new formulation on the electromagnetic field. Prog. Theor. Phys. 1956, 16, 684–685. [Google Scholar] [CrossRef]
- Milner, S.R. The classical field theory of matter and electricity I: An approach from first principles. Phil. Trans. R. Soc. A Lond. 1960, 253, 185–204. [Google Scholar]
- Aharonov, Y.; Bohm, D. Further discussion of the role of electromagnetic potentials in the quantum theory. Phys. Rev. 1963, 130, 1625–1631. [Google Scholar] [CrossRef]
- Alicki, R. Generalised electrodynamics. J. Phys. A Math. Gen. 1978, 11, 1807–1813. [Google Scholar] [CrossRef]
- Cornille, P. On the propagation of inhomogeneous waves. J. Phys. D App. Phys. 1990, 23, 129–135. [Google Scholar] [CrossRef]
- Cornille, P. An electromagnetic wave approach to matter and radiation. J. Electromagn. Waves Appl. 1994, 8, 1425–1442. [Google Scholar] [CrossRef]
- Munz, C.-D.; Ones, P.; Schneider, R.; Sonnendrucker, E.; Voss, U. Maxwell’s equations when the charge conservation is not satisfied. C. R. Acad. Sci. Paris 1999, 328, 431–436. [Google Scholar] [CrossRef]
- Van Vlaenderen, K. Generalization of classical electrodynamics to admit a scalar field and longitudinal waves. Hadron. J. 2001, 24, 609–628. [Google Scholar]
- Van Vlaenderen, K.; Waser, A. A generalization of classical electrodynamics for the prediction of scalar field effects. arXiv 2003, arXiv:physics/0305098. [Google Scholar]
- Arbab, A.I.; Satti, Z.A. On the generalized Maxwell’s equations and their prediction of the electroscalar wave. Prog. Phys. 2009, 2, 8–13. [Google Scholar]
- Arbab, A.I. The modified electromagnetism and the emergent of longitudinal wave. arXiv 2018, arXiv:physics.gen-phys/1403.2687. [Google Scholar] [CrossRef]
- Jimenez, J.C.; Maroto, A.L. Cosmological magnetic fields from inflation in extended electromagnetism. Phys. Rev. D 2011, 83, 023514. [Google Scholar] [CrossRef]
- Hively, L.M.; Gaikos, G.C. Toward a more complete electrodynamic theory. Int. J. Signals Imaging Syst. Eng. 2012, 5, 3–10. [Google Scholar] [CrossRef]
- Hively, L.M. Methods and Apparatus for Generation and Detection of a Scalar Longitudinal Electromagnetic Wave. U.S. Patent 9,306,527, 3 April 2016. [Google Scholar]
- Modanese, G. High-frequency electromagnetic emission from non-local wavefunctions. Appl. Sci. 2019, 9, 1982. [Google Scholar] [CrossRef]
- Modanese, G. Design for a test for the electromagnetic coupling of non-local wave functions. Results Phys. 2019, 12, 1056–1061. [Google Scholar] [CrossRef]
- Modanese, G. Metrics with zero and almost-zero Einstein action in quantum gravity. Symmetry 2019, 11, 1288. [Google Scholar] [CrossRef]
- Modanese, G. Covariant formulation of Aharonov-Bohm electrodynamics and its application to coherent tunneling. In Unified Field Mechanics II: Formulations and Empirical Tests; World Scientific Publishing: Singapore, 2018; pp. 268–272. [Google Scholar]
- Modanese, G. Time in quantum mechanics and the local non-conservation of the probability current. Mathematics 2018, 6, 155. [Google Scholar] [CrossRef]
- Modanese, G. Electromagnetic coupling of strongly non-local quantum mechanics. Phys. B Condens. Matter 2017, 524, 81–84. [Google Scholar] [CrossRef]
- Modanese, G. Generalized Maxwell equations and charge conservation censorship. Mod. Phys. Lett. B 2017, 31, 1750052. [Google Scholar] [CrossRef]
- Poher, C.; Modanese, G. Enhanced induction into distant coils by YBCO and silicon-graphite electrodes under large current pulses. Phys. Essays 2017, 30, 435–441. [Google Scholar] [CrossRef]
- Modanese, G. Oscillating dipole with fractional quantum source in Aharonov-Bohm electrodynamics. Results Phys. 2017, 7, 480–481. [Google Scholar] [CrossRef]
- Modanese, G. A New Formulation of Aharonov-Bohm Generalized Electrodynamics. In Proceedings of the 10th International Symposium Honouring Mathematical Physicist Jean-Pierre Vigier, PortoNovo, Italy, 25–28 July 2016; World Scientific Publishing: Singapore, 2016. Available online: https://bia.unibz.it/discovery/fulldisplay/alma991005773028701241/39UBZ_INST:ResearchRepository (accessed on 15 December 2020).
- Islamov, G.G.; Tomilin, A.K. Spectral problem in a generalized theory of electromagnetic waves. In Proceedings of the 2017 Progress in Electromagnetics Research Symposium–Spring (PIERS), St. Petersburg, Russia, 22–25 May 2017. [Google Scholar] [CrossRef]
- Banduric, R. New Electrodynamics; Displacement Field Technologies: Aurora, CO, USA, 2017. [Google Scholar]
- Celani, F.; di Tommaso, A.; Vassallo, G. Maxwell’s equations and Occam’s razor. J. Condens. Matter Nucl. Sci. 2017, 25, 1–29. [Google Scholar]
- Keller, O.; Hively, L.M. Electrodynamics in curved space-time: Free space longitudinal wave propagation. Phys. Essays. 2019, 32, 282–291. [Google Scholar] [CrossRef]
- Keller, O.; Hively, L.M. Ohmura’s extended electrodynamics: Longitudinal aspects in general relativity. J. Phys. Commun. 2019, 3, 115002. [Google Scholar] [CrossRef]
- Haralick, R.A. Notes on Generalized Maxwell Equations; Privately published. Available online: https://emediapress.com/robertharalick/scalar/?hop=robitai (accessed on 15 December 2020).
- Donev, S.; Tashkova, M. Linear Connection Interpretation of Extended Electrodynamics. In Proceedings of the 11th International Conference Geometry, Integrability and Quantization, Varna, Bulgaria, 5–10 June 2009; Mladenov, I.M., Vilasi, G., Yoshioka, A., Eds.; Avangard Prima Publishing: Sofia, Bulgaria, 2010; pp. 119–126. [Google Scholar]
- El-Nabulsi, R.A. On nonlocal complex Maxwell equations and wave motion in electrodynamics and dielectric media. Opt. Quant. Electron. 2018, 50, 170. [Google Scholar] [CrossRef]
- Müller, L.; Szabo, R.J. Extended Quantum Field Theory, Index Theory, and the Parity Anomaly. Commun. Math. Phys. 2018, 362, 1049–1109. [Google Scholar] [CrossRef]
- Milton, K.A.; Abalo, E.K.; Parashar, P.; Pourtolami, N.; Wagner, J. PT-symmetric quantum electrodynamics and unitarity. Phil. Trans. R. Soc. A 2013, 371, 20120057. [Google Scholar] [CrossRef][Green Version]
- El-Nabulsi, R.A. Fourth-order Ginzburg-Landau differential equation a la Fisher-Kolmogorov and its implications in superconductivity. Phys. C 2019, 567, 1353545. [Google Scholar] [CrossRef]
- Danese, A.E. Advanced Calculus (Vol. I); Allyn & Bacon Inc.: Boston, MA, USA, 1965. [Google Scholar]
- Valone, T. (Ed.) Nikola Tesla’s Electricity Unplugged; Adventures Unlimited Press: Kempton, IL, USA, 2013. [Google Scholar]
- Monstein, C.; Wesley, J.P. Observation of scalar longitudinal electrodynamic waves. Europhys. Lett. 2002, 59, 514–520. [Google Scholar] [CrossRef]
- Meyl, K. Teslastrahlumg—Die drahtlose Ubertragung von Skallerwellen. In Proceedings of the INET Congress Aumenergie—Technologie 2000, Bregenz, Austria, 15–16 April 2000. [Google Scholar]
- Okun, L.B. Tests of electric charge conservation and the Pauli Principle. Sov. Phys. Usp. 1989, 32, 543–547. [Google Scholar] [CrossRef]
- Agostini, M.; Appel, S.; Bellinik, G.; Benzigero, J.; Bickd, D.; Bonfinij, G.; Bravoq, D.; Caccianigak, B.; Calapricen, F.; Caminata, A.; et al. Test of electric charge conservation with borexino. Phys. Rev. Lett. 2015, 115, 231802. [Google Scholar] [CrossRef] [PubMed]
- Jedele, A.; McIntosh, A.B.; Hagel, K.; Huang, M.; Heilborn, L.; Kohley, Z.; May, L.W.; McCleskey, E.; Youngs, M.; Zarrella, A.; et al. Characterizing neutron-proton equilibration in nuclear reactions with subzeptosecond resolution. Phys. Rev. Lett. 2017, 118, 062501. Available online: https://cyclotron.tamu.edu/progress-reports/2015-2016/2%20Heavy%20Ion%20Reactions/II_37-40_Characterizing%20neutron-proton%20equilibration%20in%20nuclear%20reactions%20with%20sub-zeptosecond.pdf (accessed on 15 December 2020). [CrossRef]
- Jezouin, S.; Iftikhar, Z.; Anthore, A.; Parmentier, F.D.; Gennser, U.; Cavanna, A.; Ouerghi, A.; Levkivskyi, I.P.; Idrisov, E.; Sukhorukov, E.V.; et al. Controlling charge quantization with quantum fluctuations. Nature 2016, 536, 58–62. [Google Scholar] [CrossRef]
- Ramo, S.; Whinnery, J.R.; van Duzer, T. Fields and Waves in Communication Electronics; John Wiley & Sons: New York, NY, USA, 1967; p. 332ff. [Google Scholar]
- Park, L. Seismic Activity Detector. U.S. Patent 8,023,360, 29 August 2008. [Google Scholar]
- Zaimidoroga, O. An electroscalar energy of the sun. J. Mod. Phys. 2016, 7, 806–818. [Google Scholar] [CrossRef]
- Wesley, J.P. Weber electrodynamics: Part I—General theory, steady current effects. Found. Phys. Lett. 1990, 3, 443–469. [Google Scholar] [CrossRef]
- Camara, C.G.; Escobar, J.V.; Hird, J.R.; Putterman, S.J. Correlation between nanosecond x-ray flashes and stick-slip friction in peeling tape. Nature 2008, 455, 1089–1092. [Google Scholar] [CrossRef]
- Constable, E.; Horvat, J.; Lewis, R.A. Mechanisms of X-ray emission from peeling of adhesive tape. Appl. Phys. Lett. 2010, 97, 131502. [Google Scholar] [CrossRef]
- Szabo, I.; Sodderman, M.; Leanza, L.; Zoratti, M.; Gulbins, E. Single-point mutations of a lysine residue change function of Bax and Bcl-xL expressed in Bax- and Bak-less mouse embryonic fibroblasts: Novel insights into the molecular mechanisms of Bax-induced apoptosis. Cell Death Differ. 2011, 18, 427–438. [Google Scholar] [CrossRef]
- Peralta, R.G.; Andino, S. Electrical neuroimaging with irrotational sources. Comput. Math. Methods Med. 2015, 801037. [Google Scholar] [CrossRef]
- Andreev, E.; Dovbeshko, G.; Krasnoholovets, V. The study of the influence of the TESLAR technology on aqueous solution of some bio-molecules. Res. Lett. Phys. Chem. 2007, 94286. [Google Scholar] [CrossRef]
- Krasnoholovets, V.; Tane, J.L. An extended interpretation of the thermodynamic theory including an additional energy associated with a decrease in mass. Int. J. Simul. Model Process 2006, 2, 67–79. [Google Scholar] [CrossRef]
- Alburger, D.E.; Harbottle, G.; Norton, E.F. Half-life of 32Si. Earth Planet. Sci. Lett. 1986, 78, 168–176. [Google Scholar] [CrossRef]
- Parkhomov, A.G. Deviations from beta radioactivity exponential drop. J. Mod. Phys. 2011, 2, 8635. [Google Scholar] [CrossRef]
- Jenkins, J.H.; Fischbach, E.; Javorsek, D., II; Lee, R.H.; Sturrock, P.A. Concerning the time dependence of the decay rate of 137Cs. Appl. Radiat. Isot. 2013, 74, 50–55. [Google Scholar] [CrossRef] [PubMed]
- O’Keefe, D.; Morreale, B.L.; Lee, R.H.; Buncher, J.B.; Jenkins, J.H.; Fischbach, E.; Gruenwald, T.; Javorsek, D., II; Sturrock, P.A. Spectral content of 22Na/44Ti decay data: Implications for a solar influence. Astrophys. Space Sci. 2013, 344, 297–303. [Google Scholar] [CrossRef]
- Mohsinally, T.; Fancher, S.; Czemy, M.; Fischbach, E.; Gruenwald, J.T.; Heim, J.; Jenkins, J.H.; Nistor, J.; O’Keefe, D. Evidence for correlations between fluctuations in 54Mn decay rates and solar storms. Astropart. Phys. 2016, 75, 29–37. [Google Scholar] [CrossRef]
- Sturrock, P.A.; Steinitz, G.; Fischbach, E.; Parkhornov, A.; Scargle, J.D. Analysis of beta-decay data acquired at the Physikalisch-Technische Bundesanstalt: Evidence of a solar influence. Astropart. Phys. 2016, 84, 8–14. [Google Scholar] [CrossRef]
- Cook, N.D. Models of the Atomic Nucleus: Unification Through a Lattice of Nucleons, 2nd ed.; Springer: Berlin, Germany, 2010; ISBN 978-3642147364. [Google Scholar]
- Feynman, R. QED—The Strange Theory of Light and Matter; Princeton University Press: Princeton, NJ, USA, 1985. [Google Scholar]
- Dyson, F.J. Divergence of perturbation theory in quantum electrodynamics. Phys. Rev. 1952, 85, 631–632. [Google Scholar] [CrossRef]
- Morel, L. Determination of the fine structure constant with an accuracy of 81 parts per trillion. Nature 2020, 588, 61–65. [Google Scholar] [CrossRef]
- Beautiful Bond. Nature 2017, 547, 257–258.
- Duplantier, B.; Jolicceur, T. Short range Flaws. Nature 1982, 356, 24. [Google Scholar] [CrossRef]
- Bailin, D. Gauge Field Theory. Nature 1976, 260, 736. [Google Scholar] [CrossRef]
- Ellis, J. The need for new physics. Nature 2012, 481, 24. [Google Scholar] [CrossRef] [PubMed]
- Zilberti, L. The misconception of closed magnetic flux lines. IEEE Magn. Lett. 2017, 8, 1306005. [Google Scholar] [CrossRef]
- Arrayas, A.; Bouwmeester, D.; Trueba, J.L. Knots in electromagnetism. Phys. Rep. 2017, 667, 1–61. [Google Scholar] [CrossRef]
- Kedia, H.; Foster, D.; Dennis, M.R.; Irvine, W.T.M. Weaving knotted vector fields with tunable helicity. Phys. Rev. Lett. 2016, 117, 274501. [Google Scholar] [CrossRef]
- Jhajj, N.; Larkin, I.; Rosenthal, E.W.; Zahedpour, S.; Wahlstrand, J.K.; Milchberg, H.M. Spatiotemporal optical vortices. Phys. Rev. X 2016, 6, 031037. [Google Scholar] [CrossRef]
- Kedia, H.; Bialynicki-Birula, I.; Peralta-Salas, D.; Irvine, W.T.M. Tying Knots in Light Fields. Phys. Rev. Lett. 2013, 111, 150404. [Google Scholar] [CrossRef]
- Dalhuisen, J.W.; Bouwmeester, D. Twistors and electromagnetic knots. J. Phys. A Math. Theor. 2012, 45, 135201. [Google Scholar] [CrossRef]
- Barrio, R.; Blesa, F.; Serrano, S. Topological changes in periodicity hubs of dissipative systems. Phys. Rev. Lett. 2012, 108, 214102. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, R.E.; Moffatt, H.K.; Pesci, A.I. Topological constraints and their breakdown in dynamical evolution. Nonlinearity 2012, 25, R85–R98. [Google Scholar] [CrossRef][Green Version]
- Irvine, W.T.M.; Bouwmeester, D. Linked and knotted beams of light. Nature Phys. 2008, 4, 718–720. [Google Scholar] [CrossRef]
- Chubykalo, A.E.; Espinoza, A. Unusual formations of the free electromagnetic field in vacuum. J. Phys. A 2002, 35, 8043–8053. [Google Scholar] [CrossRef]
- Gilmore, R. Topological analysis of chaotic dynamical systems. Rev. Mod. Phys. 1998, 70, 1455–1529. [Google Scholar] [CrossRef]
- Rafiada, A.F.; Trueba, J.L. Two properties of electromagnetic knots. Phys. Lett. A 1997, 232, 25–33. [Google Scholar]
- Marsh, G.E. Force-Free Magnetic Fields: Solutions, Topology and Applications; World Scientific Publishing: Singapore, 1996. [Google Scholar]
- Ranada, A. A topological theory of the electromagnetic field. Lett. Math. Phys. 1989, 18, 97–106. [Google Scholar] [CrossRef]
- McDonald, K.L. Topology of steady current magnetic fields. Am. J. Phys. 1954, 22, 586–596. [Google Scholar] [CrossRef]
- Kedia, H.; Peralta-Salas, D.; Irvine, W.T.M. When do knots in light stay knotted? J. Phys. A Math. Theor. 2018, 51, 025204. [Google Scholar] [CrossRef]
- Martins, A.A.; Pinheiro, M.J. Fluidic electrodynamics: Approach to electromagnetic propulsion. Phys. Fluids 2009, 21, 097103. [Google Scholar] [CrossRef]
- Kleckner, D.; Irvine, W.T.M. Creation and Dynamics of knotted vortices. Nat. Phys. 2013, 9, 253–258. [Google Scholar] [CrossRef]
- Scheeler, M.W.; van Rees, W.M.; Kedia, H.; Kleckner, D.; Irvine, W.T.M. Linking fluids as they twist and writhe. Science 2017, 357, 487–491. [Google Scholar] [CrossRef] [PubMed]
- Spirichev, Y.A. About Longitudinal Waves of an Electromagnetic Field. Privately Published. 2017. Available online: https://scholar.google.com/scholar?hl=en&as_sdt=0%2C6&q=%22About+Longitudinal+Waves+of+an+Electromagnetic+Field%22&btnG= (accessed on 16 December 2020).
- Spergel, D. The dark side of cosmology: Dark matter and dark energy. Science 2015, 347, 1100–1102. [Google Scholar] [CrossRef] [PubMed]
- Saa, D. General Covariance of Maxwell’s Equations. 2019 Preprint (Eq. 3). Available online: https://www.researchgate.net/publication/332119339 (accessed on 15 December 2020).
- Li, C.; Wan, L.; Wei, Y.; Wang, J. Definition of current density in the presence of a non-local potential. Nanotechnology 2011, 19, 115412. [Google Scholar] [CrossRef]


| Item | Brief Description of Testable Prediction | Reference |
|---|---|---|
| 1 | The SLW drivers are: AL= ∇α⇔EL= ∇e⇔JL= ∇κ⇔B = 0. | Equation (15) * |
| 2 | The SLW has a dynamical scalar field, C = ∇∙A + εμ∂Φ/∂t. | Equation (12) |
| 3 | The SLW has a longitudinal E-field. | Equation (22b) |
| 4 | The SLW has a power density vector of CE/μ. | Equation (24) |
| 5 | The SLW has a momentum density of −CE/μ. | Equation (25) |
| 6 | The SLW has a power comparable to the TEM wave. | Equation (22a) * |
| 7 | The SLW is unconstrained by the skin effect. | Section 5 * |
| 8 | The SLW free-space attenuation goes like 1/r2. | Equation (23) * |
| 9 | The SLW monopole radiation is isotropic. | Equation (23) * |
| 10 | The scalar wave arises from Φ= −∂α/∂t, plus Item 1. | [3] |
| 11 | The scalar-wave has a pressure density of ∇C2/2μ. | Equation (25) |
| 12 | The scalar-wave has an energy density of C2/2μ. | Equation (24) |
| 13 | C is a pseudo-scalar. | Equation (12) |
| 14 | The scalar wave is also charge-fluctuation driven. | Equation (16) |
| 15 | The interface matching condition for C is… | Equation (17) |
| 16 | The interface matching condition for ρA is… | Equation (18) |
| 17 | The interface matching condition for JA is… | Equation (19) |
| 18 | Momentum balance has a mixed-mode term, ∇ × BC/μ. | Equation (25) |
| 19 | Momentum balance also has source term, JC. | Equation (25) |
| 20 | Energy balance has a new source, ρC/εμ. | Equation (24) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reed, D.; Hively, L.M. Implications of Gauge-Free Extended Electrodynamics. Symmetry 2020, 12, 2110. https://doi.org/10.3390/sym12122110
Reed D, Hively LM. Implications of Gauge-Free Extended Electrodynamics. Symmetry. 2020; 12(12):2110. https://doi.org/10.3390/sym12122110
Chicago/Turabian StyleReed, Donald, and Lee M. Hively. 2020. "Implications of Gauge-Free Extended Electrodynamics" Symmetry 12, no. 12: 2110. https://doi.org/10.3390/sym12122110
APA StyleReed, D., & Hively, L. M. (2020). Implications of Gauge-Free Extended Electrodynamics. Symmetry, 12(12), 2110. https://doi.org/10.3390/sym12122110




