Abstract
We study—with existence and unicity results—a variant of the SIR model for an infectious disease incorporating both the possibility of a death outcome—in a short period of time—and a regime switch that can account for the mitigation measures used to control the spreading of the infections, such as a total lockdown. This model is parametrised by three parameters: the basic reproduction number, the mortality rate of the infected, and the duration of the disease. We discuss a particular example of application to Portuguese COVID-19 data in two short periods just after the start of the epidemic in 4 March 2020, with the first two cases dated that day. We propose a simple and effective method for the estimation of the main parameters of the disease, namely, the basic reproduction number and the mortality rate of the infected. We correct these estimated values to take into account the asymptomatic non-diagnosed members of the population. We compare the outcome of the model in the cases of the existence, or not, of a regime switch, and under three different scenarios, with a remarkable agreement between model and data deaths in the case of our basis scenario. In a final short remark, we deal with the existence of symmetries for the proposed model.
1. Introduction
In this paper, we study a variant of the SIR model for an infectious disease, incorporating the possibility of a death outcome, and focus on a short period of time in order to describe the difference in the evolution of subpopulations with, or without, mitigating measures such as a lockdown. The SIR model—SIR for Susceptible, Infected, Recovered—was introduced in [1] (see also [2] for a present day account) and still is at the root of the most used models for epidemics. It is similar to the system of ordinary differential equations given in Formula (1), the difference being that in the SIR model there is no equation for the proportion of those in the population that have died once infected; that is, the equation for the variable d. The introduction of a death outcome in a SIR model has not been a widely studied subject, maybe because of the difficulties in the biological interpretation of parameters or parameter estimation (as is clearly stated in [3] (p. 34)). In the specific case of the data analysis presented here, it is possible to satisfactorily estimate a death rate parameter, and the biological interpretation is simple, within the bounds of the following caveat that pervades the data set we use: we do not distinguish deaths classified under the two categories—death caused by the infection and death caused by some other disease than COVID-19 on a person with a positive diagnostic of the infection. In the real data application we perform, our goal is to analyse a disease in a period of less than 70 days, and so the demographic fluctuations are not significative, since the lethality rate is known to be small, at this date; moreover, as it follows from [1] (p. 110): “Since the course of an epidemic is short compared with the life of an individual, the population may be considered as remaining constant, except in as far as it is modified by deaths due to the epidemic disease itself”. Nevertheless, if the disease has a rapid progression with an outcome of possible death, the death toll of the disease has a socially significant impact. Moreover, the death toll of such an epidemic can be determined daily; as such, if the model has, as one of its computed results, the deaths of the infected in the population, an assessment of the quality of the model can be performed; we attempt such an assessment in Remark 11. In this work, we need only the most elementary concepts on mathematical epidemic modelling. A very thorough introduction to epidemic modelling can be read in [2]. Some other introductory expositions of the mathematics of epidemics are, for instance, [3] (pp. 15–53) or [4] (pp. 345–410).
The modelling of the current epidemic has been the subject of many studies, and it is impossible to mention even a significant part; we chose to recall some references that we find to be closely related to our approach. For instance, in [5], the authors consider eight compartments, and they estimate the parameters using data between day 1 and day 46; the details of the estimation procedures are not given. In [6], the authors use—among other models—a compartment model of SEIR type, with an additional group of exposed patients for which there is a delay between being exposed and being infected; they refer to the use of maximum likelihood estimation with a Poisson likelihood as an estimation procedure. The work [7] also considers a SIR type model but with natural deaths, and considers explicitly a discretisation procedure to solve the differential equations. Let us stress the following author’s very important remark that justifies the care needed to consider prospective results of these kinds of models. “…Predicting the behaviour of the epidemic with high accuracy is nearly impossible due to there being many unknown factors, e.g., …and parameters of the epidemic”. We must point out that different models have different advantages and weaknesses. For instance, in [8], a review of 72 articles on the mathematical models of the COVID-19 pandemic leads the authors to the conclusion that, although epidemiological models take into account the dynamics of the spread of the infectious disease in a population, they are also highly dependent on the estimation of parameters, and do not take into account the variability of parameters during the course of the epidemic. This observation of May 2021 shows the opportunity of studying epidemiological models with regime switching, which is a major contribution of the present work.
The introduction of birth and death in compartmental SIR type models (see, for instance [9] (p. 30)) aims at describing the evolution of a disease in a long term scenario, of several years, in which demographic fluctuations have to be taken into account. We must presently stress the following caveat for these models. Relying on SIR type epidemiological models to produce predictions on the course of an epidemic can be deceiving, as the work [10] clearly shows; in it, the authors consider a SIR model, with scenarios defined by parameters adjusted for qualitative information—such as the real number of infected—and then compare the evolution given by the model with the observed data. The main conclusion is that: ...The constructed SIR model failed to forecast the actual spread and pattern of the epidemic in the long term. The study of SIR type compartmental models with a subpopulation of the deaths caused by infection, which is to be applied in shorter periods for which the mortality and birth rates of the population can be considered as irrelevant, has already been considered by several authors.
In [11], not related to the COVID-19 pandemic, there is a thorough study—with equilibrium points and stability—of a SEIR model with two additional compartments—asymptomatic infectious and dead once infected. The model has at least eleven primary parameters and a simulation study with parameters obtained from real data from a study of Ebola disease. The qualitative analysis of a system of ODE of the SIR type model can shed light on the characteristic features of the evolution of the variables, such as susceptible, infected, and recovered. Such a study is developed in [12] for a SIR model, in which the proportion of deaths caused by disease is not a variable and, having as additional parameters, the protection rate and the isolation rate; these parameters being non-estimable; due to the lack of data, the model is exploited with plausible given values for the parameters. The models proposed in [13] consider, besides the usual subpopulations in a SEIR type model “...the number of individuals that pass away due to the disease, divided by the total population”. The author considers that all variables are measurable with the exception of the exposed, and considers eight parameters for the models. The estimation procedure considered is of constrained weighted least squares type and simulation results are presented for different sets of parameters corresponding to typified disease cases such as recurrent epidemic and short lockdown period. A remarkable modelling work on the current COVID-19 pandemic is presented in [14]. The authors consider an ODE model with ten variables—susceptible, exposed, asymptomatic, quarantined asymptomatic, severely infected, hospitalised, recovered, recovered asymptomatic, deceased, and protective susceptible. They calibrate the parameters employing the least square method to the proposed model to obtain the best-fit parameters for Ghana and Egypt; they perform a sensitivity analysis and study the optimal control using two control variables that are incorporated into the ODE initial system to reduce the disease transmission and the quarantine for asymptomatic infected individuals. The work in [15] aims at describing the COVID-19 epidemics in Wuhan, Toronto, and Italy. It is a network model, as the “...individuals (are classified) by their average number of contacts in a typical day (time unit for the modelling)”, and to each of these numbers, there corresponds a set of classes of a SEIR type model with additional subpopulations of asymptomatically infected, symptomatically infected, hospitalised and dead. The main results are the theoretical derivations of the “...epidemic threshold defined as the average number of secondary cases produced by an infected individual in a completely susceptible population and of the final epidemic size”. These results are exploited in a simulation study for which the authors consider phases such as before and after lockdown. In [16], the author considers an alternative for the regime switching—of rough type—considered here, but for a SEIR type model in which the coefficients are supposed to take two (or three values) on two (or three) complementary intervals of the time domain. A study of a regime switching models for the evolution of an infected population that influenced this work is [17]. A recent study of a SI(RD) model with regime switching with a logistic function is presented in [18]; the authors use a neural network to detect the regime change points, and a grid search for the estimation of the usual parameters. A more recently published study of a SIR model with deaths and with changing parameters applied to Spanish data is given in [19]; the SI(RD) model studied in this article was, independently, being discussed by us at least since November 2020 (see [20,21]). In this work, we consider data from the first wave of the COVID-19 pandemic in Portugal. Other very recent works that also consider data from Portugal are [22,23].
We now state the main results of this work.
- We study the model proposed—a susceptible-infected-(recovered-dead) model with regime switching—proving that there are two ways to achieve the regime switching (the rough way and the smooth way), and that these are equivalent for all practical purposes;
- Given a bivariate set of data—(daily cases-lethality)—we propose a new simple method to estimate the parameters of the model specially suited to the jagged character of the observations using a binomial model; this amounts to hypothesise that there is a mechanism that corrupts, by noise, the observed trajectories of the ordinary differential equations of the model.
- We show that, taking into account important qualitative information, there are secondary parameters—that modify the primary parameters—that can be set according to reasonable scenarios, such that in one of these scenarios, the lethality rate can be recovered with a very small error.
2. The SI(RD) Model
In this section, we detail the main concepts and specify the notations used next. Some of the concepts presented in the following are classical concepts in the infectious disease modelling literature. Variants of the SIR model were considered by one of the authors in [24] and, for the COVID-19 epidemic context, in [25,26]. In the following, we will focus on the main differences between previous models and the one we study in this work. In the SI(RD) model—which is a variant of the SIR model with an additional compartment represented by D in the acronym SI(RD) for the deceased elements of the population—the members of a population are categorised into one of four groups: S, those who are susceptible to being infected; I, those who have been infected and are able to spread the disease to susceptible individuals; R, those who have recovered from the disease and are immune to subsequent re-infection and D, those who died while infected. The movement of individuals is one-way only according to the scheme: . The parameters of the model are:
- the daily infection rate of the susceptible population;
- the recovery rate is a rate which controls how fast members progress into the I and R groups, respectively;
- is the death rate among those infected;
- is a composite parameter, which—in case —is often used, and is referred to as the contact number.
The SI(RD) model is described by a system of ordinary differential equations (ODE) for the functions —given in formulas (1)—depicting the time evolution of the proportions of the population in each group, that is, s in S, i in I, r in R and d in D; as so, refer, respectively, to the fraction of the population in the susceptible, infected, recovered and dead subpopulation groups. The ODE system in the Cauchy problem of Formula (1) can also be found in [19] (p. 2).
When initial conditions for these groups—susceptible, infected, recovered and dead—are specified, the change in size of these groups may be plotted over time by solving numerically the system of four ordinary differential equations which, for constant or regular time varying parameters, has a unique regular solution.
The inspection of these equations will reveal details of the dynamics of the disease in a population (see, for a related approach of this discussion, [27] (pp. 44, 45)).
- If the fraction of the population in the infected group is initially increasing (i.e., ), an epidemic has begun. For any in a neighbourhood of zero—such that —and if almost all population is susceptible—that is, —we have that:As a consequence, for the SI(RD) model, we define the composite parameter , corresponding to in the SIR model—since in SIR model, there is no parameter—by:
- At the peak point of an epidemic—with —we should have that , by Formula (2), and so, the peak point of an epidemic occurs at a time such that:
Remark 1
(Basic reproduction number).The basic reproduction number is the expected number of secondary cases produced by a single infected individual in a completely susceptible population. Usually, it is defined as,
- T—the transmissibility which is the probability an individual infecting another given there was contact between them;
- —the average rate of contact between susceptible and infected individuals;
- —the duration of the infection in individuals; in the SI(RD) model, the infection ends with two possible outcomes: either recovered or dead.
We may identify and , and doing so, we have the identification:
The contact number —alias, the basic reproduction number—may be understood as the average number of susceptible members of the population; an infected individual spreads the disease to, while that individual is in the infected group.
Remark 2
Let us notice that, at some time , we have if, and only if, with we have,
Remark 3
(On the positive and bounded solutions of ODE system in Formula (1)). We observe that the sum of the righthand terms of the four equations in Formula (1) is zero. As a consequence of this observation, we have that, for all t and by integration, the sum is constant; since at time , we want to deal with proportions we have that and so, we may conclude that for all t, we have that . Furthermore, if the solutions are all non-negative, the relation , valid for all t, this implies that all the solutions are bounded. The proof to show that the solutions are bounded for the SIR type models may be done in several ways; the most efective proceeds by considering one equation at a time, by expressing the equation in integral form in such a way that an exponential function appears, guaranteeing the positivity of solutions (see for instance [28]). By dealing with one equation after another, it is possible to take into account relations such as the one observed in Formula (4) above.
3. SI(RD) Models with Regime Switching (Two Different Values for the Parameter )
For the modelling purposes of our work, we are interested in considering that the parameters of the SI(RD) model, namely, the basic reproduction number alias , the duration of the infection alias and the mortality rate —that have to be estimated or calibrated from the observations—may vary in disjoint and complementary intervals of time. So, firstly, we are going to select the main parameters of the model. For that, we first observe that the parameters and can be expressed as functions of the primary parameters alias , alias and . By using Formula (3) and the fact that and , we have that:
and so, the system of ODE in (1) can be rewritten as:
a formulation that only uses the parameters , the contact number, , the duration of the disease and , the mortality rate among the infected.
We now present the main ideas for the study of the SI(RD) model that we have been considering, but with regime switching. Consider a phenomena modelled by a system of ODE—such as the one in Formulas (5)—denoted for simplicity by with a chosen fixed parameter and and a regular function of the first two variables say, twice differentiable. The change in the dynamics of phenomena may be rendered, in the ODE of the model, by a change in the right-hand side of the ODE, that is, by considering with a function H different from the function F for, let us say as an example, ; this may be called a pure functional regime switching. Another basic rendition amounts to just change the parameter, that is considering for and another chosen fixed parameter different from ; this type of regime switching may be called a pure parametric regime switching. A more general mixed regime switching can be considered by changing both the righthand side of the ODE and the parameter in some subintervals of the original time domain . In this work we consider, and compare, two different forms of regime switching with the same purpose, to wit, the rough (R) regime switching and the smooth (S) regime switching. Let us consider a first example of pure parametric regime switching, the rough regime switching in the context of a standard existence and unicity theorem for ODE for instance, the global Cauchy-Lipschitz theorem (see [29] (pp. 152–154) and [30] (pp. 119–121)) or with the denomination Picard-Lindelöf theorem [31] (p. 8)).
Definition 1
(A rough regime switching for ODE). Suppose that the following conditions are verified for .
- (j)
- The function is a continuous function.
- (jj)
- For some constant , the uniform Lipschitz condition in the variable t given by,is verified for all values of the variables .
Let the first regime solution be for , the unique solution of the ODE for with a given set of initial conditions, which exists and is unique by the Cauchy–Lipschitz theorem. Let the second regime solution be for the unique solution of for taking as initial conditions , that is, the terminal value of the solution in the first regime. Then, the continuous function defined by,
is the a rough regime switching function for the ODE given by for .
We observe that is obtained in by glueing the solution for and the solution for and so is the continuous function in that coincides with for and with for .
Remark 4
(On the rough regime switching as a solution of an ODE). A question that arises naturally may be formulated in the following way: is the rough regime switching function for the ODE given by for a bona fide solution of an ODE? The answer is no in the usual sense, because of the following. The rough regime switching here described by is not differentiable at the point in general. In fact, supposing that and observing that by construction, under the hypothesis of the continuity of the function , we have that:
despite the fact that is differentiable in as is differentiable in and is differentiable in . Being so, the function may not be considered as a usual solution of a Cauchy type problem. In Theorem 2 of Section 6, we consider extended solutions of an ODE in the sense of Carathéodory, and we show that the rough regime switching function described above can, nevertheless, be considered as a solution of an ODE, although only in an extended sense.
We now define a second form of regime switching that we will also use in this work, namely the smooth (S) regime switching.
Definition 2
(A smooth regime switching with transition function G). Let , with , be some fixed values. Let the function defined for all and for every value of the parameter , be a twice differentiable function of its two variables. Suppose that there exists a value of the parameter such that , for and for . The smooth regime switching solution associated to the two Cauchy problems with ODE given by:
for the parameters and with transition function G, is the solution of the correspondent ODE given by:
An example of a function G of Definition 2 is the function given by Formula (9) and depicted in Figure 1. In this example, the parameter controls the extension of the regime changing interval .
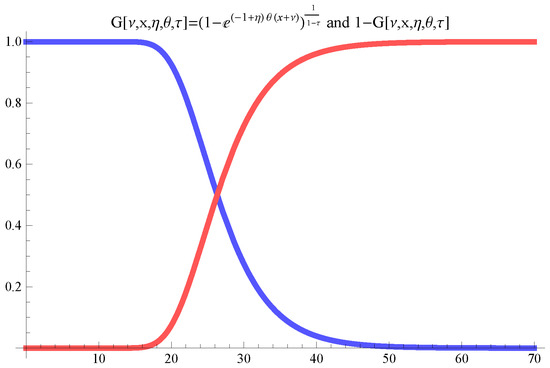
Figure 1.
Regime switching drive function (red) and its complement to one (blue).
Remark 5
(On the existence of the smooth regime switching with transition function G as in Definition 2). It is clear that, due to the regularity of the function G, if the two Cauchy problems—for the values and of the parameters—given by the ODE in Formula (7) and arbitrary initial conditions have unique solutions, then any Cauchy problem given by the ODE in Formula (8) also has a unique solution.
This second form of the regime switching here considered, namely the smooth (S) regime switching, provides a solution for the problem of the change in the dynamics of the phenomena in our ODE model representation, given a choice of function G a smooth solution in , and given a choice of fixed times .
In the following, we will consider a smooth regime switching model, as just described with a function such as the one in Figure 1, that is:
with a multidimensional parameter controlling the main characteristics of the function. Our use of the specific function G in Formula (9), in our modelling, stems from the possibility of performing a stability analysis similar to the one presented in [17]. With the following definitions: , , , and , the ODE that we consider is obtained from ODE in Formulas (5) by means of the procedure that gave the ODE in Formula (8), that is,
In order to obtain the results of the model, for the smooth regime switching case—results presented in Section 5—the system of ODE in Formula (10) is to be integrated numerically. The software used was Mathematica ™ (see [32]). The existence and uniqueness of solutions for such a model pose no problem, as pointed out in Remark 5.
4. Data and Parameter Estimation
The data considered in this study—represented in Table 1 and Table 2 and Figure 2—are composed of two daily reported time series; the series of the number of infected and the series of the number of deaths attributed to the infection.

Table 1.
Data: 208 daily infection numbers; 4 March to 27 September 2020, Portugal.

Table 2.
Data: 208 death daily numbers; 4 March to 27 September 2020, Portugal.
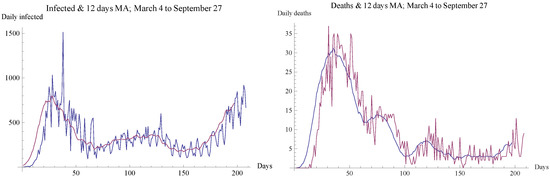
Figure 2.
Daily infected and death numbers and 12-day moving averages in Portugal.
The data used were extracted from a public available source transcribing information from the Portuguese General Direction of Health (DGS) and can be retrieved at https://pt.wikipedia.org/wiki/Predefinição:Tabela_Covid-19_Portugal_região/dia_(DGS) (the website was accessed on on 31 October 2020). The precise numbers do not really matter for our work, only the general trends matter; the methods introduced can be applied to other sets of data with the same characteristics. The number of infected is the number of individuals with positive outcome on an infection test; most commonly a PCR test.
As far as we know, with obvious exceptions, the reported deaths are of those persons who died having had a positive outcome on an infection test. There are natural questions arising from this data description; these questions do not have known answers because, for the moment, there is no practical and affordable way of getting the answers. What is the real number of infections in the whole population? What is the real lethality rate—alias, the case fatality rate—of the disease? This uncertainty is reflected on the outcomes of any model relying on parameters connected to these unknown numbers. In Section 4.5, we will consider the use of some secondary parameters to overcome this issue.
We now address the problem of estimating the parameters of the model from the data. We first observe, as it is usually observed in the usual graphic curves of epidemics evolution, e.g., Figure 2, that we may distinguish several periods the most remarkable being the initial growth period, starting 4 March 2020, with the first two cases being acknowledged and ending in 18 March (day 15)—with the emergency state declaration, effective 22 March—and the following period, ending in 9 May, day 67, as a consequence of the lockdown measures. We will concentrate our analysis in these first two periods as they correspond to a regime switch—derived from the emergency status applied from 22 March on (day 19)—for a determined set of viral clades; it is already known (see the genomic analysis of Instituto Ricardo Jorge in Portugal—https://insaflu.insa.pt/covid19/(accessed on 30 June 2020)—and, in France [33]) that the two following pairs of increasing-decreasing infection numbers corresponding to sets of different viral clads and strains—as shown in Figure 3—and so, they may require a completely different set of parameters; if not, a different model.
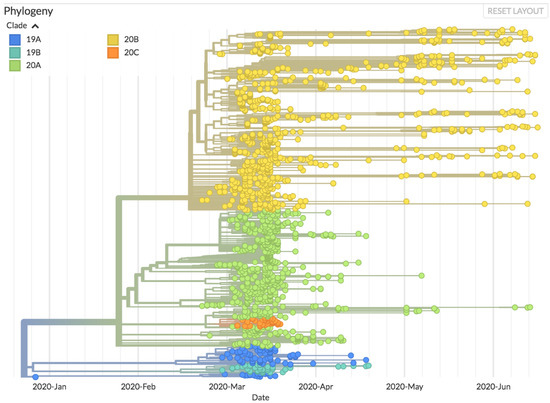
Figure 3.
Clades and strains of SARS-COVID-19 in Portugal by Instituto Ricardo Jorge.
The identification of these periods can be done, for instance, with a moving average that smoothes the rough oscillations. In Figure 2, it can be observed that there is a clear maximum in the 12th day moving average of the infected, and there is a sort of plateau of maximum values for the death numbers. This allows us to define the starting and ending dates of the two periods under consideration for computational purposes.
From the data on the infected, we can estimate the parameter and get some information on the duration of the infection, the parameter. From the mortality data, we can estimate the mortality rate and get some additional information on the parameter.
4.1. On the Assumed Value for the Duration of the Disease
It is an acknowledged fact (see [34]) that the viral load for infections of this type of disease becomes undetectable after a few days, between 6 and 14. In the particular case of this disease, it was observed that, in the vast majority of cases, after 5 days (see [35]), the viral load becomes undetectable. As a consequence, we will assume that our basis scenario corresponds to days, and we will consider two extreme scenarios with parameter values days and days. Further on—see Section 4.4—we will see that the lethality rate estimates, with a three and eleven days delay, define an interval consistent with the proposed duration day interval for the disease , as the main contagious period of the infection.
4.2. Determination of the Initial Date of the Decreasing Trend Period
Given a whole set of time labeled data points of the number of infected the determination of the date where the regime switch may be taken to happen can be performed with a moving average sequence , the average of the k day values prior to the current date, defined by:
Intuitively, the sequence , for is closer to the smaller the value of k. Moreover, for a sequence with a rising trend, we should always have , and so, the first time label n such that may be considered the time stamp of rising trend break. The same applies mutatis mutandis to a decreasing trend. For our data we know that the regime switch must have occurred between days 15 and 30 on account of the lockdown determination on 18 March 2020 (day 15). For we had for the first index n such that and so we take the date as the starting date of the decreasing trend in the data that will be used for estimation of the contact number.
4.3. Estimation of the Contact Number
We propose the following method that is suited for the type of data considered with well defined growth characteristics: data defining a jagged line such that a regularisation obtained by a moving average that smoothes the rough oscillations—see Figure 2—is increasing in the first considered sub-period and decreasing in the second sub-period. To account for the jagged characteristic of the line corresponding to the data—a characteristic that is possibly due noise contamination originated from delays in collecting and reporting the observed numbers—we will consider a binomial type model, that is, the following hypothesis for each of the sub-periods of dates .
- (1)
- The length of the period is determined and we have a sequence of daily observations of the number of infected. There is a sequence of random variables such that the initial is arbitrary but the remaining observed data is a realisation of this sample.
- (2)
- There exists a random variable , taking two values —with u representing the magnitude of the upward jump and d representing the magnitude of a downward jump—such that and with and . For a sample of we have, for , that:The values are the parameters to be estimated and they depend on the period considered.
As a consequence of these hypothesis we have the following immediate conclusions.
- (1)
- The maximum likelihood estimator of , as a consequence of the distribution of , is given by:
- (2)
- By the law of large numbers we have that for large enough,that is, may be taken as a good approximation of —the expectation of —and is a good approximation of , the variance of .
- (3)
- By the method of moments, we can determine the couple of estimators for the parameter couple as the solutions of the equations derived from the law of given by,considering the estimator of given by Formula (12) and the estimator of (respectively ) given by Formula (13). There are two sets of solutions—Formulas (14) and (15)—and we have to choose the set that corresponds to the period characteristic, that is, in the first period we should have the greatest u with the highest probability and in the second period the greatest d with the higher probability.
Finally, we will take for the first period and for the second period, and the computed results are presented in Table 3.

Table 3.
Estimates of and of for the two successive sub-periods.
Remark 6
(Comments on the estimates of Table 3). In the first period, days 1 to 25, that is, 4 March to 28 March, the estimated value of is perfectly compatible with the strongly increasing character of the observations, and the estimated values of — highlighted in boldface—are similar to other estimations of this parameter; for instance a value used in the Imperial College study paper, see [36] or [37] and for a very particular subpopulation of a cruise ship. In the second period, days 25 to 67, that is, 28 March to 9 May, we observe that there is almost equal probability for either an upward or a downward probability and the downward parameter estimate gives us a lesser but still high estimate for .
4.4. Estimation of the Lethality Rate
The estimation of the lethality rate must be accomplished by establishing some functional relation with the number of infected. Among several different models tried, including ARMA models, we finally observed that the simplest model, that is the linear fit, was the adequate model for the two periods. We then considered, for the two periods independently, a linear fit with vanishing constant, of the daily deaths given as a function of the daily infected but with varying time delays. Based on both the lowest AIC—Akaike Information Criterion (see [38] for both AIC e BIC thorough developments)—and the highest R-squared the best model was a linear fit with vanishing constant with a delay of three days in the first period and a delay of eleven days in the second period. That is,
We recall that the p-value in Table 4 is the probability of observing a t-statistic at least as far from zero as the one obtained from the data used in the estimation; given that the p-value in the table the model is adequate.

Table 4.
Estimates of the lethality for the two successive sub-periods.
Remark 7
(Comments on the estimates of Table 4). Despite the remarkable statistical properties of the estimates obtained in the two periods under analysis, the values obtained for the lethality rate —highlighted in boldface—are excessive if we consider the whole population of infected including also the undiagnosed and/or asymptomatic cases. In the following Section 4.5 we put forward an explanation and a correction to this excess of deaths.
Remark 8
(On the nature of the most adequate ODE model). The lethality model we obtained as the best fit in Formula (16) suggests that the ODE model should comprise a delay in the differential equation corresponding to the lethality. The use of delay differential equations (DDE) in epidemiology is not new, see for instance [39]. Also, in [40] there is an application to the multi-group SIR model with mass action incidence and with discrete time delay based on the construction of a Lyapunov functional for the DDE model. As it is well known, the DDE models require the study of stability that can be quite demanding (see, for instance, [41] (p. 36)).
4.5. Further Hypothesis on the Results of the Estimation Procedure
As early as 8 May 2020, it was a common assumption that the total number of infections was much higher than the officially reported (see [42]). In fact, already in [43], it is stated that the total number of infected was between 3 and 20 times the number of reported infection cases. Moreover, recently in 5 October 2020, Dr. Michael Ryan, head of emergencies at the WHO said, that… “best estimates indicate that roughly 1 in 10 people worldwide may have been infected by the coronavirus—more than 20 times the number of confirmed cases” (see https://www.cnbc.com/2020/10/05/who-10percent-of-worlds-people-may-have-been-infected-with-virus-.html (accessed on 6 October 2020)). As a consequence, since our model applies to the whole population, we will further assume the following:
- We will consider that the real number of infected is 20 times higher than the number reported. As a consequence, the model parameters and are to be modified to take this assumption in consideration.
- The estimated value for the parameter has to be replaced by the value given by,with , a secondary parameter, being the correction needed to take into account that the non diagnosed infected cases must correspond to non symptomatic cases and, as such, with a contagion force inferior to those infected with symptoms and tested with a positive outcome. Having no prior information available, we will consider that correspond to our basis scenario, and we will base our main conclusions on the observations of the outcomes of the model under this particular scenario.
- In the same way, the estimated value for the parameter should be replaced by the value given by,with , another secondary parameter, being the correction needed to take into account the mortality rate due to the infection in the asymptomatic and not tested with a positive outcome. Having no prior information available, we will suppose that correspond to our basis scenario and and to alternative scenarios.
- For the initially immune we consider that in the first period these are supposed to be 2.5% of the population. In the second period the initially immune are those who either recovered or died at the end of the preceding period.
- For the smooth regime switching model drive function G, shown in Figure 1, the parameter choice ensures that for we have , for we have , for we gave and that for we gave and so, the smooth regime switching unfolds, essentially, between day 16, the declaration of starting time of the lockdown, and day 40.
5. Results of the Model
We now apply the model given by the ODE systems in Formula (5) and in Formula (10) to the two different sub-periods considering the different set of parameters indicated above. For the second sub-period and the ODE systems in Formula (5), the initial conditions are the terminal conditions of the preceding sub-period. In the numerical integration of the rough regime switching ODE we take day 20 that is, 23 March the following day to the emergency state declaration, in Portugal, to be the beginning of the second sub-period with a different regime.
Let us give a summary of the assumptions for the basis scenario by interpreting the parameters in Table 5. In this scenario , that is, those infected but not diagnosed as such have a contagion force with being the contagion force of those with an positive diagnostic infection; and so meaning that mortality rate for the asymptomatic infected and not tested with a positive outcome is one twentieth of the mortality for those infected and with a positive outcome on a test; and, finally, states that the duration of the infection in the basis scenario is days. We will first consider the results for the basis scenario and after, the results for the extreme scenarios I and II defined for specific choices of the secondary parameters , and as in Table 5 (see Section 4.5 for the need of establishing scenarios for the secondary parameters).

Table 5.
Parameters for basis scenario and extreme scenarios I and II.
5.1. Results of the Model in the Basis Scenario
In Figure 4 we have the numerical solutions of the ODE systems for the two periods considered, for the constant parameter case—that is, with no regime switching—and for both the regime switching cases the smooth and the rough case in the case of the base scenario (see Table 5 for the values of the secondary parameters , and in the basis scenario). The yellow constant line at height one—explained in Remark 3—is just the sum of proportions and is drawn for control purposes. The terminal values, at date 67 corresponding to May 9th, for the proportions in each subpopulations—susceptible, infected, recovered and dead—are given in Table 6.
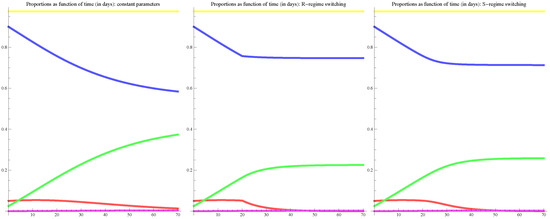
Figure 4.
Solutions of the SI(RD) ODE: constant parameters, R-RS and S-RS; .
Remark 9
(Comments on the ODE solutions displayed in Figure 4). With, susceptible in blue, infected in red, recovered in green, dead in magenta, and with the sum of proportions in yellow, the ODE model without regimes, on the left-hand side, and the ODE models with regimes are clearly different. In the case of the rough regime switching the effect of the regime change is clear both in the susceptible and the infected. At first sight, the final values of the proportions between the rough regime switching and the smooth regime switching; on the right-hand side, if they differ, they differ slightly (see Table 6).
Remark 10
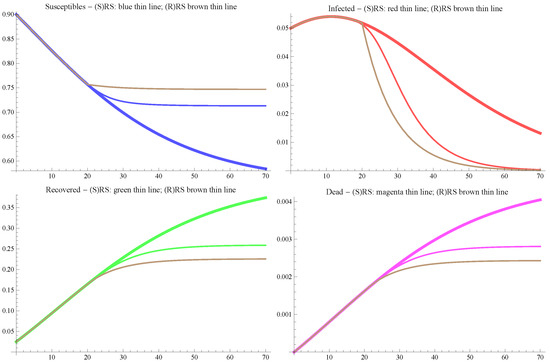
(Comments on the differences displayed in Figure 5 and on Table 6). As expected, the regime switch has the following effects: the increase of the susceptible, the sharp fall of the infected, the decline of the recovered and the most remarkable diminution of the deaths of the infected. In each instance, the change between the constant parameter evolution and the regime switching evolution was more pronounced for the rough regime switching, as expected.

Figure 5.
Comparing constant parameters with (R) and (S) regime switching; .
Remark 11

(On the agreement between the death results of the model and the death numbers of the data). The introduction of a death compartment in the model can be used to ascertain the quality of the model as well as of the parameter estimation procedures. We will now compare the results of the model with the real data. The lowest death rate—for the whole infected population corresponding to the rough regime switching—given by the model in Table 6, at day 67, is 2430.14 deaths per million; by reversing the procedure we applied to the estimated lethality rate in order to have a rate applied to the whole infected population in Formula (17) we have that the number of deaths of infected in regard to the diagnosed population is 2430.14/20 = 121.507 deaths per million. The data number of deaths caused by infection corresponding to the pandemic status at day 67, the end of the second period under analysis, should be taken at date 78 in Table 2, corresponding to 20 May 2020, due to the 11-day time lag between the deaths and the infected, and this value is 1263; in [44], we get, for 20 May, 1247 deaths because they did not count the number of deaths which occurred on 20 May, which was 37. For coherence with our computations, we will consider the death toll as 1263. Taking into account the estimate of the Portuguese population of 10,188,013 (see https://www.worldometers.info/world-population/portugal-population/ (accessed on 15 October 2020), we have the number of deaths of infected per million equal to 123.969. So, the ratio of the data number/model number is 123.969/121.507 = 1.0203, that is, an excess of 2% of the data over the model. This can be considered as a good agreement between model and data given that we used an estimate for the total population number in Portugal. We nevertheless observe that the true death toll of the epidemic may be larger than the accounted (see [45], for an early suggestion of this possibility) and that there is also the possibility that the model studied does not cover some important aspects of the epidemic evolution. This problem may be a feature common to the compartmental models; for instance in [5] (p. 857a) the authors predict a 0.06% percentage of deaths in a time horizon of 350 days—a very high value for a death of infected estimate of the whole population—which is a result comparable to the rough regime switching evolution for the extreme scenario I in Table 7 ahead.

Table 7.
Numerical results of the ODE model for extreme scenario I at date 67.
5.2. Results of the Model in the Extreme Scenarios I and II
The consideration of alternative scenarios—with a different set of secondary parameters—allows for a better overview of the descriptive power of the model. As proposed in Section 4.5, we can consider several different values for the secondary parameters , and , allowing the definition of two extreme scenarios in Table 5. The extreme scenario I has the lowest values for the secondary parameter—and, as a consequence, also for the contact number — and also for the parameter, which is the duration of the disease. The extreme scenario II, with the numerical results in Table 8, is the opposite.

Table 8.
Numerical results of the ODE model for extreme scenario II at date 67.
Remark 12
(On the results of the model for the extreme scenarios I and II and consequent conclusions about the basis scenario assumptions). With respect to the basis scenario, the extreme scenario I has a larger death toll with an increasing proportion in the susceptible population while the proportions of infected and recovered are much smaller in the extreme scenario I when compared with the same proportions in the basis scenario. In the extreme scenario II (see Table 8), the proportion of susceptible is smaller but the proportion of recovered is comparable while the proportion of deaths is larger almost 114-fold for the regime switching model. As so and given the agreement between data and model numbers for the death toll in Remark 11, we must conclude that the assumptions made for the basis scenario are the most adequate. We stress that this fact gives us important information about the disease stated in the following conclusions. For the asymptomatic and/or undiagnosed the most plausible value of the contact number is 50% of the contact number of the diagnosed. The most plausible mortality rate, caused by the disease, for the asymptomatic and/or undiagnosed is zero and the most plausible value for the duration of the disease is 7.5 days.
6. On the Regime Switching SI(RD) ODE Models: Existence and Unicity Results
An allegedly alternative to the rough regime switching considered in this work—that it seems being used by some authors (see [16], for instance)—is to consider that the coefficients of the SIR type model—for instance, SEIR or SI(RD) models—are not constant but take two (or three) different values in two (or three) complementary intervals of the time domain. In fact, we will observe in Remark 14 that the two approaches to the rough regime switching are essentially the same. For the alternative rough regime switching, the usual Lipschitz type existence theorem or even the Peano existence theorem for ODE do not apply as the function in the righthand term of the ODE—with such discontinuous time varying parameters—is not continuous. Existence and unicity of solutions for such a model is a crucial question. A different approach is needed; following [46] (pp. 41–44), we consider the definition of an extended solution of a differential equation,
Definition 3
(Extended solution of an ODE). Let a differential equation be given by,
or in the equivalent integral form with the appropriate Lebesgue measure in ,
for anonnecessarily continuous function, with and . An extended solution of the ODE in Formula (18) is an absolutely continuous function (see for a precise definition [47] (pp. 144–150)) such that for and Formula (18), or equivalently, Formula (19), is verified for all , possibly with the exception of a set of null Lebesgue measure.
We now recall Caratheodory’s existence theorem (see [46] (p. 43)), in the context of the model we are studying, a theorem that ensures the existence of an extended solution under general conditions.
Theorem 1
(Caratheodory’s existence theorem). Suppose that verifies:
- (i)
- is measurable in the variable t, for fixed , and continuous in the variable , for fixed t.
- (ii)
- there exists a Lebesgue integrable function , defined on a neighbourhood of the initial time, let us say I, such that for .
Then, for a given initial condition, given in a neighbourhood of the initial time, there exists anextended solutionaccording to Definition 3.
We now state and prove an important result for our work, showing that the rough regime switching function of Definition 1 is, essentially, an extended solution of the ODE of the SI(RD) model in Formula (1), in agreement with what was announced in Remark 4.
Theorem 2
(Existence and unicity in the SI(RD) model with rough regime switching). Consider the SI(RD) model given by the Cauchy problem n Formulas (1), that is:
with a time dependent vectorial parameter , such that for some :
Then, by Theorem 1, this Cauchy problem has an extended solution in the sense of Definition 3. Moreover, any two different solutions differ possibly only on a set of zero Lebesgue measure, and so the extended solution is unique.
Proof.
In order to address the problem of the existence of extended solutions for the rough regime switching models, we observe that the ODE in Formulas (5)—with time changing, discontinuous, parameters , and —may be represented as:
with , and:
As a consequence, the ODE in Formula (20) can be represented as in Formula (18) with such that . We have, for the Euclidean norm in , with the matrix components of and using the fact that the Frobenius norm dominates the matrix norm associated with the Euclidean norm,
with and since , with N(t) given by the expression:
By Caratheodory’s existence theorem (see Theorem 1 above), the extended solution for equation given in Formula (18)—for a given initial condition and in the case of the rough regime switching models here considered—exists as a consequence of the estimate in Formula (22) by observing that the components of are proportions, and so is bounded, and that in Formula (23) is bounded and measurable, and so it is Lebesgue-integrable in any compact interval of the time variable.
We now address the unicity of solutions for the regime switching ODE problems already mentioned in this section. For that purpose, we will prove that the function satisfies a Lipschitz condition in the variable for each fixed t. By resorting to Formulas (5) and with , and , for notation simplification, we have that,
We now use the fact that to obtain that,
where, with the same simplified notations for , and , we have:
Now, using the Euclidean norm in , the fact that the Frobenius norm dominates the matrix norm associated with the Euclidean norm, the fact that all components of are non-negative and bounded by one, as proportions always are, we have that, if the parameters , and are bounded measurable functions, then is bounded, by a bounded measurable function given by:
and then we have:
thus ensuring a boundedness condition that implies the Lipschitz character of . Now, either directly using theorem 18.4.13 in [48] (p. 337) or using Osgood’s uniqueness theorem—as presented for instance, in [49] (p. 58) or in [50] (pp. 149–151)—we may conclude that the extended solution, that we know to exist, is unique, in the sense that two solutions may only differ on a set of Lebesgue measures equal to zero. □
Remark 13
(Existence alternative proof). We could also quote Wintner’s theorem as referred by [51], stating that if with N and L piecewise continuous, positive and L nondecreasing, such that for some
then the ODE in Formula (18) has a solution for a given initial condition, by observing that the quoted theorem is valid, under the assumption that is continuous with the possible exception of points of a null Lebesgue set of the time variable, by considering extended solutions instead of usual solutions, which have a continuous derivative, and as and both satisfy the hypotheses of Wintner’s theorem for parameters , and , taking each two (or three) distinct values in two (or three) complementary intervals of the time domain.
We observe that these existence and uniqueness results are essential for a numerical integration of the ODE, but that no result of convergence numerical is implied—in the existence and uniqueness results above—for the regime switching ODE with discontinuous coefficients. Nevertheless, the Lipschitz condition with respect to the variable—such as the one in Formula (26)—is sufficient for the convergence of the Euler method (see [52] (p. 74)).
Remark 14
(On the existence of essentially only one rough regime switching model). We also observe that our definition of a rough regime switching as the continuous function obtained by glueing the usual solutions of ODE in complementary time intervals—as described in Section 3—is equal almost everywhere in the time variable, with respect to the Lebesgue measure, to any extended solution of the alternative rough regime switching obtained by solving an ODE with discontinuous parameters, which is the best we can expect for extended solutions.
Remark 15
(Existence and unicity of solutions for the smooth regime switching). It is clear that the existence and unicity of a solution for the smooth regime switching model in Section 3 may be dealt either by the usual Cauchy-Lipschitz existence and unicity theorem or by the results of this section, with the necessary adaptations of the definitions of the matrices and . An example of smooth regime switching was studied in [17] with two coupled ODE, having in each equation two evolution regimes in such a way that the transition in time, between these regimes, is achieved by a coupling function similar to the function in Formula (9).
Remark 16
(On the Lie symmetries for ODE models with regime switching). There are at least two ways of considering symmetries on the model developed in this work. The first and more simple one is the usual reversibility in time for ODE. In fact it is clear from the expression of an ODE in integral form in Formula (19)—using as the variable change—that the generalised solution of a ODE for a regime switching model proved using Carathéodory’s theorem is reversible in time. The second and profound one is related to the Lie symmetries for the differential model in Formula (5) with added regime switching as studied in this work. Lie type symmetries for ODE in general are the object of several reference works, for instance in [53]. For the SIR and the SI(RD) models, Lie symmetries were presented in [54,55], following the general proposals of using Lie symmetries in epidemiology developed in [56,57]. The study of Lie symmetries for ODE with regime switching remains to be done. A natural approach is to use the ideas of bifurcation theory, as masterfully developed in [58,59].
7. Discussion, Conclusions and Further Work
We introduced, studied, and applied a SIR type model with a compartment for deaths—occurring by force of the infection—and with regime switching to model pandemic mitigation measures such as a lockdown. The model depends on three main parameters, to wit, the basic reproduction number, the lethality rate and the duration of the disease. The statistical methodologies introduced to estimate the main parameters of the model—using real data of the initial period of the pandemia in Portugal—are natural, and provide estimates in line with values reported in the literature. Nevertheless, these values have to be resized in order to account for the true dimension of the infected population; this resizing creates secondary parameters which are impossible to estimate, due to the lack of proper data. When fed with the resized parameters—for some scenario chosen values of the secondary parameters—the model gives results in line with what is to be expected, for instance, the lowering of the death toll of mortality when a mitigating measure of lockdown type is present and, for the lethality also, a remarkable agreement within an excess of 2% of the observed data over the model. We must conclude that the assumptions made for the basis scenario are the most adequate of the three scenarios proposed; we observe that this fact gives us important information, about the disease, stated in the following. For the asymptomatic and/or undiagnosed the most plausible value of the contact number is 50% of the contact number of the diagnosed. The most plausible mortality rate—caused by the disease—for the asymptomatic and/or undiagnosed is zero and the most plausible value for the duration of the disease is 7.5 days. The methodology introduced is applicable whenever there are clear regime switchings in the evolution and correspondent estimates of the relevant parameters occurring by force of control measures such as lockdown. The main advantage of the SI(RD) model studied in this work is that, in its simplicity, it allowed us to recover the past behaviour of the lethality which is the main social nefarious consequence of an epidemic. One line of investigation that our work opens up to is to replace parameters by parametric functions depending on parametric variables that may capture the effects of our secondary parameters; this line of investigation seems justified by the importance of the secondary parameters in the conclusions we attained. An alternative to this line of investigation is to randomise the parameters; with this approach we would have to prescribe probability distributions for the parameters and then use Monte Carlo simulation to get probability distributions for the proportions of susceptible, recovered and dead, at the end of the period studied.
Author Contributions
Conceptualization, M.L.E.; Formal analysis, M.L.E.; Investigation, M.L.E., N.P.K., G.R.G. and P.P.; Software, M.L.E.; Visualization, M.L.E.; Writing—original draft, M.L.E.; Writing—review and editing, M.L.E., N.P.K., G.R.G. and P.P. All authors have read and agreed to the published version of the manuscript.
Funding
For the second author, this work was done under partial financial support of RFBR (Grant No. 19-01-00451). For the first, third and fourth authors this work was partially supported through the project of the Centro de Matemática e Aplicações, UID/MAT/00297/2020 financed by the Fundação para a Ciência e a Tecnologia (Portuguese Foundation for Science and Technology). The APC was funded by the insurance company Future Healthcare.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used were extracted from a public available source transcribing information from the Portuguese General Direction of Health (DGS) and can be retrieved at https://pt.wikipedia.org/wiki/Predefinição:Tabela_Covid-19_Portugal_região/dia_(DGS) (the website was accessed on on 31 October 2020).
Acknowledgments
This work was published with finantial support from the insurance company Future Healthcare. The authors would like to thank Future Healthcare for this generous support and for their interest in the development of models for disease and health insurance problems in Portugal. The authors wish to express their gratitude to JLS, former publisher at McGraw-Hill Book Company, for his extensive revision of the English language in this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kermack, W.O.; McKendrick, A.G.; Walker, G.T. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. A Contain. Pap. A Math. Phys. Character 1927, 115, 700–721. [Google Scholar] [CrossRef] [Green Version]
- Martcheva, M. An Introduction to Mathematical Epidemiology; Texts in Applied Mathematics; Springer: New York, NY, USA, 2015; Volume 61. [Google Scholar] [CrossRef]
- Keeling, M.J.; Rohani, P. Modeling Infectious Diseases in Humans and Animals. Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Brauer, F.; Castillo-Chavez, C. Mathematical Models in Population Biology and Epidemiology, 2nd ed.; Texts in Applied Mathematics; Springer: New York, NY, USA, 2011. [Google Scholar]
- Giordano, G.; Blanchini, F.; Bruno, R.; Colaneri, P.; Di Filippo, A.; Di Matteo, A.; Colaneri, M. Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nat. Med. 2020, 26, 855–860. [Google Scholar] [CrossRef]
- Bertozzi, A.L.; Franco, E.; Mohler, G.; Short, M.B.; Sledge, D. The challenges of modeling and forecasting the spread of COVID-19. Proc. Natl. Acad. Sci. USA 2020, 117, 16732–16738. [Google Scholar] [CrossRef]
- Carcione, J.M.; Santos, J.E.; Bagaini, C.; Ba, J. A Simulation of a COVID-19 Epidemic Based on a Deterministic SEIR Model. Front. Public Health 2020, 8, 230. [Google Scholar] [CrossRef] [PubMed]
- Shankar, S.; Mohakuda, S.S.; Kumar, A.; Nazneen, P.S.; Yadav, A.K.; Chatterjee, K.; Chatterjee, K. Systematic review of predictive mathematical models of COVID-19 epidemic. Med. J. Armed Forces India 2021, 77, S385–S392. [Google Scholar] [CrossRef]
- Brauer, F.; Castillo-Chávez, C. Mathematical Models in Population Biology and Epidemiology; Texts in Applied Mathematics; Springer: New York, NY, USA, 2001; Volume 40. [Google Scholar] [CrossRef]
- Moein, S.; Nickaeen, N.; Roointan, A.; Borhani, N.; Heidary, Z.; Javanmard, S.H.; Ghaisari, J.; Gheisari, Y. Inefficiency of SIR models in forecasting COVID-19 epidemic: A case study of Isfahan. Sci. Rep. 2021, 11, 4725. [Google Scholar] [CrossRef]
- De la Sen, M.; Ibeas, A.; Alonso-Quesada, S.; Nistal, R. On a New Epidemic Model with Asymptomatic and Dead-Infective Subpopulations with Feedback Controls Useful for Ebola Disease. Discret. Dyn. Nat. Soc. 2017, 2017, 4232971. [Google Scholar] [CrossRef] [Green Version]
- ud Din, R.; Algehyne, E.A. Mathematical analysis of COVID-19 by using SIR model with convex incidence rate. Results Phys. 2021, 23, 103970. [Google Scholar] [CrossRef]
- Sameni, R. Mathematical Modeling of Epidemic Diseases; A Case Study of the COVID-19 Coronavirus. arXiv 2020, arXiv:2003.11371. [Google Scholar]
- Asamoah, J.K.K.; Jin, Z.; Sun, G.Q.; Seidu, B.; Yankson, E.; Abidemi, A.; Oduro, F.; Moore, S.E.; Okyere, E. Sensitivity assessment and optimal economic evaluation of a new COVID-19 compartmental epidemic model with control interventions. Chaos Solitons Fractals 2021, 146, 110885. [Google Scholar] [CrossRef] [PubMed]
- Xue, L.; Jing, S.; Miller, J.C.; Sun, W.; Li, H.; Estrada-Franco, J.G.; Hyman, J.M.; Zhu, H. A data-driven network model for the emerging COVID-19 epidemics in Wuhan, Toronto and Italy. Math. Biosci. 2020, 326, 108391. [Google Scholar] [CrossRef] [PubMed]
- Glass, D.H. European and US lockdowns and second waves during the COVID-19 pandemic. Math. Biosci. 2020, 330, 108472. [Google Scholar] [CrossRef] [PubMed]
- Esquível, M.L.; Patrício, P.; Guerreiro, G.R. From ODE to Open Markov Chains, via SDE: An application to models for infections in individuals and populations. Comput. Math. Biophys. 2020, 8, 180–197. [Google Scholar] [CrossRef]
- Petrica, M.; Leordeanu, M.; Stochitoiu, R.D.; Popescu, I. A regime switching on Covid-19 analysis and prediction in Romania. arXiv 2020, arXiv:2007.13494. [Google Scholar]
- Martínez, V. A Modified SIRD Model to Study the Evolution of the COVID-19 Pandemic in Spain. Symmetry 2021, 13, 723. [Google Scholar] [CrossRef]
- Esquível, M.L. The Multi-Compartment SI(RD) Model with Regime Switching: An Application to COVID-19 Pandemic. Presentation at Seminário de Estatística e Gestão do Risco do Centro de Matemática e Aplicações, FCT Nova, New University of Lisbon, in November. 2020. Available online: https://drive.google.com/file/d/15sZZXUiB20OfeoHX5RFfYsLEWLyOvA_Y/view (accessed on 1 December 2020).
- Esquível, M.; Krasii, N.; Guerreiro, G.; Patrício, P. The Multi-Compartment SI(RD) Model with Regime Switching: An Application to COVID-19 Pandemic. Paper Submission to Journal of Applied Statistics in November. 2020. Available online: https://drive.google.com/file/d/1KKa4NEAH9O2HY38EACNfOlBTkavbCMFH/view?usp=sharing (accessed on 27 November 2020).
- Ndaïrou, F.; Torres, D.F.M. Mathematical Analysis of a Fractional COVID-19 Model Applied to Wuhan, Spain and Portugal. Axioms 2021, 10, 135. [Google Scholar] [CrossRef]
- Vaz, S.; Torres, D.F.M. A Discrete-Time Compartmental Epidemiological Model for COVID-19 with a Case Study for Portugal. Axioms 2021, 10, 314. [Google Scholar] [CrossRef]
- Doutor, P.; Rodrigues, P.; Soares, M.d.C.; Chalub, F.A.C.C. Optimal vaccination strategies and rational behaviour in seasonal epidemics. J. Math. Biol. 2016, 73, 1437–1465. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Machado, B.; Antunes, L.; Caetano, C.; Pereira, J.F.; Nunes, B.; Patrício, P. The impact of vaccination on the evolution of COVID-19 in Portugal. Math. Biosci. Eng. 2022, 19, 936–952. [Google Scholar] [CrossRef]
- Caetano, C.; Morgado, M.L.; Patrício, P.; Pereira, J.F.; Nunes, B. Mathematical Modelling of the Impact of Non-Pharmacological Strategies to Control the COVID-19 Epidemic in Portugal. Mathematics 2021, 9, 1084. [Google Scholar] [CrossRef]
- Brauer, F.; Castillo-Chavez, C.; Feng, Z. Mathematical Models in Epidemiology; Texts in Applied Mathematics; Springer: New York, NY, USA, 2019; Volume 69. [Google Scholar] [CrossRef]
- Sun, C.; Zhao, H.; Lin, Y.; Dai, Y. An SIRS Epidemic Model Incorporating Media Coverage with Time Delay. Comput. Math. Methods Med. 2014, 2014, 680743. [Google Scholar]
- Birkhoff, G.; Rota, G.C. Ordinary Differential Equations, 3rd ed.; John Wiley & Sons: New York, NY, USA; Chichester, UK; Brisbane, Australia, 1978. [Google Scholar]
- Cartan, H. Cours de Calcul Différentiel; Hermann: Paris, France, 1977. [Google Scholar]
- Hartman, P. Ordinary Differential Equations; Classics in Applied Mathematics; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 2002; Volume 38. [Google Scholar] [CrossRef]
- Wolfram Research, Inc. Mathematica, Version 12.3.1; Wolfram Research, Inc.: Champaign, IL, USA, 2021. [Google Scholar]
- Colson, P.; Levasseur, A.; Delerce, J.; Chaudet, V.; Bossi, M.; Ben Khedher, P.E.; Fournier, J.C.; Raoult, D. Dramatic increase in the SARS-CoV-2 mutation rate and low mortality rate during the second epidemic in summer in Marseille. Pre-Prints Covid Du IHU 2020, 1, 1–20. [Google Scholar] [CrossRef]
- Walsh, K.A.; Jordan, K.; Clyne, B.; Rohde, D.; Drummond, L.; Byrne, P.; Ahern, S.; Carty, P.G.; O’Brien, K.K.; O’Murchu, E.; et al. SARS-CoV-2 detection, viral load and infectivity over the course of an infection. J. Infect. 2020, 81, 357–371. [Google Scholar] [CrossRef]
- La Scola, B.; Le Bideau, M.; Andreani, J.; Hoang, V.T.; Grimaldier, C.; Colson, P.; Gautret, P.; Raoult, D. Viral RNA load as determined by cell culture as a management tool for discharge of SARS-CoV-2 patients from infectious disease wards. Eur. J. Clin. Microbiol. Infect. Dis. 2020, 39, 1059–1061. [Google Scholar] [CrossRef] [PubMed]
- Ferguson, N.M.; Laydon, D.; Nedjati-Gilani, G.; Imai, N.; Ainslie, K.; Baguelin, M.; Bhatia, S.; Boonyasiri, A.; Cucunubá, Z.; Cuomo-Dannenburg, G.; et al. Impact of Nonpharmaceutical Interventions (NPIs) to Reduce COVID-19 Mortality and Healthcare Demand; Imperial College COVID-19 Response Team, Imperial College: London, UK, 2020. [Google Scholar] [CrossRef]
- Zhang, S.; Diao, M.; Yu, W.; Pei, L.; Lin, Z.; Chen, D. Estimation of the reproductive number of novel coronavirus (COVID-19) and the probable outbreak size on the Diamond Princess cruise ship: A data-driven analysis. Int. J. Infect. Dis. 2020, 93, 201–204. [Google Scholar] [CrossRef]
- Konishi, S.; Kitagawa, G. Information Criteria and Statistical Modeling; Springer: New York, NY, USA, 2008. [Google Scholar]
- Salpeter, E.E.; Salpeter, S.R. Mathematical Model for the Epidemiology of Tuberculosis, with Estimates of the Reproductive Number and Infection-Delay Function. Am. J. Epidemiol. 1998, 147, 398–406. [Google Scholar] [CrossRef] [PubMed]
- Kajiwara, T.; Sasaki, T.; Takeuchi, Y. Construction of Lyapunov functionals for delay differential equations in virology and epidemiology. Nonlinear Anal. Real World Appl. 2012, 13, 1802–1826. [Google Scholar] [CrossRef]
- Fridman, E. Introduction to Time-Delay Systems; Systems & Control: Foundations & Applications; Birkhäuser/Springer: Cham, Switzerland, 2014. [Google Scholar] [CrossRef]
- Böhning, D.; Rocchetti, I.; Maruotti, A.; Holling, H. Estimating the undetected infections in the COVID-19 outbreak by harnessing capture, recapture methods. Int. J. Infect. Dis. 2020, 97, 197–201. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.L.; Mertens, A.N.; Crider, Y.S.; Nguyen, A.; Pokpongkiat, N.N.; Djajadi, S.; Seth, A.; Hsiang, M.S.; Colford, J.M.; Reingold, A.; et al. Substantial underestimation of SARS-CoV-2 infection in the United States. Nat. Commun. 2020, 11, 4507. [Google Scholar] [CrossRef]
- Hasell, J.; Mathieu, E.; Beltekian, D.; Macdonald, B.; Giattino, C.; Ortiz-Ospina, E.; Roser, M.; Ritchie, H. A cross-country database of COVID-19 testing. Sci. Data 2020, 7, 345. [Google Scholar] [CrossRef] [PubMed]
- The Economist. Fatal Flaws: COVID-19 death toll appears higher than official figures suggest. Economist, 4 April 2020.
- Coddington, E.A.; Levinson, N. Theory of Ordinary Differential Equations; McGraw-Hill Book Company, Inc.: New York, NY, USA; Toronto, ON, USA; London, UK, 1955. [Google Scholar]
- Rudin, W. Real and Complex Analysis, 3rd ed.; McGraw-Hill Book Co.: New York, NY, USA, 1987. [Google Scholar]
- Kurzweil, J. Ordinary Differential Equations; Studies in Applied Mechanics; Elsevier Scientific Publishing Co.: Amsterdam, The Netherlands, 1986; Volume 13, p. 440. [Google Scholar]
- Teschl, G. Ordinary Differential Equations and Dynamical Systems; Graduate Studies in Mathematics; American Mathematical Society: Providence, RI, USA, 2012; Volume 140. [Google Scholar] [CrossRef]
- Nevanlinna, F.; Nevanlinna, R. Absolute Analysis; Springer: New York, NY, USA; Heidelberg, Germany, 1973. [Google Scholar]
- Stokes, A. The Application of a fixed-point theorem to a variety of nonlinear stability problems. Proc. Natl. Acad. Sci. USA 1959, 45, 231–235. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Butcher, J.C. Numerical Methods for Ordinary Differential Equations, 3rd ed.; John Wiley & Sons, Ltd.: Chichester, UK, 2016. [Google Scholar] [CrossRef]
- Bluman, G.W.; Anco, S.C. Symmetry and Integration Methods for Differential Equations; Applied Mathematical Sciences; Springer: New York, NY, USA, 2002; Volume 154. [Google Scholar]
- Ouhadan, A.; El Kinani, E.H.; Hajar, M. Lie symmetries analysis for SIR model of epidemiology. Appl. Math. Sci. (Ruse) 2013, 7, 4595–4604. [Google Scholar] [CrossRef]
- Matadi, M.B. On the integrability of the SIRD epidemic model. Commun. Math. Biol. Neurosci. 2020, 2020, 55. [Google Scholar]
- Leach, P.G.L.; Andriopoulos, K. Application of symmetry and symmetry analyses to systems of first-order equations arising from mathematical modelling in epidemiology. In Symmetry in Nonlinear Mathematical Physics. Part 1, 2, 3; Natsīonal. Akad. Nauk Ukraïni, Īnst. Mat. Kiev: Kiev, Ukraine, 2004; Volume 3, pp. 159–169. [Google Scholar]
- Nucci, M.C. Using Lie symmetries in epidemiology. In Proceedings of the 2004 Conference on Differential Equations and Applications in Mathematical Biology, Nanaimo, BC, Canada, 18–23 July 2004. [Google Scholar]
- Golubitsky, M.; Schaeffer, D.G. Singularities and Groups in Bifurcation Theory. Vol. I; Applied Mathematical Sciences; Springer: New York, NY, USA, 1985; Volume 51. [Google Scholar] [CrossRef]
- Golubitsky, M.; Stewart, I.; Schaeffer, D.G. Singularities and Groups in Bifurcation Theory. Vol. II; Applied Mathematical Sciences; Springer: New York, NY, USA, 1988; Volume 69. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).