Abstract
MORUS is one of the finalists of the CAESAR competition. This is an ARX construction that required investigation against rotational cryptanalysis. We investigated the power of rotational cryptanalysis against MORUS. We show that all the operations in the state update function of MORUS maintain the rotational pairs when the rotation distance is set to a multiple of the sub-word size. Our investigation also confirms that the rotational pairs can be used as distinguishers for the full version of MORUS if the constants used in MORUS are rotational-invariant. However, the actual constants used in MORUS are not rotational-invariant. The introduction of such constants in the state update function breaks the symmetry of the rotational pairs. Experimental results show that rotational pairs can be used as distinguishers for only one step of the initialization phase of MORUS. For more than one step, there are not enough known differences in the rotational pairs of MORUS to provide an effective distinguisher. This is due to the XOR-ing of the constants that are not rotational-invariant. Therefore, it is unlikely for an adversary to construct a distinguisher for the full version of MORUS by observing the rotational pairs.
1. Introduction
MORUS [1,2] is a family of authenticated encryption stream cipher algorithms, one of the finalists in the CAESAR Authenticated Encryption (AE) competition [3]. There are three variants: MORUS-640-128, MORUS-1280-128 and MORUS-1280-256, where the first number represents the state size and the latter represents the key size. The cipher is intended to provide confidentiality and integrity assurance for the input data. This is a popular candidate from the CAESAR competition. Third-party security analysis is important for promoting and validating the design claims of MORUS. This paper provides a third-party analysis of MORUS subject to rotational cryptanalysis.
The MORUS family of ciphers has been subject a wide range of third-party security analyses. We first briefly discuss the existing security analyses of MORUS. Mileva et al. [4] proposed a distinguisher for MORUS-640 under the nonce-reuse scenario. This attack can analogously be used for MORUS-1280. They also reported collisions in the internal state of MORUS. However, an adversary must inject specific differences in the internal state to obtain the collisions. Dwivedi et al. [5] discussed the use of SAT solvers for state recovery with a complexity of . The complexity of this attack is beyond the designer’s claimed security margin. Dwivedi et al. [6] also performed differential and rotational cryptanalysis with a reduced version of MORUS. The best result from this work was a theoretical key recovery attack against MORUS-1280-256, where the initialization phase was reduced to 18 rounds (3.6 steps). Salam et al. [7] applied cube attacks that obtained distinguishers with up to 4/5 steps for MORUS-640/1280 with negligible complexity. Kales et al. [8] and Vaudenay et al. [9] analyzed the security of MORUS under the nonce-reuse scenario. Their attacks included state recovery, key recovery, forgery with practical complexities and a small number of nonce-misuse queries. Salam et al. [10] described key recovery and forgery against MORUS using fault attacks. This work considered different fault models. The best result from this work was a full key recovery with a transient fault model. Nozaki and Yoshikawa [11] investigated a power analysis attack against MORUS. Their work implemented the attack on an FPGA, which demonstrated the vulnerability of MORUS to power analysis. Ashur et al. [12] presented a linear correlation in the output of the full version of MORUS. This correlation can be used to distinguish the MORUS output keystream from randomness. Their work shows a plaintext recovery attack can be applied to MORUS-1280 using about blocks of data. They also presented a forgery attack on a reduced version of MORUS, where the finalization was reduced to three steps, and a key recovery attack under a nonce-reuse scenario for a reduced 10-step initialization. Li and Wang [13] analyzed division property and differential trails against MORUS. They reported 6/6.5-step integral distinguishers for MORUS-640/1280 and 4.5-step differential distinguishers for MORUS-1280. Shi and Guan [14] described a state recovery attack against MORUS under a nonce-reuse scenario. The attack reuses the nonce seven times to recover the internal state bits with practical complexity. Ye et al. [15] proposed a new existence terms detection method using the cube attack and applied it to MORUS. This method demonstrated key recovery attacks on 6/7-step MORUS-640-128 and integral distinguishers against 7-step MORUS-640-128/MORUS-1280-256. Shi et al. [16] proposed an algorithm to compute the correlation of quadratic Boolean functions. They applied the method to analyze the linear trails of MORUS. They identified a set of trails with correlation , which led to distinguishing and message-recovery attacks for all versions of MORUS with a complexity of . Chen et al. [17] discussed a method to search for cubes based on the division property. This work demonstrated a cube attack on 4.4-step MORUS-640-128 with a complexity of . He et al. [18] also investigated cube attacks against MORUS. The best result from this work used a cube of size 22 to apply a key recovery attack against 6-step MORUS-640-128.
Rotational cryptanalysis was applied [19] to ciphers composed of three operations: addition, rotation and XOR (ARX). MORUS is an ARX-like cipher, except that it uses bitwise multiplication instead of the addition operation. For ARX-like constructions, there is a need for analysis against rotational cryptanalaysis. Rotational cryptanalysis investigates the propagation of rotational pairs in the outputs of a cryptographic scheme for given rotational input pairs. The term rotational cryptanalysis was coined by Khovratovich and Nikolić in 2010 [19]; however, the attack technique was known and applied prior to this work by Biham [20]. To the best of our knowledge, there have been few third-party analyses of MORUS components and operations using rotational cryptanalysis. Therefore, we considered investigating the application of rotational cryptanalysis to MORUS, since it has similar ties to the ARX ciphers. In particular, we investigated different components and operations in MORUS and their rotational properties. Note that a rotational attack on MORUS was also investigated by Dwivedi et al. [6]. Their application of rotational cryptanalysis tried to recover the secret key of MORUS. They have developed a key recovery attack on round-reduced MORUS based on rotational cryptanalysis. On the other hand, we used rotational cryptanalysis to build a distinguisher for MORUS. Our approach of rotational cryptanalysis can build the distinguisher for just one step of the initialization phase of MORUS. Both of these works show that MORUS provides a large security margin against rotational cryptanalysis. The work by Dwivedi et al. [6] suggests that all the operations, except for the XOR-ing of constants, preserve the rotational pairs in MORUS for any arbitrary rotation distance. However, according to our analysis, this is not always true. We note that the operation in MORUS does not preserve rotational pairs in all the bits for arbitrary rotation distance; instead, it preserves the rotational pairs in all the bits when the rotation distance is a multiple of the sub-word length . This does not affect their cryptanalysis, since it uses known rotational characteristics in specific bits, which are computed in a pre-computation phase.
2. Description of MORUS
The MORUS family of stream ciphers supports a key K of either 128-bits or 256-bits. The initialization vector V is 128 bits for all the variants of MORUS. It takes an input plaintext P of arbitrary length. Confidentiality is achieved by encrypting the plaintext P by XOR-ing with the output keystream generated by the cipher to obtain the ciphertext C. The cipher also takes associated data D of arbitrary length as input. The associated data are not encrypted. MORUS provides integrity assurance for both the plaintext P and associated data D. This is done by injecting the plaintext and associated data into the internal state of the cipher and computing a tag in terms of the internal state.
MORUS has five state elements . Each element is a register of length either 128 bits or 256 bits, for MORUS-640 and MORUS-1280, respectively. This gives a total internal state size of 640 or 1280 bits, for MORUS-640 and MORUS-1280, respectively. Before going into the details of MORUS structure and operation phases, we first introduce the notations and operations used in this paper, as below:
- ⊕: Bit-wise XOR operation.
- ⊗: Bit-wise AND operation.
- ∥: Concatenation
- Word: A sequence of 32 bits or 64 bits, for MORUS-640 and MORUS-1280, respectively.
- Block: A sequence of 128 bits or 256 bits, for MORUS-640 and MORUS-1280, respectively.
- : Divide a -bit block x into 4 -bit words and rotate each word to the left by b bits.
- : The secret key of size bits.
- V: The initialization vector of size 128 bits.
- : A 128-bit constant in hexadecimal format.
- : A 128-bit constant in hexadecimal format.
- : The external input message to the state at step t.
- : The input plaintext block at step t.
- : The input associated data block at step t.
- : The output keystream block at step t.
- : The output ciphertext block at step t.
- : Authentication tag.
- : The internal state at step t.
- : The internal state at the jth round of step t.
- : kth element of state .
- : Rotation of the input X to the left by r bits.
- : operation applied to X. and assumed to be known from context.
2.1. Phases of Operation
Operations performed in MORUS can be divided into five phases:
- Initialization
- Processing associated data
- Encryption
- Finalization
- Decryption and tag verification
Note that there are two versions of the MORUS family of authenticated encryption cipher: MORUSv1 [1] and MORUSv2 [2]. The two versions differ only in the finalization phase. The general description provided in this paper is based on MORUSv2 [2]. Here we briefly describe the initialization of MORUS, as we investigated rotational cryptanalysis on this phase. Interested readers are referred to the original specifications of MORUS for further details.
Initialization of MORUS
The initialization of MORUS starts with loading the key, initialization vector and two 128-bit constants and into the internal state in a particular format. The loaded state of MORUS-640 is defined as . For MORUS-1280, two different key sizes may be used: a 128-bit key or a 256-bit key. The loaded state of MORUS-1280 with a 128-bit key is defined as . Similarly, the loaded state of MORUS-1280 with a 256-bit key is defined as . After forming the loaded state, the state of MORUS is updated for 16 clocks (steps) using the state update function . During these updates, the external input is set to zero and the cipher does not produce any output. After these 16 updates, the content of state element is XORed with the key. The state obtained at the end of this process is the initial state of MORUS-640.
2.2. Functions Used in MORUS
The operations performed in different phases of MORUS are based on several component functions. These are:
- 1.
- State Update Function
- 2.
- Keystream Generation Function
- 3.
- Combining Function
2.2.1. State Update Function
One of the main component functions of MORUS is the state update function . At each clock (step) t of the state update function, there are 5 rounds with similar operations. The operations in the state update function include AND, XOR and rotation operation. MORUS uses the bitwise left rotation , a simple rotation of the input X to the left by bits, where . It also uses the operation which divides a -bit block input x into 4 -bit words and rotates each word to the left by bits, where . The rotation constants and for different variants of MORUS are listed in Table 1.

Table 1.
Rotation constants used in MORUS.
Figure 1 shows the operations involved in the state update function of MORUS in generic form. As shown in Figure 1, in each round, two of the state elements are updated using the operations and . The state update function takes input from the internal state and external input M. Depending on the phase the cipher is in, the external input M can be: all zero bits, the associated data, the plaintext or a representation of the length of the associated data and plaintext. During the initialization phase, the external input is set to zero. The external inputs are defined in terms of the plaintext and the associated data for the encryption and associated data loading phases, respectively. The external input is defined in terms of the length of the plaintext and associated data for the finalization phase.
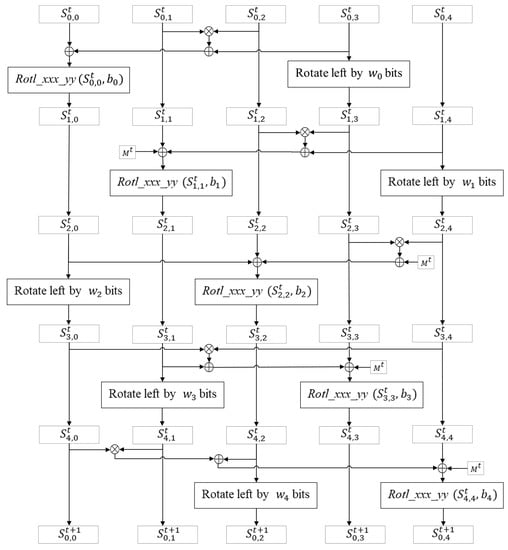
Figure 1.
State update function of MORUS.
2.2.2. Keystream Generation Function
The keystream generation function outputs a keystream block at each step of the encryption phase. The first four state elements of MORUS are used in the keystream function, as shown in
In the keystream generation function, is the left rotation constant, set to 96 bits or 192 bits for MORUS-640 and MORUS-1280, respectively.
2.2.3. Combining Function
MORUS is a binary additive stream cipher. Hence, it uses a simple XOR operation as the combining function during the encryption phase. That is, the ciphertext block is computed by XOR-ing the input plaintext block and the keystream block. At each clock t of the encryption phase, MORUS outputs a keystream block using Equation (1). This output keystream block is XOR-ed with the plaintext block to compute the respective ciphertext block. The ciphertext computation is shown in
3. Rotational Cryptanalysis of MORUS
Rotational cryptanalysis investigates the propagation of rotational pairs in the outputs of a cryptographic scheme for any given rotational input pairs. Let X and denote two input vectors, where is equivalent to the r-bit left rotated version of the input vector X. The input vector pair is called a rotational input pair. In rotational cryptanalysis, the adversary inputs such a rotational pair into the underlying cryptographic algorithm and observes the behavior of the output pairs. Let Z and denote the resulting output pair for the inputs X and , respectively; and denotes the r-bit left rotated version of Z. Having implies that the operations involved in the cryptographic algorithm do not affect the rotational relations in the output pair . That is, in such a scenario, the rotational relation is preserved in the output pair for the corresponding input pair . Clearly, if the rotational relation is preserved, the adversary can observe it in the output pair to build a distinguisher for the underlying cryptographic algorithm.
In the attack model, the adversary needs to select a pair of inputs. In the initialization phase of stream cipher based scheme, the adversary can select the rotational input pairs from the key or the initialization vector or combination of both key-initialization vector. Therefore, the attack model follows the chosen key attack, or the chosen initialization vector attack, or the chosen key-initialization vector attack. Additionally, note that the inputs in the rotational pair are related to each other; thus, this can also be considered as a related key-initialization vector attack.
This section discusses the applicability of rotational cryptanalysis to MORUS. We investigated the basic rotational properties of different operations used in the MORUS state update function. XOR-ing of constants also plays an important role in the analysis of rotational pairs. Our investigation also included the analysis of rotation invariant bits in the constants used for MORUS. We then investigated the rotational properties of MORUS state contents using the above mentioned operations. The goal of these investigations was to construct a distinguisher for MORUS, if the rotational properties were preserved in the input and the output.
3.1. Rotational Properties of Operations Used in MORUS
The operations in the state update function of MORUS include AND, XOR and rotation operations. It also uses the operation, which divides a -bit block input x into 4 -bit words and rotates each word to the left by b bits.
The rotational properties of bitwise XOR and rotation operation were investigated by Khovratovich and Nikolić [19]. In the following, we review these properties. We also analyze the properties of the ) operation, which were not explored in any previous literature.
3.1.1. Rotational Properties of XOR and Rotation Operation
Khovratovich and Nikolić stated that XOR operation preserves rotational pairs [19]. That is, for an r-bit rotation, Equation (3) is true. Their work stated that Equation (3) is true, but did not include the proof of this statement. For completeness, we provide a proof for this.
Theorem 1.
Bitwise XOR operation applied to a binary string X preserves the rotational pairs for any arbitrary rotation distance r. That is,
Proof of Theorem 1.
Suppose denotes the notation for n-bit string , where and . Similarly we define the string for n-bit string , where and . Then, for a r-bit arbitrary left rotation with , we can represent X and Y as and , respectively. We can write
and
Therefore, . □
The analysis show that the bitwise rotation operation also preserves the rotational pairs. Therefore, XOR and rotation operations in the state update function of MORUS do not break the symmetry in the rotational pairs.
3.1.2. Rotational Properties of AND Operation
Similar to the XOR operation, it is easy to prove that the bitwise AND operation always preserves the rotational pairs. That is, Equation (4) is true for any arbitrary rotation distance r.
Theorem 2.
Bitwise AND operation applied to a binary string X preserves the rotational pairs for any arbitrary rotation distance r. That is,
Proof of Theorem 2.
Suppose denotes the notation for n-bit string , where and . Similarly we define the string for n-bit string , where and . Then, for a r-bit arbitrary left rotation with , we can represent X and Y as and , respectively. We can write
and
Therefore, . □
Therefore, bitwise AND operation in the state update function of MORUS does not break the symmetry in the rotational pairs.
3.1.3. Rotational Properties of Operation
MORUS uses the operation which is a composition of two operations. This includes dividing the input word into four sub-words of equal length and then applying bitwise left rotation operation to these sub-words of MORUS. This operation can be considered as a bit-wise permutation. In general, bit-wise permutation does not preserve the rotational pairs. This is illustrated below with a simple example.
Let be a sequence of 8 bits. The application of operation on this 8-bit sequence X results in:
Following this, the application of a one-bit left rotation applied to results in:
Now, consider the alternative where first, the one bit left rotation is applied to the 8 bit sequence X, followed by the application of operation on the rotated sequence. The one bit left rotation applied to the sequence X results in:
Following that, application of operation on the rotated sequence results in:
Clearly in general, and therefore a rotational pair is not guaranteed to be preserved.
Conditions for Preserving a Rotational Pair under
We observe that the operation preserves the rotational pair, if the distance r of the left rotation applied to X equals to a multiple of the sub-word length . For the above example, the sub-word length is two. Applying two bit left rotation to the sequence X results in:
Application of operation on the rotated sequence results in:
Alternatively, application of two bit left rotation applied to results in:
As shown in the example, when the distance of the rotation applied is equal to the sub-word size. Experimental verification also confirms that the rotational pairs are preserved when the distance of the left rotation applied to X is equal to a multiple of the sub-word length . Additionally, the rotational pair will be preserved if the sequence X is rotation invariant for any arbitrary rotation distance.
We define the following theorem which identifies the condition for preserving rotation pairs when the operation is applied.
Theorem 3.
The operation applied to a binary string X preserves the rotational pairs if the distance of the rotation r applied is equal to a multiple of the sub-word size or if the input X is rotation invariant. That is,
if r is a multiple of the sub-word size.
Proof of Theorem 3.
Suppose denotes a n-bit string , where , , and . Let denote the notation for n-bit string , where and . Let b be the rotation distance applied in the operation. Then, can be represented as .
The length of the sub-word is for a n bit string. Thus, we need to show that the rotation distance , , on the operation will preserve the rotational pairs.
Therefore, when . Similarly, we can prove that Theorem 3 is true for a rotation distance . Additionally, if the input sequence X is rotation invariant for arbitrary rotation distance r, then application of to the input X will not have any effect on it. Therefore, the operation will preserve the rotational pairs if the input X is rotation invariant. □
In MORUS-640, the sub-word size is 32 bits. Thus, to maintain the rotational pairs in the operation of MORUS-640, the distance of the rotations applied should be a multiple of 32. Analogously, the sub-word size is 64 bits for MORUS-1280. Therefore, the distance of the rotations applied needs to be a multiple of 64 to preserve the rotational pair in the operation of MORUS-1280.
3.2. Rotational Properties of the Constants in MORUS
MORUS uses two constants and at the beginning of the initialization phase, which are used to load some of the state elements. These constants are XOR-ed with the contents of specific state elements as a part of the state update process. Khovratovich and Nikolić show that addition/XOR of a constant breaks the symmetry in rotational relations, if the constant is not rotation invariant [19]. Therefore, XOR-ing of constants plays an important role in the rotational cryptanalysis. In the following, we discuss the rotational properties of the constants used in MORUS.
3.2.1. Rotational Properties of MORUS-640 Constants
We analyzed the MORUS-640 constants when r-bit rotation is applied to it. We investigated the number of bits in the constant which are rotation invariant for the r-bit rotation. MORUS-640 applies the operation in its state update function. According to Theorem 3, the preserves the rotational pairs if the rotation distance is a multiple of 32 bits, i.e., 32, 64 or 96. Therefore, for the analysis of MORUS-640 constants, we set the rotation distance r as a multiple of 32.
With the above conditions, the constant also needs to be 32, 64, 96 or 128 bits rotation invariant depending on the distance of the rotations applied. If the constant is 32-bit rotation invariant (i.e., the constant can be divided into 4 small sub-word of 32 bits where each of the sub-word has same content), then there are rotation invariant constants. For a 64 bits rotation invariant constant, there are rotation invariant constants.
We investigated the rotation invariant bits in the constants for any distance of the rotation which are multiples of . For any multiples of , the constants used in MORUS-640 are not rotation invariant among all the bits; except for the trivial one which is basically the same constant. In the following, we discuss the number of bits that remain rotation invariant for different rotation distances set based on above criteria.
In MORUS-640, and are used to load the state element and . We examined the number of rotation invariant bits in these constants for any rotation distance which is a multiples of 32. The rotated constant has 74, 60 and 74 rotation invariant bits for 32, 64, and 96 bit rotation distances, respectively. Similarly, the rotated constant has 64, 62 and 64 rotation invariant bits for 32, 64, and 96 bit rotation distances, respectively. This means XOR-ing of these constants with the contents of any state element inverts about half of the bits in the corresponding state element compared to the result of XOR-ing with the rotated version of the constant.
Additionally, in the first step of the initialization phase, is used to update . The rotated version of this constant has 62, 74 and 62 rotation invariant bits for 32, 64, and 96 bit rotation distances, respectively.
The constant is used at the first step of initialization phase to update the state element . The rotated version of this constant has 72, 64 and 72 rotation invariant bits for rotation distances 32, 64, and 96 bits, respectively.
3.2.2. Rotational Properties of MORUS-1280 Constants
We investigated the constants used in MORUS-1280, when r-bit rotation is applied to it. The investigation explores the number of rotation invariant bits in the constant for rotation distance r. MORUS-1280 applies the operation in its state update function. According to Theorem 3, the operation preserves the rotational pairs if the rotation distance is a multiple of 64 bits, i.e., 64, 96, 192 or 256. Therefore, for the analysis of MORUS-1280 constants, we set the rotation distance r as a multiple of 64.
With the above conditions, the constant also needs to be 64, 128, 192 or 256 bits rotation invariant depending on the distance of rotations applied. For MORUS-1280, if the constant is 64-bit rotation invariant (i.e., the constant can be divided into four small sub-word of 64 bits where each of the sub-word has same content), then there are rotation invariant constants. For a 128 bits rotation invariant constant, there are rotation invariant constants which will preserve the rotational pairs for MORUS-1280.
We investigated the rotation invariant bits in the constants for any distances of rotation which are multiples of . For any multiples of , the constant used in MORUS-1280 is not rotation invariant among all the bits; except for the trivial one which is basically the same constant. In the following, we discuss the number of bits that remain rotation invariant for different rotation distances set based on above criteria.
In MORUS-1280, is used to load the state element . The rotated version of this constant has 138, 114 and 138 rotation invariant bits for rotation distances 64, 128 and 192 bits, respectively. This means that XOR-ing this constant with the contents of the state element will preserve the rotational pairs in 138 bits when the rotation distance in the input is set to 64 bits.
The constant used to initialize state element consists of all 1. This constant is rotation invariant for any arbitrary rotation distance. Similarly, the constant used to initialize state element consists of all 0s. This constant is also rotation invariant for any arbitrary rotation distance.
3.3. Rotational Properties of MORUS State Contents
This section investigates the rotational properties in the MORUS state contents. The contents of MORUS state elements were updated using the state update function . Rotational properties of the operations and constants used in the state update function are discussed in Section 3.1 and Section 3.2. In our investigation, we used these properties to determine the propagation of rotational pairs in MORUS state contents.
We first investigated the probability of preserving the rotational pairs in the MORUS state elements after one step of the initialization phase. We then extended our analysis for more than one step of the initialization phase.
We started our experiment by defining the key K and initialization vector V in terms of variables. We then generated equations in terms of K and V to represent the state contents of n-step MORUS. After that, we generated the equations in terms of rotated versions of the key and initialization vector to represent the state contents of n-step MORUS. Finally, we investigated the rotational pair in the state elements to determine whether they preserve the rotational pair. Preserving the rotational pair in the state elements means that the rotational pair in the output keystream is also preserved.
If the rotational pair is preserved in the output pair, then adversary can observe the output pair and use this to distinguish the MORUS output from a randomly generated output. This can be considered as a distinguisher under the related key-IV model.
3.3.1. Rotational Properties of MORUS-640 State Contents
MORUS-640 uses the operations XOR, AND, bitwise left rotation and the operation in its state update function. As illustrated in Theorems 1 and 2, bitwise XOR and AND operation will preserve the rotational pair for any arbitrary number of rotations. However, for the operation, as described in Theorem 3, the rotation distance in the input needs to be a multiple of 32 bits—i.e., 32, 64 or 92—for MORUS-640, to preserve rotational pairs in the output. Thus, in our analysis of MORUS-640 state contents, the distance of the rotation r was set to 32. We conducted our analysis with the rotation distance of 32 bits, since that preserved the rotational pairs in maximum number of bits after performing the XOR operation with the constant (see Section 3.2.1).
Rotational Pairs in MORUS-640 with 1-Step Initialization Phase
For a 32 bit rotated input, rotational pairs are preserved in 74 bits of the state element with probability 1. Rotational pairs are preserved in the rest of the 54 bits of the state element with probability 0—i.e., the corresponding bits are inverted. This is because of the the XOR of with the contents of state element , at the beginning of the initialization phase. As shown in Section 3.2.1 for bit rotation distance, has 74 bits which are rotation invariant. Thus, this introduces 54 inverted bits.
For state element , rotational pairs are preserved in 62 bits with probability 1. Rotational pairs are preserved in the rest of the 66 bits of the state element with probability 0; i.e., the corresponding bits are inverted. Note that is XOR-ed with the contents of state element . As shown in Section 3.2.1, constant has 62 rotation invariant bits. Thus, this introduces inversion in the resulting rotational pair.
Rotational pairs are preserved in 72 bits of the state element with probability 1. Rotational pairs are preserved in the remaining 56 bits of the state element with probability 0; i.e., the corresponding bits are inverted. We also observe that the constant is XOR-ed with the contents of . As illustrated in Section 3.2.1, constant has 72 rotation invariant bits. Thus, this introduces inversion in the resulting rotational pair.
Rotational pairs are preserved with probabilities 1, 0.5 and 0 in 36, 64 and 28 bits of , respectively. Finally, rotational pairs are preserved with probabilities 1, 0.5 and 0 in 14, 94 and 20 bits of , respectively. Table 2 summarizes the probability of preserving rotational pairs in the state elements of 1-step MORUS-640.

Table 2.
Probability of preserving rotational pairs after one step of the initialization of MORUS-640.
As shown in Table 2, after one step there are 482 known differences in rotational pairs based on 32-bit rotations of the state elements of MORUS. Therefore, observing these known differences in the specific output bit of a rotational pair, an adversary can distinguish the keystream of 1-step MORUS-640 from a randomly generated output.
Rotational Pairs in MORUS-640 with Initialization Phase beyond One Step
We extended our experiments to determine the probability of preserving rotational pairs in more than one step of the initialization phase of MORUS-640. For two steps of the initialization phase, we found there are only 21 known differences in rotational pairs of the state contents of MORUS-640. In particular, we found only 14 bits and 7 bits are preserved in state elements and , respectively, with a probability of 1 or 0. This is not sufficient to determine a distinguisher because there are no known differences in the rest of the state elements.
For more than two steps of the initialization phase, Sage fails to generate the equations. This is due to the fact that the equations get very complicated after two steps of the initialization phase and the software Sage runs out of memory to perform the necessary computations.
As indicated above, after the two steps of the initialization phase, there are not enough rotational pairs in the state elements to construct a distinguisher and such situation becomes worse with more steps. Therefore, it is unlikely for an adversary to construct a distinguisher for the full version of MORUS-640 based on observing the rotational pairs.
3.3.2. Rotational Properties of MORUS-1280 State Contents
MORUS-1280 uses the XOR, AND, bitwise left rotation and the operations in its state update function. As illustrated in Theorems 1 and 2, bitwise XOR and AND operation will preserve the rotational pair for any arbitrary number of rotations. However, for the operation as described in Theorem 3, the rotation distance in the input needs to be a multiple of 64 bits, i.e., 64, 128 or 192, for MORUS-1280, to preserve rotational pairs in the output. Thus, in our analysis of MORUS-1280 state contents, the distance of the rotation r is set to 64. We conducted our analysis with the rotation distance of 64 bits, since it preserved the rotational pairs in the maximum number of bits after performing the XOR operation with the constant (see Section 3.2.2).
Rotational Pairs in MORUS-1280 with 1-Step Initialization Phase
Rotational pairs are preserved in all of the 256 bits of the state element with probability 1. This is because the constant XOR-ed with the contents of this state element are all zeroes and so rotation invariant for arbitrary rotation distance r.
Rotational pairs are preserved in 138 bits of the state element with probability 1. Rotational pairs are preserved in the remaining 118 bits of the state element with probability 0; i.e., the corresponding bits are inverted. Observe that is XOR-ed with the contents of the state element . As described in Section 3.2.2, has 138 rotation invariant bits. Thus, XOR-ing of this constant introduces 118 bits of inversion in the rotational pair.
Rotational pairs are preserved in all of the 256 bits of the state element with probability 1. This is because the constant XOR-ed with the contents of this state element is , e.g., all zeroes, and rotation invariant for arbitrary rotation distance r.
Rotational pairs are preserved with probabilities 1, 0.5 and 0 in 73, 118 and 65 bits of , respectively. Rotational pairs are preserved with probabilities 1, 0.5 and 0 in 78, 118 and 60 bits of , respectively.
Table 3 summarizes the probability of preserving rotational pairs in the state elements of 1-step MORUS-1280. We found that rotational pairs are preserved with probability 1 in 801 bits of the 1-step MORUS-1280. After one step of the initialization phase, there are only 236 bits which are unknown with probability 0.5. Therefore, based on these known differences in the specific output bit of a rotational pair, an adversary can distinguish the keystream of 1-step MORUS-1280 from a randomly generated output.

Table 3.
Probability of preserving rotational pairs after one step of the initialization of MORUS-1280.
Rotational Pairs in MORUS-1280 with Initialization Phase beyond One Step
We extended our experiments to determine the probability of preserving rotational pairs in more than one step of the initialization phase of MORUS-640. For two steps of the initialization phase, we found only 30 bits and 17 bits are preserved in state elements and , respectively, with a probability of 1 or 0. This is not sufficient to determine a distinguisher because there are no known differences in the rest of the state elements.
For more than two steps of the initialization phase, Sage fails to generate the equations for MORUS-1280. This is due to the fact that the equations get very complicated after two steps of the initialization phase and the software Sage runs out of memory.
As indicated above, after the two steps of the initialization phase, there are not enough rotational pairs in the state elements to construct a distinguisher; and said situation becomes worse with more steps. Therefore, it is unlikely an adversary will be able to construct a distinguisher for the full version of MORUS-1280 based on observing the rotational pairs.
4. Conclusions
We investigated the feasibility of rotational cryptanalysis on different variants of MORUS. Our investigation showed that all the operations used in MORUS preserve the rotational pairs when the rotation distance is set to a multiple of 32 or 64 for MORUS-640 and MORUS-1280, respectively. We have also verified that an adversary can build a distinguisher for the full version of MORUS if rotational-invariant constants are used in the state update function of MORUS. However, the constants used in MORUS are not rotational-invariant, which makes it infeasible to build the distinguisher for more than one step. Due to the non-invariant constants used in the state update function of MORUS, we found that rotational cryptanalysis can distinguish the MORUS output for only one step of the initialization phase. For more than one step of the initialization phase, the probability of preserving rotational pair becomes 0.5 in most of the bits. This makes it infeasible to apply the distinguisher for more than one round.
Funding
This research was funded by Xiamen University Malaysia Research Fund (grant number XMUMRF/2019-C3/IECE/0005).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- Wu, H.; Huang, T. The Authenticated Cipher MORUS (v1). CAESAR Competition. Available online: https://competitions.cr.yp.to/round1/morusv1.pdf (accessed on 14 October 2021).
- Wu, H.; Huang, T. The Authenticated Cipher MORUS (v2). CAESAR Competition. Available online: https://competitions.cr.yp.to/round3/morusv2.pdf (accessed on 14 October 2021).
- CAESAR: Competition for Authenticated Encryption: Security, Applicability, and Robustness. Available online: https://competitions.cr.yp.to/index.html (accessed on 14 October 2021).
- Mileva, A.; Dimitrova, V.; Velichkov, V. Analysis of the authenticated cipher MORUS (v1). In Cryptography and Information Security in the Balkans—BalkanCryptSec 2015; Lecture Notes in Computer Science; Pasalic, E., Knudsen, L.R., Eds.; Springer: Cham, Switzerland, 2015; Volume 9540, pp. 45–59. [Google Scholar] [CrossRef]
- Dwivedi, A.D.; Klouček, M.; Morawiecki, P.; Nikolić, I.; Pieprzyk, J.; Wójtowicz, S. SAT-based cryptanalysis of authenticated ciphers from the CAESAR Competition. In Proceedings of the 14th International Conference on Security and Cryptography—SECRYPT 2017, Madrid, Spain, 24–26 July 2017; pp. 237–246. [Google Scholar] [CrossRef] [Green Version]
- Dwivedi, A.; Morawiecki, P.; Wójtowicz, S. Differential and rotational cryptanalysis of round-reduced MORUS. In Proceedings of the 14th International Conference on Security and Cryptography—SECRYPT 2017, Madrid, Spain, 24–26 July 2017; pp. 275–284. [Google Scholar] [CrossRef]
- Salam, I.; Simpson, L.; Bartlett, H.; Dawson, E.; Pieprzyk, J.; Wong, K.K. Investigating cube attacks on the authenticated encryption stream cipher MORUS. In Proceedings of the IEEE International Conference on Trust, Security and Privacy in Computing and Communications—TrustCom 2017, Sydney, Australia, 1–4 August 2017; pp. 961–966. [Google Scholar] [CrossRef] [Green Version]
- Kales, D.; Eichlseder, M.; Mendel, F. Note on the robustness of CAESAR candidates. IACR Cryptol. ePrint Arch. 2017, 2017, 1137. [Google Scholar]
- Vaudenay, S.; Vizar, D. Under pressure: Security of CAESAR candidates beyond their guarantees. IACR Cryptol. ePrint Arch. 2017, 2017, 1147. [Google Scholar]
- Salam, I.; Simpson, L.; Bartlett, H.; Dawson, E.; Wong, K.K. Fault attacks on the authenticated encryption stream cipher MORUS. Cryptography 2018, 2, 4. [Google Scholar] [CrossRef] [Green Version]
- Nozaki, Y.; Yoshikawa, M. Power analysis attack for a fast authenticated encryption MORUS. In Proceedings of the International Conference on Applied System Innovation—ICASI 2017, Sapporo, Japan, 13–17 May 2017; pp. 365–368. [Google Scholar] [CrossRef]
- Ashur, T.; Eichlseder, M.; Lauridsen, M.; Leurent, G.; Minaud, B.; Rotella, Y.; Sasaki, Y.; Viguier, B. Cryptanalysis of MORUS. In Advances in Cryptology—ASIACRYPT 2018; Lecture Notes in Computer Science; Peyrin, T., Galbraith, S., Eds.; Springer: Cham, Switzerland, 2018; Volume 11273, pp. 35–64. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Wang, M. Cryptanalysis of MORUS. Des. Codes Cryptogr. 2019, 87, 1035–1058. [Google Scholar] [CrossRef]
- Shi, T.; Guan, J. Real-time state recovery attack against MORUS in nonce-misuse setting. Sci. China Inf. Sci. 2019, 62, 39109. [Google Scholar] [CrossRef] [Green Version]
- Ye, T.; Wei, Y.; Meier, W. A new cube attack on MORUS by using division property. IEEE Trans. Comput. 2019, 68, 1731–1740. [Google Scholar] [CrossRef]
- Shi, D.; Sun, S.; Sasaki, Y.; Li, C.; Hu, L. Correlation of quadratic Boolean functions: Cryptanalysis of all versions of full MORUS. In Advances in Cryptology—CRYPTO 2019; Lecture Notes in Computer Science; Boldyreva, A., Micciancio, D., Eds.; Springer: Cham, Switzerland, 2019; Volume 11693, pp. 180–209. [Google Scholar] [CrossRef]
- Chen, S.; Xiang, Z.; Zeng, X.; Zhang, S. Cube attacks on round-reduced MORUS and GIMLI. Sci. China Inf. Sci. 2021, 65, 119101. [Google Scholar] [CrossRef]
- He, Y.; Wang, G.; Li, W.; Ren, Y. Improved cube attacks on some authenticated encryption ciphers and stream ciphers in the internet of things. IEEE Access 2020, 8, 20920–20930. [Google Scholar] [CrossRef]
- Khovratovich, D.; Nikolić, I. Rotational cryptanalysis of ARX. In Fast Software Encryption—FSE 2010; Lecture Notes in Computer Science; Hong, S., Iwata, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6147, pp. 333–346. [Google Scholar] [CrossRef] [Green Version]
- Biham, E. New types of cryptanalytic attacks using related keys. J. Cryptol. 1994, 7, 229–246. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).