Abstract
Minkowski spacetime provides a background framework for the kinematics and dynamics of classical particles. How the framework implements the motion of matter is not specified within special relativity. In this paper we specify how Minkowski space can implement motion in such a way that ’quantum’ propagation occurs on appropriate scales. This is done by starting in a discrete space and explicitly taking a continuum limit. The argument is direct and illuminates the special tension between ’rest’ and ’uniform motion’ found in Minkowski space, showing how the formal analytic continuations involved in Minkowski space and quantum propagation arise from the same source.
1. Prolog
Problems with the concept of ‘motion’ go back to antiquity. For example, Zeno’s paradoxes provided an early illustration that our concepts of ‘rest’ and ‘motion’ do not have clear boundaries. To this day, while the calculus provides a mathematically rigorous model of motion using limits, the model itself is outside the domain of any ‘physical reality’ accessible to an actual observer. Thus we can imagine an experiment to determine a ratio , where and represent measurements of physically small lengths and times respectively. However, under no circumstances can one conduct an experiment where, in the measurement of velocity, , or where a limit as is actually taken.
Despite the impossibility of observing or verifying the physical analogs of continuity and differentiability, the use of infinite divisibility and smoothness in classical theories has been very successful. Notably, general relativity continues to engage philosophers, physicists and mathematicians alike for the way it encodes the imagery of how space, time and gravity might interact in a smooth world [1].
Wheeler’s famous aphorism:
provides a clear visualization that, encoded mathematically with strong smoothness assumptions, yields modern relativity. The clarity of the image that Wheeler’s statement in natural language invokes and the closeness to the resulting mathematical models is so evident that, by comparison, quantum mechanics looks like a deliberate cypher. (This is not to impugn the importance or effectiveness of quantum theory. It is arguably the most accurate and useful theory we have, and the mathematical framework is no less elegant than relativity. However, the interpretations of the theory are many and varied and there is no sensible statement in natural language that illustrates what quantum propagation physically represents.)“Spacetime tells matter how to move, matter tells spacetime how to curve.”[2]
Since relativity, and in particular Minkowski space, is so clear in its ‘encoding’ of features of spacetime, the intent of this paper is to use that clarity to view the emergence of quantum propagation from within the restrictions of Minkowski space, both literally and metaphorically. With reference to the first half of Wheeler’s quote we address the question:
“What are the spacetime instructions that tell an electron how to move?”
An answer to this question may be found from the perspective of applied mathematics when we digitally encode simple features of spacetime diagrams. The digital aspect of the encoding allows us to reach underneath the smoothness assumptions of relativity and ask questions about how spacetime, that is not intrinsically smooth in the presence of discrete events, could implement instructions in such a way that a smooth continuum limit results.
In the process of finding appropriate instruction sets, we shall see quantum propagation emerge [3] as a direct consequence of the fixed speed of light. While this does not remove the peculiarities of quantum propagation, it does point directly to the light-speed postulate as the source of both quantum mechanics and special relativity. It also refers both theories back to older philosophical problems of differentiating ‘rest’ and ‘motion’. Lastly, the origin of the formal analytic continuation that distinguishes quantum mechanics from ‘classical’ theories becomes evident in this picture. Roughly speaking, in a discrete context, Minkowski’s original invocation of spacetime in terms of , so that boosts look like rotations, turns the analog of worldlines into signals on the scale of the Compton length. Classical relativity is obtained by ignoring the signal and retaining only the rotation and stretch of the Lorentz transformation; while the Dirac equation is obtained by keeping the lowest frequencies of the signal. Once this is discovered, it changes the perspective on the relationship between relativity and quantum mechanics. If you start with discrete events under the restrictions of special relativity, classical physics arises only if you deliberately ignore the fact that a discrete spacetime forces the existence of a non-trivial signal in place of the worldline.
This does become evident when you start in the discrete world and take a continuum limit. However, it is hidden if you start in the continuum and try to work backwards to the discrete. (This is arguably what happened with quantum mechanics historically. In the transition from old quantum theory to modern quantum theory, Schrödinger’s use of his partial differential equation, essentially to extract discrete eigenvalues, was preferred to Heisenberg’s matrix mechanics because of the ubiquitous presence of differential equations in physics.) In that case ‘quantum propagation’ has to be added as an overlay …, a prescription where dynamical variables are replaced by operators. While the latter is conventional and elegant, the former allows you to see that quantum propagation, whether ‘relativistic’ or not, has its origin in the Lorentz transformation and the fixed speed of light.
2. Introduction
In this paper we discuss specific instructions by which spacetime tells an electron (or a particle identified by a fixed mass) how to move in a two dimensional spacetime. We investigate a variant of special relativity that associates a characteristic length (The Compton length) with an electron’s ‘worldline’ so that the microscopic structure of the worldline identifies the particle mass. We examine the instructions for movement of such a particle in a discrete spacetime, considering the problem in such a way that a smooth continuum limit becomes available as the partition of spacetime is refined. We find that maintenance of the fixed characteristic length in a continuum limit ultimately leads to the Dirac equation, but in a context where the antecedents in the classical theory are clear.
It is notable that while this transition from ‘classical’ to ‘quantum’ appears in the continuum limit, it does so where we can examine the approach along with the limit itself. This allows us to see that the origin of ‘wave-particle duality’ and the resulting non-locality arises from within special relativity itself. By viewing the continuum limit this way we see the transition from the discrete to the continuous, thus avoiding an initial prejudice that space and time should be independently continuous.
In practical terms, the view provides a reminder that the common use of differentials like in physical situations where we are contemplating a limit , often has an attached caveat like where M is some fixed large number. If we ignore the caveat and take the limit, we are liable to get a model that describes behaviour in a regime where . A familiar statistical example of this is the diffusion equation. We can extract the diffusion equation from the theory of random walks on lattices by invoking a continuum limit where we let space scales go to zero while assuming that such scales stay above the physical length of the mean free path of the fluid being modelled. The resulting partial differential equation then works well as a model on macroscopic scales but is unreliable otherwise, as it does not recognize behaviour changes on the scale of inter-particle distance, and incorrectly predicts infinite signal velocity [4].
We shall see that classical special relativity is similar in that ‘telling matter how to move’ without building a specific mass into the kinematics, presupposes a continuum limit at the start; it is specifically this presupposition that precludes quantum propagation. By failing to recognize the Compton scale of a particle, the usual formulations of special relativity miss ‘quantum’ behaviour that results from the existence of a characteristic inner scale [5,6].
In the next section, we sketch the primary argument specifically through digital images of spacetime diagrams, where the the simplicity of the arguments is easily seen. In this section we specify what the instruction set that encodes an electron’s persistence in time must entail in terms of producing the digital images of simple spacetime diagrams. We see that, contrary to Newtonian physics, rest in Minkowski space is a derived concept, although one that is easily visualized. Uniform motion is more subtle, but is also easily accomodated through the Lorentz transformation. Subsequent sections sketch the mathematical encoding of the imaging of particles at rest and in inertial motion.
In Section 6 we discuss the calculation and the implications.
3. Imaging a Particle at Rest
In order for spacetime to specifically tell an ‘electron’ how to move, it has to recognize the particle’s mass. Conventionally in special relativity, mass and associated momentum/energy are deduced through dynamics, but if spacetime is telling an electron how to move, it is reasonable to assume that spacetime itself does not have to ‘learn’ the mass through interactions with other objects, so we are looking for identifying geometric features that could be associated with mass.
When working with special relativity it is often useful to consider spacetime diagrams to illustrate features of boosts, worldlines and clocks. A first notable feature of spacetime using such diagrams is that if we choose an origin for a spacetime frame we find that the origin partitions spacetime into four distinct regions Figure 1.
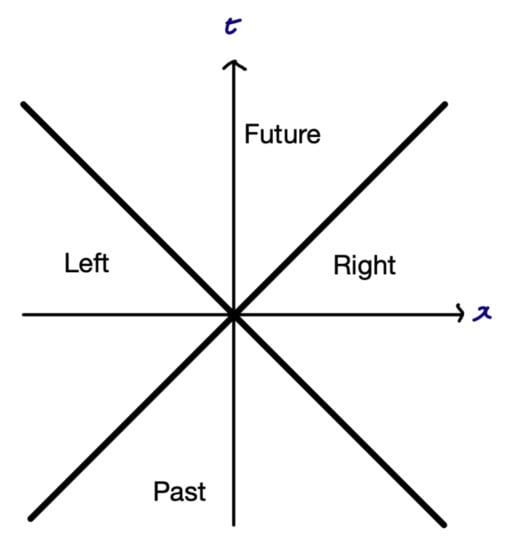
Figure 1.
Light-like lines through the origin partition spacetime into four distinct regions. The partition exists on all scales. Throughout this article all diagrams assume natural units in which .
If we imagine discrete events at positions , the intersections of the forward and backward lightcones from these points yield a sequence of causal areas that include all points time-like connected to the events in the sequence. The four different combinations of past, future, left and right suggest we colour edges in four different colours, giving rise to a sequences of what we shall call timestamps. (Alternatively, if we think of the boundaries of the causal areas as photons, there are two distinguishable photons and two directions giving rise to a four-state ’clock’. So for example in Figure 2 the red and green lines, though parallel, correspond to the two different photons.) Figure 2.
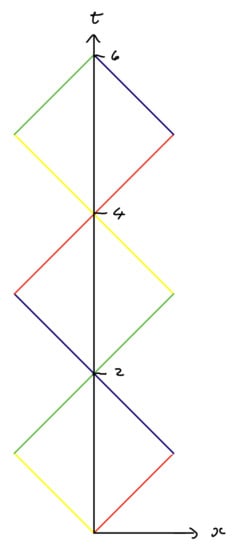
Figure 2.
Periodic events on a stationary worldline give rise to sequences of causal areas. We call a succession of two of these a timestamp. The period here is 4. The ‘worldline’ here is assumed to lie on the t-axis.
From Figure 2 we can see that successive causal areas are geometrically similar, but are not simple translations of each other. The first square, between and requires a rotation of in the plane, as well as a translation to be fully congruent to the successive rectangle. As a result, two successive squares forming a timestamp between the events at and form a unit that is congruent to the next timestamp between and . The alternation of the two types of squares in the sequence of squares can be thought of as a ‘photon clock’ [7,8,9,10] or a sequence of oriented squares [11].
The objective of this section is to build a digital instruction set to draw the 4-colour timestamp Figure 2 from the bottom up. We shall do this first at a very coarse resolution, subsequently increasing the resolution, adapting the image to a reduction of pixel size. We shall then see how to map a sequence of timestamps onto an analog of a worldline in such a way that the mapping generalizes to arbitrarily high resolution.
While the timestamp has some appeal in terms of suggesting a target for ‘spacetime telling an electron how to move’ there are two questions that need clarification to make further progress.
- What, if anything, does the timestamp have to do with quantum propagation?
- Is there a mapping of the timestamp image onto a domain that admits a smooth continuum limit?
The first question requests some indication that timestamps, as examples of spacetime instructions, are linked to quantum propagation. One visual argument would be to show how timestamp replacements of worldlines respond to Lorentz boosts. Figure 3 shows the effect of a Lorentz boost on a timestamp chain. As the relative speed of the observer with respect to the rest frame increases, the chain axis rotates and the chain itself stretches, pulling earlier links out along the direction of the chain; an example of ‘the moving clock runs slow’ of special relativity. As the velocity v increases, the intersection of the chain with a line at fixed t occurs at earlier portions of the timestamp sequence. Throughout all boosts the edges of the causal areas remain fixed in orientation due to the fixed speed c.
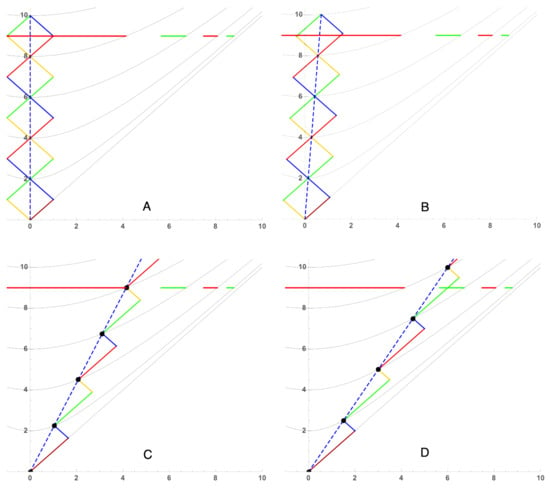
Figure 3.
A sequence of timestamps stretched and rotated by Lorentz boosts. Time is vertical and space horizontal. Clockwise from the top. (A) a Red portion of the timestamp intersects the line . In (B,C) the relative speed of the observer increases but the Red portion still intersects . In (D) velocity is high enough that the earlier Green segment intersects . As the relative speed of the observer increases, the earlier the ‘history’ recorded on the space axis.
Notice that the ensemble of these intersections provides a ‘History Map’ [4] of the chain along the x-axis, running from the current value of t back to the origin as x runs from 0 to . That is, the ensemble of images over all inertial frames maps the history of the timestamp ‘at rest’ onto the spatial axis.
Figure 4 shows the History Map of a far-field record of the intersection of the boosted images of the right side of the chains, along the x-axis [4,12].This is shown at fixed t for particle speeds . Plotted with this far-field record is the real part of the Feynman non-relativistic propagator for an electron. We can see visually the synchronization of the two. Only one parameter, the mass in appropriate units, fixes the synchronization that persists for many, many cycles. This suggests that a smoothed version of a timestamp might produce the propagator in detail, thus providing a connection between timestamps and quantum propagation.
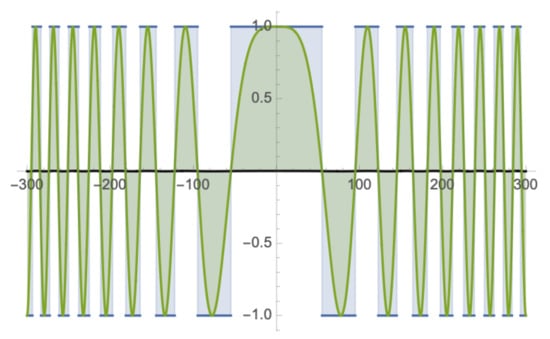
Figure 4.
The History-Map of a binary clock is the variable frequency square wave in this figure. The smooth curve is the real part of the Feynman propagator [13]. A single number mass in natural units, registers the two patterns. While the path integral assembles the propagator from an infinite number of Feynman paths, the History-Map is a mapping of a single sequence of timestamps via the Lorentz boosts. The smooth curve is standard quantum mechanics. The History Map is Special Relativity with Timestamps replacing worldlines.
To answer the second question, we shall build timestamps digitally using just two operations. We shall see that there exists a natural smoothing feature that ultimately admits a continuum formulation. We do this in the next section.
4. Building a Transfer Matrix
In the previous section we visually established a structural feature of special relativity that appears to produce a discrete form of the Dirac propagator. That is, in Figure 4 we see that the transitions of the four discrete states of the timestamp mark the nodes of the propagator, encasing a smooth curve in a discontinuous two-valued envelope curve. The inability of the envelope curve to match the smooth features of the propagator stem from the fact that the boundaries of the timestamp are null lines, along which proper time does not change. Only at corners and crossing points on the timestamp does the proper time change, and that discontinuously. Like the tick-tock of a mechanical clock, the timestamp counts time discretely with four intrinsic states. It is these discontinuities that map onto the nodes of the Feynman propagator.
However, if spacetime is responsible for maintaining fixed time intervals based on a counting process, and we wish to end up with a smooth description, the counting frequency must be much higher than the corner frequency of the electron timestamp. To end up with a differential equation, we do not need to have infinite frequencies in spacetime, but we do need to consider frequencies much higher than the Compton frequency. We can then set up a counting process for spacetime with the caveat that if we are able to take a continuum limit to extract the Dirac propagator, the result itself is an approximation, not to be taken too seriously below the Compton wavelength, but descriptive above the Compton length. (The point here is that the assumption that Nature operates in a mathematical domain containing analytic functions is a leap of faith that can never be verified on a practical level, and would in any case be inconsistent with a finite universe from a quantum mechanical perspective. In this article, limits are explicitly regarded as mathematical conveniences, so when we speak of a limit like where is a time interval, we mean that is small compared to the Compton time, but still larger than some other characteristic length like the Planck length.)
To develop an encoding for spacetime we simply encode as digital images the spacetime diagrams that give rise to Figure 1, Figure 2, Figure 3 and Figure 4. Since digital images are just arrays of numbers, the linear algebra involved in the encoding process represents the generation of the images of the spacetime diagrams that we visually interpret as features of spacetime. The algebraic manipulations we go through to map the timestamp onto an image that smoothly handles increasing resolution, gives an analogy of how spacetime might accomplish the same thing.
We first encode the timestamp as the representation of a ‘stationary’ particle. The encoding will involve number and a single fixed magnitude. The number aspect will just count frequencies of operations, there being two operations; Persist (P) and Switch (S) for persistence along a light cone and direction reversal, respectively. Thus we shall be looking at periodic sequences like
where the number of P’s between S’s is fixed in a sequence and each symbol represents a fixed small magnitude. The continuum limit will increase the number of P’s between S’s without bound but will fix the magnitude of the sum of the small magnitudes between S’s. That is, in Equation (1) n increases without bound but the ‘time’ interval between S’s remains fixed. While Equation (1) builds the timestamp out of small time intervals with a discontinuous velocity structure, spacetime itself needs structure on the small time scales of the individual steps to do the encoding. (That is, spacetime has to have a way of counting steps between corners on the timestamp, since the null edges themselves do not carry the information corresponding to the number of steps to the next switch.) To model that encoding we replace the half cycle in Equation (1) by:
This process leads to a smooth analog of the timestamp Equation (1) and provides a mapping from the visual features of timestamps to a discrete precursor of a smooth process. The S that is a corner in the timestamp is distributed over the entire length of the half period. The replacement allows us to see that provided spacetime has a bandwidth that can encode frequencies much higher than the Compton frequency, then between the discrete envelope of the timestamp and the smooth evolution of the Dirac propagator, there are intermediate piecewise linear progressions to indicate where the propagator comes from and why it is there.
As an example, we create a very low resolution digital image of the timestamp of Figure 2. Specifically, we shall create a digital image in which the width of the image is 6 pixels and its height is greater than the timestamp height of 24 pixels. Since the image involves just 4 colours on a uniform background, we can associate a 2-component intensity with each pixel as follows:
the background being represented as .
To generate the digital image in the same way that spacetime might evolve a pattern along the x-axis, we construct a discrete process that will take the initial pattern on the x-axis at and evolve the initial condition to create the timestamp image. From Figure 2 we see that the initial condition at the origin is a combination of Red and Yellow. After the first step the Red has moved one unit to the right and the Yellow one to the left. This movement is repeated in the next step. For an image that is only 6 pixels wide, at the third step Red switches to Blue and Yellow switches to Green. This persists for 6 steps and then the colours and directions reverse. In the persist or switch representation of Equation (1) the sequence is
In terms of pixel intensities with the coding of Equation (3) the initial configuration is:
Which we flatten to the ‘state’:
This can be evolved by a ‘transfer matrix’ to produce a succession of states that represents the coding of a timestamp. Below is an explicit representation of the transfer matrix on the left, and the resulting timestamp, grown from the bottom, on the right. That is, the array on the right is obtained by operating on the initial condition Equation (6) with the transfer matrix on the left. Each row of the array on the right is obtained through multiplication of the previous row by the transfer matrix.
Interpreted as an unrendered digital image with the assigned colours of Figure 2 we see the timestamp pattern in the data matrix on the right in Equation (7). The data matrix itself, rendered as an image, would be pixelated and give a coarse representation of lines compared to the sketch in Figure 2. The pixelation may be reduced by increasing the pixel density, but staying at this resolution we can examine the transfer matrix that operates on the initial state Equation (6), and see how we would increase the resolution.
Looking at the structure we can see that the two bands parallel to the main diagonal correspond to the ‘P’ instruction to persist along the null lines in the image, maintaining the colour state and direction (left, right). The element and the elements constitute the ‘S’ instruction that changes the direction and colour of the null lines at the outer corners (This is accomplished by switching states and sides of the spatial ‘box’. We could have chosen reflective boundary conditions to the same effect, but this choice is simpler.). Visually we can look at the matrix and see that to increase the number of pixels along the edges we just keep the corner elements and increase rows and columns maintaining the banded structure. We shall do this shortly, but first we address the question of mapping the timestamp onto a formulation that smooths out the switch S in time evolution. That is we want to implement Equation (2) to determine Q. In this case the transfer matrix has been specifically constructed to implement persistence three times followed by a switch, i.e., the initial path to the first corner is . So from the given initial condition, matrix multiplication three times by the transfer matrix constructs the edges to the first corner and a second three applications brings the edges back to the centre and the result is the negative of the initial condition (row 7 in the array in Equation (7)). Thus we have:
where is the negative of the identity matrix. While we may be tempted to write:
there are several possibilities for Q because there are several sixth roots of . However a relevant choice can be made by noting that Q has just two distinct eigenvalues, and that step through the entire sequence of sixth roots. Each of these two belong to one of the two edge directions. (These are also the two lowest frequency eigenvalues of the transfer matrix in the sense of transitions around the unit circle.) We can construct a suitable representation of a diagonal form of Q so that the pairs of eigenvalues alternate. With Q in this diagonal form:
where ⊗ denotes the Kronecker product. In this representation, individual pixels in the image do not pass their intensity along null edges. Instead they pass varying intensity to the same pixel at the next time step. The image of the smoothed timestamp using is, in this representation:
The central columns of the data matrix Equation (11) are plotted in Figure 5.
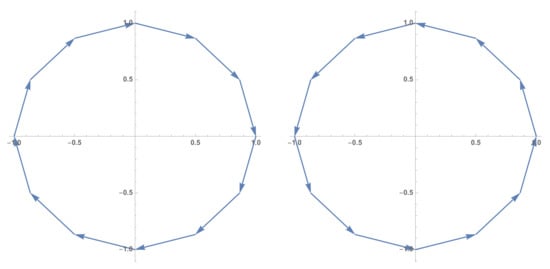
Figure 5.
The two pixel ‘intensities’ in the digital array image Equation (11). Proceeding from the initial intensity of 1 in the central two pixels, the pixel intensities plotted in the complex plane evolve through discrete spirals traversed in opposite directions.
There are a number of interesting features of this ‘digital image’:
- The edges of timestamps that enclose causal areas in spacetime have been mapped onto the two pixels corresponding to the initial conditions, introducing a form of spatial stationarity. (This is a qualitatively different approach from pre-relativistic physics where the ‘rest frame’ is special and movement is constructed assuming space and time are independent. Here the rest frame is constructed from the light cones.)
- The pixel intensities of the timestamp that were binary and could be stored in a single bit, now require a bigger ‘word’ to store the varying intensity values.
- In this diagonal formulation of instruction, the ‘intensities’ are actually complex numbers; not a data type usually used for images in the spatial domain, however the appearance in this context is welcome and instructive.
The first point indicates that the mapping, Equation (2), that was specifically chosen to smooth out the timestamp corners by distributing the effect of the switch over many steps, did so by wrapping the timestamp onto two approximate cylinders centred on the two states associated with . This has the effect of encoding the information describing the causal area boundary onto static positions in space. That is, the evolution of the causal area has been mapped onto what could be considered the analog of the worldline of a stationary particle. This mapping is an encoding of the geometry of the timestamp.
The second point indicates a compromise we have to accept in order to keep the local stationary worldline concept in this discrete version of special relativity. If you start in a continuum formulation of special relativity then the worldline of a stationary particle could be represented as , this being a distribution approximation for a particle at rest at the origin. This is clearly insufficient to represent the colour/intensity in our representation of our stationary particle. The delta function alone cannot encode the timestamp, the geometry associated with mass. As we increase the resolution of our image, our analog of the Dirac delta function is actually two Kronecker delta functions with complex intensities that vary periodically in time. (Mapping the geometry of the timestamp onto the analog of a worldline converts the worldline to a signal. As a result, the Fourier uncertainty principle becomes involved and will turn up in the image model. The principle’s sensational appearance in physics was due to Heisenberg and retains his name as a result. The absence of the principle with conventional worldlines in special relativity arises from the fact that the delta function as a distribution is an adaptation of the on-off function of a single bit of information, and itself does not carry a signal unless a signal is invoked as an overlay, as it is in the path integral formulation of quantum mechanics.) As a result, ‘telling an electron how to stay in one place’ immediately invokes elements of signal processing, bringing those elements into the physical domain.
The third point suggests why complex numbers are so convenient in quantum mechanics and why Minkowski’s original formulation of special relativity invoked the ‘time’ coordinate . Looking at Figure 2 or Figure 3, the colour designations are all period 4. At any spatial location, each colour returns after four switches and the colours stay in sequence. As a clock, the timestamp completes its cycle in four steps along the time axis. However, in terms of spatial displacement, the spatial ‘clock’ returns to the spatial origin every two steps. At each return the colours have switched to their complement giving the encoding Equation (8). Note that the initial colours in this discrete representation switch via the real matrix
and the initial colours have components that are just . However, as we refine the lattice and consider time steps shorter than the Compton time, as in the coarse resolution given by , the mapping of the timestamp geometry onto single pixel intensities cannot be done in a single component over the reals. For example, if instead of three steps between switches, as in , we have n steps between switches, we then have:
For large n we can write so that the smoothed second term of the Kronecker product becomes:
and we can think of as a measure of distance along the t-axis. Notice that T ‘registers’ with the time stamp at the even integers where the null lines cross in the centre of the timestamp. Here for integer k. For odd k, where the null lines from the origin reach their farthest extent and change colour on direction reversal, is imaginary. For real in general, maps the initial condition, the double Kronecker delta at the origin onto unimodular complex numbers. Visually, the timestamp boundaries are mapped onto two osculating spirals as in Figure 6.
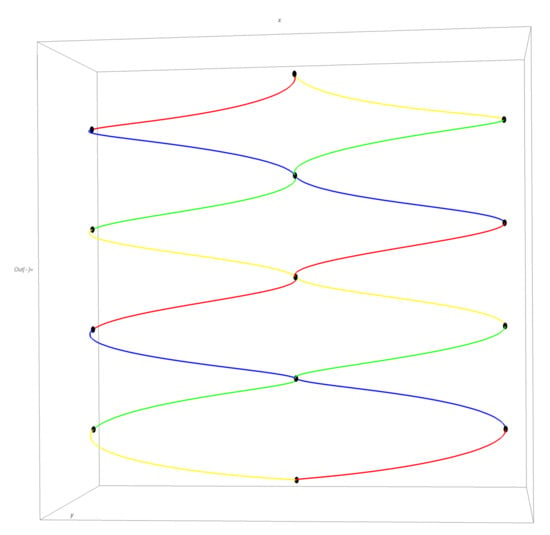
Figure 6.
A visual representation of the timestamp made smooth. The result of the filtering process is to map the two halves of the timestamp onto two cylinders that are side by side. The curves touch periodically and mimic the planar figure of the timestamp. The colours here have been retained to compare to the original planar version Figure 2.
Revisiting the idea of smoothness in this process, the idea has been to encode the information contained in the timestamp in such a way that the encoding, on lattice refinement, converges to a form that is expressible in terms of differential equations.
When we look at the 4-state timestamp of Figure 2, the figure itself is piecewise differentiable. The edges are smooth except at the corners. The transfer matrix image generator T evolves the edges smoothly via the P operation and produces the corner with the S. The effect of replacing T with Q in Equation (2) distributes the effect of S over a half cycle of the timestamp. When this is done, we can see for example in Equation (10), the transition from T to Q removes the eigenvalues and projectors from T that distribute the timestamp along the null lines, and condenses the information into the intensity of just two pixels. To do this the intensities are forced into the complex domain and the result is Equation (11). To see the ’smoothing’ aspect of this Figure 5 shows that the complex numbers are evenly distributed on the unit circle. In the limit as the step size gets small the graph of the ‘smoothed timestamp image’ is sketched in Figure 6.
It is worth noting that the smoothing operation is really that of a low pass filter. To relate this to the objective of finding the smooth propagator underneath the discontinuous History-Map in Figure 4, note that if you compare the propagator with the history map, it is essentially the History-Map with all but the lowest frequency removed in a Fourier expansion. This frequency filtering takes place in the transition from T to Q.
If we ‘undo’ the diagonalization involved in obtaining Equation (15) in order to restore the analogs of operations P and S, the similarity transformation produces in the form:
We see here that the digital clock that initially ticked between the four colours encoded via Equation (3) using the switch matrix , has been interpolated by mapping intermediate states onto the unit circle in the complex plane. Instead of there being a single step that is itself a switch (i.e., ), the refinement below the Compton scale replaces the switch with successively smaller rotations.
Note that if we take the limit of Equation (16) as with t fixed we find:
giving the time dependence of a stationary Dirac particle of mass in a 2D spacetime. (For convenience we have chosen units so that the time between crossings is 1 and the Compton time is 4, giving timestamps with corners at the integers.)
5. A Particle in a Box
In the above we found instructions that smoothed the timestamp, providing instructions for a particle to stay stationary in a fixed reference frame. We did this by placing the particle at the centre of a box that is the same spatial width as the timestamp, and requiring the crossing points of the causal boundaries to stay fixed in that box.
It is important to note that the previous section was simply about digitizing space-time diagrams. There was no formal analytic continuation to mimic either Minkowski space or quantum propagation. Complex numbers did emerge through the insistence that the pattern of causal boundaries be mapped onto digital intensities. However the emergence was by construction. It did not force us to leave the domain of applied mathematics where we understand the mathematics as an encoding of images. We know why refinement of the lattice required an expansion of an essentially planar figure (the timestamp) into another dimension that is conveniently wrapped on a circle.
Specifically, the emergence of complex numbers was a result of the need to describe the causal areas via the timestamp that has a natural period of 4, corresponding to the 4 directions of a two-dimensional spacetime. The need to do this smoothly lifted intensities from real numbers to complex numbers.
In the implementation, the colour/state switch , while a Real matrix, has eigenvalues . The smoothing operation that allows the analog of stationary worldlines then mapped the colour/intensity of the image onto the unit circle in the complex plane. The point here is that we know why complex numbers, or more generally the Pauli matrices, arise in this context. They arise because of the persistent structure of the null lines in Minkowski space.
To allow particles to move (as opposed to stay stationary) within a fixed frame, we are going to encase our images of timestamps in a box that is much larger than the width of the timestamp. To place this in a context where the ’particle in a box’ description is an electron in a box in more familiar surroundings, we shall change two aspects of notation from the previous section. Referring to Equation (17) the timestamp ‘mass’ of will be replaced by the electron mass m in units where ℏ and c are both 1. We shall also change representations and replace the switch matrix with where is the Pauli matrix.
To allow for particles that move in a fixed frame, we place the particle in a box of width that is much larger than the width of the original timestamp, and ask whether the restriction allows stationary states. To build the transfer matrix we retain the Persist instruction and replace the Switch instruction with the ‘smoothed’ version from Equation (16) to first order in . For a box of spatial width M, the transfer matrix is:
or
where is the identity, is the permuted identity with all rows cyclically shifted up one row. is the identity with the rows cyclically shifted down one. The matrices are:
and we can see that the Transfer matrix simply embeds the timestamp in a box, assumed here to be much wider than the Compton wavelength specified by m.
The matrix Equation (19) is a transfer matrix for Feynman’s Chessboard model [14,15,16,17,18,19] in a box whose solution we sketch here. For complete details see the original reference [20].
Equation (19) expresses in terms of blocks and since we are looking for eigenvalues and eigenvectors, we can partition an eigenvector into a column vector of matrices , . Now suppose that the themselves are slowly varying for large M and in fact may be written as for some and some two component vector . The eigenvalue equation can then be written in terms of :
Provided these all reduce to the same relation. Now if the length of the box is , write then the n’th root is and the eigenvalue equation becomes:
where
To first order in the eigenvalues are:
with
We would like to find the behaviour of in the continuum limit through integer values of . To do this we write:
where is the projector for the i’th eigenvalue. In the limit the eigenvalues approach:
The projectors in this limit are constructed from the right eigenvectors of the matrices in Equation (21). The normalized right eigenvector of Equation (23) is:
where . The corresponding normalized right eigenvector of the full matrix is then:
with the left eigenvector being the conjugate transpose of this. The effect of the sequential powers of in the eigenvectors is that the projectors also have a similar pattern, so for example, the first column for the projector for the n’th (+) eigenvalue is
The presence of the phase factor suggests we consider the discrete Fourier transform of the spatial amplitudes. Consider:
If, for example, we take the discrete transform of the odd component of Equation (30) we get
So the projectors in Equation (30), when their columns are transformed via Equation (31), yield non-zero results only at the appropriate eigenvalue . Thus if we take the discrete transform of the first two columns of the eigenvalue expansion Equation (30) as in Equation (32) we get a matrix, to lowest order in of
Similarly, this occurs for all the . In ‘momentum space’, the structure of the timestamp is such that for fine partitions of spacetime, below the Compton wavelength, the Fourier components of the propagator simplify and satisfy the same equation. Note that
Satisfies
a form of the Dirac equation in a 2D spacetime. By placing the timestamp in a box with a lattice spacing that is small compared to the Compton wavelength; we see that the Dirac propagator with a finite momentum spectrum, appropriate for the box, is generated. In the continuum limit the discrete series approaches the free particle propagator.
6. Conclusions
The purpose of this article was to find instructions that spacetime could use to tell an electron how to move. The model used was to take the timestamp image Figure 2 and ask the questions:
- How do we create a digital image of the timestamp?
- How do we map the digital image onto one that becomes smooth on finer resolution?
The reason for doing this is that digital image processing is an aspect of applied mathematics that we can dissect and understand without directly confronting interpretive problems. (This is in contrast to the situation involving quantum mechanics in general, and the Dirac equation in particular. Since its discovery in the early 20th century, the interpretation of Equation (34) has evolved to align with quantum field theory. However, the increased empirical accuracy involved in the reinterpretation has not been accompanied by a convergence in interpretation.)
Visually, we saw that digital versions of Figure 2 could be created using transfer matrices like Equation (7) and then refined by increasing the size of the transfer matrix appropriately. If we wanted to preserve the timestamp structure while making the scaling smooth, the resulting smoothed ‘image’ looked like Figure 6. That is, the two halves of the planar timestamp had been mapped onto osculating helices. In the context of images, the relationships between scale, colour and geometry were easy to see because of the context of encoding images of spacetime diagrams. That is, the reason for the mathematics was always known through what it encoded.
However, the appearance of Dirac-like time dependence in Equation (17) was suggestive. The timestamp and the simple switch Equation (12), smoothed to map the edges of the timestamp to the ’intensities’ of two pixels, suggested that this process could possibly mediate between the discontinuous timestamp function and Feynman’s propagator in Figure 4.
On one hand, we discovered exactly what went into the propagator as the encoding of a digital representation of the timestamp. On the other, the smoothed version of the timestamp provided a ‘clock’ appropriate to the Dirac equation.
In Section 5 we took the image processing transfer matrix for a discrete precursor of a smooth image, and modified it to sit inside a box that was much larger than the width of a timestamp. We then asked the question as to whether the box could support stationary patterns. This produced a discrete Fourier representation whose continuum limit reproduced Feynman’s propagator for his Chessboard model [13].
The result of the mathematical exercise was Equation (34) as an embodiment of spacetime telling an electron how to move or, in the original context, an encoding of digitally rendering images of a smoothed timestamp.
7. Discussion
Looking over the description of particle motion using timestamps, we can step back and compare this with classical approaches going back to Zeno. The view up to modern times is that as we partition time down to smaller and smaller intervals, we should see physical objects getting closer and closer to being ‘stationary’, where stationarity is the absence of motion in space. This view of stationarity as a special state is anthropocentric; it is what we expect from all our senses because none can register any change in objects moving at terrestrial speeds over time intervals smaller than our own perceptions can resolve. While we can always imagine moving with inertial objects to make them stationary over small time intervals, we have no direct experience with Minkowski space’s actual demarcation of spacetime via null lines that cannot be viewed in this way.
In Minkowski space, an ‘event’ at the origin , associated with an object that persists in time and is macroscopically ‘stationary’, does not give rise to an event at for arbitrarily small in such a way as to build a continuous worldline of like events. Instead it builds a ‘timestamp’, an area bounded by null lines that is much larger than the ‘event’ at the origin. This is because the fixed upper bound in velocity c is enforced on all scales in Minkowski space and the discrete analog of the worldline of a stationary particle is a sequence of causal areas, not a straight line running parallel to the t-axis.
It is the special velocity c that persists in time, not spatial position. Events as points give rise to causal areas and these are the objects that our discrete version of Minkowski space tracks, with a resolution that is band limited by the Compton frequency, the characteristic length that is the signature of a specific mass.
Minkowski’s claim [21]:
taken down to microscopic scales in spacetime implicates ‘zitterbewegung’, not stationarity in space for elementary particles. Classical special relativity, by assuming a smooth worldline, eliminates this feature immediately, having to recapture energy and momentum relations through dynamics. The Dirac equation, in its usual context, transplants features found in non-relativistic quantum mechanics into the relativistic domain. However, in its usual context, it is an overlay of quantum propagation on Minkowski space that is enforced as a recipe rather than discovered as a consequence of the Lorentz transformation.“Henceforth space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality.”
The value of the approach in this article is that the interdependence of space and time dictated by special relativity is maintained through fine scales and gives rise to a characteristic length that specifies mass. In this view, the peculiarities of quantum mechanics arise directly from the enforcement of the light-speed postulate through all scales. When ‘’ is taken below the scale of the Compton length, the classical picture of the approach to spatial stationarity on fine time scales is replaced by the ‘fixed c’ condition warranted by Minkowski space, and the result engages a form of ‘quantum propagation’ simply as a smooth mapping of the causal areas generated by a discrete process. The ‘phase’ that becomes part of the propagator is a device whereby Spacetime instructions keep the Compton scale structure of the timestamp intact.
This picture also lends some insight into the peculiarity involved in the superposition principle in quantum mechanics [12]. The path integral, useful as it is in quantum mechanics, seems to say that a single particle explores all possible paths in its trip between two observations, in violation of what it means to be a (localized) classical particle. This seems and is peculiar when you think of the paths as collections of worldlines. However, the above analysis is explicit that worldlines in Minkowski space are themselves proxies. Minkowski space is about areas, not lengths. Lorentz boosts preserve the Euclidean areas of the causal region between events. Associating a worldline or a path with a particle then involves a dimensional error. If the error is completely ignored because the Compton wavelength is much smaller than all other characteristic lengths in the problem, classical special relativity is appropriate with mass identified by dynamics and a single worldline associated with a particle.
If there are characteristic lengths that are on the order of the Compton length, then the dimensional error of paths requires compensation that is mimicked in the above by the emergence of phase. It is the presence of phase in wavefunctions that allows spacetime to keep track of the countable causal areas generated by the existence of the Compton scale and the constancy of c. It is through phase that the inner characteristic length is maintained and spacetime areas, as opposed to lengths, are treated appropriately. The ‘function’ of the wavefunction can then be seen as pre-processing the probability density function that arises from the Born rule [22]. It effectively moulds the sample space to conform to the restrictions that Minkowski space inflicts on spacetime. This restriction, the rotated ‘causality’ cone of Minkowski space, means that the encoding process by which spacetime tells an electron how to move respects causal areas. Probability density functions that we would construct to be normalized over all space at fixed t must also respect causal areas but cannot do so by just adding the effects of Wiener paths. Only by the device of allowing paths to carry the phase generated by Minkowski space can the ‘dimensional error’ of paths in Minkowski space be compensated. This is reflected in the superposition principle switching from probability density functions in classical physics to wavefunctions in quantum mechanics.
All these features are exposed when you look at Minkowski space from a discrete perspective that allows you to treat mass as a characteristic inner scale. With this as a starting point, the origin of the Dirac equation become much easier to see. Quantum mechanics then emerges from special relativity, demonstrating that we should look more closely at relativity if we wish to examine quantum foundations.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This article is dedicated to the memory of Gerhard Grössing, a pioneer in Emergent Quantum Mechanics whose vitality, insight, and integrity permeated his work and inspired his colleagues.
Conflicts of Interest
The author declares no conflict of interest.
References
- Ryckman, T.A. Early Philosophical Interpretations of General Relativity. In The Stanford Encyclopedia of Philosophy, Spring 2018 ed.; Zalta, E.N., Ed.; Metaphysics Research Lab, Stanford University: Stanford, CA, USA, 2018. [Google Scholar]
- Ford, K.; Wheeler, J.A. Geons, Black Holes, and Quantum Foam: A Life in Physics; W. W. Norton and Company: New York, NY, USA, 2010. [Google Scholar]
- Grössing, G. Sub-Quantum Thermodynamics as a Basis of Emergent Quantum Mechanics. Entropy 2010, 12, 1975–2044. [Google Scholar] [CrossRef]
- Ord, G.N. Statistical Mechanics and the Ghosts of Departed Quantities. arXiv 2019, arXiv:1901.11066. [Google Scholar]
- Ord, G.N. Fractal Space-Time a Geometric Analog of Relativistic Quantum Mechanics. J. Phys. A 1983, 16, 1869–1884. [Google Scholar] [CrossRef]
- Nottale, L. Fractals Spacetime and Microphysics; World Scientific: Singapore, 1993. [Google Scholar]
- Williamson, J.G. A New Linear Theory of Light and Matter. J. Phys. Conf. Ser. 2019, 1251, 012050. [Google Scholar] [CrossRef]
- Williamson, J.G.; van der Mark, M.B. Is the electron a photon with toroidal topology? Ann. Fond. Louis Broglie 1997, 22, 133. [Google Scholar]
- de Broglie, L. Researches sur la Theorie des Quanta. Ph.D. Thesis, Migration-Université en Cours d’Affectation, Paris, France, 1925. [Google Scholar]
- Baylis, W. De Broglie waves as an effect of clock desynchronization. Can. J. Phys. 2007, 85, 1317–1323. [Google Scholar] [CrossRef]
- Ord, G.N. Counting Oriented Rectangles and the Propagation of Waves. J. Math. Chem. 2009, 45, 65–71. [Google Scholar] [CrossRef]
- Ord, G. Superposition as a Relativistic Filter. Int. J. Theor. Phys. 2017, 56, 2243. [Google Scholar] [CrossRef]
- Feynman, R.P.; Hibbs, A.R. Quantum Mechanics and Path Integrals; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Gersch, H.A. Feynman’s Relativistic Chessboard as an Ising Model. Int. J. Theor. Phys. 1981, 20, 491. [Google Scholar] [CrossRef]
- Jacobson, T.; Schulman, L.S. Quantum Stochastics: The passage from a relativistic to a non-relativistic path integral. J. Phys. A 1984, 17, 375–383. [Google Scholar] [CrossRef][Green Version]
- Gaveau, B.; Jacobson, T.; Kac, M.; Schulman, L.S. Relativistic extension of the analogy between quantum mechanics and Brownian motion. Phys. Rev. Lett. 1984, 53, 419–422. [Google Scholar] [CrossRef]
- Kauffman, L.H.; Noyes, H.P. Discrete Physics and the Dirac Equation. Phys. Lett. A 1996, 218, 139. [Google Scholar] [CrossRef]
- Ord, G.N. A Reformulation of the Feynman Chessboard Model. J. Stat. Phys. 1992, 66, 647–659. [Google Scholar] [CrossRef]
- McKeon, D.G.C.; Ord, G.N. Time Reversal in Stochastic Processes and the Dirac Equation. Phys. Rev. Lett. 1992, 69, 3–4. [Google Scholar] [CrossRef] [PubMed]
- Ord, G.N. The Feynman Chessboard in a Box. Can. J. Phys. 1993, 71, 159–161. [Google Scholar] [CrossRef]
- Minkowski, H. Space and Time. In The Principle of Relativity: A Collection of Original Memoirs on the Special and General Theory of Relativity; Dover: New York, NY, USA, 1952; pp. 75–91. [Google Scholar]
- Ord, G.; Mann, R. How Does an Electron Tell the Time? Int. J. Theor. Phys. 2011, 51, 652–666. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).