Abstract
An antimagic labeling of a graph G is a bijection such that the weights distinguish all vertices. A well-known conjecture of Hartsfield and Ringel (1990) is that every connected graph other than admits an antimagic labeling. For a set of distances D, a D-antimagic labeling of a graph G is a bijection such that the weight is distinct for each vertex x, where is the D-neigbourhood set of a vertex x. If , for every vertex x in G, a graph G is said to be -regular. In this paper, we conjecture that a graph admits a D-antimagic labeling if and only if it does not contain two vertices having the same D-neighborhood set. We also provide evidence that the conjecture is true. We present computational results that, for , all graphs of order up to 8 concur with the conjecture. We prove that the set of -regular D-antimagic graphs is closed under union. We provide examples of disjoint union of symmetric -regular that are D-antimagic and examples of disjoint union of non-symmetric non--regular graphs that are D-antimagic. Furthermore, lastly, we show that it is possible to obtain a D-antimagic graph from a previously known distance antimagic graph.
1. Introduction
Let be a finite, simple, and undirected graph with v vertices and e edges. The notion of antimagic labeling of a graph G was introduced in Hartsfield and Ringel’s book Pearls in Graph Theory [1] as a bijection f: such that the weights () distinguish all vertices. Hartsfield and Ringel [1] also conjectured that every connected graph other than admits antimagic labeling in this seminal work.
As of today, the antimagic conjecture is still open; however, much evidence has been presented by many authors. By using a probabilistic method, Alon et al. [2] proved the conjecture for graphs with minimum degree at least , for some constant C. Eccles [3] improved this result, by proving the conjecture for graphs with average degree at least some constant . Hefetz, Saluz, and Tran [4] utilized Combinatorial Nullstellensatz to prove that if a graph on vertices, where p is an odd prime and k is a positive integer, admits a -factor, then it is antimagic. A series of articles by Cranston, Liang, and Zhu [5], Bérczi, Bernáth, and Vizer [6], and Chang et al. [7] showed that for , every k-regular graph is antimagic. For trees, Kaplan, Lev, and Roddity [8] proved that a tree with at most one vertex of degree 2 is antimagic. On the other hand, Liang, Wong, and Zhu [9] proved that a tree with many vertices of degree 2 is antimagic. The latest result on antimagic trees is by Lozano, Mora, Seara, and Tey [10] who proved that caterpillars are antimagic.
In 2017, Arumugam et al. [11] and Bensmail et al. [12] independently introduced a weaker notion of antimagic labeling, called the local antimagic labeling, where only adjacent vertices must be distinguished. Both sets of authors conjectured that any connected graph other than admits a local antimagic labeling. This conjecture has been completely settled by Haslegrave [13] using probabilistic method.
Another type of antimagic labeling was introduced by Kamatchi and Arumugam in 2013 [14]. A bijection is called a distance antimagic labeling of graph G if for two distinct vertices x and y, , where , for the open neighborhood of x, i.e., the set of all vertices adjacent to x. A graph admitting a distance antimagic labeling is called a distance antimagic graph. In the same paper, Kamatchi and Arumugam conjectured that a graph G is distance antimagic if and only if G does not have two vertices with the same open neighbourhood.
Some families of graphs have been shown to be distance antimagic, among others, the path , the cycle (), the wheel () [14], and the hypercube () [15]. In 2016, Llado and Miller [16] utilized Combinatorial Nullstellensatz to prove that a tree with l leaves and vertices is distance antimagic.
In 2011, O’Neal and Slater [17] introduced the D-magic labeling as follows. Let be a set of distances in G. The graph G is said to be D-magic if there exists a bijection and a magic constantk such that for any vertex x, , where is the D-neighborhood set of x.
When we consider the D-neighborhood set of a vertex, the regularity of a graph is defined as follows. A graph G is said to be -regular if for every vertex . Clearly, an regular graph is -regular.
Inspired by the notion of D-magic labeling, the idea of distance antimagic labeling was generalized by considering a set of distances and the D-neighborhood set of a vertex.
Definition 1.
A D-antimagic labeling of a graph G is a bijection such that the weight is distinct for each vertex x.
It is clear that if a graph contains two vertices having the same D-neighborhood set, then the graph does not admit a D-antimagic labeling. Here we boldly conjecture that the converse of the previous statement is also true, and thus we propose the following.
Conjecture 1.
A graph admits a D-antimagic labeling if and only if it does not contain two vertices having the same D-neighborhood set.
If x and y are two distinct vertices with the same D-neighborhood set, the two vertices are called D-twins of each other, denoted by . It is clear that is an equivalence relation, and thus Conjecture 1 can be rewritten as: “A graph admits a D-antimagic labeling if and only if its vertex set partition defined by contains only singletons”.
An automorphism of a graph G is a permutation of preserving adjacency. A graph G is said to be vertex-transitive if, for any two vertices x and y, there exists an automorphism of G that maps x to y and it is said to be edge-transitive if, for any two edges and , there is an automorphism of G that maps to . If G is both vertex-transitive and edge-transitive, G is symmetric. Recall that a cycle, a complete graph, and a hypercube are symmetric. A path on at least four vertices and a wheel on at least five vertices are neither vertex-transitive nor edge-transitive.
In the rest of the paper, we shall provide several pieces of evidence that Conjecture 1 is true. First, in Section 2, we provide computational results where all graphs of order up to 8 concur with Conjecture 1, for the case of . Second, in Section 3, we show that the set of -regular D-antimagic graphs is closed under union. For particular D, we provide examples of symmetric -regular graphs that are D-antimagic, so the disjoint union of those graphs is also D-antimagic. Examples of disjoint union of non--regular graphs that are neither vertex-transitive nor edge-transitive but admit D-antimagic labelings are also presented in this section. Lastly, in Section 4, we show that it is possible to obtain a D-antimagic graph from a previously known distance antimagic graph. We realize that Conjecture 1, if true, will be laborious to prove, and thus in the following sections, we propose several open problems that hopefully are more feasible to solve.
2. Computational Result
We build an exhaustive algorithm to search for all distance antimagic graphs of order v. We split the algorithm into three functions: Algorithm 1 checks whether an input graph G contains -twins by seeking two identical rows in the adjacency matrix of G. Algorithm 2 decides whether labeling is distance antimagic, and Algorithm 3 searches for distance antimagic graphs. We implemented this algorithm in C++, and the source code can be found in [18].
Let , A be the adjacency matrix of G, and the labeling matrix be a matrix whose entry is , the label of vertex .
| Algorithm 1. Check If G Contains -Twins |
|
| Algorithm 2. Evaluate Distance Anti Magic |
|
| Algorithm 3. Search Distance Anti Magic |
|
We run the algorithm to search for all distance antimagic (non-isomorphic) graphs of order up to 8 generated by nauty [19], with results as depicted in Table 1.

Table 1.
Distance antimagic graphs of order .
Thus, we obtain the following result, which supports Conjecture 1.
Theorem 1.
A graph of order admits a -antimagic labeling if and only if it does not contain two vertices having the same -neighborhood set.
3. Closedness of Union of D-Antimagic Graphs
Theorem 2.
Let D be an arbitrary set of distances and be two D-antimagic graphs. If H is -regular and , for every , then is also D-antimagic.
Proof.
Let g and h be D-antimagic labelings of G and H. Define a new labeling l for as , when , and , when .
We shall show that l is D-antimagic. Let x and y be two distinct vertices in . If both , then . If both , then
The last case is if, without loss of generality, and . Since and , then . □
Let be the set of all D- antimagic graphs and be the set of all -regular graphs. A direct consequence of Theorem 2 is
Corollary 1.
is closed under union.
Corollary 1 is a generalization of a result in [15], where it was proved that if G is a regular distance antimagic graph, then is also distance antimagic.
Direct application of Corollary 1 to known graphs in results in the following.
Corollary 2.
- 1.
- For , the disjoint union of cycles is -antimagic.
- 2.
- For , the disjoint union of cycles is -antimagic.
- 3.
- For , the disjoint union of complete graphs is -antimagic.
- 4.
- For , the disjoint union of hypercubes is -antimagic.
- 5.
- For , the disjoint union of hypercubes is -antimagic.
Proof.
Due to facts that:
- 1.
- For , the cycle is -antimagic [14].
- 2.
- For , the cycle is -antimagic [20].
- 3.
- For , the complete graph is trivially -antimagic.
- 4.
- For , the hypercube is -antimagic [15].
- 5.
- For , the disjoint union of two hypercubes is -antimagic [21].
□
Although closedness under union is still unknown for the set of non-regular graphs, in the following theorems, we shall provide some families of disjoint union of non-regular graphs admitting D-antimagic labelings for . We start by showing that particular cases of disjoint union of paths are distance antimagic.
Theorem 3.
For any positive integers , the disjoint union of two paths is distance antimagic.
Proof.
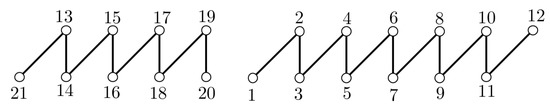
Let and . We shall consider three cases which depend on the parity of m and n.
Case 1. Without loss of generality, when m odd and n even. Define a labeling , where , for , , for , and , for .
Under this labeling, the weights are:
and
It is clear that every vertex in has a distinct weight less than any weight in . On the other hand, in , the only even weights are , all of which are different. To conclude, for the odd weights in , the following inequalities hold
Case 2. When both m and n are even. Since the case when is considered in Theorem 4, we may assume . Define a labeling , where . Under this labeling, , for .
We then define three different labelings for , depending on the value of n.
Sub Case 2.1. When and , define a labeling , where
Here the weights are:
all of which are larger the the weights of all vertices in .
Sub Case 2.2. For , define a labeling , where
This labeling results to the following weights of vertices in .
The even weights are and the odd weights , all of which are larger than the weights of vertices in .
Sub Case 2.3. When define a labeling , where
Thus, we obtain the following weights for vertices in .
Here the odd weights are and the even weights are .
Case 3. When both m and n are odd, define a labeling , where , for , and
Under the labeling g, we obtain the following weights of vertices.
and
The odd weights are and the even weights are , for , and , for . This concludes our proof.
An example of a distance magic labeling for can be viewed in Figure 1. □

Figure 1.
A distance antimagic labeling for .
Theorem 4.
For , is distance antimagic.
Proof.
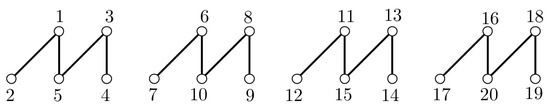
Let and . We shall consider three cases:
Case 1. When , define a labeling f of as follows.
Thus, we obtain the weight of each vertex as follows.
Case 2. When , define a labeling f of as follows.
Thus, the weight of each vertex is as follows.
Case 3. When , define a labeling f of as follows.
This leads to the following weights of vertices.
This concludes the proof since, in all three cases, all the vertex-weights are distinct. An example of a distance antimagic labeling for is depicted in Figure 2. □

Figure 2.
A distance antimagic labeling for .
In general, we are still not able to prove that the disjoint union of arbitrary paths is distance antimagic.
Problem 1.
Show that , where , is distance antimagic.
The next three theorems deal with the distance antimagicness of graphs containing many triangles, i.e., wheels, fans, and friendship graphs. A wheel is a graph obtained by joining all vertices of a cycle of order n to another vertex called the center. Let where is the center and are the vertices of the cycle.
Theorem 5.
For and , is distance antimagic.
Proof.
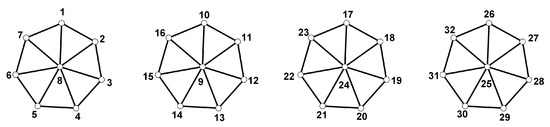
Let . We define different vertex labelings f of , depending on the value of n.
Case 1. When n is even.
Sub Case 1.1. When .
This will lead to the following weights of vertices.
Sub Case 1.2..
and so we obtain the following vertex-weights.
Case 2. When n is odd.
Sub Case 2.1. When .
The vertex-weights under this labeling are as follows.
For odd j,
and for even j,
Sub Case 2.2. For .
Thus, we obtain the following vertex-weights.
This concludes the proof since, in all the cases, all the vertex-weights are clearly distinct.
An example of a distance antimagic labeling for can be seen in Figure 3. □

Figure 3.
A distance antimagic labeling for .
A fan is a graph obtained by joining all vertices of a path of order n to a further vertex called the center. Let where is the center and are the vertices of the path.
Theorem 6.
For and , is distance antimagic.
Proof.
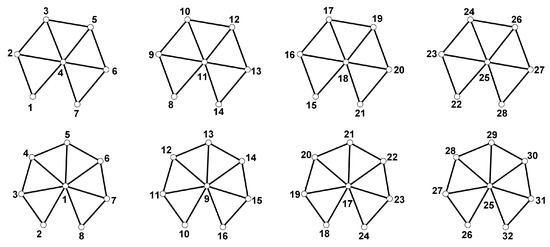
We define a vertex labeling f of as follow:
Case 1. When n is odd,
and thus we obtain the following vertex-weights.
Case 2. When n is even.
Sub Case 2.1. When ,
which leads to the following vertex-weights.
Sub Case 2.2. When ,
and so we obtain the following vertex-weights.
In all cases, we can see that all the weights are distinct.
Examples of distance antimagic labelings for for and are depicted in Figure 4. □

Figure 4.
Distance antimagic labelings for and .
A friendship graph is obtained by identifying a vertex from n copies of cycles of order 3. Let where are the vertices in the j-th , for and
Theorem 7.
For and , is distance antimagic.
Proof.
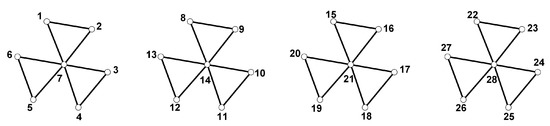
We define a vertex labeling f of as follow.
For ,
and so we obtain the following vertex-weights.
where all the weights are distinct.
An example of a distance antimagic labeling for can be viewed in Figure 5. □

Figure 5.
A distance antimagic labeling for .
We conclude this section by considering the disjoint union of unicyclic graphs. A sun is a cycle on n vertices with a leaf attached to each vertex on the cycle. Let the vertex set of sun where and .
Theorem 8.
For and , is distance antimagic.
Proof.
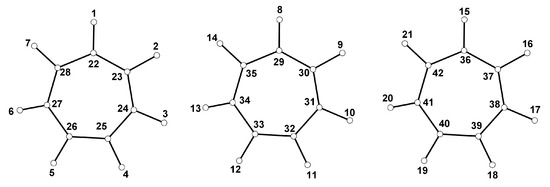
Let . We define a vertex labeling f of as follows.
and
Under the labeling f, the vertex-weights are
and
which are all distinct.
An example of a distance antimagic labeling for is in Figure 6. □

Figure 6.
A distance antimagic labeling for .
With several examples that we have presented, more general questions are in the following.
Problem 2.
If G is a non-regular graph containing no -twins, show that is distance antimagic.
Problem 3.
If are non-regular graphs containing no -twins, show that is distance antimagic.
4. Distance-D Graph and D-(Anti)magic Labeling
For any connected graph G, we denote by , the distance-k graph of G, as the graph whose vertices are those of G and whose edges are the 2-subsets of vertices at mutual distance k in G [22]. In particular, . On the other hand, the k-th power graph of a graph G, , is another graph that has the same set of vertices, but in which two vertices are adjacent when their distance in G is at most k [23]. Clearly, .
We generalize the two aforementioned graphs by defining the distance-D graph of G, , as the graph with the same vertices as G, where two vertices are adjacent when their distance in G is in D. Clearly, the distance-k graph and the kth power . (For examples, see Figure 7 and Figure 8.)
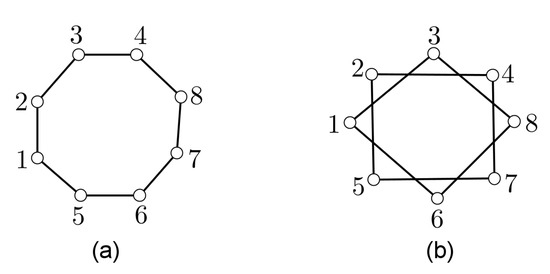
Figure 7.
(a) A -magic labeling for . (b) A distance antimagic labeling for .
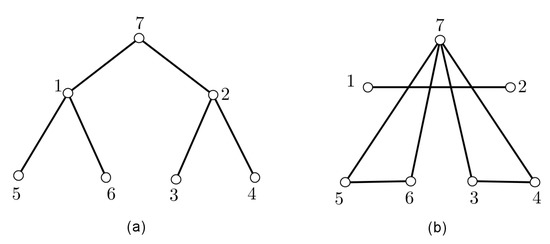
Figure 8.
(a) A -antimagic labeling for a binary tree T. (b) A -antimagic labeling for .
The next theorem shows that when G is D-(anti)magic, is either -(anti)magic or -(anti)magic.
Theorem 9.
Let G be a D-(anti)magic graph.
- 1.
- If D does not contain 0 then is -(anti)magic.
- 2.
- If D contains 0 then is -(anti)magic.
Proof.
Suppose that f is an (anti)magic labeling of G. From the definition of , for any x, in is the same with in G. If D does not contain 0, then in is the same with in G. On the other hand, if D contains 0, then in is the same with in G. □
However, since it is relatively easier to find a distance (anti)magic labeling for a graph, the converse of Theorem 9 is more interesting for us. Let be the set of graphs of order n. Define a function , where . It is clear that is neither injective nor surjective. For instance, as depicted in Figure 9, is , however there is also another graph, in this case , where . Notice that both and are -antimagic with the same vertex labeling.
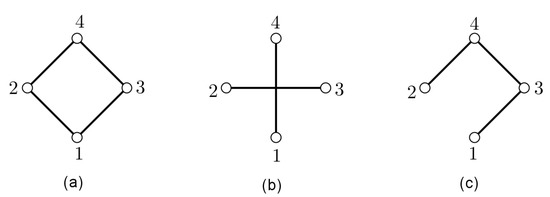
Figure 9.
(a) A -antimagic labeling for . (b) A distance antimagic labeling for . (c) A -antimagic labeling for .
Despite the fact that is not invertible, we can still state the following.
Theorem 10.
Suppose one of the following conditions holds:
- 1.
- Let D be a distance set not containing 0 and G be a -(anti)magic graph.
- 2.
- Let D be a distance set containing 0 and G be a -(anti)magic graph.
If there exists a graph H such that , then H is D-(anti)magic.
Theorem 10 hints that if we manage to find a distance (anti)magic graph, we might as well find D-(anti)magic graphs for suitable sets of Ds.
Author Contributions
Conceptualization, R.S.; methodology, R.S.; formal analysis, R.S., T.N., F.Y. and K.W.; writing—original draft preparation, R.S., T.N. and K.W.; writing—review and editing, R.S., T.N., F.Y., K.W., N.H. and K.A.S.; supervision, R.S.; funding acquisition, R.S., N.H. and K.A.S. All authors have read and agreed to the published version of the manuscript.
Funding
R.S., N.H. and K.A.S. were funded by Program Penelitian Kolaborasi Indonesia (PPKI) 2021 No. 033/IT1.B07.1/SPP-LPPM/II/2021.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hartsfield, N.; Ringel, G. Pearls in Graph Theory; Academic Press: San Diego, CA, USA, 1990. [Google Scholar]
- Alon, N.; Kaplan, G.; Lev, A.; Roditty, Y.; Yuster, R. Dense graphs are antimagic. J. Graph Theory 2004, 47, 297–309. [Google Scholar] [CrossRef] [Green Version]
- Eccles, T. Graphs of Large Linear Size Are Antimagic. J. Graph Theory 2016, 81, 236–261. [Google Scholar] [CrossRef] [Green Version]
- Hefetz, D.; Saluz, A.; Tran, H. An application of the combinatorial Nullstellensatz to a graph labelling problem. J. Graph Theory 2010, 65, 70–82. [Google Scholar] [CrossRef]
- Cranston, D.; Liang, Y.; Zhu, X. Regular Graphs of Odd Degree Are Antimagic. J. Graph Theory 2015, 80, 28–33. [Google Scholar] [CrossRef] [Green Version]
- Bérczi, K.; Bernáth, A.; Vizer, M. Regular Graphs are Antimagic. Elec. J. Combinat. 2015, 22. [Google Scholar] [CrossRef]
- Chang, F.; Liang, Y.; Pan, Z.; Zhu, X. Antimagic Labeling of Regular Graphs. J. Graph Theory 2016, 82, 339–349. [Google Scholar] [CrossRef] [Green Version]
- Kaplan, G.; Lev, A.; Roditty, Y. On zero-sum partitions and anti-magic trees. Discret. Math. 2009, 309, 2010–2014. [Google Scholar] [CrossRef] [Green Version]
- Liang, Y.; Wong, T.; Zhu, X. Anti-magic labeling of trees. Discret. Math. 2014, 331, 9–14. [Google Scholar] [CrossRef]
- Lozano, A.; Mora, M.; Seara, C.; Tey, J. Caterpillars are Antimagic. Mediterr. J. Math. 2021, 18, 39. [Google Scholar]
- Arumugam, S.; Premalatha, K.; Baca, M.; Semanicová-Fenovcíkovxax, A. Local Antimagic Vertex Coloring of a Graph. Graphs Comb. 2017, 33, 275–285. [Google Scholar] [CrossRef]
- Bensmail, J.; Senhaji, M.; Lyngsie, K.S. On a combination of the 1-2-3 conjecture and the antimagic labelling conjecture. Discret. Math. Theor. Comput. Sci. 2017, 19. Available online: https://dmtcs.episciences.org/3849/pdf (accessed on 28 September 2021).
- Haslegrave, J. Proof of a local antimagic conjecture. Discret. Math. Theor. Comput. Sci. 2018, 20, #18. [Google Scholar]
- Kamatchi, N.; Arumugam, S. Distance Antimagic Graphs. J. Combinat. Math. Combinat. Comput. 2013, 64, 61–67. [Google Scholar]
- Kamatchi, N.; Vijayakumar, G.R.; Ramalakshmi, A.; Nilavarasi, S.; Arumugam, S. Distance Antimagic Labelings of Graphs. Lect. Notes Comp. Sci. 2017, 10398, 113–118. [Google Scholar]
- Llado, A.; Miller, M. Approximate results for rainbow labelings. Period. Math. Hung. 2017, 74, 11–21. [Google Scholar] [CrossRef] [Green Version]
- O’Neal, A.; Slater, P. An introduction to distance D-magic graphs. J. Indones. Math. Soc. 2011, 89–107. [Google Scholar] [CrossRef] [Green Version]
- Yasin, F. Available online: https://github.com/fuadyasin/distance-magic-labeling (accessed on 28 September 2021).
- McKay, B.D.; Piperno, A. Practical Graph Isomorphism, II. J. Symb. Comput. 2013, 60, 94–112. [Google Scholar] [CrossRef]
- Dafik; Alfarisi, R.; Prihandini, R.M.; Adawiyah, R.; Agustin, I.H. Inclusive distance antimagic graphs. Aip Conf. Proc. 2018, 020083. [Google Scholar] [CrossRef]
- Anuwiksa, P.; Munemasa, A.; Simanjuntak, R. D-Magic and Antimagic Labelings of Hypercubes. submitted.
- Brouwer, A.E.; Cohen, A.M.; Neumaier, A. Distance-Regular Graphs; Springer: New York, NY, USA, 1989; p. 437. [Google Scholar]
- Bondy, A.; Murty, U.S.R. Graph Theory; Graduate Texts in Mathematics; Springer: Berlin/Heidelberg, Germany, 2008; Volume 244, p. 82. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).