On Forbidden Subgraphs of (K₂, H)-Sim-(Super)Magic Graphs

Abstract

A graph G admits an H-covering if every edge of G belongs to a subgraph isomorphic to a given graph H. G is said to be H-magic if there exists a bijection $f:V\left(G\right)\cup E\left(G\right)\to \{1,2,\dots ,|V\left(G\right)|+|E\left(G\right)\left|\right\}$ such that $w_f\left(H^{\prime }\right)={\sum }_{v\in V\left(H^{\prime }\right)}f\left(v\right)+{\sum }_{e\in E\left(H^{\prime }\right)}f\left(e\right)$ is a constant, for every subgraph $H^{\prime }$ isomorphic to H. In particular, G is said to be H-supermagic if $f\left(V\right(G\left)\right)=\{1,2,\dots ,|V\left(G\right)\left|\right\}$. When H is isomorphic to a complete graph $K_2$, an H-(super)magic labeling is an edge-(super)magic labeling. Suppose that G admits an F-covering and H-covering for two given graphs F and H. We define G to be $(F,H)$-sim-(super)magic if there exists a bijection $f^{\prime }$ that is simultaneously F-(super)magic and H-(super)magic. In this paper, we consider $(K_2,H)$-sim-(super)magic where H is isomorphic to three classes of graphs with varied symmetry: a cycle which is symmetric (both vertex-transitive and edge-transitive), a star which is edge-transitive but not vertex-transitive, and a path which is neither vertex-transitive nor edge-transitive. We discover forbidden subgraphs for the existence of $(K_2,H)$-sim-(super)magic graphs and classify classes of $(K_2,H)$-sim-(super)magic graphs. We also derive sufficient conditions for edge-(super)magic graphs to be $(K_2,H)$-sim-(super)magic and utilize such conditions to characterize some $(K_2,H)$-sim-(super)magic graphs.

1. Introduction

In this paper, all graphs to be considered are finite, simple, and undirected. We write $[a,b]$ to define the set of consecutive integers $\{a,a+1,a+2,\dots ,b\}$, for any positive integers $a<b$. We denote two isomorphic graphs G and H with $G\cong H$. The degree of vertex x of G, denoted by $deg\left(x\right)$, is the number of vertices in G adjacent to x.

Let G be a graph with the vertex set $V\left(G\right)$ and the edge set $E\left(G\right)$. An edge-magic total labeling (or EMT labeling for short) of a graph G is a bijection $\lambda :V\left(G\right)\cup E\left(G\right)\to \{1,2,\dots ,|V\left(G\right)|+|E\left(G\right)\left|\right\}$ with the property that there exists a constant k such that $\lambda \left(x\right)+\lambda \left(y\right)+\lambda \left(xy\right)=k$, for any edge $xy\in E\left(G\right)$. Then, G is said to be edge-magic (EMT) and k is called a magic sum. This notion was defined by Kotzig and Rosa [1], who called it magic valuation, and later rediscovered by Ringel and Lladó [2]. In [2], Ringel and Lladó conjectured that all trees are EMT. Since then, numerous papers associated with EMT labeling have been published.

In 1998, Enomoto et al. [3] introduced a special case of EMT labeling with the extra property that $\lambda \left(V\right(G\left)\right)=\{1,2,\dots ,|V\left(G\right)\left|\right\}$. It is called a super edge-magic total labeling (SEMT labeling). A graph G that admits an SEMT labeling is said to be super edge-magic (SEMT). An SEMT labeling has a significant role in graph labeling because it is related to other types of labelings. Figueroa-Centeno et al. [4] found relationships between SEMT and well-known labelings such as harmonious, sequential, and cordial labelings. Bača et al. [5] established the relationship between SEMT and EMT labelings and $(a,d)$-edge-antimagic vertex labeling. Other relationships and comprehensive surveys about SEMT and EMT graphs can be found in [6,7,8,9].

The next Lemma states a necessary and sufficient condition of an SEMT graph. We frequently use this condition to construct SEMT labelings of some graphs.

Lemma 1

([4]).A graph G is SEMT if and only if there exists a bijective function $f:V\left(G\right)\to [1,|V\left(G\right)\left|\right]$ such that the set $S=\left\{f\right(u)+f(v\left)\right|uv\in E\left(G\right)\}$ consists of $\left|E\right(G\left)\right|$ consecutive integers. In such a case, f extends to an SEMT labeling of G with magic sum $k=\left|V\right(G\left)\right|+\left|E\right(G\left)\right|+s$, where $s=min\left(S\right)$.

In [3], Enomoto et al. presented a necessary condition for an SEMT graph as stated in the following.

Lemma 2

([3]).If a graph G with order p and size q is SEMT, then $q\le 2p-3$.

We call an SEMT graph with the maximum number of edges given by Lemma 2 a maximal SEMT graph. In [10], Macdougall and Wallis provide some properties of maximal SEMT graphs and construct some particular maximal SEMT graphs such as triangulations of v-cycle, generalized prisms, and graphs with large cliques. Sugeng and Xie [11] presented a construction to extend any non-maximal SEMT graph into a maximal SEMT graph by utilizing the adjacency matrix. Thus, it is interesting to ask the question of which other graphs are maximal SEMT.

Subsequently, Gutiérrez and Lladó [12] generalized the notion of EMT and SEMT into H-(super)magic labelings in 2005. Let G be a graph where each edge belongs to at least one subgraph isomorphic to a given graph H. In this case, G admits an H-covering. An H-magic labeling of G is a bijection $g:V\left(G\right)\cup E\left(G\right)\to \{1,2,\dots ,|V\left(G\right)|+|E\left(G\right)\left|\right\}$ with the property that there exists a positive integer k such that $w_H\left(H^{\prime }\right)={\sum }_{v\in V\left(H^{\prime }\right)}g\left(v\right)+{\sum }_{e\in E\left(H^{\prime }\right)}g\left(e\right)=k$, for every subgraph $H^{\prime }$ of G isomorphic to H. The H-magic labeling g of G with the extra property that $g\left(V\right(G\left)\right)=\{1,2,\dots ,|V\left(G\right)\left|\right\}$ is called H-supermagic labeling of G. A graph G is an H-magic or H-supermagic if it has an H-magic labeling or H-supermagic labeling, respectively.

While working with H-magic graphs, we found labelings of graphs which are simultaneously H-magic and F-magic, for two non isomorphic graphs F and H. For instance, Figure 1 shows an example of a ladder $L_n=P_n\times K_2$ which is $C_4$-magic and $C_{2m}$-magic, for any $m\in [3,\lceil \frac{n}{2}\rceil ]$, at the same time [13]. This leads us to generalize the concept of H-magic with two or more non-isomorphic covers.

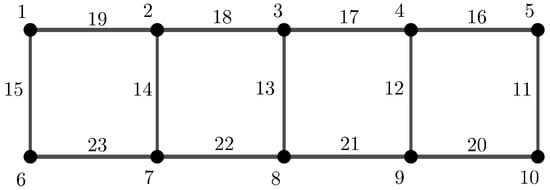
Figure 1. A $C_4$-supermagic and $C_6$-supermagic labelings of ladder.

Given two non-isomorphic graphs F and H, let G be a graph admitting an F-covering and H-covering simultaneously. An $(F,H)$-simultaneously-magic labeling of G, denoted by $(F,H)$-sim-magic labeling, is a bijective function $f:V\left(G\right)\cup E\left(G\right)\to \{1,2,\dots ,|V\left(G\right)|+|E\left(G\right)\left|\right\}$ with the property that there exist two positive integers $k_F$ and $k_H$ (not necessarily the same) such that $w_f\left(F^{\prime }\right)={\sum }_{v\in V\left(F^{\prime }\right)}f\left(v\right)+{\sum }_{e\in E\left(F^{\prime }\right)}f\left(e\right)=k_F$ and $w_f\left(H^{\prime }\right)={\sum }_{v\in V\left(H^{\prime }\right)}f\left(v\right)+{\sum }_{e\in E\left(H^{\prime }\right)}f\left(e\right)=k_H$, for each subgraph $F^{\prime }$ of G isomorphic to F and each subgraph $H^{\prime }$ of G isomorphic to H. In such a case that $f\left(V\right(G\left)\right)=\{1,2,\dots ,|V\left(G\right)\left|\right\}$, we call f an $(F,H)$-simultaneously-supermagic labeling, denoted by $(F,H)$-sim-supermagic labeling. The graph G is said to be $(F,H)$-sim-magic or $(F,H)$-sim-supermagic if it has an $(F,H)$-sim-magic labeling or $(F,H)$-sim-supermagic labeling, respectively. By the definition of these notions, the construction of $(F,H)$-sim-(super)magic labelings of graphs can enlarge the collection of graphs that are known to be F-(super)magic and H-(super)magic.

In [13], we established the existence of a $(K_2+H,2K_2+H)$-sim-supermagic labeling of a join product graph $G+H$ and a $(C_4,H)$-sim-supermagic labeling of a Cartesian product graph $G\times K_2$ where H is isomorphic to a ladder or an even cycle. We also presented the relationship between an $\alpha$ labeling of a tree T not isomorphic to a star and a $(C_4,C_6)$-sim-supermagic of the Cartesian product $T\times K_2$.

Since SEMT and EMT labelings are known to be related to other well-known graph labelings, in this paper we focus on the study of $(K_2,H)$-sim-(super)magic labelings; in particular for a graph H that is isomorphic to a path, a star, or a cycle. We denote a path on n vertices by $P_n$ and a cycle on n vertices by $C_n$. A star $S_n$ is a tree on $n+1$ vertices with one vertex, called the center, having degree n and the remaining vertices having degree one.

An automorphism of a graph G is a permutation of $V\left(G\right)$ preserving adjacency. A graph G is said to be vertex-transitive if, for any two vertices u and w, there is an automorphism of G that maps u to w and it is said to be edge-transitive if, for any two edges u and w, there is an automorphism of G that maps u to w. If G is both vertex-transitive and edge-transitive, G is said to be symmetric. Recall that a cycle is symmetric; a star is edge-transitive but not vertex-transitive; and a path on at least 4 vertices is neither vertex-transitive nor edge-transitive. In other words, in this paper we study $(K_2,H)$-sim-(super)magic labelings for three classes of graphs H with varied symmetry.

Some of our results enlarge the collection of known (S)EMT and H-(super)magic graphs. To show this, in Section 2 we list some necessary or sufficient conditions for a graph to be H-(super)magic, for H isomorphic to a path, a star, or a cycle.

To recognize whether a graph is not $(K_2,H)$-sim-(super)magic, we determine forbidden subgraphs for $(K_2,H)$-sim-(super)magic graphs. In Section 3, Section 4 and Section 5 some forbidden subgraphs for $(K_2,H)$-sim-(super)magic labelings, where H is isomorphic to a path, a star, or a cycle, are presented. In those sections, we say that G is H-free if G does not contain H as a subgraph.

Additionally, in Section 3, we characterize $(K_2,P_n)$-sim-(super)magic graphs of small order and establish sufficient conditions for $(K_2,P_n)$-sim-(super)magic graphs. In Section 4, we characterize $(K_2,S_n)$-(super)magic graphs. In Section 5, we characterize $(K_2,C_n)$-(super)magic graphs of order $n\ge 3$ by establishing a relation between (S)EMT and $C_n$-(super)magic labelings and construct some cycles with chords that are $(K_2,C_n)$-(super)magic. Our constructions subsequently extend known maximal SEMT graphs and cycle-(super)magic graphs. In Section 5, we present sufficient conditions for an SEMT graph with order m to be $(K_2,C_n)$-sim-(super)magic for $n<m$.

2. Previous Results on H-(Super)Magic Labelings

In this paper, we first survey some known necessary conditions of H-(super)magic graphs for H isomorphic to a path and a star. These results are immediately necessary conditions for a $(K_2,H)$-sim-(super)magic graph. We also list some graphs known to be cycle-(super)magic.

In [12], it is proved that if G is a $P_h$-magic graph, $h>2$, then G is $C_h$-free as stated in the following theorem.

Theorem 1

([12]).Let G be a $P_h$-magic graph, $h>2$. Then G is $C_h$-free.

A cycle on n vertices $C_n$ with one pendant edge is denoted by $C_n^{+1}$ (See Figure 2 for $C_5^{+1}$). Maryati et al. [14] gave the following necessary conditions for path-magic graphs.

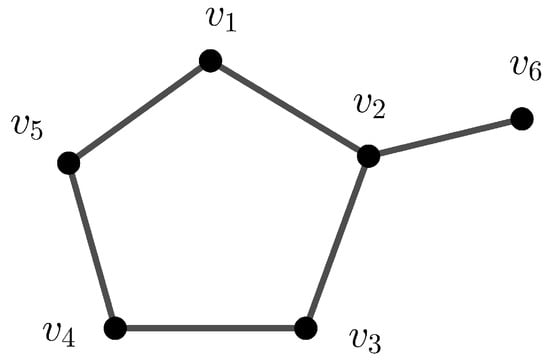
Figure 2. The cycle with one pendant edge $C_5^{+1}$.

Theorem 2

([14]).Let $n\ge 4$ be a positive integer.

1 .

If G is $P_n$-magic, then G is $C_{n-1}^{+1}$-free.

2 .

If G is $P_n$-magic, then G is $C_{n+1}^{+1}$-free.

In [14,15], Maryati et al. provided another forbidden subgraph of path-magic graphs by defining an $H_n$ graph. The $H_n$ graph is a graph with $V\left(H_n\right)=\{v_{1,i},v_{2,i}|i\in [1,2n+1]\}$ and $E\left(H_n\right)=\{v_{1,i}{v}_{1,i+1},v_{2,i}{v}_{2,i+1}$$|i\in [1,2n]\}\cup \left\{v_{1,c}{v}_{2,c}\right|c=n+1\}$ (Figure 3 illustrates the graph $H_3$).

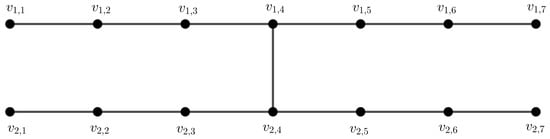
Figure 3. The graph $H_3$.

Theorem 3

([14,15]).Let $n\ge 3$ be a positive integer. If G is $P_n$-magic, then G is $H_{n+2}$-free.

In [12], Gutiérrez and A. Lladó also established some necessary conditions of star-magic graphs by considering the degree of vertices.

Theorem 4

([12]).Let f be a $S_h$-magic labeling of a graph G with magic constant $m_f$. If the degree of vertex $x\in V\left(G\right)$ verifies $deg\left(x\right)>h$, then for every vertex y adjacent to x, we have $f\left(y\right)+f\left(xy\right)=\frac{1}{h}(m_f-f\left(x\right))$.

Corollary 1

([12]).Let G be a $S_h$-magic graph with $h>1$. Then, for every edge $e=xy$ of G, $min\left\{deg\right(x),deg(y\left)\right\}\le h$.

In the following theorems, we present some known classes of cycle-supermagic graphs, a more complete list can be found in [7]. We recall the definition of the graphs mentioned in the theorems. A fan $F_n$ is a graph obtained from connecting a single vertex to all vertices in cycle $P_n$. A wheel $W_n$ is a graph with $n+1$ vertices obtained from connecting a single vertex to all vertices in cycle $C_n$. For $k\ge 2$, a windmill $W(r,k)$ is a graph obtained by identifying one vertex in each of the k disjoint copies of the cycle $C_r$. For $n\ge 2$, a ladder $L_n$, is defined as $P_n\times K_2$, whose vertex set is $V\left(L_n\right)=V\left(P_n\right)\times V\left(K_2\right)=\left\{(x_i,y_j)\right|i\in [1,n]$ and $j\in [1,2]\}$ and edge set is $E\left(L_n\right)=\left\{(x_i,y_j)(x_{i+1},y_j)\right|i\in [1,n-1]$ and $j\in [1,2]\}\cup \left\{(x_i,y_1)(x_i,y_2)\right|i\in [1,n]\}$. Illustrations of a wheel, a fan, and a ladder can be seen in Figure 4.

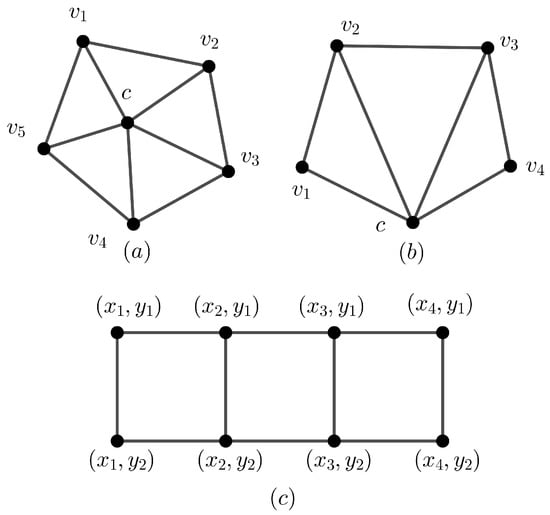
Figure 4. (a) The wheel $W_5$, (b) the fan $F_4$, and (c) the ladder $L_4$.

Theorem 5

([16,17]).For $n\ge 4$, the wheel $W_n$ is $C_3$-supermagic.

Theorem 6

([16]).For any two integers $k\ge 2$ and $r\ge 3$, the windmill $W(r,k)$ is $C_r$-supermagic.

Theorem 7

([18]).Let $n\ge 4$ be a positive integer.

1 .

The fan $F_n$ is $C_m$-supermagic for any integer $4\le m\le \lfloor \frac{n+4}{2}\rfloor$;

2 .

The ladder $L_n$ is $C_m$-supermagic for any positive integer $3\le m\le \lfloor \frac{n}{2}\rfloor +1$.

One important observation on H-magicness is the following.

Observation 1.

If G is H-magic then $G\bigcup n{K}_1$ is also H-magic.

The converse of Observation 1 is not true. For example, $2P_3\cup K_1$ is $P_3$-supermagic (as shown in Figure 5) but $2P_3$ is not $P_3$-magic (as a result of Theorem 1 in [14]).

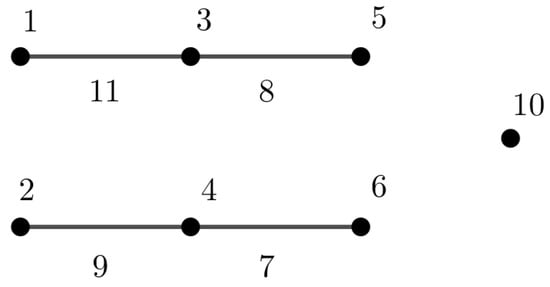
Figure 5. $P_3$-magic of $2P_3\cup K_1$.

Due to this fact, in the rest of the paper, we restrict our observation to graphs with components not isomorphic to $K_1$.

3. $({\mathit{K}}_{\mathbf{2}},{\mathit{P}}_{\mathit{n}})$-Sim-Supermagic Labelings

In this section, we provide the collection of forbidden subgraphs and characterize a $(K_2,P_n)$-sim-supermagic graph.

Let $m\ge 3$ and $n\ge 2$ be two integers. We denote the edge sets of a path $P_n$ and a cycle $C_m$ as $E\left(P_n\right)=\left\{w_i{w}_{i+1}\right|i\in [1,n-1]$ and $E\left(C_m\right)=\{v_i{v}_{i+1}$$|i\in [1,m-1]\cup \left\{v_1{v}_m\right\}$, respectively. An $(m,n)$-tadpole is a graph obtained by joining the end vertex $w_1$ of $P_{n-1}$ to the vertex $v_1$ of $C_m$. Figure 6 shows the $(4,5)$-tadpole graph.

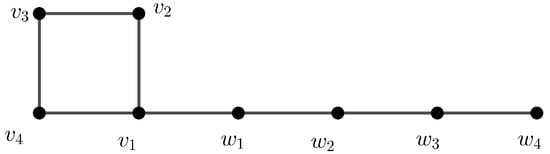
Figure 6. The $(4,5)$-tadpole graph.

We denote the star with n pendant edges as $S_n$. Consider the star $S_3$ with three pendant edges denoted by $e_1,e_2,e_3$. We define $S(S_3;e_1,e_2,e_3;n,3,3)$ as a subdivision of the star $S_3$ by replacing the edge $e_1$ with a path on n vertices and the remaining edges by paths on three vertices. Figure 7 illustrates the subdivided star $S(S_3;e_1,e_2,e_3;5,3,3)$.

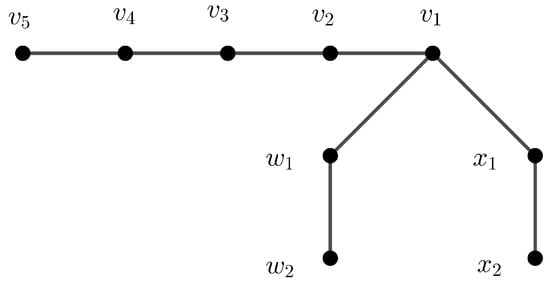
Figure 7. The $S(S_3;e_1,e_2,e_3;5,3,3)$ graph.

In [19], Maryati et al. introduced a subgraph-amalgamation. For $n\ge 2$, let ${\left\{G_i\right\}}_{i=1}^n$ be a collection of graphs $G_i$s where each $G_i$ contains $H_i^{*}\cong H$ as a fixed subgraph and let $\mathcal{H}={\left\{H_i^{*}\right\}}_{i=1}^n$ be the collection of $H_i^{*}$s. The H-amalgamation of ${\left\{G_i\right\}}_{i=1}^n$, denoted by $Amal(G_1,G_2,\dots ,G_n;\mathcal{H};n)$, is a graph constructed from identifying the $H_i^{*}$ of each $G_i$. If $G_i$ is isomorphic to a given graph G, we write the H-amalgamation as $Amal(G;\mathcal{H};n)$.

Let $G_1$ be an $(m,n)$-tadpole containing a subgraph $H_1^{*}=v_2{v}_3$ isomorphic to $P_2$; let $G_2$ be a path $P_k$, whose edge set is $E\left(P_k\right)=\left\{x_i{x}_{i+1}\right|i\in [1,k-1]\}$, containing a subgraph $H_2^{*}=x_3{x}_4$ isomorphic to $P_2$; and $\mathcal{H}={\left\{H_i^{*}\right\}}_{i=1}^2$. Figure 8 illustrates the $Amal\left(\right(5,3)$-tadpole,$P_8;\mathcal{H};2)$.

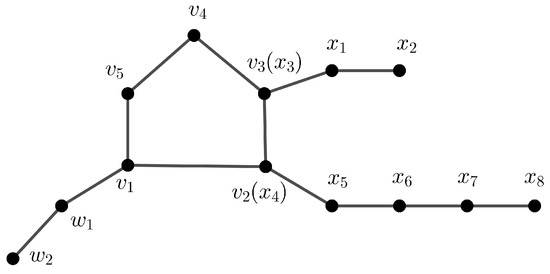
Figure 8. The $Amal\left(\right(5,3)$-tadpole,$P_8;\mathcal{H};2)$ graph.

The next theorem stated forbidden subgraphs of $(K_2,P_n)$-sim-(super)magic graphs.

Theorem 8.

If G is $(K_2,P_n)$-sim-(super)magic, then G is H-free where

1 .

$H\cong C_m$, for any $n\ge 4$ and $m\in [n-1,n+1]$;

2 .

$H\cong H_{n+2}$, for any $n\ge 3$;

3 .

$H\cong P_{n+1}$, for any $n\ge 3$;

4 .

$H\cong S(S_3;e_1,e_2,e_3;n-2,3,3)$, for any $n\ge 5$;

5 .

$H\cong (k,n-k)$-tadpole, for any $n>4$ and $k\in [3,n-2]$;

6 .

$H\cong Amal\left(\right(m,3)$-tadpole, $P_{n-m};\mathcal{H};2)$, for any $n\ge 7,$ and $m\in [3,n-4]$.

Proof. 

The case where $H\cong C_m$, for any $n\ge 4$ and $m\in [n-1,n+1]$, is an immediate consequence of Theorems 1 and 2; and the case where $H\cong H_{n+2}$, for any $n\ge 3$, is an immediate consequence of Theorem 3. The rest of the cases are proven as follows.

Case 3. $H\cong P_{n+1}$, for any $n\ge 3$.

Suppose that G is a $(K_2,P_n)$-sim-(super)magic graph and G is not $P_{n+1}$-free. Let f be a $(K_2,P_n)$-sim-(super)magic labeling of G. Consider two subgraphs isomorphic to $P_n$ with edges $v_1{v}_2,v_2{v}_3,\dots ,v_{n-1}{v}_n$ and $v_2{v}_3,v_3{v}_4,\dots ,v_n{v}_{n+1}$. Since G is $(K_2,P_n)$-magic,

$$\sum _{i=1}^{n}f\left(v_i\right)+\sum _{i=1}^{n-1}f\left(v_i{v}_{i+1}\right)=\sum _{i=2}^{n+1}f\left(v_i\right)+\sum _{i=2}^{n}f\left(v_i{v}_{i+1}\right).$$

(1)

By eliminating ${\sum }_{i=2}^{n}f\left(v_i\right)+{\sum }_{i=2}^{n-1}f\left(v_i{v}_{i+1}\right)$ in both sides of Equation (1), we have

$$f\left(v_1\right)+f\left(v_1{v}_2\right)=f\left(v_n{v}_{n+1}\right)+f\left(v_{n+1}\right).$$

However, ${\sum }_{i=1}^{2}f\left(v_i\right)+f\left(v_1{v}_2\right)={\sum }_{i=n}^{n+1}f\left(v_i\right)+f\left(v_n{v}_{n+1}\right)$. This clearly forces $f\left(v_2\right)=f\left(v_n\right)$, a contradiction.

Case 4. $H\cong S(S_3;e_1,e_2,e_3;n-2,3,3)$, for any $n\ge 5$.

Assume to the contrary that G is $(K_2,P_n)$-sim-(super)magic and G contains $S(S_3;e_1,e_2,e_3;$$n-2,3,3)$ as a subgraph. Let f be a $(K_2,P_n)$-sim-(super)magic labeling of G. Consider a subgraph H isomorphic to $S(S_3;e_1,e_2,e_3;n-2,3,3)$. Label the vertex set $V\left(H\right)=\left\{v_i\right|i\in [1,n-2]\}\cup \{w_i,x_i|i\in [1,2]\}$ and the edge set $E\left(H\right)=\left\{v_i{v}_{i+1}\right|i\in [1,n-3]\}\cup \{v_1{w}_1,v_1{x}_1,w_1{w}_2,x_1{x}_2\}$. There exist two paths isomorphic to $P_n$ with edges $v_{n-2}{v}_{n-3},v_{n-3}{v}_{n-4},\dots ,v_2{v}_1,$$v_1{w}_1,w_1{w}_2$ and $v_{n-2}{v}_{n-3},v_{n-3}{v}_{n-4},\dots ,$$v_2{v}_1,v_1{x}_1,x_1{x}_2$. As f is a $(K_2,P_n)$-sim-(super)magic labeling, we have ${\sum }_{i=1}^{n-2}f\left(v_i\right)+{\sum }_{i=1}^{2}f\left(w_i\right)+f\left(v_1{w}_1\right)+{\sum }_{i=1}^{n-3}f\left(v_i{v}_{i+1}\right)+f\left(w_1{w}_2\right)={\sum }_{i=1}^{n-2}f\left(v_i\right)+{\sum }_{i=1}^{2}f\left(x_i\right)+{\sum }_{i=1}^{n-3}f\left(v_i{v}_{i+1}\right)+f\left(v_1{x}_1\right)+$ $f\left(x_1{x}_2\right).$ Thus, we obtain $f\left(v_1{w}_1\right)=f\left(v_1{x}_1\right)$, a contradiction.

Case 5. $H\cong (k,n-k)$-tadpole, for any $n>4$ and $k\in [3,n-2]$.

Suppose that G is $(K_2,P_n)$-sim-(super)magic and contains $(k,n-k)$-tadpole as a subgraph. Let f be a $(K_2,P_n)$-sim-(super)magic labeling of G. Next, let k be an arbitrary positive integer with $k\in [3,n-2]$. Consider a subgraph H isomorphic to $(k,n-k)$-tadpole. Denote the vertex set $V\left(H\right)=\{v_i,w_j|i\in [1,k],j\in [1,n-k]\}$ and the edge set $E\left(H\right)=\left\{v_i{v}_{i+1}\right|i\in [1,k-1]\}\cup \{v_1{v}_k,v_1{w}_1\}\cup \left\{w_j{w}_{j+1}\right|j\in [1,n-k-1]\}$. Consider two paths isomorphic to $P_n$ with edges $w_{n-k}{w}_{n-k-1},w_{n-k-1}{w}_{n-k-2},\dots ,w_2{w}_1,w_1{v}_1,v_1{v}_2,v_2{v}_3,\dots ,v_{k-1}{v}_k$ and $w_{n-k}{w}_{n-k-1},w_{n-k-1}{w}_{n-k-2},\dots ,w_2{w}_1,w_1{v}_1,v_1{v}_k,v_k{v}_{k-1},\dots ,$$v_3{v}_2$. Since G is $(K_2,P_n)$-sim-(super)magic, ${\sum }_{i=1}^{n-k}f\left(w_i\right)+{\sum }_{i=1}^{k}f\left(v_i\right)+{\sum }_{i=1}^{n-k-1}f\left(w_i{w}_{i+1}\right)+f\left(v_1{w}_1\right)+{\sum }_{i=1}^{k-1}f\left(v_i{v}_{i+1}\right)={\sum }_{i=1}^{n-k}f\left(w_i\right)+{\sum }_{i=1}^{k}f\left(v_i\right)+{\sum }_{i=1}^{n-k-1}f\left(w_i{w}_{i+1}\right)+f\left(v_1{w}_1\right)+f\left(v_1{v}_k\right)+{\sum }_{i=2}^{k-1}f\left(v_i{v}_{i+1}\right)$. As a result, we have $f\left(v_1{v}_k\right)=f\left(v_1{v}_2\right)$, a contradiction.

Case 6. $H\cong Amal\left(\right(m,3)$-(tadpole), $P_{n-m};\mathcal{H};2)$, for any $n\ge 7$ and $m\in [3,n-4]$.

Assume to the contrary that G is $(K_2,P_n)$-sim-(super)magic and contains a subgraph isomorphic to $Amal\left(\right(m,3)$-(tadpole), $P_{n-m};\mathcal{H};2)$. Let f be a $(K_2,P_n)$-sim-(super)magic labeling of G. Then, let m be an arbitrary positive integer with $m\in [3,n-4]$. Consider a subgraph H of G isomorphic to $Amal\left(\right(m,3)$-(tadpole), $P_{n-m};\mathcal{H};2)$. Denote the vertex set $V\left(H\right)=\left\{v_i\right|i\in [1,m]\}\cup \left\{w_i\right|i\in [1,n-m-2]\}\cup \{x_i,y_i|i\in [1,2]\}$ and the edge set $E\left(H\right)=\left\{v_i{v}_{i+1}\right|i\in [1,m-1]\}\cup \left\{w_i{w}_{i+1}\right|i\in [1,n-m-3]\}\cup \{v_1{v}_m,v_1{w}_1,v_2{x}_1,v_m{y}_1,x_1{x}_2,$ $y_1{y}_2\}$. Consider two paths isomorphic to $P_n$ with edges $w_{n-m-2}{w}_{n-m-3},w_{n-m-3}{w}_{n-m-4},\dots ,w_1{v}_1,v_1{v}_2,v_2{v}_3,\dots ,v_{m-1}{v}_m,v_m{y}_1,y_1{y}_2$ and $w_{n-m-2}{w}_{n-m-3},w_{n-m-3}{w}_{n-m-4},\dots ,$ $w_1{v}_1,v_1{v}_m,v_m{v}_{m-1},\dots ,v_3{v}_2,v_2{x}_1,x_1{x}_2$. As G is $(K_2,P_n)$-sim-(super)magic, we have

${\sum }_{i=1}^{n-m-2}f\left(w_i\right)+f\left(w_1{v}_1\right)+{\sum }_{i=1}^{m}f\left(v_i\right)+{\sum }_{i=1}^{2}f\left(y_i\right)+{\sum }_{i=1}^{n-m-3}f\left(w_i{w}_{i+1}\right)+{\sum }_{i=1}^{m-1}f\left(v_i{v}_{i+1}\right)$$+f\left(v_m{y}_1\right)+f\left(y_1{y}_2\right)={\sum }_{i=1}^{2}f\left(x_i\right)+{\sum }_{i=1}^{m}f\left(v_i\right)+{\sum }_{i=1}^{n-m-2}f\left(w_i\right)+{\sum }_{i=1}^{n-m-3}f\left(w_i{w}_{i+1}\right)+$${\sum }_{i=2}^{m-1}f\left(v_i{v}_{i+1}\right)+f\left(v_1{v}_m\right)+f\left(v_2{x}_1\right)+f\left(x_1{x}_2\right)+f\left(w_1{v}_1\right)$. Thus, we have $f\left(x_1\right)=f\left(y_1\right)$, a contradiction. □

We remark that if G is $(K_2,P_n)$-sim-(super)magic, then $P_n$ is the longest path of G. Notice that, for $n\in [3,4]$, $S(S_3;e_1,e_2,e_3;n-2,3,3)$ contains $P_5$ as a subgraph. By Theorem 8, such graphs are not $(K_2,P_n)$-sim-supermagic. The converse of Theorem 8 is not true as shown in the following example.

Example 1.

The graph $m{P}_3$ is not $(K_2,P_3)$-sim-(super)magic for any integer $m\ge 3$.

Proof. 

Suppose that there exists a $(K_2,P_3)$-sim-(super)magic labeling on $m{P}_3$. Let $X_i$ be the set of the internal vertex label in a $P_3^i$ for $i\in [1,m]$. Clearly $|X_i|=1$. For each edge $xy\in P_3^i$, the $xy$-weight, $f\left(xy\right)+f\left(x\right)+f\left(y\right)=k$. Thus, the $P_3$-weight of $P_3^i$ is $2k-\sum X_i$ for every $i\in [1,m]$. Consequently, $\sum X_i$ should be a constant for every $i\in [1,m]$, a contradiction. □

Problem 1.

What are the other forbidden subgraphs of $(K_2,P_n)$-sim-(super)magic graph?

As a consequence of Theorem 8 where $H\cong P_{n+1}$, for any integer $n\ge 3$, we have the following two results.

Corollary 2.

Let $n\ge 3$ be a positive integer and G be a graph that admits $P_n$-covering. If G is $(K_2,P_n)$-sim-(super)magic, then $n\ge diam\left(G\right)+1$.

Corollary 3.

Let $n\ge 3$ be a positive integer and G be a graph that admits $P_n$-covering. If G is $(K_2,P_n)$-sim-(super)magic, then G is $C_h$-free for any $h>n$.

By the previous two corollaries, Theorem 8, and Example 1, we have the following corollaries.

Corollary 4.

Let $n\in \{3,4\}$ and G be a graph that admits $P_n$-covering. If G is $(K_2,P_n)$-sim-(super)magic, then G is a forest. In particular, if G is $(K_2,P_n)$-sim-(super)magic, then G is a tree.

Let $n\ge 2$ be a positive integer. In [12], it is proved that the star $S_n$ is $S_m$-supermagic for each $m<n$. Moreover, the $S_m$-supermagic labeling of $S_n$ in [12] is also an SEMT labeling of $S_n$. Combining with Example 1 and Corollary 4, we obtain the following.

Corollary 5.

A graph G is $(K_2,P_3)$-sim-(super)magic if and only if G is isomorphic to the star $S_n$ for any positive integer $n\ge 3$.

A caterpillar $S_{n_1,n_2,\cdots ,n_k}$ is a graph derived from a path $P_k$, $k\ge 2$, where the vertex $w_i\in V\left(P_k\right)$ is adjacent to $m_i\ge 0$ leaves, $i\in [1,k]$. A special case of caterpillars when $k=2$, $m_1\ge 1$, and $m_2\ge 1$ is called a double star $S_{m_1,m_2}$. An illustration of the double star $S_{5,3}$ and a $(K_2,P_4)$-sim-supermagic labeling on $S_{5,3}$ can be seen in Figure 9. Since Kotzig and Rosa [1] have proved that all caterpillars are SEMT, utilizing Corollary 4, we have the following.

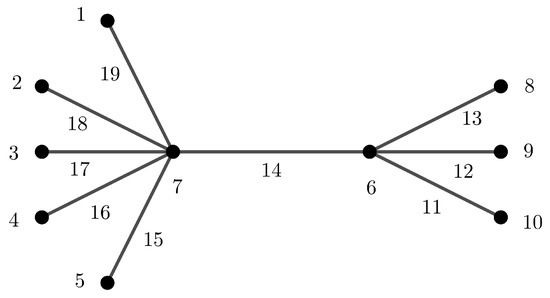
Figure 9. A $(K_2,P_4)$-sim-supermagic labeling of the double star $S_{5,3}$.

Corollary 6.

A connected graph G is $(K_2,P_4)$-sim-(super)magic if and only if G is isomorphic to a double star $S_{m,n}$ for any two positive integers m and n.

Problem 2.

Characterize $(K_2,P_n)$-sim-(super)magic graphs for any $n\ge 5$.

We conclude this section by presenting sufficient conditions for an (S)EMT graph to be $(K_2,P_n)$-sim-(super)magic.

Lemma 3.

Let k and n be two positive integers. Let G be a graph of order at least $n+1$ that admits $P_n$-covering. Let ${\left\{P_n^i\right\}}_{i=1}^k$ be the family of all subgraphs of G isomorphic to $P_n$ and let $\sum X_i$ be the sum of all internal vertices labels in $P_n^i$ for every $i\in [1,k]$. If f is an (S)EMT labeling in G such that $\sum X_i$ is constant, for each $i\in [1,k]$, then G is $(K_2,P_n)$-sim-(super)magic.

Proof. 

Let $m_f$ be the magic sum of the labeling. Let $i\ne j$ be two positive integers in $[1,k]$. Consider two arbitrary paths $P_n^i$ and $P_n^j$ in ${\left\{P_n^i\right\}}_{i=1}^k$. Thus, $\sum X_i=\sum X_j$. Hence, we have the following:

$$\begin{array}{ccc}\hfill w\left(P_n^i\right)& =& \sum _{v\in V\left(P_n^i\right)}f\left(v\right)+\sum _{e\in E\left(P_n^i\right)}f\left(e\right)\hfill \\ & =& (n-1)m_f-\sum X_i\hfill \\ & =& (n-1)m_f-\sum X_j\hfill \\ & =& \sum _{v\in V\left(P_n^j\right)}f\left(v\right)+\sum _{e\in E\left(P_n^j\right)}f\left(e\right)\hfill \\ & =& w\left(P_n^j\right)\hfill \end{array}$$

As a result, the sum of all edges and vertices labels associated to a subgraph of G isomorphic to $P_n$ is a constant. Therefore, G is a $P_n$-(super)magic. Since f is simultaneously SEMT and $P_n$-(super)magic, G is $(K_2,P_n)$-sim-(super)magic. □

As an immediate consequence of Lemma 3, we have the following special cases of caterpillars that are $(K_2,P_n)$-sim-magic. The broom $B_{m,n}$ is defined as a graph isomorphic to the caterpillar $S_{n_1,n_2,\cdots ,n_{m-n}}$ where $n_1=n_2=\cdots =n_{m-n-1}=0$ and $n_{m-n}=n$. The double broom $D{B}_{m,k_1,k_2}$ is a graph isomorphic to the caterpillar $S_{n_1,n_2,\cdots ,n_{m-k_1-k_2}}$ where $n_1=k_1$, $n_2=n_3=\cdots$$=n_{m-k_1-k_2-1}=0$, and $n_{m-k_1-k_2}=k_2$. Figure 10 illustrates the broom $B_{11,6}$ and the double broom $D{B}_{14,3,6}$.

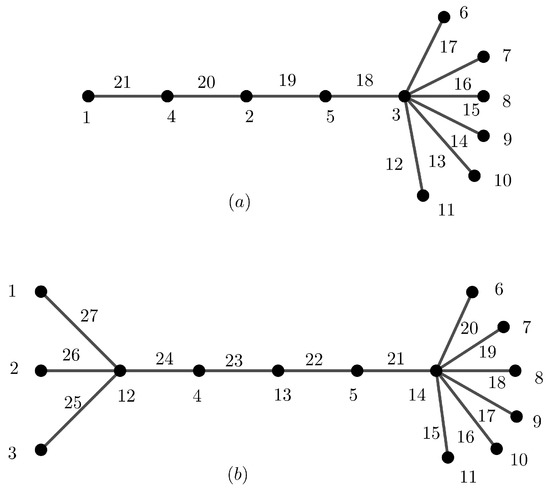
Figure 10. (a) A $(K_2,P_6)$-sim-supermagic labeling of the broom $B_{11,6}$ and (b) A $(K_2,P_7)$-sim-supermagic labeling of the double broom $D{B}_{14,3,6}$.

Corollary 7.

Let $n_1,n_2,$ and m be three positive integers at least two and $n\ge 3$. The broom $B_{m+n-1,m}$ and the double broom $D{B}_{n+n_1+n_2-2,n_1,n_2}$ are $(K_2,P_n)$-sim-magic.

Proof. 

It is known that all caterpillars are edge magic [1]. Moreover, all subgraphs isomorphic to $P_k$ have the same internal vertices. This completes the proof. □

Figure 10 illustrates $(K_2,P_n)$-sim-supermagic labelings of the broom $B_{11,6}$ and the double broom $D{B}_{14,3,6}$ for $n=6$ and $n=7$, respectively.

4. A $({\mathit{K}}_{\mathbf{2}},{\mathit{S}}_{\mathit{n}})$-Sim-Supermagic Labelings

In this section, we characterize $(K_2,S_n)$-sim-(super)magic graphs. Clearly, necessary conditions of $S_n$-magic graphs in Theorem 4 and Corollary 1 are also necessary conditions of $(K_2,S_n)$-sim-(super)magic graphs. In the following Lemma, we strengthen the degree condition of Corollary 1 for $(K_2,S_n)$-sim-(super)magic graphs.

Lemma 4.

Let $n\ge 2$ be a positive integer and G be a $(K_2,S_n)$-sim-(super)magic. Then, there is only one vertex x of G with $deg\left(x\right)\ge n$.

Proof. 

Suppose that there are two vertices v and w in $V\left(G\right)$ such that $deg\left(v\right)\ge n$ and $deg\left(w\right)\ge n$. Let f be a $(K_2,S_n)$-sim-(super)magic labeling of G. Hence, there exist two positive integers $k_1$ and $k_2$ such that each edge $xy\in E\left(G\right)$ satisfies $f\left(x\right)+f\left(y\right)+f\left(xy\right)=k_1$ and each subgraph H of G isomorphic to $S_n$ satisfies ${\sum }_{u\in V\left(H\right)}f\left(u\right)+{\sum }_{e\in E\left(H\right)}f\left(e\right)=k_2$. Consider two arbitrary stars with center v and w that are isomorphic to $S_n$ as $S^1$ and $S^2$. Thus,

$$\begin{array}{ccc}\hfill \sum _{v\in V\left(S^1\right)}f\left(v\right)+\sum _{e\in S^1}f\left(e\right)& =& \sum _{w\in V\left(S^2\right)}f\left(w\right)+\sum _{e\in E\left(S^2\right)}f\left(e\right)\hfill \\ \hfill n{k}_1-(n-1)f\left(v\right)& =& n{k}_1-(n-1)f\left(w\right).\hfill \end{array}$$

As a result, we have $f\left(v\right)=f\left(w\right)$, a contradiction. □

Recall that Gutiérrez and Lladó [12] proved the following theorem. The labeling in the proof of the theorem will be utilized to characterize $(K_2,S_n)$-sim-supermagic graphs.

Theorem 9

( [12]). The star $S_m$ is $S_n$-supermagic for any $n\in [1,m]$.

Proof. 

Denote the vertex set of $S_m$ by $V\left(S_m\right)=\{v_1,v_2,\dots ,$$v_m,$$v_{m+1}\}$, where $v_{m+1}$ is the maximum degree vertex, and the edge set of $S_m$ by $E\left(S_m\right)=\left\{v_{m+1}{v}_i\right|i\in [1,m]\}$. Define a bijection $f:V\left(S_m\right)\cup E\left(S_m\right)\to [1,2m+1]$ with $f\left(v_i\right)=i$ and $f\left(v_{m+1}{v}_i\right)=2(m+1)-i$, for any $i\in [1,m]$, and $f\left(v_{m+1}\right)=m+1$. Thus, $f\left(V\left(S_m\right)\right)=[1,m+1]$. We can verify that $w\left(H\right)={\sum }_{v\in V\left(H\right)}f\left(v\right)+{\sum }_{e\in E\left(H\right)}f\left(e\right)=(m+1)+n(i+(2(m+1)-i))=(m+1)(2n+1)$ (constant) for every subgraph H of $S_m$ isomorphic to $S_n$. Therefore, $S_m$ is $S_n$-supermagic for each $n\in [1,m]$. □

Now we are ready to characterize $(K_2,S_n)$-sim-supermagic graphs.

Theorem 10.

Let $n\ge 1$ be a positive integer. A graph G is $(K_2,S_n)$-sim-supermagic if and only if G is isomorphic to the star $S_m$ for $m>n$.

Proof. 

(⇐) First, we prove that, for $m>n$, the star $S_m$ is $(K_2,S_n)$-sim-supermagic. Recall the $S_n$-supermagic labeling of $S_m$ in the proof of Theorem 9, where $w\left(v_{n+1}{v}_i\right)=f\left(v_{n+1}\right)+f\left(v_i\right)+f\left(v_{n+1}{v}_i\right)=n+1+i+2(m+1)-i=n+1+2(m+1)$ (constant), for each edge $v_{n+1}{v}_i$ in $E\left(S_m\right)$. Hence, $S_m$ is $(K_2,S_n)$-sim-supermagic for $m>n$.

$(\Rightarrow )$ Conversely, we prove that if G is $(K_2,S_n)$-sim-supermagic, then G is isomorphic to the star $S_m$ for $m>n$. Clearly, a connected graph G with order two and three is isomorphic to $S_1$ and $S_2$, respectively. Then, consider G with order at least four. Suppose to the contrary that G is not isomorphic to any star $S_m,m>n$. Let e be an arbitrary edge in G. Suppose that e belongs to $S^{*}$, a subgraph isomorphic to $S_n$, where e is incident with c, the center of $S^{*}$. Since G is not isomorphic to a star, there exists another edge $e^{\prime }$ which is not incident with c. Since G admits $S_n$-covering, then $e^{\prime }$ belongs to a subgraph that is isomorphic to $S_n$ where the center is not c, a contradiction by Lemma 4. □

We remark that by considering $n=2$, we can derive another proof of Corollary 5 from Theorem 10.

5. A $({\mathit{K}}_{\mathbf{2}},{\mathit{C}}_{\mathit{n}})$-Sim-Supermagic Labelings

In this section, we list some forbidden subgraphs and some $(K_2,C_n)$-sim-(super)magic graphs. We start by presenting results for $(K_2,C_n)$-sim-(super)magic graphs of order n by considering the relation between two well-known magic labelings: (S)EMT and $C_n$-(super)magic.

Lemma 5.

Let G be a graph of order n admitting a $C_n$ covering. If G is (S)EMT then G is $C_n$-(super)magic.

Proof. 

Let f be an $\left(S\right)$EMT labeling of G. Thus, there exists a positive integer $k_1$ such that $f\left(x\right)+f\left(y\right)+f\left(xy\right)=k_1$ for each edge $xy$ in $E\left(G\right)$. Denote $\left\{x_i\right|i\in [1,n]\}$ as the set of vertices in G. Define a bijection $g:V\left(G\right)\cup E\left(G\right)\to [1,|V\left(G\right)|+|E\left(G\right)\left|\right]$ with $g\left(x\right)=f\left(x\right)$ for all $x\in$V(G)$\cup E\left(G\right)$. Consider an arbitrary subgraph C isomorphic to $C_n$. Since the label of each vertex x is counted twice in $w\left(C\right)={\sum }_{v\in V\left(C\right)}f\left(v\right)+{\sum }_{e\in E\left(C\right)}f\left(e\right)$, then $w\left(C\right)=n{k}_1-{\sum }_{i=1}^{n}f\left(x_i\right)$, a constant. Therefore, G is $C_n$-(super)magic. □

The converse of Lemma 5 is not true since $K_4$ is $C_4$-(super)magic, although it is known that $K_4$ is neither EMT [1,3] nor SEMT [3] (See Figure 11). However, it is clear that we have the following necessary and sufficient condition for a graph of order n to admit a $(K_2,C_n)$-sim-(super)magic labeling.

Figure 11. (a) A $C_4$-supermagic labeling of $K_4$ and (b) A $C_4$-magic labeling of $K_4$.

Corollary 8.

Let G be a graph order n admitting a $C_n$ covering. G is (S)EMT if and only if G is $(K_2,C_n)$-sim-(super)magic.

It is known that the complete graph $K_n$ is EMT if and only if $n=3,5,6$ [1]. Since each pair of vertices in $K_n$ are adjacent, the number of subgraphs of $K_n$ isomorphic to $C_n$ is the number of n-cycles in the symmetric group $S_n$, which is $\frac{n!}{n}=(n-1)!$ Thus, the number of subgraphs of $K_5$ and $K_6$ isomorphic to $C_5$ and $C_6$ is 24 and 120, respectively.

Corollary 9.

Let $n>3$ be a positive integer. A complete graph $K_n$ is $(K_2,C_n)$-sim-magic if and only if $n=5$ or $n=6$.

Proof. 

(⇐) Recall the known EMT labeling f in $K_n$ for $n=5$ or 6 [1]. By Lemma 5, f is a $C_n$-magic labeling. This gives $K_n$ as $(K_2,C_n)$-sim-magic for $n=5$ or 6.

(⇒) Conversely, it is immediately known from the fact that $K_n$ is not EMT according to Kotzig and Rosa [1]. □

Figure 12 shows $(K_2,C_5)$-sim-supermagic and $(K_2,C_6)$-sim-supermagic graphs.

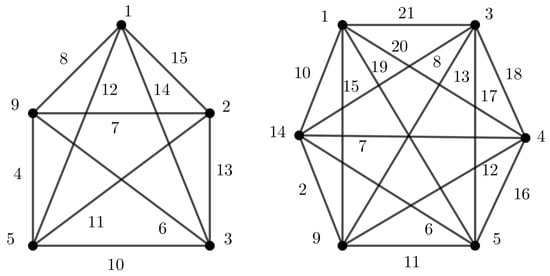
Figure 12. A $(K_2,C_n)$-sim-supermagic labeling for $n\in [5,6]$.

Kotzig and Rosa [1] proved that the complete bipartite graph $K_{m,n}$ is EMT for all m and n. Philips et al. [20] constructed an EMT labeling of the wheel $W_n$ for $n\equiv 0,1,$ or 2(mod 4). By Lemma 5, we have the following Corollary.

Corollary 10.

Let $n\ge 3$ be a positive integer.

1 .

$K_{n,n}$ is $(K_2,C_{2n})$-sim-magic;

2 .

$W_n$ is $(K_2,C_{n+1})$-sim-magic for $n\equiv 0,1,$ or 2(mod 4).

In the next two theorems, we consider a $(K_2,C_m)$-sim-supermagic labeling of a cycle with chords. A chord is an edge joining two non-adjacent vertices in a cycle. An n-power of graph $G^n$ is a graph with the vertex set $V\left(G^n\right)=V\left(G\right)$ and any two vertices are adjacent when their distance in G is at most n. Recall from Lemma 2 that $C_n^2$ is not SEMT, so it is if we remove at most two edges from $C_n^2$. Thus, it is interesting to construct a maximal SEMT graph, where the number of edges is equal to the upper bound of inequality in Lemma 2, from $C_n^2$.

Let $n\ge 3$ be a positive integer and $\left\{x_i\right|i\in [1,n]\}$ be the vertex set of the cycle $C_n$. Let $E=\{x_{\lfloor \frac{n}{2}\rfloor }{x}_{\lfloor \frac{n}{2}\rfloor +2},x_{n-1}{x}_1,x_n{x}_2\}$ be the set of three edges in $C_n^2$. We define the cycle with chords $C{C}_n^1$ where the vertex set is $V\left(C_n\right)$ and the edge set is $E\left(C_n^2\right)\backslash E$. It is clear that $C{C}_n^1$ admits a $C_n$-covering for every odd integer $n\ge 7$ and we have the following theorem.

Theorem 11.

Let $n\ge 7$ be an odd integer. A cycle with chords $C{C}_n^1$ is $(K_2,C_n)$-sim-supermagic.

Proof. 

Let $\left\{x_i\right|i\in [1,n]\}$ be the vertex set of $C{C}_n^1$. Define a bijection $f:V\left(C{C}_n^1\right)\to [1,|V\left(C{C}_n^1\right)\left|\right]$ as $f\left(x_i\right)=i$, for $i\in [1,n]$. Thus, for each edge $x_i{x}_j\in E\left(C{C}_n^1\right)$, we have

1 .

$f\left(x_i\right)+f\left(x_{i+1}\right)=2i+1$, for each $i\in [1,n-1]$;

2 .

$f\left(x_n\right)+f\left(x_1\right)=n+1$;

3 .

$f\left(x_i\right)+f\left(x_j\right)=i+i+2=2i+2$, for $j=(i+2)modn$ and $i\in [1,n-2]$.

Consequently, $3\le f\left(x_i\right)+f\left(x_j\right)\le 2n-1$ and the set $S=\{f\left(x_i\right)+f\left(x_j\right)|x_i{x}_j\in E\left(G\right)\}$ consists of $\left|E\right(G\left)\right|$ consecutive integers. By Lemma 1, $C{C}_n^1$ is SEMT and f is the SEMT labeling with magic sum $k=\left|V\right(G\left)\right|+\left|E\right(G\left)\right|+min\left(S\right)=n+2n-3+3=3n$. By Lemma 5, f is also a $C_n$-supermagic labeling of $C{C}_n^1$. This concludes that $C{C}_n^1$ is $(K_2,C_n)$-sim-supermagic. □

Figure 13a illustrates a $(K_2,C_7)$-sim-supermagic labeling of $C{C}_7^1$.

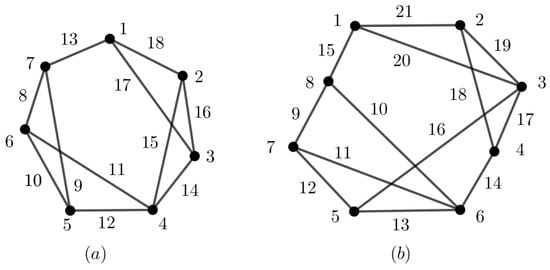
Figure 13. (a) A $(K_2,C_7)$-sim-supermagic labeling $C{C}_7^1$ and (b) A $(K_2,C_8)$-sim-supermagic labeling of $C{C}_8^2$.

Let $n\ge 8$ be an even integer. Let $E^{*}=\{x_{\frac{n}{2}-1}{x}_{\frac{n}{2}+1},x_{\frac{n}{2}}{x}_{\frac{n}{2}+2},x_{\frac{n}{2}+2}{x}_{\frac{n}{2}+4},$$x_{n-1}{x}_1,$ $x_n{x}_2\}$. We define the cycle with chords $C{C}_n^2$ as a graph where the vertex set is $V\left(C_n\right)$ and the edge set is $E\left(C_n^2\right)\backslash E^{*}\bigcup \{x_{\frac{n}{2}-1}{x}_{\frac{n}{2}+2},$$x_{\frac{n}{2}+1}{x}_{\frac{n}{2}+4}\}$. Such a cycle with chords admits $C_n$-covering for each $n\ge 8$ an even integer.

Theorem 12.

Let $n\ge 8$ be an even integer. A cycle with chords $C{C}_n^2$ is $(K_2,C_n)$-sim-supermagic.

Proof. 

Let $\left\{x_i\right|i\in [1,n]\}$ be the vertex set of $C{C}_n^2$. Define a bijection $f:V(C{C}_n^2)\to [1,|V(C{C}_n^2)\left|\right]$ as follows.

• $f(x_i)=i$, for every $i\in [1,\frac{n}{2}]$ and $i\in [\frac{n}{2}+3,n]$;
• $f(x_{\frac{n}{2}+1})=\frac{n}{2}+2$;
• $f(x_{\frac{n}{2}+2})=\frac{n}{2}+1$.

For each $x_i{x}_j\in E(C{C}_n^2)$, we have

• $f(x_i)+f(x_{i+1})=2i+1$, for each $i\in [1,\frac{n}{2}-1]$ and $i\in [\frac{n}{2}+2,n-1]$;
• $f(x_{\frac{n}{2}})+f(x_{\frac{n}{2}+1})=n+2$;
• $f(x_{\frac{n}{2}+1})+f(x_{\frac{n}{2}+2})=n+3$;
• $f(x_n)+f(x_1)=n+1;$
• $f(x_i)+f(x_{i+2})=2i+2$, for each $x_i{x}_{i+2}\in E(C{C}_n^2)$, $i\in [1,\frac{n}{2}]$ and $i\in [\frac{n}{2}+3,n-2]$;
• $f(x_{\frac{n}{2}+1})+f(x_{\frac{n}{2}+3})=n+5$;
• $f(x_{\frac{n}{2}-1})+f(x_{\frac{n}{2}+2})=n$;
• $f(x_{\frac{n}{2}+1})+f(x_{(\frac{n}{2}+4)})=n+6$.

It can be counted that $3\le f\left(x_i\right)+f\left(x_j\right)\le 2n-1$ and the set $S=\{f\left(x_i\right)+f\left(x_j\right)|x_i{x}_j\in E\left(G\right)\}$ consists of $\left|E\right(G\left)\right|$ consecutive integers. By Lemma 1, $C{C}_n^2$ is SEMT and f is the SEMT labeling with magic sum $k=|V\left(C{C}_n^2\right)|+|E\left(C{C}_n^2\right)|+min\left(S\right)=n+2n-3+3=3n$. By Lemma 5, f is also a $C_n$-supermagic labeling of $C{C}_n^2$. This concludes that $C{C}_n^2$ is $(K_2,C_n)$-sim-supermagic. □

Figure 13b shows a $(K_2,C_8)$-sim-supermagic labeling of cycle with chords $C{C}_8^2$.

In addition to maximal SEMT graphs construction, we remark that Theorems 11 and 12 also enlarge the classes of graphs known to be $C_n$-supermagic and SEMT.

Notice that up to Theorem 12 we only consider $(K_2,C_n)$-sim-supermagic graphs of order n. Therefore, it is interesting to ask whether an (S)EMT graph G of order n can admit a $C_m$-(super)magic labeling, for $m<n$. We start by presenting some forbidden subgraphs of $(K_2,C_n)$-sim-(super)magic graphs, for $n\ge 3$.

Theorem 13.

If G is $(K_2,C_n)$-sim-(super)magic, then G is H-free, where

1 .

$H\cong Amal(C_n;P_{n-1};2)$, for any $n\ge 3$;

2 .

$H\cong Amal(C_n;P_{n-2};2)$, for any $n\ge 3$.

Proof. 

Suppose that G is $(K_2,C_n)$-sim-(super)magic and G is not H-free. Then, G contains a subgraph that is isomorphic to H. Let f be a $(K_2,C_n)$-sim-(super)magic labeling of G, such that there exist two positive integers $k_1$ and $k_2$, satisfying $f\left(x\right)+f\left(y\right)+f\left(xy\right)=k_1$ and ${\sum }_{v\in V\left(C\right)}f\left(v\right)+{\sum }_{e\in E\left(C\right)}f\left(e\right)=k_2$, for each edge $xy\in E\left(G\right)$ and for each subgraph C isomorphic to $C_n$, respectively. We consider the following two cases.

Case 1. $H\cong Amal(C_n;P_{n-1};2)$.

Consider a subgraph $H\cong Amal(C_n;P_{n-1};2)$ of a graph G. Denote the vertices in $Amal(C_n;P_{n-1};2)$ by $\left\{v_n\right\}\cup \left\{u_i\right|i\in [1,n-1]\}\cup \left\{w_n\right\}$ such that the edge set is $\left\{u_i{u}_{i+1}\right|i\in [1,n-2]\}\cup \{v_n{u}_i,w_n{u}_i|i\in \{1,n-1\}\}$. There are two cycles $C^1$ and $C^2$ isomorphic to $C_n$ with $V\left(C^1\right)=v_n,u_1,u_2,\dots ,u_{n-2},u_{n-1}$ and $V\left(C^2\right)=w_n,u_1,u_2,\dots ,u_{n-2},$$u_{n-1}$. Then,

$$\begin{array}{c}\hfill \sum _{i=1}^{n-1}f\left(u_i\right)+f\left(v_n\right)+\sum _{i=1}^{n-2}f\left(u_i{u}_{i+1}\right)+f\left(v_n{u}_1\right)+f\left(v_n{u}_{n-1}\right)=\\ \hfill \sum _{i=1}^{n-1}f\left(u_i\right)+f\left(w_n\right)+\sum _{i=1}^{n-2}f\left(u_i{u}_{i+1}\right)+f\left(w_n{u}_1\right)+f\left(w_n{u}_{n-1}\right)\end{array}$$

or

$$f\left(v_n\right)+f\left(v_n{u}_1\right)+f\left(v_n{u}_{n-1}\right)=f\left(w_n\right)+f\left(w_n{u}_1\right)+f\left(w_n{u}_{n-1}\right).$$

Since $f\left(x\right)+f\left(y\right)+f\left(xy\right)=k_1$ for each edge $xy\in E\left(G\right)$, $f\left(v_n\right)+f\left(v_n{u}_1\right)=f\left(w_n\right)+f\left(w_n{u}_1\right)$. Hence, $f\left(v_n{u}_{n-1}\right)=f\left(w_n{u}_{n-1}\right)$, a contradiction.

Case 2. $H\cong Amal(C_n;P_{n-2};2)$.

Consider a subgraph $H\cong Amal(C_n;P_{n-2};2)$ of a graph G. Denote the vertices in $Amal(C_n;P_{n-2};2)$ by $\{v_{n-1},v_n\}\cup \left\{u_i\right|i\in [1,n-2]\}\cup \{w_{n-1},w_n\}$ such that the edge set is $\left\{u_i{u}_{i+1}\right|i\in [1,n-3]\}\cup \{u_1{v}_{n-1},v_{n-1}{v}_n,v_n{u}_{n-2},u_1{w}_{n-1},w_{n-1}{w}_n,w_n{u}_{n-2}\}$. There are two cycles $C^1$ and $C^2$ isomorphic to $C_n$ with $V\left(C^1\right)=v_n,v_{n-1},u_1,u_2,\dots ,u_{n-2}$ and $V\left(C^2\right)=w_n,w_{n-1},u_1,u_2,\dots ,$ $u_{n-2}$. Then

$$\begin{array}{ccc}\hfill \sum _{i=1}^{n-2}f\left(u_i\right)+\sum _{i=n-1}^{n}f\left(v_i\right)+\sum _{i=1}^{n-3}f\left(u_i{u}_{i+1}\right)+f\left(v_{n-1}{u}_1\right)+f\left(v_n{u}_{n-2}\right)+f\left(v_n{v}_{n-1}\right)& =& \\ \hfill \sum _{i=1}^{n-2}f\left(u_i\right)+\sum _{i=n-1}^{n}f\left(w_i\right)+\sum _{i=1}^{n-3}f\left(u_i{u}_{i+1}\right)+f\left(w_{n-1}{u}_1\right)+f\left(w_n{u}_{n-2}\right)+f\left(w_n{w}_{n-1}\right)\end{array}$$

or

$$\begin{array}{ccc}\hfill \sum _{i=n-1}^{n}f\left(v_i\right)+f\left(v_n{v}_{n-1}\right)+f\left(v_{n-1}{u}_1\right)+f\left(v_n{u}_{n-2}\right)& =& \\ \hfill \sum _{i=n-1}^{n}f\left(w_i\right)+f\left(w_n{w}_{n-1}\right)+f\left(w_{n-1}{u}_1\right)+f\left(w_n{u}_{n-2}\right).\end{array}$$

Thus $f\left(v_{n-1}\right)+f\left(v_{n-1}{u}_1\right)=f\left(w_{n-1}\right)+f\left(w_{n-1}{u}_1\right)$ and $f\left(v_n\right)+f\left(v_n{u}_{n-2}\right)=f\left(w_n\right)$$+f\left(w_n{u}_{n-2}\right)$. Hence, $f\left(v_{n-1}{v}_n\right)=f\left(w_{n-1}{w}_n\right)$, a contradiction. □

The converse of Theorem 13 is not true. Consider m copies of isomorphic cycles of order n, $m{C}_n$. It is clear that $m{C}_n$ admits $C_n$-covering and is H-free, for H isomorphic to the forbidden subgraphs in Theorem 13. However $m{C}_n$ is SEMT if and only if m and n are odd [21], and so $m{C}_n$, for even $m\ge 2$, is not $(K_2,C_n)$-sim-supermagic. Therefore, the two subgraphs in Theorem 13 are not the only forbidden subgraphs of $(K_2,C_n)$-sim-supermagic graphs.

Problem 3.

What are the other forbidden subgraphs of $(K_2,C_n)$-sim-(super)magic graphs?

In the following lemma, we state sufficient conditions for an (S)EMT graph to be a $(K_2,C_n)$-sim-(super)magic graph.

Lemma 6.

Let $k\ge 2$ and $n\ge 3$ be two positive integers. Let G be a graph order at least $n+1$ that admits $C_n$-covering. Let ${\left\{C_n^i\right\}}_{i=1}^k$ be the family of all subgraph of G isomorphic to $C_n$ and $\sum Y_i$ be the sum of all vertices labels in $C_n^i$, for each $i\in [1,k]$. If f is an (S)EMT labeling in G such that $\sum Y_i$ is constant, for every $i\in [1,k]$, then G is $(K_2,C_n)$-sim-(super)magic.

Proof. 

Let $m_f$ as the magic sum of the labeling. Let $i\ne j$ be two positive integers in $[1,k]$. Consider two arbitrary cycles $C_n^i$ and $C_n^j$ in ${\left\{C_n^i\right\}}_{i=1}^k$. Thus, $\sum Y_i=\sum Y_j$. Hence, we have that

$$\begin{array}{ccc}\hfill w\left(C_n^i\right)& =& \sum _{v\in V\left(C_n^i\right)}f\left(v\right)+\sum _{e\in E\left(C_n^i\right)}f\left(e\right)\hfill \\ & =& n{m}_f-\sum Y_i=n{m}_f-\sum Y_j\hfill \\ & =& \sum _{v\in V\left(C_n^j\right)}f\left(v\right)+\sum _{e\in E\left(C_n^j\right)}f\left(e\right)\hfill \\ & =& w\left(C_n^j\right).\hfill \end{array}$$

Hence, the sum of all edges and vertices labels associated to a subgraph of G isomorphic to $C_n$ is a constant. Therefore, G is a $C_n$-(super)magic for each $n\ge 3$. Since f is simultaneously an (S)EMT and $C_n$-(super)magic, G is $(K_2,C_n)$-sim-(super)magic. □

Consequently, by Lemma 6, we have the following corollary.

Corollary 11.

Let $m\ge 3$ be an odd integer. The disjoint copies of cycle on 3 vertices, $m{C}_3$, is $(K_2,C_3)$-sim-supermagic.

Proof. 

Recall an SEMT labeling of $m{C}_3$, for odd m, from [21]. We denote $V\left(m{C}_3\right)=\left\{u_{i,j}\right|i\in [1,m]$ and $j\in [1,3]\}$ and $E\left(m{C}_3\right)=\left\{u_{i,j}{u}_{i,j+1}\right|i\in [1,m]$ and $j\in [1,2]\}\cup \left\{u_{i,1}{u}_{i,3}\right|i\in [1,m]\}$ and define

$$\begin{array}{ccc}\hfill f\left(u_{i,j}\right)& =& \left\{\begin{array}{cc}i,\hfill & \mathrm{if}i\in [1,m]\mathrm{and}j=1;\hfill \\ 2m+\frac{2i+1+m}{2},\hfill & \mathrm{if}i\in [1,\frac{m-1}{2}]\mathrm{and}j=2;\hfill \\ 2m+\frac{2i+1-m}{2},\hfill & \mathrm{if}i\in [\frac{m+1}{2},m]\mathrm{and}j=2;\hfill \\ 2m+1-2i,\hfill & \mathrm{if}i\in [1,\frac{m-1}{2}]\mathrm{and}j=3;\hfill \\ 3m+1-2i,\hfill & \mathrm{if}i\in [\frac{m+1}{2},m]\mathrm{and}j=3.\hfill \end{array}\right.\hfill \end{array}$$

Let $C_3^i$ be a subgraph of $m{C}_3$ isomorphic to $C_3$ and $\sum Y_i$ be the sum of all vertices labels in $C_3^i$. Hence, for $1\le i\le \frac{m-1}{2}$, we have

$$\begin{array}{ccc}\hfill \sum Y_i& =& i+2m+\frac{2i+1+m}{2}+2m+1-2i\hfill \\ & =& i+2m+i+\frac{1+m}{2}+2m+1-2i\hfill \\ & =& \frac{3}{2}(3m+1)\hfill \end{array}$$

and, for $\frac{m+1}{2}\le i\le m$, we have

$$\begin{array}{ccc}\hfill \sum Y_i& =& i+2m+\frac{2i+1-m}{2}+3m+1-2i\hfill \\ & =& i+2m+i+\frac{1-m}{2}+3m+1-2i\hfill \\ & =& \frac{3}{2}(3m+1).\hfill \end{array}$$

Therefore, $\sum Y_i$ is constant for $1\le i\le m$. By Lemma 6, $m{C}_3$ is $(K_2,C_3)$-sim-supermagic. □

6. Open Problems

We conclude by listing open problems from the previous sections that could be interesting for further investigation.

• What are the other forbidden subgraphs of $(K_2,P_n)$-sim-(super)magic graph?
• What are the other forbidden subgraphs of $(K_2,C_n)$-sim-(super)magic graphs?
• Characterize $(K_2,P_n)$-sim-(super)magic graphs for any $n\ge 5$.