Dynamic Response Analysis of a Multiple Square Loops-String Dome under Seismic Excitation

Abstract

The interaction between multiple loops and string cables complicates the dynamic response of triple square loops-string dome structures under seismic excitation. The internal connection between the multiple square loops-string cables and the grid beams was studies to provide a favorable reference for an anti-seismic structure. With a finite element model of the Fuzhou Strait Olympic Sports Center Gymnasium, established by SAP2000 software, the structural dynamic characteristic parameters were obtained first, and then this study adopted a time-history analysis method to study the internal force response of the cables and the roof grid beams of the multiple square loops-string dome (MSLSD) under three types of seismic array excitation. The influence of two factors, namely the seismic pulse and the near and far seismic fields, on the dynamic response of this structure was analyzed by three groups of different types of seismic excitation (PNF, NNF, PFF). As shown from the results, the first three-order vibration modes were torsional deformations caused by cables, the last five were mainly the overall roof plane vibration and antisymmetric vibration. Under the excitation of the three seismic arrays, the internal force responses of stay cables, square cables in the outer ring and the string cables were largest, while the maximum internal force response of the struts changed with the direction of seismic excitation. The largest internal force response of the roof grid beams occurred in local components such as BX3, BX7 and BY7, and the largest deformation of the beam nodes occurred in JX7, JX12 and JY4. In general, the seismic pulse and the near seismic field weakened the internal force response of the struts and cables but increased the internal force response and deformation of the dome beams, while the near and far seismic fields outweighed the seismic pulse. All the above provides an important reference for structural monitoring and seismic resistance.

1. Introduction

With the recent continuous development of long-span spatial structures, the string dome, as a roof structure boasting light weight, high rigidity, good stability and strong spanning capability, has been widely adopted in large gymnasiums, opera houses and other public buildings such as the Tianbao Center Lobby, the 2008 Olympic Badminton Stadium, and the Jinan Olympic Sports Center Gymnasium [1,2]. The new square loops-string (SL-S) structure is one with pre-tensioned square ring cables and stay cables, in which struts bear axial compression and form a reliable support to arch up the lattice cylindrical shell. Compared with the traditional large-scale string dome structure, the square loops-string structure is simpler in lines, clearer in force transmission paths and better in force-bearing and antideformation performance of the roof grid beam structure. Such a structure has been integrated into the canopies of Shenzhen North Railway Station and the Fuzhou Strait Olympic Sports Center Gymnasium [3,4].

In addition to exhibition competitions and large-scale mass activities, the dome-structure gymnasium can also serve as an earthquake refuge. Collapse of buildings during earthquakes causes serious casualties and economic losses. Much research has been carried out on recent years carried out by Chinese and foreign experts on the mechanical properties and stability of the string dome structure, such as seismic response and anti-seismic analysis [5,6,7,8], buckling and dynamic response under friction [9], model optimization design based on artificial neural networks [10], elastoplastic dynamic response [11], structural optimization algorithm and design [12,13,14], long-span discontinuous mechanical properties [15], initial geometric defect analysis [16], cable tension estimation [17], static and the dynamic analysis by finite element method [18,19], and thrust line analysis of masonry domes [20]. Gong, S.Y. [21] summarized the research on shape selection, statics and stability, dynamic and seismic resistance, prestress and optimization of the string dome. Li, X.Y. [22] used a simplified soil model through a modified SR method to analyze the dynamic characteristics and seismic response of a string dome structure under soil-structure interaction (SSI). Jiang, Z.R. [23] studied the nonlinear dynamic buckling of a long-span elliptic paraboloid string dome by introducing such factors as geometric nonlinearity, initial geometric defects, material elastoplasticity, and half-span live load distribution. Ruggieri, S. [24,25] developed a new numerical practical procedure to investigate the evaluation of floor deformability in the performance of a simple linear analysis on 3D numerical models by removing the rigid floor hypothesis and adopting a simple floor model, and defined a new approach for predicting the fundamental period of vibration for reinforced concrete buildings through regression analysis procedures of 40 new buildings using a numerical model with elastic dynamic parameters.

However, most of the current seismic response analyses on string structures are limited to the traditional string dome structure, without enough research on the dynamic characteristics of the latest string dome structure, i.e., the Multiple Square Loops-String (MSL-S) structure. Thus, a project adopting the MSL-S dome structure with the Fuzhou Strait Olympic Sports Center Gymnasium as the object of study, we used the time history method to analyze the internal force of cables and grid beams and the displacement response of grid beams under seismic excitation to provide a favorable reference for antiseismic responses of the MSL-S. The influence of two factors, namely, the near and far seismic fields and the seismic pulse, on the dynamic response of this structure was analyzed.

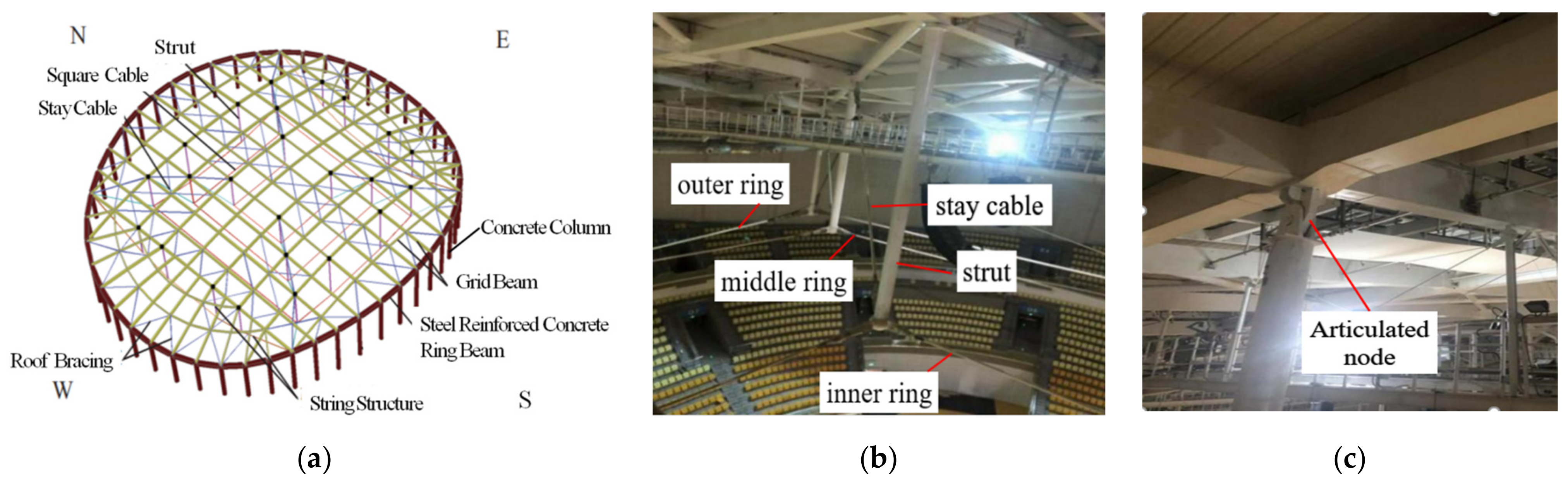
2. Project Overview

The Fuzhou Strait Olympic Sports Center Gymnasium covers about 42,000 m². The roof has an elliptical MSL-S structure with a span of 116 m × 97 m and the roof structure is mainly composed of grid frame beams, triple square loops and the surrounding concrete columns, in which the frame beams include outer steel concrete ring beams, grid steel beams and the roof support, while the string structure consists of struts, stay cables, square ring cables and string beams. The dome is symmetrical in the east-west direction but asymmetrical in the north-south direction, with the north top higher than the south. The model structure is shown in Figure 1a. The grid beams are made from rectangular steel and the struts have circular steel pipes. The grid beams are rigidly connected with reinforced bases and the struts are articulated with cables and roof grid beams, the nodes of which are shown in Figure 1b,c.

3. Numerical Simulation and Model Validation

3.1. Modelling Parameters

3.1.1. Geometric Dimension

The elevation of the dome reaches 39.7 m, the span of the square loop-string structure is 106.5 m, the span of the main truss of grid beams peaks at 97.5 m with the distance between main trusses ranging from 6.3 m to 7.6 m and the distance between secondary trusses is 9.5 m. The four sides of the dome have a relatively large load area with long-span horizontal cables. To increase the vertical rigidity of the structure, two middle struts (SC13~SC16) are added on the north and south sides of the outer square ring cables and independent string beams (SH13~SH14) are erected both on the east and west sides, the maximum span of which is 75.9 m. The struts and cables of the MSL-S structure system are shown in Figure 2.

3.1.2. Material Characteristics

The grid beams, struts and additional roof support of the MSL-S roof structure are all made of the Q345 steel with an elasticity modulus of 2.06 × 10⁵ N/mm² and a volume density of 7.85 × 10³ kg/m³. While the cables have PE finished products composed of Φ5 or Φ7 high-strength steel wires with an elasticity modulus of 1.95 × 10⁵ N/mm² and a tensile strength of 1.67 × 10³ MPa.

3.1.3. Finite Element Model Creation

General finite element software SAP2000 V19 was used to establish the three-dimensional finite element model of the string dome structure of the gymnasium. The roof grid beams used the steel box-sections simulated by the Frame unit, the prestressed cables were simulated by the Cable unit and the struts were simulated by the Link unit. The struts nodes at both ends were simulated as articulated to ensure the smooth rotation during the prestressing process. The berm under the roof, an auxiliary structure of grid structure system, was applied to the corresponding struts in the form of a line load (1.5 kN/m) after simplification; Given the additional load of the cable connection device, PE pipes and fillers, the weight of the cables was multiplied by a coefficient of 1.05. With the ring beams outside the grid beams connected with the concrete column nodes, the degrees of freedom in six directions were coupled, and the bottom of concrete column was a fixed end constraint. The three-dimensional finite element model is shown in Figure 1a.

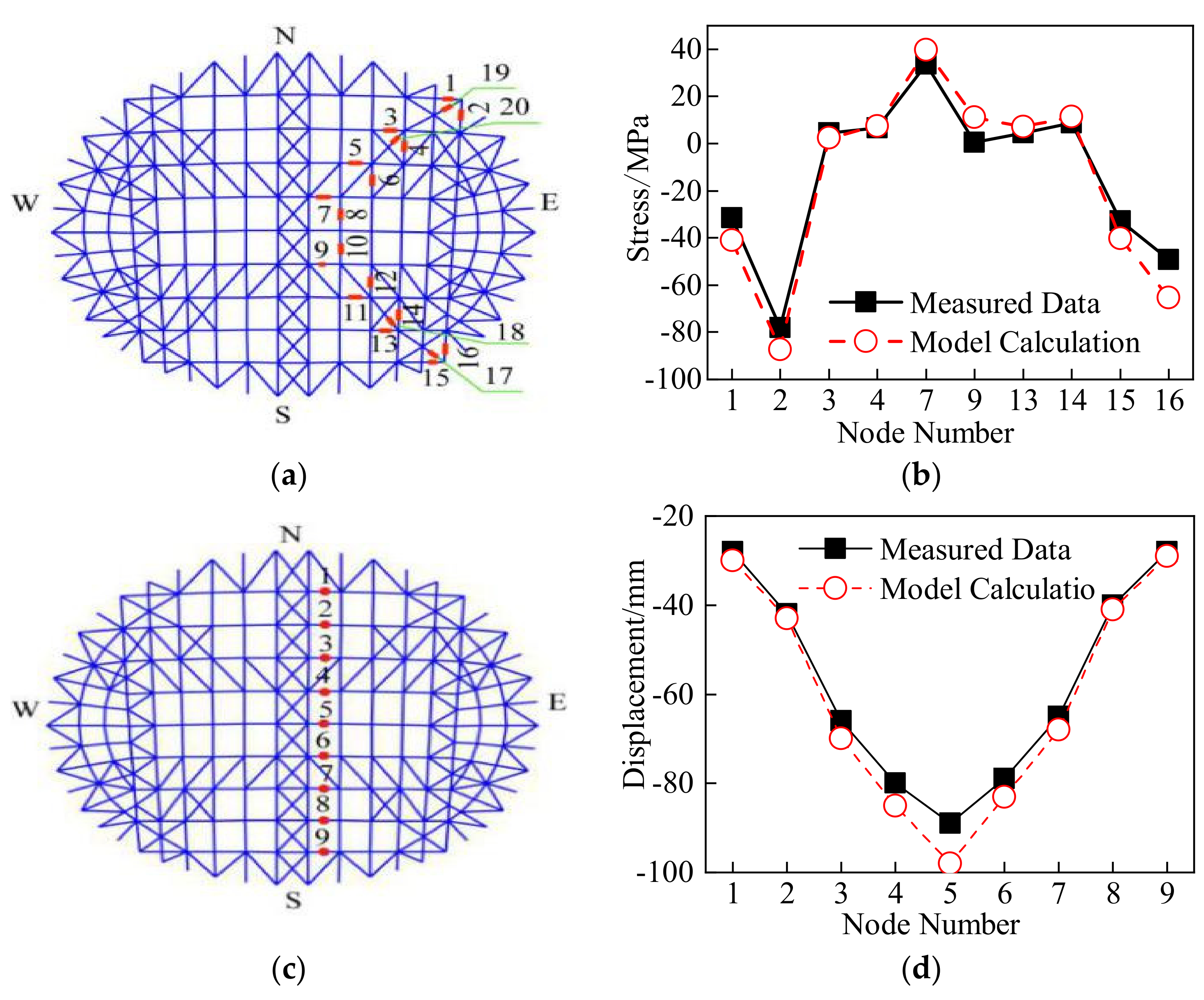
3.2. Model Validation

To verify the accuracy and reliability of the finite element numerical model, the stress monitoring data and displacement monitoring data of the key roof nodes during the construction process were determined [26]. Stress monitoring distributions of roof grid beams was conducted at 16 different places with strain gauges installed on both the upper and lower surfaces of the beam spans, as shown in Figure 3a; while deformation monitoring was conducted in nine places with the measuring points set in the middle of the grid beams, as shown in Figure 3c.

A comparison of the results between the measured data and the model calculation of grid beam stress and node vertical displacement are, respectively, displayed in Figure 3b,d, from which we can see that the overall difference between the two data sets is small. Among them, No. 16 beam is the one with the biggest stress error, which is 16.1 MPa between the actual measurement and theoretical calculation, and No. 5 beam has the biggest displacement error, which is 10.1 mm. Given the good agreement between the simulation and experiment results in each construction stage with acceptable errors, the numerical model was used as the simulation analysis model.

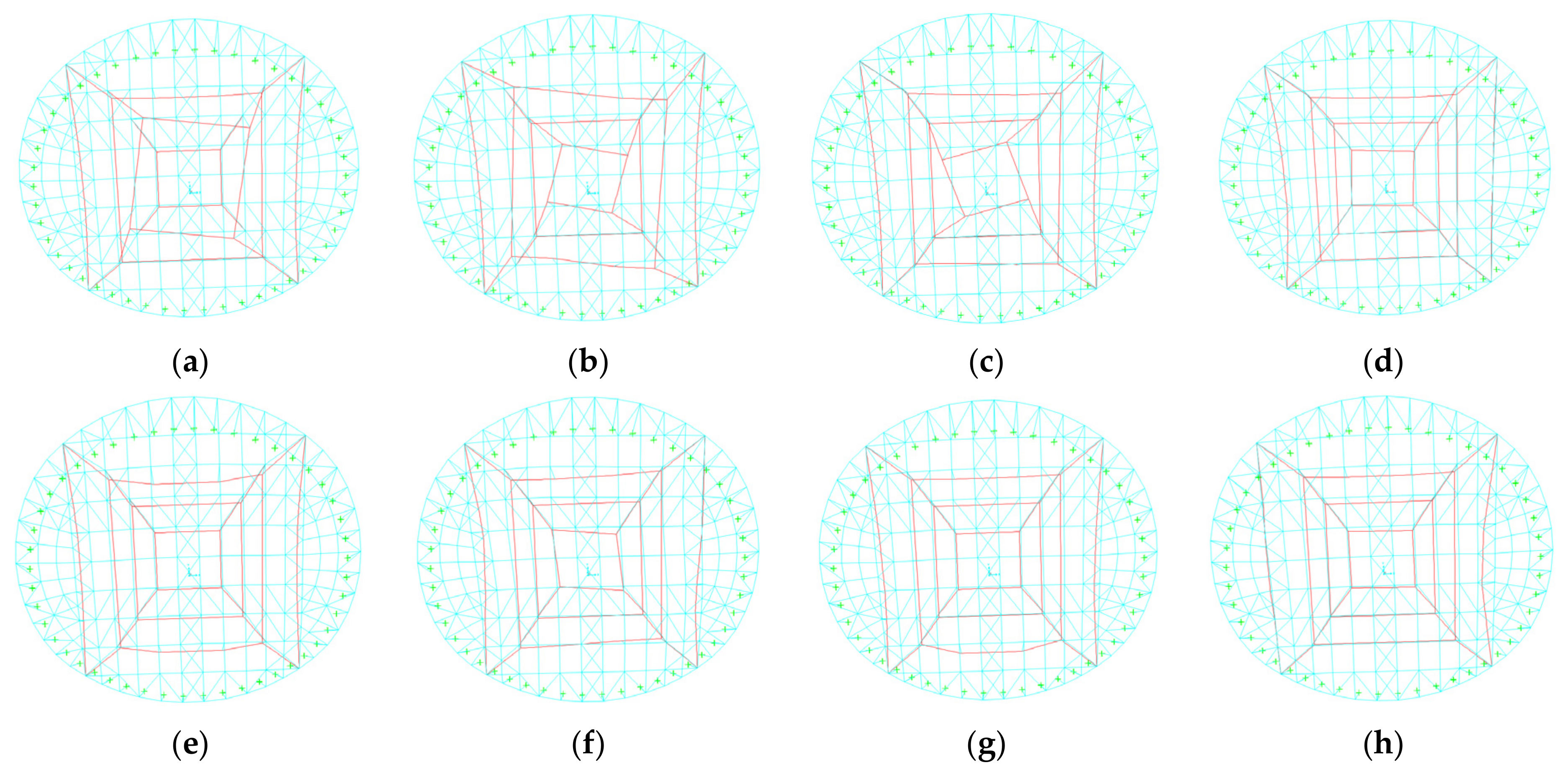
3.3. Structural Dynamic Characteristics

The first eight orders of vibration modes simulated and analyzed by the finite element model are shown in Figure 4. The natural frequency and participating mass ratios in the main directions are shown in

Table 1. Structural natural frequency.

Order	1	2	3	4	5	6	7	8
Natural Frequency (Hz)	0.76	0.86	0.86	0.91	1.13	1.17	1.28	1.29
Main Direction	RZ	RZ	RZ	UX	UY	UX	UY	UX
Partecipating Masses Ratio	1.342 × 10−3	7.96 × 10−3	5.452 × 10−4	0.07886	0.02809	0.09835	0.03773	0.63

. It can be seen from the model analysis that the first-order vibration mode demonstrates the torsion of the middle ring cable, the second one as the torsion of the inner and outer ring cables, the third as the torsion of the inner ring cable, the fourth as the antisymmetric vertical vibration of the whole roof along the short span, the fifth as the antisymmetric vertical vibration of the whole roof along the long span, the sixth as the symmetric vertical vibration of the whole roof along 45 degree, the seventh as the outer vibration of the south outer ring cables, and the eighth as the coupling of the translational motion and antisymmetric vibration of roof along the long-span direction. Therefore, the first three vibration modes are dominated by the torsional deformation of square ring cables while the last five ones are mainly the overall roof plane vibration and antisymmetric vibration.

4. Seismic Response Law of Roof Structure under Different Seismic Arrays

To facilitate the analysis of the seismic excitation response of the roof frame within the ring-cable structure of the gymnasium, the key structural components were numbered. As the central grid beams cover the longest span with the largest internal force value and displacement amount, they were selected as the research object. The numbers of grid beams and beam nodes are shown in Figure 5, where B represents the grid frame beam, J represents the node, X and Y, respectively, stand for the EW direction and SN direction. The numbers of struts and cables are shown in Figure 2.

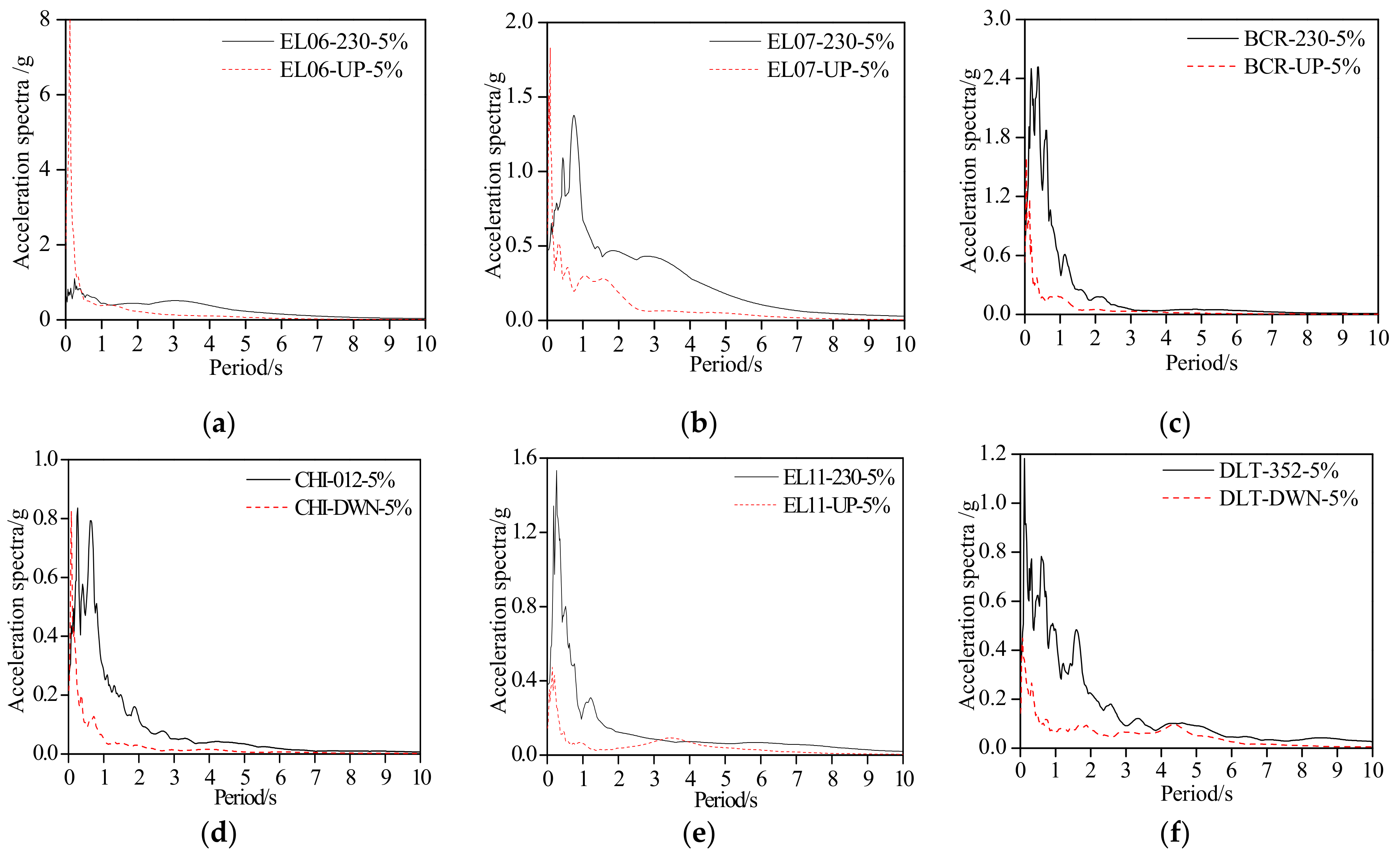
4.1. Seismic Arrays Input

The degree of seismic fortification intensity of the gymnasium is seven, and falls into the third seismic group. In light of the rules of seismic grouping, the Imperial Valley-06 far-field seismic wave files, DLT-352 and DLT-DWN, were collected from Pacific Earthquake Engineering Research Center (PEERC). The seismic acceleration curve and response spectrum curve are showed in Figure 6a–d. The horizontal seismic waves (X or Y direction) of DLT-352 were combined with the vertical seismic waves (Z direction) of DLT-DWN, and the seismic excitation effect partial coefficients, γ_Eh and γ_Ev, were, respectively, set as 1.3 and 0.5 under two components, and set as 1.0, 0.85 and 0.65 under three components [27]. The combination formulas are as follows.

No. 1 Seismic Array: K1 = 1.3 × X + 0.5 × Z,

(1)

No. 2 Seismic Array: K2 = 1.3 × Y + 0.5 × Z,

(2)

No. 3 Seismic Array: K3 = 1.0 × X + 0.85 × Y + 0.65 × Z,

(3)

To better analyze the response of the structure under seismic excitation, the peak ground acceleration (PGA) was adjusted to 0.22 g in consideration of the impact of earthquakes that rarely occur. Meanwhile, when analyzing the elastoplasticity of dome structure in the context of rarely occurring earthquakes, the damping ratio was set as 0.05 and the nonlinear time history analysis method based on “self-weight” was used to analyze the seismic response.

4.2. Dynamic Response under the Excitation of No. 1 Seismic Array

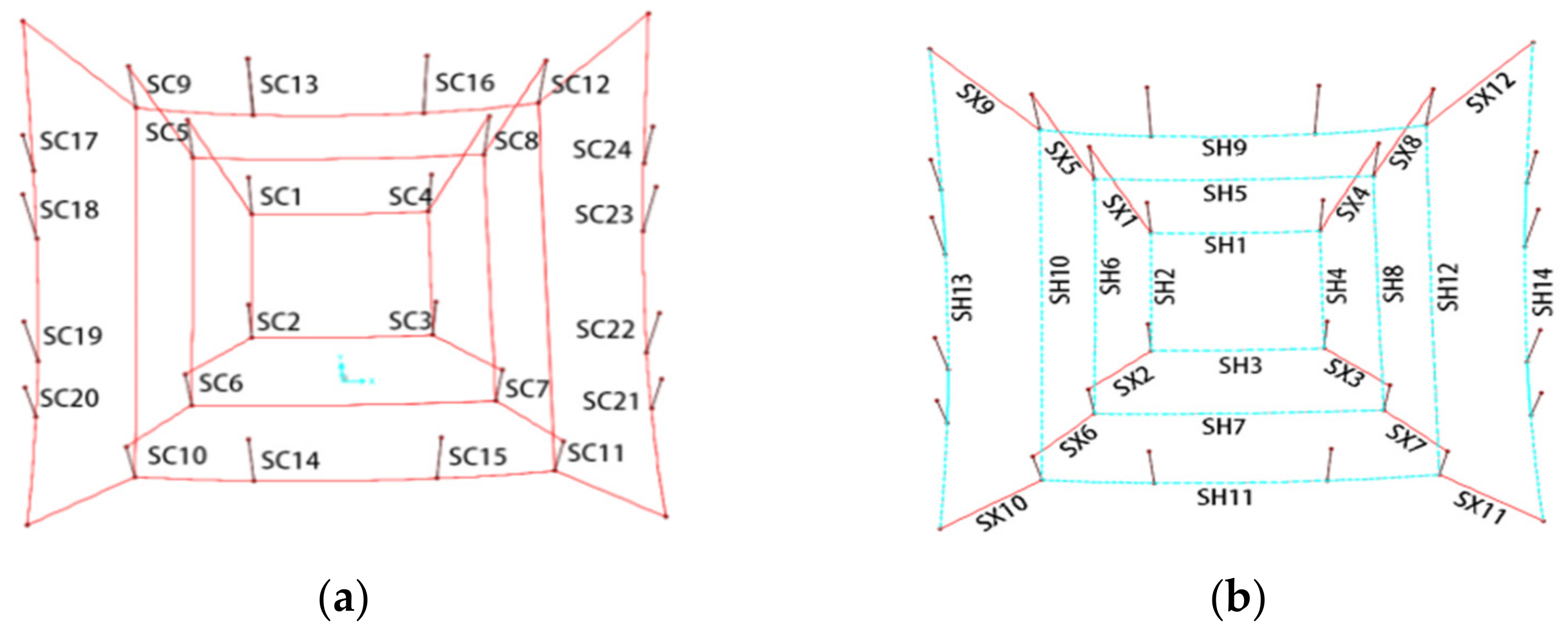
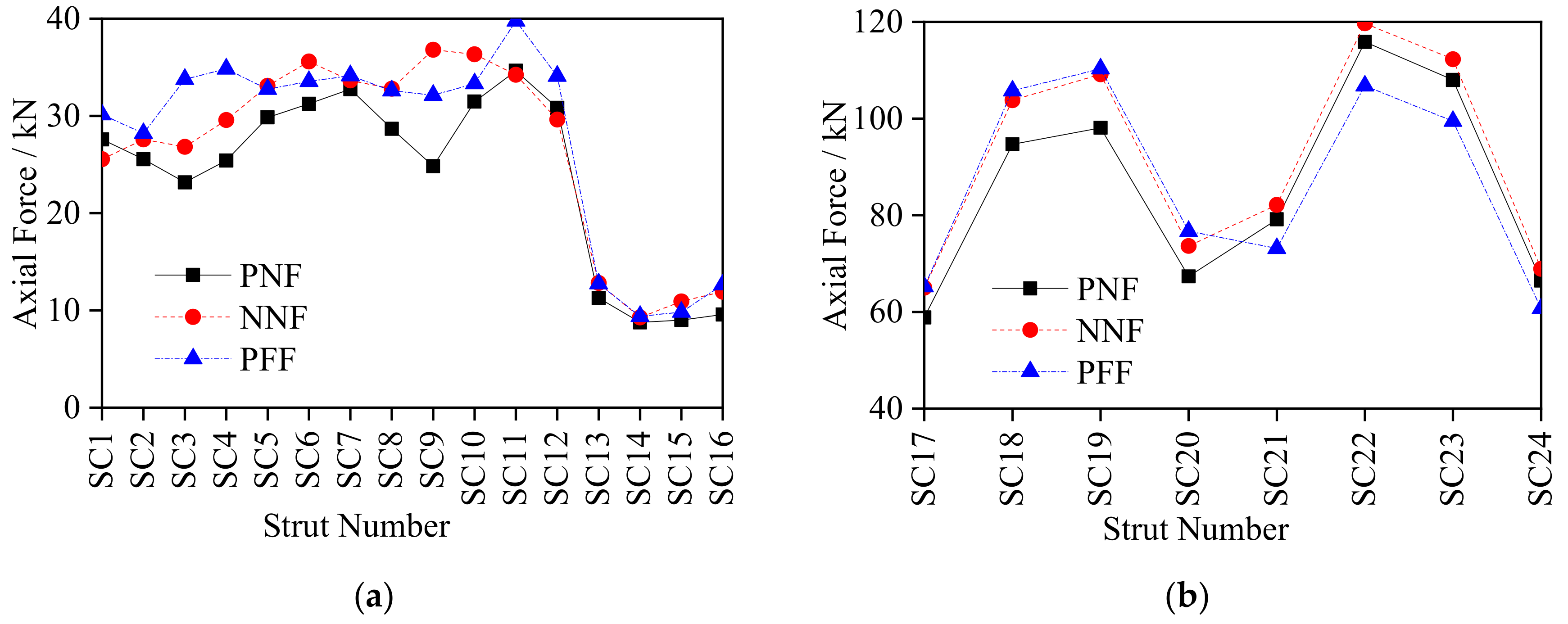
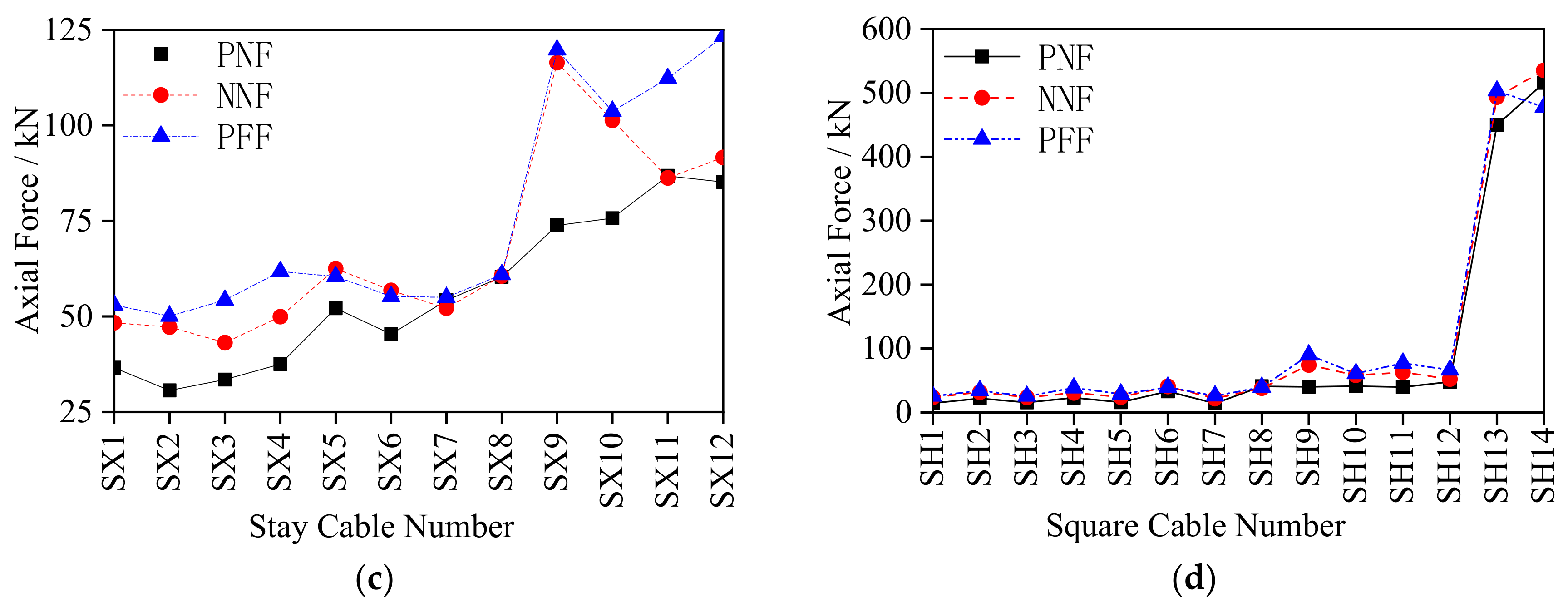
4.2.1. Analysis of the Internal Force Response of Roof Square Ring Cables

As the stay cables and square ring cables unite to mainly transfer tensions, and the struts units transfer compressions, the internal force response of cables and struts of the ring-cable structure under No. 1 seismic array excitation is shown in Figure 7, where the structural dynamics remain relatively small due to the equal altitudes at both ends of the EW (X) direction, as well as great rigidity. It can be seen from the figure that struts (SC1 to SC16) tend to be more average in force and smaller in internal force response with comparable values, and the smallest internal force response occurs in the additional struts (SC1 to SC16) at the north and south sides of the outer ring. The inner ring and middle ring stay cables (SX1 to SX8) and ring cables (SH1 to SH8) share a relatively small internal force response within 90 kN, while the outer ring stay cables (SX9 to SX12) and ring cables (SH9 to SH12) experience a significantly increased internal force response, almost double that of the inner ring and middle ring. String cables are long in span and unilaterally connected, and the cables (SH13 to SH14) and struts (SC17 to SC24) have the largest internal force response.

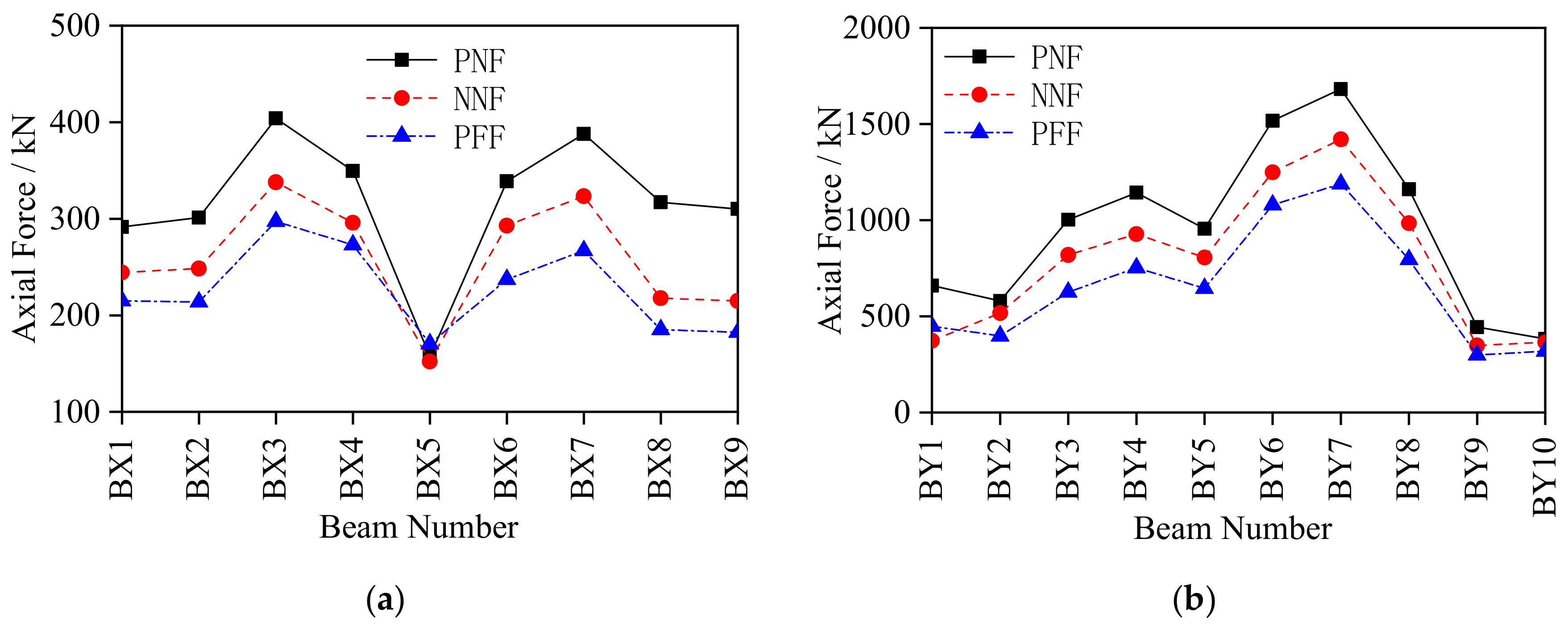
4.2.2. Analysis of the Internal Force Response of Roof Grid Beams

The internal force response of the grid beams under No. 1 seismic array excitation is shown in Figure 8. The ring-cable structural frame system is irregular, and the internal force of the roof frame (BX1 to BX9) in the EW direction is distributed axisymmetrically with the mid-span beam BX5, which has the smallest internal force response. The X-shaped steel pipes set in the SN direction in the mid-span grid beam strengthen the local roof stiffness. As there is a long span between BX3 and BX7, their internal force response is the largest. The internal force response of the roof grid beams (BY1 to BY10) are irregularly distributed and generally greater than that in the EW direction. As the input direction of combined seismic waves is perpendicular to the roof framing elements, a larger internal force response occurs in out-of-plane vibration, maximizing at BY7 about 1440 kN.

4.2.3. Analysis of the Roof Node Deformation

The vertical displacement of roof nodes moving along the positive direction of the Z axis is represented as positive displacement, and vice versa. It can be seen from Figure 9 that the displacement and deformation of the roof grid beam nodes (JX1 to JX18) in the EW direction are basically symmetrically distributed. While the maximal displacement is reached at nodes JX7 and JX12, the increased local stiffness at the middle span greatly decreases the displacement of JX9 and JX10. The vertical displacement of roof grid beam nodes (JY1 to JY11) in the SN direction is distributed asymmetrically, with the greatest displacement appearing at node JY7, which is about 45 mm. Comparing Figure 8a with Figure 8b, the difference between the node displacement and internal force response of the roof grid beams can be seen. The reason why the overall grid beam node displacement in the SN direction is smaller than that in the EW direction is that the long-span arch structure facilitates the antisymmetrical vibration mode under combined seismic excitation, leading to a large vertical displacement.

4.3. Dynamic Response under Excitation of No. 2 and No. 3 Seismic Arrays

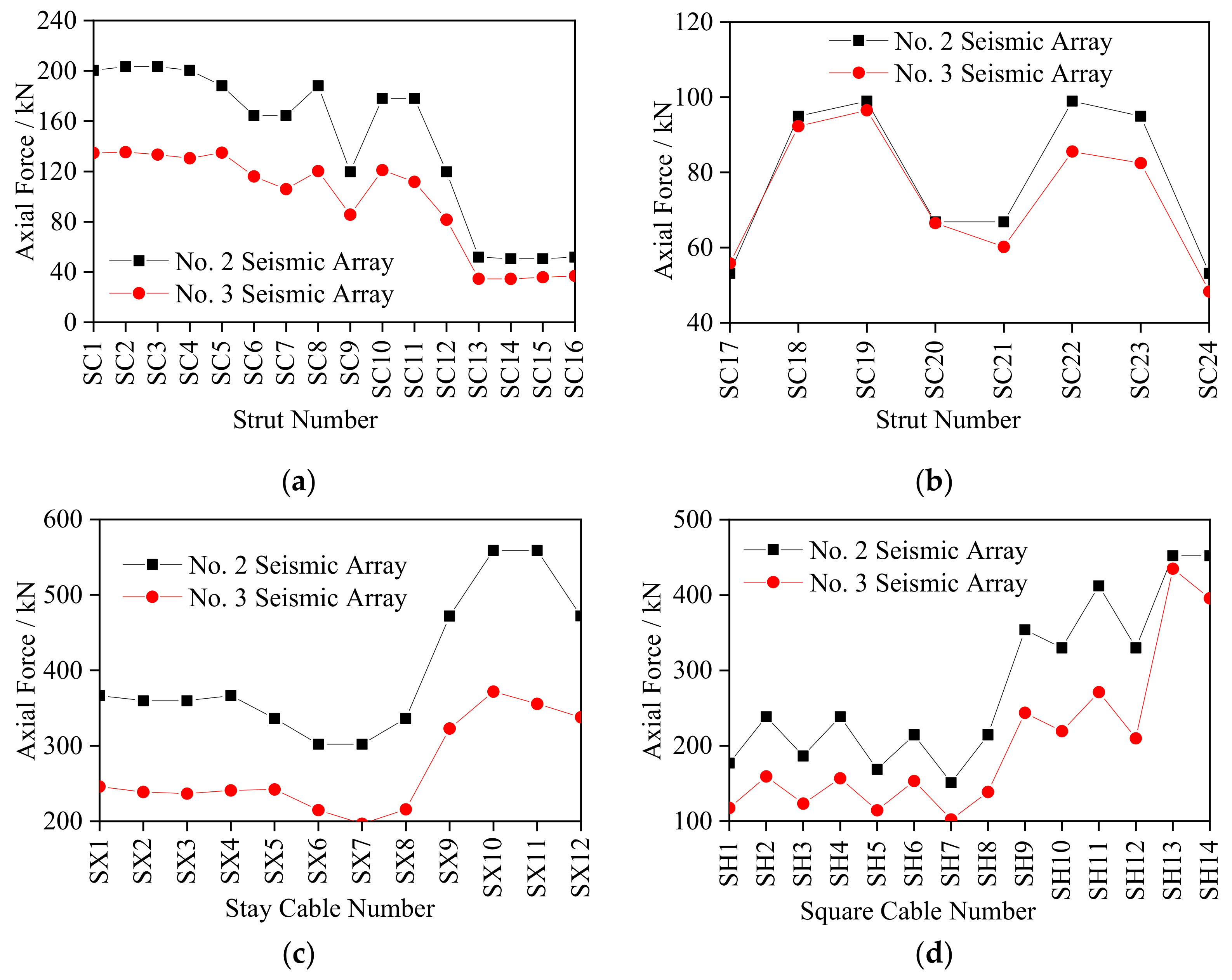
4.3.1. Analysis on the Internal Force Response of Roof Square Ring Cables

The structural stiffness of the gymnasium in the SN direction is relatively weak, and the structural dynamic response is larger and similar under the Excitation of No. 2 and No. 3 seismic arrays. Therefore, these two seismic arrays were considered simultaneously for better comparison and analysis.

As seen in Figure 10, the internal force response of the struts and the cables under No. 2 seismic array excitation was larger than that under the No. 3 seismic array and was about four to six times larger than that under the No. 1 seismic array. As an additional vertical acceleration is generated by the altitude difference between the north and south sides when the seismic waves move along the Y direction, the small rise span of the roof structure in this direction, coupled with less out-of-plane stiffness than in-plane stiffness, resulting in a greater structural dynamic response. In addition, the internal force response of the struts (SC1 to SC12) shows a downward trend from the inner ring to the outer ring. The additional struts (SC13 to SC16) of the outer ring have the least internal force response, followed by the struts in the string cables (SC17 to SC24), with an average value of about 80 kN. The internal force response of the middle ring stay cables (SX5 to SX8) and loop cables (SH5 to SH8) are slightly smaller than those of the inner ring. The outer ring stay cables (SX9 to SX12), loop cables and string cables (SH9 to SH14) have the largest internal force response.

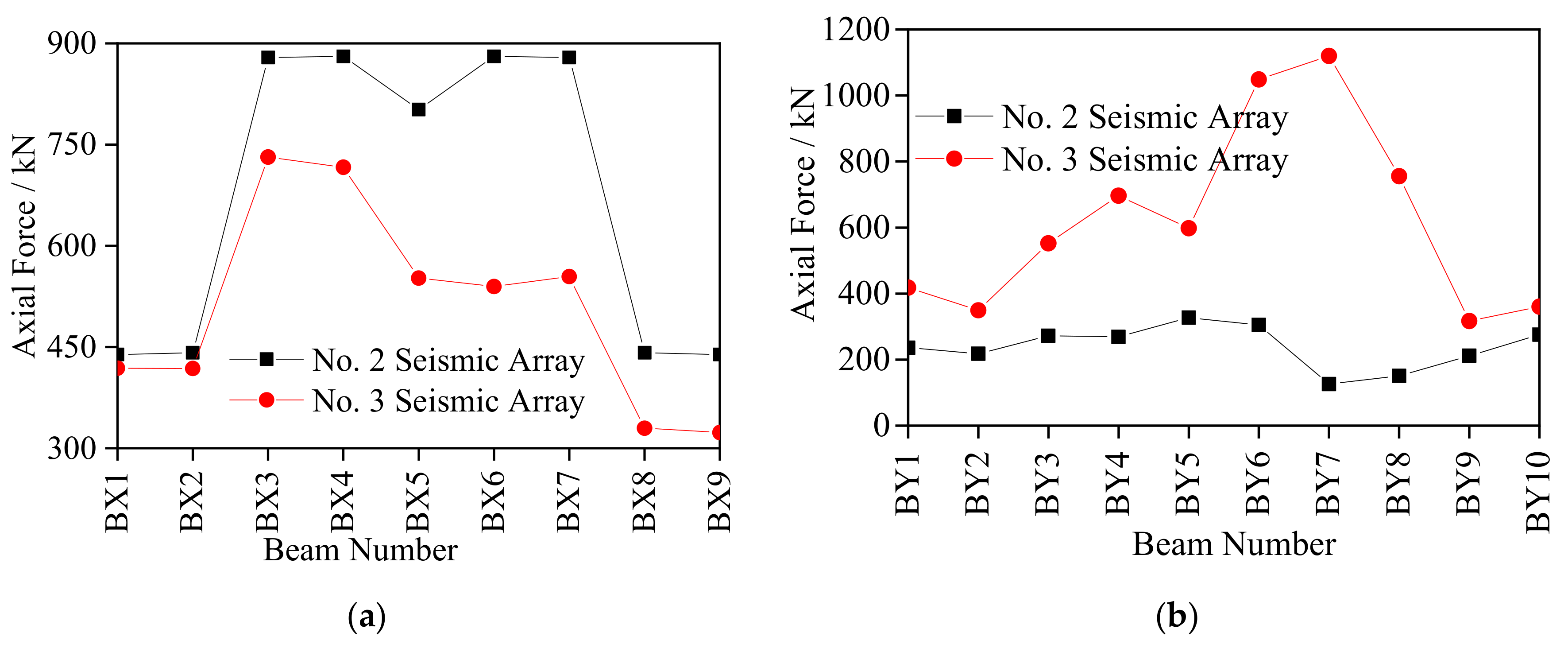
4.3.2. Analysis of the Internal Force Response of Roof Grid Beams

As seen in Figure 11, the internal force response of the roof grid beams (BX1 to BX9) in the EW direction under No. 2 seismic array is larger than that under No. 3 seismic array, which is contrary to that of the beams from BY1 to BY10. The internal force response of the roof grid beams from BX1 to BX9 under No. 2 seismic array is symmetrically distributed, in which the grid beams BX3 and BX7 have the largest internal force response that is obviously greater than that in the SN direction, thus serving as the main stress component of the structural system. The internal force response of the grid beam in the SN direction is irregularly distributed with an average value of about 200 kN under No. 2 seismic array, and with the largest value of 1120 kN under No. 3 seismic array.

Compared with No. 1 seismic array excitation, the internal force response of the roof grid beams in the EW direction under No. 2 seismic array excitation has a significant increase, the maximum value of which is about 2.5 times that of No. 1, while a substantial decrease occurs in the internal force response of the roof grid beams in the SN direction, the maximum value of which only accounts for about 25% of that in the EW direction. The reason is that when the seismic wave moves in the Y direction, the grid beams in the EW direction become perpendicular to the moving direction of combined seismic waves and thus generate out-of-plane vibration, greatly increasing the internal force of grid beams. As the grid beams in the SN direction are parallel to the moving direction of the seismic wave, they suffer less an effect.

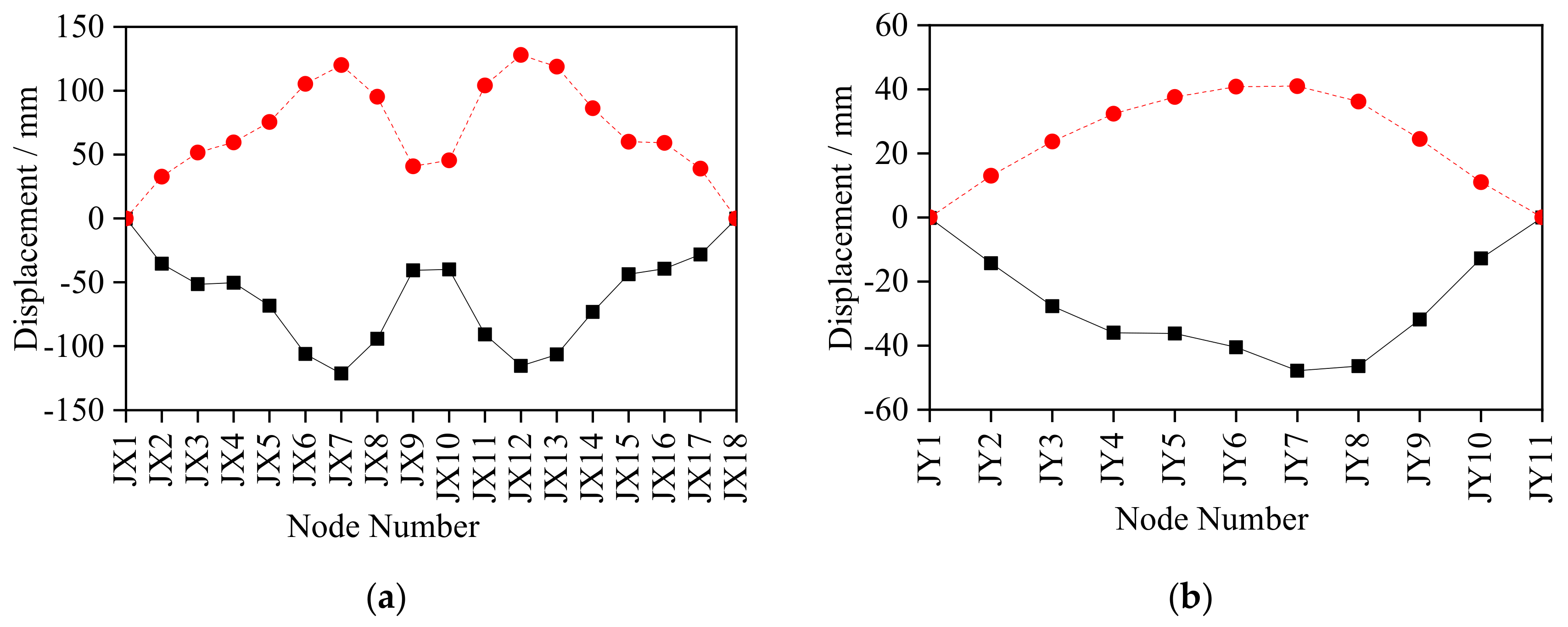
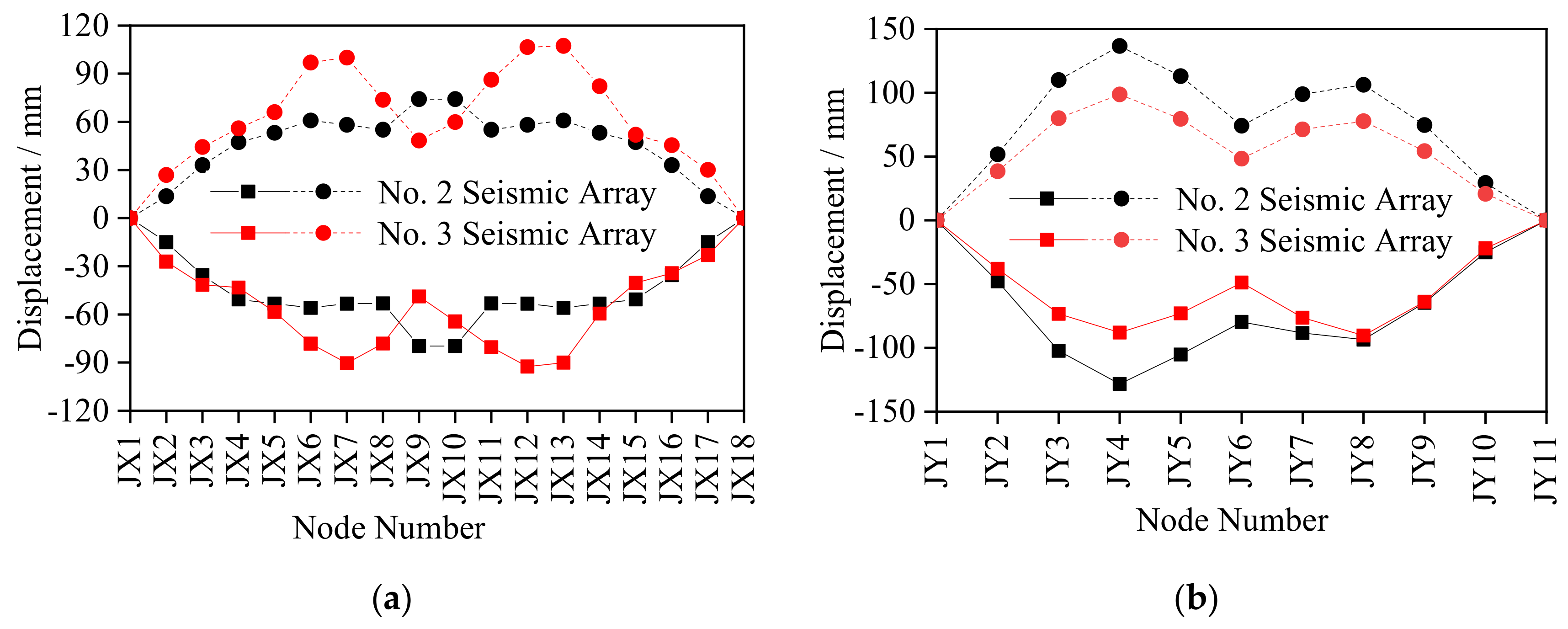
4.3.3. Analysis of the Roof Nodes Deformation

The displacement response of roof grid beam nodes under No. 2 and No. 3 seismic array excitation is displayed in Figure 12. The displacement response in the EW direction under No. 2 seismic array excitation is weaker than that under No. 3 seismic array excitation, in addition to nodes JX9 and JX10, while the displacement response in the SN direction is different. The displacement response is basically symmetrically arranged in the EW direction (JX1 to JX18), with the displacement maximizing at the midspan nodes of JX9 and JX10 under No. 2 seismic array, and at the nodes of JX7 and JX13 under No. 3 seismic array excitation. The displacement peak in the SN direction appears at JY4, and the displacement of the north nodes (JY2 to JY5) under seismic excitation exceeds that of the south nodes (JY7 to JY10), because of weak lateral rigidity caused by the longer steel pipe columns on the north side. Compared with No. 1 seismic array, the displacement of the roof grid beam nodes under No. 2 seismic array excitation experiences a decrease in the EW direction, while an increase is seen in the SN direction, with the maximum value almost doubled.

5. Effect Law of Different Types of Ground Motions on the Seismic Response of Roof Structures

Seismic action comes with strong randomness and uncertainty. Located at the junction of the Pacific plate and the Asia-Europe plate, Fuzhou has witnessed the occurrence of different types of earthquakes from time to time. Therefore, further research on the dynamic response of the gymnasium structure under different seismic fields and seismic impulses is of great significance for seismic monitoring and emergency response tasks related to the gymnasium.

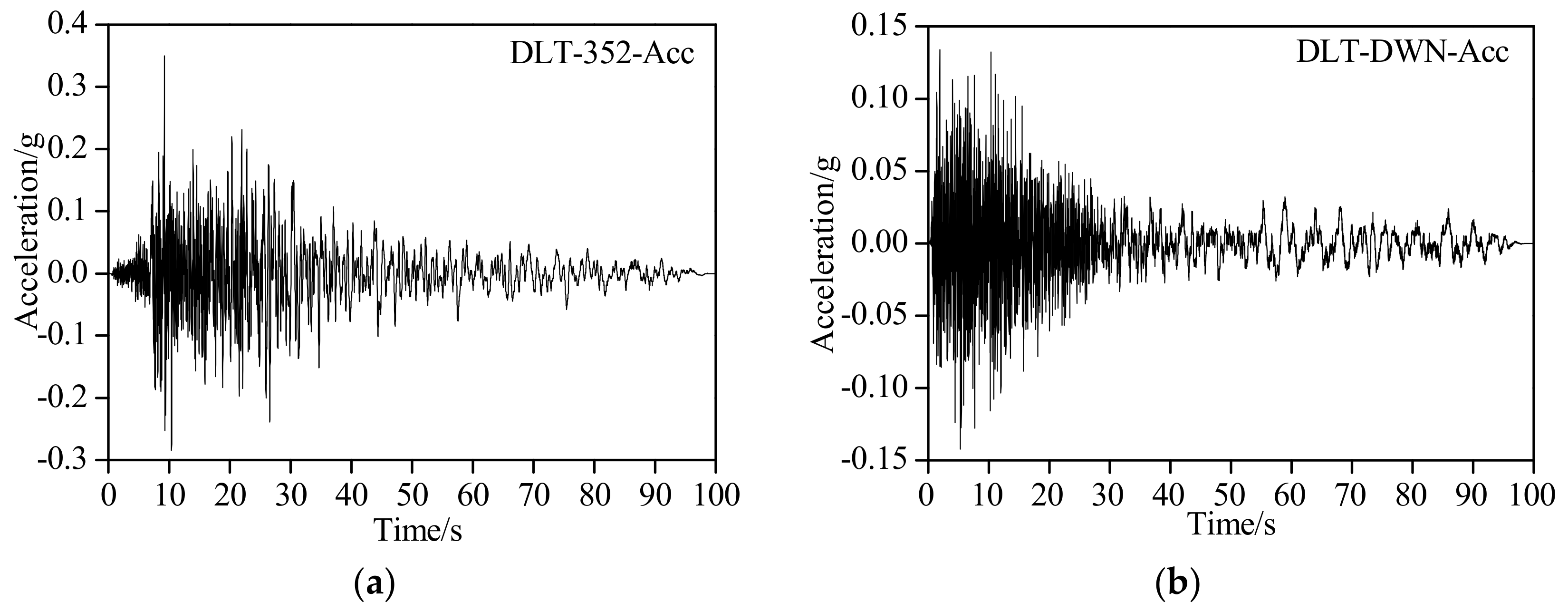
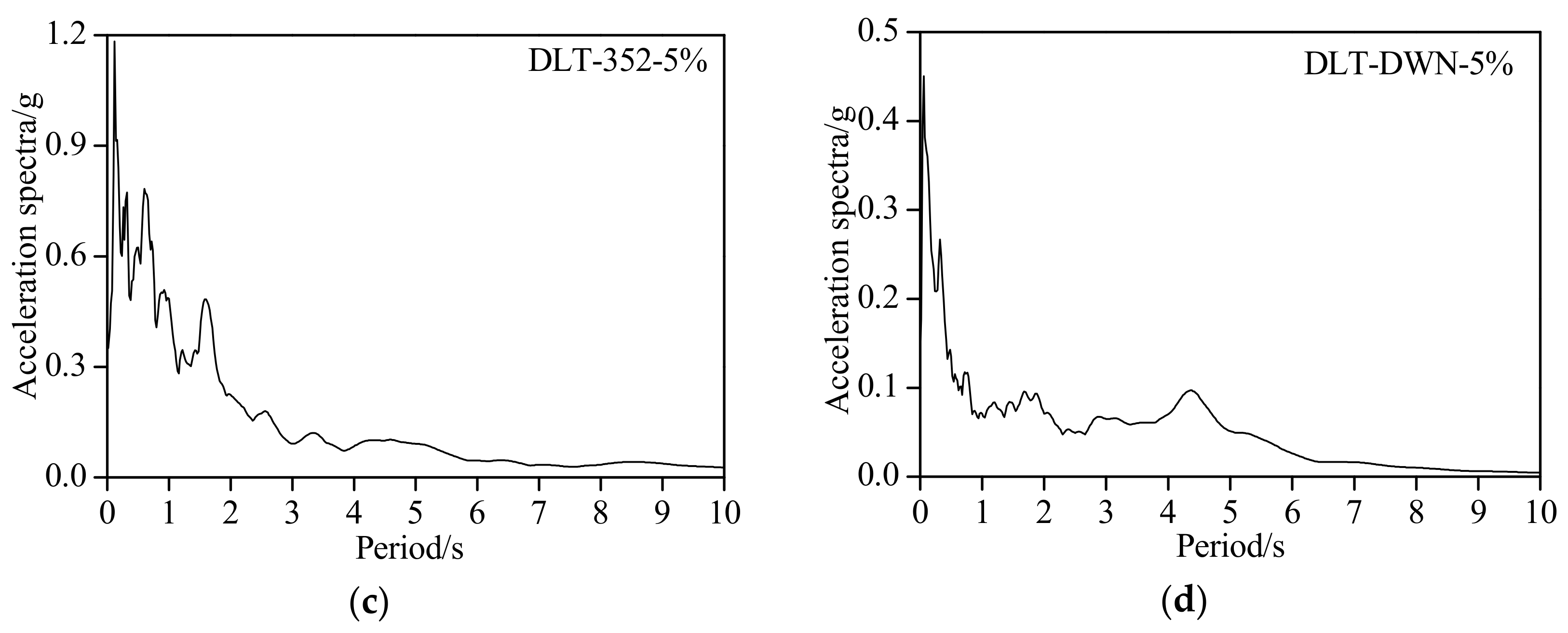
5.1. Input of Different Types of Seismic Waves

Imperial Valley-06 far-field seismic wave files from the PEERC were selected, including two groups of pulse near field(PNF) seismic waves, two groups of nonpulse near field (NNF) seismic waves and two groups of pulse far field(PFF) seismic waves. The spectrum curve of seismic wave acceleration response (ARS) is displayed in Figure 13. In consideration of rarely occurring earthquakes, the PGA was adjusted to 0.22 g and the horizontal direction (X-direction) and vertical direction (Z-direction) of the six sets of seismic waves were chosen as the earthquake inputs according to the partial coefficients. The seismic parameter information is detailed in

Table 2. Table of Seismic Load Cases.

ID	Type	Load Case	Seismic Wave Measurement	PGA (g)	Partial Factor (Direction)	Input Proportionality Factor
F1	Pulse Near Field (PNF)	EL06	EL06-230	0.449	1.3(Ux)	6242
			EL06-UP	1.895	0.5(Uz)	569
F2		EL07	EL07-230	0.469	1.3(Ux)	5976
			EL07-UP	0.578	0.5(Uz)	1865
F3	Nonpulse Near Field (NNF)	BCR	BCR-230	0.777	1.3(Ux)	3607
			BCR-UP	0.532	0.5(Uz)	2026
F4		CHI	CHI-012	0.270	1.3(Ux)	10381
			CHI-DWN	0.216	0.5(Uz)	4991
F5	Pulse Far Field (PFF)	EL11	EL11-230	0.379	1.3(Ux)	7395
			EL11-UP	0.144	0.5(Uz)	7486
F6		DLT	DLT-352	0.350	1.3(Ux)	8008
			DLT-DWN	0.142	0.5(Uz)	7592

, where the nonlinear time history analysis method based on “self-weight” is used. The damping ratio was set as 0.05 and the average value of the response under various types of seismic array conditions was selected as the structural dynamic response.

5.2. Analysis of the Internal Force Response of Roof Square Ring Cables

The internal force responses of the structural components of the multiple square ring cables under the excitation of the three types of seismic waves are shown in Figure 14. It can be seen from Figure 14a,b that the internal force response law of the struts (SC1 to SC24) remains basically the same with comparable values. Except for some struts (such as SC1, SC11, SC21, etc.), the internal force response under the excitation of the PNF combined seismic wave is the smallest, indicating that, in general, seismic impulses weaken the internal force response of the struts, while the near and far seismic fields equip the struts with greater internal force response.

The internal force response of stay cables and ring cables are shown in Figure 14c,d. In general, the internal force response under the PFF combined seismic wave is the biggest, while that under the PNF combined seismic wave is the smallest. The outer ring stay cables (SX9 to SX12) and the ring cables (SH9 to SH14) undergo the largest increase in the internal force response under the NNF and PFF seismic excitation, and the smallest under the PFF seismic excitation. SH13, under the PFF seismic excitation, has the largest internal force response with an axial force value of 503 kN, while SH14, under the NNF seismic excitation, has the largest internal force response with an axial force value of 535 kN and an increase of 0.203. That proves that the seismic impulse fails to cause larger internal force responses of stay cables and ring cables. Instead, it weakens their internal force response. Other than SH14, the seismic excitation in the far field generates a greater internal force response than the near field.

5.3. Analysis of the Internal Force Response of Roof Grid Beams

Figure 15 shows the internal force response of the roof grid beams under the three types of seismic excitation. It can be seen that the change law of the structure system under different seismic excitation remains basically the same. The PNF seismic array has the biggest excitation, followed by NNF and then PFF, which indicates that the seismic impulse generates a larger structural dynamic response to the roof grid frame beams, the near seismic field produces a greater internal force response than that of the far seismic field under the same impulse, and the influence of the near and far seismic fields exceed that of the impulse. In addition, as the frame beam BX5 of the roof vault is rigid enough and the axial forces under different seismic conditions are equivalent, with the smallest value, the aforementioned two factors exert little effect on this cross-grid beam.

5.4. Analysis of the Roof Nodes Deformation

The vertical displacement response of the roof grid beam nodes under three types of seismic excitation is shown in Figure 16, in which the overall distribution law is consistent with that of the grid beam internal force response. PNF combined seismic excitation has the largest vertical displacement, followed by NNF and then PFF. In addition, the positive deformation of nodes JX11–JX17 and the negative deformation of JX2–JX8 are distributed alternately under the excitation of NNF and PFF, with little difference. This indicates that the seismic impulse excitation further increases the displacement response of the roof grid beam nodes, and the seismic excitation of the near field produces a greater nodal displacement response than the far field. Overall, the near field factor exceeds the impulse factor.

6. Conclusions and Future Plans

With the establishment of a finite element numerical model of the MSL-S roof structure of the Fuzhou Strait Olympic Sports Center Gymnasium, this study analyzed the dynamic characteristics of string structures. The structural dynamic response under combined seismic excitation was studied through the nonlinear time history analysis method based on “self-weight” and the influence of different seismic impulses and near and far seismic fields on the dynamic response of the structure was studied. The conclusions are as follows.

• The natural frequency of the first eight-order vibration modes gradually increased from 0.762 to 1.292, with the main vibration mode being the torsional deformation caused by the cables, while the last five mainly related to the overall roof plane vibration and antisymmetric vibration. Therefore, attention must be paid to the cable vibration of the structure.
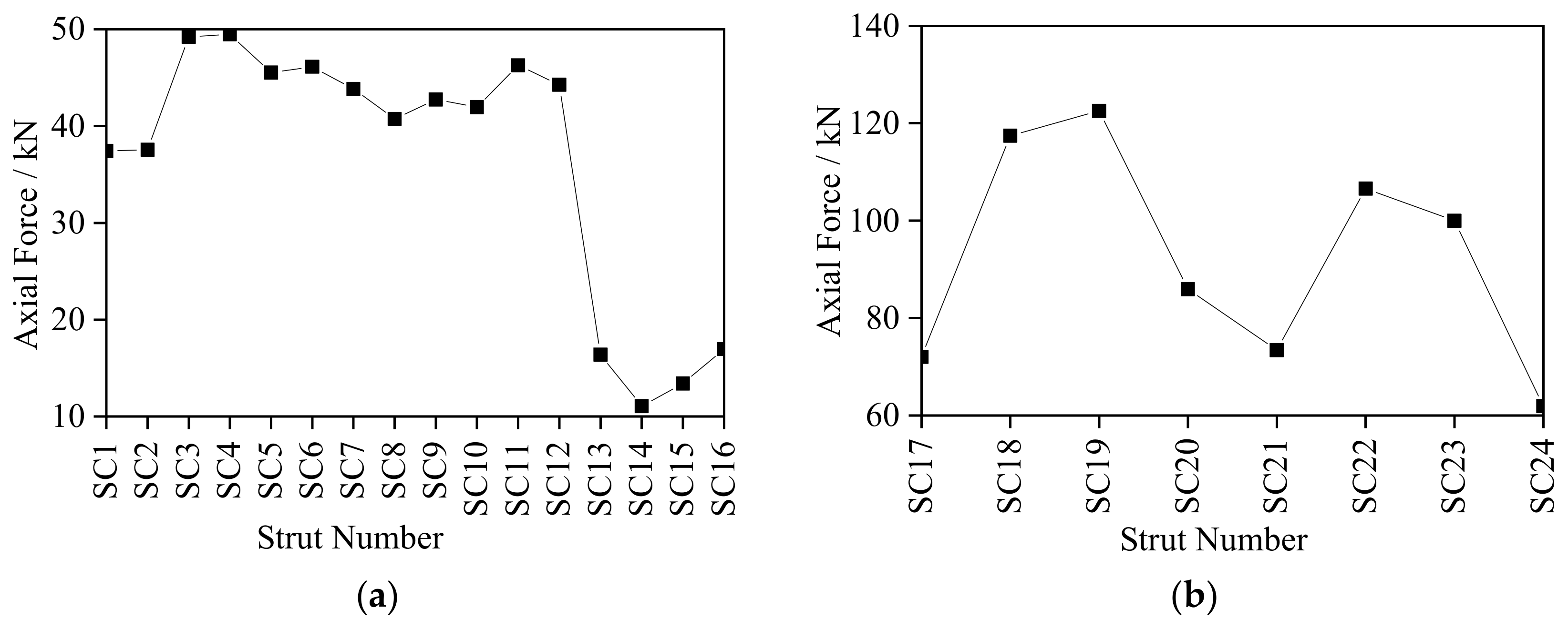
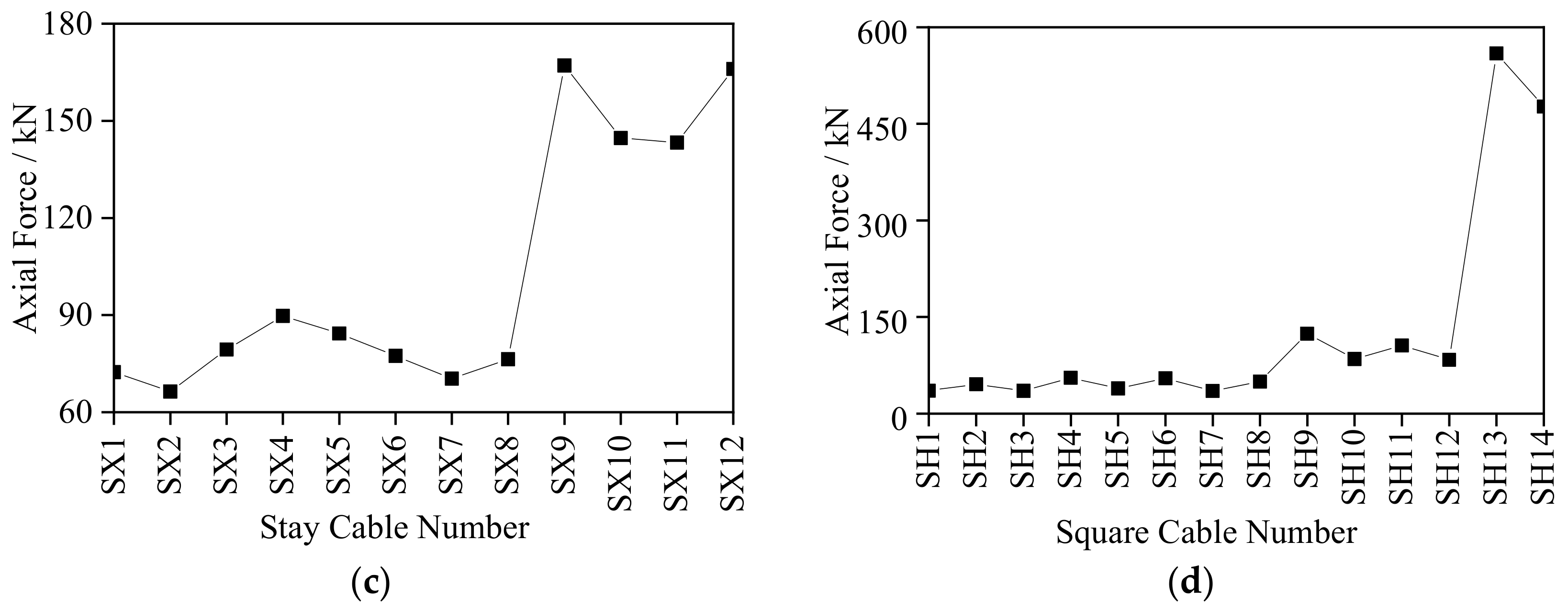
• Under excitation of the No. 1 seismic array, the internal force responses of structural struts, stay cables and ring cables were relatively small. The internal force of the struts of each ring remained equivalent within 50 kN, and weaker than that of the string cables between 60 kN to 125 kN. The largest internal force response of the stay cables was in outer ring between 140 kN to 170 kN, and the internal force of the string cables was the largest between 450 kN to 600 kN. The internal force response of the roof grid beam was symmetrically arranged in the EW direction with the largest internal force response occurring in BX3 and BX7 (about 350 kN). The response in the SN direction was generally larger, among which BY7 had the largest response of 1441.31 kN. The vertical displacement of the grid beam in the EW direction exceeded that in the SN direction. Therefore, emphasis must be laid on monitoring the stress and deformation of the local components of BX3, BX7 and BY7 and the internal force of the string cables.
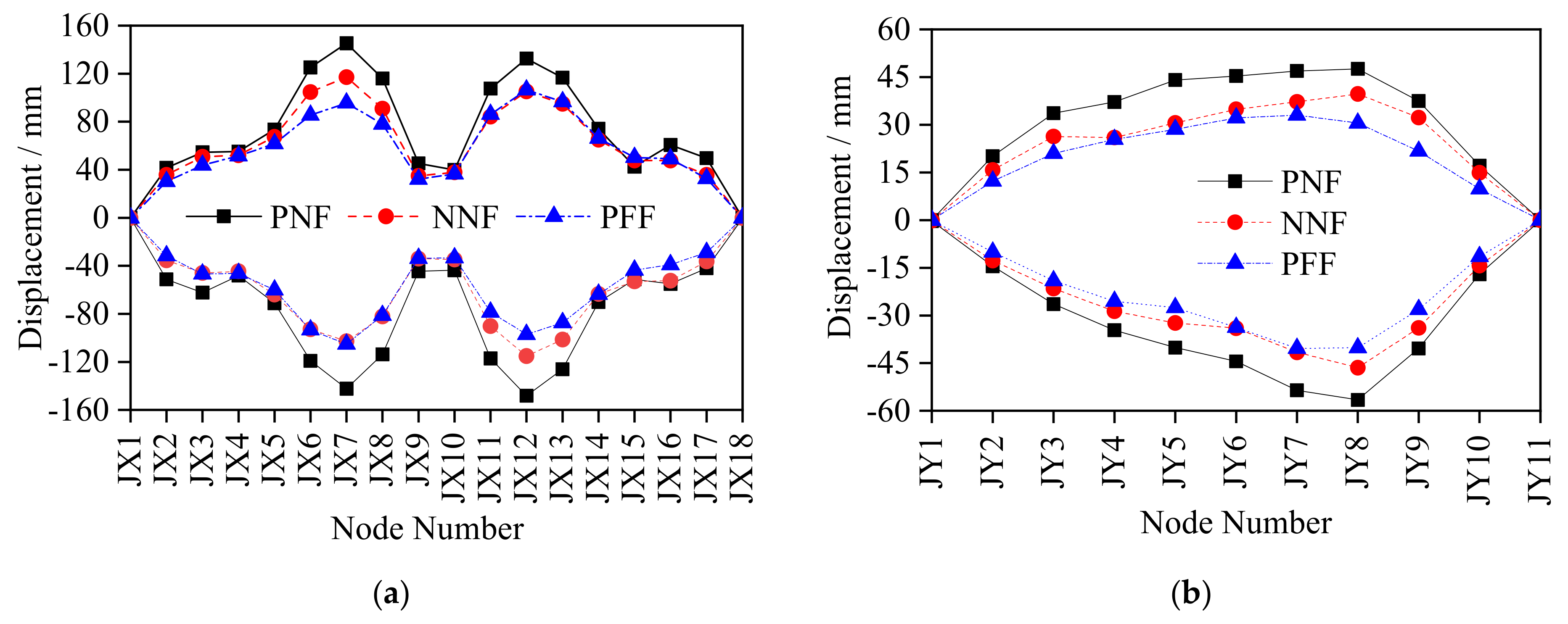
• The structural dynamic response under excitation of No. 2 seismic array was larger than that under the excitation of No. 3 seismic array except for the internal force response of the roof grid beams in the SN direction and the displacement response of the roof grid beam nodes in the EW direction. The internal force response of struts showed a downward trend from the inner ring to the outer ring, with the largest internal force response appearing in stay cables, ring cables and string cables of the outer ring. Under excitation of No. 2 and No. 3 seismic arrays, the internal force response of the struts of each ring was within 200 kN, while the internal force of the outer ring stay cables was the largest with a peak value of 559.71 kN, and the peak value of the internal force of the square cables was 452.22 kN (SH13). The internal force response of the roof grid beam was relatively large, with the peak value in the EW direction of 880.64 kN and in the SN direction of 1119.97 kN. The maximum value of displacement of the grid beam nodes in the SN direction was about twice that in the EW direction, with the largest displacement in node JY4 (136.72 mm). Thus, emphasis must be placed on monitoring the struts in the inner ring and the stay cables, ring cables and string cables in the outer ring, the stress of the roof mid-span grid beam and the deformation of local nodes such as JX7, JX12 and JY4.
• The seismic impulse factor weakened the internal force response of cables and struts. The internal force response of the cables under the seismic excitation in the far field was larger than that in the near field. The seismic impulse increased the internal force response and displacement deformation of the roof grid beam and the seismic excitation in the near field produced greater internal force response and displacement deformation of the grid beam than the far field. The influence of near and far fields exceeded that of the impulse. Thus, attention must be paid to the internal force response and displacement deformation of the roof grid beam when the seismic excitation contains an impulse factor, especially in the near field.

The research focuses on the internal connection of the structural dynamic response between the cables, strut and roofs in the structural system of MSLSD, which predicted possible damage of the structure under different types of seismic excitation in advance and provided an important reference for structural seismic resistance. In addition, the research is relevant to the operation and maintenance of the building, including regular inspections. Due to the limitation of monitoring equipment, the existing monitoring system cannot collect corresponding data for all the key roof nodes to improve the monitoring database; the actual structure and the finite element model needs to be further optimized to analyze the structure dynamic response more accurately. At the same time, compared with the traditional string dome structure, the advantages and disadvantages of this new structure system (MSLSD) need to be further studied to provide a reference for promotion and improvement.