Parameterized Design and Dynamic Analysis of a Reusable Launch Vehicle Landing System with Semi-Active Control
Abstract
1. Introduction
2. Working Principles of the RLV Landing System
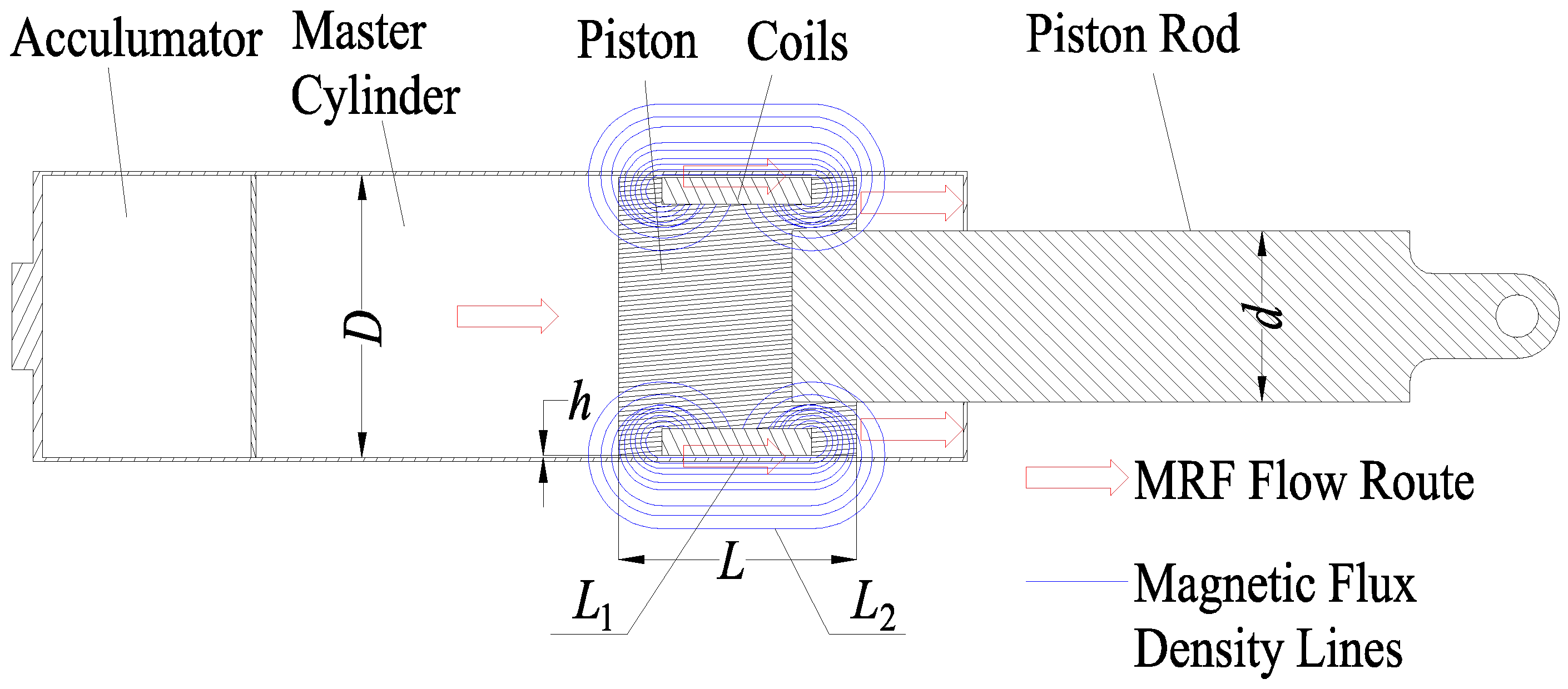
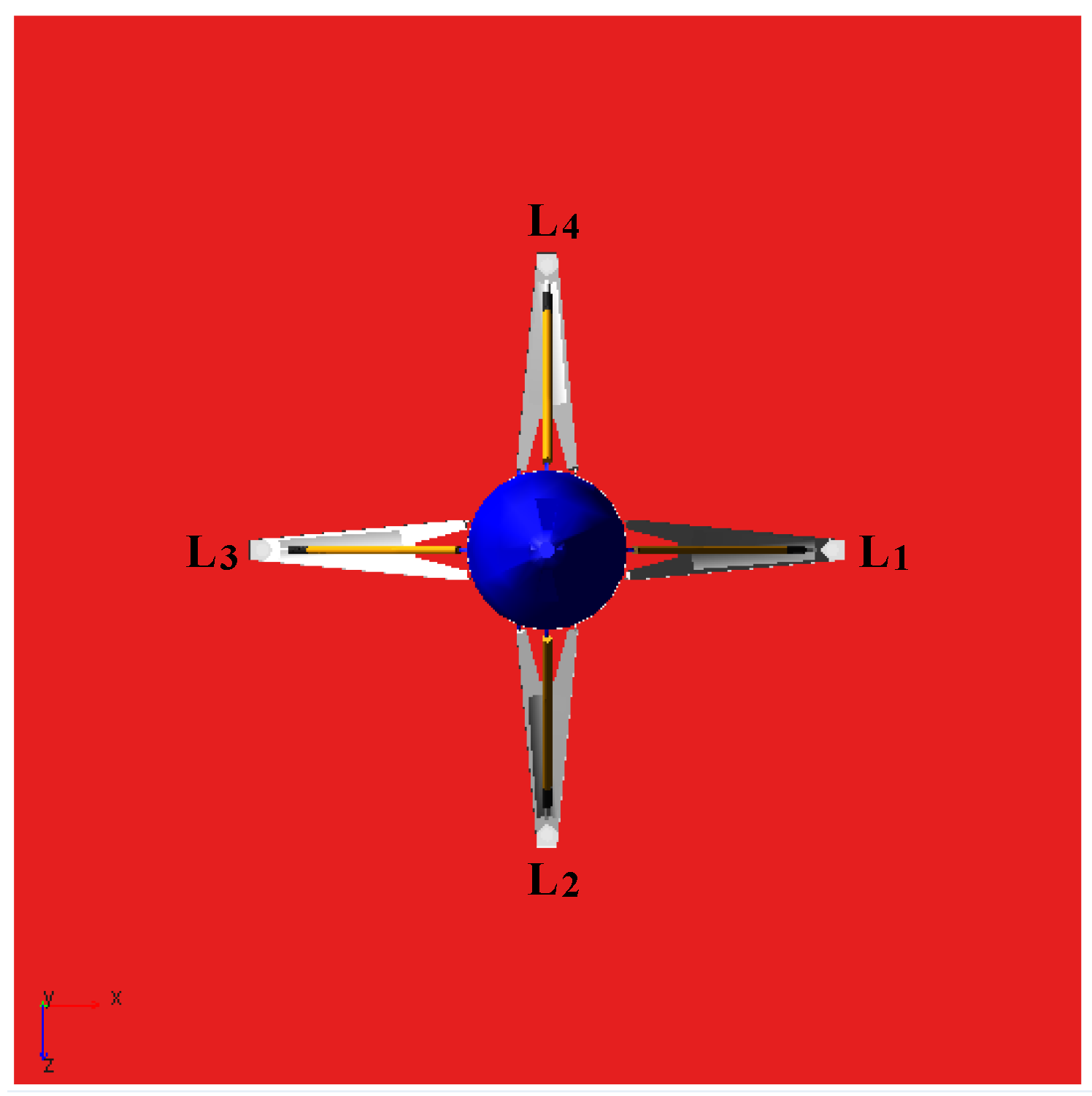
2.1. Overall Scheme of the RLV Landing System with MRF Dampers
2.2. Working Principles of the RLV Landing System
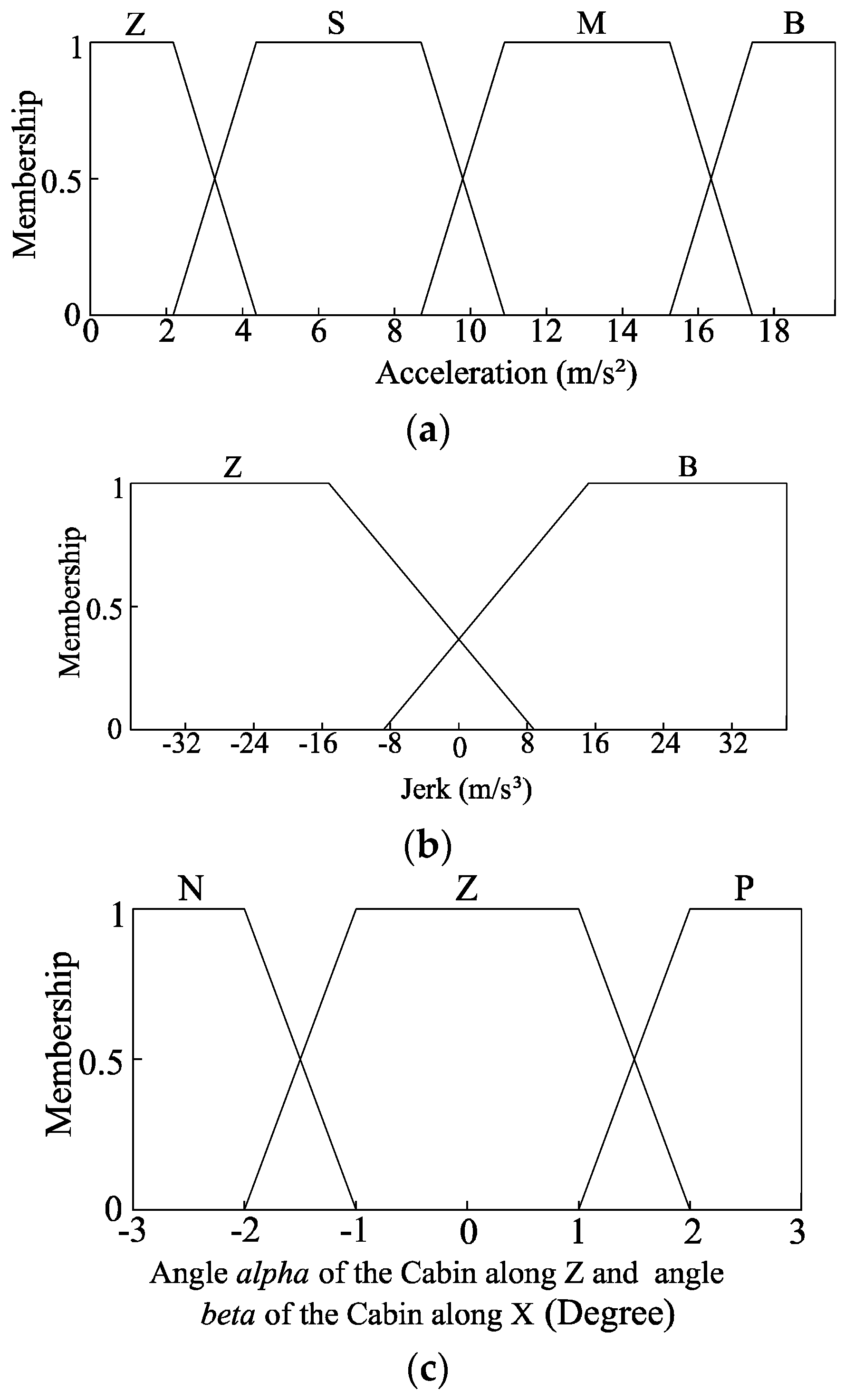
2.3. Control Approach of the RLV Landing System
3. Landing Dynamic Analysis and Parameterized Design of RLV Landing System
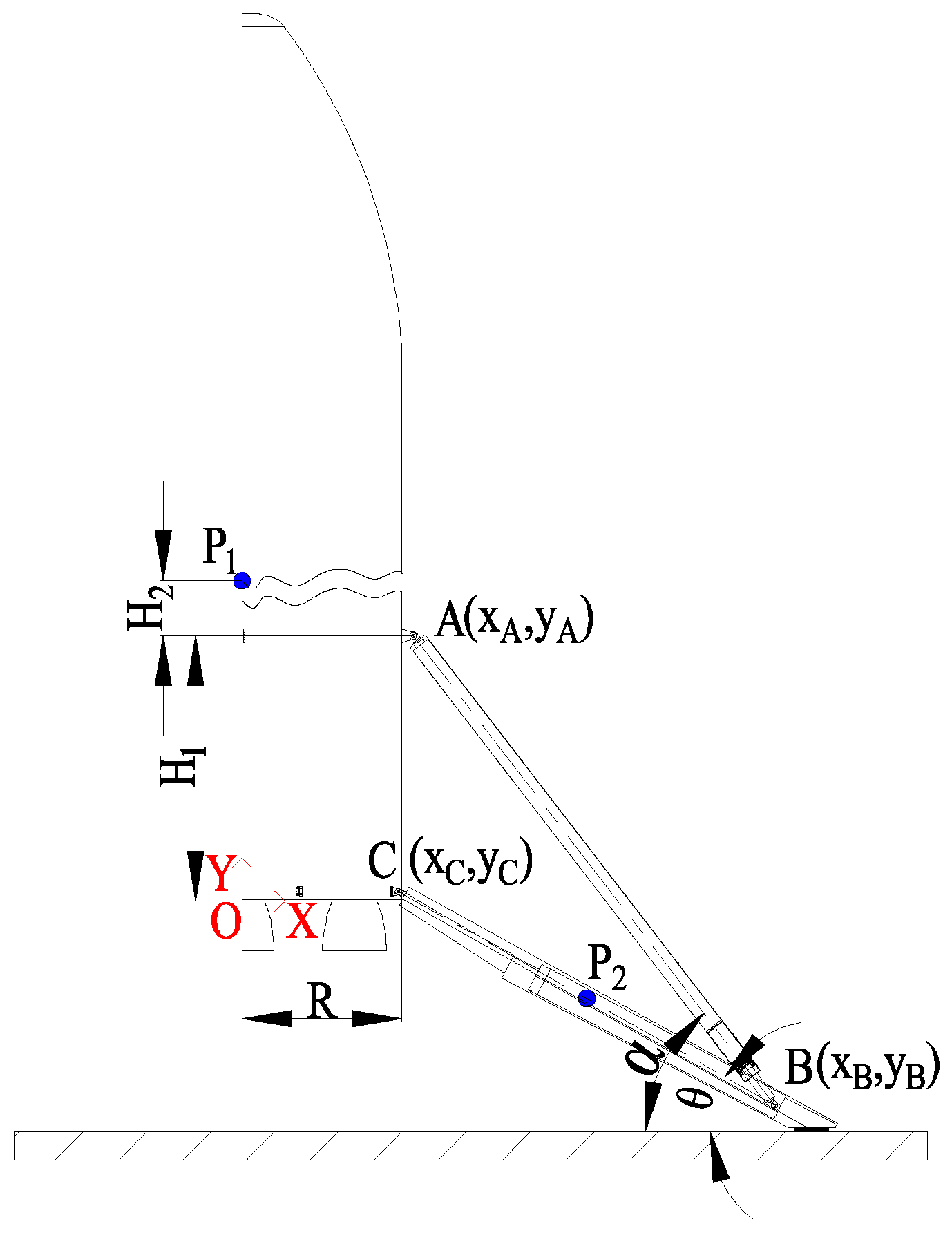
3.1. Landing Dynamic Analysis of the RLV Landing System
3.2. Parameterized Design of the RLV Landing System
4. Landing Dynamic Simulations
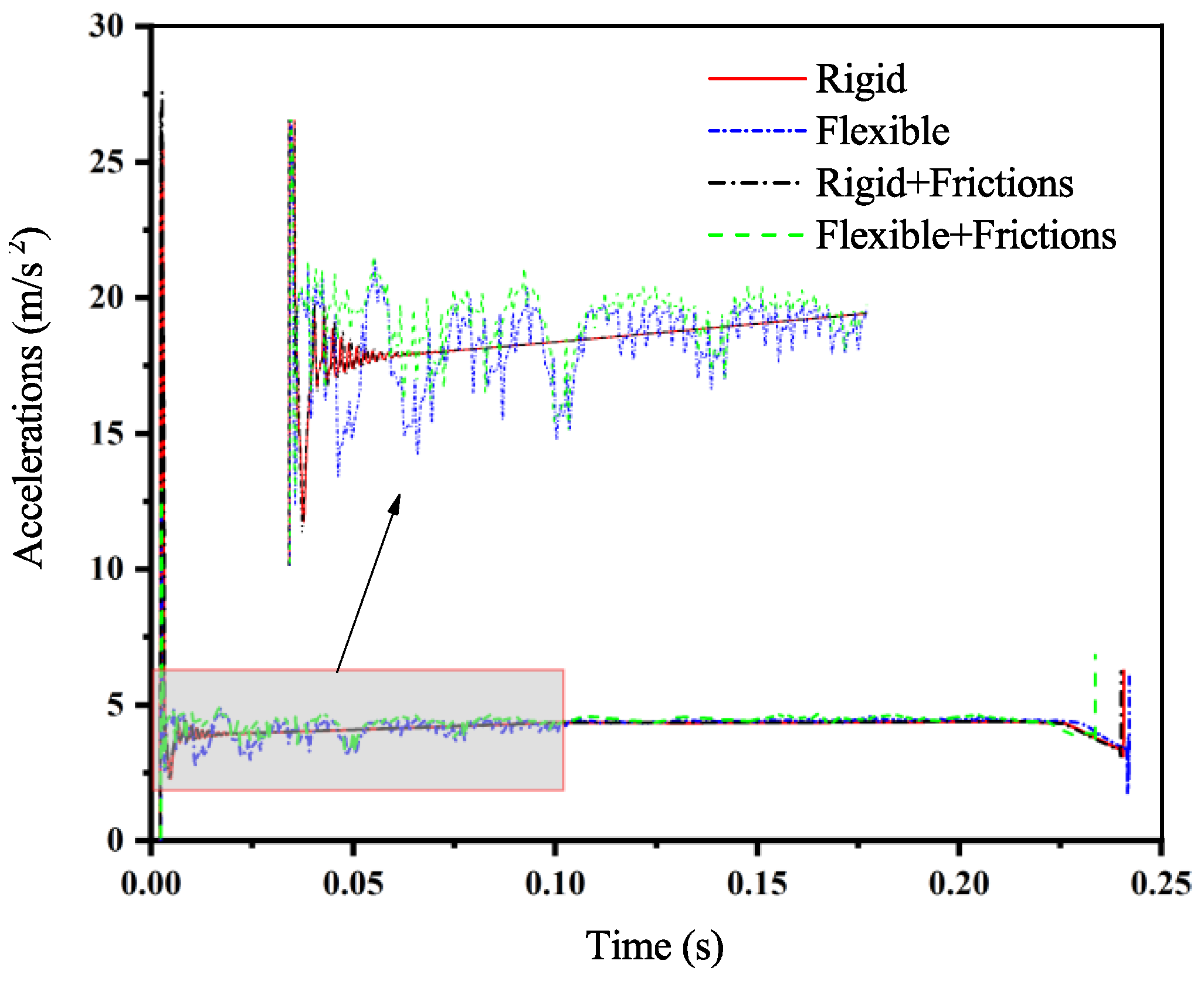
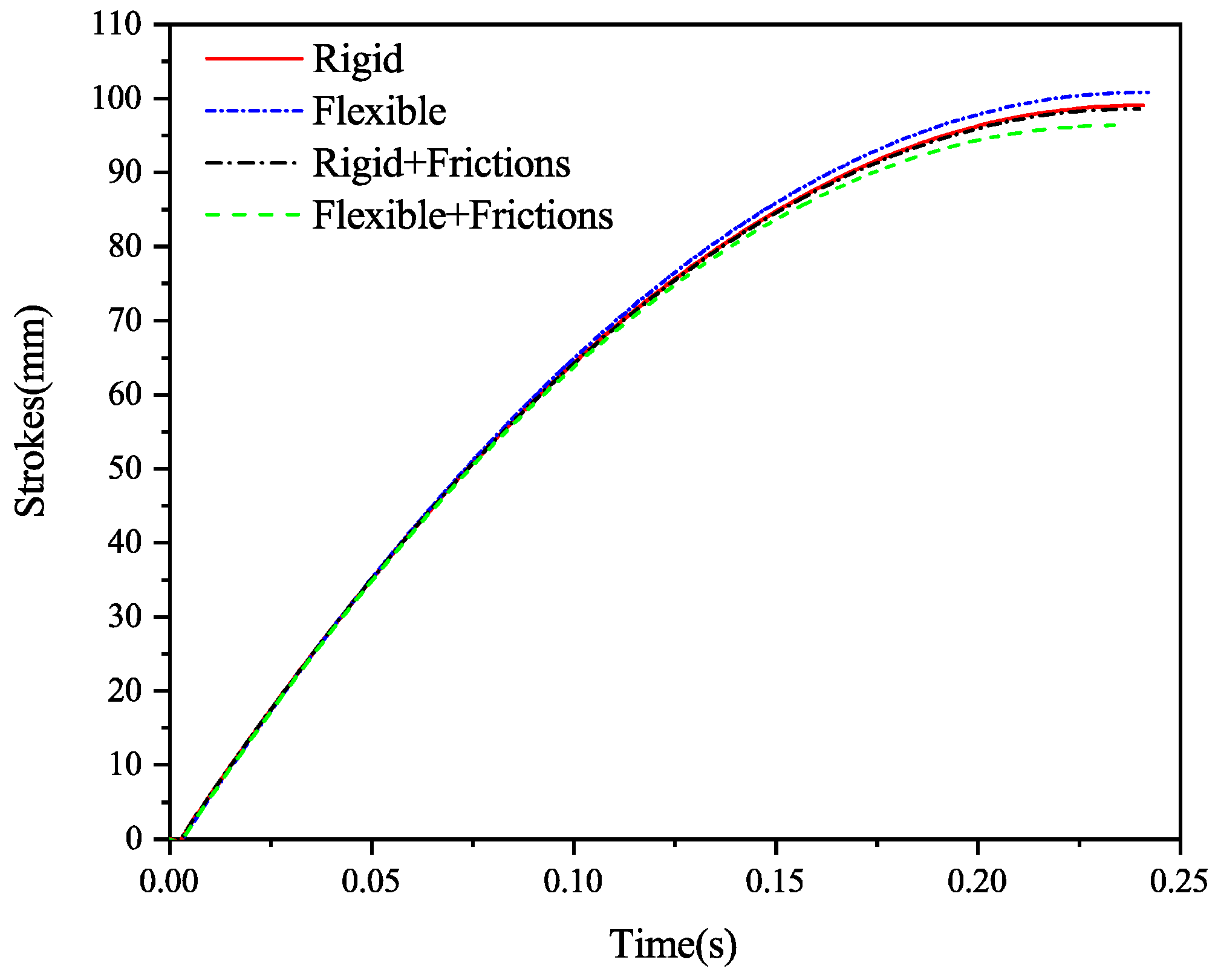
4.1. Highest Rocket Acceleration Condition
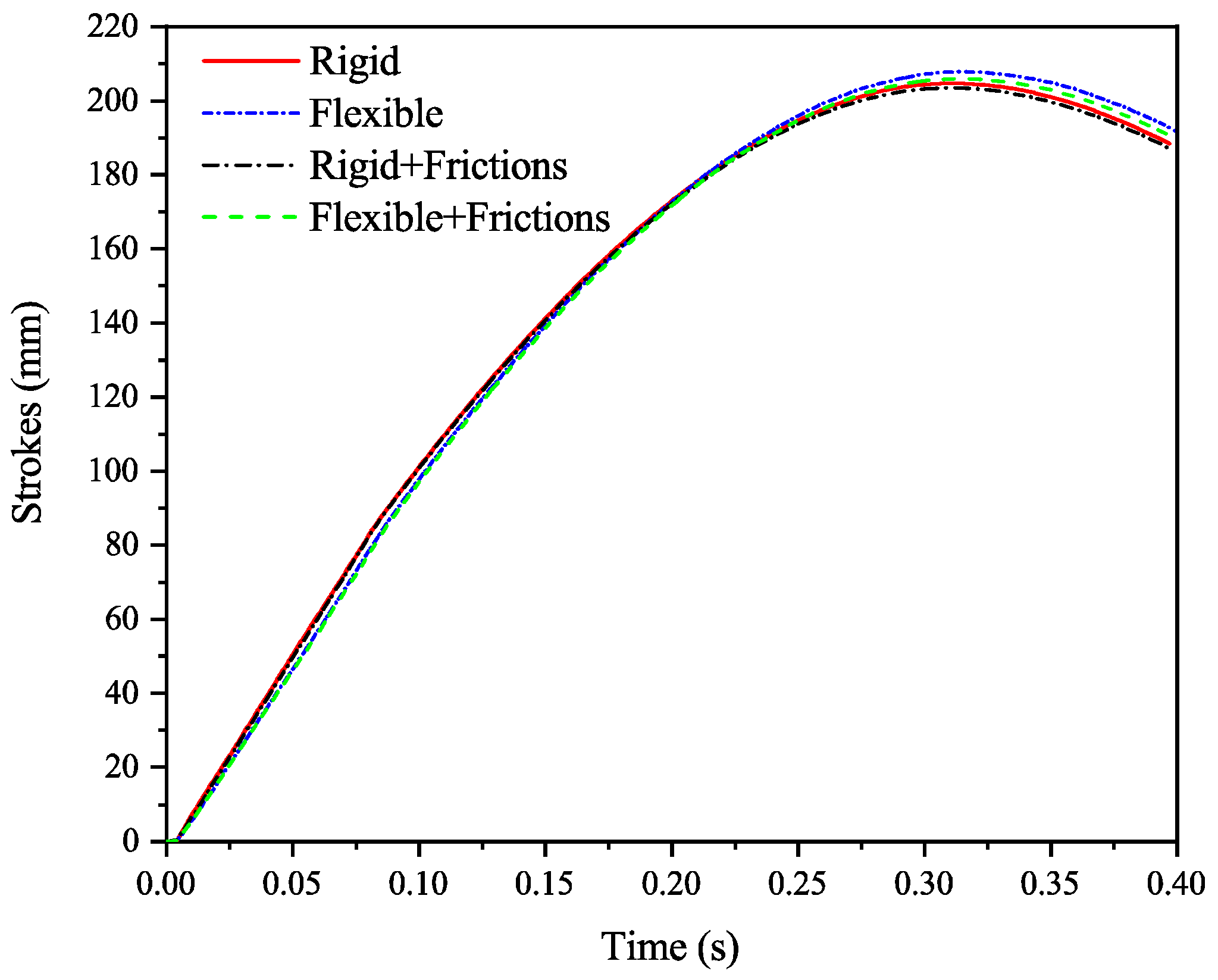
4.2. Greatest Damper Compressions Condition
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Notation
| α | Angle between the primary strut and ground |
| θ | Angle between the auxiliary strut and ground |
| μ | Friction coefficient |
| τ | Maximum yield stress of MRF |
| ρ | Density of MRF |
| η | Viscosity of MRF |
| a0 | undetermined coefficient of the constant term |
| aj | the undetermined coefficient of one-degree term |
| aij | the undetermined coefficient of the quadratic term. |
| c | Contact damping of the impact function |
| d | Penetration depth of the impact function |
| e | Contact force exponent of the impact function |
| k | Stiffness of the impact function |
| q | Distance function of the impact function |
| q0 | Trigger distance of the impact function |
| v | Piston velocity |
| Ap | Piston area |
| Agap | The gap area between the master cylinder and piston |
| An | Cross-section area of the master cylinder |
| D | Diameter of piston |
| D | Diameter of piston rod |
| Fa | Force of auxiliary strut acting at point C |
| Fc | Controllable damping force of MRF damper |
| Fp | Force of primary strut acting at point A |
| Fu | Uncontrollable damping force of MRF damper |
| FNi | Air-spring force caused by the accumulator |
| Kentry | Local resistance coefficient of the entry |
| Kentry | Local resistance coefficient of the exit |
| H1 | Vertical distance between the origin and point A |
| H2 | Vertical distance between the mass center P1 of elastic parts and point A |
| L | Length of coils |
| R | Horizontal distance between the origin of rocket coordinate system and point C |
| R1 | Highest rocket acceleration |
| R2 | Greatest compression stroke |
| R3 | Distance between rocket and ground |
| R4 | Mass of a set of landing gear |
| RP1 | Initial distance between the mass center of the rocket and the ground |
| V | Volume of accumulator |
| V0 | Initial volume of accumulator |
Appendix A
| Inputs | Outputs | ||||||
|---|---|---|---|---|---|---|---|
| Acceleration | Jerk | alpha | beta | τ1 | τ2 | τ3 | τ4 |
| B | All | All | All | Z | Z | Z | Z |
| Z | Z | Z | Z | B | B | B | B |
| Z | B | Z | Z | MB | MB | MB | MB |
| S | Z | Z | Z | SB | SB | SB | SB |
| S | B | Z | Z | M | M | M | M |
| M | Z | Z | Z | SM | SM | SM | SM |
| M | B | Z | Z | S | S | S | S |
| Z | Z | P | Z | S | SB | MB | SB |
| Z | B | P | Z | S | M | SB | M |
| Z | Z | N | Z | MB | SB | S | SB |
| Z | B | N | Z | SB | M | S | M |
| Z | Z | Z | P | SB | S | SB | MB |
| Z | B | Z | P | M | S | M | SB |
| Z | Z | Z | N | SB | MB | SB | S |
| Z | B | Z | N | M | SB | M | S |
| Z | Z | N | P | MB | SB | SB | MB |
| Z | B | N | P | SB | M | M | SB |
| Z | Z | P | N | SB | MB | MB | SB |
| Z | B | P | Z | M | SB | SB | M |
| Z | Z | N | N | SB | MB | MB | SB |
| Z | B | N | N | SB | SB | M | M |
| Z | Z | P | P | SB | SB | MB | MB |
| Z | B | P | P | M | M | SB | SB |
| S | Z | P | Z | Z | M | SB | M |
| S | B | P | Z | Z | SM | M | SM |
| S | Z | N | Z | SB | M | Z | M |
| S | B | N | Z | M | SM | Z | SM |
| S | Z | Z | P | M | Z | M | SB |
| S | B | Z | P | SM | Z | SM | M |
| S | Z | Z | N | M | SB | M | Z |
| S | B | Z | N | SM | M | SM | Z |
| S | Z | P | P | M | M | SB | SB |
| S | B | P | P | SM | SM | M | M |
| S | Z | N | N | SB | SB | M | M |
| S | B | N | N | M | M | SM | SM |
| S | Z | P | N | M | SB | SB | M |
| S | B | P | N | SM | M | M | SM |
| S | Z | N | P | SB | M | M | SB |
| S | B | N | P | M | SM | SM | M |
| M | Z | P | Z | Z | SM | M | SM |
| M | B | P | Z | Z | S | SM | S |
| M | Z | N | Z | SM | Z | M | SM |
| M | B | N | Z | S | Z | SM | S |
| M | Z | Z | N | SM | M | SM | Z |
| M | B | Z | N | S | SM | S | Z |
| M | Z | Z | P | SM | Z | SM | M |
| M | B | Z | N | S | SM | S | Z |
| M | Z | N | N | M | M | SM | SM |
| M | B | N | N | SM | SM | S | S |
| M | Z | N | P | M | SM | SM | M |
| M | B | N | P | SM | S | S | SM |
| M | Z | P | N | SM | M | M | SM |
| M | B | P | N | S | SM | SM | S |
| M | Z | P | P | SM | SM | M | M |
| M | B | P | P | S | S | SM | SM |
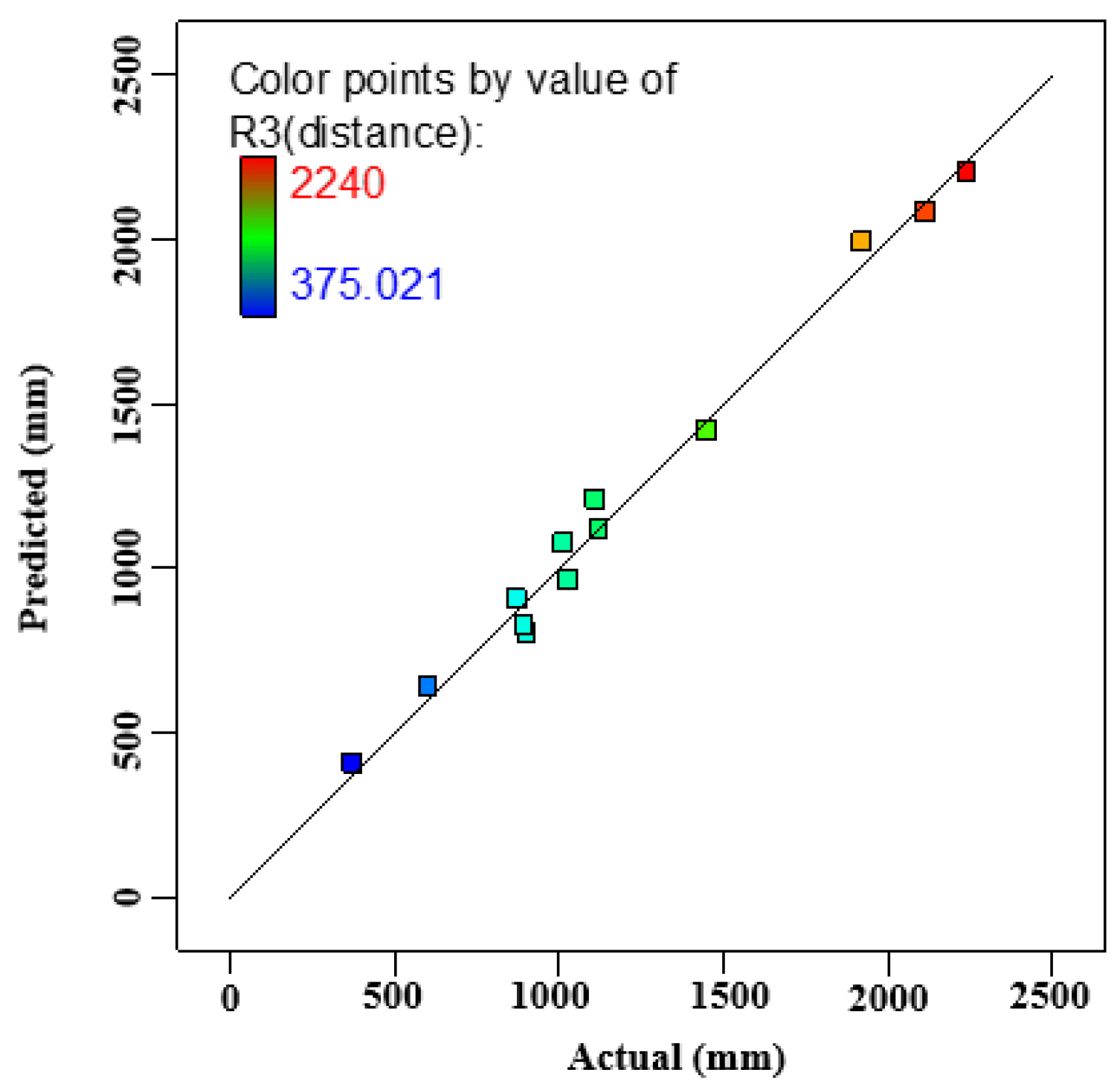
| Run | Factor 1: A(θ/°) | Factor 2: B(α/°) | Factor 3: C(H1/mm) | Response 1: R1 (amax/m/s2) | Response 2: R2 (Strokes/mm) | Response 3: R3 (Distance/mm) | Response 4: R4 (Mass/kg) |
|---|---|---|---|---|---|---|---|
| 1 | 27 | 42 | 1800 | 23.3495 | 79.5787 | 2240 | 108.446 |
| 2 | 24 | 42 | 1500 | 17.7913 | 64.4743 | 1112.8 | 91.6878 |
| 3 | 30 | 42 | 1500 | 33.193 | 113.355 | 2113.5 | 109.83 |
| 4 | 27 | 42 | 1200 | 20.5145 | 82.2504 | 1448.6 | 89.412 |
| 5 | 30 | 53 | 1500 | 30.0239 | 46.4953 | 902.999 | 79.913 |
| 6 | 27 | 47.5 | 1500 | 61.8792 | 21.4722 | 1121 | 85.2949 |
| 7 | 27 | 47.5 | 1500 | 61.8792 | 21.4722 | 1121 | 85.2949 |
| 8 | 24 | 47.5 | 1800 | 69.0255 | 18.5479 | 1028.8 | 87.5495 |
| 9 | 24 | 47.5 | 1200 | 21.6645 | 56.0716 | 894.954 | 85.2949 |
| 10 | 27 | 47.5 | 1500 | 61.8792 | 21.4722 | 1121 | 85.2949 |
| 11 | 27 | 53 | 1800 | 29.5464 | 40.7394 | 873.652 | 82.5555 |
| 12 | 30 | 47.5 | 1200 | 44.3331 | 70.8267 | 1013.2 | 82.452 |
| 13 | 30 | 47.5 | 1800 | 36.5785 | 62.3615 | 1923.2 | 98.0229 |
| 14 | 27 | 53 | 1200 | 27.7053 | 43.8536 | 602.336 | 72.0231 |
| 15 | 24 | 53 | 1500 | 31.3973 | 95.6979 | 375.021 | 75.1617 |
| 16 | 27 | 47.5 | 1500 | 61.8792 | 21.4722 | 1121 | 85.2949 |
| 17 | 27 | 47.5 | 1500 | 61.8792 | 21.4722 | 1121 | 85.2949 |
References
- Wang, Z.G.; Luo, S.B.; Wu, J.J. Developments of Reusable Launch Vehicles; National University of Defense Technology Press: Changsha, China, 2004. (In Chinese) [Google Scholar]
- Lei, B. Design and Analysis of Landing Absorber System for Vertical Takeoff and Landing Launch Vehicle. Ph.D. Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2020. [Google Scholar]
- Yue, S.; Nie, H.; Zhang, M.; Huang, M.; Zhu, H.; Xu, D. Dynamic analysis for vertical soft landing of reusable launch vehicle with landing strut flexibility. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2018, 233, 1377–1396. [Google Scholar] [CrossRef]
- Xu, D.; Zhang, Z.; Wu, K.; Li, H.; Lin, J.; Zhang, X.; Guo, X. Recent progress on development trend and key technologies of vertical take-off vertical landing reusable launch vehicle. Chin. Sci. Bull. 2016, 61, 3453–3463. [Google Scholar] [CrossRef]
- Sgarlata, P.; Weegar, R. Operational lessons of the DC-X propulsion system operations. In Proceedings of the 31st Joint Propulsion Conference and Exhibit, San Diego, CA, USA, 10–12 July 1995. [Google Scholar] [CrossRef]
- Wagner, E.; DeForest, C.E. Opportunities for Suborbital Space and Atmospheric Research Facilities on Blue Origin’s New Shepard Crew Capsule; AGU Fall Meeting Abstracts: Washington, DA, USA, 2016. [Google Scholar]
- Bjelde, B.; Capozzoli, P.; Shotwell, G. The SpaceX Falcon 1 Launch Vehicle Flight 3 Results, Future Developments, and Falcon 9 Evolution; Space Exploration Technologies: Hawthorne, LA, USA, 2008. [Google Scholar]
- Dreyer, L. Latest developments on SpaceX’s Falcon 1 and Falcon 9 launch vehicles and Dragon spacecraft. In Proceedings of the 2009 IEEE Aerospace Conference, IEEE, Big Sky, MT, USA, 7–14 March 2009. [Google Scholar] [CrossRef]
- SpaceX. Falcon 9 Launch Vehicle Payload User’s Guide. 2008. Available online: https://www.spaceflightnow.com/falcon9/001/f9guide.pdf (accessed on 17 September 2020).
- Tatiossian, P.; Desmariaux, J.; Garcia, M. Callisto Project-Reusable First Stage Rocket Demonstrator. In Proceedings of the 7th European Conference for Aeronautics and Space Sciences (EUCASS), Paris, France, 3–6 July 2017. [Google Scholar] [CrossRef]
- Dumont, E.; Ecker, T.; Witte, L.; Chavagnac, C.; Windelberg, J.; Klevanski, J.; Giagkozoglou, S. CALLISTO-Reusable VTVL launcher first stage demonstrator. In Proceedings of the Space Propulsion Conference, Sevilla, Spain, 14–18 May 2018; p. SP2018_00406. [Google Scholar]
- Shuai, Y. Retraction and Landing Dynamic Analysis of Landing gear for Vertical Takeoff and Landing Reusable Launch Vehicle. Ph.D. Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2019. [Google Scholar]
- Yue, S.; Nie, H.; Zhang, M.; Wei, X.; Gan, S. Design and landing dynamic analysis of reusable landing leg for a near-space manned capsule. Acta Astronaut. 2018, 147, 9–26. [Google Scholar] [CrossRef]
- Yue, S.; Nie, H.; Zhang, M.; Huang, M.; Dafu, X. Optimization and Performance Analysis of Oleo-Honeycomb Damper Used in Vertical Landing Reusable Launch Vehicle. J. Aerosp. Eng. 2018, 31, 04018002. [Google Scholar] [CrossRef]
- Yue, S.; Titurus, B.; Nie, H.; Zhang, M. Liquid spring damper for vertical landing Reusable Launch Vehicle under impact conditions. Mech. Syst. Signal Process. 2019, 121, 579–599. [Google Scholar] [CrossRef]
- Bo, L.; Ming, Z.; Shuai, Y. Design and Optimization of a Crashworthy Damper Used for Reusable Launch Vehicles. J. Astronaut. 2019. (In Chinese) [Google Scholar] [CrossRef]
- LORD. Viscosity vs. Temp and Yield Stress vs. H [R]. 2010. Available online: https://mar-lord-mr.worldsecuresystems.com/lord-mr-products/mrf-132dg-magneto-rheological-fluid (accessed on 17 September 2020).
- LORD. Yield Strength versus H for any MR fluid [R]; LORD: Cary, NC, USA, 2011. [Google Scholar]
- Rabinow, J. The magnetic fluid clutch. Electr. Eng. 1948, 67, 1167. [Google Scholar] [CrossRef]
- Zhao, X.; Chen, J.; Wang, C.; Wei, J. Research on Magnetorheological Fluid Damper for Lunar Lander and Its Design. Mach. Build. Autom. 2018. (In Chinese) [Google Scholar] [CrossRef]
- Heckenthaler, T.; Engell, S. Approximately time-optimal fuzzy control of a two-tank system. IEEE Control. Syst. 1994, 14, 24–30. [Google Scholar] [CrossRef]
- Kickert, W.; Lemke, H.V.N. Application of a fuzzy controller in a warm water plant. Automatica 1976, 12, 301–308. [Google Scholar] [CrossRef]
- King, P.; Mamdani, E. The application of fuzzy control systems to industrial processes. Automatica 1977, 13, 235–242. [Google Scholar] [CrossRef]
- Dutta, S. Fuzzy logic applications: Technological and strategic issues. IEEE Trans. Eng. Manag. 1993, 40, 237–254. [Google Scholar] [CrossRef]
- Qing, L. Investigation on Several Key Problems for Performance of Lunar Lander Soft Landing. Ph.D. Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2012. [Google Scholar]
- Verheul, C. ADAMS Methodology-Contact Modeling”, Benelux ADAMS User Meeting. 2012. Available online: https://www.insumma.nl/wp-content/uploads/SayField_Verheul_ADAMS_Contacts.pdf (accessed on 17 September 2020).
- Yutang, T. Design and Fuzzy Control of Magnetorheological Shock Absorber. Ph.D. Thesis, Nanjing University of Science and Technology, Nanjing, China, 2006. [Google Scholar] [CrossRef]
- Zhaochun, L. Performances and Control Method of Magnetorheological Shock Isolation Device. Ph.D. Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2012. [Google Scholar] [CrossRef]
- Mikułowski Grzegorz, M. Adaptive Impact Absorbers Based on Magnetorheological Fluids. Ph.D. Thesis, Psnc Poznan Supercomputer & Networking Center, Warsaw, Poland, 2008. Available online: http://www.ippt.pan.pl/_download/doktoraty/2008mikulowski_g_doktorat.pdf (accessed on 17 September 2020).
- Weixiong, R.G. Preliminary Design of Reusable Lunar Lander Landing System. Ph.D. Thesis, Luleå University of Technology, Luleå, Sweden, 2017. [Google Scholar]
- Heng, C. Investigation on Energy-Absorption Nanomaterials for Lunar Lander and Analysis on Soft-Landing Performance. Ph.D. Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2017. CNKI:CDMD:1.1019.801155. [Google Scholar]
- Saxena, D.; Rathore, H. Vibration control of MR damper landing gear. Int. J. Adv. Res. Artif. Intell. 2013, 2, 72–76. [Google Scholar] [CrossRef]
- Taylor, A.; Benney, R.; Bagdonovich, B. Investigation of the Application of Airbag Technology to Provide a Softlanding Capability for Military Heavy Airdrop. In Proceedings of the 16th Aiaa Aerodynamic Decelerator Systems Technology Conference & Seminar, Boston, MA, USA, 21–24 May 2001. [Google Scholar] [CrossRef]
- Zhu, G.N. Structure Design and Analysis on Landing Support of Vertical Takeoff and Vertical Landing Launch Vehicle. Ph.D. Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2019. [Google Scholar]
- Mingyang, H. Control strategy of launch vehicle and lander with adaptive landing gear for sloped landing. Acta Astronaut. 2019, 161, 509–523. [Google Scholar] [CrossRef]
- Yunkang, S.; Huiping, Y. Improvement of Response Surface Methodology and Application to Engineering Optimization; Science Press of China: Beijing, China, 2011. (In Chinese) [Google Scholar]
- Anderson, M.J.; Whitcomb, P.J.; Shari, L.K. Handbook for Experimenters; Stat-Ease: Minneapolis, MN, USA, 2017; Available online: https://cdnm.statease.com/pubs/handbk_for_exp_sv.pdf (accessed on 27 November 2017).
- Junlin, W.; Hong, N.; Lichun, L.; Jinbao, C.; Fuming, Z. Analysis of Landing Performance and Multi-factor Effects with Lunar Lander. J. Nanjing Univ. Aeronaut. Astronaut. 2010, 288–293. [Google Scholar] [CrossRef]
- Wang, C.; Nie, H.; Chen, J.; Lee, H.P. The design and dynamic analysis of a lunar lander with semi-active control. Acta Astronaut. 2019, 157, 145–156. [Google Scholar] [CrossRef]












| Structure | Material | Relative Permeability | Conductivity (S/m) | Relative Permittivity |
|---|---|---|---|---|
| Cylinders | Aluminum | 1 | 3.774 × 107 | 1.000022202 |
| Magnetic core | AISI1010 | 500 | 6.452 × 106 | 1 |
| Coils | Copper | 1 | 5.998 × 107 | 0.9999935542 |
| Gas in the accumulator | Nitrogen | 1 | 0 | 1 |
| Parameters | Value |
|---|---|
| Viscosity | 0.112 Pa s |
| Density | 2.95 g/cm3 |
| Solid content by Weight | 20.98% |
| Maximum Yield Stress | 48 kPa |
| Operating Temperature | −40∼+130 °C |
| Codes | Design Parameters | Lower Limits | Upper Limits |
|---|---|---|---|
| A | The angle between the auxiliary strut and ground (θ) | 24° | 30° |
| B | Angle between the primary strut and ground (α) | 42° | 53° |
| C | The vertical distance between point A and C (H1) | 1200 mm | 1800 mm |
| Responses | Design Targets | Goal |
|---|---|---|
| R1 | Highest rocket acceleration (m/s2) | Minimize |
| R2 | Greatest compression stroke (mm) | Minimize |
| R3 | Distance between rocket and ground (mm) | Maximum |
| R4 | Mass of a set of landing gear (kg) | Minimize |
| Response | Fitted Functions |
|---|---|
| R1 | R1 = +61.879 + 0.531A + 2.978B + 5.535C − 4.194AB − 13.779AC − 0.248BC − 8.078A2 − 25.670B2 − 10.901C2 |
| R2 | R2 = +21.472 + 7.281A − 14.109B − 6.472C − 24.521AB + 7.265AC − 0.111BC + 24.440A2 + 34.093B2 + 6.040C2 |
| R3 | R3 = +1121.000 + 317.666A − 520.112B + 263.320C − 118.180AB + 194.039AC − 130.021BC − 35.514A2 + 40.594B2 + 129.553C2 |
| R4 | R4 = +87.578 + 3.815A − 11.215B + 5.924 C − 3.3477AB + 3.329AC − 2.125BC |
| Parameters (Design Parameters) | Responses (Design Targets) | |||||
|---|---|---|---|---|---|---|
| A (θ) | B (α) | C (H1) | Highest rocket acceleration | Greatest compression stroke | Distance between rocket and ground | Mass |
| 29.58° | 52.42° | 1800 mm | 17.79 m/s2 | 47.31 mm | 1286.82 mm | 85.12 Kg |
| Landing Condition | Vertical Velocity | Horizontal Velocity | Pitch Angle |
|---|---|---|---|
| Highest acceleration | −2 m/s | 1 m/s | 0° |
| Greatest compression | −2 m/s | 1 m/s | 3° |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Chen, J.; Jia, S.; Chen, H. Parameterized Design and Dynamic Analysis of a Reusable Launch Vehicle Landing System with Semi-Active Control. Symmetry 2020, 12, 1572. https://doi.org/10.3390/sym12091572
Wang C, Chen J, Jia S, Chen H. Parameterized Design and Dynamic Analysis of a Reusable Launch Vehicle Landing System with Semi-Active Control. Symmetry. 2020; 12(9):1572. https://doi.org/10.3390/sym12091572
Chicago/Turabian StyleWang, Chen, Jinbao Chen, Shan Jia, and Heng Chen. 2020. "Parameterized Design and Dynamic Analysis of a Reusable Launch Vehicle Landing System with Semi-Active Control" Symmetry 12, no. 9: 1572. https://doi.org/10.3390/sym12091572
APA StyleWang, C., Chen, J., Jia, S., & Chen, H. (2020). Parameterized Design and Dynamic Analysis of a Reusable Launch Vehicle Landing System with Semi-Active Control. Symmetry, 12(9), 1572. https://doi.org/10.3390/sym12091572





