Prospective Teachers’ Development of Meta-Cognitive Functions in Solving Mathematical-Based Programming Problems with Scratch
Abstract
1. Introduction
2. Literature Review
2.1. Meta-Cognition in Problem-Solving
2.2. Programming in Mathematical Problem-Solving and Meta-Cognition
- How and when do prospective teachers use meta-cognitive functions while solving mathematical-based programming problems in the Scratch environment?
- How are the meta-cognitive functions related to the programming or mathematical aspects of solving mathematical-based programming problems in the Scratch environment?
3. Method
3.1. Context and Participants
3.2. Research Procedure
3.3. Data Sources
3.3.1. Video Recording of the Learning Process
3.3.2. The Prospective Teachers’ Reports
3.4. Data Analyses
3.4.1. Video Recording of the Learning Process
3.4.2. The Prospective Teachers’ Reports
Awareness: ‘I thought about what I already know’, ‘I tried to remember if I had ever done a problem like this before’, ‘I thought about something I had done another time that had been helpful’, ‘I thought ‘I know what to do’’, ‘I thought ‘I know this sort of problem’’.
Evaluation: ‘I thought about how I was going’, ‘I thought about whether what I was doing was working’, ‘I checked my work’, ‘I thought ‘Is this right?’’, ‘I thought ‘I can’t do it’’.
Regulation: ‘I made a plan to work it out’. ‘I thought about a different way to solve the problem’, ‘I thought about what I would do next’, ‘I changed the way I was working’.
3.5. Learning Sequences
3.6. Learning Activities
3.6.1. First Problem
3.6.2. Second Problem
3.6.3. Third Problem
4. Findings
4.1. Development of Meta-Cognitive Functions Among Prospective Teachers
4.1.1. First Stage: Approaching the Problems without Utilizing Regulation
4.1.2. Second Stage: Approaching the Problems with the Utilization of Meta-Cognitive Functions Only in the Mathematical Processes or the Programming Processes
- (100)
- Salam: We need to plan our solution.
- (101)
- Seham: First, we must organize the data.
- (102)
- Alla: Then, we must move from the initial point.
- (103)
- Salam: We need to know the length of the side.
- …
- (The prospective teachers continue to discuss and construct their mathematical ideas. Then, they began implementing their ideas in Scratch)
- (145)
- Salam: Do repetition
- (146)
- Alaa: Turn with angle 30 to the right.
- (147)
- Salam: The sides are a and b.
- (148)
- Alaa: Turn with angle 120 and move b, three times.
- (149)
- Salam: (after trying to run the program) Oh, it is a hexagon.
- (150)
- Alaa: Let us see what mathematical mistakes we made.
- (153)
- Maha: We need to plan how to do that in Scratch.
- (154)
- Namareq: If we get to the edge, we must use the ‘rotation’ block if we were at a particular point on the edge.
- (155)
- Maha: When it gets to the edge, it must turn around at a certain angle
- (156)
- Nora: It means we want to keep it walking a certain distance to get to the edge, then turn around at a certain angle, and continue walking for a certain distance.
4.1.3. Third Stage: Approaching the Problems with the Regulation in Both Aspects (Mathematical Aspect and Programming Aspect)
- (314)
- Mai: We begin by looking at the givens of the problem. This will help us plan our solution.
- (315)
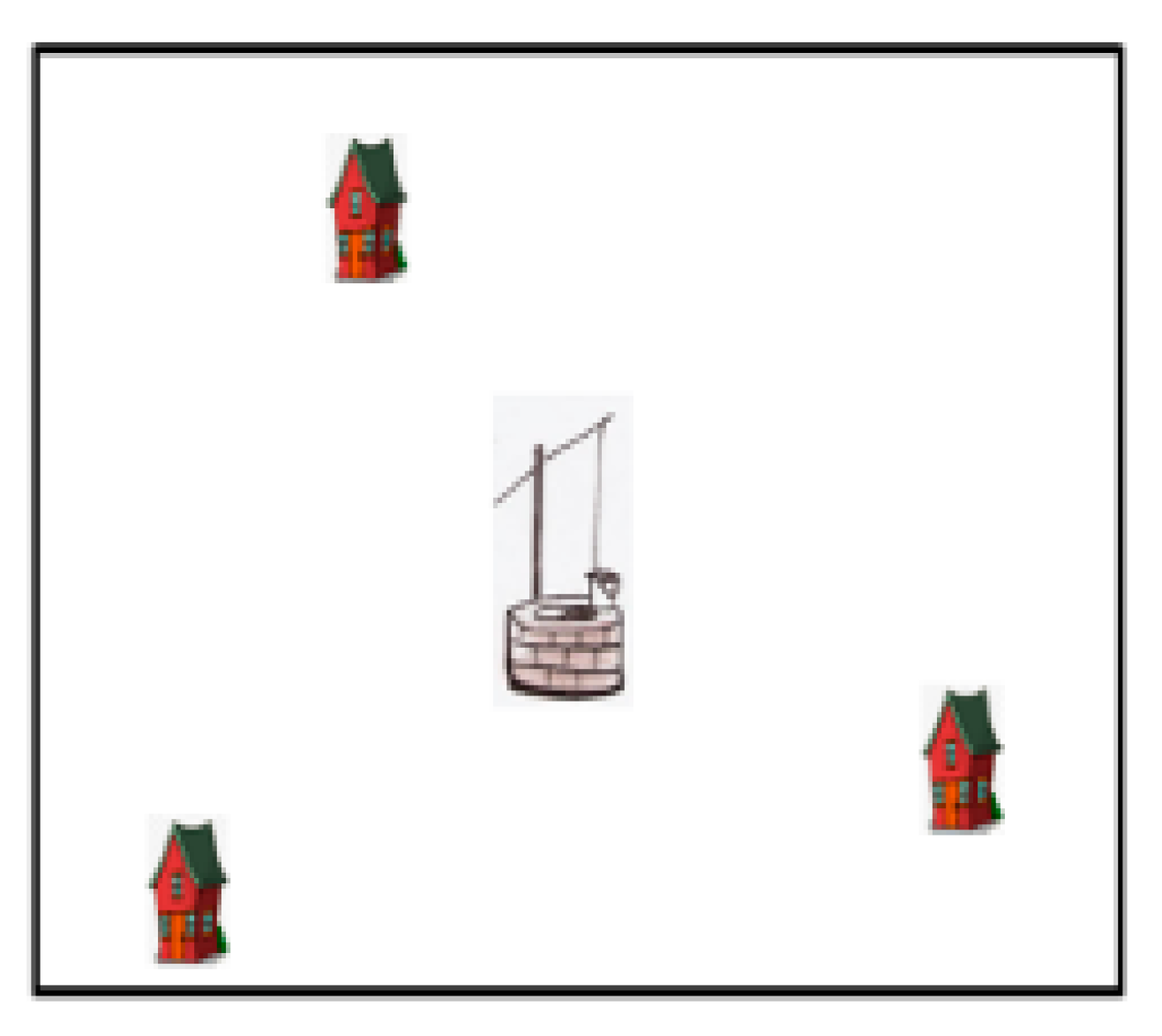
- Rina: We have three houses that are not located on a straight line.
- (316)
- Rand: We can say that we have three coordinates of three points
- (317)
- Mai: This situation makes me think of a circle; the houses could be points on the circle, and the well could be the centre of the circle. Here, we can use the mathematical features of the circle’s centre.
- (318)
- Rand: So, we need to assign the three points, and then find the coordinates of the circle’s centre.
- (319)
- Rina: We can locate geometrically the coordinates of the circle’s centre by connecting the three points with three segments and drawing the perpendicular bisectors of two of them. The intersection point of the two perpendicular bisectors is the centre of the circle—the location of the well.
- …
- (The prospective teachers continued doing the mathematical calculations of the problem)
- (378)
- Mai: We need now to assign the coordinates in Scratch.
- …
- (Before performing in Scratch, the prospective teachers discussed how to use the features of Scratch to get the best solution).
- (390)
- Rina: We can use the ‘random position’ block for the locations of the houses.
- (391)
- Rand: After drawing the points, we need to show the drawings of the segments and perpendicular bisectors in Scratch.
- (392)
- Rand: We use the geometrical calculations of the circle’s centre to present the location of the well on the Scratch screen.
4.2. Frequencies of Meta-Cognitive Functions
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Flavell, J. Meta-cognitive Aspects of Problem Solving. In The Nature of Intelligence; Resnick, L., Ed.; Erlbaum: Hillsdale, NJ, USA, 1976; pp. 231–235. [Google Scholar]
- Schneider, W.; Artelt, C. Metacognition and mathematics education. ZDM 2010, 42, 149–161. [Google Scholar] [CrossRef]
- Silver, E. The Teaching and Assessing of Mathematical Problem Solving; National Council of Teachers of Mathematics [NCTM]: Reston, VA, USA, 1985. [Google Scholar]
- Veenman, M.V.J.; Spaans, M.A. Relation between intellectual and meta-cognitive skills: Age and task differences. Learn. Individ. Differ. 2005, 15, 159–176. [Google Scholar] [CrossRef]
- Desoete, A.; Roeyers, H. Off-line metacognition—A domain-specific retardation in young children with learning disabilities. Learn. Disabil. Q. 2002, 25, 123–139. [Google Scholar] [CrossRef]
- Özsoy, G. An investigation of the relationship between metacognition and mathematics achievement. Asia Pac. Educ. Rev. 2011, 12, 227–235. [Google Scholar] [CrossRef]
- Mevarech, Z.R.; Fan, L. Cognition, Metacognition, and Mathematics Literacy. In Cognition, Metacognition, and Culture in STEM Education; Springer: Cham, Switzerland, 2018; pp. 261–278. [Google Scholar]
- Duangnamol, T.; Supnithi, T.; Srijuntongsiri, G.; Ikeda, M. Computer-Supported Meta-reflective Learning Model via mathematical word problem learning for training metacognition. Res. Pract. Technol. Enhanc. Learn. 2018, 13, 14. [Google Scholar] [CrossRef]
- Teong, S.K. The effect of metacognitive training on mathematical word-problem solving. J. Comput. Assist. Learn. 2003, 19, 46–55. [Google Scholar] [CrossRef]
- Baya’a, N.; Daher, W.; Jaber, O.; Anabousy, A. Educating pre-service teachers in meta-cognitive activities. In Proceedings of the Fifth ERME Topic Conference; Weigand, H.-G., Clark-Wilson, A., Donevska-Todorova, A., Faggiano, E., Grønbæk, N., Trgalova, J., Eds.; University of Copenhagen: Copenhagen, Denmark, 2018; pp. 35–42. Available online: https://static-curis.ku.dk/portal/files/215182839/MEDA_2018_Proceedings.pdf (accessed on 10 September 2020).
- Eteläpelto, A. Metacognition and the expertise of computer program comprehension. Scand. J. Educ. Res. 1993, 37, 243–254. [Google Scholar] [CrossRef]
- Rum, S.N.; Ismail, M. Meta-cognitive awareness assessment and introductory computer programming course achievement at university. Int. Arab J. Inf. Technol. (IAJIT) 2016, 13, 667–675. [Google Scholar]
- Cetin, I.; Sendurur, E.; Sendurur, P. Assessing the Impact of Meta-Cognitive Training on Students’ Understanding of Introductory Programming Concepts. J. Educ. Comput. Res. 2014, 50, 507–524. [Google Scholar] [CrossRef]
- Breed, B.; Mentz, E.; Van der Westhuizen, G. A meta-cognitive approach to pair programming: Influence on meta-cognitive awareness. Electron. J. Res. Educ. Psychol. 2014, 12, 33–60. [Google Scholar] [CrossRef]
- Dindar, M.; Järvelä, S.; Järvenoja, H. Interplay of metacognitive experiences and performance in collaborative problem solving. Comput. Educ. 2020, 154, 103922. [Google Scholar] [CrossRef]
- Leikin, R.; Berman, A.; Zaslavsky, O. Applications of symmetry to problem solving. Int. J. Math. Educ. Sci. Technol. 2000, 31, 799–809. [Google Scholar] [CrossRef]
- Righini, G.; Salani, M. Symmetry helps: Bounded bi-directional dynamic programming for the elementary shortest path problem with resource constraints. Discret. Optim. 2006, 3, 255–273. [Google Scholar] [CrossRef]
- Wilson, J.; Clarke, D. Towards the modelling of mathematical metacognition. Math. Educ. Res. J. 2004, 16, 25–48. [Google Scholar] [CrossRef]
- Flavell, J.H. Metacognition and cognitive monitoring: A new area of cognitive–developmental inquiry. Am. Psychol. 1979, 34, 906. [Google Scholar] [CrossRef]
- Flavell, J.H. Cognitive Monitoring. In Children’s Oral Communication Skills; Dickson, W.P., Ed.; Academic Press: New York, NY, USA, 1981. [Google Scholar]
- Efklides, A. Metacognitive experiences: The missing link in the self-regulated learning process. Educ. Psychol. Rev. 2006, 18, 287–291. [Google Scholar] [CrossRef]
- Veenman, M.V.J.; Kok, R.; Blöte, A.W. The relation between intellectual and metacognitive skills at the onset of metacognitive skill development. Instr. Sci. 2005, 33, 193–211. [Google Scholar] [CrossRef]
- Cross, D.R.; Paris, S.G. Developmental and instructional analyses of children’s metacognition and reading comprehension. J. Educ. Psychol. 1988, 80, 131–142. [Google Scholar] [CrossRef]
- Brown, A.L. Metacognition, Executive Control, Self-regulation and Other Mysterious Mechanisms. In Metacognition, Motivation and Understanding; Weinert, F., Kluwe, R., Eds.; Lawrence Erlbaum: Hillsdale, NJ, USA, 1987; pp. 65–115. [Google Scholar]
- Veenman, M.V.J. The Role of Intellectual and Metacognitive Skills in Math Problem Solving. In Metacognition in Mathematics Education; Desoete, A., Veenman, M., Eds.; Nova Science: Haupauge, NY, USA, 2006; pp. 35–50. [Google Scholar]
- Desoete, A.; Roeyers, H.; De Clercq, A. Can offline metacognition enhance mathematical problem solving? J. Educ. Psychol. 2003, 95, 188–200. [Google Scholar] [CrossRef]
- Kramarski, B.; Mevarech, Z.R. Enhancing mathematical reasoning in the classroom: The effects of cooperative learning and metacognitive training. Am. Educ. Res. J. 2003, 40, 281–310. [Google Scholar] [CrossRef]
- Özsoy, G.; Ataman, A. The effect of meta-cognitive strategy training on mathematical problem solving achievement. Int. Electron. J. Elem. Educ. 2017, 1, 67–82. [Google Scholar]
- Shahbari, J.A.; Daher, W.; Rasslan, S. Mathematical knowledge and the cognitive and meta-cognitive processes emerged in model-eliciting activities. Int. J. New Trends Educ. Their Implic. 2014, 5, 209–219. [Google Scholar]
- Batista, S.C.F.; Baptista, C.B.F. Learning object for linear systems: Scratch in mathematics. Int. J. New Trends Educ. Their Implic. 2014, 5, 71–81. [Google Scholar]
- Calder, N.; Taylor, M. Scratching Below the Surface: Mathematics through an Alternative Digital Lens? In Shaping the Future of Mathematics Education, Proceedings of the 33rd Annual Conference of the Mathematics Education Research Group of Australasia, Freemantle, Australia, 3–7 July 2010; Sparrow, L., Kissane, B., Hurst, C., Eds.; MERGA: Freemantle, UK, 2010. [Google Scholar]
- Zavala, L.A.; Gallardo, S.C.H.; García-Ruíz, M.Á. Designing interactive activities within Scratch 2.0 for improving abilities to identify numerical sequences. In Proceedings of the 12th International Conference on Interaction Design and Children, New York, NY, USA, 24–27 June 2013; pp. 423–426. [Google Scholar]
- Chiang, F.K.; Qin, L. A Pilot study to assess the impacts of game-based construction learning, using Scratch, on students’ multi-step equation-solving performance. Interact. Learn. Environ. 2018, 26, 803–814. [Google Scholar] [CrossRef]
- Ke, F. An implementation of design-based learning through creating educational computer games: A case study on mathematics learning during design and computing. Comput. Educ. 2014, 73, 26–39. [Google Scholar] [CrossRef]
- Bernard, M.; Bachu, E. Enhancing the Meta-cognitive Skill of Novice Programmers through Collaborative Learning. In Metacognition: Fundaments, Applications, and Trends; Springer: Cham, Switzerland, 2015; pp. 277–298. [Google Scholar]
- Deek, F.P.; McHugh, J.A.; Turoff, M. Problem solving and cognitive foundations for program development: An integrated model. In Proceedings of the Sixth International Conference on Computer Based Learning in Science (CBLIS), Nicosia, Cyprus, 5–10 July 2003; pp. 266–271. [Google Scholar]
- Volet, S.E. Modeling and coaching of relevant meta-cognitive strategies for enhancing university students’ learning. Learn. Instr. 1991, 1, 319–336. [Google Scholar] [CrossRef]
- Glaser, B.; Strauss, A. The Discovery of Grounded Theory: Strategies for Qualitative Research; Weidenfeld and Nicolson: London, UK, 1967. [Google Scholar]
- Daher, W.; Awawdeh Shahbari, J. Secondary Students’ Identities in the Virtual Classroom. Sustainability 2020, 12, 4407. [Google Scholar] [CrossRef]
- Shahbari, J.A.; Daher, W. Learning Congruent Triangles through Ethnomathematics: The Case of Students with Difficulties in Mathematics. Appl. Sci. 2020, 10, 4950. [Google Scholar] [CrossRef]
- Akpinar, Y.; Aslan, Ü. Supporting children’s learning of probability through video game programming. J. Educ. Comput. Res. 2015, 53, 228–259. [Google Scholar] [CrossRef]
- Calao, L.A.; Moreno-León, J.; Correa, H.E.; Robles, G. Developing mathematical thinking with Scratch: An experiment with 6th grade students. In Design for Teaching and Learning in a Networked World, 10th European Conference on Technology Enhanced Learning, EC-TEL 2015; Springer: Toledo, Spain, 2015; pp. 17–27. Available online: https://www.researchgate.net/publication/282861505_Developing_Mathematical_Thinking_with_Scratch_An_Experiment_with_6th_Grade_Students (accessed on 10 September 2020). [CrossRef]
- Kurland, D.M.; Pea, R.D.; Clement, C.; Mawby, R. A study of the development of programming ability and thinking skills in high school students. J. Educ. Comput. Res. 1986, 2, 429–458. [Google Scholar] [CrossRef]
- Daher, W.; Anabousy, A.; Jabarin, R. Metacognition, positioning and emotions in mathematical activities. Int. J. Res. Educ. Sci. (IJRES) 2018, 4, 292–303. [Google Scholar] [CrossRef]
- Winne, P.H. Experimenting to bootstrap self-regulated learning. J. Educ. Psychol. 1997, 89, 1–14. [Google Scholar] [CrossRef]
- Vula, E.; Avdyli, R.; Berisha, V.; Saqipi, B.; Elezi, S. The impact of meta-cognitive strategies and self-regulating processes of solving math word problems. Int. Electron. J. Elem. Educ. 2017, 10, 49–59. [Google Scholar]
- Moreno-León, J.; Robles, G.; Román-González, M. Dr. Scratch: Automatic analysis of scratch projects to assess and foster computational thinking. RED-Rev. Educ. Distancia 2015, 46. [Google Scholar] [CrossRef]
- Moreno-León, J.; Robles, G.; Román-González, M. Code to learn: Where does it belong in the K-12 curriculum? J. Inf. Technol. Educ. Res. 2016, 15, 283–303. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shahbari, J.A.; Daher, W.; Baya’a, N.; Jaber, O. Prospective Teachers’ Development of Meta-Cognitive Functions in Solving Mathematical-Based Programming Problems with Scratch. Symmetry 2020, 12, 1569. https://doi.org/10.3390/sym12091569
Shahbari JA, Daher W, Baya’a N, Jaber O. Prospective Teachers’ Development of Meta-Cognitive Functions in Solving Mathematical-Based Programming Problems with Scratch. Symmetry. 2020; 12(9):1569. https://doi.org/10.3390/sym12091569
Chicago/Turabian StyleShahbari, Juhaina Awawdeh, Wajeeh Daher, Nimer Baya’a, and Otman Jaber. 2020. "Prospective Teachers’ Development of Meta-Cognitive Functions in Solving Mathematical-Based Programming Problems with Scratch" Symmetry 12, no. 9: 1569. https://doi.org/10.3390/sym12091569
APA StyleShahbari, J. A., Daher, W., Baya’a, N., & Jaber, O. (2020). Prospective Teachers’ Development of Meta-Cognitive Functions in Solving Mathematical-Based Programming Problems with Scratch. Symmetry, 12(9), 1569. https://doi.org/10.3390/sym12091569






