Prospective Teachers’ Development of Meta-Cognitive Functions in Solving Mathematical-Based Programming Problems with Scratch

Abstract

Transformations, including symmetry and rotations, are important in solving mathematical problems. Meta-cognitive functions are considered critical in solving mathematical problems. In the current study, we examined prospective teachers’ use of meta-cognitive functions while solving mathematical-based programming problems in the Scratch environment. The study was conducted among 18 prospective teachers, who engaged in a sequence of mathematical problems that utilize Scratch. The data sources included video recordings and solution reports while they performed mathematical problems. The findings indicated that the participants developed their meta-cognitive functions as problem solvers related to both mathematics and programming aspects. The findings also indicated that the participants developed regulation meta-cognitive functions more than awareness and evaluation ones in mathematical and programming aspects.

1. Introduction

The meta-cognitive concept was proposed by Flavell [1], who defined meta-cognitive knowledge as the individual’s knowledge of the regulation of his cognitive activity. Meta-cognition was highlighted in education, in general, and mathematics, in particular [2]. Using meta-cognition has an essential role in the failure or success of solving mathematical problems [3]. Moreover, there are positive relationships between meta-cognition and achievements [4]. Evidence has been found among different studies [5,6]. A learner who uses meta-cognitive skills is more likely to solve the task correctly than a learner who does not activate meta-cognitive skills [7]. For that, it is important to foster meta-cognitive processes among learners.

To the end of developing meta-cognitive processes, several researchers have emphasized the use of technology. Duangnamol, Supnithi, Srijuntongsiri, and Ikeda [8] indicated that the use of a technological application encouraged students to think about their thinking. Teong [9] found that meta-cognitive training within computer environments has a positive impact on the success of solving mathematical word problems among low-achievement students, and on the development of their abilities on when to make metacognitive decisions. Meta-cognition is considered an important topic in education, in general, and mathematics education, in particular [10]. On the other hand, researchers point to the role of technology in developing meta-cognition, in general, and in programming, in particular [11,12]. The present research addresses the intersection of the two fields. Moreover, meta-cognitive skills have not been adequately studied in computer programming education [13]. More specifically, little research had been done on the role of meta-cognition in the teaching and learning of computer programming skills [14]. In addition, generally, studies on meta-cognitive processes are limited to individual math problem-solving [15]. This is especially true when learners solve mathematics-based programming problems that are based on transformations. It is important to study such learning because transformations like symmetry lie at the heart of mathematics [16] and Scratch programming [17].

In the current study, we adopted Wilson and Clark’s [18] model of meta-cognitive functions that was suggested for studying meta-cognitive behavior. The model includes the tracing of three meta-cognitive functions: Awareness, evaluation, and regulation (we will elaborate on them later in the literature review Section 2.1). We use the model to examine prospective teachers’ use of meta-cognitive functions while solving mathematical-based programming problems in the Scratch environment by focusing on group work. In addition, we trace the changes in the meta-cognitive functions along the learning sequences.

2. Literature Review

2.1. Meta-Cognition in Problem-Solving

Meta-cognition was defined by Flavell [19] as “cognition about cognitive phenomena”, or in more simple words, thinking about our own thinking. Meta-cognitive thinking includes two main aspects: Meta-cognitive knowledge and meta-cognitive experience [20,21]. Meta-cognitive knowledge is declarative knowledge about the interaction between human characteristics, mission, and strategy [19]. The meta-cognitive experience refers to cognitive or affective experiences; this is knowledge of a specific task during its implementation, including knowledge of mission characteristics and the procedures required to carry it out [22]. Since the definition of Flavell, different definitions have been suggested; for example, Schneider and Artelt [2] defined meta-cognition as knowledge of cognitive tasks and strategies for coping with such tasks. Cross and Paris [23] defined meta-cognition as the knowledge and control children have over their own thinking and learning activities. Brown [24] defined meta-cognition as one’s own knowledge about cognition and the regulation of cognitive processes toward specific goals. Most of the different definitions of meta-cognition can be separated into knowledge about cognition and self-regulation of cognition. Veenman [25] suggested that the most common distinction in meta-cognition separates meta-cognitive knowledge from skills. From the earlier definition, we can say that the first component is the meta-cognitive knowledge, while the second component is termed differently by several researchers. However, it has the same meaning as the individual’s procedural knowledge for regulating one’s problem-solving and learning activities [25].

Wilson and Clark [18] claimed that the research had ignored nonregulation functions, such as awareness and evaluations of thought processes. Therefore, Wilson and Clark [18] depended on the literature related to the definition of metacognition to extend it to include three meta-cognitive components, which they termed as functions: Awareness, evaluation, and regulation. Meta-cognitive awareness “relates to individuals’ awareness of where they are in the learning process or in the process of solving a problem, of their content-specific knowledge, and of their knowledge about their personal learning or problem-solving strategies” [18]. Meta-cognitive regulation is based on knowledge about oneself, the task, and strategies to engage with in executive processes, such as planning, self-correcting, setting goals, and improving and enhancing cognitive activity. It occurs when individuals use their meta-cognitive processes such as planning to direct their thinking and their knowledge [18]. Meta-cognitive evaluation refers to judgements made regarding one’s thinking processes, capacities, and limitations as these are employed in a particular situation or as self-attributes. For example, a person or a group could make an evaluation regarding the effectiveness of their solution method [18]. This meta-cognitive function assumes some awareness of the individual’s processes and knowledge.

Meta-cognition is widely recognized as an essential part of learning; particularly, it plays a vital role in success in mathematical problem-solving [4]. Generally, there are two directions for studies on meta-cognition in learning. The first direction is adapting meta-cognitive interventions and examining their effectiveness, e.g., [26,27,28]. Özsoy and Ataman [28] reported that meta-cognitive treatment improved mathematical problem-solving achievement among students. Desoete, Roeyers, and De Clercq [26] reported that students in the meta-cognitive group had significantly higher post-test mathematical problem-solving scores than the other four interventions. The positive treatment outcomes were obtained by adding an aspect of offline meta-cognition to mathematical problem-solving treatments [26]. The second direction follows the development of components in meta-cognitive knowledge and experiences as a result of the specific environment, e.g., Shahbari, Daher, and Rasllan [29]. Shahbari and her colleagues reported that engagement in modeling activities fostered participants’ meta-cognitive skills. In the current study, we joined the second direction, by tracing the meta-cognitive functions as defined by Wilson and Clark [18] in the learning sequences that were based on the solution of mathematics-based programming problems.

2.2. Programming in Mathematical Problem-Solving and Meta-Cognition

Programming languages, as employed in mathematics education, allow students to develop programs that can solve mathematical problems and provide teachers with a platform to assist childhood education [30]. The Scratch environment is an interactive graphical programming language that provides support for students in creative problem-solving [31]. Scratch is pointed at as having a positive effect on learning mathematics, improvements in mathematical processes, competencies such as identification and comparison of numbers [32], and equation-solving performance [33], besides increasing the positive attitudes toward learning mathematics [34]. On the other hand, acquiring basic programming skills is not enough, as Bernard and Bachu [35] reported that, although students acquire basic programming skills, they are unable to use them in a meaningful way to solve non-routine problems, and they are unable to validate their solutions.

Deek, McHugh, and Turoff [36] presented a six-step problem-solving and program development model: Formulating the problem; planning the solution; designing the solution; translation; testing and delivery. These steps are covered by the meta-cognitive functions, which emphasize that employment of meta-cognitive training has an important role in programming education. For example, the meta-cognitive instruction helped novices to develop a strong conceptual and strategic knowledge base to design a program for a novel problem [37]. Intervention based on meta-cognition caused significantly better acquisition of introductory programming concepts, and participants also reported positive feelings toward meta-cognitive instruction [13]. Despite the previous attempts of researchers to examine the impact of using meta-cognitive skills on programming education, little research has verified the development of using metacognitive skills; here, we are concerned with meta-cognitive functions, when solving mathematics-based programming problems. We attempt to do that in the present research.

Research questions:

• How and when do prospective teachers use meta-cognitive functions while solving mathematical-based programming problems in the Scratch environment?
• How are the meta-cognitive functions related to the programming or mathematical aspects of solving mathematical-based programming problems in the Scratch environment?

3. Method

3.1. Context and Participants

The study was conducted in a college of education among 18 third-year prospective teachers majoring in teaching mathematics and computers in middle school. The learning context was that of pedagogical training, where we utilized this context for educating our prospective teachers in integrating new technologies and teaching strategies, e.g., [10], with special emphasis on using the Scratch environment for programming. The prospective teachers were requested to use the Scratch environment as a means for drawing geometric shapes or developing knowledge of other mathematical fields like algebra. In addition, they were advised to use meta-cognitive functions through their mathematical problem-solving and Scratch programming processes. Two of the authors were responsible for the preparation process that was implemented in a workshop held each day where the actual practical training in the schools took place. Those authors accompanied the prospective teachers in their practical training in two middle schools as pedagogical supervisors.

The prospective teachers did not have previous knowledge of the Scratch environment. The participants worked in groups of 3–4 members. We chose to document three groups based on the acceptance of the groups to be documented in video, and their volunteering to be interviewed after their solving of the mathematical problems. All prospective teachers were required to participate in the learning sequence as part of their B.Ed. studies in college.

3.2. Research Procedure

The research was conducted along one year; the prospective teachers were engaged in solving a sequence of mathematical problems that require the utilization of Scratch for graphical and programming purposes.

3.3. Data Sources

The data were collected using a couple of tools: Video recordings of the learning process of the prospective teachers and the prospective teachers’ reports.

3.3.1. Video Recording of the Learning Process

We documented the prospective teachers’ solving and discussing of the problems in all the learning sequences for each one of three groups.

3.3.2. The Prospective Teachers’ Reports

The participating prospective teachers’ discussions and solutions of the problems were documented in each group and delivered to the authors at the end of each activity. After solving each problem, each group watched the video recording that documented their activity in solving the problem. The participants got Wilson and Clarke’s [18] fourteen cards; each card included meta-cognitive action statements that associated with one of the three meta-cognitive functions (awareness, regulation, and evaluation) in the mathematical and programming aspects. The participants were asked to choose the card that appropriates to their engagement in the problem’s solving.

3.4. Data Analyses

3.4.1. Video Recording of the Learning Process

We used the deductive and inductive constant comparative method [38] to analyze the problem-solving processes for each problem. Doing that, we followed works that we did earlier [39,40]. We considered the video recording of the learning process together with the solution texts of the participating prospective teachers.

3.4.2. The Prospective Teachers’ Reports

We considered the mathematical processes and the programming processes. For each group, we constructed a chain that presents their meta-cognitive functions used in the solution process of each problem. The deductive method was based on Wilson and Clark’s [18] fourteen cards, which included the following statements for each of the meta-cognitive functions:

Awareness: ‘I thought about what I already know’, ‘I tried to remember if I had ever done a problem like this before’, ‘I thought about something I had done another time that had been helpful’, ‘I thought ‘I know what to do’’, ‘I thought ‘I know this sort of problem’’.

Evaluation: ‘I thought about how I was going’, ‘I thought about whether what I was doing was working’, ‘I checked my work’, ‘I thought ‘Is this right?’’, ‘I thought ‘I can’t do it’’.

Regulation: ‘I made a plan to work it out’. ‘I thought about a different way to solve the problem’, ‘I thought about what I would do next’, ‘I changed the way I was working’.

Due to the finer analyses of this data, we chose to analyze our data resources in three stages along the learning sequence: At the beginning, at the middle, and at the end of the learning process.

3.5. Learning Sequences

The learning sequence was based on solving mathematical-based programming problems by the prospective teachers in the Scratch environment. In detail, the sequence included five phases. The first phase addressed assessing the prospective teachers’ abilities in Scratch and meta-cognition, which was done through requesting them to solve a problem individually and detail their thinking processes while solving it. The second phase addressed discussing the meta-cognitive processes in the solutions, and examining the intuitive use of meta-cognition in the solutions—when such use was present. The third phase addressed introducing the Scratch programming and the meta-cognitive functions as tools for improving the prospective teachers’ solution processes. In the fourth phase, the prospective teachers were requested to work in groups to solve mathematical-based programming problems, while discussing their use of meta-cognitive functions and documenting their solution steps and their thinking processes. In the fifth phase, the prospective teachers used their improved Scratch skills and meta-cognitive functions independently to solve new problems. At this phase, the prospective teachers worked individually first and then in groups to solve the problems. Afterward, they discussed in the whole class their use of the meta-cognitive functions in their solutions.

3.6. Learning Activities

Here, we present three problems that the prospective teachers engaged with in different stages of the learning sequence. The prospective teachers were requested to write the steps of their drawing, their planning, thoughts, and reflections during the programming, as well as how they proceeded in this programming.

3.6.1. First Problem

The following shape (see Figure 1) includes a sequence of embedded squares: You are requested to draw these squares with Scratch.

3.6.2. Second Problem

You need to construct a series of embedded equilateral triangles as presented in the following shape (see Figure 2).

3.6.3. Third Problem

Given 3 houses (see Figure 3), not located on a straight line, we want to dig a well that is equidistant from the three houses. Where should the well be located?

Show this in the Scratch environment.

4. Findings

The analyses of the participants’ discourse through their engagement in problem-solving indicated two main effects of the learning sequence on the prospective teachers’ utilization of the meta-cognitive functions. The first is related to the development of meta-cognitive functions among the participants, while the second is related to the differences between the frequencies of the three types of meta-cognitive functions (awareness, regulation, and evaluation) in both the mathematical and programming aspects.

4.1. Development of Meta-Cognitive Functions Among Prospective Teachers

The findings indicated differences in using meta-cognitive functions among the prospective teachers in three stages of the learning sequence. In the first stage, prospective teachers approached the problems without any process of regulation. In the second stage, the prospective teachers approached the problems utilizing regulation within the programming processes or within the mathematical processes. In the third stage, the prospective teachers approached utilizing regulation in both mathematical processes and programming processes. Below, we describe each of these stages, taking care of the three types of meta-cognitive functions: Awareness, regulation, and evaluation.

4.1.1. First Stage: Approaching the Problems without Utilizing Regulation

The prospective teachers’ approach at this stage to the problem; the first problem in the learning activities above was characterized by spontaneous solving, where no regulated activity was identified. Doing that, the prospective teachers discussed several ideas and moved from one to another without an in-depth investigation of the problem.

4.1.2. Second Stage: Approaching the Problems with the Utilization of Meta-Cognitive Functions Only in the Mathematical Processes or the Programming Processes

At this stage, we identified regulation actions. However, these actions occurred while performing mathematical processes or while performing programming processes. Episode 1 presents prospective teachers’ regulation of their mathematical processes without regulating their programming processes. This happened while one group (Salam, Seham, and Alla) solved the second problem in the learning activities above.

Episode 1: Utilizing meta-cognitive functions in the mathematical processes

(100)

Salam: We need to plan our solution.

(101)

Seham: First, we must organize the data.

(102)

Alla: Then, we must move from the initial point.

(103)

Salam: We need to know the length of the side.

…

(The prospective teachers continue to discuss and construct their mathematical ideas. Then, they began implementing their ideas in Scratch)

(145)

Salam: Do repetition

(146)

Alaa: Turn with angle 30 to the right.

(147)

Salam: The sides are a and b.

(148)

Alaa: Turn with angle 120 and move b, three times.

(149)

Salam: (after trying to run the program) Oh, it is a hexagon.

(150)

Alaa: Let us see what mathematical mistakes we made.

Episode 1 shows that the prospective teachers became aware of the meta-cognitive process; i.e., planning, needed for their solving of the problem (100). This awareness supported them in regulating their mathematical actions (101–103). However, they started their programming spontaneously without planning their programming processes, which resulted in another shape (145–149). This made them decide to evaluate their mathematical actions (150).

Episode 2 presents the prospective teachers’ utilization of meta-cognitive functions in their programming without taking care of their mathematical processes. This happened while one group (Maha, Namareq, and Nora) solved the second problem in the learning activities above.

Episode 2: Regulation of the programming processes

(153)

Maha: We need to plan how to do that in Scratch.

(154)

Namareq: If we get to the edge, we must use the ‘rotation’ block if we were at a particular point on the edge.

(155)

Maha: When it gets to the edge, it must turn around at a certain angle

(156)

Nora: It means we want to keep it walking a certain distance to get to the edge, then turn around at a certain angle, and continue walking for a certain distance.

Episode 2 shows that prospective teachers did not discuss the problem mathematically, but showed awareness of the need to plan their programming in Scratch (153). They discussed and planned how to apply their solution in Scratch by regulating their programming toward using features such as the ‘rotation’ block (154).

4.1.3. Third Stage: Approaching the Problems with the Regulation in Both Aspects (Mathematical Aspect and Programming Aspect)

The prospective teachers’ approach to the problems, at the third stage, is characterized by the characterization of their working in both mathematical solving and programming. They analyzed the problems’ data, followed by planning the mathematical solution and then planning the programming in Scratch. At this stage, unlike the previous stages, the prospective teachers did not apply the trial and error method as part of their problem-solving processes. This is presented in Episode 3, which describes part of the solution of one group (Mai, Rina, and Rand) for the third problem in the learning activities above.

Episode 3: Regulation of the mathematical and programming processes

(314)

Mai: We begin by looking at the givens of the problem. This will help us plan our solution.

(315)

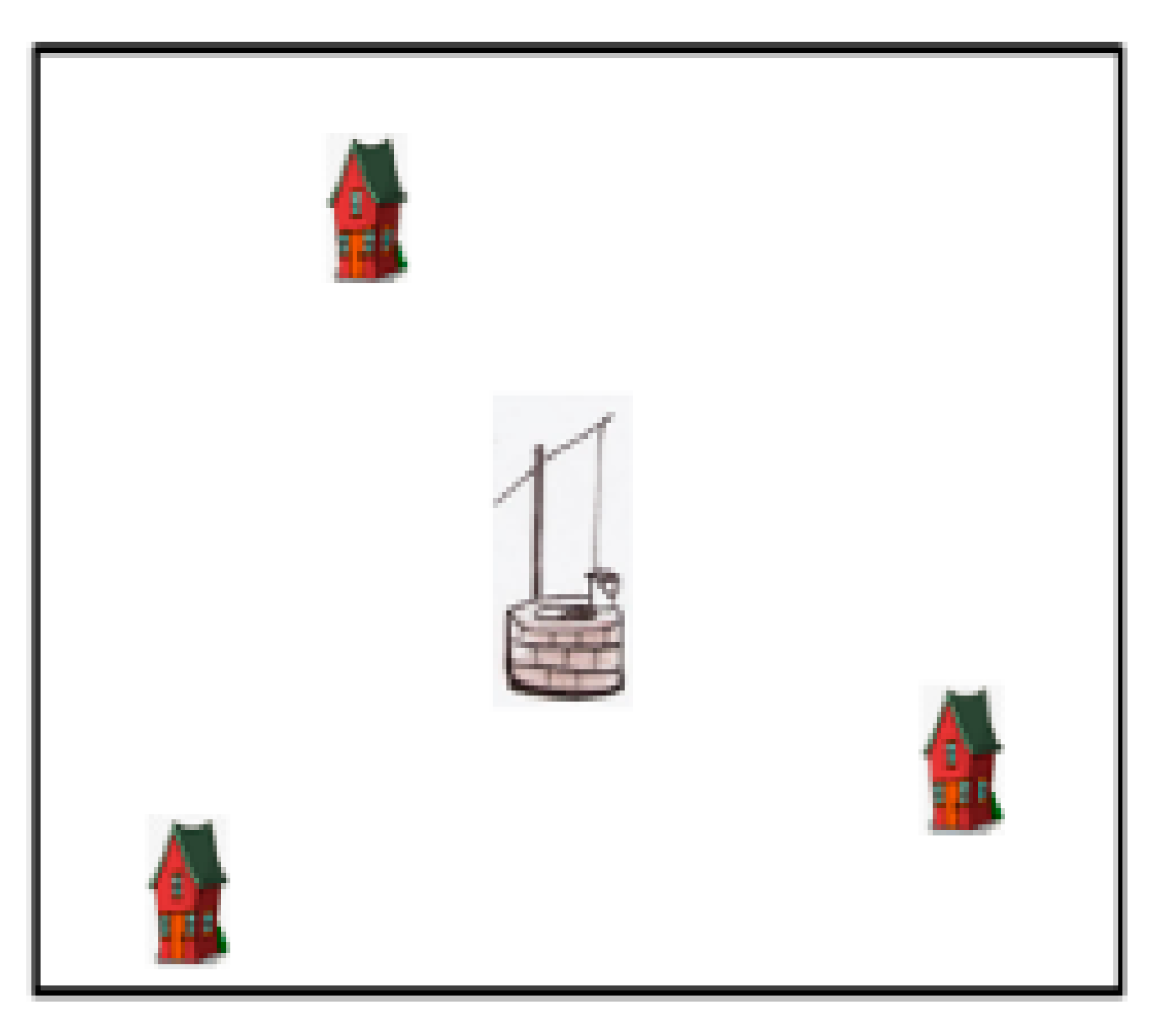
Rina: We have three houses that are not located on a straight line.

(316)

Rand: We can say that we have three coordinates of three points

(317)

Mai: This situation makes me think of a circle; the houses could be points on the circle, and the well could be the centre of the circle. Here, we can use the mathematical features of the circle’s centre.

(318)

Rand: So, we need to assign the three points, and then find the coordinates of the circle’s centre.

(319)

Rina: We can locate geometrically the coordinates of the circle’s centre by connecting the three points with three segments and drawing the perpendicular bisectors of two of them. The intersection point of the two perpendicular bisectors is the centre of the circle—the location of the well.

…

(The prospective teachers continued doing the mathematical calculations of the problem)

(378)

Mai: We need now to assign the coordinates in Scratch.

…

(Before performing in Scratch, the prospective teachers discussed how to use the features of Scratch to get the best solution).

(390)

Rina: We can use the ‘random position’ block for the locations of the houses.

(391)

Rand: After drawing the points, we need to show the drawings of the segments and perpendicular bisectors in Scratch.

(392)

Rand: We use the geometrical calculations of the circle’s centre to present the location of the well on the Scratch screen.

Episode 3 shows that the prospective teachers were aware of the meta-cognitive process of organizing the data (314); a process that precedes the planning process. This helped them advance toward regulating their mathematical (317–319), as well as programming (390, 392), processes. The prospective teachers determined, at the beginning, the specific givens of the problem. Then, they planned their mathematical solution and, afterward, discussed and planned their programming options in Scratch.

4.2. Frequencies of Meta-Cognitive Functions

The findings obtained from analysis of the prospective teachers’ reports indicated different frequencies of the meta-cognitive functions in the three problems. These findings indicated an increase in the regulation of meta-cognitive functions utilized in the mathematical and programming processes. In Figure 4, we present the sequence of participants’ meta-cognitive functions only among one group through the three problems. The frequencies in the other two groups showed a similar pattern of frequencies.

Figure 4 indicates that at the final stage in the learning process, the regulation meta-cognitive function is more frequent than the awareness and evaluation meta-cognitive functions in both the mathematical and programming processes. Besides, we notice that in this final stage, the use of meta-cognitive functions in the mathematical processes was more frequent than in the programming processes.

5. Discussion

The current study aimed to examine the use of meta-cognitive functions among prospective teachers while solving mathematical-based programming problems with Scratch. Previous studies examined whether programming with Scratch improves students’ outcomes related to students’ cognitive performance and cognitive processes in the mathematics class. These studies showed that the Scratch programmed activities led to significant improvement in conceiving mathematical concepts like the learning of probability concepts by middle-school students [41], which was achieved in Scratch-based video games, or Scratch-based mathematical thinking by sixth-grade students [42]. The present study was interested in a field related to cognitive processes; i.e., meta-cognition, and specifically, in the prospective teachers’ development of meta-cognitive functions in solving mathematical-based programming problems with Scratch. The findings indicated that at the beginning of the learning process, the prospective teachers approached the problems without any indications of awareness, regulation, or evaluation. This result is expected as the prospective teachers did not have sufficient experience in using meta-cognitive functions in their problem-solving. This is especially true as they were engaged in problem-solving in new contexts, like programming with Scratch here. Later, as the prospective teachers were introduced to meta-cognition and programming with Scratch, they developed meta-cognitive functions either in the programming processes or in the mathematical processes. As the prospective teachers advanced in programming experience through problem-solving and meta-cognition utilization, they approached the problems using meta-cognitive functions in both mathematical and programming processes. These findings join the various studies that indicated the effectiveness of using Scratch in learning and teaching mathematics, e.g., [18,19]. More specifically, it emphasizes the role of technology [8] and the role of programming [43] in fostering the meta-cognitive functions that positively influence the different aspects of problem-solving activity [44]. Here, it positively influenced the prospective teachers’ utilization of meta-cognitive processes in a field that combines mathematical and programming problem-solving.

The findings also indicated that the prospective teachers developed regulation of meta-cognitive functions more than awareness and evaluation ones in both mathematical and programming aspects. This indicates that the participants recognized the need to regulate their solving processes, especially in a context that includes different learning components like problem-solving, mathematical thinking, and programming thinking. This implies that the participating prospective teachers acknowledged the importance of regulation in facilitating the solution of complex problems [45], especially in succeeding to solve mathematical problems [46], and mathematics-based programming problems here.

Finally, it is important to note that the present research studied the solving of mathematical-based programming problems with Scratch by only one class of prospective teachers. Further research is needed to target the intersection of meta-cognition, mathematics-based problems, and programming. Future research could address different student populations in the different school levels. This is especially needed as programming has been suggested lately for improving various skills of learners, like computational thinking (CT) [47] and logical thinking [48].

6. Conclusions

The current study highlighted the importance of the engagement in a sequence of mathematics-based programming problems in the Scratch environment for fostering meta-cognitive functions in both mathematical and programming processes. It targets a field that has been studied little, i.e., the meta-cognition in solving mathematical-based programming problems with Scratch.

We can conclude that the role of the sequence of mathematics-based programming problems, side-by-side with the guidelines of the instructor, had an important role in supporting the developments of learner’s meta-cognitive functions in programming and in mathematics problem-solving. Moreover, we can conclude that the development of only mathematical meta-cognitive functions or programming meta-cognitive functions is inefficient for solving mathematics-based programming problems successfully. Therefore, in such intervention, it is important to emphasize the meta-cognitive functions in both aspects, mathematics and programming. Another implication of the current study emphasizes the implementation of such a learning sequence in the teacher’s education training in order to develop prospective teacher’s meta-cognitive functions.

The present research goes one step further in this direction. It proved that complex meta-cognitive activity is subject to education. Through the problem-solving of sequences of problems and the mediation of the teacher, learners can advance their utilization of meta-cognitive processes, even in new contexts that combine more than one discipline. More research is needed regarding meta-cognition instruction for the different school levels.