Contention-Free Scheduling for Mixed-Criticality Multiprocessor Real-Time System
Abstract
:1. Introduction
- We propose a method to calculate an upper bound of the number of contention-free slots for each task;
- We then propose MC-CF;
- We develop the DA test for MC-CF.
2. Related Work
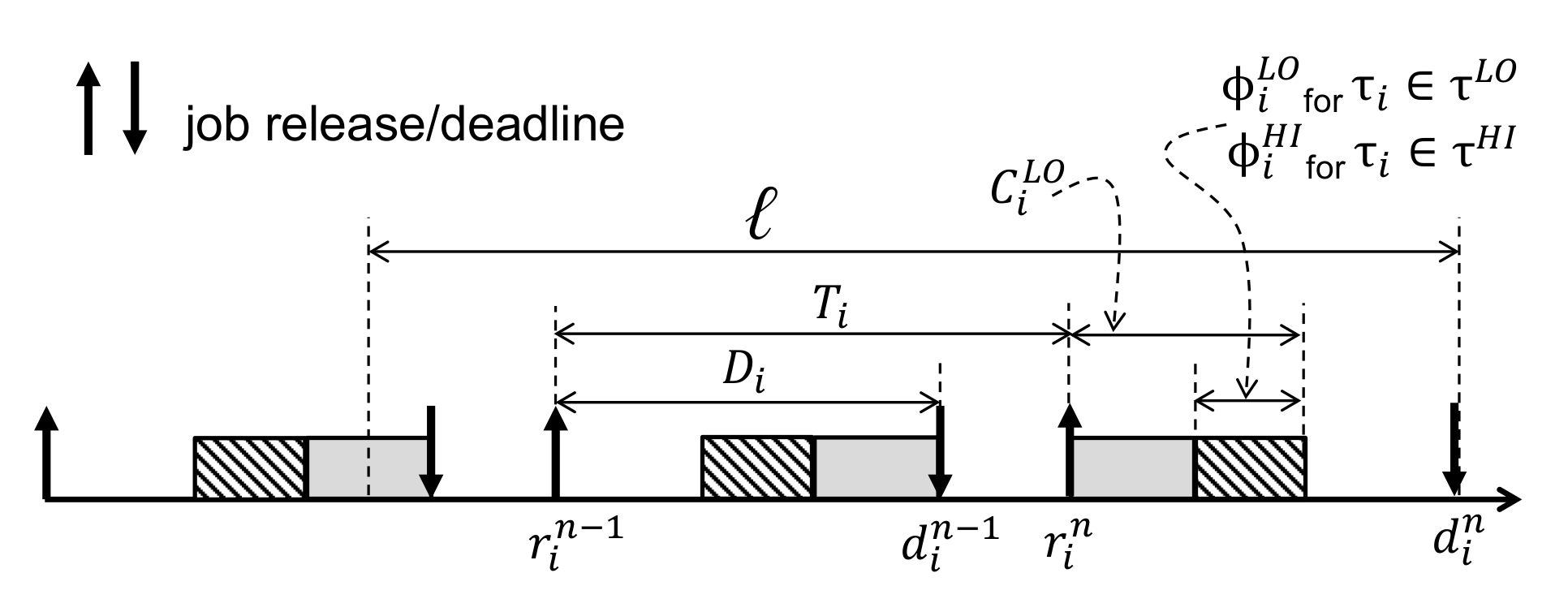
3. System Model
- is the criticality of a task, and a task with or is either a HI-criticality or LO-criticality task, respectively.
- and denote the worst-case execution times (WCETs) for the low and high criticalities, respectively. We assume that because a task with higher criticality requires a more conservative analysis for WCET.
- and represent the relative deadline and the period of the task, respectively, and is satisfied.
- In the LO-mode, every task is schedulable; and
- In the HI-mode, every task is schedulable.
4. MC-CF
4.1. MC-CF Scheme
| Algorithm 1 CF policy for MC multiprocessor systems. |
|
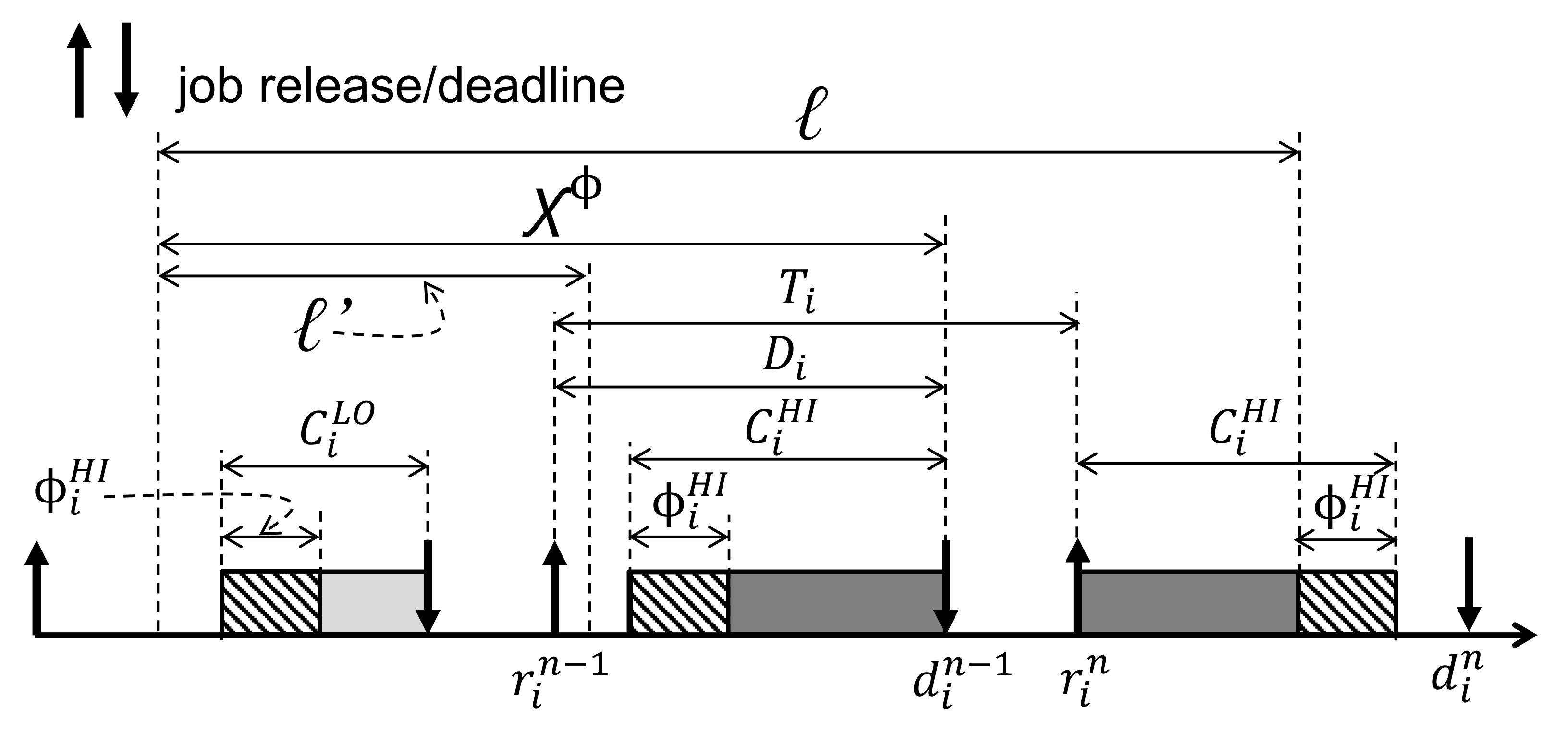
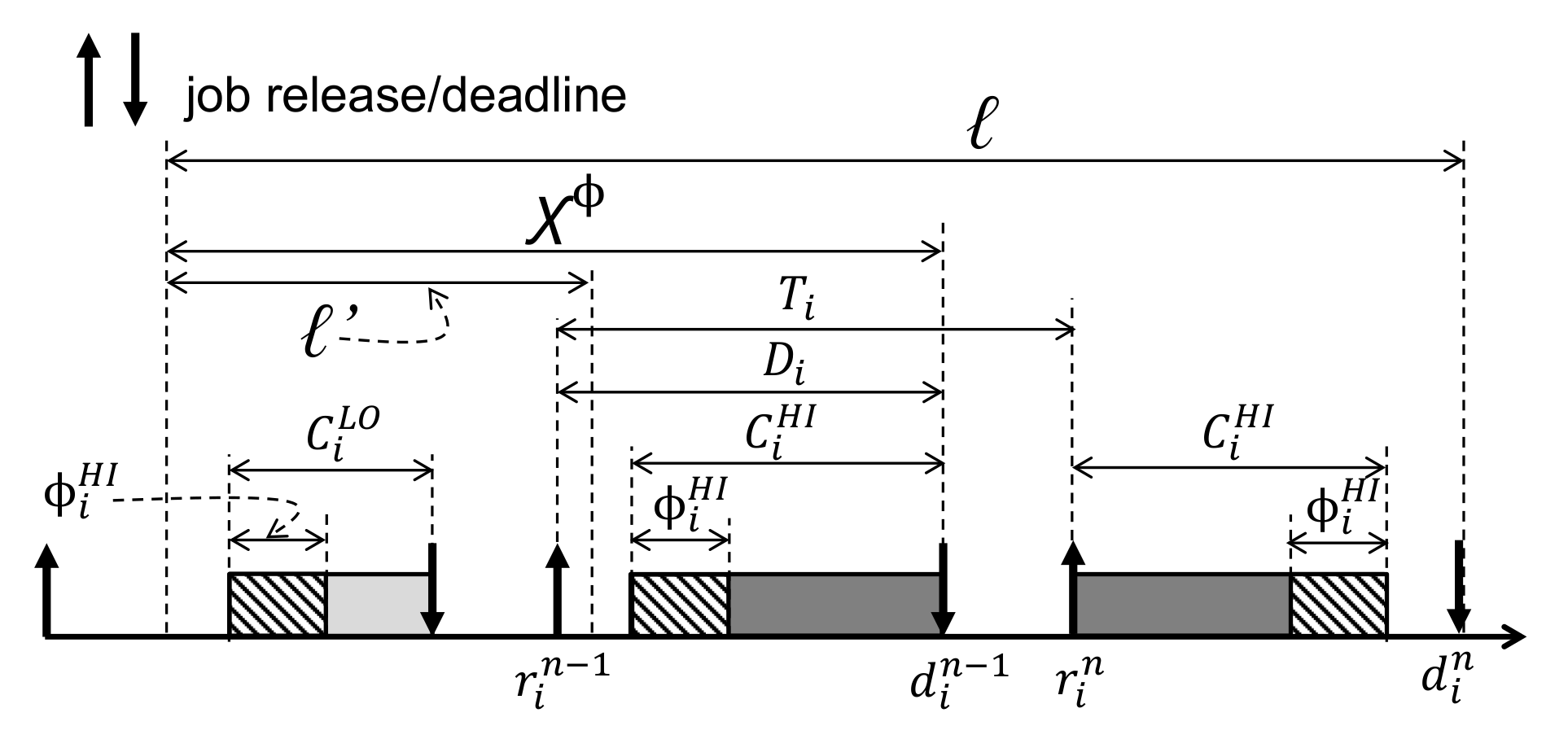
4.2. Lower Bound of Contention-Free Slots
5. Schedulability Analysis for MC-CF
5.1. Schedulability Analysis for LO-Mode
5.2. Schedulability Analysis for HI-Mode
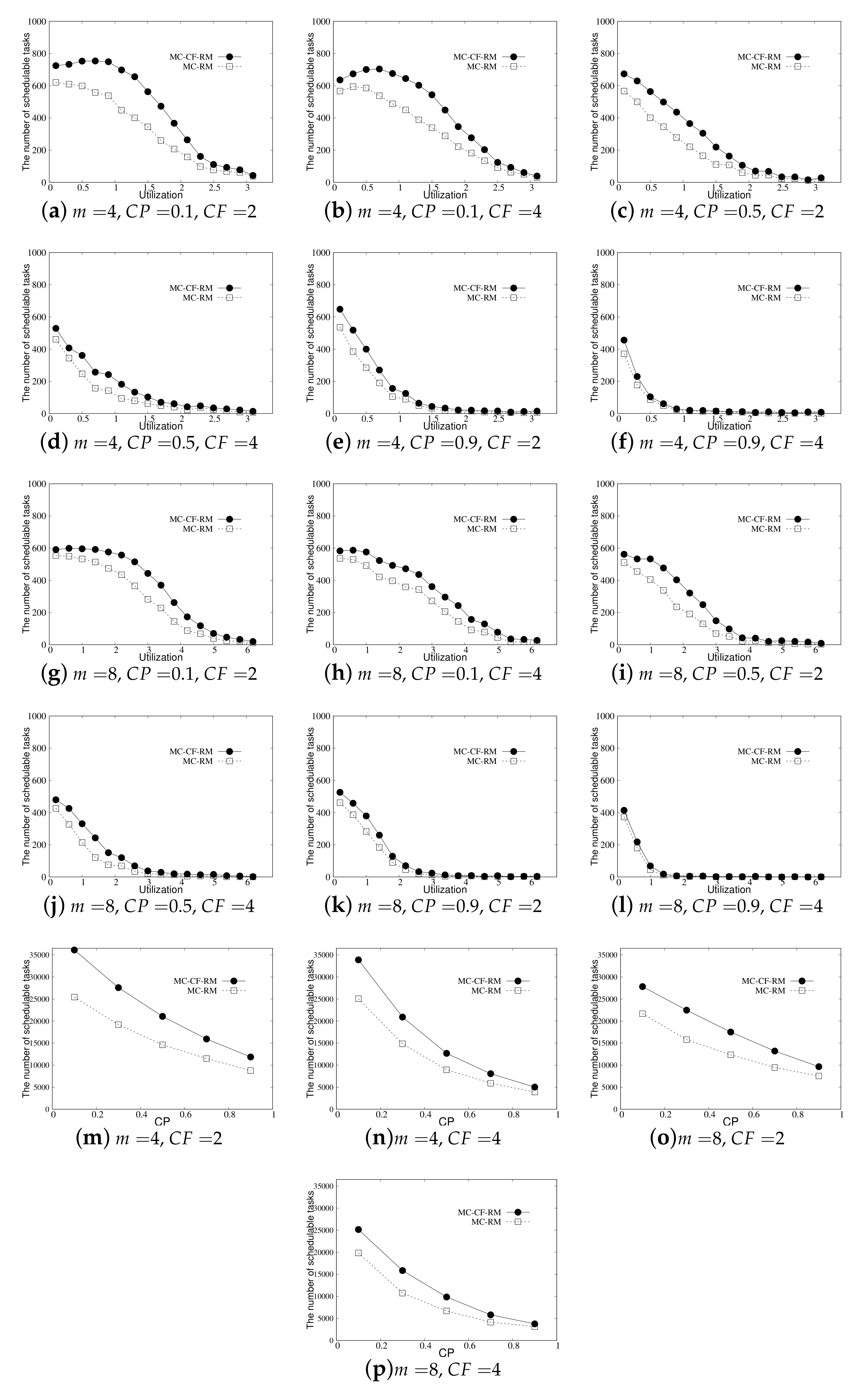
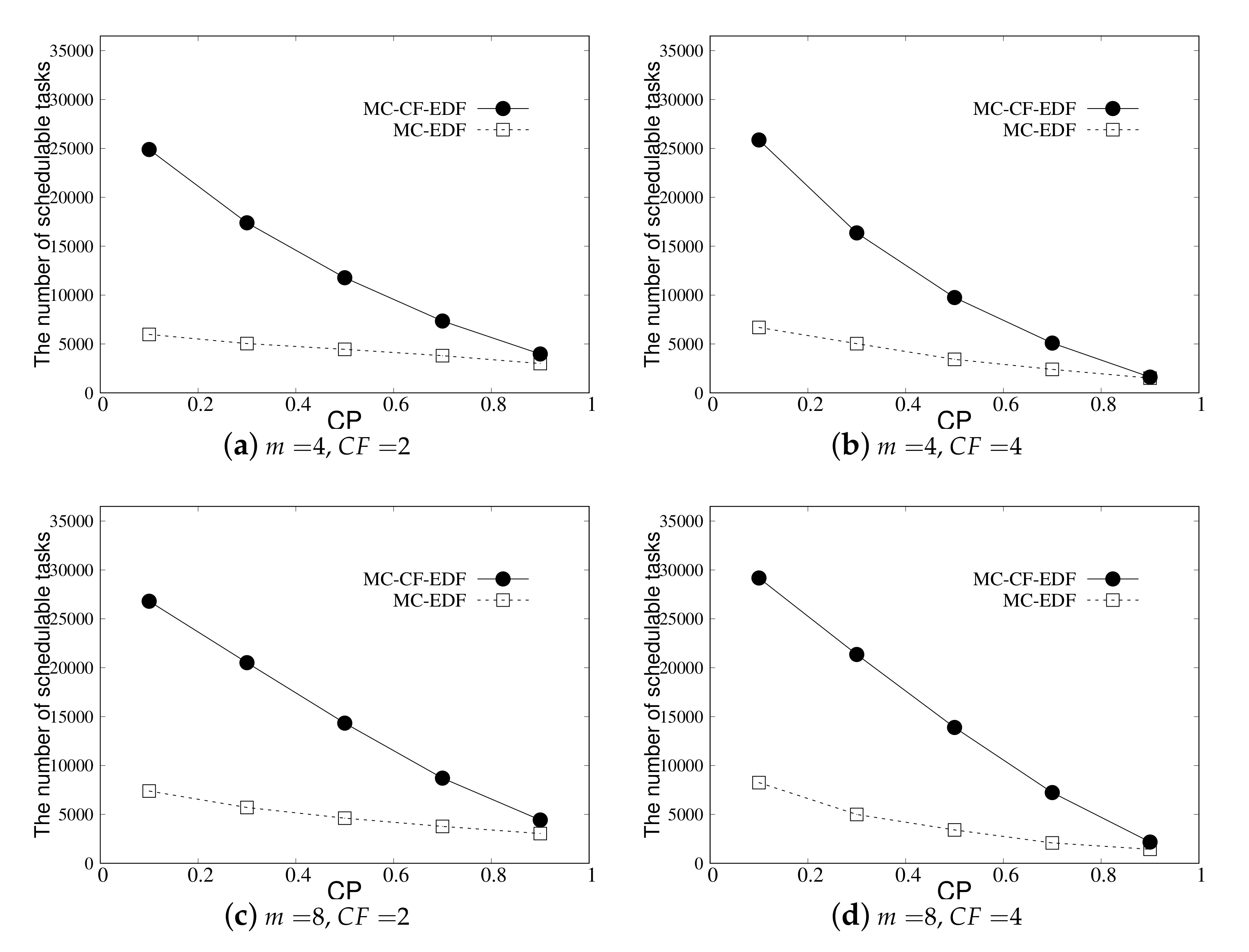
6. Evaluation
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Baruah, S.; Mok, A.; Rosier, L. Preemptively scheduling hard-real-time sporadic tasks on one processor. In Proceedings of the IEEE Real-Time Systems Symposium (RTSS), Lake Buena Vista, FL, USA, 5–7 December 1990; pp. 182–190. [Google Scholar]
- Anderson, J.H.; Srinivasan, A. Early-release fair scheduling. In Proceedings of the 12th Euromicro Conference on Real-Time Systems, Euromicro, RTSECRTS, Stockholm, Sweden, 19–21 June 2000; pp. 35–43. [Google Scholar]
- Cho, H.; Ravindran, B.; Jensen, E.D. An Optimal Real-Time Scheduling Algorithm for Multiprocessors. In Proceedings of the 27th IEEE International Real-Time Systems Symposium (RTSS’06), Rio de Janeiro, Brazil, 5–8 December 2006; pp. 101–110. [Google Scholar]
- Regnier, P.; Lima, G.; Massa, E.; Levin, G.; Brandt, S. RUN: Optimal Multiprocessor Real-Time Scheduling via Reduction to Uniprocessor. In Proceedings of the IEEE Real-Time Systems Symposium (RTSS), Vienna, Austria, 29 November–2 December 2011; pp. 104–115. [Google Scholar]
- Andersson, B.; Tovar, E. Multiprocessor Scheduling with Few Preemptions. In Proceedings of the 12th IEEE International Conference on Embedded and Real-Time Computing Systems and Applications (RTCSA’06), Sydney, Australia, 16–18 August 2006; pp. 322–334. [Google Scholar]
- Levin, G.; Funk, S.; Sadowski, C.; Pye, I.; Brandt, S. DP-FAIR: A Simple Model for Understanding Optimal Multiprocessor Scheduling. In Proceedings of the Euromicro Conference on Real-Time Systems (ECRTS), Brussels, Belgium, 6–9 July 2010; pp. 3–13. [Google Scholar]
- Ernst, R.; Natale, M.D. Mixed Criticality Systems—A History of Misconceptions? IEEE Des. Test 2016, 33, 65–74. [Google Scholar] [CrossRef]
- Anderson, J.H.; Baruah, S.; Brandenburg, B.B. Multicore operating-system support for mixed criticality. In Proceedings of the Workshop on Mixed-Criticality: Roadmap to Evolving UAV Certification, San Francisco, CA, USA, 16 April 2009. [Google Scholar]
- Pathan, R. Schedulability Analysis of Mixed-Criticality Systems on Multiprocessors. In Proceedings of the Euromicro Conference on Real-Time Systems (ECRTS), Pisa, Italy, 11–13 July 2012; pp. 309–320. [Google Scholar]
- Baek, H.; Jung, N.; Chwa, H.S.; Shin, I.; Lee, J. Non-Preemptive Scheduling for Mixed-Criticality Real-Time Multiprocessor Systems. IEEE Trans. Parallel Distrib. Syst. 2018, 29, 1766–1779. [Google Scholar] [CrossRef]
- Baker, T.P.; Cirinei, M.; Bertogna, M. EDZL Scheduling Analysis. Real Time Syst. 2008, 40, 264–289. [Google Scholar] [CrossRef]
- Lee, J.; Easwaran, A.; Shin, I. Maximizing Contention-Free Executions in Multiprocessor Scheduling. In Proceedings of the IEEE Real-Time Technology and Applications Symposium (RTAS), Chicago, IL, USA, 11–14 April 2011; pp. 235–244. [Google Scholar]
- Lee, J.; Easwaran, A.; Shin, I. Contention-Free Executions for Real-Time Multiprocessor Scheduling. ACM Trans. Embed. Comput. Syst. 2014, 13, 1–69. [Google Scholar] [CrossRef]
- Jung, N.; Baek, H.; Lim, D.; Lee, J. Incorporating Zero-Laxity Policy into Mixed-Criticality Multiprocessor Real-Time Systems. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2018, 101, 1888–1899. [Google Scholar] [CrossRef]
- Burns, A.; Davis, R.I. Mixed Criticality Systems—A Review; University of York: York, UK, 2015. [Google Scholar]
- Bertogna, M.; Cirinei, M. Response-Time Analysis for Globally Scheduled Symmetric Multiprocessor Platforms. In Proceedings of the 28th IEEE International Real-Time Systems Symposium (RTSS 2007), Tucson, AZ, USA, 3–6 December 2008; pp. 149–160. [Google Scholar]
- Baek, H.; Lee, J.; Shin, I. Multi-Level Contention-Free Policy for Real-Time Multiprocessor Scheduling. J. Syst. Softw. 2018, 137, 36–49. [Google Scholar] [CrossRef]
- Baek, H.; Lee, J. Improved Schedulability Analysis of the Contention-Free Policy for Real-Time Systems. J. Syst. Softw. 2019, 154, 112–124. [Google Scholar] [CrossRef]
- Vestal, S. Real-Time Sampled Signal Flows through Asynchronous Distributed Systems. In Proceedings of the IEEE Real-Time Technology and Applications Symposium (RTAS), San Francisco, CA, USA, 7–10 March 2005; pp. 170–179. [Google Scholar]
- Baruah, S.; Bonifaci, V.; D’Angelo, G.; MarchettiSpaccamela, A.; van der Ster, S.; Stougie, L. Mixed-criticality scheduling of sporadic task systems. In Proceedings of the 19th Annual European Symposium on Algorithms, Saarbrücken, Germany, 5–9 September 2011; pp. 555–566. [Google Scholar]
- Baruah, S.; Bonifaci, V.; D’Angelo, G.; Marchetti-Spaccamela, H.L.A.; van der Ster, S.; Stougie, L. The Preemptive Uniprocessor Scheduling of Mixed-Criticality Implicit-Deadline Sporadic Task Systems. In Proceedings of the Euromicro Conference on Real-Time Systems (ECRTS), Pisa, Italy, 11–13 July 2012; pp. 145–154. [Google Scholar]
- Baruah, S.; Burns, A.; Davis, R.I. Response-Time Analysis for Mixed Criticality Systems. In Proceedings of the IEEE Real-Time Systems Symposium (RTSS), Vienna, Austria, 29 November–2 December 2011; pp. 34–43. [Google Scholar]
- Baruah, S.; Li, H.; Stougie, L. Toward the design of certifiable mixed-criticality systems. In Proceedings of the IEEE Real-Time Technology and Applications Symposium (RTAS), Stockholm, Sweden, 12–15 April 2010; pp. 13–22. [Google Scholar]
- Li, H.; Baruah, S. An algorithm for scheduling certifiable mixed-criticality sporadic task systems. In Proceedings of the IEEE Real-Time Systems Symposium (RTSS), San Diego, CA, USA, 30 November–3 December 2010; pp. 183–192. [Google Scholar]
- Baruah, S. Schedulability Analysis for a General Model of Mixed-Criticality Recurrent Real-Time Tasks. In Proceedings of the IEEE Real-Time Systems Symposium (RTSS), Porto, Portugal, 29 November–2 December 2016. [Google Scholar]
- Li, H.; Baruah, S. Global mixed-criticality scheduling on multiprocessors. In Proceedings of the Euromicro Conference on Real-Time Systems (ECRTS), Pisa, Italy, 10–13 July 2012; pp. 166–175. [Google Scholar]
- Lee, J.; Phan, K.; Gu, X.; Lee, J.; Easwaran, A.; Shin, I.; Lee, I. MC-Fluid: Fluid Model-Based Mixed-Criticality Scheduling on Multiprocessorss. In Proceedings of the IEEE Real-Time Systems Symposium (RTSS), Rome, Italy, 2–5 December 2014; pp. 41–52. [Google Scholar]
- Davis, R.; Burns, A. Priority Assignment for Global Fixed Priority Pre-emptive Scheduling in Multiprocessor Real-Time Systems. In Proceedings of the IEEE Real-Time Systems Symposium (RTSS), Washington, DC, USA, 1–4 December 2009; pp. 398–409. [Google Scholar]
- Bini, E.; Buttazzo, G. Measuring the performance of schedulability tests. Real Time Syst. 2005, 30, 129–154. [Google Scholar] [CrossRef]



| Notation | Description | Notation | Description |
|---|---|---|---|
| m | the number of processors | a task set | |
| a task in | the criticality of | ||
| WCET for the low criticality | WCET for high criticality | ||
| the relative deadline of | the period of | ||
| a set of tasks of which the criticality is low | a set of tasks of which the criticality is high | ||
| the n-th job invoked by | the release time of | ||
| the finishing time of | the absolute deadline of | ||
| a set of tasks of which the priority of each is higher than | the lower bound of the contention-free slots for | ||
| the lower bound of the contention-free slots for | the remaining execution time of at t | ||
| the remaining contention-free slots of at t | the queue in which tasks have their original priorities | ||
| the queue in which tasks have demoted priorities | the lower bound of the contention-free slots for , assuming that a mode transition occurs at | ||
| the interference of on in the LO-mode | the interference of on , assuming that a mode transition occurs at |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baek, H.; Lee, K. Contention-Free Scheduling for Mixed-Criticality Multiprocessor Real-Time System. Symmetry 2020, 12, 1515. https://doi.org/10.3390/sym12091515
Baek H, Lee K. Contention-Free Scheduling for Mixed-Criticality Multiprocessor Real-Time System. Symmetry. 2020; 12(9):1515. https://doi.org/10.3390/sym12091515
Chicago/Turabian StyleBaek, Hyeongboo, and Kilho Lee. 2020. "Contention-Free Scheduling for Mixed-Criticality Multiprocessor Real-Time System" Symmetry 12, no. 9: 1515. https://doi.org/10.3390/sym12091515
APA StyleBaek, H., & Lee, K. (2020). Contention-Free Scheduling for Mixed-Criticality Multiprocessor Real-Time System. Symmetry, 12(9), 1515. https://doi.org/10.3390/sym12091515





