Magnetized Flow of Cu + Al2O3 + H2O Hybrid Nanofluid in Porous Medium: Analysis of Duality and Stability
Abstract
1. Introduction
2. Mathematical Modeling
3. Stability Analysis
4. Results and Discussion
5. Conclusions
- The present results show good agreements with the previously published results.
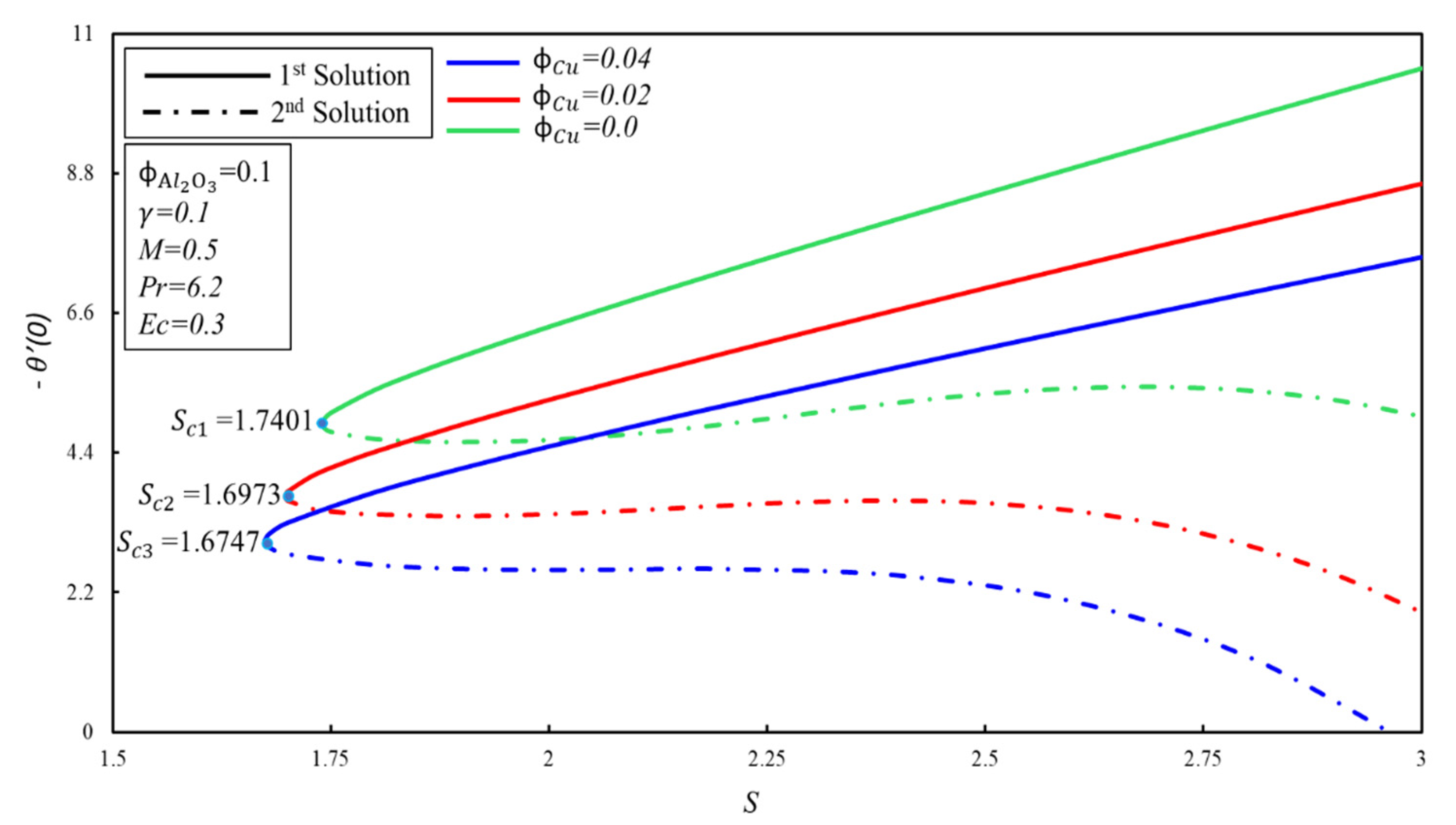
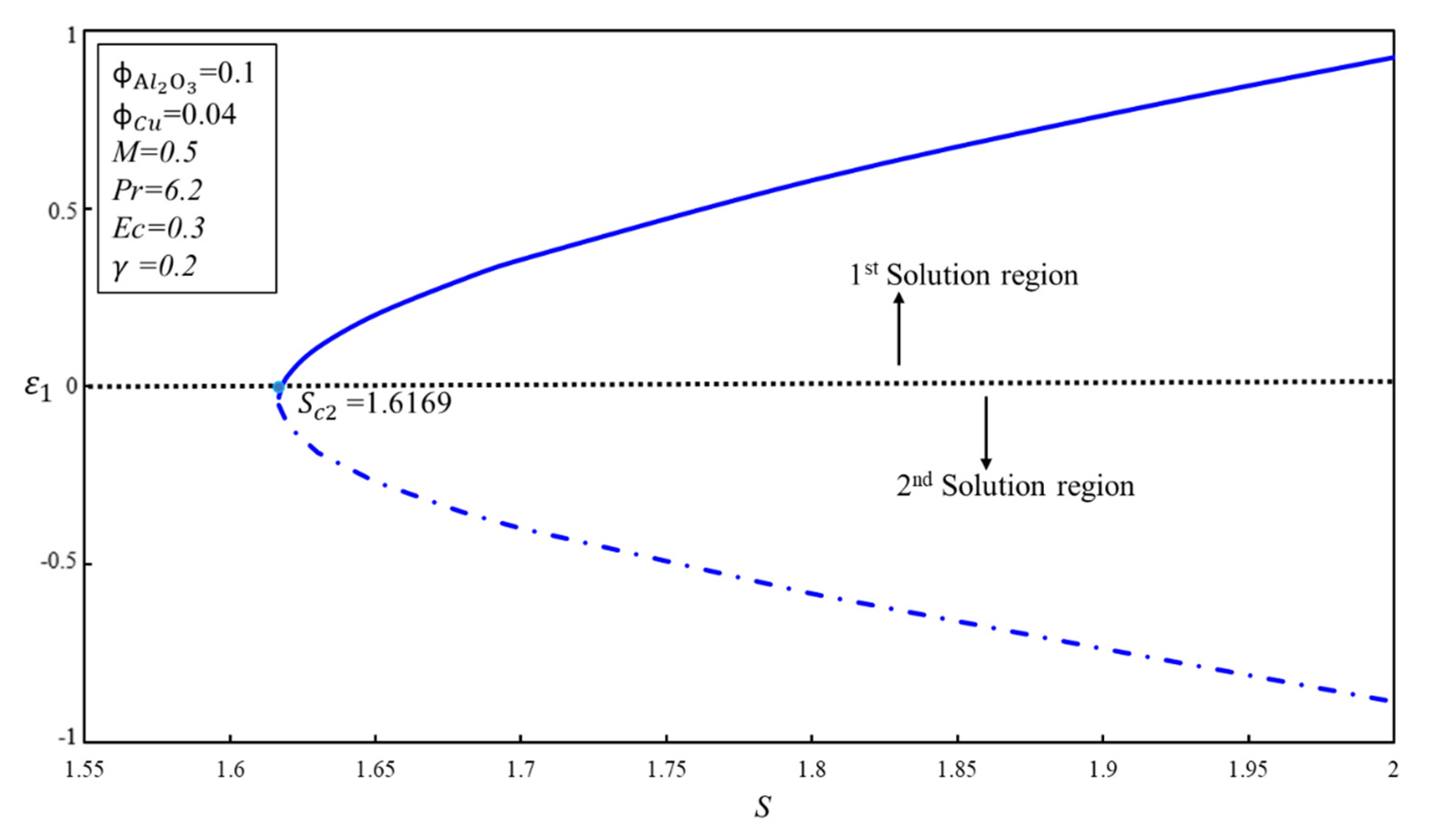
- Dual solutions exist when , while no solution exists .
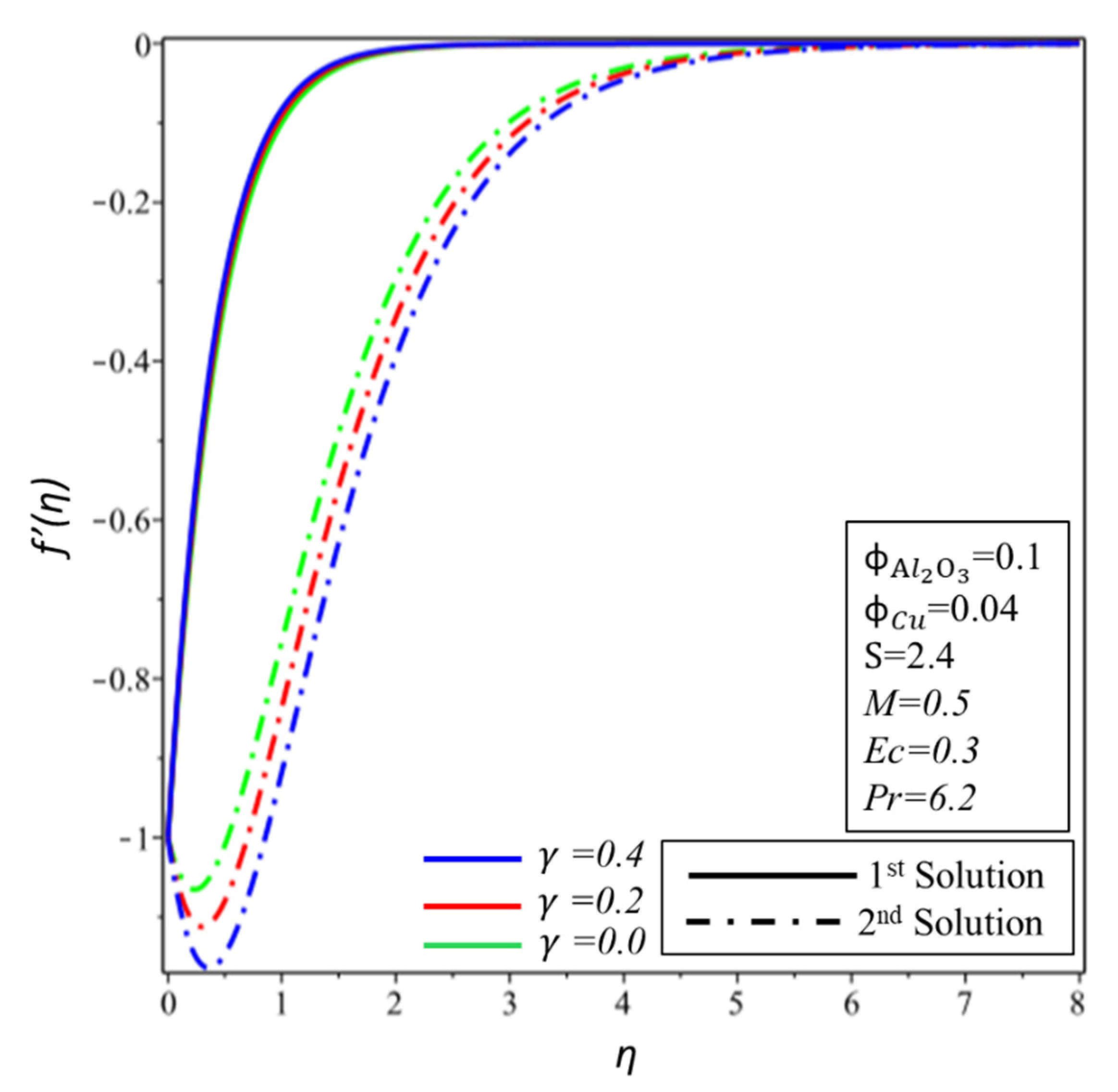
- Shear stress rises in the first solution then declines in the second solution for the rising values of , , , and .
- For the first solution, the heat transfer rate rises as S and M parameters are enhanced, while this is lower when is up.
- Enhancement in the volume fraction of the nanoparticles pushes forward the boundary layer separation. Therefore, ranges of solutions increase.
- Compared with nanofluid and viscous fluid, hybrid nanofluid seems to be more efficient in cooling processes.
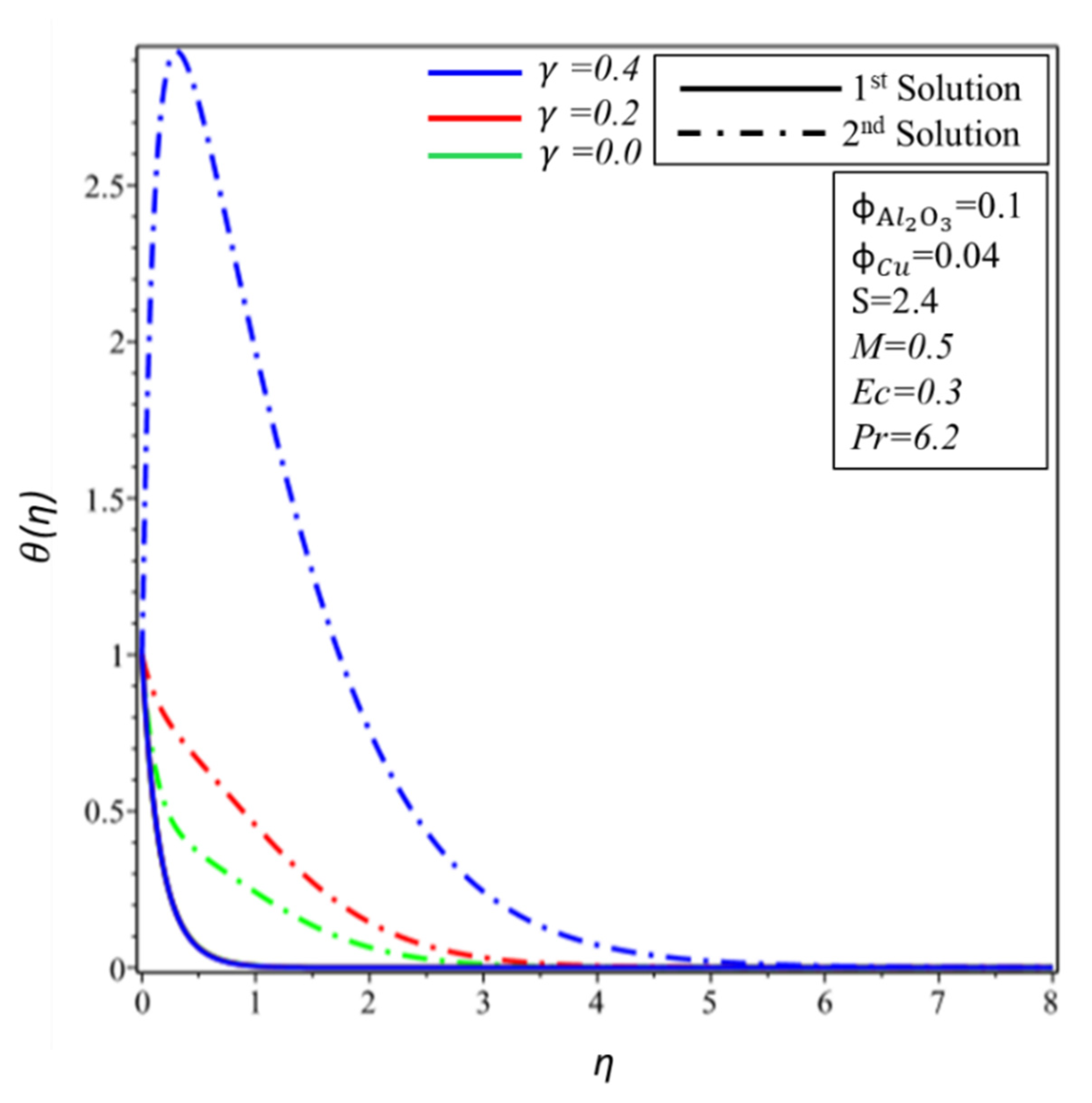
- The first is stable, and the second is unstable.
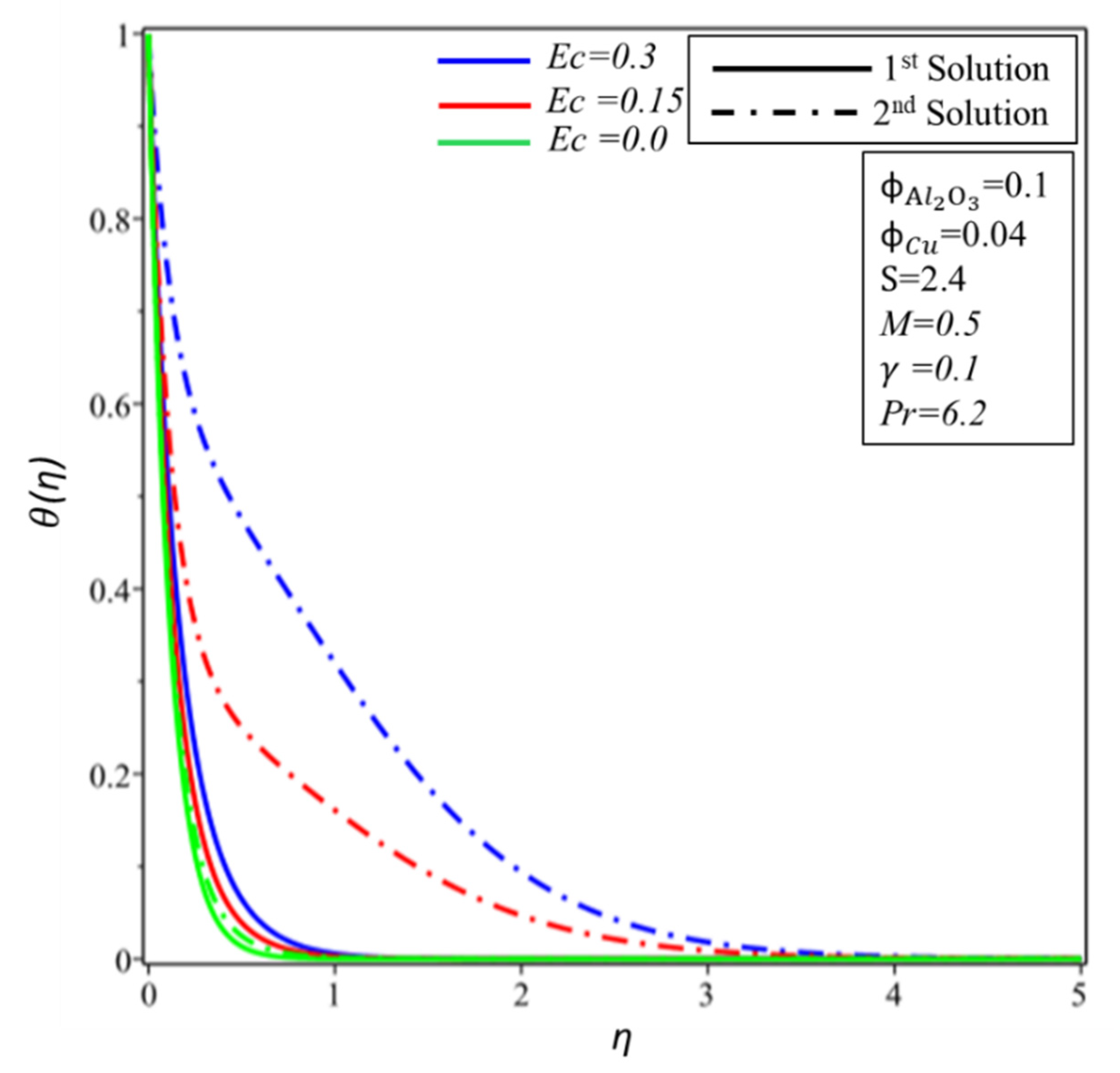
- The Eckert number and temperature profiles are directly proportional.
- The highest value of Eckert number does not affect the boundary layer separation against suction.
- This model does not function outside the critical points, so there is no solution.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; No. ANL/MSD/CP-84938; CONF-951135-29; Argonne National Lab.: Argonne, IL, USA, 1995. [Google Scholar]
- Ahmad, M.; Muhammad, T.; Ahmad, I.; Aly, S. Time-dependent 3D flow of viscoelastic nanofluid over an unsteady stretching surface. Phys. A Stat. Mech. Appl. 2020, 124004. [Google Scholar] [CrossRef]
- Ghazvini, M.; Maddah, H.; Peymanfar, R.; Ahmadi, M.H.; Kumar, R. Experimental evaluation and artificial neural network modeling of thermal conductivity of water based nanofluid containing magnetic copper nanoparticles. Phys. A Stat. Mech. Appl. 2020, 124127. [Google Scholar] [CrossRef]
- Tassaddiq, A.; Khan, I.; Nisar, K.S. Heat transfer analysis in sodium alginate based nanofluid using MoS2 nanoparticles: Atangana–Baleanu fractional model. Chaos Solitons Fractals 2020, 130, 109445. [Google Scholar] [CrossRef]
- Nadeem, S.; Abbas, N.; Elmasry, Y.; Malik, M.Y. Numerical analysis of water based CNTs flow of micropolar fluid through rotating frame. Comput. Methods Programs Biomed. 2020, 186, 105194. [Google Scholar] [CrossRef]
- Mitra, D.; Howli, P.; Das, B.K.; Das, N.S.; Chattopadhyay, P.; Chattopadhyay, K.K. Size and phase dependent thermal conductivity of TiO2-water nanofluid with theoretical insight. J. Mol. Liq. 2020, 302, 112499. [Google Scholar] [CrossRef]
- Sahoo, R.R.; Kumar, V. Development of a new correlation to determine the viscosity of ternary hybrid nanofluid. Int. Commun. Heat Mass Transf. 2020, 111, 104451. [Google Scholar] [CrossRef]
- Shafiq, A.; Khan, I.; Rasool, G.; Sherif, E.S.M.; Sheikh, A.H. Influence of Single-and Multi-Wall Carbon Nanotubes on Magnetohydrodynamic Stagnation Point Nanofluid Flow over Variable Thicker Surface with Concave and Convex Effects. Mathematics 2020, 8, 104. [Google Scholar] [CrossRef]
- Gireesha, B.J.; Umeshaiah, M.; Prasannakumara, B.C.; Shashikumar, N.S.; Archana, M. Impact of nonlinear thermal radiation on magnetohydrodynamic three dimensional boundary layer flow of Jeffrey nanofluid over a nonlinearly permeable stretching sheet. Phys. A Stat. Mech. Appl. 2020, 124051. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, U.; Khan, I.; Baleanu, D.; Nisar, K.S. Stability Analysis and Dual Solutions of Micropolar Nanofluid over the Inclined Stretching/Shrinking Surface with Convective Boundary Condition. Symmetry 2020, 12, 74. [Google Scholar] [CrossRef]
- Ghasemi, H.; Aghabarari, B.; Alizadeh, M.; Khanlarkhani, A.; Abu-Zahra, N. High efficiency decolorization of wastewater by Fenton catalyst: Magnetic iron-copper hybrid oxides. J. Water Process Eng. 2020, 37, 101540. [Google Scholar] [CrossRef]
- Rasool, G.; Shafiq, A.; Baleanu, D. Consequences of Soret–Dufour Effects, Thermal Radiation, and Binary Chemical Reaction on Darcy Forchheimer Flow of Nanofluids. Symmetry 2020, 12, 1421. [Google Scholar] [CrossRef]
- Mozaffari, S. Rheology of Bitumen at the Onset of Asphaltene Aggregation and Its Effects on the Stability of Water-In-Oil Emulsion. Master’s Thesis, University of Alberta, Alberta, AB, Canada, 2015. [Google Scholar] [CrossRef]
- Darjani, S.; Koplik, J.; Banerjee, S.; Pauchard, V. Liquid-hexatic-solid phase transition of a hard-core lattice gas with third neighbor exclusion. J. Chem. Phys. 2019, 151, 104702. [Google Scholar] [CrossRef] [PubMed]
- Shafiq, A.; Rasool, G.; Khalique, C.M. Significance of thermal slip and convective boundary conditions in three dimensional rotating Darcy-Forchheimer nanofluid flow. Symmetry 2020, 12, 741. [Google Scholar] [CrossRef]
- Mozaffari, S.; Li, W.; Dixit, M.; Seifert, S.; Lee, B.; Kovarik, L.; Mpourmpakis, G.; Karim, A.M. The role of nanoparticle size and ligand coverage in size focusing of colloidal metal nanoparticles. Nanoscale Adv. 2019, 1, 4052–4066. [Google Scholar] [CrossRef]
- Darjani, S.; Koplik, J.; Pauchard, V. Extracting the equation of state of lattice gases from random sequential adsorption simulations by means of the Gibbs adsorption isotherm. Phys. Rev. E 2017, 96, 052803. [Google Scholar] [CrossRef] [PubMed]
- Shafiq, A.; Rasool, G.; Khalique, C.M.; Aslam, S. Second Grade Bioconvective Nanofluid Flow with Buoyancy Effect and Chemical Reaction. Symmetry 2020, 12, 621. [Google Scholar] [CrossRef]
- Esfe, M.H.; Alirezaie, A.; Rejvani, M. An applicable study on the thermal conductivity of SWCNT-MgO hybrid nanofluid and price-performance analysis for energy management. Appl. Therm. Eng. 2017, 111, 1202–1210. [Google Scholar] [CrossRef]
- Sundar, L.S.; Sharma, K.V.; Singh, M.K.; Sousa, A.C.M. Hybrid nanofluids preparation, thermal properties, heat transfer and friction factor–a review. Renew. Sustain. Energy Rev. 2017, 68, 185–198. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I.; Seikh, A.H.; Sherif, E.S.M.; Nisar, K.S. Stability analysis and multiple solution of Cu–Al2O3/H2O nanofluid contains hybrid nanomaterials over a shrinking surface in the presence of viscous dissipation. J. Mater. Res. Technol. 2020, 9, 421–432. [Google Scholar] [CrossRef]
- Devi, S.A.; Devi, S.S.U. Numerical investigation of hydromagnetic hybrid Cu–Al2O3/water nanofluid flow over a permeable stretching sheet with suction. Int. J. Nonlinear Sci. Numer. Simul. 2016, 17, 249–257. [Google Scholar] [CrossRef]
- Suresh, S.; Venkitaraj, K.P.; Selvakumar, P.; Chandrasekar, M. Synthesis of Al2O3–Cu/water hybrid nanofluids using two step method and its thermo physical properties. Colloids Surf. A Physicochem. Eng. Asp. 2011, 388, 41–48. [Google Scholar] [CrossRef]
- Hayat, T.; Nadeem, S. Heat transfer enhancement with Ag–CuO/water hybrid nanofluid. Results Phys. 2017, 7, 2317–2324. [Google Scholar] [CrossRef]
- Jamshed, W.; Aziz, A. Cattaneo–Christov based study of TiO2–CuO/EG Casson hybrid nanofluid flow over a stretching surface with entropy generation. Appl. Nanosci. 2018, 8, 685–698. [Google Scholar] [CrossRef]
- Rostami, M.N.; Dinarvand, S.; Pop, I. Dual solutions for mixed convective stagnation-point flow of an aqueous silica–alumina hybrid nanofluid. Chin. J. Phys. 2018, 56, 2465–2478. [Google Scholar] [CrossRef]
- Aly, E.H.; Pop, I. MHD flow and heat transfer over a permeable stretching/shrinking sheet in a hybrid nanofluid with a convective boundary condition. Int. J. Numer. Methods Heat Fluid Flow 2019. [Google Scholar] [CrossRef]
- Khan, A.S.; Khan, M.I.; Hayat, T.; Faisal Javed, M.; Alsaedi, A. Mixed convective non-linear radiative flow with TiO2-Cu-water hybrid nanomaterials and induced magnetic field. Int. J. Numer. Methods Heat Fluid Flow 2019. [Google Scholar] [CrossRef]
- Olatundun, A.T.; Makinde, O.D. Analysis of Blasius flow of hybrid nanofluids over a convectively heated surface. In Defect and Diffusion Forum; Trans Tech Publications: Stafa-Zurich, Switzerland, 2017; Volume 377, pp. 29–41. [Google Scholar]
- Abbas, N.; Nadeem, S.; Malik, M.Y. Theoretical study of micropolar hybrid nanofluid over Riga channel with slip conditions. Phys. A Stat. Mech. Appl. 2020, 124083. [Google Scholar] [CrossRef]
- Maskeen, M.M.; Zeeshan, A.; Mehmood, O.U.; Hassan, M. Heat transfer enhancement in hydromagnetic alumina–copper/water hybrid nanofluid flow over a stretching cylinder. J. Therm. Anal. Calorim. 2019, 138, 1127–1136. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Dogonchi, A.S.; Ganji, D.D. Magneto-hydrodynamic flow and heat transfer of a hybrid nanofluid in a rotating system among two surfaces in the presence of thermal radiation and Joule heating. AIP Adv. 2019, 9, 025103. [Google Scholar] [CrossRef]
- Khan, M.I.; Khan, S.A.; Hayat, T.; Waqas, M.; Alsaedi, A. Modeling and numerical simulation for flow of hybrid nanofluid (SiO2/C3H8O2) and (MoS2/C3H8O2) with entropy optimization and variable viscosity. Int. J. Numer. Methods Heat Fluid Flow 2019. [Google Scholar] [CrossRef]
- Sharma, A.K.; Singh, R.K.; Dixit, A.R.; Tiwari, A.K.; Singh, M. An Investigation on Tool Flank Wear Using Alumina/MoS2 Hybrid Nanofluid in Turning Operation. In Advances in Manufacturing Engineering and Materials; Springer: Cham, Switzerland, 2019; pp. 213–219. [Google Scholar]
- Al-Mdallal, Q.M.; Indumathi, N.; Ganga, B.; Hakeem, A.A. Marangoni radiative effects of hybrid-nanofluids flow past a permeable surface with inclined magnetic field. Case Stud. Therm. Eng. 2020, 17, 100571. [Google Scholar] [CrossRef]
- Ramesh, G.K. Three different hybrid nanometrial performances on rotating disk: A non-Darcy model. Appl. Nanosci. 2019, 9, 179–187. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I. Mathematical analysis of magnetohydrodynamic (MHD) flow of micropolar nanofluid under buoyancy effects past a vertical shrinking surface: Dual solutions. Heliyon 2019, 5, e02432. [Google Scholar] [CrossRef] [PubMed]
- Ghadikolaei, S.S.; Gholinia, M.; Hoseini, M.E.; Ganji, D.D. Natural convection MHD flow due to MoS2–Ag nanoparticles suspended in C2H6O2H2O hybrid base fluid with thermal radiation. J. Taiwan Inst. Chem. Eng. 2019, 97, 12–23. [Google Scholar] [CrossRef]
- Magyari, E.; Keller, B. Heat and mass transfer in the boundary layers on an exponentially stretching continuous surface. J. Phys. D Appl. Phys. 1999, 32, 577. [Google Scholar] [CrossRef]
- Mushtaq, A.; Farooq, M.A.; Sharif, R.; Razzaq, M. The impact of variable fluid properties on hydromagnetic boundary layer and heat transfer flows over an exponentially stretching sheet. J. Phys. Commun. 2019, 3, 095005. [Google Scholar] [CrossRef]
- Reddy, G.B.; Goud, B.S.; Shekar, M.R. Numerical Solution of MHD Mixed Convective Boundary Layer Flow of a Nanofluid through a Porous Medium due to an Exponentially Stretching Sheet with Magnetic Field Effect. Int. J. Appl. Eng. Res. 2019, 14, 2074–2083. [Google Scholar]
- Rahman, A.N.H.; Bachok, N.; Rosali, H. Numerical Solutions of MHD Stagnation-Point Flow over an Exponentially Stretching/Shrinking Sheet in a Nanofluid. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2019; Volume 1366, p. 012012. [Google Scholar]
- Farooq, U.; Lu, D.; Munir, S.; Ramzan, M.; Suleman, M.; Hussain, S. MHD flow of Maxwell fluid with nanomaterials due to an exponentially stretching surface. Sci. Rep. 2019, 9, 1–11. [Google Scholar] [CrossRef]
- Dero, S.; Rohni, A.M.; Saaban, A. MHD micropolar nanofluid flow over an exponentially stretching/shrinking surface: Triple solutions. J. Adv. Res. Fluid Mech. Therm. Sci. 2019, 56, 165–174. [Google Scholar]
- Lund, L.A.; Omar, Z.; Khan, I. Steady incompressible magnetohydrodynamics Casson boundary layer flow past a permeable vertical and exponentially shrinking sheet: A stability analysis. Heat Transf. Asian Res. 2019, 48, 3538–3556. [Google Scholar] [CrossRef]
- Ali Lund, L.; Ching, D.L.C.; Omar, Z.; Khan, I.; Nisar, K.S. Triple local similarity solutions of Darcy-Forchheimer Magnetohydrodynamic (MHD) flow of micropolar nanofluid over an exponential shrinking surface: Stability analysis. Coatings 2019, 9, 527. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I.; Raza, J.; Sherif, E.S.M.; Seikh, A.H. Magnetohydrodynamic (MHD) Flow of Micropolar Fluid with Effects of Viscous Dissipation and Joule Heating Over an Exponential Shrinking Sheet: Triple Solutions and Stability Analysis. Symmetry 2020, 12, 142. [Google Scholar] [CrossRef]
- Bachok, N.; Ishak, A.; Pop, I. Boundary layer stagnation-point flow and heat transfer over an exponentially stretching/shrinking sheet in a nanofluid. Int. J. Heat Mass Transf. 2012, 55, 8122–8128. [Google Scholar] [CrossRef]
- Dzulkifli, N.; Bachok, N.; Yacob, N.; Md Arifin, N.; Rosali, H. Unsteady stagnation-point flow and heat transfer over a permeable exponential stretching/shrinking sheet in nanofluid with slip velocity effect: A stability analysis. Appl. Sci. 2018, 8, 2172. [Google Scholar] [CrossRef]
- Anuar, N.S.; Bachok, N.; Arifin, N.M.; Rosali, H.; Pop, I. Stagnation-Point Flow and Heat Transfer over an Exponentially Stretching/Shrinking Sheet in Hybrid Nanofluid with Slip Velocity Effect: Stability Analysis. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2019; Volume 1366, p. 012002. [Google Scholar]
- Waini, I.; Ishak, A.; Pop, I. Hybrid nanofluid flow induced by an exponentially shrinking sheet. Chin. J. Phys. 2019. [Google Scholar] [CrossRef]
- Jain, S.; Choudhary, R. Effects of MHD on boundary layer flow in porous medium due to exponentially shrinking sheet with slip. Procedia Eng. 2015, 127, 1203–1210. [Google Scholar] [CrossRef]
- Ali Lund, L.; Omar, Z.; Khan, I.; Raza, J.; Bakouri, M.; Tlili, I. Stability Analysis of Darcy-Forchheimer Flow of Casson Type Nanofluid Over an Exponential Sheet: Investigation of Critical Points. Symmetry 2019, 11, 412. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I. Quadruple solutions of mixed convection flow of magnetohydrodynamic nanofluid over exponentially vertical shrinking and stretching surfaces: Stability analysis. Comput. Methods Programs Biomed. 2019, 182, 105044. [Google Scholar] [CrossRef]
- Harris, S.D.; Ingham, D.B.; Pop, I. Mixed convection boundary-layer flow near the stagnation point on a vertical surface in a porous medium: Brinkman model with slip. Transp. Porous Media 2009, 77, 267–285. [Google Scholar] [CrossRef]
- Rahman, M.M.; Roşca, A.V.; Pop, I. Boundary layer flow of a nanofluid past a permeable exponentially shrinking/stretching surface with second order slip using Buongiorno’s model. Int. J. Heat Mass Transf. 2014, 77, 1133–1143. [Google Scholar] [CrossRef]
- Bhattacharyya, K.; Pop, I. MHD boundary layer flow due to an exponentially shrinking sheet. Magnetohydrodynamics 2011, 47, 337–344. [Google Scholar]
- Miklavčič, M.; Wang, C. Viscous flow due to a shrinking sheet. Q. Appl. Math. 2006, 64, 283–290. [Google Scholar] [CrossRef]
- Fang, T. Boundary layer flow over a shrinking sheet with power-law velocity. Int. J. Heat Mass Transf. 2008, 51, 5838–5843. [Google Scholar] [CrossRef]
- Hamid, M.; Usman, M.; Khan, Z.H.; Ahmad, R.; Wang, W. Dual solutions and stability analysis of flow and heat transfer of Casson fluid over a stretching sheet. Phys. Lett. A 2019, 383, 2400–2408. [Google Scholar] [CrossRef]

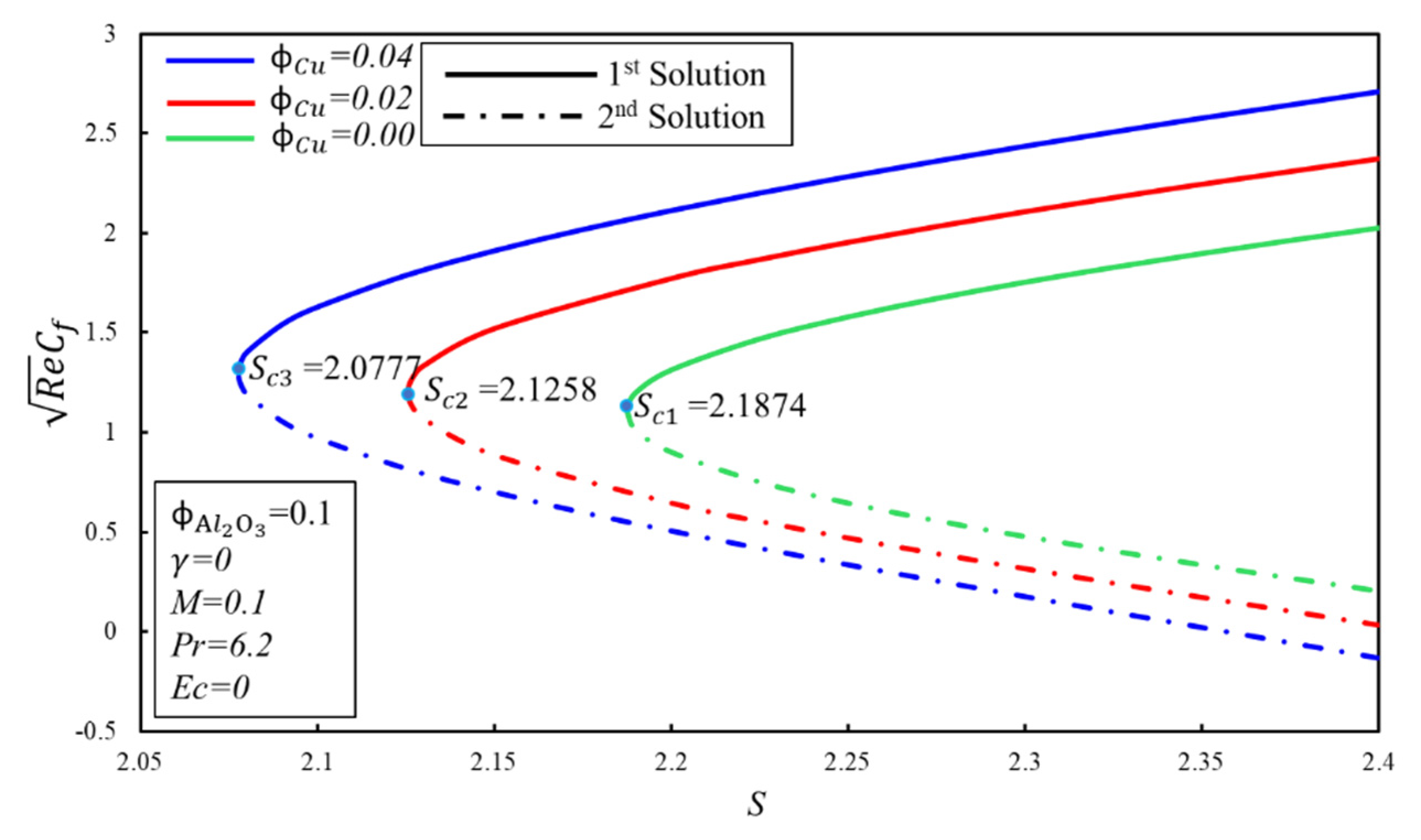
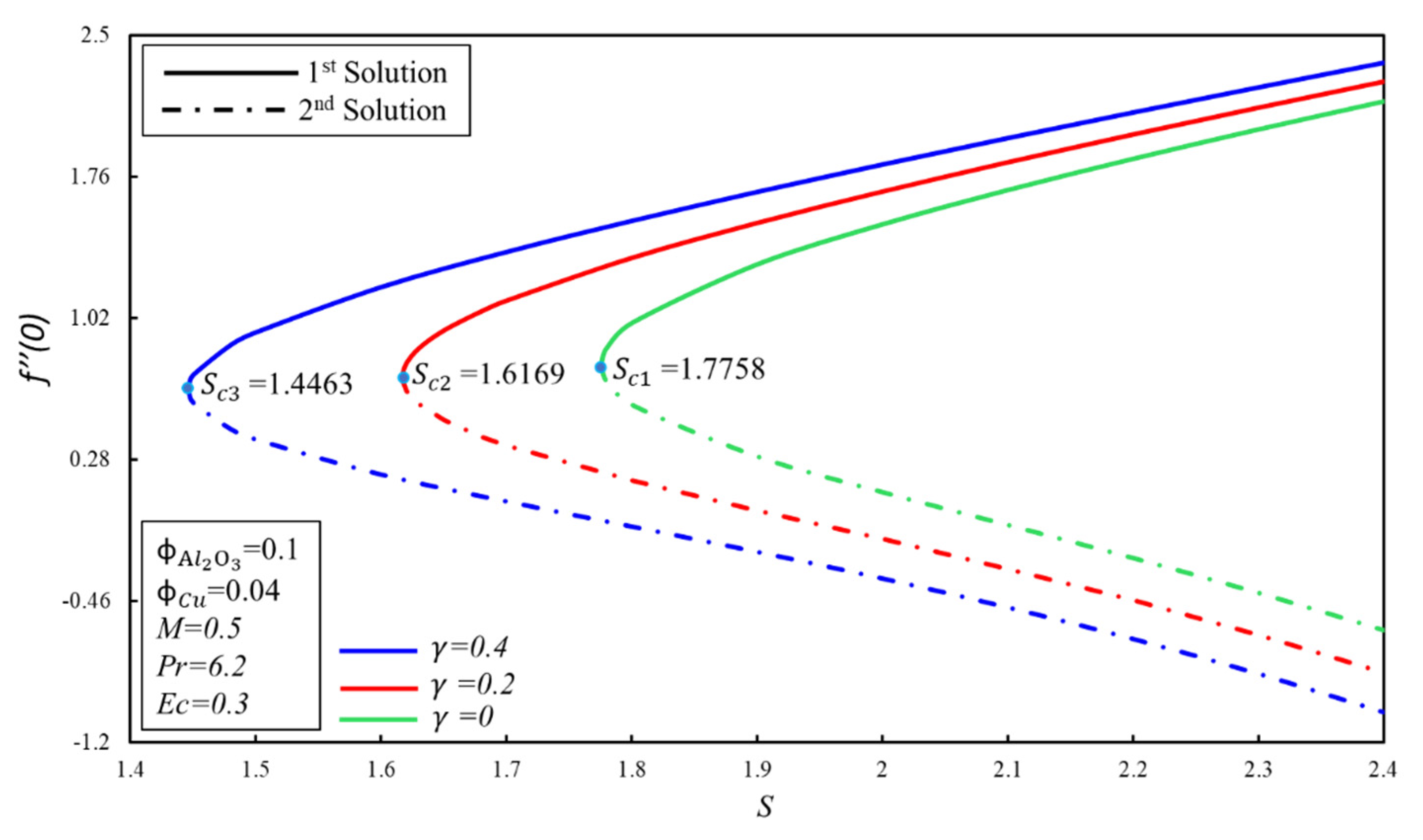
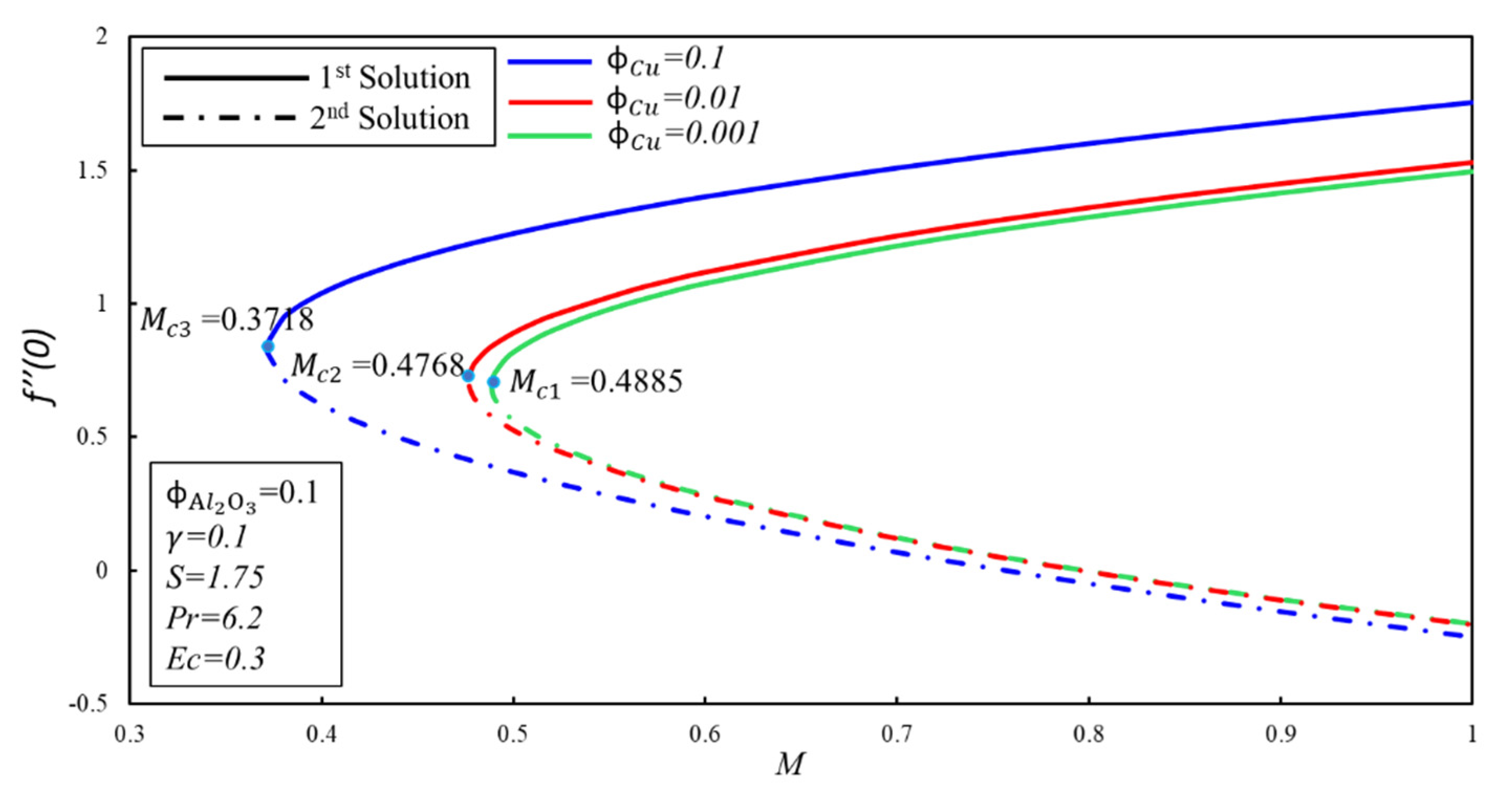

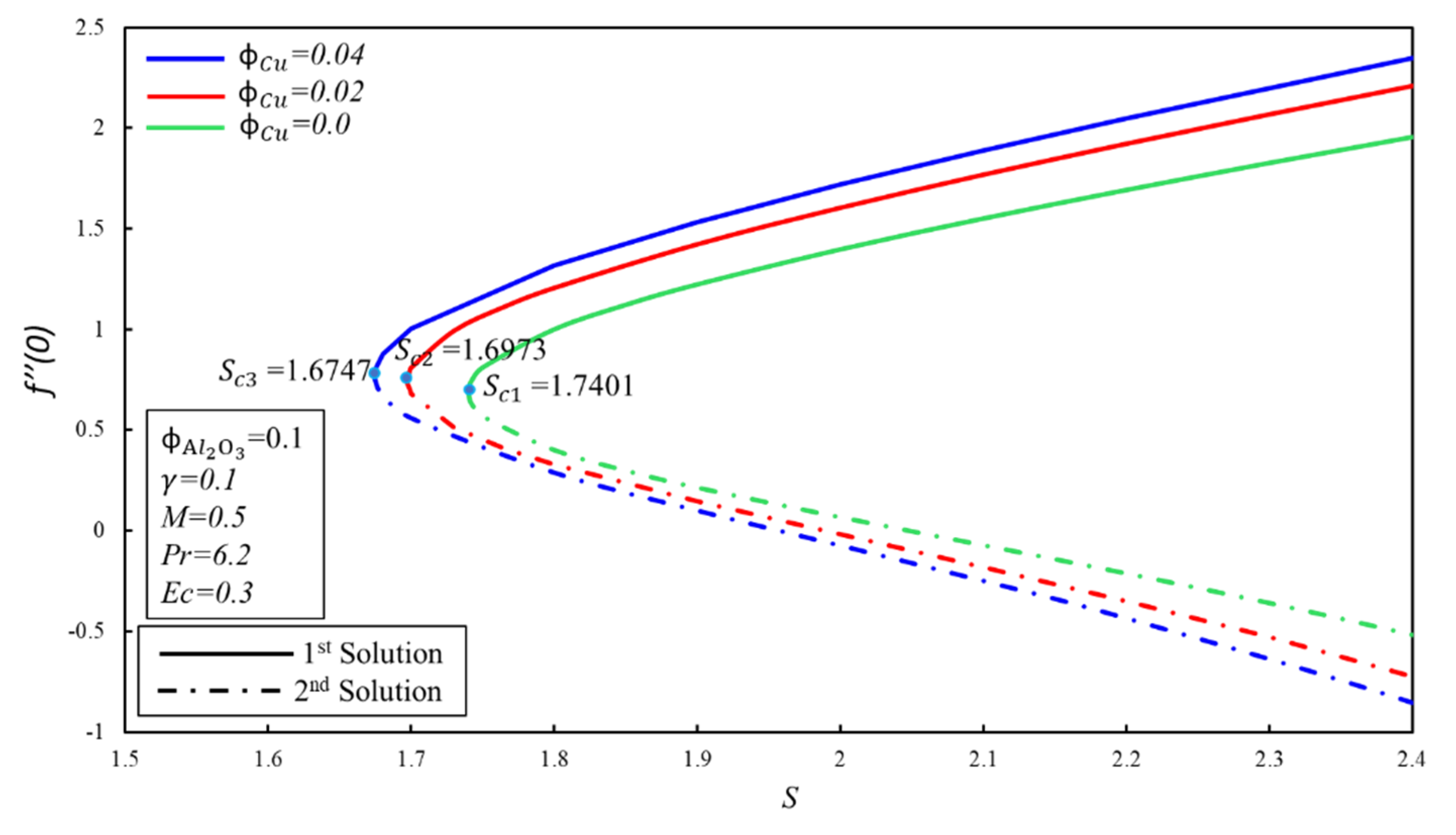

| Names | Properties |
|---|---|
| Viscosity of Dynamic | |
| Density | |
| Thermal conductivity | where |
| Heat capacity | |
| Electrical conductivity | where |
| Fluids | (kg/m3) | (J/kg K) | k (W/m K) |
|---|---|---|---|
| Alumina (Al2O3) | 3970 | 765 | 40 |
| Copper (Cu) | 8933 | 385 | 400 |
| Water (H2O) | 997.1 | 4179 | 0.613 |
| M | |||||
|---|---|---|---|---|---|
| First Solution | Second Solution | ||||
| 0.01 | 0 | 0 | 3 | 2.4863 | −1.1077 |
| 0.05 | 2.8189 | −1.6261 | |||
| 0.1 | 3.0749 | −2.0807 | |||
| 0.1 | 3.1146 | −2.2302 | |||
| 0.3 | 3.1908 | −2.5230 | |||
| 0.5 | 3.2633 | −2.8077 | |||
| 0.1 | 3.2967 | −2.9403 | |||
| 0.3 | 3.3614 | −3.1999 | |||
| 0.5 | 3.4236 | −3.4519 | |||
| 2.75 | 3.0944 | −2.4453 | |||
| 2.5 | 2.7590 | −1.6382 | |||
| 2.25 | 2.4142 | −1.0062 |
| Pr | M | ||||
|---|---|---|---|---|---|
| First Solution | Second Solution | ||||
| 0.01 | 6.2 | 0 | 0 | 12.7302 | 12.5387 |
| 0.05 | 11.2238 | 10.9591 | |||
| 0.1 | 9.6302 | 9.2758 | |||
| 5 | 7.6893 | 7.2426 | |||
| 3 | 4.4876 | 3.7171 | |||
| 2 | 2.9193 | 1.8444 | |||
| 6.2 | 0.1 | 9.6319 | 9.2613 | ||
| 0.3 | 9.6354 | 9.2315 | |||
| 0.5 | 9.6386 | 9.2000 | |||
| 0.1 | 8.5867 | 5.9024 | |||
| 0.3 | 6.4827 | 0.6929 | |||
| 0.5 | 4.3787 | 7.2883 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lund, L.A.; Omar, Z.; Dero, S.; Khan, I.; Baleanu, D.; Nisar, K.S. Magnetized Flow of Cu + Al2O3 + H2O Hybrid Nanofluid in Porous Medium: Analysis of Duality and Stability. Symmetry 2020, 12, 1513. https://doi.org/10.3390/sym12091513
Lund LA, Omar Z, Dero S, Khan I, Baleanu D, Nisar KS. Magnetized Flow of Cu + Al2O3 + H2O Hybrid Nanofluid in Porous Medium: Analysis of Duality and Stability. Symmetry. 2020; 12(9):1513. https://doi.org/10.3390/sym12091513
Chicago/Turabian StyleLund, Liaquat Ali, Zurni Omar, Sumera Dero, Ilyas Khan, Dumitru Baleanu, and Kottakkaran Sooppy Nisar. 2020. "Magnetized Flow of Cu + Al2O3 + H2O Hybrid Nanofluid in Porous Medium: Analysis of Duality and Stability" Symmetry 12, no. 9: 1513. https://doi.org/10.3390/sym12091513
APA StyleLund, L. A., Omar, Z., Dero, S., Khan, I., Baleanu, D., & Nisar, K. S. (2020). Magnetized Flow of Cu + Al2O3 + H2O Hybrid Nanofluid in Porous Medium: Analysis of Duality and Stability. Symmetry, 12(9), 1513. https://doi.org/10.3390/sym12091513








