Hybrid Nanofluid Flow Past a Shrinking Cylinder with Prescribed Surface Heat Flux

Abstract

This numerical study was devoted to examining the occurrence of non-unique solutions in boundary layer flow due to deformable surfaces (cylinder and flat plate) with the imposition of prescribed surface heat flux. The hybrid Al${}_2$O${}_3$-Cu/water nanofluid was formulated using the single phase model with respective correlations of hybrid nanofluids. The governing model was simplified by adopting a similarity transformation. The transformed differential equations were then numerically computed using the efficient bvp4c solver with the ranges of the control parameters $0.5\%\le {\varphi }_1,{\varphi }_2\le 1.5\%$ (Al${}_2$O${}_3$ and Cu volumetric concentration), $0\le K\le 0.2$ (curvature parameter), $2.6<S\le 3.2$ (suction parameter) and $-2.5<\lambda \le 0.5$ (stretching/shrinking parameter). Dual steady solutions are presentable for both a cylinder $(K>0)$ and a flat plate $(K=0)$ with the inclusion of only the suction (transpiration) parameter. The real and stable solutions were mathematically validated through the stability analysis. The Al${}_2$O${}_3$-Cu/water nanofluid with ${\varphi }_1=0.5\%$ (alumina) and ${\varphi }_2=1.5\%$ (copper) has the highest skin friction coefficient and heat transfer rate, followed by the hybrid nanofluids with volumetric concentrations $({\varphi }_1=1\%,{\varphi }_2=1\%)$ and $({\varphi }_1=1.5\%,{\varphi }_2=0.5\%)$, respectively. Surprisingly, the flat plate surface abates the separation of boundary layer while it enhances the heat transfer process.

1. Introduction

Over recent decades, the investigation in the field of fluid flow has gained interest due to the wide range of industrial applications. The explorations so far have covered Newtonian and non-Newtonian fluids with multiple effects and single or multi-phases [1,2,3,4,5]. The applications of the study of fluid flow can be found in mechanical and chemical engineering, biological systems and astrophysics. The inquisitiveness in this field grew significantly in the past few years after Choi [6] embedded the nanoparticle in the investigation of fluid flow to develop an advanced heat transfer fluid with substantially higher conductivities. The analysis revealed that the fluid with nanoparticles enhanced the thermophysical properties as compared to the classical working fluid. Since then, many researchers gained interest and contributed to this field by considering experimental and numerical studies. Wang and Su [7] conducted an experimental study on the boiling heat transfer of a nanofluid in a vertical tube with diverse pressure conditions. The continuation of the study has been reported in Wang et al. [8]. The experimental works on nanofluids also have been documented by Ahmadi and Willing [9], Masuda et al. [10], Das et al. [11] and Pak and Cho [12]. Meanwhile, study via a mathematical approach with various effects and surfaces was reported in work done by Kuznetsov and Nield [13], Mahat et al. [14], Zokri et al. [15] and Waini et al. [16].

As nanofluids are extensively used as coolants; lubricants; and also in practical applications, including refrigeration, air-conditioning, microelectronics and processors of mobile computers, the advancements in this topic are being further investigated by considering fluids containing more than one type of nanoparticle called hybrid nanofluids. This new invention has new thermal characteristics as compared to conventional nanofluids. The application of Al${}_2$O${}_3$-Cu/water in the boundary layer flow was further analyzed by Waini et al. [17,18] for thin needle and sensor surfaces, respectively; Khashi’ie et al. [19,20] for Riga plate and cylinder surfaces, respectively; and Zainal et al. [21,22,23] specifically for the flat plate cases. They also performed a stability analysis to justify the stability of the dual solutions. Moreover, the collection of documents on hybrid nanofluids can be found in works done by Yen et al. [24], Labib et al. [25], Nasrin and Alim [26], Takabi and Shokouhmand [27], Devi and Devi [28,29], Yousefi et al. [30], Hayat et al. [31], Ghadikolaei et al. [32], Tayebi and Chamkha [33] and Ashorynejad and Shahriari [34].

According to the current studies on the fluid mechanics of fluid flow, the flow characteristics depend on what type of geometry the fluid is moving over. A group of researchers focused on the fluid flow problem over different types of stretching/shrinking surfaces. For instance, Kasim et al. [35] investigated the interaction on a fluid and solid moving over a stretching sheet, and Lund et al. [36] considered the study of fluid flow past an inclined stretching/shrinking surface. Waini et al. [37] and Anuar et al. [38] deliberated on the problem of fluid flow under an exponentially shrinking sheet. The fluid flow passing over a shrinking cylinder was first discussed by Wang [39]. The exponential transformation was used to facilitate numerical integration in order to compute the solution. His work was further investigated by Mukhopadhyay [40], Vajravelu et al. [41], Butt and Ali [42], Abbas et al. [43], Malik et al. [44] and Shafik et al. [45]. Besides, the problem of the flow past a cylinder has important applications in the study of geological formations that includes the exploration and thermal recovery of oil, geothermal reservoirs and underground nuclear waste storage sites. The outcomes from this study will be beneficial to the engineers in the prediction of flow, heat transfer and solute or contaminant dispersion about intrusive bodies such as salt domes, magnetic intrusions, piping and casting systems (see Ganesan and Loganathan [46]). Recent works on flow past a stretching cylinder with various physical phenomena can be found in Ferdows et al. [47] (gyrotactic microorganism), Ullah et al. [48] (chemical reaction and heat generation/absorption) and Suleman et al. [49] (homogeneous-heterogeneous reactions).

The choices of the thermal boundary conditions for the fluid flow problem are very crucial, since a difference in conditions leads one to describe a different situation for the problem. They are four types of boundary conditions which are generally used. They are constant wall temperature (CWT), constant/prescribe heat flux (PHF), Newtonian heating (NH) and convective boundary condition (CBC). According to Muthtamilselvan and Prakash [50], the constant thermal boundary conditions that are imposed on the surface are not adequate in some cases, for example, in a microelectromechanical (MEM) condensation application where a fixed heat dissipation due to condensation on the lower surface of the plate is removed by the gas flowing over the top surface. Therefore, a lot of research work was replaced with a different heating process. The condition of CWT is generally used to describe bodies with very high heat conductivity while PHF is used to present the problem with the supplied thermal energy from the surface. The NH and CBC correspond to the existence of convection heating (or cooling) at the surface and are obtained from the surface energy balance. They are many reported articles that considered those thermal boundary conditions. The present problem considered the case of PHF, since it seems more realistic. The existing studies involving the particular thermal boundary condition can be found in [51,52,53,54,55].

Motivated by the above literature, the present paper aims to extend the existing investigation of hybrid nanofluids by considering the flow past a shrinking cylinder through adopting the model of nanofluids proposed by Tiwari and Das [56]. The hybrid nanofluid deliberated with two elements, which were Al${}_2$O${}_3$ and Cu in pure water. The governing equations with thermal condition heat flux were first transformed into a system of ordinary differential equations by using an appropriate similarity transformation. The system of equations was then solved numerically using the boundary value problem solver (bvp4c) which is embedded in Matlab software. The validation of the present works was done by direct comparison with the current output in the literature for special cases (limiting cases). The effects of pertinent parameters on the flow and heat transfer characteristics are presented in tabular and graphical form. To the best of the authors’ knowledge, minimal studies have been reported in the literature regarding the investigation of flow over a shrinking cylinder in hybrid nanofluids embedded in the heat flux thermal condition.

2. Mathematical Formulation

A steady, incompressible and laminar boundary layer flow of hybrid nanofluid (Cu-Al${}_2$O${}_3$/water) towards a horizontal cylinder is studied here. The circular cylinder with radius a is deformed (stretch/shrink) with velocity $u_w\left(x\right)=u_{0}x/L$ where constant $u_0$ is a characteristic velocity and L is the characteristic length of the cylinder. Figure 1 illustrates the physical model and coordinate system $(x,r)$ of this problem. The deformable cylinder is subjected to the prescribed heat flux $q_w\left(x\right)=T_{0}x/L$ where $T_0$ is a characteristic temperature.

The governing model in the PDEs (partial differential equations) is given as (see Khashi’ie et al. [20], Qasim et al. [57])

$$\frac{\partial \left(ru\right)}{\partial x}+\frac{\partial \left(rv\right)}{\partial r}=0,$$

(1)

$$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial r}=\frac{{\mu }_{hnf}}{{\rho }_{hnf}}\left(\frac{{\partial }^{2}u}{\partial r^2}+\frac{1}{r}\frac{\partial u}{\partial r}\right),$$

(2)

$$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial r}=\frac{k_{hnf}}{{\left(\rho C_p\right)}_{hnf}}\left(\frac{{\partial }^{2}T}{\partial r^2}+\frac{1}{r}\frac{\partial T}{\partial r}\right),$$

(3)

while the boundary conditions are

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & v=v_w\left(r\right),u=\lambda u_w\left(x\right),k_{hnf}\frac{\partial T}{\partial r}=-q_w\left(x\right),\mathrm{at}r=a\hfill \\ \hfill & u\to 0,T\to T_{\infty },\mathrm{as}r\to \infty \hfill \end{array}\end{array}$$

(4)

where $v_w\left(r\right)$ represents the mass flux velocity through the permeable surface such that $v_w\left(r\right)>0$ for mass injection and $v_w\left(r\right)<0$ for mass suction. For the case of an impermeable surface, $v_w\left(r\right)=0$. Besides, u and v denote the velocities along $x-$ and $r-$axes, correspondingly and T is the temperature of the hybrid nanofluid. In this work, the constant far-field temperature $T_{\infty }$ is considered while the cylinder wall is subjected to the variable heat flux $q_w\left(x\right)$. In addition, the constant stretching/shrinking parameter $\lambda$ signifies the shrinking cylinder when $\lambda <0$ and stretching cylinder when $\lambda >0$. The static cylinder is symbolized by $\lambda =0$. The correlations of the nanofluids (regular and hybrid) are presented in

Table 1. The correlations of single $\left(nf\right)$ and hybrid nanofluids $\left(hnf\right)$ (see Tiwari and Das [56], Takabi and Salehi [58]).

Properties	Nanofluids
Density $\left(\rho \right)$	${\displaystyle {\rho }_{nf}=\left(1-\varphi \right){\rho }_{bf}+\varphi {\rho }_s}$
	${\displaystyle {\rho }_{hnf}=(1-{\varphi }_{hnf}){\rho }_{bf}+{\varphi }_1{\rho }_{s1}+{\varphi }_2{\rho }_{s2}}$
Heat Capacity $\left(\rho C_p\right)$	${\displaystyle {\left(\rho C_p\right)}_{nf}=(1-\varphi ){\left(\rho C_p\right)}_{bf}+\varphi {\left(\rho C_p\right)}_s}$
	${\displaystyle {\left(\rho C_p\right)}_{hnf}=\left(1-{\varphi }_{hnf}\right){\left(\rho C_p\right)}_{bf}+{\varphi }_1{\left(\rho C_p\right)}_{s1}+{\varphi }_2{\left(\rho C_p\right)}_{s2}}$
Dynamic Viscosity $\left(\mu \right)$	${\displaystyle \frac{{\mu }_{nf}}{{\mu }_{bf}}=\frac{1}{{(1-\varphi )}^{2.5}}}$
	${\displaystyle \frac{{\mu }_{hnf}}{{\mu }_{bf}}=\frac{1}{{(1-{\varphi }_{hnf})}^{2.5}}}$
Thermal Conductivity $\left(k\right)$	${\displaystyle \frac{k_{nf}}{k_{bf}}=\left[\frac{k_s+2k_{bf}-2\varphi \left(k_{bf}-k_s\right)}{k_s+2k_{bf}+\varphi \left(k_{bf}-k_s\right)}\right]}$
	${\displaystyle \frac{k_{hnf}}{k_{bf}}=\left[\frac{\frac{{\varphi }_1{k}_1+{\varphi }_2{k}_2}{{\varphi }_{hnf}}+2k_{bf}+2\left({\varphi }_1{k}_1+{\varphi }_2{k}_2\right)-2{\varphi }_{hnf}kbf}{\frac{{\varphi }_1{k}_1+{\varphi }_2{k}_2}{{\varphi }_{hnf}}+2k_{bf}-\left({\varphi }_1{k}_1+{\varphi }_2{k}_2\right)+{\varphi }_{hnf}{k}_{bf}}\right]}$

where $s1$ and $s2$ denote the alumina and copper nanoparticles, respectively; ${\varphi }_1$ and ${\varphi }_2$ are the volumetric concentrations of the alumina and copper nanoparticles, accordingly. Besides, the subscript $bf$ denotes the base fluid (pure water); $nf$ and $hnf$ are single and hybrid nanofluids, respectively. In Table 1, ${\varphi }_{hnf}={\varphi }_1+{\varphi }_2$ where ${\varphi }_{hnf}\approx 0$ corresponds to water—base fluid. The thermophysical properties of the water and both nanoparticles are presented in

Table 2. Thermo-physical properties of the nanoparticles and water (see Oztop and Abu-Nada [59]).

Thermophysical Properties	Base Fluid	Nanoparticles
	Pure Water	Alumina	Copper
${\mathbf{C}}_{\mathbf{p}}$(J/kgK)	4179	765	385
$\mathbf{\rho }$ (kg/m${}^{\mathbf{3}}$)	997.1	3970	8933
$\mathbf{k}$(W/mK)	0.6130	40	400

.

The following similarity variables are introduced as (Qasim et al. [57], Giri et al. [60])

$$u=\frac{u_{0}x}{L}{f}^{\prime }\left(\eta \right),v=-\frac{a}{r}\sqrt{\frac{u_0{\nu }_f}{L}}f\left(\eta \right),T=T_{\infty }+\frac{q_w}{k_f}\sqrt{\frac{{\nu }_{f}L}{u_0}}\theta \left(\eta \right),\eta =\sqrt{\frac{u_0}{{\nu }_{f}L}}\frac{r^2-a^2}{2a},$$

(5)

so that

$$v_w\left(r\right)=-\frac{a}{r}\sqrt{\frac{u_0{\nu }_f}{L}}S,$$

(6)

where ${\nu }_f$ is the kinematic viscosity of the water, S is the dimensionless mass flux parameter and categorized as $S>0$ and $S<0$ for suction and injection, respectively. The continuity equation in Equation (1) is obeyed by adopting the transformation in Equation (5). Hence, considering this transformation, Equations (2)–(4) are transformed and simplified to

$$\frac{{\mu }_{hnf}/{\mu }_f}{{\rho }_{hnf}/{\rho }_f}\left[(1+2K\eta )f^{″}+2K{f}^{″}\right]+f{f}^{″}-f^{\prime 2}=0,$$

(7)

$$\frac{1}{\mathrm{Pr}}\frac{k_{hnf}/k_f}{{\left(\rho C_p\right)}_{hnf}/{\left(\rho C_p\right)}_f}\left[(1+2K\eta ){\theta }^{″}+2K{\theta }^{\prime }\right]+f{\theta }^{\prime }-f^{\prime }\theta =0,$$

(8)

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & f^{\prime }\left(0\right)=\lambda ,f\left(0\right)=S,{\theta }^{\prime }\left(0\right)=-\frac{k_f}{k_{hnf}},\hfill \\ \hfill & f^{\prime }(\infty )\to 0,\theta (\infty )\to 0,\hfill \end{array}\end{array}$$

(9)

where $K=\sqrt{{\nu }_{f}L/u_0{a}^2}$ is the curvature parameter and Pr $={\left(\mu C_p\right)}_f/k_f$ is the Prandtl number. The local skin friction coefficient $C_f$ and the local Nusselt number $N{u}_x$ (heat transfer rate) are defined as

$$C_f=\frac{{\mu }_{hnf}}{{\rho }_f{u_w}^2}{\left(\frac{\partial u}{\partial r}\right)}_{r=a},N{u}_x=-\frac{x{k}_{hnf}}{k_f(T_w-T_{\infty })}{\left(\frac{\partial T}{\partial r}\right)}_{r=a}.$$

(10)

By substituting Equation (5) into Equation (10), we obtain

$$R{e}_x^{1/2}{C}_f=\frac{{\mu }_{hnf}}{{\mu }_f}{f}^{″}\left(0\right),R{e}_x^{-1/2}N{u}_x=\frac{1}{\theta \left(0\right)}$$

(11)

where $R{e}_x=u_w\left(x\right)x/{\nu }_f$ is the local Reynolds number.

3. Stability Analysis

Consider an unsteady problem of Equations (2) and (3) to test the stability of the particular similarity solutions such that

$$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial r}=\frac{{\mu }_{hnf}}{{\rho }_{hnf}}\left(\frac{{\partial }^{2}u}{\partial r^2}+\frac{1}{r}\frac{\partial u}{\partial r}\right),$$

(12)

$$\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial r}=\frac{k_{hnf}}{{\left(\rho C_p\right)}_{hnf}}\left(\frac{{\partial }^{2}T}{\partial r^2}+\frac{1}{r}\frac{\partial T}{\partial r}\right).$$

(13)

The disturbance in a solution may grow or decay with time; hence, it is worth using an unsteady model. The relevant similarity transformation which is applicable to reducing Equations (12) and (13) is

$$u=\frac{u_{0}x}{L}\frac{\partial f(\eta ,\tau )}{\partial \eta },v=-\frac{a}{r}\sqrt{\frac{u_0{\nu }_f}{L}}f(\eta ,\tau ),T=T_{\infty }+\frac{q_w}{k_f}\sqrt{\frac{{\nu }_{f}L}{u_0}}\theta (\eta ,\tau ),\eta =\sqrt{\frac{u_0}{{\nu }_{f}L}}\frac{r^2-a^2}{2a},$$

(14)

where $\tau =u_{0}t/L$ is a time variable. Thus, the reduced differential equations including the boundary conditions are

$$\frac{{\mu }_{hnf}/{\mu }_f}{{\rho }_{hnf}/{\rho }_f}\left[(1+2K\eta )\frac{{\partial }^{3}f}{\partial {\eta }^3}+2K\frac{{\partial }^{2}f}{\partial {\eta }^2}\right]+f\frac{{\partial }^{2}f}{\partial {\eta }^2}-{\left(\frac{\partial f}{\partial \eta }\right)}^2-\frac{{\partial }^{2}f}{\partial \eta \partial \tau }=0,$$

(15)

$$\frac{1}{\mathrm{Pr}}\frac{k_{hnf}/k_f}{{\left(\rho C_p\right)}_{hnf}/{\left(\rho C_p\right)}_f}\left[(1+2K\eta )\frac{{\partial }^2\theta }{\partial {\eta }^2}+2K\frac{\partial \theta }{\partial \eta }\right]+f\frac{\partial \theta }{\partial \eta }-\theta \frac{\partial f}{\partial \eta }-\frac{\partial \theta }{\partial \tau }=0,$$

(16)

$$f(0,\tau )=S,\frac{\partial f(0,\tau )}{\partial \eta }=\lambda ,\frac{\partial \theta (0,\tau )}{\partial \eta }=-\frac{k_f}{k_{hnf}},\frac{\partial f(\infty ,\tau )}{\partial \eta }\to 0,\theta (\infty ,\tau )\to 0.$$

(17)

Further, to examine the solution’s stability, the following perturbation equations in (18) can be substituted into Equations (15)–(17) to generate a list of unknown eigenvalues $\beta$ where ${\beta }_1<{\beta }_2<\dots <{\beta }_n$. The positive or negative sign from the smallest eigenvalue ${\beta }_1$ is important in determining a solution’s stability. The perturbation equations are (Merkin [61], Weidman et al. [62])

$$f(\eta ,\tau )=f_0\left(\eta \right)+e^{-\beta \tau }F\left(\eta \right),\theta (\eta ,\tau )={\theta }_0\left(\eta \right)+e^{-\beta \tau }G\left(\eta \right),$$

(18)

where $f_0\left(\eta \right)=f\left(\eta \right)$, ${\theta }_0\left(\eta \right)=\theta \left(\eta \right)$; and $F\left(\eta \right)$ and $G\left(\eta \right)$ are small relatives to $f_0\left(\eta \right)$ and ${\theta }_0\left(\eta \right)$, respectively. The linearized eigenvalue problem is represented by

$$\frac{{\mu }_{hnf}/{\mu }_f}{{\rho }_{hnf}/{\rho }_f}\left[(1+2K\eta )F^{‴}+2K{F}^{″}\right]+F^{″}{f}_0-(2f_0^{\prime }-\beta )F^{\prime }+f_0^{″}F=0,$$

(19)

$$\frac{1}{\mathrm{Pr}}\frac{k_{hnf}/k_f}{{\left(\rho C_p\right)}_{hnf}/{\left(\rho C_p\right)}_f}\left[(1+2K\eta )G^{″}+2K{G}^{\prime }\right]+G^{\prime }{f}_0+(\beta -f_0^{\prime })G-{\theta }_0{F}^{\prime }+F{\theta }_0^{\prime }=0,$$

(20)

and the homogeneous boundary condition is

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & F\left(0\right)=0,G^{\prime }\left(0\right)=0,F^{\prime }\left(0\right)=0,\hfill \\ \hfill & F^{\prime }(\infty )\to 0,G(\infty )\to 0.\hfill \end{array}\end{array}$$

(21)

As recommended by Harris et al. [63], the trivial eigenvalue solution can be prevented by replacing and relaxing $F^{\prime }(\infty )\to 0$ in Equation (21) with $F^{″}\left(0\right)=1$. ${\beta }_1>0$ implies that the solution is stable and realistic while ${\beta }_1<0$ concludes that the solution is unreal or unstable.

4. Results and Discussion

The essential factor for the computation of flow behaviors and the heat transfer performance of a nanofluid is the preparation of appropriate mono/hybrid nanofluids. The selection of alumina-copper/water (Al${}_2$O${}_3-$Cu/water) hybrid nanofluid in this study was motivated by Suresh et al. [64] who set up an experiment to examine the thermophysical properties of Al${}_2$O${}_3-$Cu/water hybrid nanofluids. Their investigational work proved that the stability of a hybrid nanofluid relies on the nanoparticles’ volume concentration, and the stability of a nanofluid with a higher concentration is poor. Additionally, the experimental results indicate that the prepared hybrid nanofluid substantially improved in efficiency of thermal conductivity and stability. Thus, the impacts of the aggregation and sedimentation of mono/hybrid nanoparticles can be ignored in this numerical work. It is worth mentioning that the Prandtl number was fixed at 6.2 (representing water) throughout the analysis of this study (Oztop and Abu Nada [59]). Obeying the remarkable work of Suresh et al. [64], the nanoparticles’ volume concentration of this study was set within the range of $0.005\le {\varphi }_1,{\varphi }_2\le 0.015$ to ensure the stability of the hybrid nanofluid. Meanwhile, the other parameters were used between these ranges (excluding the validation part): $0\le K\le 0.2$ (curvature parameter), $2.6<S\le 3.2$ (suction parameter) and $-2.5<\lambda \le 0.5$ (stretching/shrinking parameter). Further, the bvp4c in Matlab was fully utilized to solve the ordinary and reduced differential equation systems of Equations (7) and (8) together with the boundary equations (see Equation (9)). This recognized solver has been utilized extensively by many other investigators to address the boundary value issue. With the aim of achieving the required precision of the solutions, an initial approximation shall be offered at an initial mesh point and for a certain step size. The appropriate initial approximation and the thickness of the boundary layer ${\eta }_{\infty }$ must be selected in accordance with the values of the parameter listed.

In pursuance of the numerical outcomes, verification and accuracy of the utilized method, i.e., bvp4c, the comparison values of $\theta \left(0\right)$ when $S=0$, $\lambda =1$ and ${\varphi }_1,{\varphi }_2\approx 0$ (viscous fluid) with a different value of the curvature parameter K were assessed and are presented in

Table 3. Comparison values of $\theta \left(0\right)$ when $S=0$, $\lambda =1$ and ${\varphi }_1,{\varphi }_2\approx 0$ (viscous fluid).

K	Pr	Present	Qasim et al. [57]	Bachok et al. [66]
0.0	0.72	1.23666	1.23664	1.2367
	1.0	1.00000	1.00000	1.0000
	6.7	0.33330	0.33330	0.3333
	10	0.26877	0.26876	0.2688
1.0	0.72	0.87058	0.87018	0.8701
	1.0	0.74395	0.74406	0.7439
	6.7	0.29653	0.29661	0.2966
	10.0	0.24412	0.24217	0.2442

. It is important to note here when $K=0$ the cylindrical surface is reduced to a flat plate, while the increment value of K, i.e., $K=1$ denotes as a cylinder with $100\%$ curvature.

Table 4. Comparison values of Re${}_x^{1/2}$C${}_{fx}$ when $K=0$, $S=2.5$, $\lambda =-1$, Pr$=6.2$, ${\varphi }_1=0.1$ and various ${\varphi }_2$.

${\mathit{\varphi }}_2$	Present		Khashi’ie et al. [65]
	First Solution	Second Solution	First Solution	Second Solution
0	2.594177	0.645222	2.594178	0.645222
0.01	2.781516	0.655350	2.781516	0.655350
0.02	2.967257	0.666893	2.967257	0.666894
0.03	3.151544	0.679725	3.151544	0.679725

provides the comparison values of Re${}_x^{1/2}$C${}_{fx}$ when $K=0$ (flat plate), $S=2.5$, $\lambda =-1$, Pr$=6.2$, ${\varphi }_1=0.1$ and various ${\varphi }_2$, and it is evident that the obtained results are in outstanding agreement with the formerly published results of Qasim et al. [57], Khashi’ie et al. [65] and Bachok et al. [64]. The results of several parameters on the coefficient of skin friction and the local Nusselt number together with the velocity and temperature profiles are provided by Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 in graphical form. The impacts of the curvature parameter and various nanoparticles volumetric concentrations towards the suction/injection parameter and the stretching/shrinking parameter are discussed in detail. As a matter of fact, this current work confirms the existence of dual solutions, i.e., the first and second solutions, and a unique solution for a certain range of controlling parameters.

Figure 2 and Figure 3 depict the variation of Re${}_x^{1/2}$C${}_f$ and Re${}_x^{-1/2}$Nu${}_x$ towards S when $\lambda =-1.9$, ${\varphi }_1={\varphi }_2=0.01$ with different values of the curvature parameter where $K=0.0,0.1,0.2$ in Al${}_2$O${}_3-$Cu/H${}_2$O hybrid nanofluid, respectively. The results of Re${}_x^{1/2}$C${}_f$ rise with the intensification of K in the first solution, and decrease in the second solution when the cylinder is in the shrinking state, as demonstrated in Figure 2. Similar outcome patterns for both solutions can also be found in Re${}_x^{-1/2}$Nu${}_x$, as evaluated in Figure 3. The deployment of appropriate wall mass suction parameters $(S>0)$ in the present work was able to produce the dual similarity solutions, which is clearly proven in Figure 2 and Figure 3. On the other hand, in the state of the impermeable cylinder where no suction/injection parameter is being considered $(S=0)$ or if the injection parameter $(S<0)$ is added, no equivalent solutions can be achieved, including the unique or dual solutions. Notably, Figure 2 also illustrates that when K upsurges, the additional value of suction parameter S (more magnitude) is required in Al${}_2$O${}_3-$Cu/H${}_2$O hybrid nanofluid. In the present work, however, the authors merely evaluated the value of K within the scope of $0\le K\le 0.2$ in Al${}_2$O${}_3-$Cu/water hybrid nanofluid, and the authors would like to declare that the outcome could be varied if different values of the curvature parameter or distinctive type of hybrid nanofluid are measured. Surprisingly, Figure 3 reveals that the inclusion of K in the shrinking cylinder eventually declines the heat transfer rate of Al${}_2$O${}_3-$Cu/water hybrid nanofluid. The results oppose the fact that the augmentation in K supposedly improves the heat transfer performance in a nanofluid. This is because the increase in curvature parameter causes diminution of the curvature radius, which consequently lessens the area of the cylinder. The cylinder encounters less resistance from the fluid particles, increases the fluid velocity and ultimately boosts the rate of heat transfer. However, the authors believe that the selection of governing parameter values and the presence of prescribing heat flux at the shrinking surface of the cylinder are the explanations for this behavior. The presence of prescribed heat flux at the boundary condition system imposes some amount of heat flowing, and this consequently may worsen the process of heat transfer. Overall, the Al${}_2$O${}_3-$Cu/water hybrid nanofluid has better heat transfer efficiency in a flat plate $(K=0)$ compared to the cylinder case $(K=0.1,0.2)$.

Figure 4 and Figure 5 display the diversity of Re${}_x^{1/2}$C${}_f$ and Re${}_x^{-1/2}$Nu${}_x$ towards $\lambda$ when $S=3$, ${\varphi }_1={\varphi }_2=0.01$ with distinct values of K in Al${}_2$O${}_3-$Cu/water hybrid nanofluid. The dual solutions are observed in the shrinking surface where $\lambda <0$, whereas no dual solutions can be perceived when the surface is stretching, i.e., $\lambda >0$. Figure 4 proves that an increment of K decreases Re${}_x^{1/2}$C${}_f$ in the first solution, but upsurges the results in the second solution. Meanwhile, Figure 5 portrays the heat transfer rate of the shrinking surface where Re${}_x^{-1/2}$Nu${}_x$ is clearly diminished when the values of K rises in Al${}_2$O${}_3-$Cu/H${}_2$O hybrid nanofluid. From here, we note that the same pattern is observed in Figure 2 and Figure 3, when K increases. However, these results may vary if different values of the controlling parameter are taken into account. On another note, the effect of the volumetric concentration is also examined in this study. It was observed that the Re${}_x^{1/2}$C${}_f$ and Re${}_x^{-1/2}$Nu${}_x$, as presented in Figure 6 and Figure 7, respectively, improve with the rise of the Cu nanoparticle concentration in the first solution. In fact, the higher concentration of Cu nanoparticles creates more kinetic energy, and thereby increases the heat transfer of the fluid particles. Nevertheless, Figure 6 and Figure 7 also disclose that the second solution can be obtained only for a small value of negative $\lambda$ in the opposing or shrinking region.

Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 establish the distribution of temperature $\theta \left(\eta \right)$ and velocity profiles $f^{\prime }\left(\eta \right)$ with different controlling parameter, for instance, the suction/injection parameter S, the curvature parameter K and the stretching/shrinking parameter $\lambda$. All profiles asymptotically fulfilled the boundary condition (9) when ${\eta }_{\infty }=20$ is implemented. Figure 8 and Figure 9 depict the impact of S on $f^{\prime }\left(\eta \right)$ and $\theta \left(\eta \right)$, accordingly. The findings show that the increasing value of S is proven to boost the resistance of the flow in $f^{\prime }\left(\eta \right)$ of the first solution; however, an opposite behaviour is observed in the second solution. Meanwhile, Figure 9 exposes a reduction trend of $\theta \left(\eta \right)$ in the first and second solutions. The temperature distribution with the inclusion of the suction parameter is discussed to inspect the deterioration in temperature, which hence cools the system. As the temperature of the system reduces, the heat transfer rate is enhanced, and this is proven in Figure 3 above.

Figure 10 and Figure 11 exhibit the variation of K on $f^{\prime }\left(\eta \right)$ and $\theta \left(\eta \right)$, appropriately. $f^{\prime }\left(\eta \right)$ is reduced in the first solution but decreases (second solution) when K is added, as displayed in Figure 10. Figure 11 illustrates the rises of $\theta \left(\eta \right)$ with increments of K in both solutions, i.e, the first and second solutions. The reduction in the fluid velocity and the increases of temperature profiles are inline with the results obtained in Figure 3, where the addition of K in the shrinking state at last worsens the heat transfer rate of Al${}_2$O${}_3-$Cu/water hybrid nanofluid. Further, the influences of the static cylinder $(\lambda =0)$, the stretching parameter $(\lambda =0.3,0.5)$ and the shrinking parameter $(\lambda =-0.3,-0.5)$ on the velocity and temperature profiles are illustrated in Figure 12 and Figure 13. The findings reveal a unique solution, and no second solution appeared in either profile. That obviously indicates that the changes in behavior from shrinking to stretching state in the cylinder concurrently increase $f^{\prime }\left(\eta \right)$, as clarified in Figure 12. Meanwhile, the temperature profiles $\theta \left(\eta \right)$ decrease with the enhancement of the stretching/shrinking parameter $\lambda$.

A temporal stability analysis was conducted by solving the linearized eigenvalue problem in (19)–(21) with the inclusion of the new boundary condition $F^{″}\left(0\right)=1$. The results in Figure 14 exhibit that the first solution has ${\beta }_1>0$ (positive smallest eigenvalues). The second solution contributes to the negative smallest eigenvalue. This shows that the first solution is more realistic than the second solution. Meanwhile, as $\lambda \to {\lambda }_c$, ${\beta }_1\to 0$ from both solutions, which is in accordance with Merkin [61] and Weidman et al. [62], the transitions from stable $\left({\beta }_1>0\right)$ to unstable $\left({\beta }_1<0\right)$ occur at the turning point $\lambda ={\lambda }_c$.

5. Conclusions

The present work scrutinized the laminar and two-dimensional Al${}_2$O${}_3$-Cu/water nanofluid flow and heat transfer towards a permeable stretching/shrinking cylinder with prescribed surface heat flux. The respective differential equations can be reduced to a flat plate case when the curvature parameter $K=0$, while $K>0$ represents a circular cylinder surface. The conclusions are:

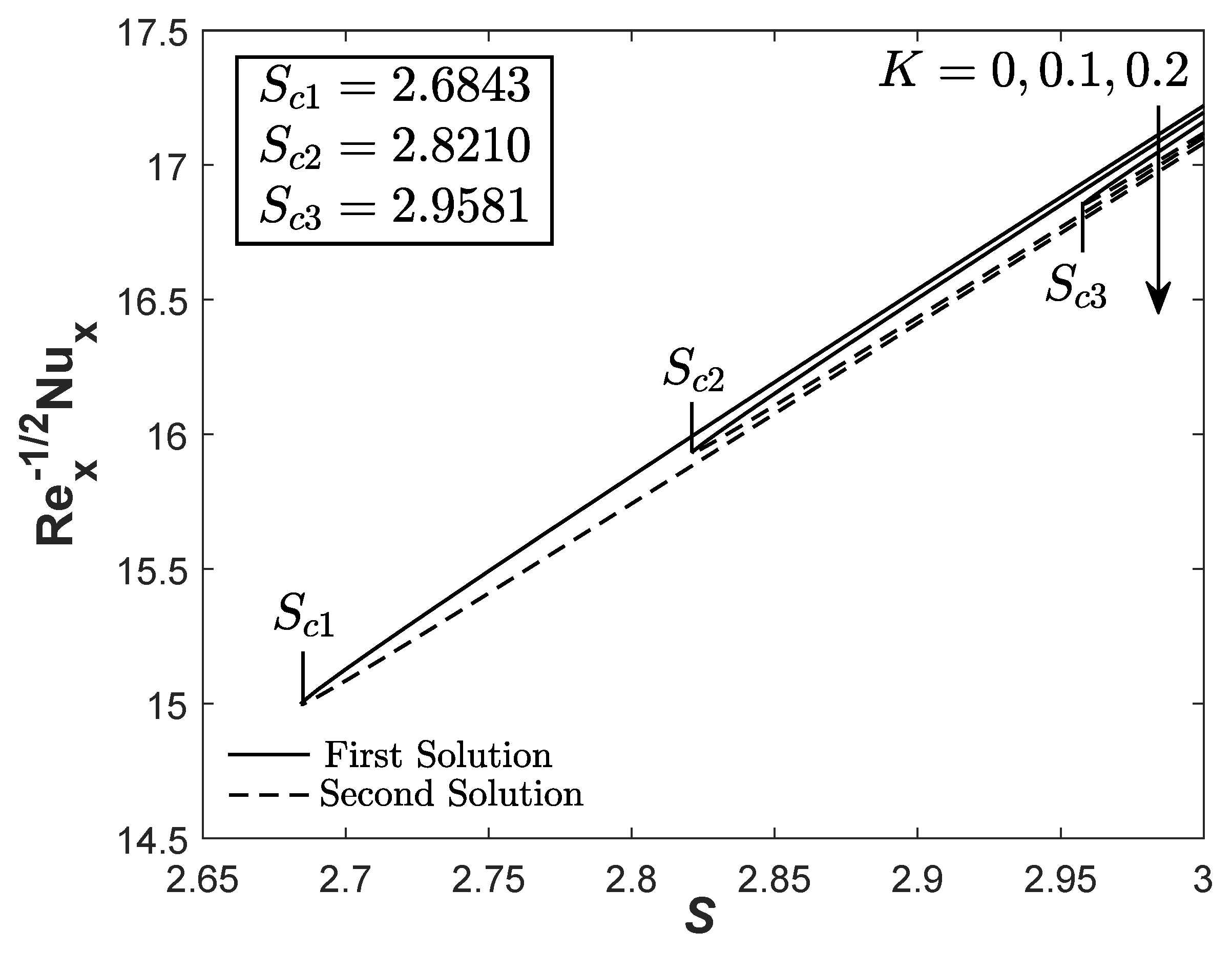
• For both shrinking cylinder and flat plate surfaces with the prescribed surface heat flux, the steady flow solutions are obtainable when the suction parameter is $S>2.6$. No second solution was observed when considering the stretching surface.
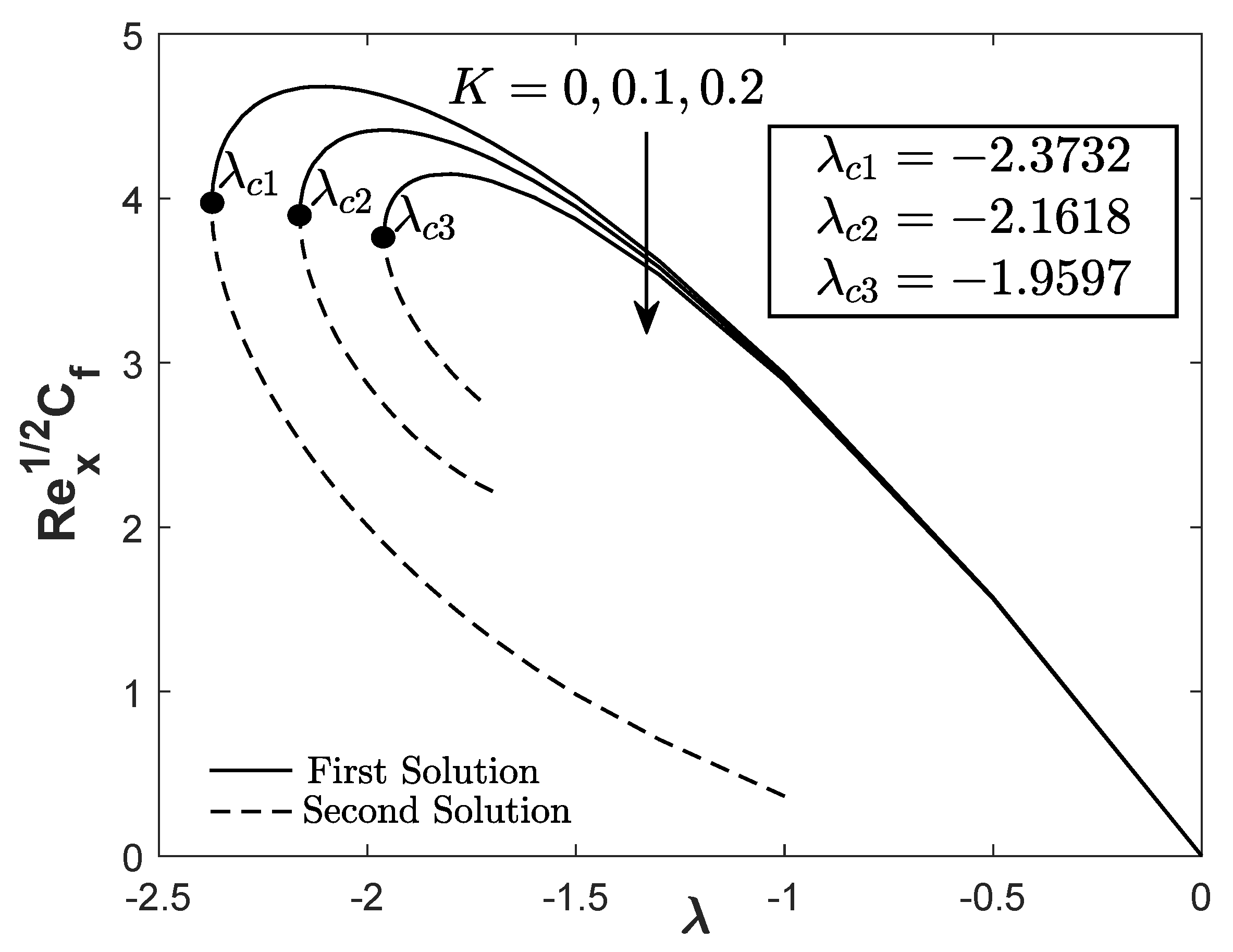
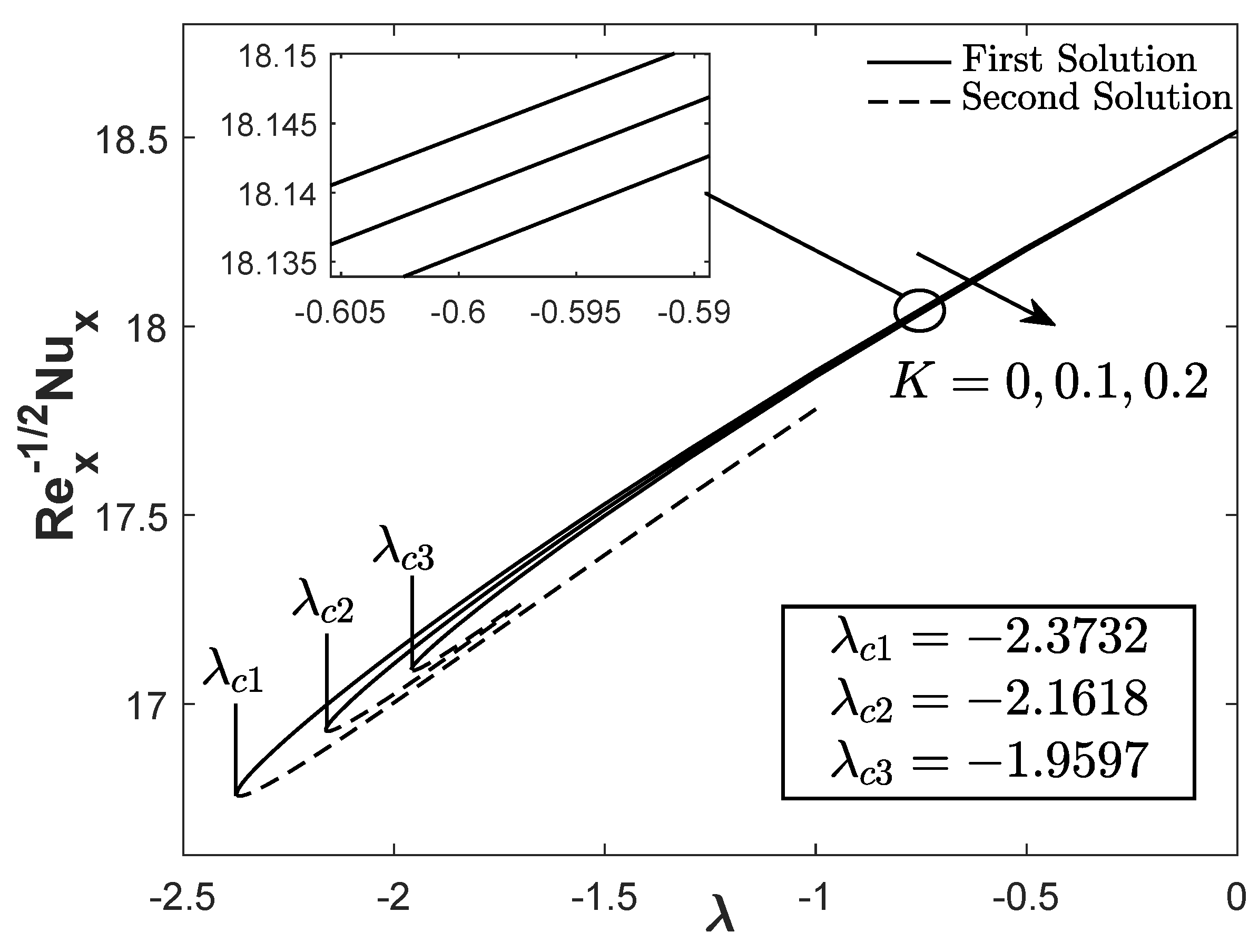
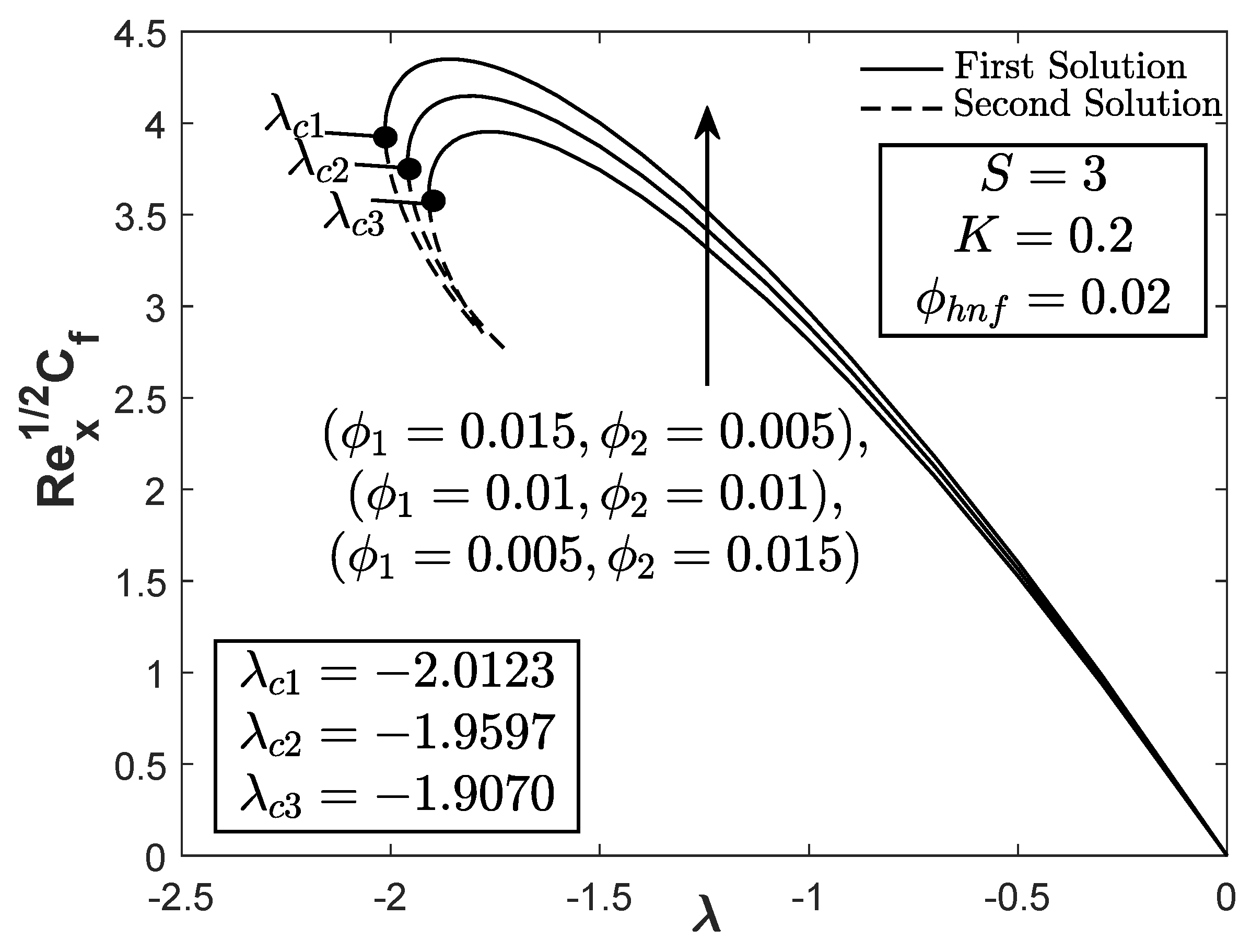
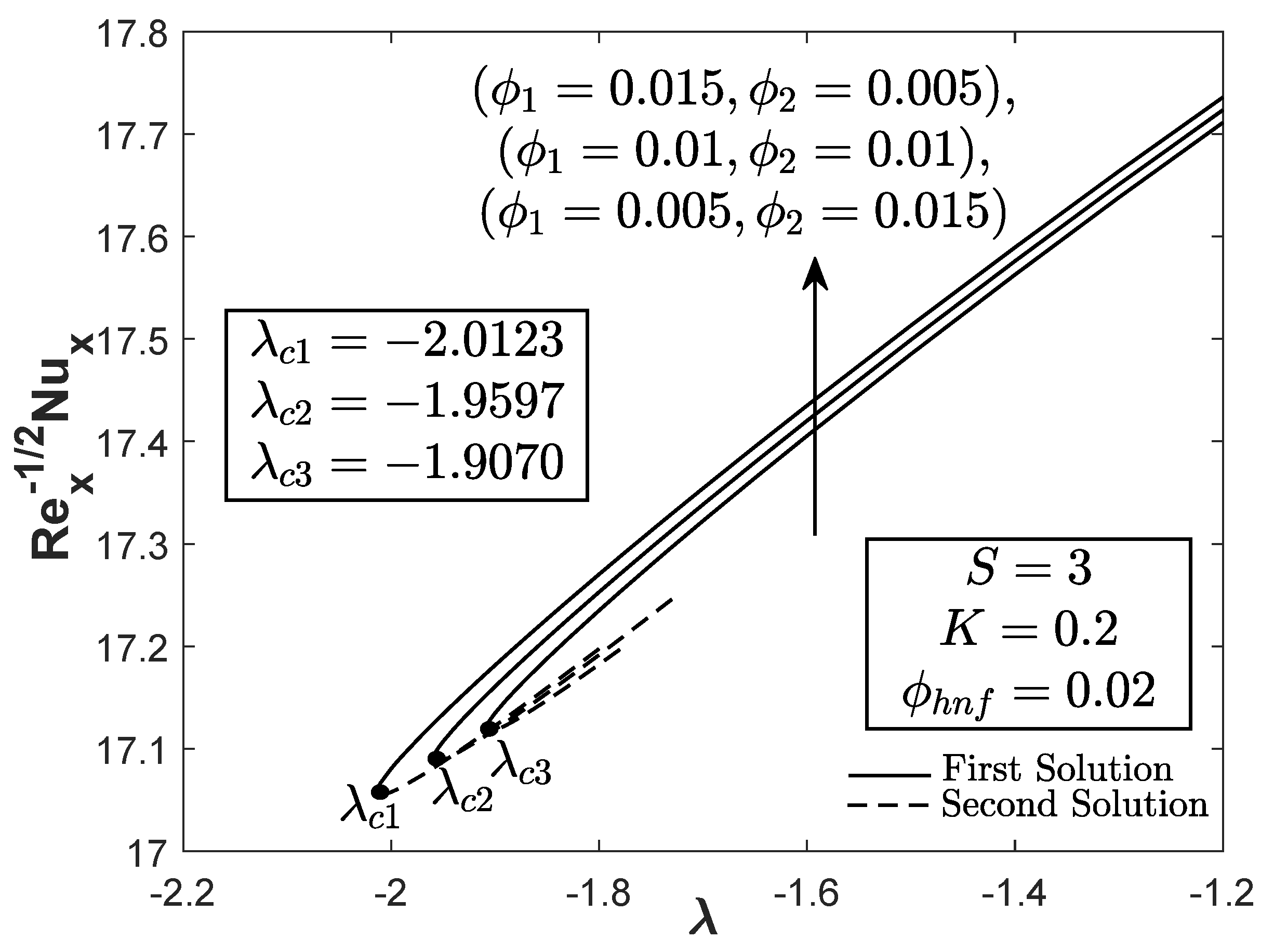
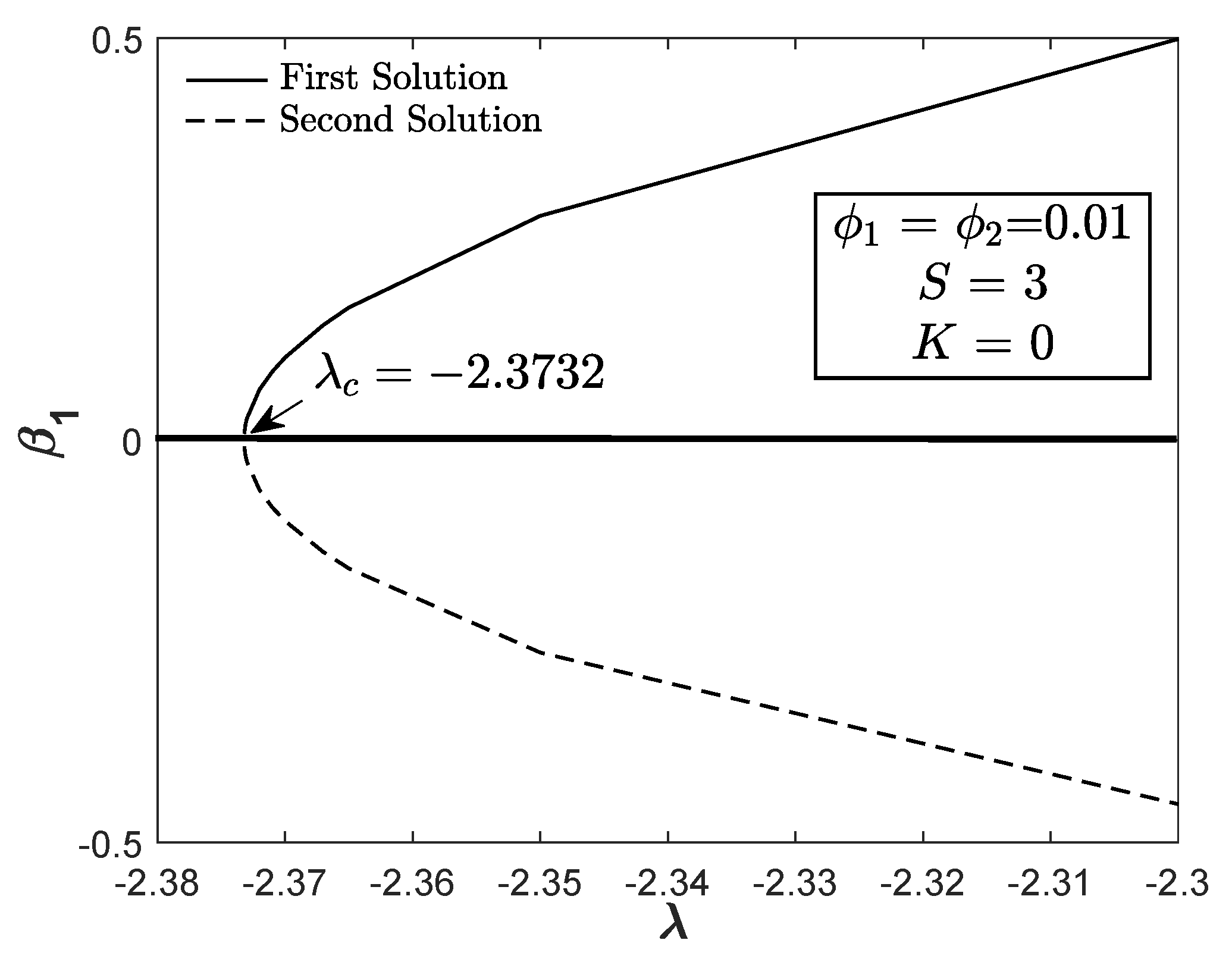
• The separation of boundary layer can be decelerated by the extension of the critical value when $K=0$. The flat plate surface also contributes to the maximum heat transfer rate.
• Among the three sets of hybrid Al${}_2$O${}_3$-Cu nanoparticle concentrations such that $({\varphi }_1=0.5\%$, ${\varphi }_2=1.5\%)$, $({\varphi }_1=1\%,{\varphi }_2=1\%)$ and $({\varphi }_1=1.5\%,{\varphi }_2=0.5\%)$, the hybrid nanofluids with concentration $({\varphi }_1=0.5\%,{\varphi }_2=1.5\%)$ provided the greatest heat transfer rate and skin friction coefficient.
• The stability analysis mathematically supports the reliability of the first solution.
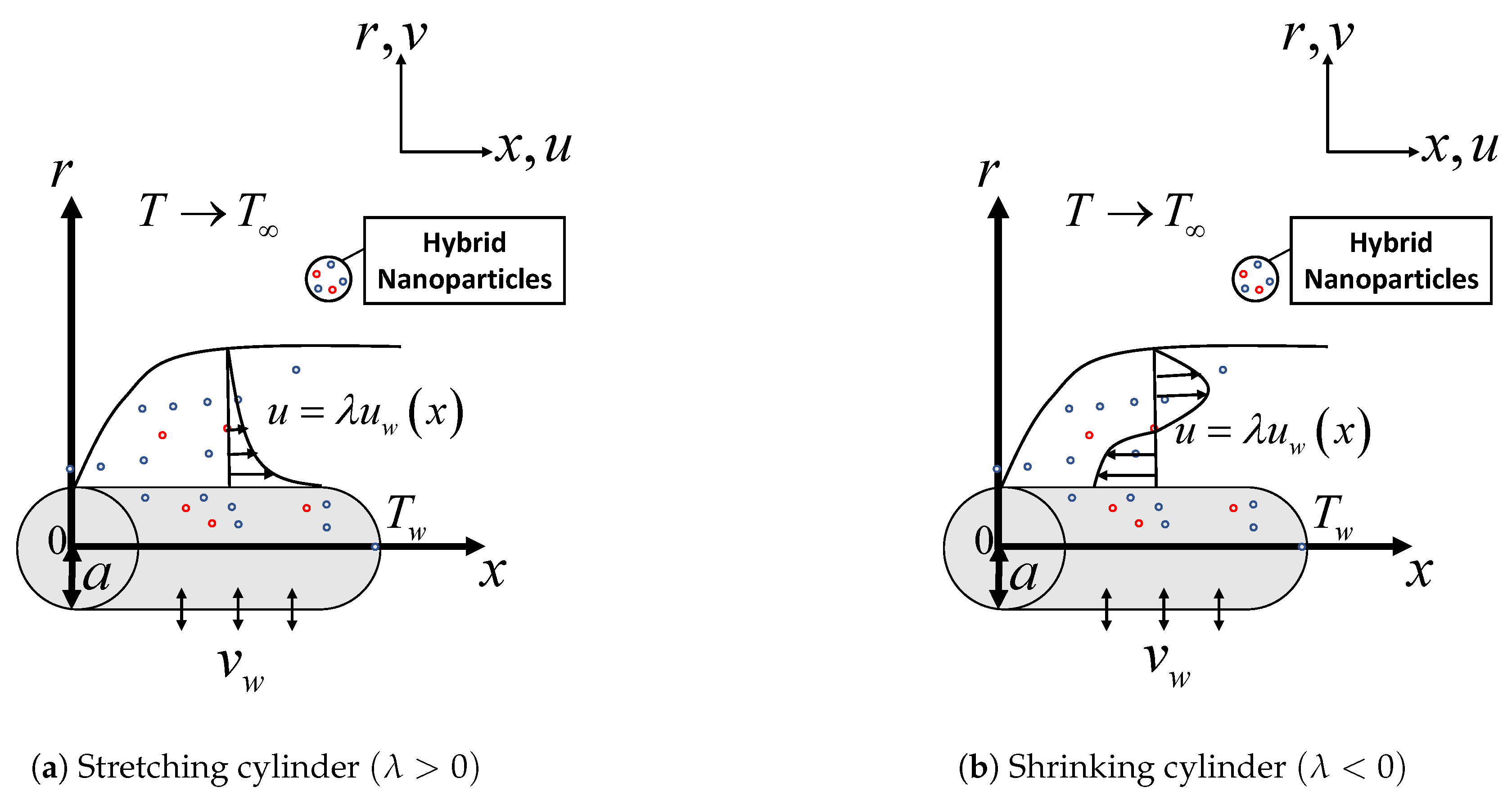
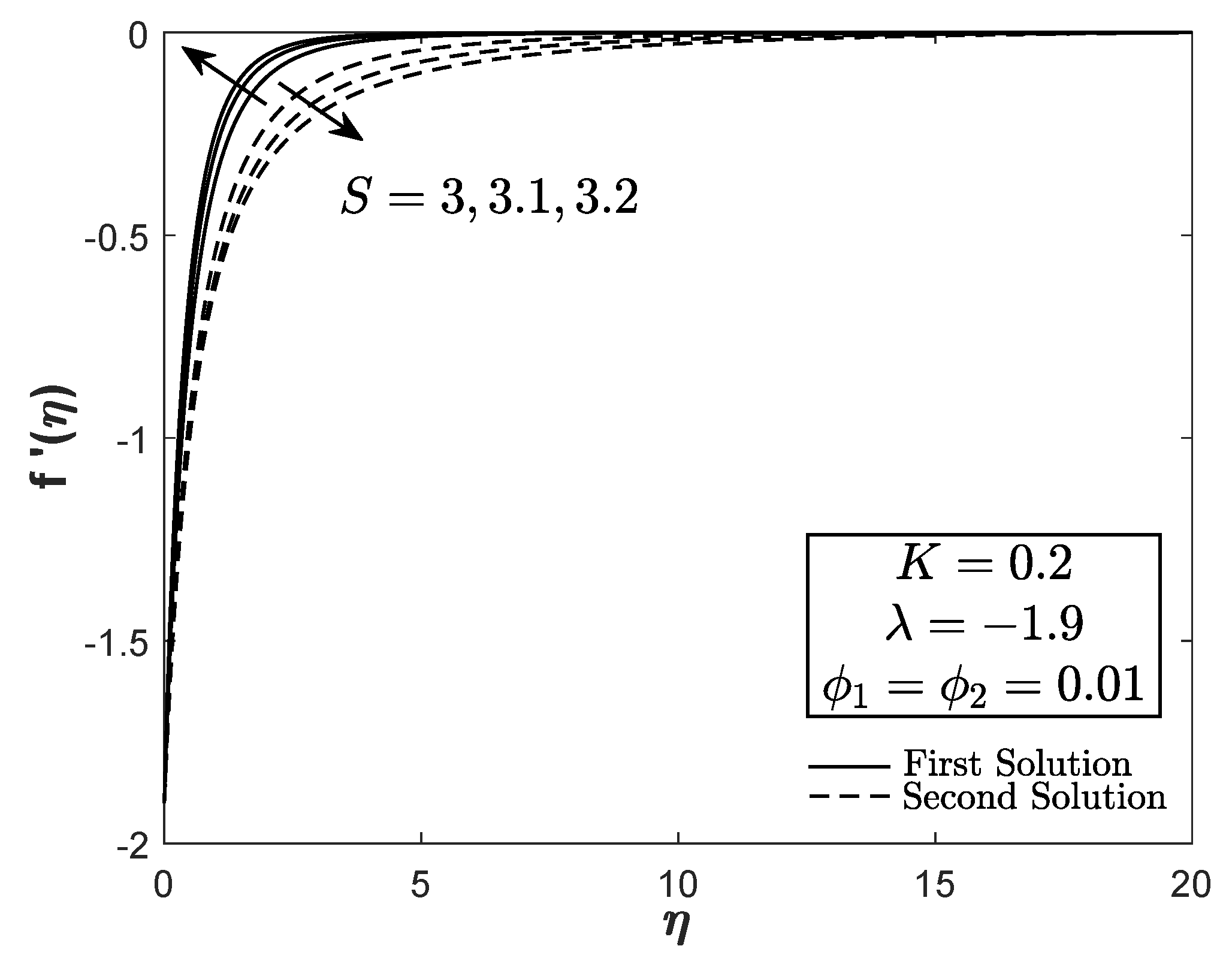
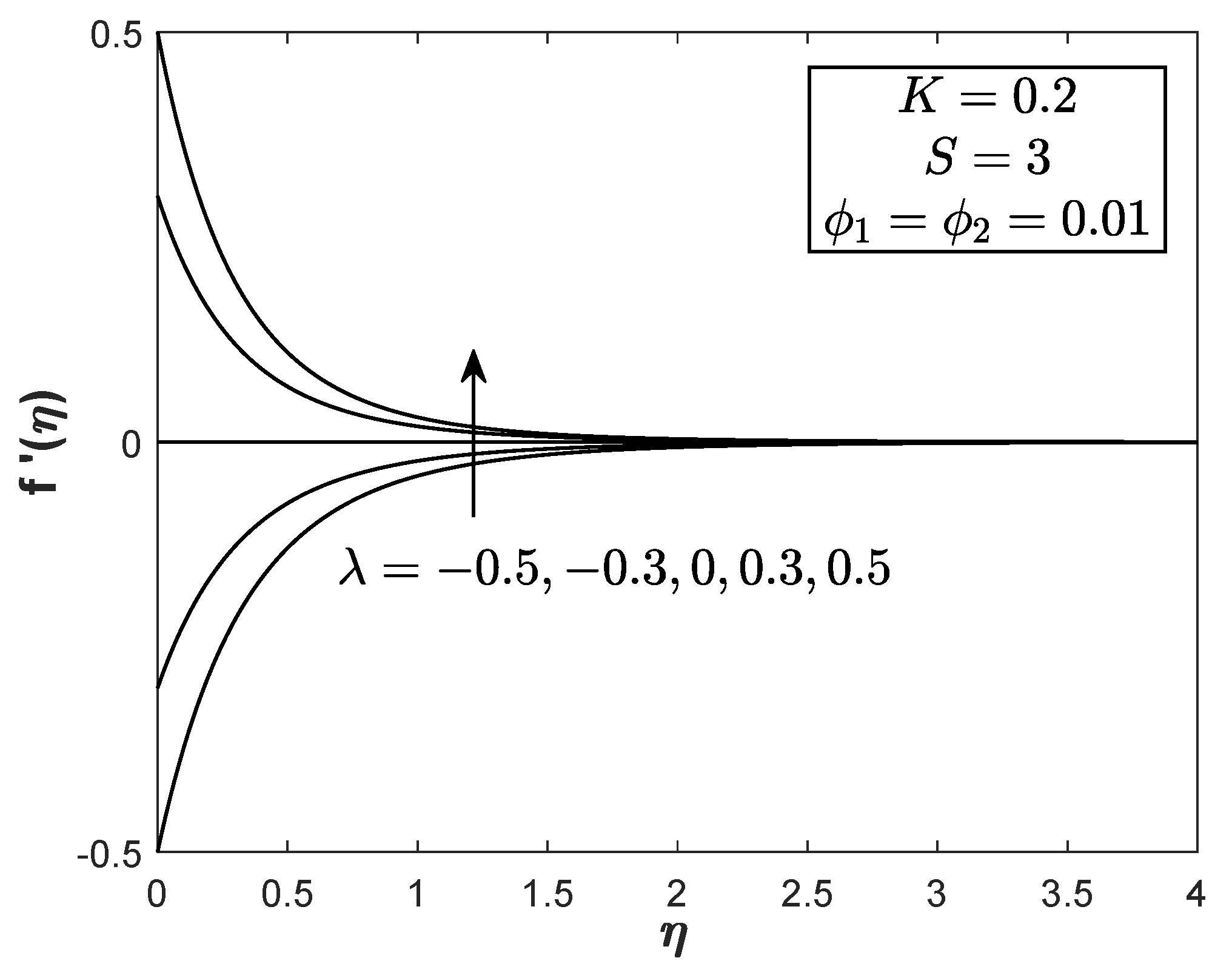
• The hybrid nanofluid flow due to the shrinking surfaces is a reverse (opposite) flow from the stretching surfaces. The velocity profile for the shrinking case $(\lambda <0)$ shows a negative value and contradicts the positive velocity profile for the stretching case $(\lambda >0)$.
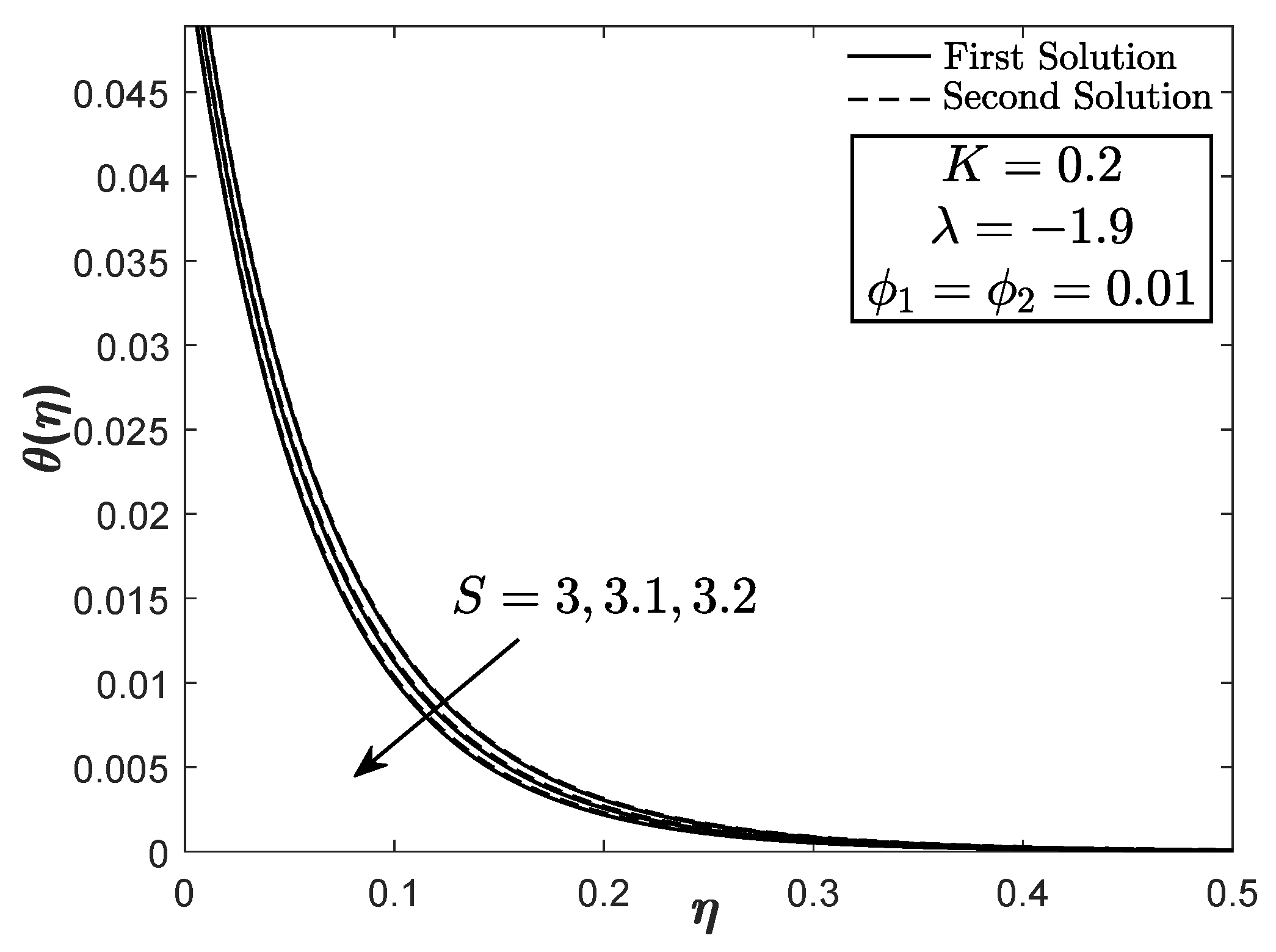
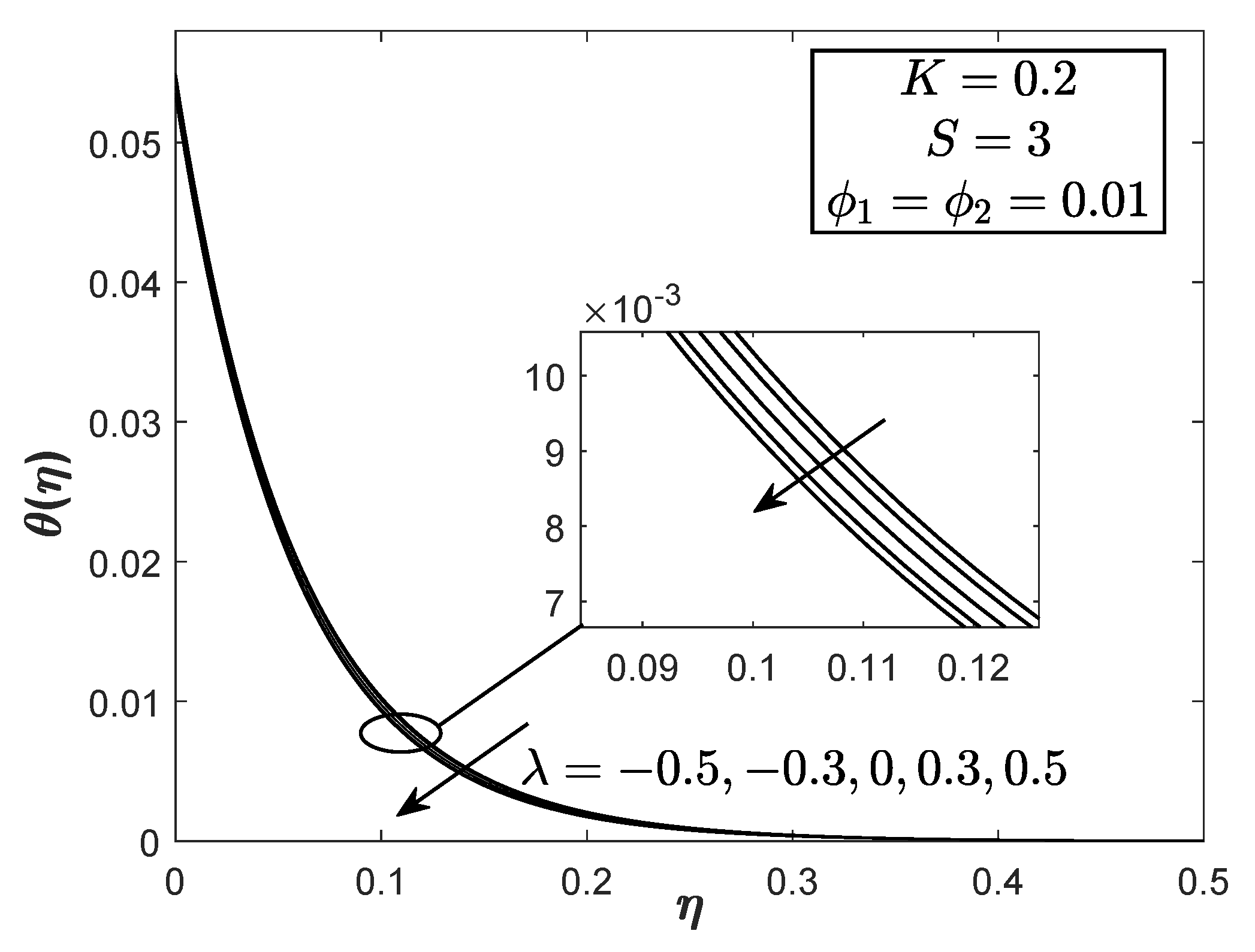
• The hybrid nanofluid temperature for the stretching case is lower than the shrinking case.

6. Recommendations for Future Work

The present findings are limited to the combination of Al${}_2$O${}_3$ and Cu nanoparticles only with ${\varphi }_{hnf}=2\%$. For future work, it will be worth studying the significance of the cylinder in augmenting the heat transfer rate while delaying the separation of boundary layer flow by considering:

• Different hybrid nanofluids (other stable combinations based on the experimental work of hybrid nanofluids);
• Stagnation point flow (exclusion of the wall mass suction parameter);
• Other physical parameters, such as magnetic field, thermal radiation, viscous dissipation and Joule heating.