A Novel Family of Efficient Weighted-Newton Multiple Root Iterations

Abstract

We propose a novel family of seventh-order iterative methods for computing multiple zeros of a nonlinear function. The algorithm consists of three steps, of which the first two are the steps of recently developed Liu–Zhou fourth-order method, whereas the third step is based on a Newton-like step. The efficiency index of the proposed scheme is 1.627, which is better than the efficiency index 1.587 of the basic Liu–Zhou fourth-order method. In this sense, the proposed iteration is the modification over the Liu–Zhou iteration. Theoretical results are fully studied including the main theorem of local convergence analysis. Moreover, convergence domains are also assessed using the graphical tool, namely, basins of attraction which are symmetrical through the fractal like boundaries. Accuracy and computational efficiency are demonstrated by implementing the algorithms on different numerical problems. Comparison of numerical experiments shows that the new methods have an edge over the existing methods.

1. Introduction

Approximating the solution of nonlinear equations by numerical methods is an important problem in many branches of science and engineering. For example, problems from many areas such as Physics, Chemistry, Mathematical Biology, and Engineering science are reduced to finding solution of nonlinear equations [1,2,3,4]. In general, closed form solutions can not be obtained so researchers use iterative methods for approximating the solution. In this paper, our aim is to construct higher order multi-point iterative methods for the multiple zeros of the univariate function $f\left(x\right)$, where $f:\mathbb{C}\to \mathbb{C}$ is analytic about the required zero. The advantages of multi-point methods over one-point methods are discussed in Traub’s well-known book [4].

Many higher-order methods, with or without using the classical Newton’s method [5]

$$x_{n+1}=x_n-m\frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)},n=0,1,2,\dots$$

(1)

are available in literature, see in [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]. Here, m is the multiplicity of a zero (say, $\alpha$) of the function $f\left(x\right)$, i.e., $f^{\left(j\right)}\left(\alpha \right)=0,j=0,1,\dots ,m-1$ and $f^{\left(m\right)}\left(\alpha \right)\ne 0$. Such methods require the evaluation of derivatives of either first-order or both first- and second-order. In particular, Liu and Zhou [13] have recently proposed the following scheme of two-point Newton-like methods,

$$\begin{array}{cc}\hfill & y_n=x_n-m\frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)},\hfill \\ \hfill & x_{n+1}=y_n-mG\left(u_n\right)\frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)},\hfill \end{array}$$

(2)

where $u_n={\left(\frac{f^{\prime }\left(y_n\right)}{f^{\prime }\left(x_n\right)}\right)}^{\frac{1}{m-1}}$ and $G:\mathbb{C}\to \mathbb{C}$ is a holomorphic function in neighborhood about zero. They have shown that this iterative scheme attains fourth-order convergence provided that the function $G\left(u\right)$ satisfies the conditions

$$G\left(0\right)=0,G^{\prime }\left(0\right)=1,G^{\prime \prime }\left(0\right)=\frac{4m}{m-1},m\ne 1.$$

In this article, we aim to develop multiple root solvers of high efficiency, meaning the methods with rapid convergence that require less computations. Proceeding in this way, we develop a family of seventh-order three-point Newton-type methods for computing multiple zeros. The proposed iterative scheme is the composition of three steps that uses the Liu–Zhou iteration (2) as the first two steps and a Newton-type iteration in the third step. The algorithm requires four function evaluations per iteration and, therefore, possesses the efficiency index $7^{1/4}\approx 1.627$, which is better than the efficiency index $4^{1/3}\approx 1.587$ of the basic method (2). In this sense, the proposed iteration is the modification over the iteration (2). Some special methods of the new family are established. The usefulness of the methods is demonstrated by performing numerical tests on several applied science problems. Thereby, we observe in each example that the new methods have far better numerical results than the existing methods. The convergence domains are also assessed using the graphical tool, namely, basins of attraction, which is an useful technique to check the convergence regions visually.

We summarize the contents of this article. In Section 2, the family of seventh-order iterative solvers is derived and its local convergence is studied. In order to check the convergence regions of the methods graphically, the basins of attractors are assessed in Section 3. Some numerical experiments are performed in Section 4 to verify the theoretical results and to compare the performance with the existing methods. In Section 5, concluding remarks are reported.

2. Development of Scheme

Our aim is to develop an iterative method for computing a multiple root with multiplicity $m>1$, which accelerates the convergence rate of the two-step Liu–Zhou iteration (2) using a minimum number of functions and derivative evaluations. Thus, it will turn out to be judicious if we consider a somewhat complicated three-step iterative scheme of the following form,

$$\left\{\begin{array}{c}{y}_n=x_n-m\frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)},\hfill \\ z_n=y_n-mG\left(u_n\right)\frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)},\hfill \\ x_{n+1}=z_n-m{v}_n\left(1+a\frac{v_n}{u_n}\right)H\left(u_n\right)\frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)},\hfill \end{array}\right.$$

(3)

where $u={\left(\frac{f^{\prime }\left(y\right)}{f^{\prime }\left(x\right)}\right)}^{\frac{1}{m-1}}$, $v={\left(\frac{f\left(z\right)}{f\left(x\right)}\right)}^{\frac{1}{m}}$, a is scalar, and $G,H:\mathbb{C}\to \mathbb{C}$ are analytic functions about a neighborhood of 0. Note that the second and third steps are weighted by the factors $G\left(u\right)$ and $H\left(u\right)$, and, as a result, these are called weight factors or weight functions.

Note that u and v are one-to-$m-1$ and one-to-m multi-valued functions, respectively. Therefore, it is convenient to treat them as the principal root. As an example, we consider the case of v. The principal root is given by $v=\exp \left[\frac{1}{m}\mathrm{Log}\left(\frac{f\left(z\right)}{f\left(x\right)}\right)\right]$, with $\mathrm{Log}\left(\frac{f\left(z\right)}{f\left(x\right)}\right)=\mathrm{Log}\left|\frac{f\left(z\right)}{f\left(x\right)}\right|+i\mathrm{Arg}\left(\frac{f\left(z\right)}{f\left(x\right)}\right)$ for $-\pi <\mathrm{Arg}\left(\frac{f\left(z\right)}{f\left(x\right)}\right)\le \pi$; this convention of $\mathrm{Arg}\left(Z\right)$ for $Z\in \mathbb{C}$ agrees with that of $\mathrm{Log}\left[Z\right]$ command of Mathematica [21]. We employ this command in the later section of numerical simulation. Similarly, we treat for u.

In the following theorem, we shall prove the seventh-order convergence of the proposed scheme (3).

Theorem 1.

Let the function $f:\mathbb{C}\to \mathbb{C}$ be analytic in a domain containing multiple zero α of multiplicity m. Suppose that the starter $x_0$ is close enough to α. Then, the iterative technique expressed by (3) possesses seventh-order convergence, provided that the functions $G\left(u\right)$ and $H\left(u\right)$ satisfy the conditions

$$\left\{\begin{array}{c}G\left(0\right)=0,G^{\prime }\left(0\right)=1,G^{\prime \prime }\left(0\right)=\frac{4m}{m-1}\hfill \\ a=\frac{m-1}{m},H\left(0\right)=1,H^{\prime }\left(0\right)=2,H^{\prime \prime }\left(0\right)=\frac{2(m^2-2m-1)}{m(m-1)}.\hfill \end{array}\right.$$

(4)

Proof. 

Let the error at n-th stage be $e_n=x_n-\alpha$. Using the Taylor’s expansion of $f\left(x_n\right)$ about $\alpha$, we have that

$$f\left(x_n\right)=\frac{f^{\left(m\right)}\left(\alpha \right)}{m!}{e}_n^m\left(1+C_1{e}_n+C_2{e}_n^2+C_3{e}_n^3+C_4{e}_n^4+C_5{e}_n^5+C_6{e}_n^6+C_7{e}_n^7+O\left(e_n^8\right)\right)$$

(5)

and

$$\begin{array}{cc}\hfill f^{\prime }\left(x_n\right)=\frac{f^{\left(m\right)}\left(\alpha \right)}{m!}{e}_n^{m-1}(m& +C_1(m+1)e_n+C_2(m+2)e_n^2+C_3(m+3)e_n^3+C_4(m+4)e_n^4\hfill \\ \hfill & +C_5(m+5)e_n^5+C_6(m+6)e_n^6+C_7(m+7)e_n^7+O\left(e_n^8\right)),\hfill \end{array}$$

(6)

where $C_k=\frac{m!}{(m+k)!}\frac{f^{(m+k)}\left(\alpha \right)}{f^{\left(m\right)}\left(\alpha \right)}$, $k\in \mathbb{N}$.

From (5), (6), and the first step of (3), we have that

$$\begin{array}{cc}\hfill {\overline{e}}_n=y_n-\alpha =& \frac{C_1}{m}{e}_n^2+\sum _{i=1}^5{\omega }_i{e}_n^{i+2}+O\left(e_n^8\right),\hfill \end{array}$$

(7)

where ${\omega }_i={\omega }_i(m,C_1,C_2,\dots ,C_7)$ are given in terms of $m,C_1,C_2,\dots ,C_7$ with two explicitly written coefficients, ${\omega }_1=\frac{2m{C}_2-(m+1)C_1^2}{m^2}$ and ${\omega }_2=\frac{1}{m^3}\left(3m^2{C}_3+{(m+1)}^2{C}_1^3-m(4+3m)C_1{C}_2\right)$. The remaining expressions of ${\omega }_i(i=3,4,5)$ are not being produced explicitly as these are very lengthy.

Expansion of $f\left(y_n\right)$ and $f^{\prime }\left(y_n\right)$ about $\alpha$ leads us to the expression

$$\begin{array}{cc}\hfill f\left(y_n\right)=& \frac{f^{\left(m\right)}\left(\alpha \right)}{m!}{\left({\overline{e}}_n\right)}^m\left(1+C_1{\overline{e}}_n+C_2{\left({\overline{e}}_n\right)}^2+C_3{\left({\overline{e}}_n\right)}^3+O\left({\left({\overline{e}}_n\right)}^4\right)\right)\hfill \end{array}$$

(8)

and

$$f^{\prime }\left(y_n\right)=\frac{f^{\left(m\right)}\left(\alpha \right)}{m!}{\left({\overline{e}}_n\right)}^{m-1}\left(m+C_1(m+1){\overline{e}}_n+C_2(m+2){\left({\overline{e}}_n\right)}^2+C_3(m+3){\left({\overline{e}}_n\right)}^3+O\left({\left({\overline{e}}_n\right)}^4\right)\right).$$

(9)

By using (6) and (9), we get expression of $u_n$ as

$$\begin{array}{c}\hfill u_n=\frac{C_1}{m}{e}_n+\frac{2C_2(m-1)-C_1^2(m+1)}{m(m-1)}{e}_n^2+\sum _{i=1}^5{\eta }_i{e}_n^{i+2}+O\left(e_n^8\right),\end{array}$$

(10)

where ${\eta }_i={\eta }_i(m,C_1,C_2,\dots ,C_7)$ are given in terms of $m,C_1,C_2,\dots ,C_7$ with one explicitly written coefficient, ${\eta }_1=\frac{1}{2m^3{(m-1)}^2}\left(C_1^3(2m^4+3m^3+2m^2-m-2)-2m^2(3m^2+m-4)C_1{C}_2+6{(m-1)}^2{m}^2{C}_3)\right)$.

Expanding the function $G\left(u\right)$ about origin using Taylor series

$$G\left(u_n\right)\approx G\left(0\right)+u_n{G}^{\prime }\left(0\right)+\frac{1}{2}{u}^2{G}^{\prime \prime }\left(0\right)+O\left(u_n^3\right).$$

(11)

By inserting the expressions (5), (6), and (11) in the second step of scheme (3) and simplifying,

$$\begin{array}{c}\hfill z_n-\alpha =-G\left(0\right)e_n+\frac{1+G\left(0\right)-G^{\prime }\left(0\right)}{m}{C}_1{e}_n^2+\sum _{i=1}^4{\gamma }_i{e}_n^{i+2}+O\left(e_n^8\right),\end{array}$$

(12)

where ${\gamma }_i={\gamma }_i(m,G\left(0\right),G^{\prime }\left(0\right),C_1,C_2,\dots ,C_7)$.

In order to obtain higher order convergence, the coefficients of $e_n$, $e_n^2$, and $e_n^3$ should vanish. The resulting equations yield

$$G\left(0\right)=0,G^{\prime }\left(0\right)=1G^{\prime \prime }\left(0\right)=\frac{4m}{m-1}.$$

(13)

Combining Equations (12) and (13), we obtain that

$$\begin{array}{c}\hfill z_n-\alpha =\frac{(2+m+8m^2+m^3)C_1^3-2(m-1)m^2{C}_1{C}_2}{2m^3{(m-1)}^2}{e}_n^4+\sum _{i=1}^3{\gamma }_i{e}_n^{i+4}+O\left(e_n^8\right).\end{array}$$

(14)

Developing $f\left(z_n\right)$ about $\alpha$, it follows that

$$\begin{array}{c}\hfill f\left(z_n\right)=\frac{f^{\left(m\right)}\left(\alpha \right)}{m!}{(z_n-\alpha )}^m\left(1+C_1(z_n-\alpha )+C_2{(z_n-\alpha )}^2+O\left({(z_n-\alpha )}^3\right)\right).\end{array}$$

(15)

Inserting (5) and (15) in the expression of $v_n$, then

$$\begin{array}{c}\hfill v_n=\frac{(2+m+8m^2+m^3)C_1^3-2m^2(m-1)C_1{C}_2}{2m^3(m-1)}{e}_n^3+\sum _{i=1}^4{\tau }_i{e}_n^{i+3}+O\left(e_n^8\right),\end{array}$$

(16)

where ${\tau }_i={\tau }_i(m,C_1,C_2,\dots ,C_7)$.

The Taylor expansion of $H\left(u_n\right)$ about origin 0 is given by

$$H\left(u_n\right)\approx H\left(0\right)+u_n{H}^{\prime }\left(0\right)+\frac{u_n^2}{2}{H}^{\prime \prime }\left(0\right).$$

(17)

Therefore, by substituting (5), (6), (10), (16), and (17) into the last step of scheme (3), we obtain the error equation

$$\begin{array}{cc}\hfill e_{n+1}=& -\frac{(1+H\left(0\right))C_1\left(\left(2+m+8m^2+m^3\right)C_1^2-2\left(m-1)m^2{C}_2\right)\right)}{2m^3{(m-1)}^2}{e}_n^4+\sum _{i=1}^3{\xi }_i{e}_n^{i+4}+O\left(e_n^8\right),\hfill \end{array}$$

(18)

where ${\xi }_i={\xi }_i(m,H\left(0\right),H^{\prime }\left(0\right),H^{\prime \prime }\left(0\right),C_1,C_2,\dots ,C_7)$.

Error Equation (18) shows that at least fifth-order convergence is attained if $H\left(0\right)=1$. Using this value in ${\xi }_1=0$, we will obtain

$$H^{\prime }\left(0\right)=2.$$

Then, using $H\left(0\right)=1$ and $H^{\prime }\left(0\right)=2$ in ${\xi }_2=0$, the following equation is obtained,

$$\begin{array}{cc}\hfill & C_1\left(\left(2+m+8m^2+m^3\right)C_1^2-2(-1+m)m^2{C}_2\right)(-2m(m-1)(1+(-1+a)m)C_2\hfill \\ \hfill & +C_1^2\left(a(2+m+8m^2+m^3)-(-1+m)(-3+m^2-m(-10+H^{\prime \prime }\left(0\right))+H^{\prime \prime }\left(0\right)\right)\left)\right)=0,\hfill \end{array}$$

(19)

which further yields

$$a=\frac{m-1}{m}\mathrm{and}{H}^{\prime \prime }\left(0\right)=\frac{2(m^2-2m-1)}{m(m-1)}.$$

(20)

Combining (20) with (18), we obtain the final error equation,

$$\begin{array}{ll}{e}_{n+1}=& \frac{1}{6m^7{(m-1)}^4}\left(C_1^2\right((-6-25m-87m^2-99m^3-204m^4+49m^5+33m^6+3m^7)C_1^4\\ & -4m(3+3m+10m^2+9m^3-40m^4+12m^5+3m^6)C_1^2{C}_2+12{(-1+m)}^2{m}^3(-1-m+m^2)C_2^2)e_n^7\\ & +O\left(e_n^8\right).\end{array}$$

(21)

Therefore, the seventh-order convergence is established.□

Remark 1.

The computational efficiency $\left(E\right)$ is computed as $E=p^{1/\theta }$ (see [22]), where p denotes the convergence order of the iterative method and θ denotes the number of function evaluations per iteration (see in [22]). With the conditions (4) the proposed scheme (3) reaches seventh-order convergence by using only four functional evaluations (viz. $f\left(x_n\right)$, $f\left(z_n\right)$, $f^{\prime }\left(x_n\right)$, and $f^{\prime }\left(y_n\right)$) per iteration. Thus, the E-value of the new scheme is $7^{1/4}\approx 1.627$, which is much better than the E-values of Newton’s method ($E=2^{1/2}\approx 1.414$), the fourth-order Liu–Zhou method ($E=4^{1/3}\approx 1.587$), and sixth-order methods by Geum et al. [8,9] ($E=6^{1/4}\approx 1.565$).

Remark 2.

Kung and Traub [23] have conjectured that the multi-point methods without memory requiring n functional evaluations can attain the maximum convergence order $2^{n-1}$. That means that with four functional evaluations one can develop a method of optimal order eight. The methods qualifying Kung–Traub hypothesis are also called optimal methods. Such methods are rare for multiple roots due to the complexity in finding the convergence order. Nevertheless, the proposed seventh methods are better than the existing sixth-order methods by Geum et al. [8] (see Formula (30) in the numerical section) in the sense that latter also require same number of evaluations, i.e., two functions and two derivatives.

Remark 3.

The proposed algorithm requires the knowledge of multiplicity m of a root. To estimate m, we can employ the formula

$$m\approx \frac{x_{n+1}-x_n}{F\left(x_{n+1}\right)-F\left(x_n\right)},$$

where in $F\left(x_n\right)=\frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)}$ (see [24]).

Some Special Cases

We can generate numerous special cases of the family (3) based on the forms of weight functions $G\left(u\right)$ and $H\left(u\right)$ that satisfy the conditions of Theorem 1. Some simple forms are given as follows,

Case I: Let us describe the following polynomial forms of G and H directly from the proposed Theorem 1:

$$G\left(u\right)=u+\frac{2m}{m-1}{u}^2\mathrm{and}H\left(u\right)=1+2u+\frac{m^2-2m-1}{m(m-1)}{u}^2.$$

(22)

Thus, the corresponding new seventh-order method (denoted by NM-I) is given by

$$\left\{\begin{array}{c}{y}_n=x_n-m\frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)},\hfill \\ z_n=y_n-m\left(u_n+\frac{2m}{m-1}{u}_n^2\right)\frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)},\hfill \\ x_{n+1}=z_n-m{v}_n\left(1+\frac{m-1}{m}\frac{v_n}{u_n}\right)\left(1+2u_n+\frac{m^2-2m-1}{m(m-1)}{u}_n^2\right)\frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)}.\hfill \end{array}\right.$$

(23)

Case II: Let us describe the following functions that satisfy the conditions of Theorem 1:

$$G\left(u\right)=u\left(\frac{1+u}{1+\frac{1+m}{1-m}u+\frac{2m(m+1)}{{(m-1)}^2}{u}^2}\right)\mathrm{and}H\left(u\right)=1+2u+\frac{m^2-2m-1}{m(m-1)}{u}^2.$$

(24)

Thus, the corresponding seventh-order method (now denoted by NM-II) is expressed as

$$\left\{\begin{array}{c}{y}_n=x_n-m\frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)},\hfill \\ z_n=y_n-m{u}_n\left(\frac{1+u_n}{1+\frac{1+m}{1-m}{u}_n+\frac{2m(m+1)}{{(m-1)}^2}{u}_n^2}\right)\frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)},\hfill \\ x_{n+1}=z_n-m{v}_n\left(1+\frac{m-1}{m}\frac{v_n}{u_n}\right)\left(1+2u_n+\frac{m^2-2m-1}{m(m-1)}{u}_n^2\right)\frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)}.\hfill \end{array}\right.$$

(25)

Case III: Let us consider the following forms satisfying the conditions of Theorem 1:

$$G\left(u\right)=u\left(\frac{1+\frac{1-2m+5m^2}{2m(m-1)}u+u^2}{1+\frac{m-1}{2m}u}\right)\mathrm{and}H\left(u\right)=1+2u+\frac{m^2-2m-1}{m(m-1)}{u}^2.$$

(26)

The corresponding new method (denoted by NM-III) is given by

$$\left\{\begin{array}{c}{y}_n=x_n-m\frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)},\hfill \\ z_n=y_n-m{u}_n\left(\frac{1+\frac{1-2m+5m^2}{2m(m-1)}{u}_n+u_n^2}{1+\frac{m-1}{2m}{u}_n}\right)\frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)},\hfill \\ x_{n+1}=z_n-m{v}_n\left(1+\frac{m-1}{m}\frac{v_n}{u_n}\right)\left(1+2u_n+\frac{m^2-2m-1}{m(m-1)}{u}_n^2\right)\frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)}.\hfill \end{array}\right.$$

(27)

Case IV: Next, let us consider the following forms satisfying the conditions of Theorem 1:

$$G\left(u\right)=u{\left(1-\frac{mu}{m-1}+\frac{3m^2{u}^2}{2{(m-1)}^2}\right)}^{-2}\mathrm{and}H\left(u\right)=1+2u+\frac{m^2-2m-1}{m(m-1)}{u}^2.$$

(28)

Then, the corresponding seventh-order iterative scheme (denoted by NM-IV) is given by

$$\left\{\begin{array}{c}{y}_n=x_n-m\frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)},\hfill \\ z_n=y_n-m{u}_n{\left(1-\frac{mu}{m-1}+\frac{3m^2{u}_n^2}{2{(m-1)}^2}\right)}^{-2}\frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)},\hfill \\ x_{n+1}=z_n-m{v}_n\left(1+\frac{m-1}{m}\frac{v_n}{u_n}\right)\left(1+2u_n+\frac{m^2-2m-1}{m(m-1)}{u}_n^2\right)\frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)}.\hfill \end{array}\right.$$

(29)

3. Complex Geometry of Methods

Here, we aim to assess the complex dynamics of new methods based on the geometrical technique, namely, basins of attraction, of the zeros of a polynomial $f\left(z\right)$ in complex domain. Using this tool, one can get an important information about the stability and convergence of a method. The idea was introduced initially by Vrscay and Gilbert [25]. Recently, many authors have used this tool in their work, see, for example, in [2,26,27] and the references cited therein.

The initial point $z_0$ is chosen in a rectangular region $R\in \mathbb{C}$ containing all the zeros of $f\left(z\right).$ Starting from the point $z_0$, the method either converges to the zero of $f\left(z\right)$ or eventually diverges. We choose the tolerance value ${10}^{-3}$ up to maximum 25 iterations to stop the iteration process. If this tolerance is not attained in required iterations, then the method does not converge to any root. To plot the basins, we adopt the following strategy. A color is assigned to each point $z_0$ lying in the basin of corresponding root. Then, the point represents the attraction basin with that particular color provided that the method converges. Contrary to this, if the method fails to converge in specified iterations, then the point paints the black color.

In what follows we assess the basins of attraction by employing the methods NM-I–NM-IV on the following three polynomials.

Problem 1.

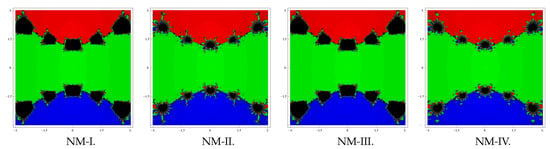
As the first example, consider the polynomial $f_1\left(z\right)={(z^3+4z)}^3$ which has zeros $\{0,\pm 2i\}$ each with multiplicity 3. For drawing basins, we use a rectangle R of size $[-3,3]\times [-3,3]$ and fix the color green to each initial point in the basin of zero “$-0$”, the color red to each point in the basin of zero “$2i$”, and the color blue to every point in the basin of zero “$-2i$”. Basins so drawn for the methods NM-I–NM-IV are shown in Figure 1. It is clear that the methods NM-IV and NM-II posses fewer divergent points (painted with black color), followed by NM-I and NM-III.

Problem 2.

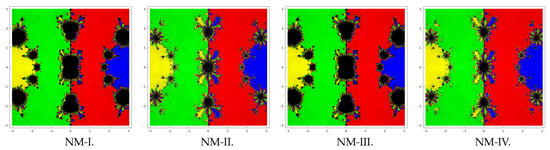
Consider the polynomial $f_2\left(z\right)={(z^4-6z^2+8)}^2$ that has four zeros $\{\pm 2,\pm 1.414\dots \}$ with multiplicity two. In this case also, we use a rectangle $R\in \mathbb{C}$ of size $[-3,3]\times [-3,3]$ and paint the basins with blue, yellow, red, and green colors of the zeros 2, $-2$, $1.414\dots$, and $-1.414\dots$, respectively. From the graphics displayed in Figure 2, we conclude that the methods NM-II and NM-IV have better convergence than NM-I and NM-III.

Problem 3.

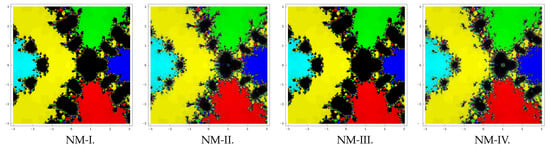
Lastly, consider the polynomial $f_3\left(z\right)=z^2{(z^2-4)}^2{(z^2-2z+2)}^2$ that has five zeros $\{0,\pm 2,1\pm i\}$ each with multiplicity two. We use a rectangle $R\in \mathbb{C}$ of size $[-3,3]\times [-3,3]$ and assign the red, blue, green, cyan, and yellow colors to the basins of attraction of these five zeros. Basins so assessed by the methods are shown in Figure 3. Like previous examples, in this case also the methods NM-II and NM-IV possess better convergence than NM-I and NM-III.

These graphics easily depict the convergence behavior of any method. If we select a value of $z_0$ in a place where different basins meet each other, it is difficult to guess which zero is going to be obtained by the method. Therefore, the selection of $z_0$ in such a region is not preferable. The zones with black color and with amalgam of different colors can not be suitable to choose the initial guess $z_0$ to acquire a unique root. The most attractive pictures are those with intricate boundaries between the basins of attraction. These boundaries have fractal-like shapes and correspond to the cases where the method is more demanding with choice of initial point. At such regions the dynamic behavior of initial guess is more unpredictable.

4. Numerical Examples

In this section, we employ the special cases NM-i, i = I, II, III, IV of family (3) on some nonlinear equations to test the validity of theoretical results derived in previous sections. Performance is compared with some well-known sixth-order methods such as the two- and three-point methods by Geum et al. [8,9]. The two-point method [8], applicable for $m>1$, is given as

$$\begin{array}{cc}\hfill & y_n=x_n-m\frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)},\hfill \\ \hfill & x_{n+1}=y_n-Q_f(u,s)\frac{f\left(y_n\right)}{f^{\prime }\left(y_n\right)},\hfill \end{array}$$

(30)

where $u={\left(\frac{f\left(y_n\right)}{f\left(x_n\right)}\right)}^{\frac{1}{m}}$ and $s={\left(\frac{f^{\prime }\left(y_n\right)}{f^{\prime }\left(x_n\right)}\right)}^{\frac{1}{m-1}}$, and $Q_f:{\mathbb{C}}^2\to \mathbb{C}$ is a holomorphic function in neighborhood of origin $(0,0)$. Considering the following cases of function $Q_f(u,s)$ in the Formula (30) and denoting the corresponding iterative method by GKN-1(j), j = a, b, c, d:

(a)

$Q_f(u,s)=m(1+2(m-1)(u-s)-4us+s^2).$

(b)

d $Q_f(u,s)=m(1+2(m-1)(u-s)-u^2-2us).$

(c)

$Q_f(u,s)=\frac{m+au}{1+bu+cs+dus},$ where $a=\frac{2m}{m-1}$, $b=2-2m$, $c=\frac{2(2-2m+m^2)}{m-1}$ and $d=-2m(m-1)$.

(d)

$Q_f(u,s)=\frac{m+a_{1}u}{1+b_{1}u+c_1{u}^2}\frac{1}{1+d_{1}s},$ where $a_1=\frac{2m(4m^4-16m^3+31m^2-30m+13}{(m-1)(4m^2-8m+7)}$, $b_1=\frac{4(2m^2-4m+3)}{(m-1)(4m^2-8m+7)}$, $c_1=-\frac{4m^2-8m+3}{4m^2-8m+7}$ and $d_1=2(m-1)$.

Next, the three-point method [9] for $m\ge 1$ is expressed as

$$\begin{array}{cc}\hfill & y_n=x_n-m\frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)},\hfill \\ \hfill & z_n=x_n-m{Q}_f\left(u\right)\frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)},\hfill \\ \hfill & x_{n+1}=x_n-m{K}_f(u,v)\frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)},\hfill \end{array}$$

(31)

wherein $u={\left(\frac{f\left(y_n\right)}{f\left(x_n\right)}\right)}^{\frac{1}{m}}$ and $v={\left(\frac{f\left(z_n\right)}{f\left(x_n\right)}\right)}^{\frac{1}{m}}$. Functions $Q_f$ and $K_f$ are analytic in a neighborhood of 0 and $(0,0)$, respectively. We consider the following combinations of $Q_f\left(u\right)$ and $K_f(u,v)$, and denote the corresponding iterative schemes by GKN-2(j), j = a, b, c, d:

(a)

$Q_f\left(u\right)=\frac{1+u^2}{1-u}$, $K_f(u,v)=\frac{1+u^2-v}{1-u+(u-2)v}$.

(b)

$Q_f\left(u\right)=1+u+2u^2$, $K_f(u,v)=1+u+2u^2+(1+2u)v$.

(c)

$Q_f\left(u\right)=\frac{1+u^2}{1-u}$, $K_f(u,v)=1+u+2u^2+2u^3+2u^4+(2u+1)v$.

(d)

$Q_f\left(u\right)=\frac{(2u-1)(4u-1)}{1-7u+13u^2}$, $K_f(u,v)=\frac{(2u-1)(4u-1)}{1-7u+13u^2-(1-6u)v}$.

Computations are performed in the programming package of Mathematica software using multiple-precision arithmetic. The results displayed in

Table 1. Numerical results for Example 1.

Methods	n	$|{\mathit{e}}_{\mathit{n}-2}|$	$|{\mathit{e}}_{\mathit{n}-1}|$	$|{\mathit{e}}_{\mathit{n}}|$	COC	CPU-Time
GKN-1(a)	4	$1.06e-09$	$3.86e-56$	$9.03e-335$	6.0000	0.1797
GKN-1(b)	4	$1.06e-09$	$3.91e-56$	$9.85e-335$	6.0000	0.1757
GKN-1(c)	4	$1.06e-09$	$4.34e-56$	$2.02e-334$	6.0000	0.1797
GKN-1(d)	4	$1.07e-09$	$1.17e-55$	$2.02e-331$	6.0000	0.1757
GKN-2(a)	4	$1.19e-06$	$5.39e-38$	$4.56e-226$	5.9999	0.2032
GKN-2(b)	4	$1.20e-06$	$1.61e-37$	$9.49e-223$	5.9999	0.2070
GKN-2(c)	4	$1.20e-06$	$1.12e-37$	$7.51e-224$	5.9999	0.2110
GKN-2(d)	4	$1.20e-06$	$1.87e-37$	$2.76e-222$	5.9999	0.2030
NM-I	3	$1.08e-07$	$4.33e-51$	0	7.0000	0.1172
NM-II	3	$1.08e-07$	$8.31e-52$	0	7.0000	0.1250
NM-III	3	$1.08e-07$	$4.33e-51$	0	7.0000	0.1367
NM-IV	3	$1.08e-07$	$8.31e-52$	0	7.0000	0.1365

,

Table 2. Numerical results for Example 2.

Methods	n	$|{\mathit{e}}_{\mathit{n}-2}|$	$|{\mathit{e}}_{\mathit{n}-1}|$	$|{\mathit{e}}_{\mathit{n}}|$	COC	CPU-Time
GKN-1(a)	4	$2.17e-08$	$4.61e-25$	$1.01e-152$	6.0000	1.4687
GKN-1(b)	4	$2.17e-08$	$4.60e-25$	$2.27e-151$	6.0000	1.4570
GKN-1(c)	4	$2.11e-08$	$4.21e-25$	$1.03e-150$	6.0000	1.5040
GKN-1(d)	4	$1.77e-08$	$2.48e-25$	$2.68e-151$	6.0000	1.4960
GKN-2(a)	4	$4.83e-07$	$1.36e-41$	$6.84e-249$	6.0000	1.3437
GKN-2(b)	4	$4.90e-07$	$2.89e-41$	$1.21e-246$	6.0000	1.3867
GKN-2(c)	4	$4.88e-07$	$2.22e-41$	$1.98e-247$	6.0000	1.4257
GKN-2(d)	4	$4.89e-07$	$3.22e-41$	$2.62e-246$	6.0000	1.3945
NM-I	3	$1.44e-08$	$6.35e-59$	0	7.0000	0.9610
NM-II	3	$1.43e-08$	$1.60e-59$	0	7.0000	0.9767
NM-III	3	$1.44e-08$	$6.35e-59$	0	7.0000	0.9492
NM-IV	3	$1.44e-08$	$1.89e-59$	0	7.0000	0.9532

,

Table 3. Numerical results for Example 3.

Methods	n	$|{\mathit{e}}_{\mathit{n}-2}|$	$|{\mathit{e}}_{\mathit{n}-1}|$	$|{\mathit{e}}_{\mathit{n}}|$	COC	CPU-Time
GKN-1(a)	4	$1.20e-05$	$6.82e-31$	$2.31e-182$	5.9999	0.5908
GKN-1(b)	4	$1.20e-05$	$6.86e-31$	$2.40e-182$	5.9999	0.5864
GKN-1(c)	4	$1.21e-05$	$7.72e-31$	$5.18e-182$	5.9999	0.5787
GKN-1(d)	4	$1.58e-05$	$1.00e-29$	$6.51e-175$	5.9999	0.5897
GKN-2(a)	4	$3.17e-05$	$1.64e-28$	$3.21e-168$	5.9999	0.5625
GKN-2(b)	4	$3.50e-05$	$6.90e-28$	$4.05e-164$	5.9999	0.5702
GKN-2(c)	4	$3.41e-05$	$4.42e-28$	$2.09e-165$	5.9999	0.5702
GKN-2(d)	4	$3.54e-05$	$8.45e-28$	$1.56e-163$	5.9999	0.5470
NM-I	4	$4.56e-06$	$9.64e-39$	$1.84e-267$	6.9999	0.4725
NM-II	4	$4.51e-06$	$4.52e-39$	$4.60e-270$	6.9999	0.4687
NM-III	4	$4.56e-06$	$9.64e-39$	$1.84e-267$	6.9999	0.4842
NM-IV	4	$4.51e-06$	$4.32e-39$	$3.21e-270$	6.9999	0.4647

and

Table 4. Numerical results for Example 4.

Methods	n	$|{\mathit{e}}_{\mathit{n}-2}|$	$|{\mathit{e}}_{\mathit{n}-1}|$	$|{\mathit{e}}_{\mathit{n}}|$	COC	CPU-Time
GKN-1(a)	5	$3.14e-21$	$9.67e-65$	$2.05e-195$	3.0000	0.03502
GKN-1(b)	5	$3.47e-21$	$9.47e-65$	$1.95e-195$	3.0000	0.03525
GKN-1(c)	5	$3.64e-21$	$1.09e-64$	$2.94e-195$	3.0000	0.03525
GKN-1(d)	5	$3.49e-21$	$9.68e-65$	$2.05e-195$	3.0000	0.04300
GKN-2(a)	4	$4.86e-04$	$1.78e-23$	$4.29e-140$	5.9997	0.03900
GKN-2(b)	4	$4.83e-04$	$1.75e-23$	$4.03e-140$	5.9996	0.03525
GKN-2(c)	4	$4.83e-04$	$1.74e-23$	$3.84e-140$	5.9997	0.03525
GKN-2(d)	4	$4.85e-04$	$1.79e-23$	$4.54e-140$	5.9996	0.03925
NM-I	3	$3.14e-07$	$1.99e-50$	0	6.9999	0.02752
NM-II	3	$3.14e-07$	$1.87e-50$	0	6.9999	0.02351
NM-III	3	$3.14e-07$	$1.99e-50$	0	6.9999	0.03125
NM-IV	3	$3.14e-07$	$1.89e-50$	0	6.9999	0.02725

contain (i) the iteration number $\left(n\right)$ in which the solution is obtained with required accuracy, (ii) the last three errors $e_n=|x_{n+1}-x_n|$, (iii) the computational order of convergence (COC), and (iv) the CPU time (CPU-time) elapsed during the execution of program. The required iteration number $\left(n\right)$ and elapsed time are recorded when the criterion $|x_{n+1}-x_n|+|f\left(x_n\right)|<{10}^{-350}$ is satisfied. Computational order of convergence (COC) is calculated by the formula (see [28])

$$\mathrm{COC}=\frac{ln|(x_{n+1}-\alpha )/(x_n-\alpha )|}{ln|(x_n-\alpha )/(x_{n-1}-\alpha )|}.$$

For numerical testing we choose the following problems.

Example 1.

Finding the eigenvalues of the characteristic equation of a square matrix of order greater than 4 is a big problem [29]). We consider the following 9 × 9 matrix.

$$M=\frac{1}{8}\left[\begin{array}{ccccccccc}-12& 0& 0& 19& -19& 76& -19& 18& 437\\ -64& 24& 0& -24& 24& 64& -8& 32& 376\\ -16& 0& 24& 4& -4& 16& -4& 8& 92\\ -40& 0& 0& -10& 50& 40& 2& 20& 242\\ -4& 0& 0& -1& 41& 4& 1& 0& 25\\ -40& 0& 0& 18& -18& 104& -18& 20& 462\\ -84& 0& 0& -29& 29& 84& 21& 42& 501\\ 16& 0& 0& -4& 4& -16& 4& 16& -92\\ 0& 0& 0& 0& 0& 0& 0& 0& 24\end{array}\right].$$

The characteristic polynomial of the matrix $\left(M\right)$ is given by

$$\begin{array}{c}\hfill f_1\left(x\right)=x^9-29x^8+349x^7-2261x^6+8455x^5-17663x^4+15927x^3+6993x^2-24732x+12960.\end{array}$$

One of the eigen values is 3 with multiplicity 4. Numerical results produced for this example, taking initial guess $x_0$$=2.25$, are shown in Table 1.

Example 2.

We consider the manning problem arising in isentropic supersonic flow around a sharp expansion corner. Let $b=\frac{\gamma +1}{\gamma -1}$, where γ is the specific heat ratio of the gas. The following relation is developed between the Mach numbers before the corner and after the corner denoted by $M_1$ and $M_2$, respectively (see [3]),

$$\delta =b^{1/2}\left({tan}^{-1}{\left(\frac{M_2^2-1}{b}\right)}^{1/2}-{tan}^{-1}{\left(\frac{M_1^2-1}{b}\right)}^{1/2}\right)-\left({tan}^{-1}{(M_2^2-1)}^{1/2}-{tan}^{-1}{(M_1^2-1)}^{1/2}\right).$$

Let us consider a particular case: To solve the equation for $M_2$ given that $M_1=1.5$, $\gamma =1.4$, and $\delta ={10}^0$. Then, we have that

$$6^{1/2}\left({tan}^{-1}{\left(\frac{x^2-1}{6}\right)}^{1/2}-{tan}^{-1}{\left(\frac{1}{12}\right)}^{1/2}\right)-\left({tan}^{-1}{(x^2-1)}^{1/2}-{tan}^{-1}{\left(\frac{1}{2}\right)}^{1/2}\right)-\pi /18=0.$$

where $x=M_2$.

Now considering this equation for three times, the required nonlinear function is given as

$$f_2\left(x\right)={\left[{tan}^{-1}\left(\frac{\sqrt{5}}{2}\right)-{tan}^{-1}\left(\sqrt{x^2-1}\right)+\sqrt{6}\left({tan}^{-1}\left(\sqrt{\frac{x^2-1}{6}}\right)-{tan}^{-1}\left(\frac{1}{2}\sqrt{\frac{5}{6}}\right)\right)-\frac{11}{63}\right]}^3.$$

This function has one zero $1.8411027704\dots$ with multiplicity 3. To find the zero, we choose initial approximation $x_0$$=1.50$. The obtained results are shown in Table 2.

Example 3.

Next we assume nonlinear test function (see [8])

$$f_3\left(x\right)=\left(x-\sqrt{3}{x}^{3}cos\left(\frac{\pi x}{6}\right)+\frac{1}{x^2+1}-\frac{11}{5}+4\sqrt{3}\right){(x-2)}^4$$

The multiple zero of function $f_3$ is 2 with multiplicity 5, which is calculated using initial approximation $x_0=1.5$. The obtained results are shown in Table 3.

Example 4.

Consider the isothermal continuous stirred tank reactor (CSTR) problem [30]. Components A and R are fed to the reactor at the corresponding rates of Q and $q-Q$. Then, the following scheme develops in the reactor (see [30]),

$$\begin{array}{cc}\hfill A+R& \to B\hfill \\ \hfill B+R& \to C\hfill \\ \hfill C+R& \to D\hfill \\ \hfill C+R& \to E.\hfill \end{array}$$

(32)

This reaction scheme was analyzed in [30] to design simple feedback control system. In the analysis, the following equation was given for the transfer function of the reactor,

$$K_C\frac{2.98(x+2.25)}{(x+1.45){(x+2.85)}^2(x+4.35)}=-1.$$

$K_C$ is called the gain of the proportional controller. The control system is stable for those $K_C$ values which yield zeros of the transfer function with negative real part. For $K_C=0$, we obtain poles of the open-loop transfer function as roots of the equation:

$$f_4\left(x\right)=x^4+11.50x^3+47.49x^2+83.06325x+51.23266875=0,$$

that are given as $x=-1.45,-2.85,-2.85,-4.35$. We see the root $-2.85$ is multiple with multiplicity 2. The results so produced by the methods using $x_0=-2.80$ are shown in Table 4.

We observe from the numerical results that the errors become smaller as the iterations proceed, which points to the increasing accuracy in the values of successive approximations. Per iteration, the number of significant figures gained by the proposed methods is larger than the existing methods because of the higher order. The reading $‘0^{\prime }$ of error $|e_n|$ indicates that at this stage the stopping condition $|x_{n+1}-x_n|+|f\left(x_n\right)|<{10}^{-350}$ has been reached. The results of penultimate column of each table support the theoretical seventh-order of convergence. This shows that the convergence order is preserved. However, this is not true for the existing sixth-order methods GKN-1(j), j= a, b, c, d, as the sixth-order convergence is not preserved in last problem. The computational efficiency can be observed by the readings of elapsed CPU-time displayed in the last column of each table. Indeed, the new methods are more efficient since they consume less execution time than the existing ones. We have also applied the methods on other different problems to confirm the accuracy and efficiency and results are found on a par with the above conclusions.

5. Conclusions

A class of seventh-order numerical methods has been designed for computing multiple zeros of nonlinear functions. Local convergence analysis has been shown under standard assumptions which proves the convergence order seven. Some particular cases have been explored and their performance has been checked by using two different ways viz. by numerical testing and by graphical tool of attraction basins. Comparison of performance of the methods with existing methods has also been shown. In addition, a comparison of estimated CPU-time has been performed in order to rank the algorithms. We emphasize that the ranking obtained in this way matches well with the ranking obtained from the computational efficiency. As remarked earlier that according to Kung–Traub conjecture one can develop a method with optimal eighth convergence using four function evaluations. Therefore, this will be a motivational factor for us in future endeavor to develop such methods