Generating Optimal Eighth Order Methods for Computing Multiple Roots
Abstract
:1. Introduction
2. Construction of the Method
3. Some Special Cases of Weight Functions of G(u) and H(v)
4. Numerical Results
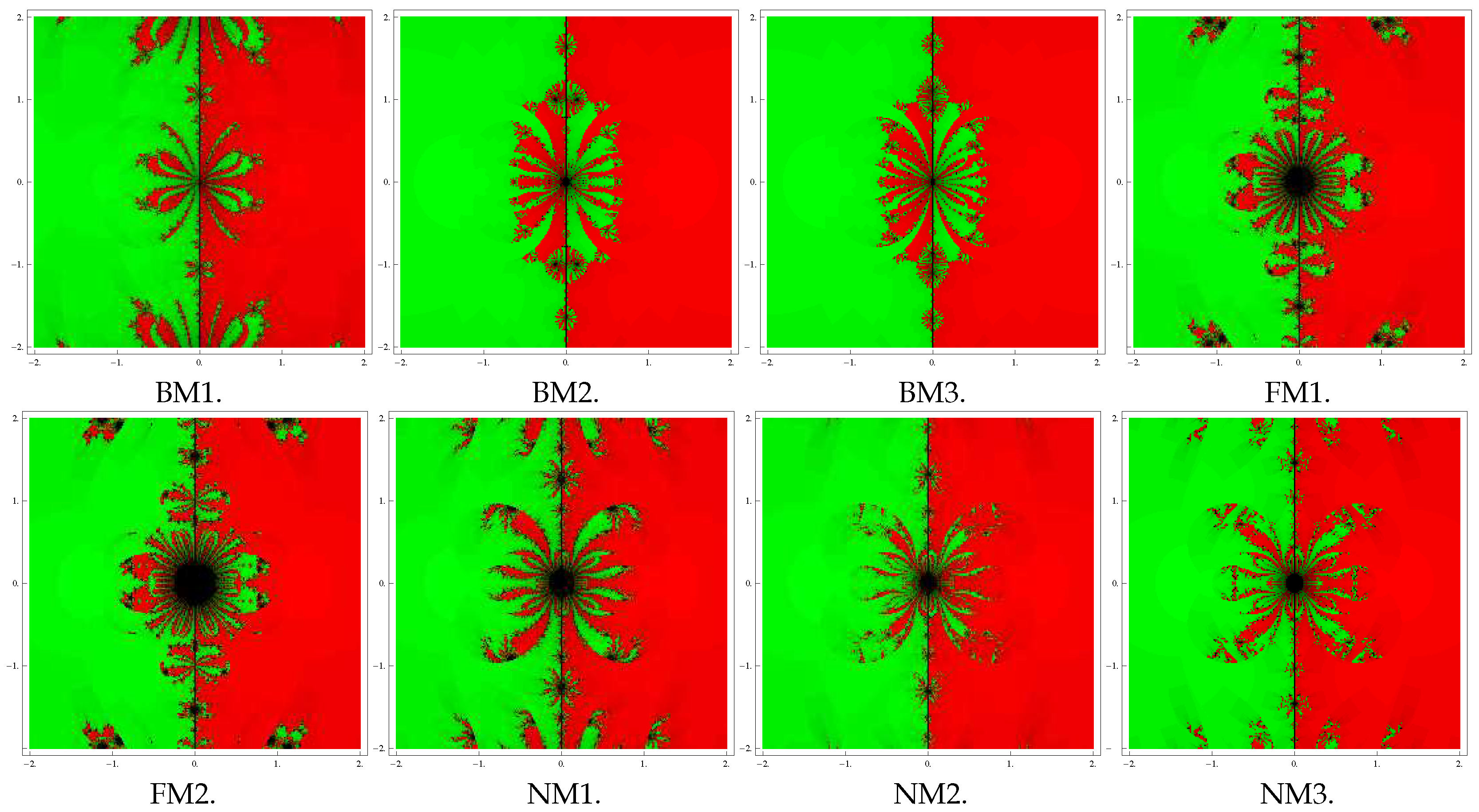
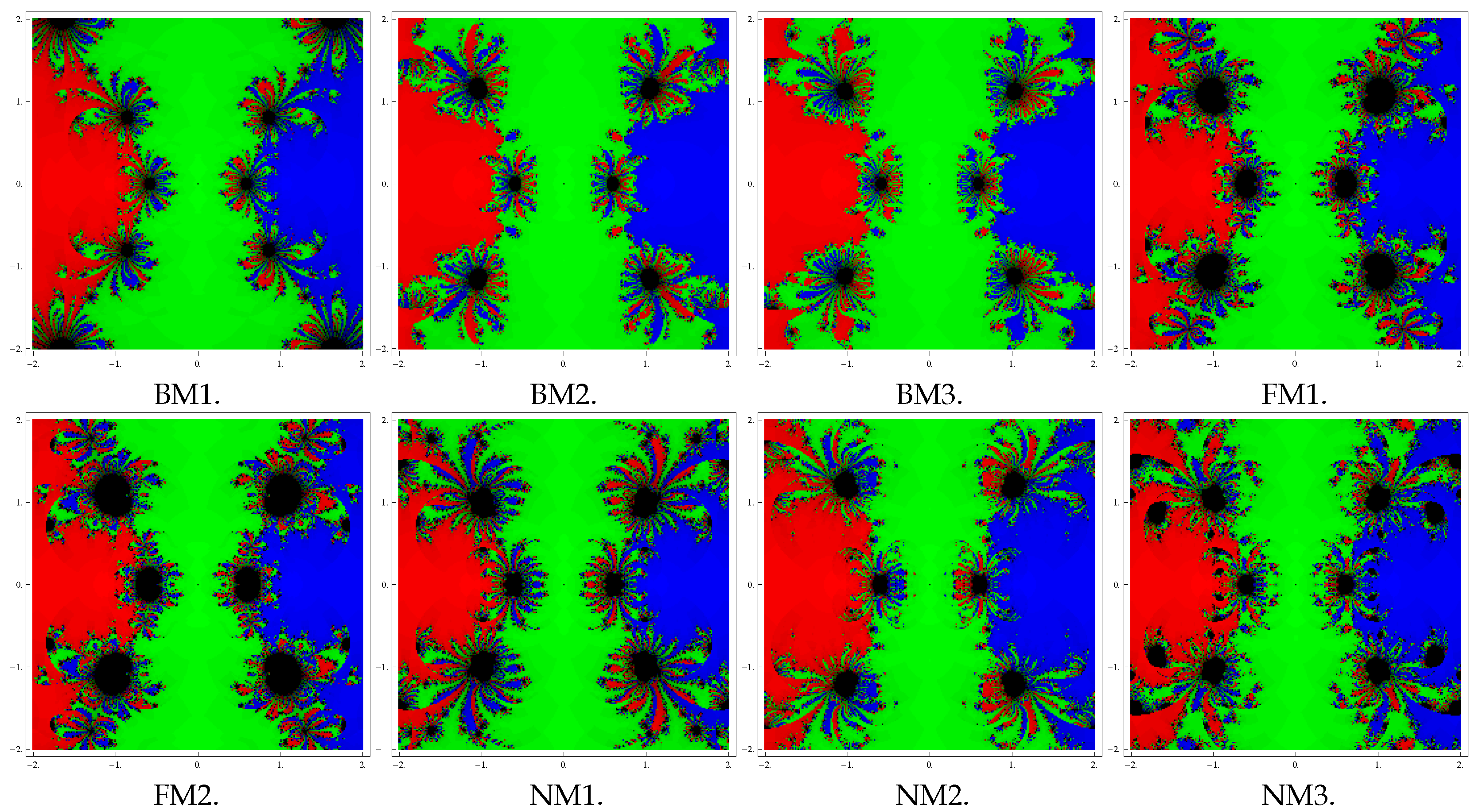
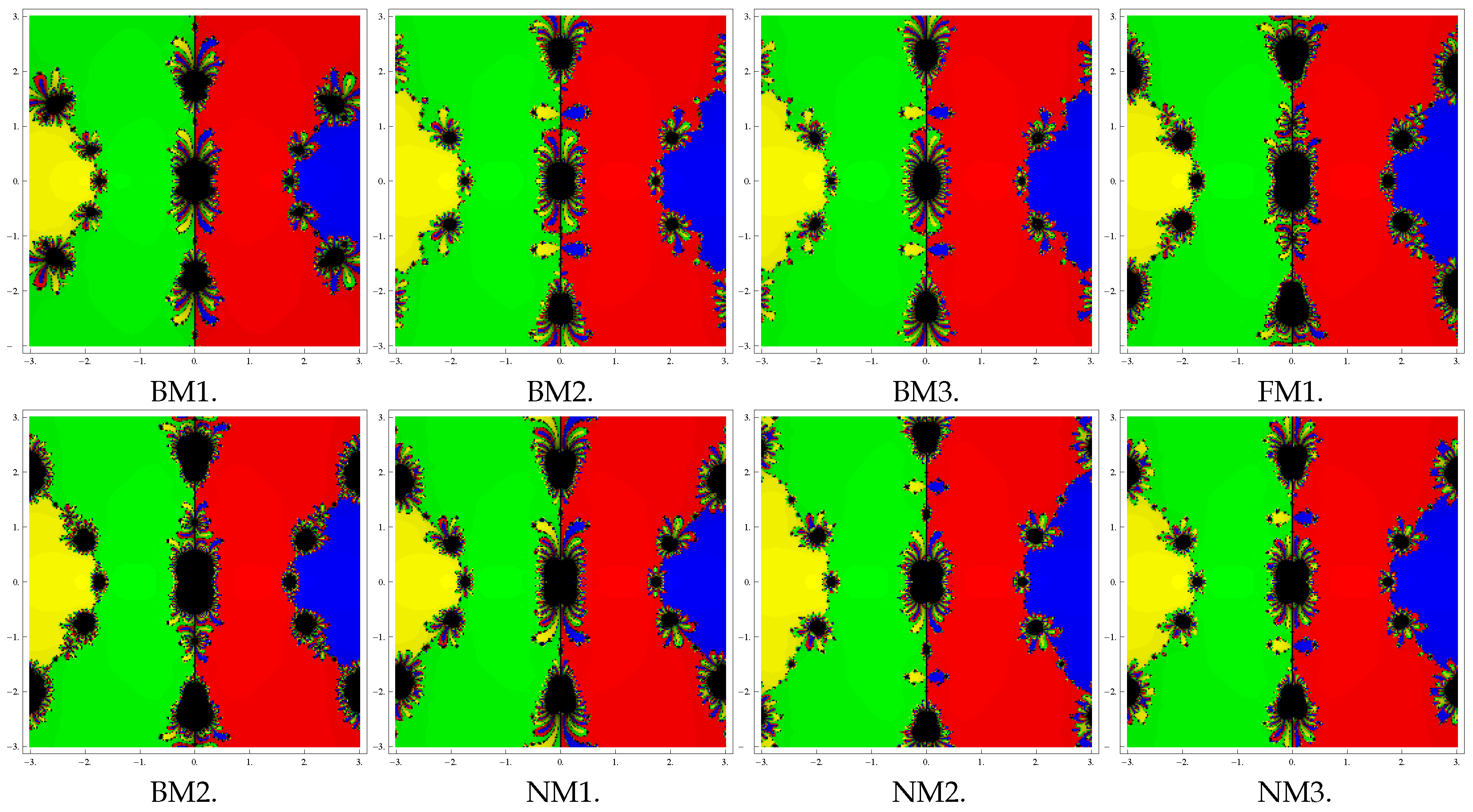
5. Basins of Attraction
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Argyros, I.K. Convergence and Applications of Newton-Type Iterations; Springer: New York, NY, USA, 2008. [Google Scholar]
- Constantinides, A.; Mostoufi, N. Numerical Methods for Chemical Engineers with MATLAB Applications; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Kung, H.T.; Traub, J.F. Optimal order of one-point and multipoint iteration. J. Assoc. Comput. Mach. 1974, 21, 643–651. [Google Scholar] [CrossRef]
- Ostrowski, A.M. Solution of Equations and Systems of Equations; Academic Press: New York, NY, USA, 1966. [Google Scholar]
- Traub, J.F. Iterative Methods for the Solution of Equations; Chelsea Publishing Company: New York, NY, USA, 1982. [Google Scholar]
- Schröder, E. Über unendlich viele Algorithmen zur Auflösung der Gleichungen. Math. Ann. 1870, 2, 317–365. [Google Scholar] [CrossRef] [Green Version]
- Hansen, E.; Patrick, M. A family of root finding methods. Numer. Math. 1977, 27, 257–269. [Google Scholar] [CrossRef]
- Victory, H.D.; Neta, B. A higher order method for multiple zeros of nonlinear functions. Int. J. Comput. Math. 1983, 12, 329–335. [Google Scholar] [CrossRef]
- Osada, N. An optimal multiple root-finding method of order three. J. Comput. Appl. Math. 1994, 51, 131–133. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Liao, X.; Cheng, L. A new fourth-order iterative method for finding multiple roots of nonlinear equations. Appl. Math. Comput. 2009, 215, 1288–1292. [Google Scholar]
- Li, S.G.; Cheng, L.Z.; Neta, B. Some fourth-order nonlinear solvers with closed formulae for multiple roots. Comput Math. Appl. 2010, 59, 126–135. [Google Scholar] [CrossRef] [Green Version]
- Sharma, J.R.; Sharma, R. Modified Jarratt method for computing multiple roots. Appl. Math. Comput. 2010, 217, 878–881. [Google Scholar] [CrossRef]
- Neta, B. Extension of Murakamis high-order nonlinear solver to multiple roots. Int. J. Comput. Math. 2010, 87, 1023–1031. [Google Scholar] [CrossRef]
- Zhou, X.; Chen, X.; Song, Y. Constructing higher-order methods for obtaining the multiple roots of nonlinear equations. J. Comput. Math. Appl. 2011, 235, 4199–4206. [Google Scholar] [CrossRef] [Green Version]
- Sharifi, M.; Babajee, D.K.R.; Soleymani, F. Finding the solution of nonlinear equations by a class of optimal methods. Comput. Math. Appl. 2012, 63, 764–774. [Google Scholar] [CrossRef] [Green Version]
- Soleymani, F.; Babajee, D.K.R.; Lotfi, T. On a numerical technique for finding multiple zeros and its dynamics. J. Egypt. Math. Soc. 2013, 21, 346–353. [Google Scholar] [CrossRef]
- Geum, Y.H.; Kim, Y.I.; Neta, B. A class of two-point sixth-order multiple-zero finders of modified double-Newton type and their dynamics. Appl. Math. Comput. 2015, 270, 387–400. [Google Scholar] [CrossRef] [Green Version]
- Kansal, M.; Kanwar, V.; Bhatia, S. On some optimal multiple root-finding methods and their dynamics. Appl. Appl. Math. 2015, 10, 349–367. [Google Scholar]
- Soleymani, F.; Babajee, D.K.R. Computing multiple zeros using a class of quartically convergent methods. Alex. Eng. J. 2013, 52, 531–541. [Google Scholar] [CrossRef] [Green Version]
- Liu, B.; Zhou, X. A new family of fourth-order methods for multiple roots of nonlinear equations. Nonlinear Anal. Model. Cont. 2013, 18, 143–152. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.; Chen, X.; Song, Y. Families of third and fourth order methods for multiple roots of nonlinear equations. Appl. Math. Comput. 2013, 219, 6030–6038. [Google Scholar] [CrossRef]
- Thukral, R. A new family of fourth-order iterative methods for solving nonlinear equations with multiple roots. J. Numer. Math. Stoch. 2014, 6, 37–44. [Google Scholar]
- Behl, R.; Cordero, A.; Motsa, S.S.; Torregrosa, J.R. On developing fourth-order optimal families of methods for multiple roots and their dynamics. Appl. Math. Comput. 2015, 265, 520–532. [Google Scholar] [CrossRef] [Green Version]
- Hueso, J.L.; Martz, E.; Teruel, C. Determination of multiple roots of nonlinear equations and applications. J. Math. Chem. 2015, 53, 880–892. [Google Scholar] [CrossRef] [Green Version]
- Behl, R.; Cordero, A.; Motsa, S.S.; Torregrosa, J.R.; Kanwar, V. An optimal fourth-order family of methods for multiple roots and its dynamics. Numer. Algorithms 2016, 71, 775–796. [Google Scholar] [CrossRef]
- Geum, Y.H.; Kim, Y.I.; Neta, B. A sixth-order family of three-point modified Newton-like multiple-root finders and the dynamics behind their extraneous fixed points. Appl. Math. Comput. 2016, 283, 120–140. [Google Scholar] [CrossRef] [Green Version]
- Behl, R.; Cordero, A.; Motsa, S.S.; Torregrosa, J.R. An eighth-order family of optimal multiple root finders and its dynamics. Numer. Algorithms 2018, 77, 1249–1272. [Google Scholar] [CrossRef]
- Zafar, F.; Cordero, A.; Rana, Q.; Torregrosa, J.R. Optimal iterative methods for finding multiple roots of nonlinear equations using free parameters. J. Math. Chem. 2018, 56, 1884–1901. [Google Scholar] [CrossRef] [Green Version]
- Geum, Y.H.; Kim, Y.I.; Neta, B. Constructing a family of optimal eighth-order modified Newton-type multiple-zero finders along with the dynamics behind their purely imaginary extraneous fixed points. J. Comput. Appl. Math. 2018, 333, 131–156. [Google Scholar] [CrossRef]
- Behl, R.; Zafar, F.; Alshomrani, A.S.; Junjua, M.; Yasmin, N. An optimal eighth-order scheme for multiple zeros of univariate function. Int. J. Comput. Math. 2018, 15, 14. [Google Scholar] [CrossRef]
- Behl, R.; Alshomrani, A.S.; Motsa, S.S. An optimal scheme for multiple roots of nonlinear equations with eighth-order convergence. J. Math. Chem. 2018, 56, 2069–2084. [Google Scholar] [CrossRef]
- Zafar, F.; Cordero, A.; Torregrosa, J.R. An efficient family of optimal eighth-order multiple root finder. Mathematics 2018, 6, 310. [Google Scholar] [CrossRef] [Green Version]
- Weerakoon, S.; Fernando, T.G.I. A variant of Newton’s method with accelerated third-order convergence. Appl. Math. Lett. 2000, 13, 87–93. [Google Scholar] [CrossRef]
- Vrscay, E.R.; Gilbert, W.J. Extraneous fixed points, basin boundaries and chaotic dynamics for Schröder and König rational iteration functions. Numer. Math. 1988, 52, 1–16. [Google Scholar] [CrossRef]
- Varona, J.L. Graphic and numerical comparison between iterative methods. Math. Intell. 2002, 24, 37–46. [Google Scholar] [CrossRef]
- Scott, M.; Neta, B.; Chun, C. Basin attractors for various methods. Appl. Math. Comput. 2011, 218, 2584–2599. [Google Scholar] [CrossRef]
| Example | Root | Multiplicity | Initial Guess | |||
|---|---|---|---|---|---|---|
| Example 1: Standard nonlinear function [26]: | ||||||
| 1.000 | 3 | 1.50 | ||||
| Example 2: Standard nonlinear function [17]: | ||||||
| 4 | ||||||
| Example 3: Standard nonlinear function [26]: | ||||||
| 1.29179850… | 2 | 1.50 | ||||
| Example 4: Eigen value problem [18]: | ||||||
| 1 | 2 | 0.50 |
| Methods | n | COC | CPU-Time | ||||
|---|---|---|---|---|---|---|---|
| BM1 | 4 | 7.9957 | 0.078 | ||||
| BM2 | 4 | 2.2710 | 0.140 | ||||
| BM3 | 4 | 2.2582 | 0.094 | ||||
| FM1 | 4 | 7.9964 | 0.078 | ||||
| FM2 | 4 | 7.9965 | 0.078 | ||||
| NM1 | 4 | 7.9969 | 0.093 | ||||
| NM2 | 4 | 7.9980 | 0.094 | ||||
| NM2 | 4 | 7.9974 | 0.094 |
| Methods | n | COC | CPU-Time | ||||
|---|---|---|---|---|---|---|---|
| BM1 | 4 | 7.9947 | 0.360 | ||||
| BM2 | 4 | 3.0000 | 0.344 | ||||
| BM3 | 4 | 2.2550 | 0.344 | ||||
| FM1 | 4 | 7.9947 | 0.360 | ||||
| FM2 | 4 | 7.9948 | 0.344 | ||||
| NM1 | 4 | 7.9968 | 0.343 | ||||
| NM2 | 4 | 7.9990 | 0.328 | ||||
| NM2 | 4 | 7.9977 | 0.360 |
| Methods | n | COC | CPU-Time | ||||
|---|---|---|---|---|---|---|---|
| BM1 | 4 | 7.9999 | 0.250 | ||||
| BM2 | 4 | 3.0000 | 0.219 | ||||
| BM3 | 4 | 2.2711 | 0.219 | ||||
| FM1 | 4 | 7.9999 | 0.187 | ||||
| FM2 | 4 | 0 | 7.9999 | 0.203 | |||
| NM1 | 4 | 0 | 7.9999 | 0.188 | |||
| NM2 | 4 | 0 | 7.9999 | 0.203 | |||
| NM2 | 4 | 0 | 7.9999 | 0.204 |
| Methods | n | COC | CPU-Time | ||||
|---|---|---|---|---|---|---|---|
| BM1 | 4 | 7.9995 | 0.078 | ||||
| BM2 | 4 | 2.2747 | 0.172 | ||||
| BM3 | 4 | 2.2621 | 0.157 | ||||
| FM1 | 4 | 7.9996 | 0.109 | ||||
| FM2 | 4 | 7.9996 | 0.093 | ||||
| NM1 | 4 | 7.9997 | 0.109 | ||||
| NM2 | 4 | 7.9997 | 0.109 | ||||
| NM2 | 4 | 7.9997 | 0.125 |
| S. No. | Test Problems | m | Roots | Color of Fractal | Best Performer | Poor Performer |
|---|---|---|---|---|---|---|
| 1 | 3 | green | BM1, NM2, NM3, | FM1, FM2 | ||
| 1 | red | BM2, BM3, NM1 | ||||
| 2 | 3 | red | BM3, BM2, NM2 | FM1, FM2 | ||
| 0 | green | NM1, BM1 | ||||
| 1 | blue | |||||
| 3 | 1 | red | BM3, NM2, BM2 | FM1, FM2 | ||
| −1.414 | green | NM3, NM1, BM1 | ||||
| 1.414 | yellow | |||||
| 2 | blue |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, D.; Kumar, S.; Sharma, J.R.; d’Amore, M. Generating Optimal Eighth Order Methods for Computing Multiple Roots. Symmetry 2020, 12, 1947. https://doi.org/10.3390/sym12121947
Kumar D, Kumar S, Sharma JR, d’Amore M. Generating Optimal Eighth Order Methods for Computing Multiple Roots. Symmetry. 2020; 12(12):1947. https://doi.org/10.3390/sym12121947
Chicago/Turabian StyleKumar, Deepak, Sunil Kumar, Janak Raj Sharma, and Matteo d’Amore. 2020. "Generating Optimal Eighth Order Methods for Computing Multiple Roots" Symmetry 12, no. 12: 1947. https://doi.org/10.3390/sym12121947
APA StyleKumar, D., Kumar, S., Sharma, J. R., & d’Amore, M. (2020). Generating Optimal Eighth Order Methods for Computing Multiple Roots. Symmetry, 12(12), 1947. https://doi.org/10.3390/sym12121947




