An Extended Shapley TODIM Approach Using Novel Exponential Fuzzy Divergence Measures for Multi-Criteria Service Quality in Vehicle Insurance Firms
Abstract
1. Introduction
2. Preliminaries
2.1. Fuzzy Sets (FSs)
2.2. Divergence Measure for FSs
3. New Divergence Measure for FSs
Jensen–Shannon Exponential Divergence Measures for FSs
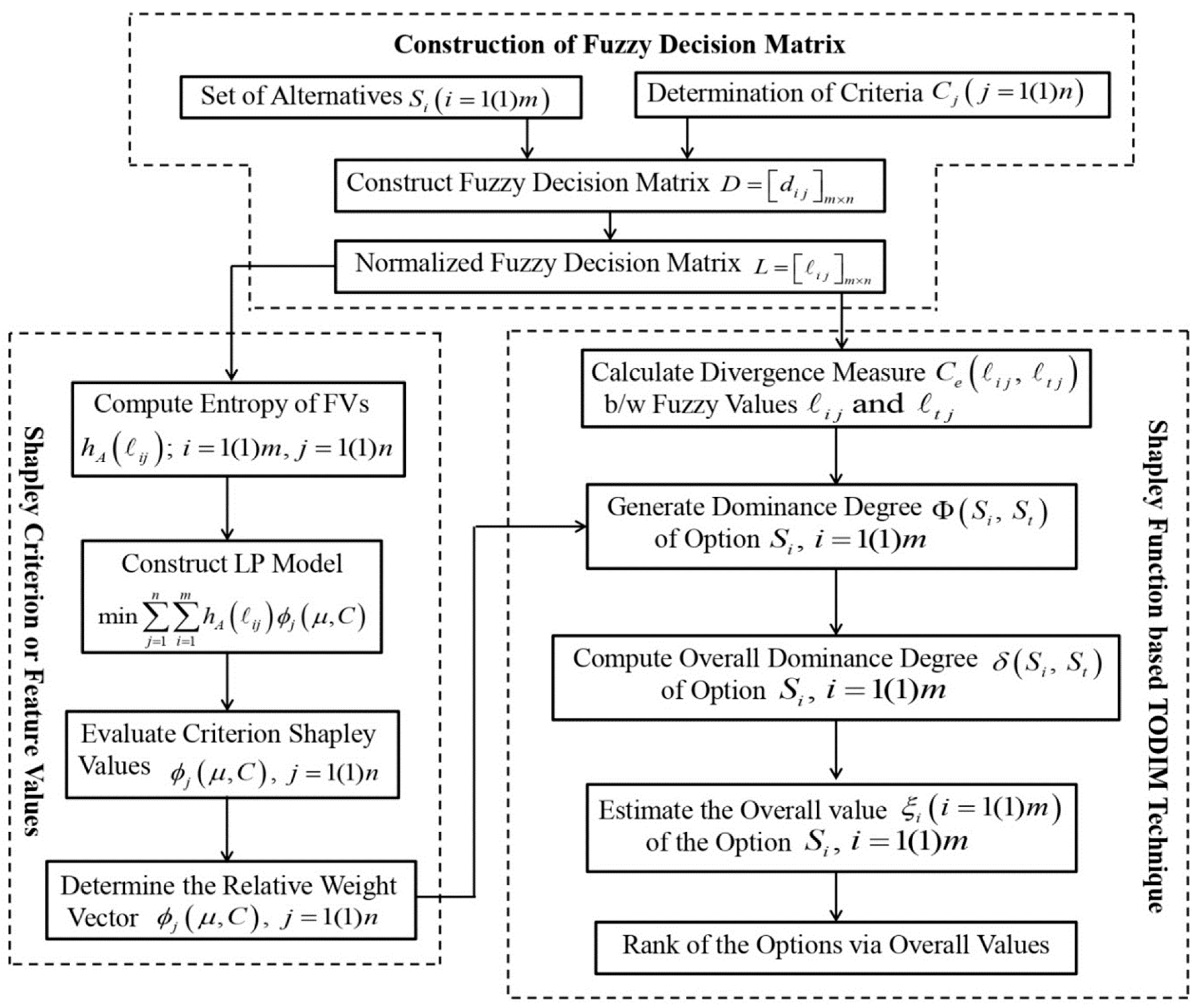
4. An Integrated TODIM Approach Using the Shapley Function and Divergence Measure
4.1. Shapley Function
4.2. Models for Criteria Weight Based on the Optimal Additive Measure
4.3. Shapley Function-Based TODIM Technique for MCDM
5. Case Study of the Proposed Method
Comparative Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix A.1. Proof of Theorem 1
Appendix A.2. Proof of Proposition 1
Appendix A.3. Proof of Proposition 2
References
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Rényi, A. On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Contributions to the Theory of Statistics; The Regents of the University of California: Berkeley, CA, USA, 1961; Volume 1. [Google Scholar]
- Sharma, B.; Mittal, D. New non-additive measures of relative information. J. Comb. Inf. Syst. Sci. 1977, 2, 122–132. [Google Scholar]
- Lin, J. Divergence measures based on the Shannon entropy. IEEE Trans. Inf. Theory 1991, 37, 145–151. [Google Scholar] [CrossRef]
- Ghosh, M.; Das, D.; Chakraborty, C.; Ray, A.K. Automated leukocyte recognition using fuzzy divergence. Micron 2010, 41, 840–846. [Google Scholar] [CrossRef] [PubMed]
- Neagoe, I.M.; Popescu, D.; Niculescu, V. Applications of entropic divergence measures for DNA segmentation into high variable regions of cryptosporidium spp. gp60 gene. Rom. Rep. Phys. 2014, 66, 1078–1087. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- De Luca, A.; Termini, S. A definition of a nonprobabilistic entropy in the setting of fuzzy sets theory. Inf. Control 1972, 20, 301–312. [Google Scholar] [CrossRef]
- Pal, N.R.; Pal, S.K. Object-background segmentation using new definitions of entropy. IEE Proc. E Comput. Digit. Tech. 1989, 136, 284–295. [Google Scholar] [CrossRef]
- Hooda, D.S. On generalized measures of fuzzy entropy. Math. Slovaca 2004, 54, 315–325. [Google Scholar]
- Verma, R.K.; Sharma, B.D. On generalized exponential fuzzy entropy. World Acad. Sci. Eng. Technol. 2011, 60, 1402–1405. [Google Scholar]
- Mishra, A.R.; Jain, D.; Hooda, D.S. On logarithmic fuzzy measures of information and discrimination. J. Inf. Optim. Sci. 2016, 37, 213–231. [Google Scholar] [CrossRef]
- Kvalseth, T.O. On exponential entropies. IEEE Int. Conf. Syst. Man Cybern. 2000, 4, 2822–2826. [Google Scholar]
- Mishra, A.R.; Hooda, D.S.; Jain, D. On exponential fuzzy measures of information and discrimination. Int. J. Comput. Appl. 2015, 119, 1–7. [Google Scholar]
- Montes, I.; Pal, N.R.; Montes, S. Entropy measures for Atanassov intuitionistic fuzzy sets based on divergence. Soft Comput. 2018, 22, 5051–5071. [Google Scholar] [CrossRef]
- Mishra, A.R.; Jain, D.; Hooda, D.S. On fuzzy distance and induced fuzzy information measures. J. Inf. Optim. Sci. 2016, 37, 193–211. [Google Scholar] [CrossRef]
- Bhandari, D.; Pal, N.R. Some new information measures for fuzzy sets. Inf. Sci. 1993, 67, 209–228. [Google Scholar] [CrossRef]
- Fan, J.; Xie, W. Distance measure and induced fuzzy entropy. Fuzzy Sets Syst. 1999, 104, 305–314. [Google Scholar] [CrossRef]
- Rani, P.; Kannan, G.; Mishra, A.R.; Mardani, A.; Alrasheedi, M.; Hooda, D.S. Unified fuzzy divergence measures with multi-criteria decision making problems for sustainable planning of an e-waste recycling job selection. Symmetry 2020, 12, 90. [Google Scholar] [CrossRef]
- Arora, H.D.; Dhiman, A. On some generalised information measure of fuzzy directed divergence and decision making. Int. J. Comput. Sci. Math. 2016, 7, 263–273. [Google Scholar] [CrossRef]
- Xiao, F.; Ding, W. Divergence measure of Pythagorean fuzzy sets and its application in medical diagnosis. Appl. Soft Comput. 2019, 79, 254–267. [Google Scholar] [CrossRef]
- Thao, N.X.; Smarandache, F. Divergence measure of neutrosophic sets and applications. Neutrosophic Sets Syst. 2018, 21, 142–152. [Google Scholar]
- Ju, F.; Yuan, Y.; Yuan, Y.; Quan, W. A divergence-based distance measure for intuitionistic fuzzy sets and its application in the decision-making of innovation management. IEEE Access 2019, 8, 1105–1117. [Google Scholar] [CrossRef]
- Joshi, R.; Kumar, S. An exponential Jensen fuzzy divergence measure with applications in multiple attribute decision-making. Math. Probl. Eng. 2018, 2018, 4342098. [Google Scholar] [CrossRef]
- Dahooie, J.H.; Zavadskas, E.K.; Firoozfar, H.R.; Vanaki, A.S.; Mohammadi, N.; Brauers, W.K.M. An improved fuzzy MULTIMOORA approach for multi-criteria decision making based on objective weighting method (CCSD) and its application to technological forecasting method selection. Eng. Appl. Artif. Intell. 2019, 79, 114–128. [Google Scholar] [CrossRef]
- Keshavarz Ghorabaee, M.; Amiri, M.; Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J. A new hybrid simulation-based assignment approach for evaluating airlines with multiple service quality criteria. J. Air Transp. Manag. 2017, 63, 45–60. [Google Scholar] [CrossRef]
- Mardani, A.; Jusoh, A.; Zavadskas, E.K.; Khalifah, Z.; Nor, K.M.D. Application of multiple-criteria decision-making techniques and approaches to evaluating of service quality: A systematic review of the literature. J. Bus. Econ. Manag. 2015, 16, 1034–1068. [Google Scholar] [CrossRef]
- Calabrese, A.; Costa, R.; Levialdi, N.; Menichini, T. Integrating sustainability into strategic decision-making: A fuzzy AHP method for the selection of relevant sustainability issues. Technol. Forecast. Soc. Chang. 2019, 139, 155–168. [Google Scholar] [CrossRef]
- Cavallaro, F.; Zavadskas, E.K.; Streimikiene, D.; Mardani, A. Assessment of concentrated solar power (CSP) technologies based on a modified intuitionistic fuzzy topsis and trigonometric entropy weights. Technol. Forecast. Soc. Chang. 2019, 140, 258–270. [Google Scholar] [CrossRef]
- Akram, M.; Adeel, A. Novel TOPSIS method for group decision-making based on hesitant m−polar fuzzy model. J. Intell. Fuzzy Syst. 2019. [Google Scholar] [CrossRef]
- Han, Q.; Li, W.; Lu, Y.; Zheng, M.; Quan, W.; Song, Y. TOPSIS method based on novel entropy and distance measure for linguistic Pythagorean fuzzy sets with their application in multiple attribute decision making. IEEE Access 2019, 8, 14401–14412. [Google Scholar] [CrossRef]
- Deveci, M.; Canitez, F.; Gökaşar, I. WASPAS and TOPSIS based interval type-2 fuzzy MCDM method for a selection of a car sharing station. Sustain. Cities Soc. 2018, 41, 777–791. [Google Scholar] [CrossRef]
- Badalpur, M.; Nurbakhsh, E. An application of WASPAS method in risk qualitative analysis: A case study of a road construction project in Iran. Int. J. Constr. Manag. 2019. [Google Scholar] [CrossRef]
- Pamučar, D.; Božanić, D. Selection of a location for the development of multimodal logistics center: Application of single-valued neutrosophic MABAC model. Oper. Res. Eng. Sci. Theory Appl. 2019, 2, 55–71. [Google Scholar] [CrossRef]
- Mishra, A.R.; Chandel, A.; Motwani, D. Extended MABAC method based on divergence measures for multi-criteria assessment of programming language with interval-valued intuitionistic fuzzy sets. Granul. Comput. 2020, 5, 97–117. [Google Scholar] [CrossRef]
- Chatterjee, K.; Kar, S. Unified Granular-number-based AHP-VIKOR multi-criteria decision framework. Granul. Comput. 2017, 2, 199–221. [Google Scholar] [CrossRef]
- Chen, T.-Y. A novel VIKOR method with an application to multiple criteria decision analysis for hospital-based post-acute care within a highly complex uncertain environment. Neural Comput. Appl. 2019, 31, 3969–3999. [Google Scholar] [CrossRef]
- Fei, L.; Xia, J.; Feng, Y.; Liu, L. An ELECTRE-based multiple criteria decision making method for supplier selection using dempster-Shafer theory. IEEE Access 2019, 7, 84701–84716. [Google Scholar] [CrossRef]
- Liao, H.; Jiang, L.; Lev, B.; Fujita, H. Novel operations of PLTSs based on the disparity degrees of linguistic terms and their use in designing the probabilistic linguistic ELECTRE III method. Appl. Soft Comput. 2019, 80, 450–464. [Google Scholar] [CrossRef]
- Rani, P.; Jain, D. Intuitionistic fuzzy PROMETHEE technique for multi-criteria decision making problems based on entropy measure. In Proceedings of Communications in Computer and Information Science (CCIS); Springer: Singapore, 2017; Volume 721, pp. 290–301. [Google Scholar]
- Wu, X.; Zhang, C.; Jiang, L.; Liao, H. An integrated method with PROMETHEE and conflict analysis for qualitative and quantitative decision-making: Case study of site selection for wind power plants. Cogn. Comput. 2019, in press. [Google Scholar] [CrossRef]
- Alali, F.; Tolga, A.C. Portfolio allocation with the TODIM method. Expert Syst. Appl. 2019, 124, 341–348. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Y.-M.; Martínez, L. Fuzzy TODIM method based on alpha-level sets. Expert Syst. Appl. 2019, 112899. [Google Scholar] [CrossRef]
- Kai-Ineman, D.; Tversky, A. Prospect theory: An analysis of decision under risk. Econometrica 1979, 47, 363–391. [Google Scholar]
- Gomes, L.; Lima, M. TODIM: Basics and application to multicriteria ranking of projects with environmental impacts. Found. Comput. Decis. Sci. 1992, 16, 113–127. [Google Scholar]
- Liang, D.; Zhang, Y.; Xu, Z.; Jamaldeen, A. Pythagorean fuzzy VIKOR approaches based on TODIM for evaluating internet banking website quality of Ghanaian banking industry. Appl. Soft Comput. 2019, 78, 583–594. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, J.; Hu, Y.; Ke, Y.; Li, L. An extended TODIM-PROMETHEE method for waste-to-energy plant site selection based on sustainability perspective. Energy 2018, 156, 1–16. [Google Scholar] [CrossRef]
- Gomes, L.F.A.M.; Machado, M.A.S.; da Costa, F.F.; Rangel, L.A.D. Criteria interactions in multiple criteria decision aiding: A choquet formulation for the TODIM method. Procedia Comput. Sci. 2013, 17, 324–331. [Google Scholar] [CrossRef]
- Qin, J.; Liu, X.; Pedrycz, W. An extended TODIM multi-criteria group decision making method for green supplier selection in interval type-2 fuzzy environment. Eur. J. Oper. Res. 2017, 258, 626–638. [Google Scholar] [CrossRef]
- Mishra, A.R.; Rani, P. Biparametric information measures-based TODIM technique for interval-valued intuitionistic fuzzy environment. Arab. J. Sci. Eng. 2018, 43, 3291–3309. [Google Scholar] [CrossRef]
- Fan, Z.P.; Zhang, X.; Chen, F.D.; Liu, Y. Extended TODIM method for hybrid multiple attribute decision making problems. Knowl. Based Syst. 2013, 42, 40–48. [Google Scholar] [CrossRef]
- Liu, P.; Shen, M. An extended C-TODIM method with linguistic intuitionistic fuzzy numbers. J. Intell. Fuzzy Syst. 2019, 37, 3615–3627. [Google Scholar] [CrossRef]
- Zhang, D.; Li, Y.; Wu, C. An extended TODIM method to rank products with online reviews under intuitionistic fuzzy environment. J. Oper. Res. Soc. 2020, 71, 322–334. [Google Scholar] [CrossRef]
- Wang, J.Q.; Li, J.J. Multi-criteria fuzzy decision-making method based on cross entropy and score functions. Expert Syst. Appl. 2011, 38, 1032–1038. [Google Scholar] [CrossRef]
- Xia, M.; Xu, Z. Entropy/cross entropy-based group decision making under intuitionistic fuzzy environment. Inf. Fusion 2012, 13, 31–47. [Google Scholar] [CrossRef]
- Shao, Y.; Mou, Q.; Gong, Z. On retarded fuzzy functional differential equations and nonabsolute fuzzy integrals. Fuzzy Sets Syst. 2019, 375, 121–140. [Google Scholar] [CrossRef]
- Montes, S.; Couso, I.; Gil, P.; Bertoluzza, C. Divergence measure between fuzzy sets. Int. J. Approx. Reason. 2002, 30, 91–105. [Google Scholar] [CrossRef]
- Jain, K.; Chhabra, P. A new exponential directed divergence information measure. J. Appl. Math. Inform. 2016, 34, 295–308. [Google Scholar] [CrossRef]
- Sugeno, M. Theory of Fuzzy Integral and its Application; Tokyo Institute of Technology: Tokyo, Japan, 1974. [Google Scholar]
- Rani, P.; Jain, D.; Hooda, D.S. Shapley function based interval-valued intuitionistic fuzzy VIKOR technique for correlative multi-criteria decision making problems. Iran. J. Fuzzy Syst. 2018, 15, 25–54. [Google Scholar]
- Kumari, R.; Mishra, A.R.; Sharma, D.K. Intuitionistic fuzzy Shapley-TOPSIS method for multi-criteria decision making problems based on information measures. Recent Adv. Comput. Sci. Commun. 2020. [Google Scholar] [CrossRef]
- Meng, F.; Wang, C.; Chen, X.; Zhang, Q. Correlation coefficients of interval-valued hesitant fuzzy sets and their application based on the Shapley function. Int. J. Intell. Syst. 2016, 31, 17–43. [Google Scholar] [CrossRef]
- Shapley, L.S. A value for n-person games. Contrib. Theory Games 1953, 2, 307–317. [Google Scholar]
- Kahneman, D.; Tversky, A. Prospect theory: An analysis of decision under risk. In Handbook of the Fundamentals of Financial Decision Making: Part I. World Scientific; World Scientific: Singapore, 2013; pp. 99–127. [Google Scholar]
- Toloie, A.; Nasimi, M.; Poorebrahimi, A. Assessing quality of insurance companies using multiple criteria decision making. Eur. J. Sci. Res. 2011, 54, 448–457. [Google Scholar]
- Mishra, A.R. Intuitionistic fuzzy information measures with application in rating of township development. Iran. J. Fuzzy Syst. 2016, 13, 49–70. [Google Scholar]
- Mishra, A.R.; Jain, D.; Hooda, D.S. Exponential intuitionistic fuzzy information measure with assessment of service quality. Int. J. Fuzzy Syst. 2017, 19, 788–798. [Google Scholar] [CrossRef]
- Krohling, R.A.; de Souza, T.T.M. Combining prospect theory and fuzzy numbers to multi-criteria decision making. Expert Syst. Appl. 2012, 39, 11487–11493. [Google Scholar] [CrossRef]
| Option | E1 | E2 | E3 | E4 |
|---|---|---|---|---|
| S1 | 0.5395 | 0.7655 | 0.6770 | 0.5915 |
| S2 | 0.7015 | 0.6990 | 0.7725 | 0.7650 |
| S3 | 0.7365 | 0.5350 | 0.6595 | 0.6340 |
| S4 | 0.7800 | 0.6985 | 0.5995 | 0.7455 |
| Entropy | E1 | E2 | E3 | E4 |
|---|---|---|---|---|
| H(S1) | 0.6029 | 0.4400 | 0.5329 | 0.5869 |
| H(S2) | 0.5111 | 0.5134 | 0.4310 | 0.4406 |
| H(S3) | 0.4747 | 0.6037 | 0.5468 | 0.5644 |
| H(S4) | 0.4211 | 0.5139 | 0.5834 | 0.4644 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mishra, A.R.; Rani, P.; Mardani, A.; Kumari, R.; Zavadskas, E.K.; Kumar Sharma, D. An Extended Shapley TODIM Approach Using Novel Exponential Fuzzy Divergence Measures for Multi-Criteria Service Quality in Vehicle Insurance Firms. Symmetry 2020, 12, 1452. https://doi.org/10.3390/sym12091452
Mishra AR, Rani P, Mardani A, Kumari R, Zavadskas EK, Kumar Sharma D. An Extended Shapley TODIM Approach Using Novel Exponential Fuzzy Divergence Measures for Multi-Criteria Service Quality in Vehicle Insurance Firms. Symmetry. 2020; 12(9):1452. https://doi.org/10.3390/sym12091452
Chicago/Turabian StyleMishra, Arunodaya Raj, Pratibha Rani, Abbas Mardani, Reetu Kumari, Edmundas Kazimieras Zavadskas, and Dilip Kumar Sharma. 2020. "An Extended Shapley TODIM Approach Using Novel Exponential Fuzzy Divergence Measures for Multi-Criteria Service Quality in Vehicle Insurance Firms" Symmetry 12, no. 9: 1452. https://doi.org/10.3390/sym12091452
APA StyleMishra, A. R., Rani, P., Mardani, A., Kumari, R., Zavadskas, E. K., & Kumar Sharma, D. (2020). An Extended Shapley TODIM Approach Using Novel Exponential Fuzzy Divergence Measures for Multi-Criteria Service Quality in Vehicle Insurance Firms. Symmetry, 12(9), 1452. https://doi.org/10.3390/sym12091452








