Intuitionistic Fuzzy Sets in Multi-Criteria Group Decision Making Problems Using the Characteristic Objects Method
Abstract
1. Introduction
2. Basic Concepts
- if then
- if and
- (i)
- then
- (ii)
- then
- ,
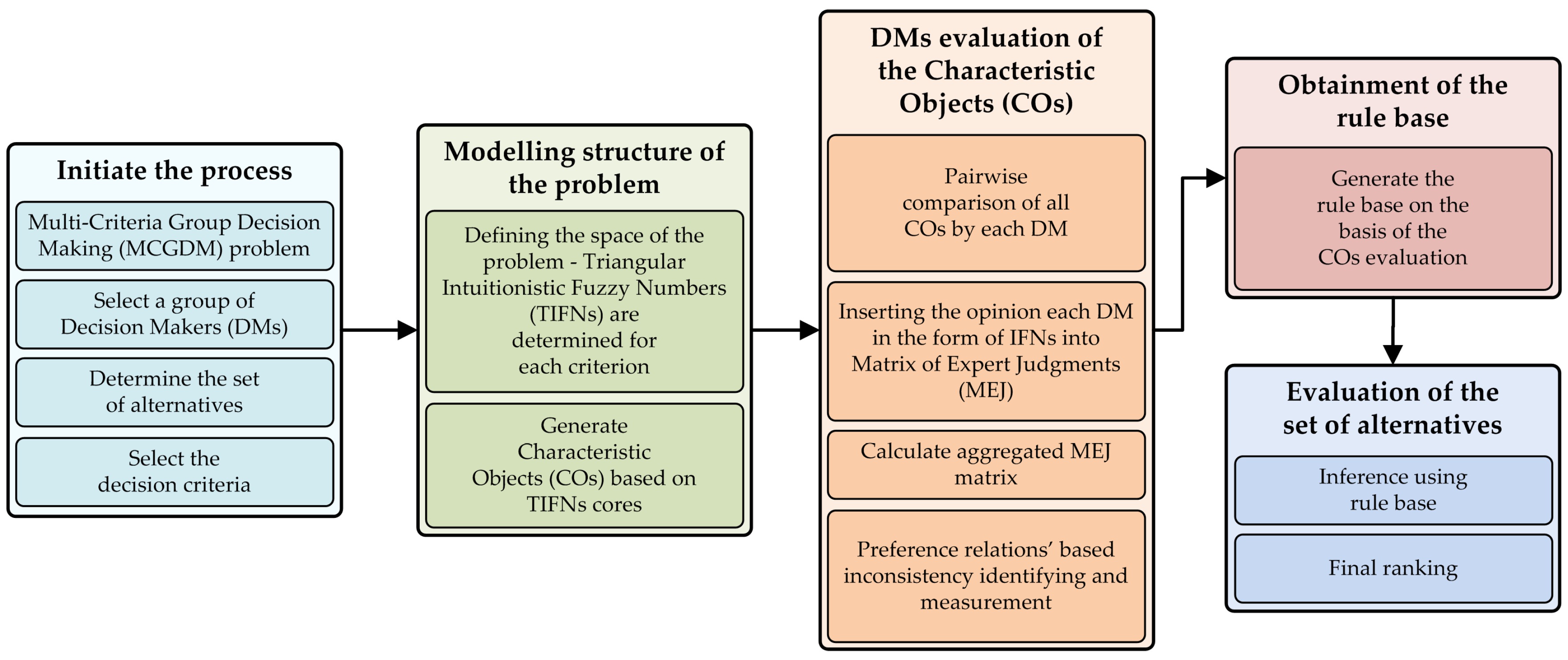
3. MCDM with COMET Method Using IFSs
4. Illustrative Example
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MCGDM | Multi-Criteria Group Decision Making |
| MCDM | Multi-Criteria Decision Making |
| GDM | Group Decision Making |
| DM | Decision Maker |
| IF | Intuitionistic Fuzzy |
| IFS | Intuitionistic Fuzzy Set |
| IFN | Intuitionistic Fuzzy Number |
| TIFN | Triangular Intuitionistic Fuzzy Number |
| IPR | Intuitionistic Preference Relations |
| HFS | Hesitant Fuzzy Set |
| COMET | Characteristic Objects METhod |
| MEJ | Matrix of Expert Judgments |
References
- Božanić, D.; Pamučar, D.; Bojanić, D. Modification of the analytic hierarchy process (AHP) method using fuzzy logic: Fuzzy AHP approach as a support to the decision making process concerning engagement of the group for additional hindering. Serbian J. Manag. 2015, 10, 151–171. [Google Scholar] [CrossRef]
- Xu, J.; Wu, Z. A discrete consensus support model for multiple attribute group decision making. Knowl.-Based Syst. 2011, 24, 1196–1202. [Google Scholar] [CrossRef]
- Atanassov, K.T. New operations defined over the intuitionistic fuzzy sets. Fuzzy Sets Syst. 1994, 61, 137–142. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Roy, J.; Das, S.; Kar, S.; Pamučar, D. An extension of the CODAS approach using interval-valued intuitionistic fuzzy set for sustainable material selection in construction projects with incomplete weight information. Symmetry 2019, 11, 393. [Google Scholar] [CrossRef]
- Chen, T.Y. The inclusion-based TOPSIS method with interval-valued intuitionistic fuzzy sets for multiple criteria group decision making. Appl. Soft Comput. 2015, 26, 57–73. [Google Scholar] [CrossRef]
- Park, J.H.; Cho, H.J.; Kwun, Y.C. Extension of the VIKOR method for group decision making with interval-valued intuitionistic fuzzy information. Fuzzy Optim. Decis. Mak. 2011, 10, 233–253. [Google Scholar] [CrossRef]
- Wu, J.; Chiclana, F. A social network analysis trust–consensus based approach to group decision-making problems with interval-valued fuzzy reciprocal preference relations. Knowl.-Based Syst. 2014, 59, 97–107. [Google Scholar] [CrossRef]
- Wu, J.; Chiclana, F. A risk attitudinal ranking method for interval-valued intuitionistic fuzzy numbers based on novel attitudinal expected score and accuracy functions. Appl. Soft Comput. 2014, 22, 272–286. [Google Scholar] [CrossRef]
- Xu, Z. An integrated model-based interactive approach to FMAGDM with incomplete preference information. Fuzzy Optim. Decis. Mak. 2010, 9, 333–357. [Google Scholar] [CrossRef]
- Xu, J.; Shen, F. A new outranking choice method for group decision making under Atanassov’s interval-valued intuitionistic fuzzy environment. Knowl.-Based Syst. 2014, 70, 177–188. [Google Scholar] [CrossRef]
- Faizi, S.; Sałabun, W.; Ullah, S.; Rashid, T.; Więckowski, J. A New Method to Support Decision-Making in an Uncertain Environment Based on Normalized Interval-Valued Triangular Fuzzy Numbers and COMET Technique. Symmetry 2020, 12, 516. [Google Scholar] [CrossRef]
- Xu, Z.; Liao, H. Intuitionistic fuzzy analytic hierarchy process. IEEE Trans. Fuzzy Syst. 2013, 22, 749–761. [Google Scholar] [CrossRef]
- Shen, F.; Xu, J.; Xu, Z. An outranking sorting method for multi-criteria group decision making using intuitionistic fuzzy sets. Inf. Sci. 2016, 334, 338–353. [Google Scholar] [CrossRef]
- Saaty, T.L. Decision making with the analytic hierarchy process. Int. J. Serv. Sci. 2008, 1, 83–98. [Google Scholar] [CrossRef]
- Wang, Z.J. Geometric consistency based interval weight elicitation from intuitionistic preference relations using logarithmic least square optimization. Fuzzy Optim. Decis. Mak. 2015, 14, 289–310. [Google Scholar] [CrossRef]
- Xu, Z.; Liao, H. A survey of approaches to decision making with intuitionistic fuzzy preference relations. Knowl.-Based Syst. 2015, 80, 131–142. [Google Scholar] [CrossRef]
- Xu, Z. Intuitionistic fuzzy aggregation operators. IEEE Trans. Fuzzy Syst. 2007, 15, 1179–1187. [Google Scholar]
- Xu, Z. Intuitionistic preference relations and their application in group decision making. Inf. Sci. 2007, 177, 2363–2379. [Google Scholar] [CrossRef]
- Xu, Z.; Cai, X.; Szmidt, E. Algorithms for estimating missing elements of incomplete intuitionistic preference relations. Int. J. Intell. Syst. 2011, 26, 787–813. [Google Scholar] [CrossRef]
- Gong, Z.W.; Li, L.S.; Forrest, J.; Zhao, Y. The optimal priority models of the intuitionistic fuzzy preference relation and their application in selecting industries with higher meteorological sensitivity. Expert Syst. Appl. 2011, 38, 4394–4402. [Google Scholar] [CrossRef]
- Wan, S.P.; Wang, Q.Y.; Dong, J.Y. The extended VIKOR method for multi-attribute group decision making with triangular intuitionistic fuzzy numbers. Knowl.-Based Syst. 2013, 52, 65–77. [Google Scholar] [CrossRef]
- Wang, Z.J. Derivation of intuitionistic fuzzy weights based on intuitionistic fuzzy preference relations. Appl. Math. Model. 2013, 37, 6377–6388. [Google Scholar] [CrossRef]
- Shu, M.H.; Cheng, C.H.; Chang, J.R. Using intuitionistic fuzzy sets for fault-tree analysis on printed circuit board assembly. Microelectron. Reliab. 2006, 46, 2139–2148. [Google Scholar] [CrossRef]
- Li, D.F. A ratio ranking method of triangular intuitionistic fuzzy numbers and its application to MADM problems. Comput. Math. Appl. 2010, 60, 1557–1570. [Google Scholar]
- Yu, D. Prioritized information fusion method for triangular intuitionistic fuzzy set and its application to teaching quality evaluation. Int. J. Intell. Syst. 2013, 28, 411–435. [Google Scholar] [CrossRef]
- Otay, İ.; Oztaysi, B.; Onar, S.C.; Kahraman, C. Multi-expert performance evaluation of healthcare institutions using an integrated intuitionistic fuzzy AHP&DEA methodology. Knowl.-Based Syst. 2017, 133, 90–106. [Google Scholar]
- Qin, Q.; Liang, F.; Li, L.; Chen, Y.W.; Yu, G.F. A TODIM-based multi-criteria group decision making with triangular intuitionistic fuzzy numbers. Appl. Soft Comput. 2017, 55, 93–107. [Google Scholar] [CrossRef]
- Saini, N.; Bajaj, R.K.; Gandotra, N.; Dwivedi, R.P. Multi-criteria decision making with triangular intuitionistic fuzzy number based on distance measure & parametric entropy approach. Procedia Comput. Sci. 2018, 125, 34–41. [Google Scholar]
- Mishra, A.R.; Rani, P.; Pardasani, K.R.; Mardani, A.; Stević, Ž.; Pamučar, D. A novel entropy and divergence measures with multi-criteria service quality assessment using interval-valued intuitionistic fuzzy TODIM method. Soft Comput. 2020, 24, 11641–11661. [Google Scholar] [CrossRef]
- Faizi, S.; Rashid, T.; Sałabun, W.; Zafar, S.; Wątróbski, J. Decision making with uncertainty using hesitant fuzzy sets. Int. J. Fuzzy Syst. 2018, 20, 93–103. [Google Scholar] [CrossRef]
- Watróbski, J.; Sałabun, W. The characteristic objects method: A new intelligent decision support tool for sustainable manufacturing. In Proceedings of the International Conference on Sustainable Design and Manufacturing, Chania, Greece, 5–6 April 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 349–359. [Google Scholar]
- Sałabun, W. The Characteristic Objects Method: A New Distance-based Approach to Multicriteria Decision-making Problems. J. Multi-Criteria Decis. Anal. 2015, 22, 37–50. [Google Scholar] [CrossRef]
- Sałabun, W.; Ziemba, P.; Wątróbski, J. The rank reversals paradox in management decisions: The comparison of the ahp and comet methods. In Proceedings of the International Conference on Intelligent Decision Technologies, Puerto de la Cruz, Spain, 15–17 June 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 181–191. [Google Scholar]
- Sałabun, W.; Karczmarczyk, A.; Wątróbski, J.; Jankowski, J. Handling data uncertainty in decision making with COMET. In Proceedings of the 2018 IEEE Symposium Series on Computational Intelligence (SSCI), Bengaluru, India, 18–21 November 2018; pp. 1478–1484. [Google Scholar]
- Wątróbski, J.; Sałabun, W.; Karczmarczyk, A.; Wolski, W. Sustainable decision-making using the COMET method: An empirical study of the ammonium nitrate transport management. In Proceedings of the 2017 Federated Conference on Computer Science and Information Systems (FedCSIS), Prague, Czech Republic, 3–6 September 2017; pp. 949–958. [Google Scholar]
- Wątróbski, J.; Sałabun, W. Green supplier selection framework based on multi-criteria decision-analysis approach. In Proceedings of the International Conference on Sustainable Design and Manufacturing, Chania, Greece, 5–6 April 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 361–371. [Google Scholar]
- Pujadas, P.; Pardo-Bosch, F.; Aguado-Renter, A.; Aguado, A. MIVES multi-criteria approach for the evaluation, prioritization, and selection of public investment projects. A case study in the city of Barcelona. Land Use Policy 2017, 64, 29–37. [Google Scholar] [CrossRef]
- Roigé Montornés, N.; Pujadas Álvarez, P.; Cardús González, J.; Aguado de Cea, A. Water network renewal strategy: A case study of Aigües de Barcelona. In Water Management; ICE: London, UK, 2019. [Google Scholar]
- Pamucar, D.S.; Pejcic Tarle, S.; Parezanovic, T. New hybrid multi-criteria decision-making DEMATELMAIRCA model: Sustainable selection of a location for the development of multimodal logistics centre. Econ. Res.-Ekon. Istraživanja 2018, 31, 1641–1665. [Google Scholar] [CrossRef]
- Wątróbski, J.; Jankowski, J.; Ziemba, P.; Karczmarczyk, A.; Zioło, M. Generalised framework for multi-criteria method selection. Omega 2019, 86, 107–124. [Google Scholar] [CrossRef]
- Bashir, Z.; Rashid, T.; Wątróbski, J.; Sałabun, W.; Malik, A. Hesitant probabilistic multiplicative preference relations in group decision making. Appl. Sci. 2018, 8, 398. [Google Scholar] [CrossRef]
- Atanassov, K.T. Interval valued intuitionistic fuzzy sets. In Intuitionistic Fuzzy Sets; Springer: Berlin/Heidelberg, Germany, 1999; pp. 139–177. [Google Scholar]
- Chen, S.M.; Tan, J.M. Handling multicriteria fuzzy decision-making problems based on vague set theory. Fuzzy Sets Syst. 1994, 67, 163–172. [Google Scholar] [CrossRef]
- Hong, D.H.; Choi, C.H. Multicriteria fuzzy decision-making problems based on vague set theory. Fuzzy Sets Syst. 2000, 114, 103–113. [Google Scholar] [CrossRef]
- Xu, Z.; Yager, R.R. Some geometric aggregation operators based on intuitionistic fuzzy sets. Int. J. Gen. Syst. 2006, 35, 417–433. [Google Scholar] [CrossRef]
- Tong, X.; Wang, Z.J. A group decision framework with intuitionistic preference relations and its application to low carbon supplier selection. Int. J. Environ. Res. Public Health 2016, 13, 923. [Google Scholar] [CrossRef]
- Piegat, A. Fuzzy Modeling and Control; Springer: Berlin/Heidelberg, Germany, 2013; Volume 69. [Google Scholar]
- Cutello, V.; Montero, J. Fuzzy rationality measures. Fuzzy Sets Syst. 1994, 62, 39–54. [Google Scholar] [CrossRef]
- Herrera-Viedma, E.; Herrera, F.; Chiclana, F.; Luque, M. Some issues on consistency of fuzzy preference relations. Eur. J. Oper. Res. 2004, 154, 98–109. [Google Scholar] [CrossRef]
- Saaty, T.L. A scaling method for priorities in hierarchical structures. J. Math. Psychol. 1977, 15, 234–281. [Google Scholar] [CrossRef]
- Faizi, S.; Sałabun, W.; Rashid, T.; Wątróbski, J.; Zafar, S. Group decision-making for hesitant fuzzy sets based on characteristic objects method. Symmetry 2017, 9, 136. [Google Scholar] [CrossRef]
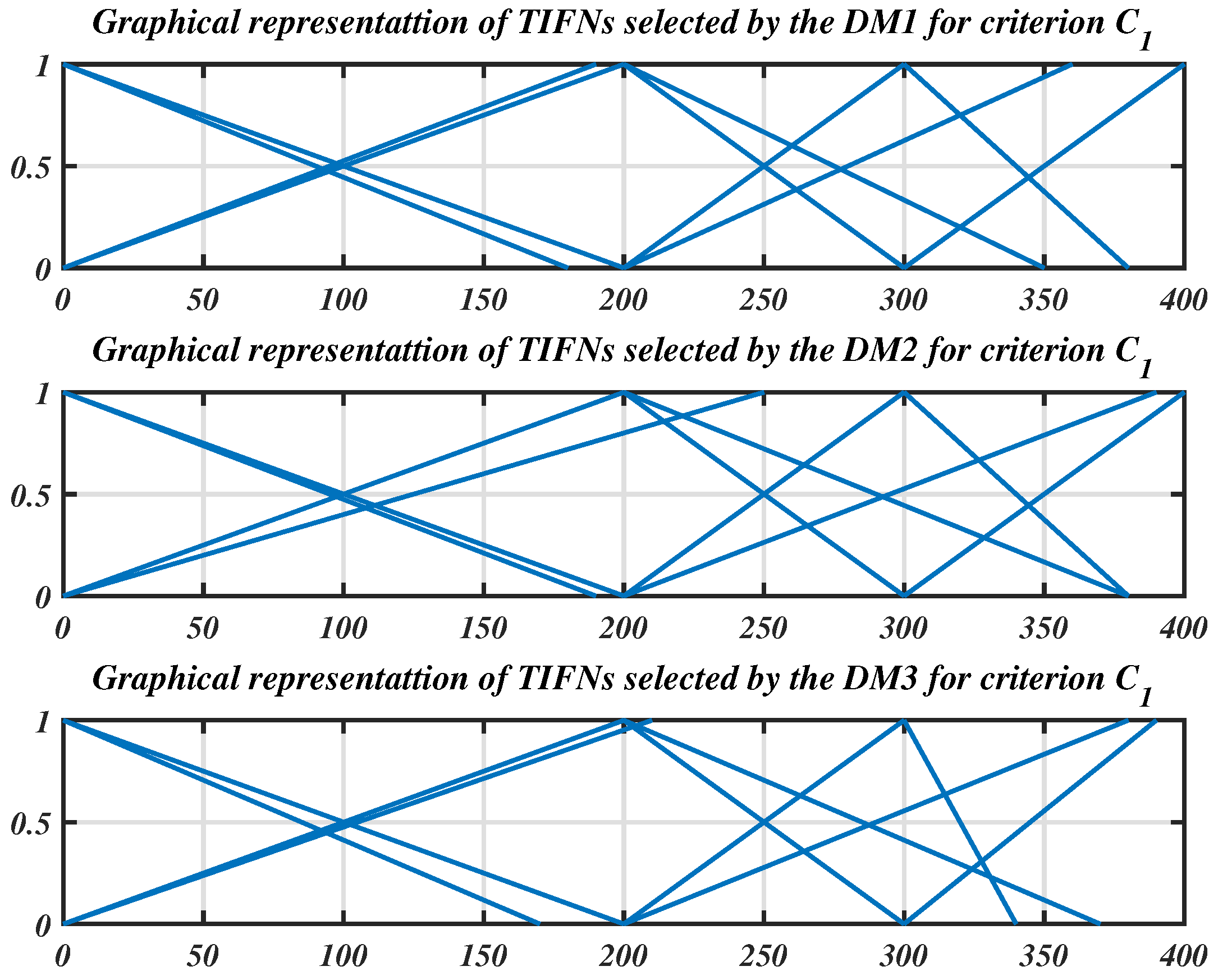
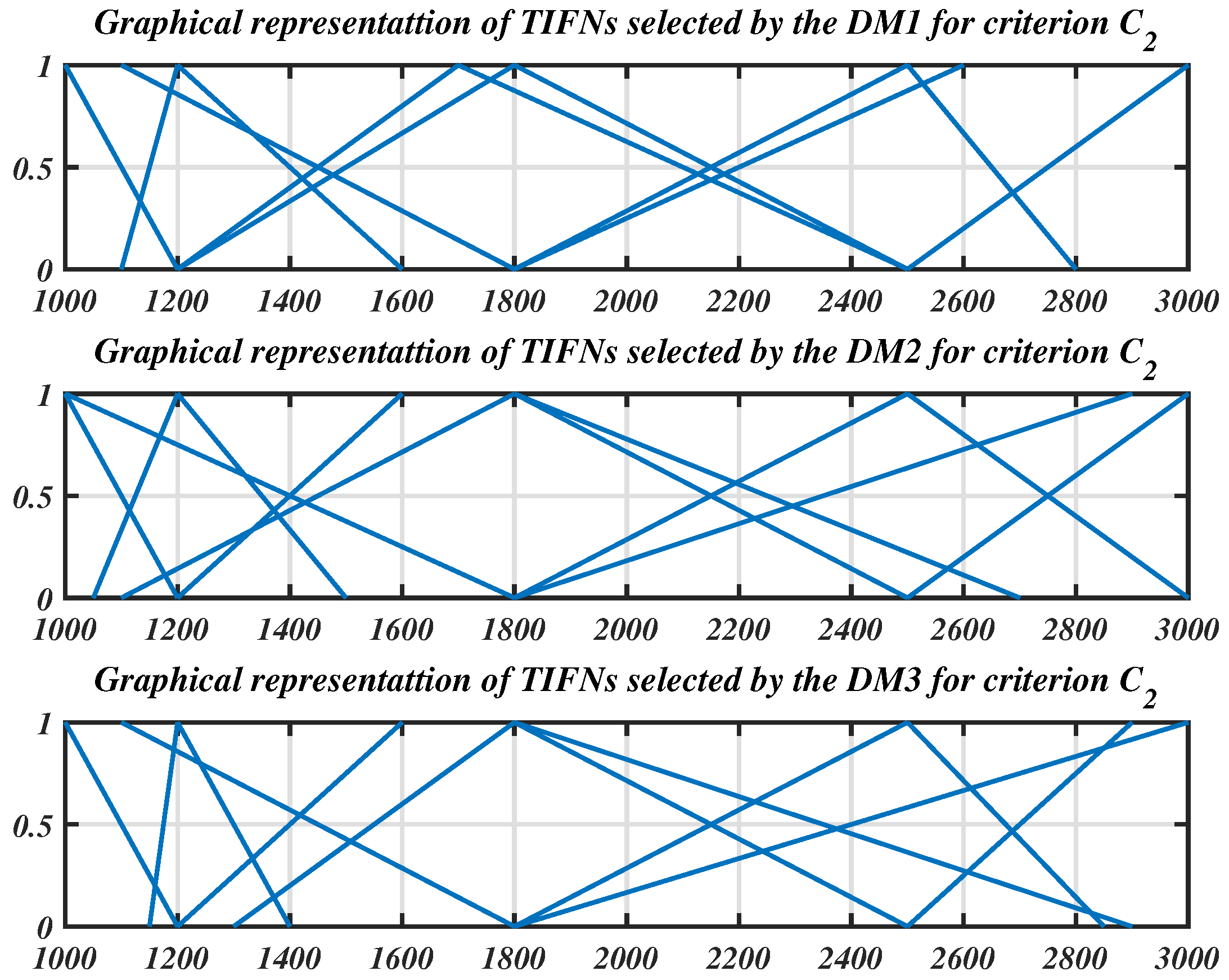
| Alternatives | (LR) | (R/U) | Bill Amount | Original Rank |
|---|---|---|---|---|
| 150 | 1650 | 2 | ||
| 50 | 2 | 2050 | 3 | |
| 250 | 1500 | 1 | ||
| 30 | 2180 | 4 |
| DM1 | |
| DM2 | |
| DM3 |
| DM1 | |
| DM2 | |
| DM3 | |
| Alternatives | Original | Ranking | Preference | Ranking | ||
|---|---|---|---|---|---|---|
| (LR) | (R/U) | Ranking | Using | Values Using | Using | |
| HFSs | IFSs | IFSs | ||||
| 150 | 2 | 3 | 3 | |||
| 50 | 2 | 3 | 2 | 2 | ||
| 250 | 1 | 1 | 1 | |||
| 30 | 4 | 4 | 4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faizi, S.; Sałabun, W.; Rashid, T.; Zafar, S.; Wątróbski, J. Intuitionistic Fuzzy Sets in Multi-Criteria Group Decision Making Problems Using the Characteristic Objects Method. Symmetry 2020, 12, 1382. https://doi.org/10.3390/sym12091382
Faizi S, Sałabun W, Rashid T, Zafar S, Wątróbski J. Intuitionistic Fuzzy Sets in Multi-Criteria Group Decision Making Problems Using the Characteristic Objects Method. Symmetry. 2020; 12(9):1382. https://doi.org/10.3390/sym12091382
Chicago/Turabian StyleFaizi, Shahzad, Wojciech Sałabun, Tabasam Rashid, Sohail Zafar, and Jarosław Wątróbski. 2020. "Intuitionistic Fuzzy Sets in Multi-Criteria Group Decision Making Problems Using the Characteristic Objects Method" Symmetry 12, no. 9: 1382. https://doi.org/10.3390/sym12091382
APA StyleFaizi, S., Sałabun, W., Rashid, T., Zafar, S., & Wątróbski, J. (2020). Intuitionistic Fuzzy Sets in Multi-Criteria Group Decision Making Problems Using the Characteristic Objects Method. Symmetry, 12(9), 1382. https://doi.org/10.3390/sym12091382







