A Stochastic Modelling Framework for Single Cell Migration: Coupling Contractility and Focal Adhesions
Abstract
1. Introduction
2. The Cell Motility Model
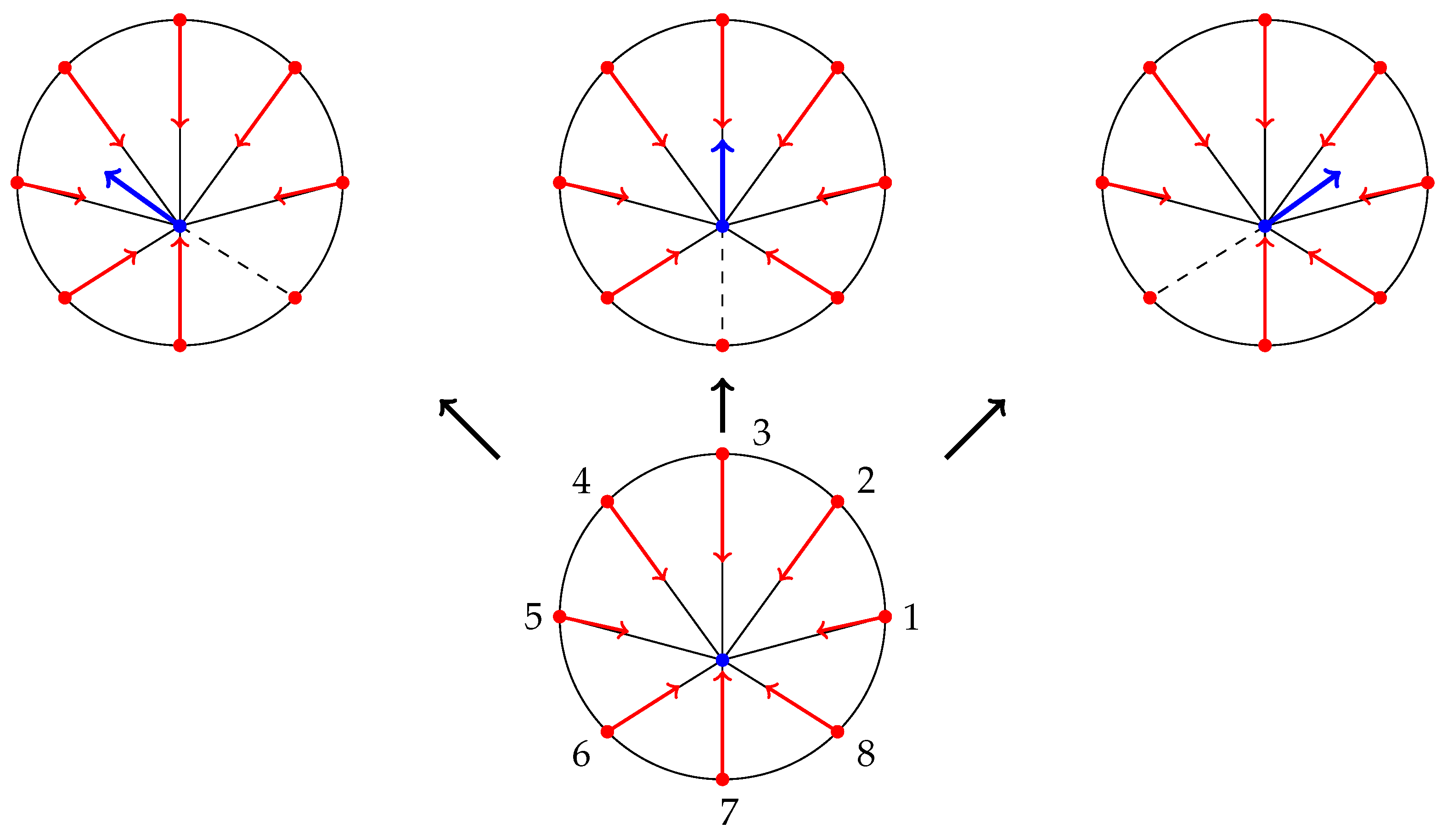
2.1. The Cell Representation
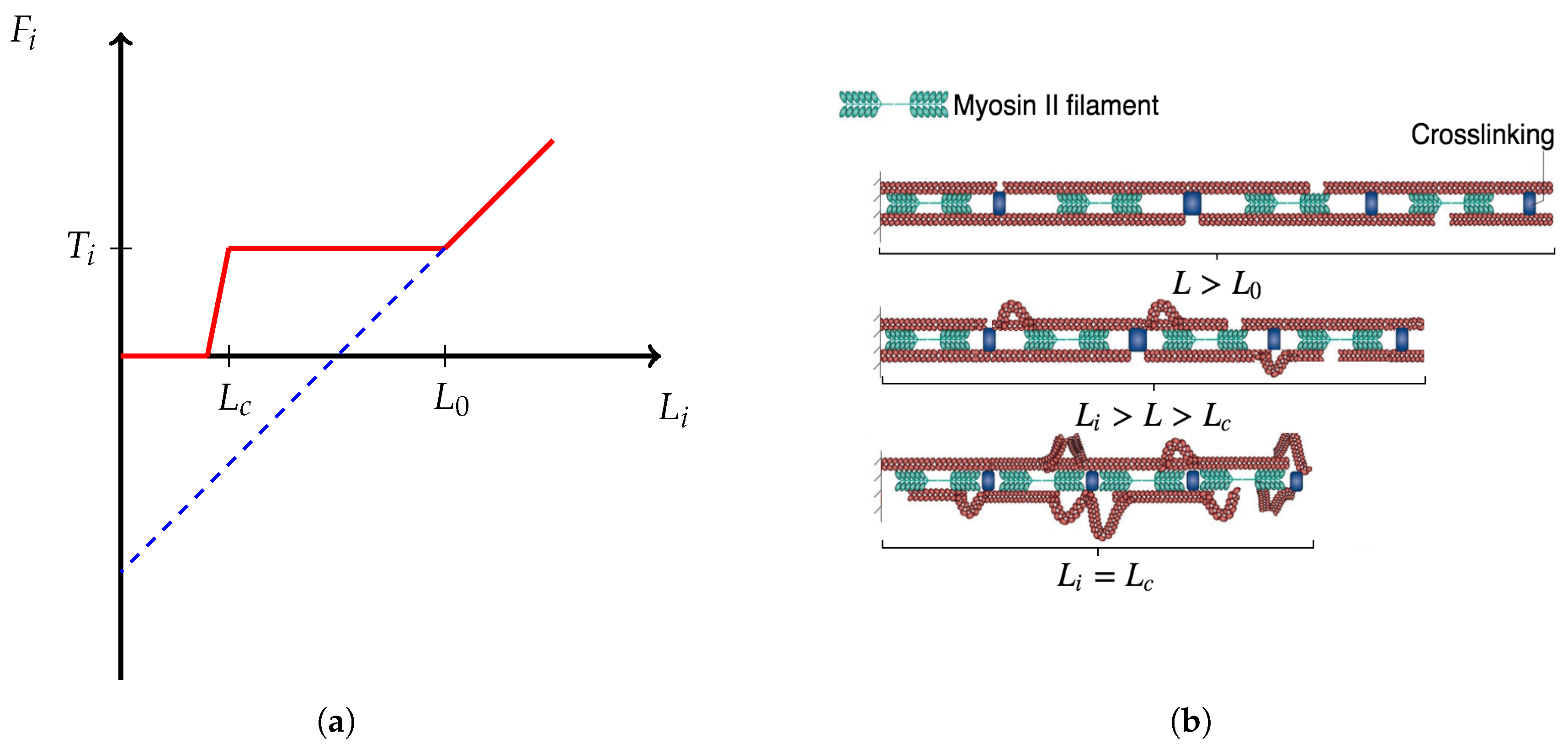
- The traction stresses are largely applied on the cell periphery and their magnitude decays rapidly towards the centre [46,47]. Thus, the cell body SF ends are at or near mechanical equilibrium. Since contractile forces are generated by SFs, then a cell body SF end must be balanced by all other SFs (due to the equilibrium). Hence, it is reasonable to have a single connecting node of radial SFs which is either at mechanical equilibrium (for stationary cells) or tends to it.
- Paul et al. [48] demonstrated that application of force, originating from nuclear region, on FAs by star-like SF arrangement, results in cells acquiring morphologies typical for motile cells. Since the forces applied on FAs by SFs determine which one ruptures, then it also influences the motion of a cell (due to retraction). Since I am primarily interested in cell migration, it is justified to assume that this architecture represents a realistic situation. Furthermore, Oakes et al. [49] found that modelling SFs embedded in contractile networks, where only SFs actively contract, yields a behaviour mimicking their experimental results—the cytoskeletal flow was directed along the stress fibres. In the same study, the authors concluded that it is appropriate to treat an SF as a 1D viscoelastic contractile element, which also justifies neglecting inertia in Equation (2).
- Since motile cells assume a wide variety of cell shapes and continuously remodel their actin cytoskeleton, one can view this representation as a cell shape normalization (it is implicitly assumed that a cell volume remains constant). That is, Figure 1b depicts a cell normalized to a circle. Möhl et al. [46] applied the shape normalization technique to a timelapse series data of migrating keratinocytes and demonstrated that this allows consistent analysis of FA dynamics, actin flow and traction forces. In view of their results, a particular cell traction force map and FA configuration normalized to a circle can be effectively captured by our representation.
2.2. The Cell Migration Cycle
2.2.1. Focal Adhesion Binding
2.2.2. Focal Adhesion Unbinding
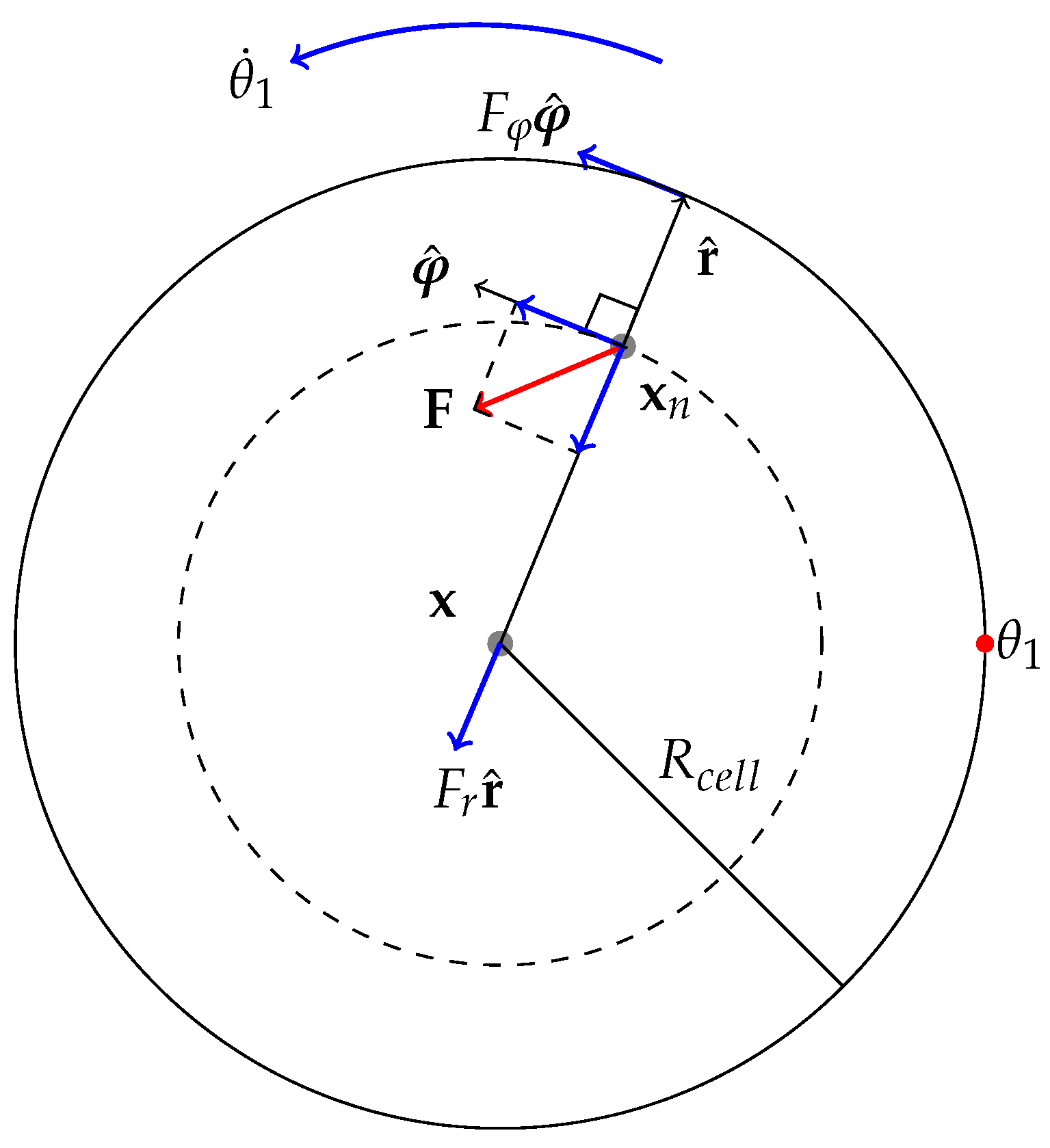
2.3. Specification of Kinematics
- The spatial and cell length scales are defined by cell radii .
- The time scale is set by FA disassociation rate , since FA unbinding of leads to locomotion.
- The force scale is defined by the characteristic force usually observed at an FA.
3. FA Event Model
3.1. Focal Adhesion Events
3.2. Combining the Cell Motility and the FA Event Model
- The time of the FA event is chosen such that .
- The system evolves according to Equation (7) for .
- At time , the index j of the FA event is chosen with probability and jump to new values:where is the standard basis vector. Note that due to Equation (8), we always have , since the probability of (un)binding of (un)bound FA is zero.
- The cycle starts anew with initial time and initial values of other variables at this time: starting at the time of the FA event is chosen such that
- The system evolves according to Equation (7) for and so on.
4. Piecewise Deterministic Process
4.1. PDMP Overview
- I
- Vector fields such that for all there exists a unique global solution to the following equation:Let denote the flow corresponding to Equation (12), i.e.,
- II
- A measurable function such that the function is integrable.
- III
- A transition measure , such that for fixed , is measurable for and is a probability measure for all on .
4.2. Cell Motility and PDMP
- I
- By Proposition 4 we see that for all , there exists a unique global solution to (12).
- II
- Note that in our case the rate function is given by (recalling Section 3.1):Here, I abuse the notation introduced in Section 3.1: for . Thus, for the integrability condition to be satisfied, I assume that each probability rate function is integrable along the solution of Equation (12). An exact form of the rates satisfying this condition will be given in the subsequent section. Note that is nonzero, which follows from Equation (8).
- III
- In our case, the measure is given by (recalling Section 3):where is the Kronecker delta function, is the Dirac measure at , and correspond to, respectively, the binding and unbinding probability rates at FA site j, and is the component of the vector .
- is the probability that the FA event j occurs, given and .
- is the probability of a jump into cell state , given and , and that the FA event j occurred.
5. Adhesion Kinetics
5.1. Unbinding Rate
5.2. Binding Dynamics
5.2.1. Rac Dependence
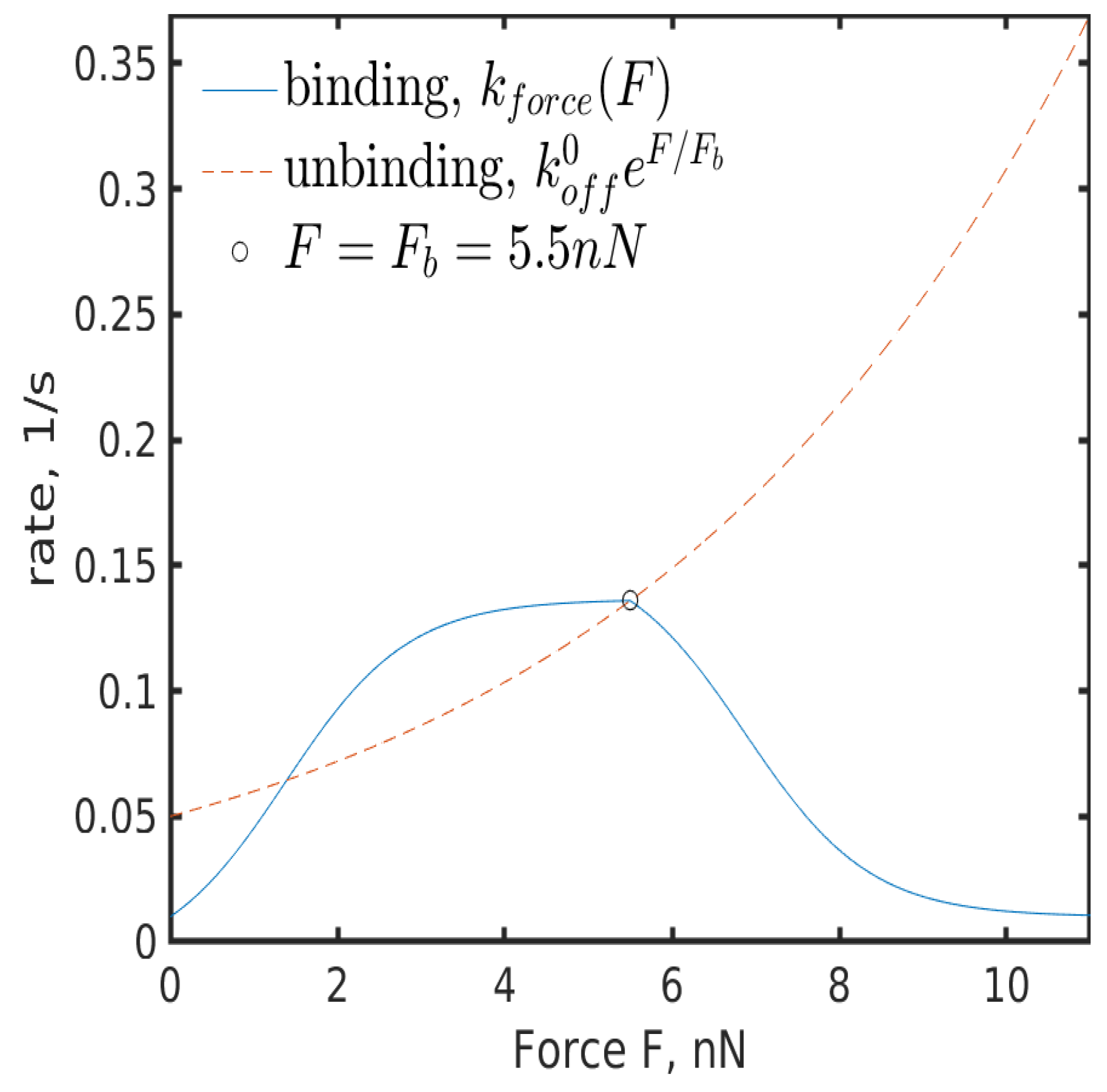
5.2.2. Force Dependence
- , i.e., if there is no force applied, the rate is .
- If the applied force is below the characteristic force , then is greater than the unbinding rate, i.e., it is more likely that an FA increases in size than that it ruptures.
- If the characteristic force is applied, the rate should equal the unbinding rate, i.e., I assume that there is a dynamic equilibrium in some sense.
- If the applied force is larger than , then the unbinding rate dominates the binding rate. Note that as FA increases in size, the force dependence diminishes [59]. Thus, should plateau around . I also assume that for large applied forces plateaus at , since exceeding loads rupture integrin bonds frequently and impede stable maturation.
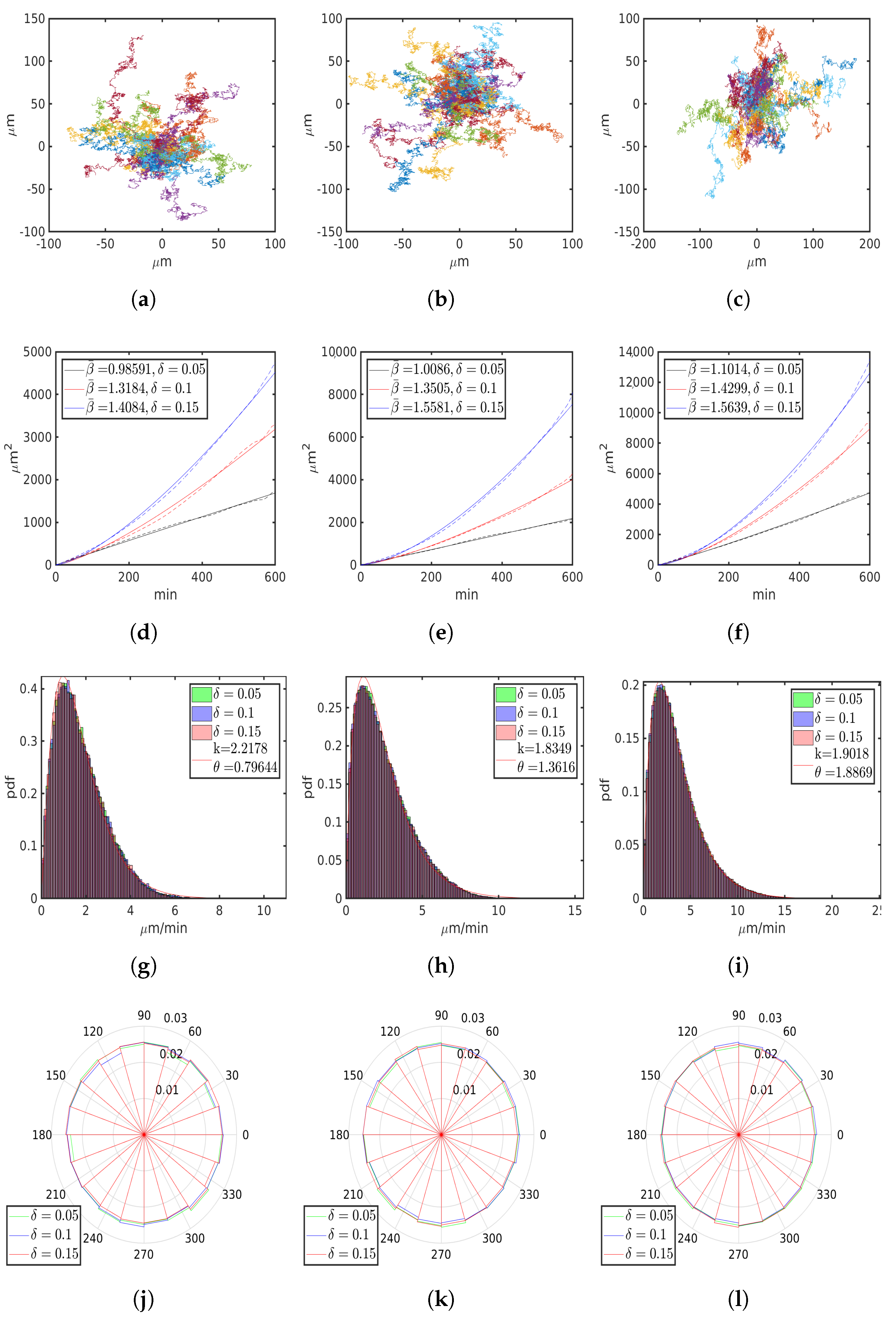
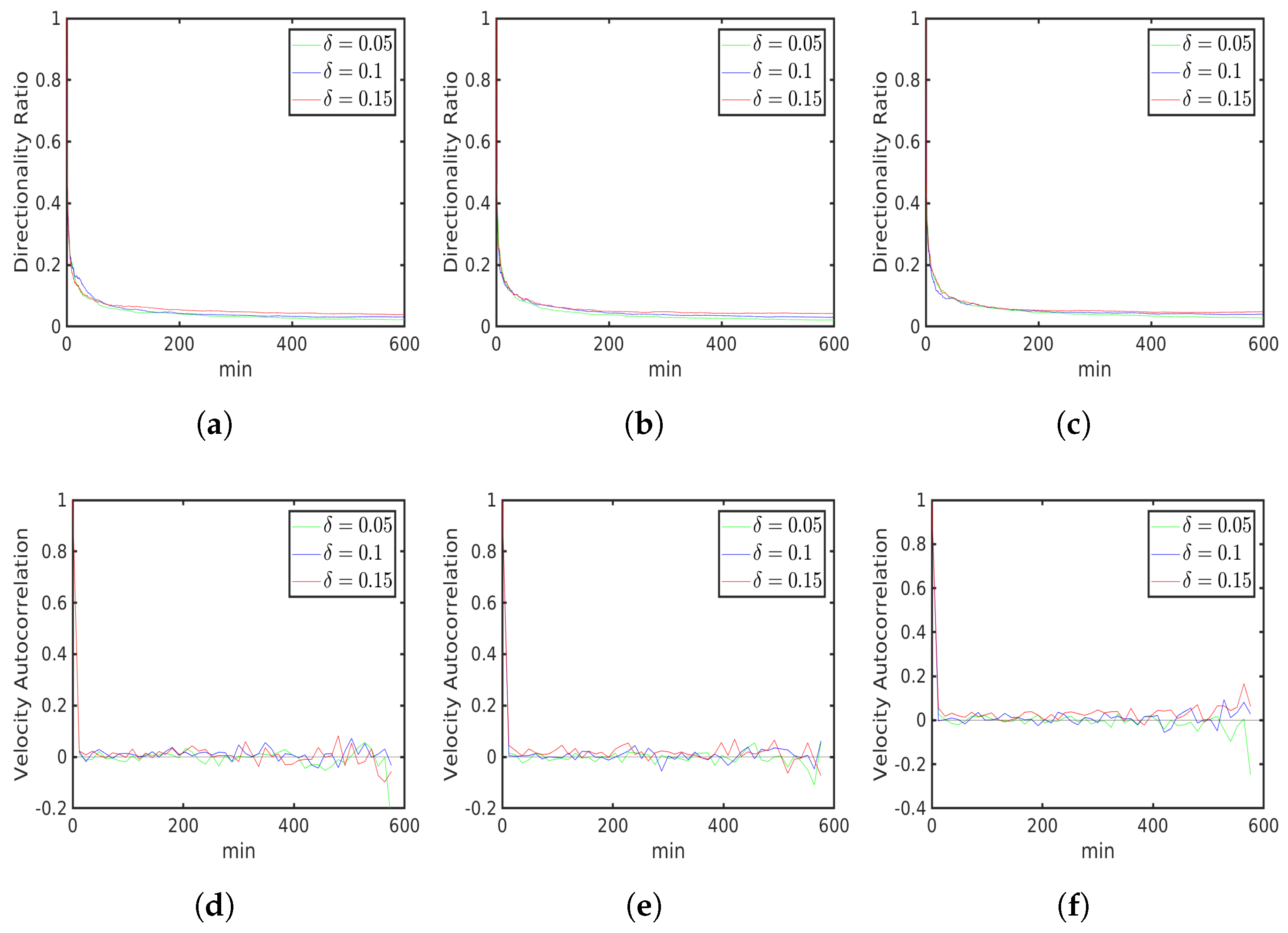
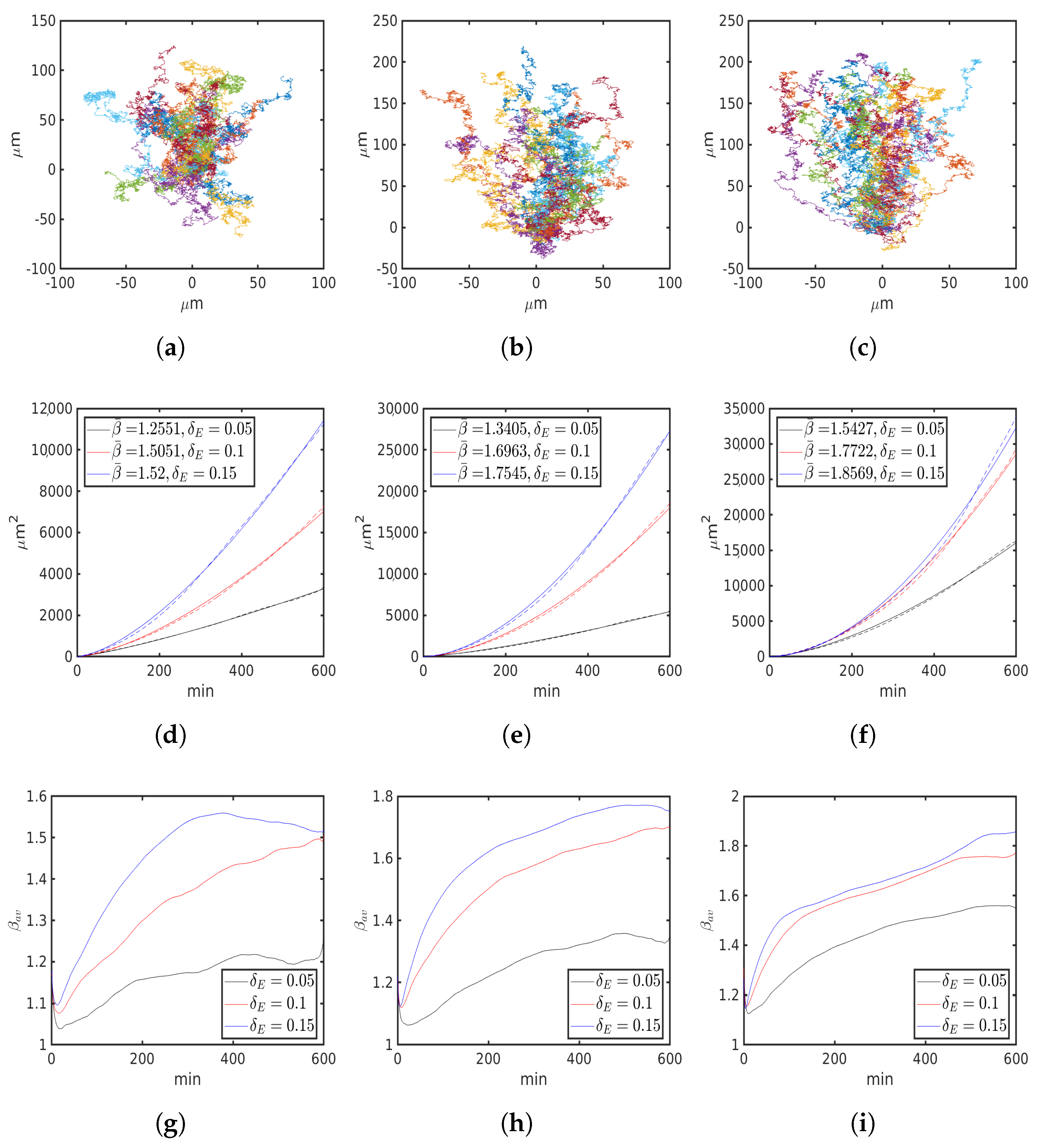
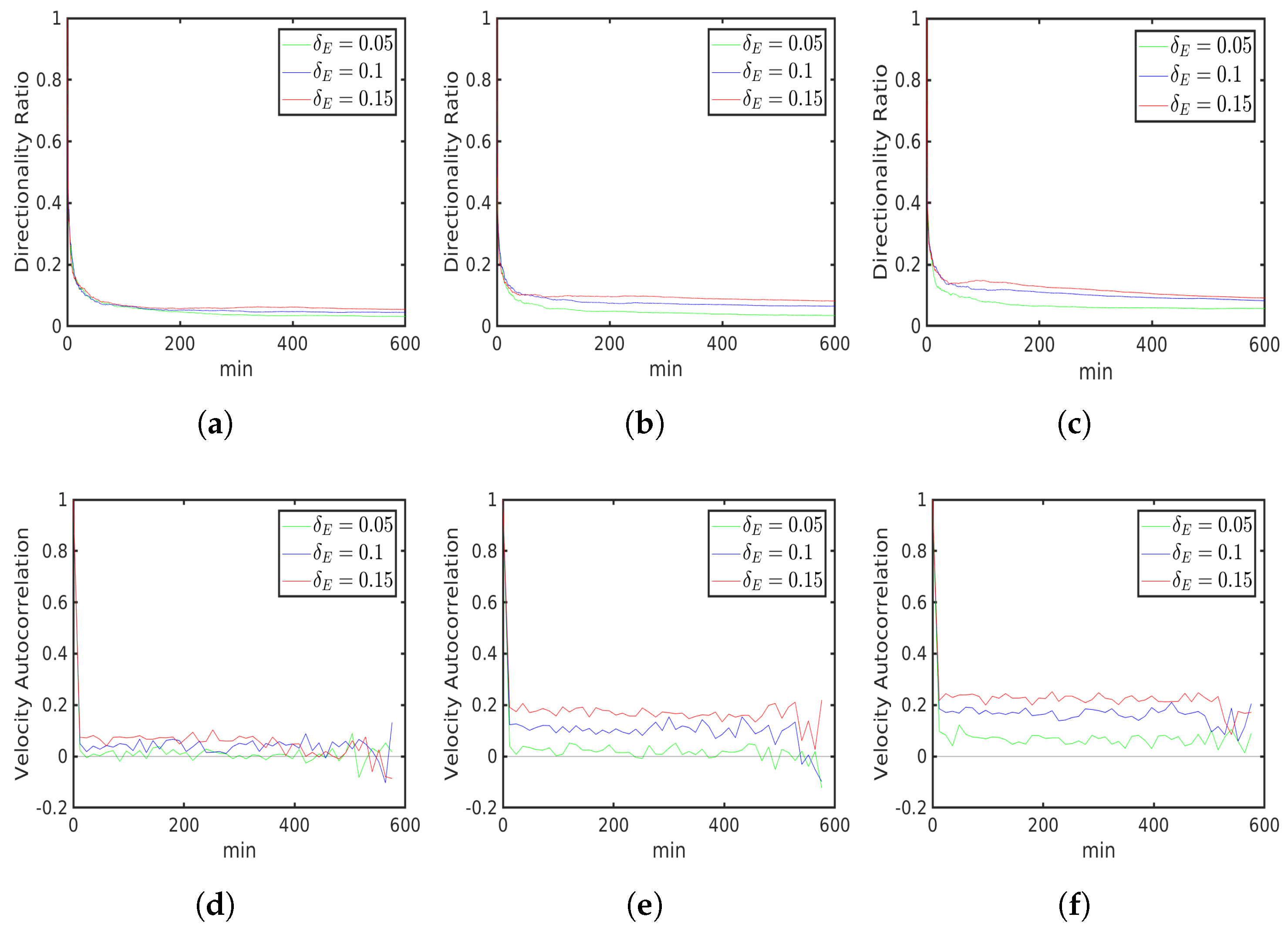
6. Numerical Simulations
- Uniform environment with no cues.
- Non-uniform environment with external cue gradient and uneven myosin motor activity within a cell.
- Striped ECM architecture.
- is at the origin, is uniformly distributed on a circle with radius , and .
- Each FA is in (un)bound state and each cell is in moving state with probability .
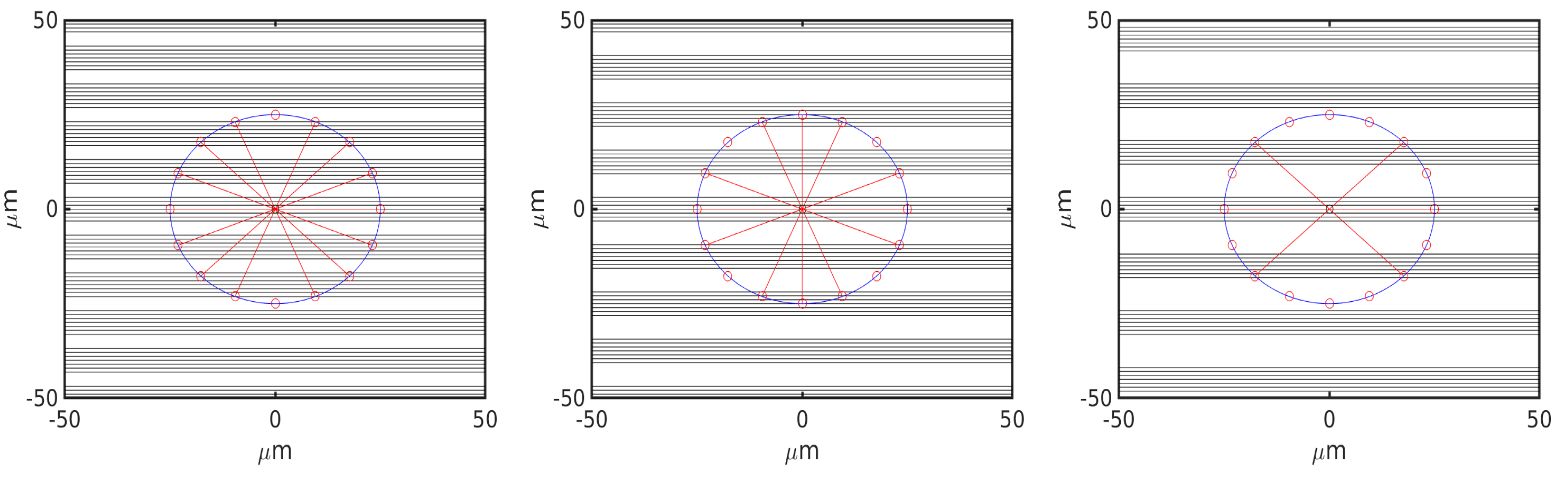
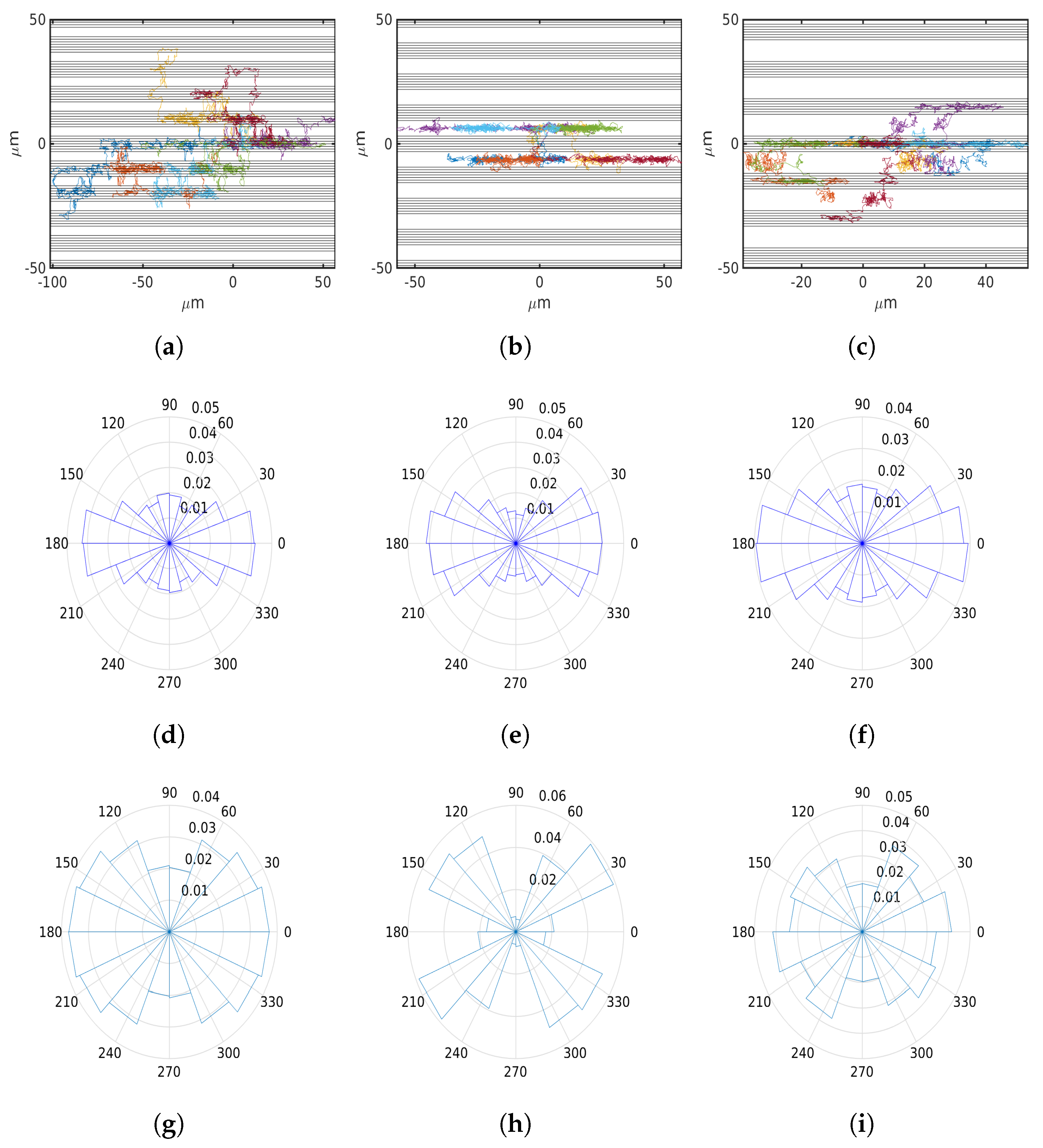
6.1. Uniform Environment
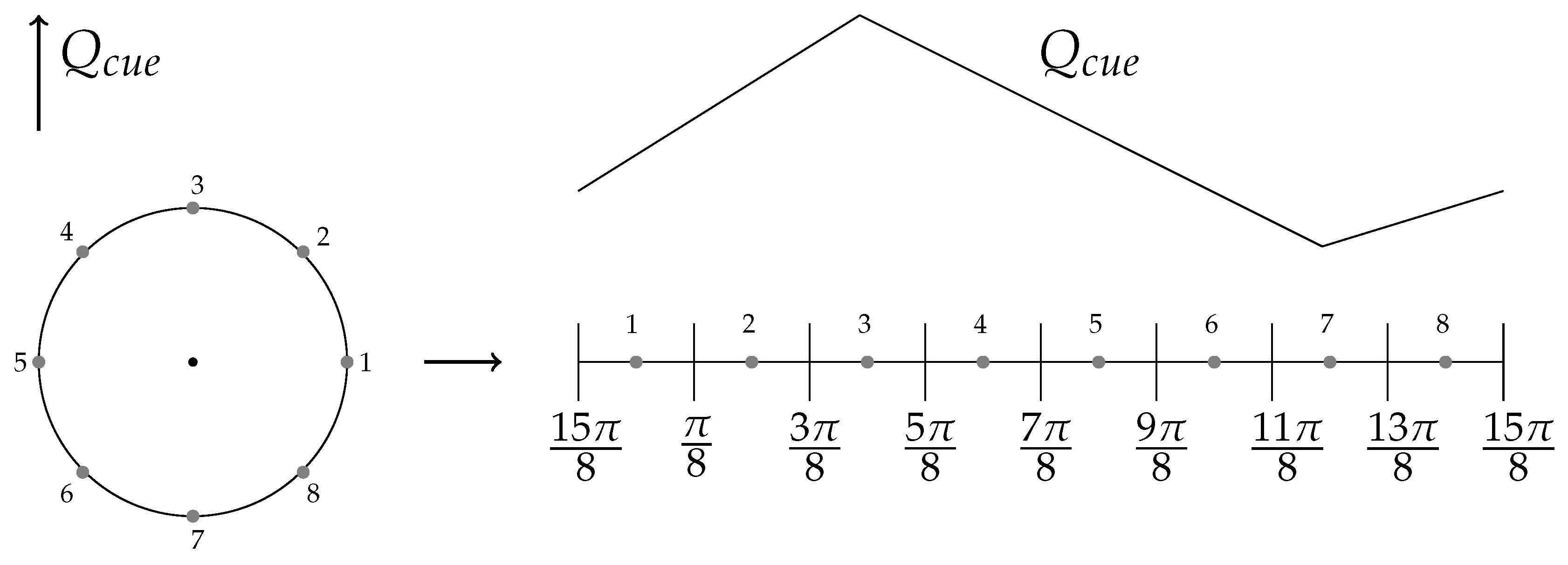
6.2. External Cue Gradient
6.3. Fibrillar Architecture of ECM
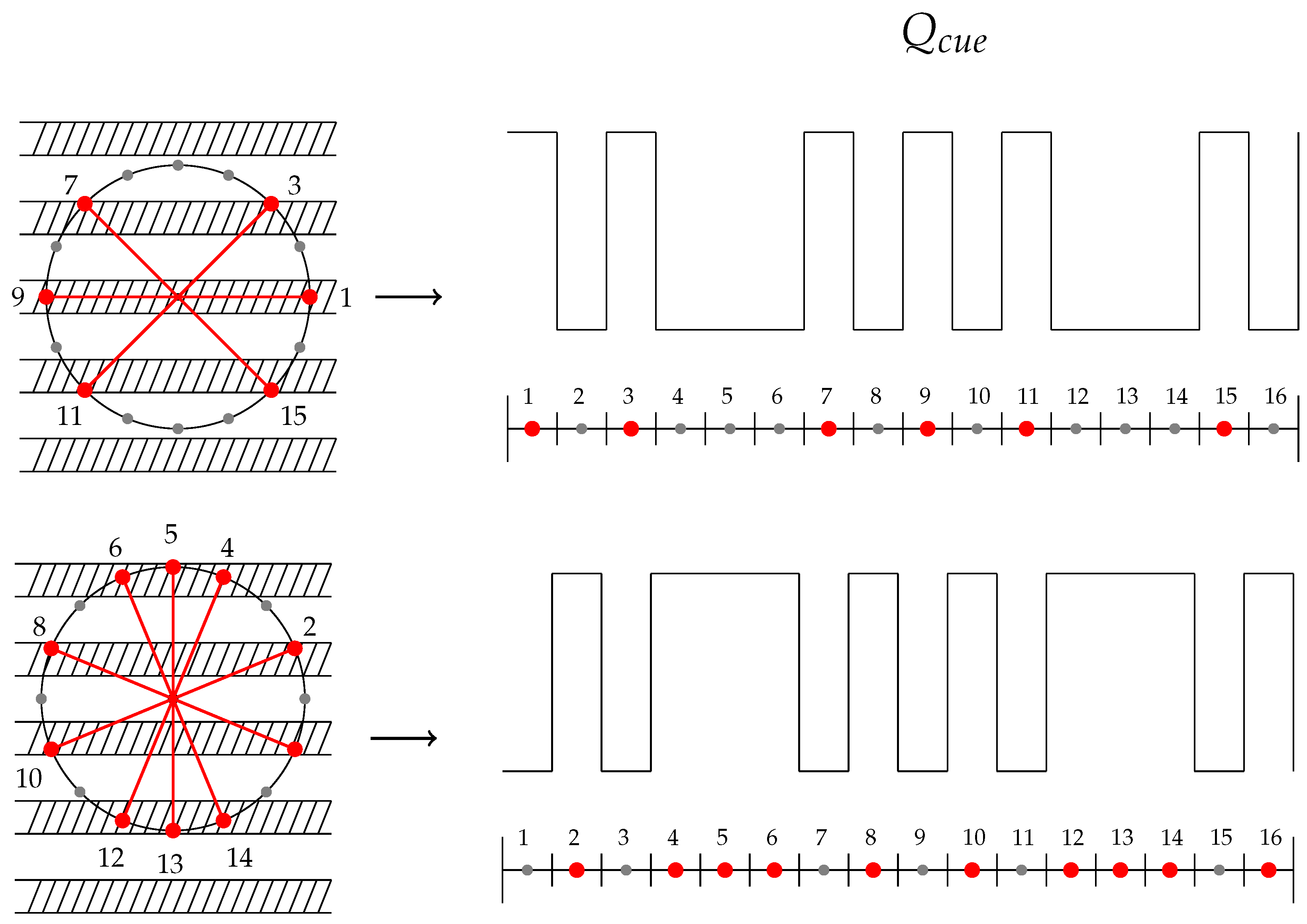
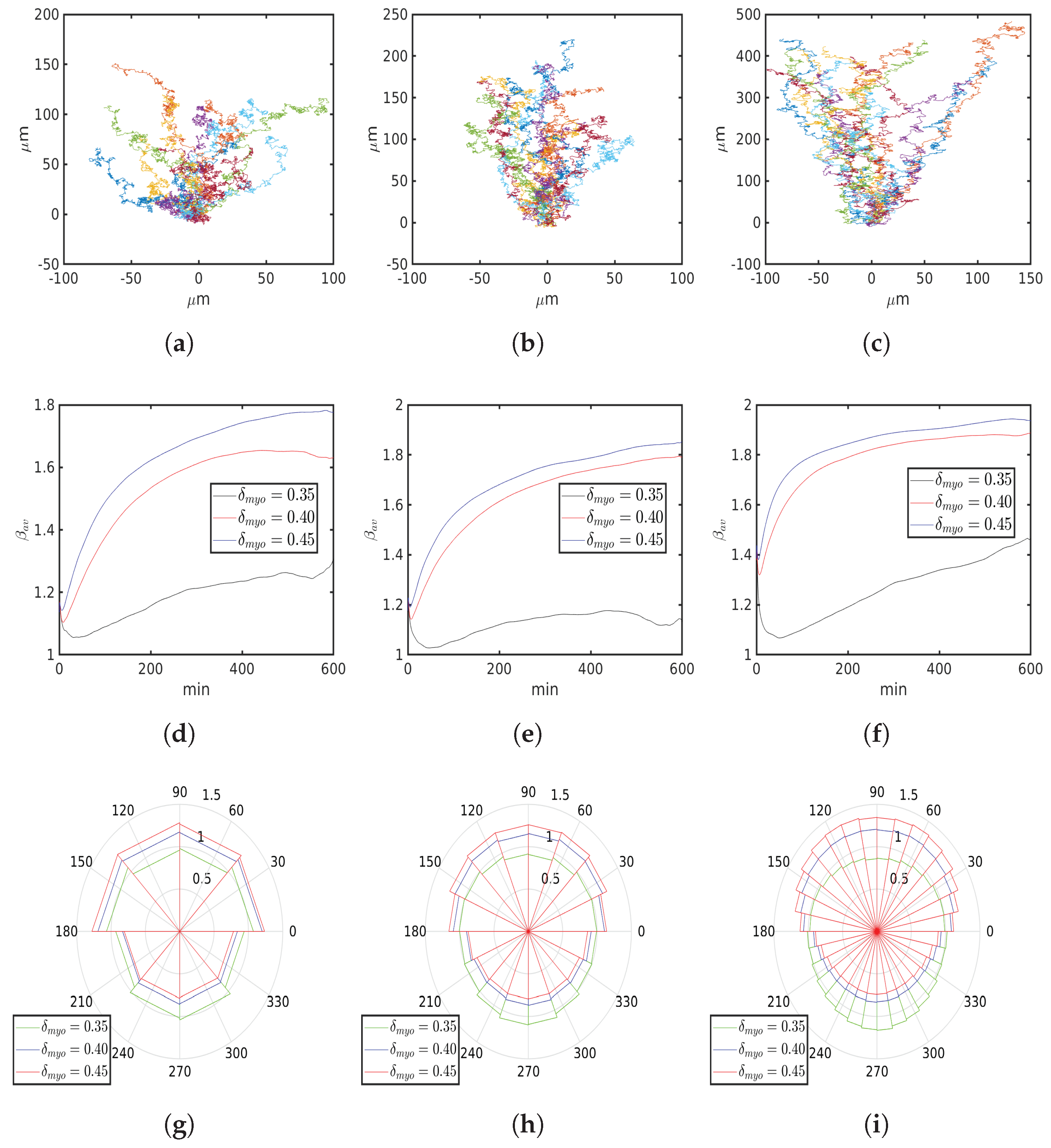
6.4. Asymmetric Contractility
7. Discussion and Outlook
- The migration cycle is reduced to two steps: FA unbinding leads to movement and cytoskeletal reconfiguration, while binding to the latter only (Section 2).
- Cell shape is assumed to be spherical and constant (Section 2.1).
- The number of adhesion sites (occupied and unoccupied) is constant (Section 2.3).
- Adhesion binding and unbinding depend on the force applied by stress fibres and position of the cell, i.e., we omit intracellular biochemical interactions (Section 5).
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| FA | Focal adhesion |
| ECM | Extracellular matrix |
| SF | Stress fibre |
| PDMP | Piecewise deterministic Markov process |
| MSD | Mean-squared displacement |
Appendix A. Equations of Cell Motion
Appendix B. Parameter Assessment
| Parameter | Value | Value | Parameter | Value | Value |
|---|---|---|---|---|---|
| 4 nN | 0.72 | 25 m | 1 | ||
| 15 nN | 2.72 | 27.5 m | 1.1 | ||
| 5.5 nN | 1 | 5 m | 0.2 | ||
| 0.05 s−1 | 1 | 5.68 | |||
| 0.01 s−1 | 0.2 | 0.11 | |||
| 5 m | 0.2 | 1.14 |
Appendix C. Data Analysis
Data Variability
Appendix D. Simulation of the PDMP
| Algorithm A1 Simulation of the PDMP. |
|
Appendix D.1. Simulation of the Next Event Time
- Piecewise constantForward: .Backward:
- Average: .
- Piecewise linear:
| Algorithm A2 Event time computation. |
|
Appendix D.2. Sampling from the Transition Measure
References
- Lauffenburger, D.A.; Horwitz, A.F. Cell migration: A physically integrated molecular process. Cell 1996, 84, 359–369. [Google Scholar] [CrossRef]
- Abercrombie, M. The Croonian Lecture, 1978—The crawling movement of metazoan cells. Proc. R. Soc. Lond. B Biol. Sci. 1980, 207, 129–147. [Google Scholar]
- Raftopoulou, M.; Hall, A. Cell migration: Rho GTPases lead the way. Dev. Biol. 2004, 265, 23–32. [Google Scholar] [CrossRef] [PubMed]
- Ridley, A.J.; Schwartz, M.A.; Burridge, K.; Firtel, R.A.; Ginsberg, M.H.; Borisy, G.; Parsons, J.T.; Horwitz, A.R. Cell migration: Integrating signals from front to back. Science 2003, 302, 1704–1709. [Google Scholar] [CrossRef]
- Holmes, W.R.; Edelstein-Keshet, L. A comparison of computational models for eukaryotic cell shape and motility. PLoS Comput. Biol. 2012, 8, e1002793. [Google Scholar] [CrossRef] [PubMed]
- Ziebert, F.; Aranson, I.S. Computational approaches to substrate-based cell motility. Npj Comput. Mater. 2016, 2, 16019. [Google Scholar] [CrossRef]
- Mogilner, A. Mathematics of cell motility: Have we got its number? J. Math. Biol. 2009, 58, 105. [Google Scholar] [CrossRef]
- Camley, B.A.; Zhao, Y.; Li, B.; Levine, H.; Rappel, W.J. Crawling and turning in a minimal reaction-diffusion cell motility model: Coupling cell shape and biochemistry. Phys. Rev. E 2017, 95, 012401. [Google Scholar] [CrossRef]
- Oelz, D.; Schmeiser, C. How Do Cells Move? Mathematical Modeling of Cytoskeleton Dynamics and Cell Migration. Cell Mechanics: From Single Scale-Based Models to Multiscale Modeling; Chapman and Hall: New York, NY, USA, 2010. [Google Scholar]
- Manhart, A.; Oelz, D.; Schmeiser, C.; Sfakianakis, N. An extended Filament Based Lamellipodium Model produces various moving cell shapes in the presence of chemotactic signals. J. Theor. Biol. 2015, 382, 244–258. [Google Scholar] [CrossRef]
- Preziosi, L.; Vitale, G. A multiphase model of tumor and tissue growth including cell adhesion and plastic reorganization. Math. Model. Methods Appl. Sci. 2011, 21, 1901–1932. [Google Scholar] [CrossRef]
- Rubinstein, B.; Jacobson, K.; Mogilner, A. Multiscale Two-Dimensional Modeling of a Motile Simple-Shaped Cell. Multiscale Model. Simul. 2005, 3, 413–439. [Google Scholar] [CrossRef] [PubMed]
- Shao, D.; Rappel, W.J.; Levine, H. Computational model for cell morphodynamics. Phys. Rev. Lett. 2010, 105, 108104. [Google Scholar] [CrossRef] [PubMed]
- Copos, C.A.; Walcott, S.; del Álamo, J.C.; Bastounis, E.; Mogilner, A.; Guy, R.D. Mechanosensitive Adhesion Explains Stepping Motility in Amoeboid Cells. Biophys. J. 2017, 112, 2672–2682. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Mogilner, A. Comparison of cell migration mechanical strategies in three-dimensional matrices: A computational study. Interface Focus 2016, 6, 20160040. [Google Scholar] [CrossRef]
- Marée, A.F.; Jilkine, A.; Dawes, A.; Grieneisen, V.A.; Edelstein-Keshet, L. Polarization and movement of keratocytes: A multiscale modelling approach. Bull. Math. Biol. 2006, 68, 1169–1211. [Google Scholar] [CrossRef]
- Marée, A.F.M.; Grieneisen, V.A.; Edelstein-Keshet, L. How Cells Integrate Complex Stimuli: The Effect of Feedback from Phosphoinositides and Cell Shape on Cell Polarization and Motility. PLoS Comput. Biol. 2012, 8, 1–20. [Google Scholar] [CrossRef]
- Arrieumerlou, C.; Meyer, T. A local coupling model and compass parameter for eukaryotic chemotaxis. Dev. Cell 2005, 8, 215–227. [Google Scholar] [CrossRef]
- Dickinson, R.B.; Tranquillo, R.T. A stochastic model for adhesion-mediated cell random motility and haptotaxis. J. Math. Biol. 1993, 31, 563–600. [Google Scholar] [CrossRef]
- Groh, A.; Louis, A.K. Stochastic modelling of biased cell migration and collagen matrix modification. J. Math. Biol. 2010, 61, 617–647. [Google Scholar] [CrossRef]
- Satulovsky, J.; Lui, R.; Wang, Y.l. Exploring the control circuit of cell migration by mathematical modeling. Biophys. J. 2008, 94, 3671–3683. [Google Scholar] [CrossRef]
- Tranquillo, R.T.; Lauffenburger, D.A.; Zigmond, S. A stochastic model for leukocyte random motility and chemotaxis based on receptor binding fluctuations. J. Cell Biol. 1988, 106, 303–309. [Google Scholar] [CrossRef] [PubMed]
- Dieterich, P.; Klages, R.; Preuss, R.; Schwab, A. Anomalous dynamics of cell migration. Proc. Natl. Acad. Sci. USA 2008, 105, 459–463. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Nørrelykke, S.F.; Cox, E.C. Persistent Cell Motion in the Absence of External Signals: A Search Strategy for Eukaryotic Cells. PLoS ONE 2008, 3, e2093. [Google Scholar] [CrossRef] [PubMed]
- Selmeczi, D.; Mosler, S.; Hagedorn, P.H.; Larsen, N.B.; Flyvbjerg, H. Cell Motility as Persistent Random Motion: Theories from Experiments. Biophys. J. 2005, 89, 912–931. [Google Scholar] [CrossRef] [PubMed]
- Othmer, H.G.; Dunbar, S.R.; Alt, W. Models of dispersal in biological systems. J. Math. Biol. 1988, 26, 263–298. [Google Scholar] [CrossRef]
- Engwer, C.; Hillen, T.; Knappitsch, M.; Surulescu, C. Glioma follow white matter tracts: A multiscale DTI-based model. J. Math. Biol. 2015, 71, 551–582. [Google Scholar] [CrossRef]
- Kelkel, J.; Surulescu, C. A multiscale approach to cell migration in tissue networks. Math. Model. Methods Appl. Sci. 2012, 22, 1150017. [Google Scholar] [CrossRef]
- Davis, M.H. Piecewise-deterministic Markov processes: A general class of non-diffusion stochastic models. J. R. Stat. Soc. Ser. B Methodol. 1984, 46, 353–388. [Google Scholar] [CrossRef]
- Davis, M.H.A. Markov Models and Optimization; Chapman and Hall: New York, NY, USA, 1993. [Google Scholar]
- Liu, Y.J.; Le Berre, M.; Lautenschlaeger, F.; Maiuri, P.; Callan-Jones, A.; Heuzé, M.; Takaki, T.; Voituriez, R.; Piel, M. Confinement and low adhesion induce fast amoeboid migration of slow mesenchymal cells. Cell 2015, 160, 659–672. [Google Scholar] [CrossRef]
- Ramirez-San Juan, G.R.; Oakes, P.W.; Gardel, M.L. Contact guidance requires spatial control of leading-edge protrusion. Mol. Biol. Cell 2017, 28, 1043–1053. [Google Scholar] [CrossRef]
- Verkhovsky, A.B.; Svitkina, T.M.; Borisy, G.G. Self-polarization and directional motility of cytoplasm. Curr. Biol. 1999, 9, 11-S1. [Google Scholar] [CrossRef]
- Yam, P.T.; Wilson, C.A.; Ji, L.; Hebert, B.; Barnhart, E.L.; Dye, N.A.; Wiseman, P.W.; Danuser, G.; Theriot, J.A. Actin–myosin network reorganization breaks symmetry at the cell rear to spontaneously initiate polarized cell motility. J. Cell Biol. 2007, 178, 1207–1221. [Google Scholar] [CrossRef] [PubMed]
- Uatay, A. A mathematical model of contact inhibition of locomotion: Coupling contractility and focal adhesions. arXiv 2019, arXiv:1901.02386. [Google Scholar]
- Uatay, A. Multiscale Mathematical Modeling of Cell Migration: From Single Cells to Populations. Ph.D. Thesis, Technische Universität Kaiserslautern, Kaiserslautern, Germany, 2019. [Google Scholar]
- Bellomo, N.; Knopoff, D.; Soler, J. On the difficult interplay between life, ”complexity”, and mathematical sciences. Math. Model. Methods Appl. Sci. 2013, 23, 1861–1913. [Google Scholar] [CrossRef]
- Knopoff, D.A.; Nieto, J.; Urrutia, L. Numerical simulation of a multiscale cell motility model based on the kinetic theory of active particles. Symmetry 2019, 11, 1003. [Google Scholar] [CrossRef]
- Gardel, M.L.; Schneider, I.C.; Aratyn-Schaus, Y.; Waterman, C.M. Mechanical integration of actin and adhesion dynamics in cell migration. Annu. Rev. Cell Dev. Biol. 2010, 26, 315–333. [Google Scholar] [CrossRef]
- Murrell, M.; Oakes, P.W.; Lenz, M.; Gardel, M.L. Forcing cells into shape: The mechanics of actomyosin contractility. Nat. Rev. Mol. Cell Biol. 2015, 16, 486–498. [Google Scholar] [CrossRef]
- Guthardt Torres, P.; Bischofs, I.B.; Schwarz, U.S. Contractile network models for adherent cells. Phys. Rev. Lett. E 2012, 85, 011913. [Google Scholar] [CrossRef]
- Kassianidou, E.; Brand, A.C.; Schwarz, U.S.; Kumar, S. Geometry and network connectivity govern the mechanics of stress fibers. Proc. Natl. Acad. Sci. USA 2017, 114, 2622–2627. [Google Scholar] [CrossRef]
- Kumar, S.; Maxwell, I.Z.; Heisterkamp, A.; Polte, T.R.; Lele, T.P.; Salanga, M.; Mazur, E.; Ingber, D.E. Viscoelastic Retraction of Single Living Stress Fibers and Its Impact on Cell Shape, Cytoskeletal Organization, and Extracellular Matrix Mechanics. Biophys. J. 2006, 90, 3762–3773. [Google Scholar] [CrossRef]
- Russell, R.J.; Xia, S.L.; Dickinson, R.B.; Lele, T.P. Sarcomere mechanics in capillary endothelial cells. Biophys. J. 2009, 97, 1578–1585. [Google Scholar] [CrossRef] [PubMed]
- Deguchi, S.; Ohashi, T.; Sato, M. Tensile properties of single stress fiber isolated from cultured vascular smooth muscle cells. J. Biomech. 2006, 39, 2603–2610. [Google Scholar] [CrossRef] [PubMed]
- Möhl, C.; Kirchgessner, N.; Schäfer, C.; Hoffmann, B.; Merkel, R. Quantitative mapping of averaged focal adhesion dynamics in migrating cells by shape normalization. J. Cell Sci. 2012, 125, 155–165. [Google Scholar] [CrossRef] [PubMed]
- Schwarz, U.S.; Gardel, M.L. United we stand integrating the actin cytoskeleton and cell matrix adhesions in cellular mechanotransduction. J. Cell Sci. 2012, 125, 3051–3060. [Google Scholar] [CrossRef] [PubMed]
- Paul, R.; Heil, P.; Spatz, J.P.; Schwarz, U.S. Propagation of mechanical stress through the actin cytoskeleton toward focal adhesions: Model and experiment. Biophys. J. 2008, 94, 1470–1482. [Google Scholar] [CrossRef]
- Oakes, P.W.; Wagner, E.; Brand, C.A.; Probst, D.; Linke, M.; Schwarz, U.S.; Glotzer, M.; Gardel, M.L. Optogenetic Control of RhoA Reveals Zyxin-mediated Elasticity of Stress Fibers. Nat. Commun. 2017, 8, 15817. [Google Scholar] [CrossRef]
- Gillespie, D.T. A rigorous derivation of the chemical master Equation. Phys. A Stat. Mech. Its Appl. 1992, 188, 404–425. [Google Scholar] [CrossRef]
- Ananthakrishnan, R.; Ehrlicher, A. The Forces Behind Cell Movement. Int. J. Biol. Sci. 2007, 3, 303–317. [Google Scholar] [CrossRef]
- Cramer, L.P. Forming the cell rear first: Breaking cell symmetry to trigger directed cell migration. Nat. Cell Biol. 2010, 12, 628–632. [Google Scholar] [CrossRef]
- Bell, G.I. Models for the specific adhesion of cells to cells. Science 1978, 200, 618–627. [Google Scholar] [CrossRef]
- Ridley, A.J. Rho GTPases and cell migration. J. Cell Sci. 2001, 114, 2713–2722. [Google Scholar] [PubMed]
- Giverso, C.; Preziosi, L. Mechanical perspective on chemotaxis. Phys. Rev. E 2018, 98, 062402. [Google Scholar] [CrossRef]
- Holmes, W.R.; Lin, B.; Levchenko, A.; Edelstein-Keshet, L. Modelling cell polarization driven by synthetic spatially graded Rac activation. PLoS Comput. Biol. 2012, 8, e1002366. [Google Scholar] [CrossRef] [PubMed]
- Narang, A. Spontaneous polarization in eukaryotic gradient sensing: A mathematical model based on mutual inhibition of frontness and backness pathways. J. Theor. Biol. 2006, 240, 538–553. [Google Scholar] [CrossRef]
- Choi, C.K.; Vicente-Manzanares, M.; Zareno, J.; Whitmore, L.A.; Mogilner, A.; Horwitz, A.R. Actin and α-actinin orchestrate the assembly and maturation of nascent adhesions in a myosin II motor-independent manner. Nat. Cell Biol. 2008, 10, 1039–1050. [Google Scholar] [CrossRef]
- Stricker, J.; Aratyn-Schaus, Y.; Oakes, P.W.; Gardel, M.L. Spatiotemporal constraints on the force-dependent growth of focal adhesions. Biophys. J. 2011, 100, 2883–2893. [Google Scholar] [CrossRef]
- Zaidel-Bar, R.; Cohen, M.; Addadi, L.; Geiger, B. Hierarchical assembly of cell–matrix adhesion complexes. Biochem. Soc. Trans. 2004, 32, 416–420. [Google Scholar] [CrossRef]
- Balaban, N.Q.; Schwarz, U.S.; Riveline, D.; Goichberg, P.; Tzur, G.; Sabanay, I.; Mahalu, D.; Safran, S.; Bershadsky, A.; Addadi, L.; et al. Force and focal adhesion assembly: A close relationship studied using elastic micropatterned substrates. Nat. Cell Biol. 2001, 3, 466–472. [Google Scholar] [CrossRef]
- Soiné, J.R.D.; Brand, C.A.; Stricker, J.; Oakes, P.W.; Gardel, M.L.; Schwarz, U.S. Model-based Traction Force Microscopy Reveals Differential Tension in Cellular Actin Bundles. PLoS Comput. Biol. 2015, 11, e1004076. [Google Scholar] [CrossRef]
- Alexandrova, A.Y.; Arnold, K.; Schaub, S.; Vasiliev, J.M.; Meister, J.J.; Bershadsky, A.D.; Verkhovsky, A.B. Comparative dynamics of retrograde actin flow and focal adhesions: formation of nascent adhesions triggers transition from fast to slow flow. PLoS ONE 2008, 3, e3234. [Google Scholar] [CrossRef]
- Vicente-Manzanares, M.; Zareno, J.; Whitmore, L.; Choi, C.K.; Horwitz, A.F. Regulation of protrusion, adhesion dynamics, and polarity by myosins IIA and IIB in migrating cells. J. Cell Biol. 2007, 176, 573–580. [Google Scholar] [CrossRef] [PubMed]
- Chan, C.E.; Odde, D.J. Traction Dynamics of Filopodia on Compliant Substrates. Science 2008, 322, 1687–1691. [Google Scholar] [CrossRef] [PubMed]
- Paňková, K.; Rösel, D.; Novotnỳ, M.; Brábek, J. The molecular mechanisms of transition between mesenchymal and amoeboid invasiveness in tumor cells. Cell. Mol. Life Sci. 2010, 67, 63–71. [Google Scholar] [CrossRef] [PubMed]
- Friedl, P.; Noble, P.; Shields, E.; Zänker, K. Locomotor phenotypes of unstimulated CD45RAhigh and CD45ROhigh CD4+ and CD8+ lymphocytes in three-dimensional collagen lattices. Immunology 1994, 82, 617. [Google Scholar]
- Gorelik, R.; Gautreau, A. Quantitative and unbiased analysis of directional persistence in cell migration. Nat. Protoc. 2014, 9, 1931. [Google Scholar] [CrossRef]
- Petrie, R.J.; Doyle, A.D.; Yamada, K.M. Random versus directionally persistent cell migration. Nat. Rev. Mol. Cell Biol. 2009, 10, 538–549. [Google Scholar] [CrossRef]
- Kubow, K.E.; Shuklis, V.D.; Sales, D.J.; Horwitz, A.R. Contact guidance persists under myosin inhibition due to the local alignment of adhesions and individual protrusions. Sci. Rep. 2017, 7, 14380. [Google Scholar] [CrossRef]
- Shellard, A.; Szabó, A.; Trepat, X.; Mayor, R. Supracellular contraction at the rear of neural crest cell groups drives collective chemotaxis. Science 2018, 362, 339–343. [Google Scholar] [CrossRef]
- Fletcher, A.; Osterfield, M.; Baker, R.; Shvartsman, S. Vertex Models of Epithelial Morphogenesis. Biophys. J. 2014, 106, 2291–2304. [Google Scholar] [CrossRef]
- Mori, Y.; Jilkine, A.; Edelstein-Keshet, L. Wave-pinning and cell polarity from a bistable reaction-diffusion system. Biophys. J. 2008, 94, 3684–3697. [Google Scholar] [CrossRef]
- Roycroft, A.; Mayor, R. Molecular basis of contact inhibition of locomotion. Cell. Mol. Life Sci. 2016, 73, 1119–1130. [Google Scholar] [CrossRef] [PubMed]
- Svitkina, T.M.; Surguchova, I.G.; Verkhovsky, A.B.; Gelfand, V.I.; Moeremans, M.; De Mey, J. Direct visualization of bipolar myosin filaments in stress fibers of cultured fibroblasts. Cell Motil. Cytoskelet. 1989, 12, 150–156. [Google Scholar] [CrossRef] [PubMed]
- Aratyn-Schaus, Y.; Oakes, P.W.; Gardel, M.L. Dynamic and structural signatures of lamellar actomyosin force generation. Mol. Biol. Cell 2011, 22, 1330–1339. [Google Scholar] [CrossRef] [PubMed]
- Verkhovsky, A.B.; Borisy, G.G. Non-sarcomeric mode of myosin II organization in the fibroblast lamellum. J. Cell Biol. 1993, 123, 637–652. [Google Scholar] [CrossRef] [PubMed]
- Finer, J.T.; Simmons, R.M.; Spudich, J.A. Single myosin molecule mechanics: Piconewton forces and nanometre steps. Nature 1994, 368, 113–119. [Google Scholar] [CrossRef]
- Molloy, J.E.; Burns, J.E.; Kendrick-Jones, J.; Tregear, R.T.; White, D.C. Movement and force produced by a single myosin head. Nature 1995, 378, 209–212. [Google Scholar] [CrossRef]
- Gardel, M.L.; Valentine, M.T.; Crocker, J.C.; Bausch, A.R.; Weitz, D.A. Microrheology of Entangled F-Actin Solutions. Phys. Rev. Lett. 2003, 91, 158302. [Google Scholar] [CrossRef]
- Kalwarczyk, T.; Ziȩbacz, N.; Bielejewska, A.; Zaboklicka, E.; Koynov, K.; Szymański, J.; Wilk, A.; Patkowski, A.; Gapiński, J.; Butt, H.J.; et al. Comparative analysis of viscosity of complex liquids and cytoplasm of mammalian cells at the nanoscale. Nano Lett. 2011, 11, 2157–2163. [Google Scholar] [CrossRef]
- Mastro, A.M.; Babich, M.A.; Taylor, W.D.; Keith, A.D. Diffusion of a small molecule in the cytoplasm of mammalian cells. Proc. Natl. Acad. Sci. USA 1984, 81, 3414–3418. [Google Scholar] [CrossRef]
- Arcizet, D.; Meier, B.; Sackmann, E.; Rädler, J.O.; Heinrich, D. Temporal Analysis of Active and Passive Transport in Living Cells. Phys. Rev. Lett. 2008, 101, 248103. [Google Scholar] [CrossRef]
- Lammerding, J. Mechanics of the Nucleus. In Comprehensive Physiology; American Cancer Society: Atlanta, GA, USA, 2011; pp. 783–807. [Google Scholar]
- Burridge, K.; Chrzanowska-Wodnicka, M. Focal adhesions, contractility, and signaling. Annu. Rev. Cell Dev. Biol. 1996, 12, 463–519. [Google Scholar] [CrossRef]
- Geiger, B.; Spatz, J.P.; Bershadsky, A.D. Environmental sensing through focal adhesions. Nat. Rev. Mol. Cell Biol. 2009, 10, 21. [Google Scholar] [CrossRef]
- Erdmann, T.; Schwarz, U.S. Stability of Adhesion Clusters under Constant Force. Phys. Rev. Lett. 2004, 92, 108102. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Redick, S.D.; Erickson, H.P.; Moy, V.T. Force measurements of the α5β1 integrin–fibronectin interaction. Biophys. J. 2003, 84, 1252–1262. [Google Scholar] [CrossRef]
- Kassianidou, E.; Kumar, S. A biomechanical perspective on stress fiber structure and function. Biochim. Biophys. Acta BBA Mol. Cell Res. 2015, 1853, 3065–3074. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.T. Mechanism of retraction of the trailing edge during fibroblast movement. J. Cell Biol. 1981, 90, 187–200. [Google Scholar] [CrossRef] [PubMed]
- Hotulainen, P.; Lappalainen, P. Stress fibers are generated by two distinct actin assembly mechanisms in motile cells. J. Cell Biol. 2006, 173, 383–394. [Google Scholar] [CrossRef]
- Kuragano, M.; Uyeda, T.Q.; Kamijo, K.; Murakami, Y.; Takahashi, M. Different contributions of nonmuscle myosin IIA and IIB to the organization of stress fiber subtypes in fibroblasts. Mol. Biol. Cell 2018, 29, 911–922. [Google Scholar] [CrossRef]
- Lewis, P.A.; Shedler, G.S. Simulation of nonhomogeneous Poisson processes by thinning. Nav. Res. Logist. 1979, 26, 403–413. [Google Scholar] [CrossRef]
- Bouchard-Côté, A.; Vollmer, S.J.; Doucet, A. The bouncy particle sampler: A non-reversible rejection-free Markov chain Monte Carlo method. arXiv 2015, arXiv:1510.02451. [Google Scholar] [CrossRef]
- Vose, M.D. A linear algorithm for generating random numbers with a given distribution. IEEE Trans. Softw. Eng. 1991, 17, 972–975. [Google Scholar] [CrossRef][Green Version]


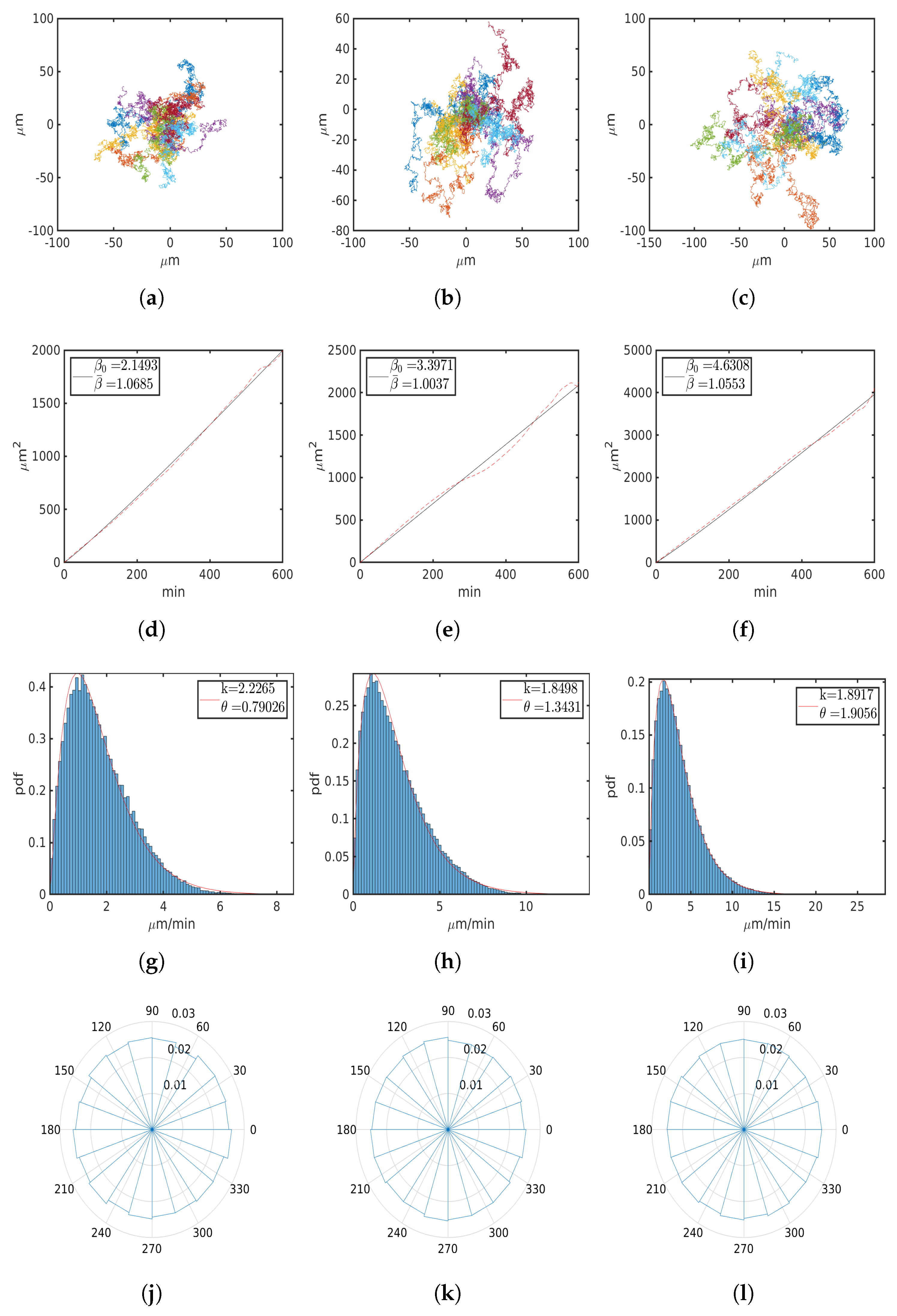





| M | 8 | 16 | 32 |
|---|---|---|---|
| , m/min | 1.7595 | 2.4845 | 3.6047 |
| , m/min | 1.4557 | 2.217 | 3.1787 |
| , 1 | 1.0683 | 1.0035 | 1.0552 |
| , m2/ | 2.1493 | 3.3971 | 4.6308 |
| , 1 | 0.0483 | 0.0408 | 0.0497 |
| M | 8 | 16 | 32 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.05 | 0.1 | 0.15 | 0.05 | 0.1 | 0.15 | 0.05 | 0.1 | 0.15 | |
| , 1 | 0.9859 | 1.3184 | 1.4084 | 1.0086 | 1.3505 | 1.5581 | 1.1014 | 1.4299 | 1.5639 |
| , m/min | 1.7656 | 1.7768 | 1.7557 | 2.4918 | 2.5009 | 2.5021 | 3.5818 | 3.5735 | 3.6104 |
| , m/min | 1.3964 | 1.4319 | 1.472 | 2.24 | 2.2322 | 2.2355 | 3.2136 | 3.1108 | 3.0269 |
| , m2/ | 3.0846 | 0.6934 | 0.5534 | 3.4517 | 0.7103 | 0.3543 | 4.1257 | 0.9536 | 0.5716 |
| , 1 | 0.0452 | 0.0519 | 0.0597 | 0.0440 | 0.0513 | 0.0587 | 0.0522 | 0.05 | 0.0623 |
| M | 8 | 16 | 32 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.05 | 0.1 | 0.15 | 0.05 | 0.1 | 0.15 | 0.05 | 0.1 | 0.15 | |
| , 1 | 1.2551 | 1.5051 | 1.52 | 1.3405 | 1.6963 | 1.7545 | 1.5427 | 1.7722 | 1.8569 |
| , m/min | 1.8136 | 1.9133 | 2.0365 | 2.5235 | 2.5972 | 2.6089 | 3.5819 | 3.4218 | 3.3074 |
| , m/min | 1.7384 | 1.5461 | 1.6434 | 2.0398 | 2.1999 | 2.1180 | 2.8058 | 2.9067 | 3.0175 |
| , m2/ | 1.0697 | 0.4625 | 0.6845 | 1.0312 | 0.3496 | 0.3654 | 0.8319 | 0.3412 | 0.2242 |
| , 1 | 0.0523 | 0.0607 | 0.0693 | 0.053 | 0.08 | 0.097 | 0.0726 | 0.1 | 0.1223 |
| M | 8 | 16 | 32 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.35 | 0.40 | 0.45 | 0.35 | 0.40 | 0.45 | 0.35 | 0.4 | 0.45 | |
| , 1 | 1.3072 | 1.6325 | 1.7759 | 1.1311 | 1.7905 | 1.8524 | 1.4650 | 1.8892 | 1.9353 |
| , m/min | 1.6230 | 1.5639 | 1.5103 | 2.3742 | 2.3798 | 2.3516 | 3.5861 | 3.7414 | 3.7701 |
| , m/min | 1.3827 | 1.4534 | 1.4607 | 2.0273 | 2.0186 | 2.2693 | 3.1370 | 3.2738 | 3.1152 |
| , m2/ | 0.7767 | 0.3659 | 0.2493 | 2.3088 | 0.2893 | 0.3037 | 1.0713 | 0.9894 | 1.2787 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uatay, A. A Stochastic Modelling Framework for Single Cell Migration: Coupling Contractility and Focal Adhesions. Symmetry 2020, 12, 1348. https://doi.org/10.3390/sym12081348
Uatay A. A Stochastic Modelling Framework for Single Cell Migration: Coupling Contractility and Focal Adhesions. Symmetry. 2020; 12(8):1348. https://doi.org/10.3390/sym12081348
Chicago/Turabian StyleUatay, Aydar. 2020. "A Stochastic Modelling Framework for Single Cell Migration: Coupling Contractility and Focal Adhesions" Symmetry 12, no. 8: 1348. https://doi.org/10.3390/sym12081348
APA StyleUatay, A. (2020). A Stochastic Modelling Framework for Single Cell Migration: Coupling Contractility and Focal Adhesions. Symmetry, 12(8), 1348. https://doi.org/10.3390/sym12081348





