Chirality: The Backbone of Chemistry as a Natural Science

Abstract

Chemistry as a natural science occupies the length and temporal scales ranging between the formation of atoms and molecules as quasi-classical objects, and the formation of proto-life systems showing catalytic synthesis, replication, and the capacity for Darwinian evolution. The role of chiral dissymmetry in the chemical evolution toward life is manifested in how the increase of chemical complexity, from atoms and molecules to complex open systems, accompanies the emergence of biological homochirality toward life. Chemistry should express chirality not only as molecular structural dissymmetry that at the present is described in chemical curricula by quite effective pedagogical arguments, but also as a cosmological phenomenon. This relates to a necessarily better understanding of the boundaries of chemistry with physics and biology.

1. Introduction

Cosmological evolution toward the actual world of classical objects passes through many hierarchical stages of increasing complexity (complexity is used here in its definition of interactions forming “complex adaptive systems,” which show attributes not expected when their parts are isolated. Such complex systems show adaptive and memory phenomena, dynamic dependence on their initial states, etc.; see, e.g., Gell-Mann [1] and Bak [2]), which implies two symmetry violations (time and charge parity (CP)) and several symmetry breakdowns. As pointed out by Barron [3], “symmetry breaking” is a process leading to a symmetry inferior to that of the initial Hamiltonian but “symmetry violation” defines a process that does not fulfill the physics symmetry conservation theorems [4]. The increase in complexity in the interactions between elementary particles leads to atoms and molecules. The latter are the building blocks of chemical substances and materials, which exhibit a behavior in agreement with our perception of a world constituted by classical objects. The non-classical objects of the elementary particle world reveal phenomena, such as the quantum superposition of states, the double-slit experiment [5], or the experimental demonstrations [6], disabling the so-called Einstein-Podolsky-Rosen paradox of quantum physics [7], which cannot be understood through our sensorial perception. However, the human brain is able to explain, through abstract mathematical reasoning, the world of non-classical objects. The behaviour of objects in the quasi-classical domain (e.g., atoms or molecules) corresponds to the emergence of new properties due to the increase of complexity in the elementary particle interactions. In fact, from a pure quantum field physics point of view, the paradoxical behaviour is not that of the elementary particles but rather that of our classical world. In this regard, the natural sciences are arranged in a hierarchical order (mathematics, physics, chemistry, and biology) where each one is an unconstrained reductionism of the higher one. However, each scientific discipline works with its own terms of complexity [1]. For example, mathematics covers all the natural sciences, but when applied to physics and chemistry it must take into account constraints such as symmetry conservation laws, the symmetry violations occurring in cosmological evolution [3,4], and fundamental thermodynamic principles [8,9], otherwise, nonsensical interpretations can arise.

Chemists work using a methodology based on the following two points:

(i)

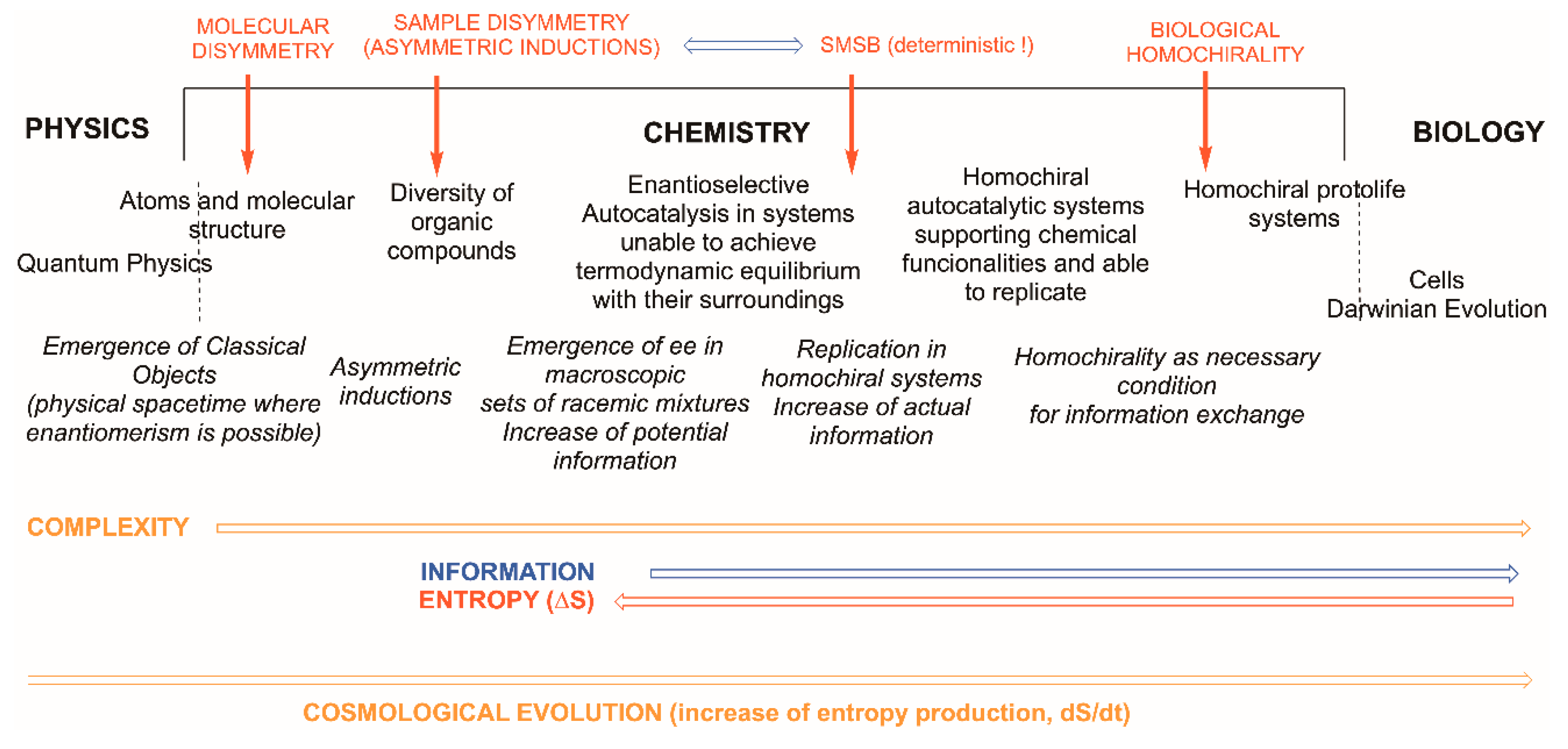
Consideration of atoms and molecules as quasi-classical objects. In fact, chemistry teaching mostly extrapolated them to atoms as robust classical objects. Atoms and molecules correspond to the frontier, or boundary, of chemistry at its lower level of complexity, that is, to the emergence of the classical from the quantum physics world. This lower frontier of chemistry is well understood by physicists and chemical physicists [10,11] but is generally ignored by chemists.

(ii)

Application of the constraints originated by the thermodynamic principles and the description of the behaviour of chemical substances and materials as very large sets of atoms and molecules, i.e., of real chemical samples. Complex chemical systems working in open systems to matter and energy exchange, whose stability derives from the dissipation of energy, are those that represent the upper boundary between biology and chemistry and are still poorly understood.

Despite the above points, chemistry, as a natural science, should study how the complexity of coupled transformations and systems can lead to the replicative and evolutive phenomena of life. The reports on these topics here were mostly restricted to theoretical works [12,13,14,15,16]. However, in the last years several research groups are paying attention to the cooperative role between many reactants in complex reaction networks that has been proposed and even experimentally explored [17,18,19,20,21,22]. Furthermore, experimental studies in bistable and oscillatory reaction networks in open systems [23,24,25] have been reported.

The intense and extensive studies in the 20th century on biological chemistry are concerned with the study of the chemical processes of current and actual living beings, but a lack of knowledge of how specific complex adaptive systems determine the emergence of the properties defining life persists. How life’s properties emerge from the behaviour of complex adaptive systems may explain why some experts in biological chemistry can believe in creationism theories. An example of the scant interest this has for chemists is shown in the topic of artificial cells, a 21st century topic that is driven by the cooperation between researchers in systems biology and in mathematical physics, but in our opinion it is very unlikely that significant results may be obtained without the collaboration of chemistry. The fault of all this must be placed on the side of the chemical community, which judges the study of chemical evolution as a part of cosmological evolution as a topic of little scientific interest, or as a high-risk research area with low professional rewards. Chemistry today is mostly regarded as a mere applied science, but not as a natural science for the understanding of the world/universe. This problem was already quoted by Hans Primas (ref. [26], pp. 3–4), that chemistry through the overproduction of “specialized” truth is losing the relationship with its neighboring sciences.

Chirality is a well-studied topic in chemistry, but only from a factual point of view. Chemical chirality is mostly treated by pedagogical effective statements, which arise from a factual consideration of the enantiomerism phenomenon, but the cause of it is mostly overlooked (Box 1). This has little bearing in the case of applied chemistry, but at the two frontiers of chemistry, one with the elementary particle world and the other with biological processes, chirality appears as a central element. But we have little understanding of its role:

(a)

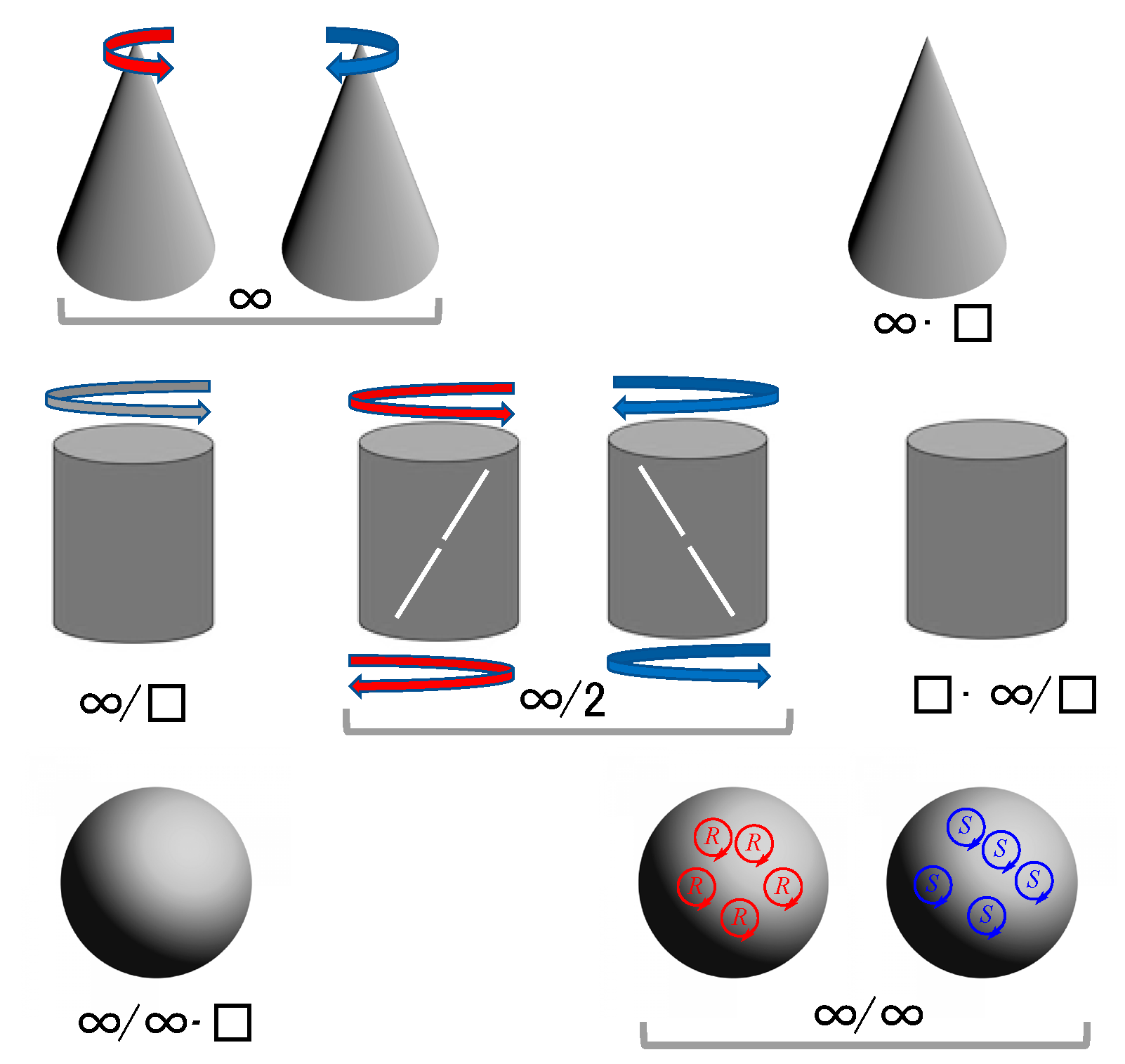
At the molecular level there is the question of enantiomerism; that chemical curricula study chirality as a part of stereochemistry is only related to the existence of structures that break parity, and parity breaking is the consequence of the symmetry violations—time the primordial one—implied in the cosmological emergence of space–time, already dissymmetric [27], and matter. The metaphysics of nature has long ago observed, and been aware of, the chirality phenomenon within the topic of the nature of space [28], well before chemistry was established as a science (see ref. [29] and cites herein).

(b)

At the frontier with biology, the dramatic experimental evidence of biological homochirality, overcoming the racemic mixture (racemate), suggests the advantage of chirality for sustaining the information related to the chemical functionalities of biological macromolecules and supramolecular systems implied in replication and in Darwinian evolution, i.e., in the properties that characterize the phenomenon of life.

Box 1. Chemical Chirality.

Chiral dissymmetry is defined by the breaking of the parity operation—simplified as the non-superposition of mirror images—of the molecular structure or of the unit cell of an anisotropic chemical sample. The geometrical representation of these “shapes” is an indirect representation of a chiral electron distribution in space: in molecules, the molecular orbitals; in solids, the electronic bands; in cholesteric liquid phases, the helicoidal solitons, etc.

Dissymmetry of Molecules: Chemists, for example, synthetic chemists working with solutions, use the term “chirality” to refer to the molecular species as defined by a chiral point group [30]. This leads to an incomplete description for isotropic sets of a very large number of units: liquids and solutions of achiral compounds, racemates, enantiopure compounds, and scalemic mixtures.

Dissymmetry of Materials: In the case of crystals, the space point group of the crystal ordering defines chirality when it belongs to one of the 65 Söhncke space groups. For lower anisotropic materials than crystals (e.g., liquid crystals), their symmetry is described by the seven Curie limiting points groups, three of them being enantiomorphic. They also define the dissymmetry of isotropic solutions and liquids: isotropic achiral and racemate samples belong to the same limiting point group, but different from that of enantiopure or scalemic mixtures. See Section 3.

Spontaneous mirror symmetry breaking (SMSB): this can involve enantioselective autocatalytic reaction networks, of high nonlinearity in the enantiomer kinetics, working in systems open to matter or energy exchange. Symmetry changes in SMSB are those of the material’s dissymmetry, and correspond to a spontaneous deracemization. Furthermore, trying to explain SMSB on the basis of molecular dissymmetry of molecular reaction mechanisms leads to misunderstandings on the origin of the SMSB phenomenon and how it can be explained (see Section 4).

Physics, in the study of the origin of the universe and of the elementary particle world, necessarily shares questions with the metaphysics of nature. With chemistry at the frontier with quantum physics and with biology, chemistry is also necessarily confronted with metaphysical questions [26,31,32]. However, chemistry as a natural science is concerned with the study of classical and quasi-classical objects, therefore, chemical methodology is freed of any metaphysical considerations [33]. This explains, in our opinion, the general reluctance of chemists to work on topics related to the origin of life that are suspected of being parascientific topics.

Section 1 discusses the role of chirality at the boundary with physics. Section 2 is concerned with the pure chemical domain and discusses the meaning of chemical chirality with respect to the dissymmetry of molecules and chemical materials. Section 3 briefly discusses the conditions to achieve non-racemic stable stationary states instead of racemic ones. Section 4 discusses the role of the scenarios described in Section 3 with respect to the boundary between systems chemistry and systems biology (chemistry/biology boundary). The arguments given in Section 1 are not based on the author’s expertise, but on well-established physical concepts (see Acknowledgments). The arguments given in Section 2 and Section 3, despite having a well-known physico-chemical basis, are surprisingly mostly ignored by the chemistry community working in chiral synthesis. The discussion in Section 4 is based on reasonable scenarios and some of the statements there are speculative and strongly reflect a personal opinion.

2. Chemical Chirality: Molecular Structures and Chemical Materials

The representation of molecules as classical objects is an approximation that chemistry applies at the borderline between theoretical physics and chemistry (see, e.g., Section 5.6 in ref. [26] and [34,35,36,37]). The formation of atoms and molecules is a critical transition due to the increase of complexity in the interactions between elementary particles (Box 2). Totally isolated chiral molecules, as well as the absence of the universal background radiation, will be represented by a superposition of the chiral states that appear as one of the enantiomers through an interaction with the surroundings [26,37].

Box 2. Molecules as Classical Objects.

Molecular structure, therefore molecular dissymmetry, emerges in chemical evolution in the increase of complexity of the interactions between elementary particles. C. F. von Weizsäcker’s analysis of physical space (ref [38], pp. 557–560) states that the differentiation between Space and Object of our classical world does not exist in the pure quantum field description. The formulation of the Einstein–Podolsky–Rosen paradox [7] against the quantum mechanical description of elementary particles—today experimentally proven as erroneous—will arise from this attempt to describe the elementary particle world in terms of our emergent space–time world. Therefore, the emergence of our “real” physical space is the emergence of the molecular structure and molecular enantiomorphism: the interactions with the external world leads to wave function collapse, reducing the superposition of states to single-state classical objects.

The understanding of the structure of atoms and molecules is essential in chemistry. As was foreseen by Werner, one of the fathers of chemical science, chemistry today uses knowledge of molecular structure (electronic energy levels and their spatial distribution) to explain the chemical properties of compounds (Figure 1). The use of the geometrical models of molecules to correlate electronic distributions and the properties of chemical substances and materials was successfully introduced in 1947 by Pauling [39], and today this approach is one of the pillars that sustain the study of chemistry. However, pure quantum field mechanisms cannot describe the spatial structure of atoms and molecules. Quantum mechanics requires the collapse of the wave function to describe molecular structures as robust objects, and this occurs because of the quantum decoherence exerted by the interaction with the surroundings and the observer [26,37]: the collapse of the wave function occurs in the irreversible coupling with time as represented by a kinematical superposition of states on a time scale much faster than that of the dynamics leading to thermal equilibrium. Molecular structure would be one of the consequences of the violation of time (reversal) symmetry yielding the thermodynamic arrow of time. Quantum chemistry assumes, in the Born–Oppenheimer approximation, wave function collapse because implicitly it describes a time superposition of states: this allows to calculate molecular structures and molecular properties (e.g., dipole moments). Notice that without wave function collapse, i.e., without decoherence originated by interactions with the surroundings, molecular structure does not exist. In summary, molecular structure can be considered as an emergent “property” arising from the increase of complexity from elementary particles toward classical objects.

Once we assume the existence of molecular structure, the question of enantiomerism needs to solve an unexpected question in order to bring quantum mechanisms in agreement with chemical experience. In the case of chirality, the quantum chemical Hamiltonian does not describe enantiomers as different objects. The wave function of an achiral molecule is represented by only a true ground state, but enantiomers are represented by two strictly degenerate ground states [26,41,42,43,44] Under the Born–Oppenheimer approximation, a chiral molecular structure yields a double-well potential (Figure 2) that is invariant with respect to space inversion, and therefore tunneling should be expected, which means that for a large set of molecules spontaneous racemization should be unavoidable. The problem is considered to be solved through the linear combination of ground and excited state (Figure 2, right), but in this case oscillations of the natural optical activity should be expected [45], something that, to best of our knowledge, chemists have never observed. Enantiomer stability requires an increase to infinite height of the barrier (that shown in Figure 2, right) between both minima to avoid tunneling and oscillations of natural optical activity. Many effects have been proposed to bring the quantum chemistry description of enantiomers in agreement with actual chemical experience, i.e., how the barrier between both energy minima might increase to infinity [46]. In respect to the cosmological evolution scenario, the more significant effect is that attributed to the violation of charge parity (VCP) in the weak interaction forming atom nuclei: the Hamiltonian loses the space-inversion symmetry so that the chiral states of the double well are no longer strictly degenerate and will become the eigenstates. Therefore, the minute energy differences between enantiomers arising from the VCP will be the cause of the existence of enantiomers as stable molecular objects and not, as is often proposed in chemistry, as the cause of the bias of the racemic composition in macroscopic samples to yield biological homochirality (see Section 3). Molecular structure and enantiomerism are consequences of the symmetry violations of time reversal and charge parity.

In summary, despite the fact that quantum mechanics gives a certain probability for tunneling between enantiomers, synthetic chemists, with the experimental evidence at hand, exclude racemization by tunneling because it has never been experimentally detected for carbon atoms as an asymmetric center, and potential chiral amines racemize because of the low inversion barrier to bond angle changes, yielding racemization (in contrast to phosphines): a large set of pure enantiopure molecules should show spontaneous racemization, even in the absence of any racemization reaction.

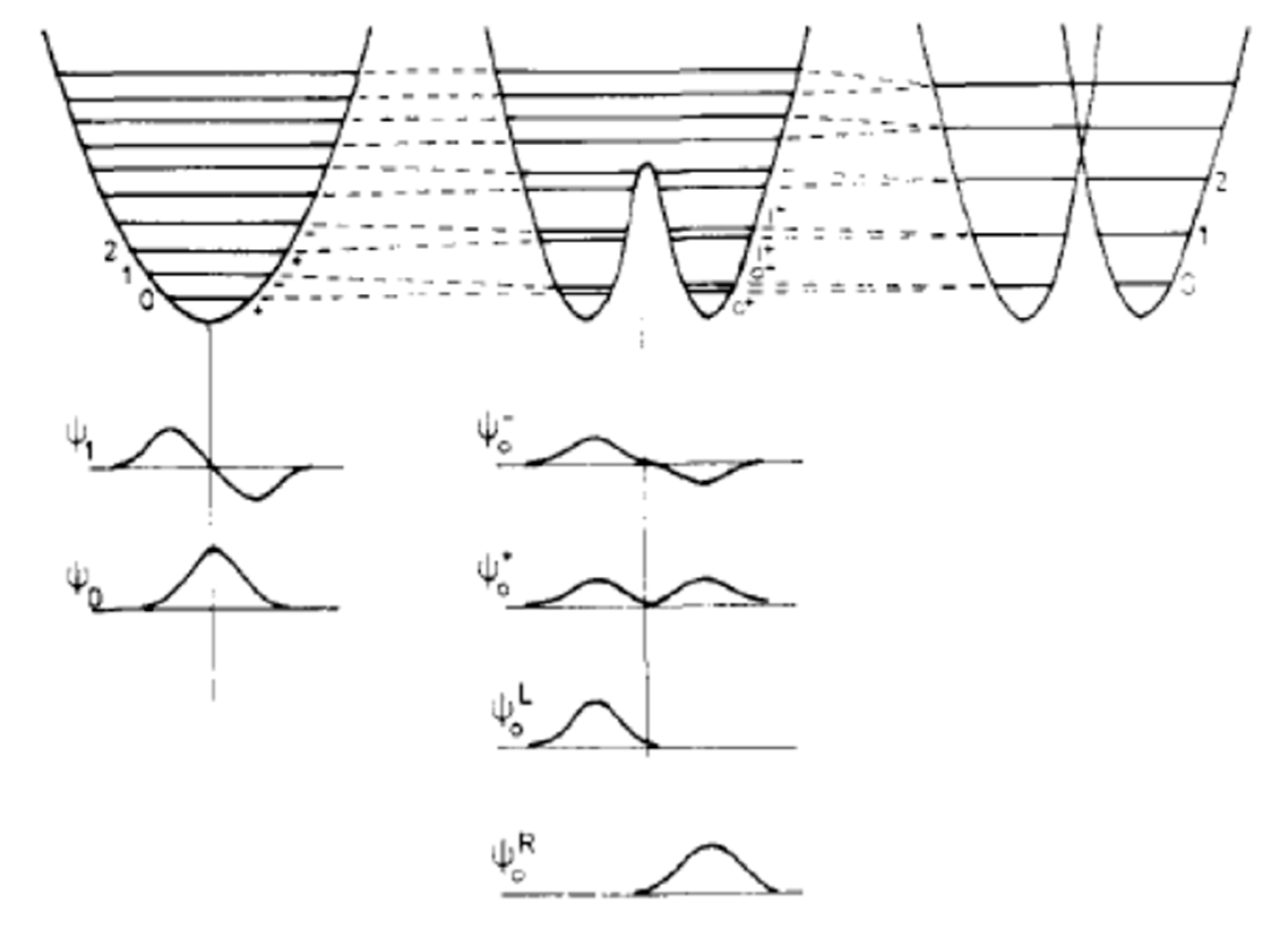
The Question of Distinguishability between Enantiomers

Enantiomerism is recognized as the breaking of parity. The practical rule to detect it is that the mirror image cannot be superimposed on the original object by translations and rotations. However, this is a factual definition; the causal one should be, as discussed in the following, that homo- and heterochiral interactions are different. In fact, the superposition procedure of the mirror image indicates that homo and heterochiral interactions must be necessarily different, as well as chiral recognition with chiral molecules and physical phenomena arising through the interaction with physical fields showing adequate dissymmetries. Dissymmetry is defined by a set of missing symmetry elements [47] that, for Pasteur, dissymmetry (chemical chirality) corresponds to the absence of any S_n (improper rotation), which obviously implies the absence of symmetry planes and inversion center. Therefore, enantiomerism is classified by the point groups of the molecular structure that break parity [30].

Stereochemistry and organic chemistry handbooks consider enantiomerism/chirality as a singular subgroup of space isomerism. This is a good method for recognizing enantiomeric structures, but underlying the cause of how it is possible that enantiomers, being geometrically identical, must be considered distinguishable particles/molecules. Structures of the same geometry, meaning those defined by historical metaphysical considerations on the nature of space (see [28] and cites therein), lead to the enantiomerism phenomenon only because they show parity breaking independently of any other stereochemical argument. The discussion on the existence of “incongruent counterpart objects”, i.e., enantiomeric objects, was Kant’s (circa 1770) preliminary step in the consideration of space and time as a priori knowledges of human reasoning (see ref. [29] for English translation and discussion of Kant’s texts). The a priori perception of space and time would have originated from the chiral nature of our brain’s sensorial systems, which, being chiral, allow for the perception of 3D physical space and, being based in dynamical chemical processes, are also bonded to the arrow of time (see Avnir in ref. [48]).

Metaphysical discussions of nature arrived a long time ago at the conclusion that, without chiral recognition, enantiomerism cannot be detected. Discussions on the existence of enantiomeric objects realized the necessity of mutual recognition in order to identify enantiomers: an “incongruent” (chiral) object can only be recognized as such when it can be compared with its counterpart. For example, the Ozma Gedanken experiment describes the impossibility to communicate the chiral sign of an asymmetric object between two cultures located on different planets in the universe [see in ref. [29], pp. 75–95, the Gardner contribution], or also Kant’s consideration that two planets having only one handedness, left or right, cannot know if, in the other one-handed planet, the handedness is the same or not (see Kant’s considerations on “incongruent objects” (1770–1783) as translated and discussed in [29]). Perhaps human reflections on chirality are as old as the reasoning arising from our sensorial chiral recognition of objects: we may speculate on the first nonwritten reports, but these are graphically expressed in prehistorical hand prints on cave rocks (Figure 3). There the shaman detects a parallel world inside the mountain rock because the being inside the rock shows him the reversed hands to those of the real world.

The question of enantiomers as distinguishable particles arose already in the inability of theoretical ideal gas models to include enantiomerism. Lifschitz and Pitayesvski [49], when considering gas kinetics (in a physics textbook!), stated that a pure enantiomer seems not to obey the detailed balance principle (the so-called micro-reversibility principle in chemistry). The detailed balance principle as described by time reversal plus parity should be an even conservation phenomenon, however, for a pure chiral compound, the parity operation leads to a different compound, i.e., to its enantiomer. The detailed balance principle, in the framework of the second principle of thermodynamics, must be necessarily followed; therefore, for the ideal gas model chirality does not exist. Ideal gas conditions assume point molecules and no interactions between them, so that, with such conditions, any differences in the physical properties between ideal gas systems, e.g., heat capacities, can only arise because of differences between molecular masses. Therefore, assuming ideal gas behaviour, the mixtures of enantiomers of different compositions—from homochiral to racemic—should show the same chemical potentials. In the case where we consider non-point-like molecules (i.e., molecules showing extended geometries), but with no differences between the homo- or heterochiral molecular collisions, the heat capacity of homochiral, scalemic, or racemic gas mixtures should be also the same because both enantiomers have the same (average) kinetic energy as well as any other forms of potential energy. Therefore, enantiomeric molecules should be indistinguishable/identical particles. However, in an actual scenario, there are differences between homochiral and heterochiral impacts, interactions, and collisions, and the heat capacities of homochiral, scalemic, and racemic gas mixtures cannot be the same, i.e., the enthalpies of these mixtures are different. Excess enthalpies in enantiomer mixtures may be detected in liquid and dense phases, but in rarified gases and diluted solutions they are under the experimental detection limit. However, despite such an enthalpy difference between homo- and heterochiral collisions being undetectable, there is no obstacle to the contribution of a configurational entropy of mixing (∆S_mix = − R ln2 in the racemic composition) to the free energy of the sample, because it is independent of the degree of the interactions leading to chiral enthalpy excesses. This is the Gibbs paradox [50], which describes the configurational entropy of mixing as a non-extensive property (degree of distinguishability) and as a consequence of the distinguishability/identity, or not, between particles. For example, the entropy of mixing, such as pointed out by Schrödinger in 1921 [51], has the same value for a CH₄/CCl₄ mixture as for an isotopical mixture ¹²CH₄/¹³CH₄. The Gibbs paradox has been “solved” by many authors, but probably the best chemical explanation is that of Denbigh and Denbigh [52] that takes into account that the entropy of mixing must be equal and of the opposite sign to that of the reverse process, i.e., the separation of the components of the mixtures through an infinite number of reversible steps (e.g., an ideal isothermic distillation). In consequence, the entropy of mixing corresponds to the value in the infinite limit of reversible separation stages. In this case the uniform convergence of the extensive character of entropy is manifested. This means that distinguishable compounds are those theoretically able to be separated. Therefore, the chemical criterion for indistinguishability is the impossibility of separation. Important is that, in the case of enantiomers, such an enantiomer resolution/separation requires chiral recognition interactions, for example, those of a chiral semi-permeable membrane or of interactions with an enantiopure pure chemical compound or with a chiral force. We can consider that the enthalpic mutual chiral recognition between enantiomers (enantiomeric discrimination ∆H_homochir ≠ 0 ≠ ∆H_heterochir, and ∆H_heterochir ≠ ∆H_homochir.), i.e., the difference between homochiral and heterochiral interactions, is a causal definition of enantiomerism: the condition for distinguishability, and therefore for the existence of a configurational entropy of mixing ∆S_mix, will arise from the enantiomeric discrimination. Notice that all this is equivalent to saying that, without mutual chiral recognition between enantiomers, chemical chirality is not manifested.

In summary, the ultimate chemical definition of chemical chirality should be the existence of enantiomeric discrimination between enantiomers. This has been stated in some chemistry manuals (for example, ref. [53], p. 154), but mostly at the end of the chirality-teaching syllabus. However, the causal significance of enantiomeric discrimination is mostly overlooked; for example, it has been commented that “Homochiral and heterochiral interactions among molecules of like constitution are unlikely ever to be exactly equal in magnitude (∆G_homo ≠ ∆G_hetero) because the two types of aggregates are anisometric (diasteromeric). The difference between these interactions was heretofore generally assumed to be nonexistent in the solution or the liquid or gaseous state, or at least too small to be measurable, and of no significant consequence” (ref. [54], p. 3). Notice that without such a small excess enthalpy of mixing, “of no significant consequence”, enantiomers would be indistinguishable species and the configurational entropy of mixing, determining the thermodynamic stability of the racemic mixture, would not exist: the entropy of mixing can be considered as the driving force toward the racemic mixture but the cause of this is the existence of an enthalpic discrimination. To forget this has little, if any, consequence in applied chemistry, but may lead to misunderstandings when comparing the stability of non-interacting enantiomers, that is, of pure enantiomers located in different systems and of spontaneous mirror symmetry breaking (SMSB) processes.

In the following we discuss an example of well-established experimental facts pointing at how, in the case of chiral crystals, the existence (or not) of interactions between them reveals (or not) the enantiomerism phenomenon.

The works of Gibbs (1874–1878) on thermodynamic stability, which led to the Phase Rule, were introduced in Europe simultaneously with the experimental verifications of the rule’s validity and with the definition of components (C), phases (P), and degrees of freedom (F) for different chemical scenarios. The Phase Rule (F = C − P + 2) is a general principle governing thermodynamic equilibrium of states completely described by pressure, volume, and temperature. Concerning chirality, a paradox was already detected by van ’t Hoff [55,56] when considering a one-component chemical system (achiral or racemizing in the solution) crystallizing into chiral enantiomorphic crystals (the so-called racemic conglomerates, e.g., the case of NaClO₃) [57]: when an excess of crystals are in equilibrium with their saturated solution, to be congruent with the experimental behavior of the system, the two enantiomorphic phases must be considered to be thermodynamically identical, i.e., as a unique solid phase (Figure 3). A trivial experimental evidence for this, which to our knowledge is never discussed in physical chemistry text books [58], is that in such a system, pure enantiomorphic crystals or a scalemic mixture of them in contact with its saturated solution, the crystal mixture does not change its enantiomeric excess (ee). For such enantiomorphic solid phases under the experimental conditions of equilibrium, it seems that chemical chirality does not exist. This occurs because in the saturated solution, i.e., at equilibrium, each crystal is isolated from the other ones: here equilibrium is expressed by the corresponding chemical potentials in the interactions between species in the solution and between the species in the solution with the solids, but not between the solids, and when such an interaction does not exist then crystal enantiomorphism cannot be manifested [59]. In summary, in the absence of chiral recognition, enantiomorphic objects are thermodynamically identical objects. This apparent paradox is experimentally observed in the final phase of the procedure of Viedma deracemization [60]. In Viedma deracemization, the wet grinding of racemic conglomerates of one chemical component, yielding enantiomorphic crystals, leads to supersaturation for the bigger crystals because of the higher solubility of the very small ones, and a cyclic process of crystal dissolution and crystal growth is established, which shows a nonlinear enantioselective dynamics leading to deracemization [61]. Any mechanism trying to explain the deracemization process must take into account that there is chiral recognition between the clusters growing to crystals (homochiral interactions occur instead of heterochiral ones). However, when the selective energy input to the system is suppressed, any fluctuation away from thermodynamic equilibrium occurs by monomer (achiral) to crystal (chiral) mechanisms, i.e., there is no chiral recognition, and the enantiomorphic crystals maintain their ee value. Depending on the mechanisms of crystal solution exchange, chirality exists or not and, as manifested by the experimental behavior at the equilibrium, there is only a thermodynamic solid phase (Figure 4).

3. Molecular Chirality vs. Chirality of Materials

Chemists work with chemical samples and interpret the results with molecular models. For example, the pathways of a synthetic transformation are explained through molecular mechanisms. The physical phenomena arising from the interaction of a material with external forces do not depend on the symmetry/dissymmetry of the molecular structure, but on that of the set of the very large number of molecules composing the material. The properties of a material in its interaction with an external force is given by the Curie principle of symmetry superposition [47,62] determined by the material symmetry elements and the symmetry classes of the external forces [63].

In the case of crystals, for example, racemic conglomerates obtained from compounds that are achiral in solution, the chiral dissymmetry of the solid is given by its classification in one of the 65 Söhncke space point groups. By contrast, chirality in solutions is generally considered by the point group of the molecular components. The latter does not give the right description to interpret the chiral physical response of the solution and may lead to misunderstandings on the meaning of SMSB in enantioselective autocatalysis (see Section 3).

The classical example of the nucleophilic addition to a prochiral carbonyl group (Figure 5) gives us an insight on the differences when the reaction is considered from the point of view of one molecule, or from that of a very large number of molecules. The addition of one molecule can only lead either to the D- or to the L-alcohol. However, since the reaction paths are reversible for single molecule fluctuations between positive, negative, and zero, then optical activity must occur. The change of the achiral point group C_S, of the prochiral carbonyl to the chiral C₁ of the alcohol, is a decrease of the symmetry order [64] and can be described as a symmetry breaking, but has no sense for a real reacting solution that obviously should lead to the racemate. SMSB refers to the spontaneous formation of a bias from the racemic composition. Notice that the racemate is stable and, in contrast to the single molecule scenario, does not show a chiral response to external forces, and therefore its symmetry (that of the external force) does not break parity.

Dissymmetry for one molecule is that of the point groups lacking Sn symmetry elements. The symmetry elements of a racemic solution compared to those of the dissymmetry of enantiopure or scalemic solutions are seldom taken into account in organic chemistry, but these can be also described. This is because sample dissymmetry can be described not only by the 65 Söhncke groups, but also by three of the seven Curie limiting point groups [64,65] (see Figure 6), which describe lower anisotropies than those of crystals. The limiting point groups describe not only the symmetry elements of amorphous materials, glasses, liquid crystals, but also ideal liquids and solutions. Limiting point groups able to represent enantiomorphism are the conical $\infty$, the cylindrical $\infty /2,$ and the spherical $\infty /\infty$ groups [47,63]. These are the space groups describing the absence or presence of dissymmetry of solutions and ideal liquids. They also describe anisotropies of oriented molecules in flows, for example, vortices in the conical point groups. The cylindrical limiting groups describe, for example, nematic and smectic liquid crystal phases and also describe the enantiomorphism generated by a shear force at the longitudinal axis of an achiral nematic phase. With respect to molecular solutions, they are described by the spherical groups: $\frac{\infty }{\infty }·m$ lacks dissymmetry, i.e., these describe the symmetry elements of achiral and racemate ideal solutions, and $\infty /\infty$ is the space point group of enantiopure solutions and scalemic mixture solutions.

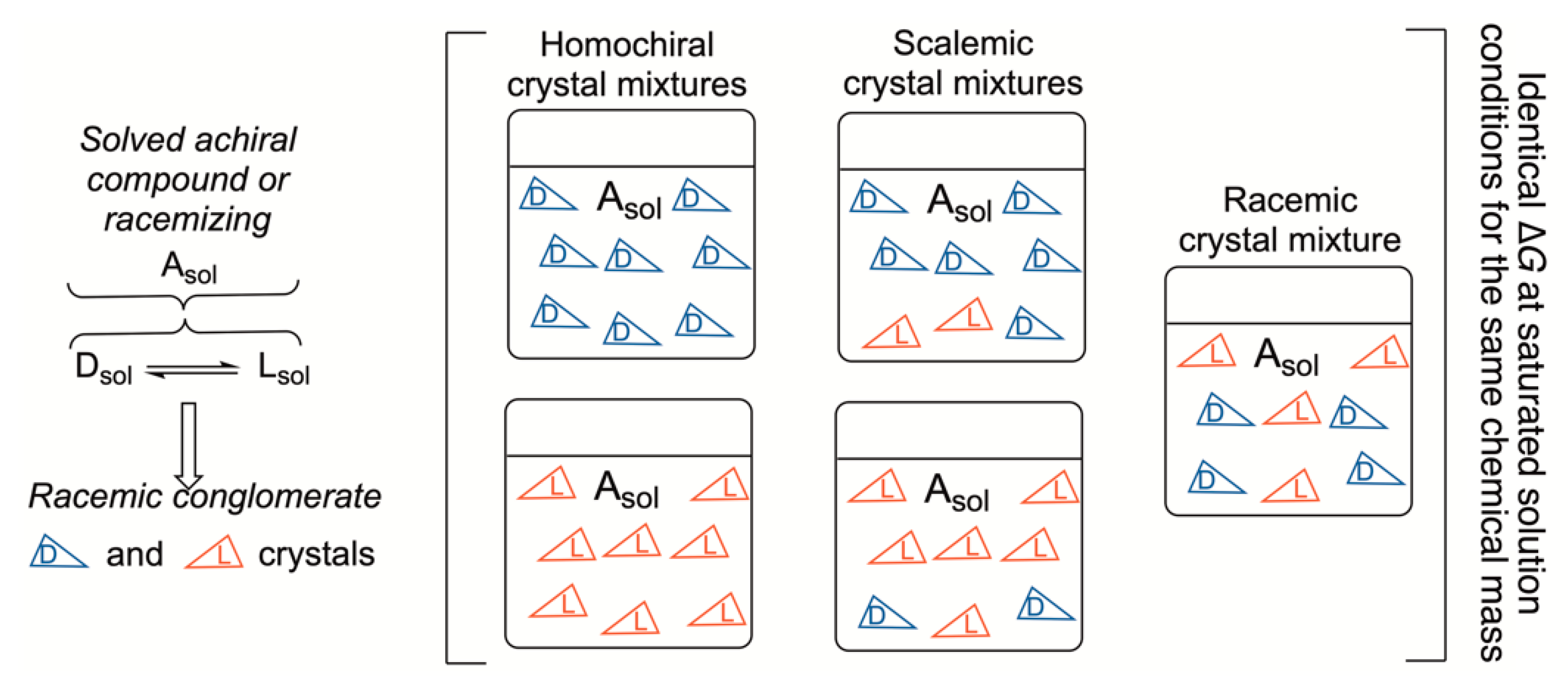
4. Racemates vs. Scalemic Mixtures in Chemical Reactions and Phase Transitions

Obtaining outputs in enantioselective reactions showing biases from the racemic composition is related to the chemical selectivity. Selectivity in the chemical transformation depends on the kinetic and thermodynamic parameters of the reactions, and on the boundary conditions (presence or absence of exchange interactions with the surroundings). A very recent review reported SMSB in crystals, mesophases, and solutions [65]. A brief summary of possible outputs for reversible or irreversible reactions in closed and in open systems is discussed in the following.

Kinetically and Thermodynamically Controlled Reactions

Irreversible reactions or exergonic transformations where the backward reaction rate constant is so small that the return to the initial compounds during the reaction workup may be approximated by zero, as for example,

$$\mathrm{A}\to \mathrm{B};\left(k_{\mathrm{B}}\right) \mathrm{A}\to \mathrm{C};\left(k_{\mathrm{C}}\right),$$

(1)

then the selectivity is that given, for initially zero concentrations of B and C, by

[B]/[C] = k_B/k_C.

(2)

In the case of reversible reaction (forward f and backward b reaction paths):

$$\mathrm{A}\rightleftharpoons \mathrm{B};(k_{f\mathrm{B}}; k_{b\mathrm{B}}) \mathrm{A}\rightleftharpoons \mathrm{C};(k_{f\mathrm{C}}; k_{b\mathrm{C}}).$$

(3)

The reaction affinities of (5) at any composition (for ideal solutions) are

$$A{f}_{\mathrm{B}}=-RTln\left\{\frac{k_{f\mathrm{B}}\left[\mathrm{A}\right]}{k_{b\mathrm{B}}\left[\mathrm{B}\right]}\right\} A{f}_{\mathrm{C}}=-RTln\left\{\frac{k_{f\mathrm{C}}\left[\mathrm{A}\right]}{k_{b\mathrm{C}}\left[\mathrm{C}\right]}\right\}.$$

(4)

Therefore, at any compositional state the [B]/[C] ratio is given by

$$\frac{\left[\mathrm{B}\right]}{\left[\mathrm{C}\right]}=\frac{K_{eq\mathrm{C}}}{K_{eq\mathrm{B}}}exp\left\{{\frac{(A{f}_{\mathrm{B}}-A{f}_{\mathrm{C}})}{RT}}^{}\right\},$$

(5)

and at thermodynamic equilibrium ($A{f}_{\mathrm{C}}$ = $A{f}_{\mathrm{B}}=0$) the selectivity ratio corresponds to the ratio of the equilibrium constants,

$$[\mathrm{B}]/[\mathrm{C}]=\frac{K_{eq\mathrm{C}}}{K_{eq\mathrm{B}}}.$$

(6)

In the case of enantiomerism (D and L enantiomers):

$$\mathrm{A}\rightleftharpoons \mathrm{D};(k_f; k_b) \mathrm{A}\rightleftharpoons \mathrm{L};(k_f; k_b),$$

(7)

$$\frac{\left[\mathrm{D}\right]}{\left[\mathrm{L}\right]}=exp\left\{{\frac{A{f}_{\mathrm{D}}-A{f}_{\mathrm{L}}}{RT}}^{}\right\},$$

(8)

the equilibrium constants and the pairs of reaction rate constants have the same value, therefore

at thermodynamic equilibrium

[D]/[L] = 1.

(9)

In systems open to matter and/or energy exchange with the surroundings (boundary conditions), the system behavior cannot be explained solely by the internal reactions, but as a whole [8,66,67,68], including its interactions with the surroundings. In non-isolated systems, a thermodynamic controlled “equilibrium” final state is in fact a stable non-equilibrium stationary state (NESS). The NESSs show non-zero affinity values and under “thermodynamic control” the species concentration ratios are expressed by Equations (5) and (8). In the case of common selectivity, the ratio [B]/[C] decreases when the boundary conditions drive the system further toward far from equilibrium conditions, but it is always ≠ 1. In contrast, in the case of enantiomerism, all possible NESSs should show racemic composition. The former stable final NESSs are those composing the so-called “thermodynamic branch” of the system. In summary, in the absence of any chiral polarization in enantioselective reactions, at thermodynamic branch scenario, any NESS must be a racemate and, for chemical isomerism and diastereoisomerism, the selective ratio decreases as the NESS moves further away from thermodynamic equilibrium.

However, the central question in energy dissipative systems is that the stability of the NESS does not depend upon whether the energy state functions form a potential well or not, but upon the entropy production (entropy production given by the product of force (affinity) by the current, absolute rate) that it originates [8,9,67,68]. The NESS of the thermodynamic branch becomes unstable at high entropy production values and, under very small fluctuations, the system is driven away from these NESSs toward new states [69].

Common reactions such as (7), which have no nonlinear kinetic dependences, achieve the critical entropy production only at very high affinities and absolute rates, and this occurs for very large species concentrations, where the medium’s viscosity is large, leading to diffusion-controlled rates and the breakdown of the mean field assumption, which leads to inhomogeneous distributions of matter and energy [69]. This may lead to ordered structures, called dissipative structures, because their stability occurs thanks to the energy dissipated by the system. However, catalyzed reactions compared to uncatalyzed ones have a higher entropy production because the entropy production rate arises from the product of the force by the current. Therefore, in complex catalytic networks showing direct or indirect autocatalysis, the critical entropy value of a bifurcation can be achieved also for reactions at ideal solution conditions [69]: the NESSs on the thermodynamic branch may become unstable and new stable NESSs can appear. The system may then transit toward other stable NESSs and may exhibit bistability and oscillatory phenomena, and even chaotic behavior [9].

In the former thermodynamic scenario, autocatalytic enantioselective reaction networks giving rise to SMSB have been theoretically predicted for a long time and were later confirmed by the experimental SMSB examples of Soai’s reaction [70,71] and of Viedma’s deracemization of racemic conglomerate crystal mixtures [60]. These dramatic experimental evidences of SMSB show how the absence of any chiral polarization leads to a stochastic distribution of the chiral signs [72] between experiments, but under the action of extremely weak chiral polarizations, the perfect symmetric bifurcation transforms into an imperfect (biased) one, leading deterministically to only one of the two chiral signs [73,74]. In the following, we comment on some points in enantioselective autocatalysis in regard to its ability, or not, to exhibit SMSB in open systems.

The irreversible enantioselective autocatalysis of first order,

A + D → 2 D (k_auto)   A + L → 2 L (k_auto),

(10)

in isolated systems may lead to kinetically controlled biases from the racemic composition. For example, in a system that, in addition to (12), contains the direct reaction

A → D (k_dir)   A → L (k_dir),

(11)

where k_dir << k_auto. When starting at zero concentrations of D and L, the very first ee values, due to the unavoidable stochastic deviations in (11), are transferred to reaction (10) and to the final reaction output [75,76]. Stochastic kinetics simulations show a distribution centered around the racemate of experiments showing ee ≠ 0, and this distribution becomes wider toward higher ee values for higher values of k_auto.

However, with respect to SMSB, the interest is in reversible reaction networks. The reversible enantioselective autocatalysis of first order (quadratic in products)

A + D ⇆ 2 D   A + L ⇆ 2 L,

(12)

where A is an achiral compound, and D/L an enantiomeric pair of compounds, has a nonlinear dependence on the enantiomer concentrations, but that does not suffice for achieving the critical entropy production for the destabilization of the racemic NESSs of the thermodynamic branch. Only when coupled to other enantioselective reactions can the autocatalytic growth dynamics be sufficiently nonlinear to lead to SMSB [72,77]. Reaction networks that may achieve this are (i) the Frank model [78,79], (ii) Viedma-like deracemizations [60,61], or (iii) enantioselective replicators showing autocatalysis [80,81]. The entropy production analysis and the energy relationships in an open system, where the effect of coupled enantioselective reactions has been studied [68], by simplifying the effect of the coupling of (12) to other enantioselective reactions SMSB, by changing the autocatalytic order (0.1 ≤ n ≤ 2) in the reaction

A + n D ⇆ (n + 1) D   A + L ⇆ 2 L,

(13)

has been recently reported. There [68], it has been shown how enantioselective autocatalysis is able to depart from the thermodynamic branch, showing multi-stability phenomenon and SMSB.

The emergence of bifurcations on the racemic thermodynamic branch, i.e., the stability or instability of the NESSs and the evolution of any non-equilibrium state, can only be understood when the system is considered as a whole, taking into account their coupling between the boundary conditions and the internal reaction network. Reaction coordinate models lose their meaning in open systems: reaction mechanisms describe the racemic thermodynamic branch as well as the scalemic stable NESSs, hence modelling by reaction coordinates and activation energies (Eyring reaction coordinate model) cannot predict the fate in open systems, which are described by the internal entropy production and entropy exchange flows with the surroundings. Moreover, the evolution of any non-equilibrium state is governed by the General Evolution Criterion (GEC) [70,71]: the partial temporal derivative of the entropy production with respect to the forces/affinities must always be negative, and zero at a NESS.

Clearer statements on this would require a detailed discussion and lie beyond the objective of this report. The interested reader may refer to the recent refs. [67,68,82,83] on this and in the specific case of SMSB systems (see Box 3). However, we can summarize as follows. The evolution and stability of the NESSs in open systems is not represented by changes in the energy state function of the internal reaction network; stable NESSs are attractors of other compositional states, through thermodynamically irreversible paths determined by a physical potential—non-thermodynamical state function—related to dissipating entropy production flows. Note the contrast with the reaction coordinate model of reversible thermodynamics, which is not a thermodynamic state function.

Box 3. SMSB: Racemic Biases Near Homochirality.

Nowadays, the Soai reaction [84] and the Viedma deracemization [60] are dramatic experimental examples of the previous theoretical reports on the possibility of SMSB in open systems. However, there are extended misunderstandings of this phenomenon.

Irreversible Thermodynamics in Open Systems. In a chemical system, the irreversibility of natural processes (breaking of time reversal invariance) is expressed by the entropy production flows of the internal reaction and by those of the exchange with the surroundings [85]. The increase of the internal entropy production, due to an increase of absolute rates and affinities, may lead to the emergence of new non-equilibrium stationary states (NESSs). In the specific case of SMSB, this leads to the destabilization of the racemic NESS and emergence of stable enantiomorphic NESSs. The physical–chemical description of this is well supported in sound concepts, thanks to the work of physical chemists of the stature, for example, of Glansdorff, Prigogine, and Eigen [8,14,69]. The physical potential governing evolution and stability in these energy dissipative systems is not a state function, in contrast to the role of the energy state functions in reversible thermodynamics. The latter allows for the fertile reaction coordinate model that today underlies our understanding and description of chemical reactions. Notice that the reaction mechanism based in mechanics is time reversible. Therefore, it cannot describe or predict the time irreversible SMSB. Notice that the same reaction mechanisms can lead to a racemate NESS or to a scalemic NESS. The entropy production flows (in units of power) originating from the coupling between the internal currents of matter and energy with those of the surrounding interactions [67,81] are the origin of the NESS.

Meaning of Far from Equilibrium Conditions in Reversible and Irreversible Thermodynamics: Reversible thermodynamics assumes the time reversibility along the chemical path, and even in quantum chemical calculations. Here in the isolated system, the evolution of a composition very far from thermodynamic equilibrium can be simulated assuming local equilibrium conditions and a reversible transformation. The reaction coordinate model is based on this, where a hypersurface, defined by the geometrical parameters of atoms or molecules participating in the reaction, is represented as a function of an energy state function, e.g., ∆G. This is a useful, fast, exclusive tool, used qualitatively in current day chemistry and quantitatively in the quantum chemical description of reaction paths. The coordinate reaction model can be approximated for its use in open systems, when the final NESS belongs to the so-called thermodynamic branch. However, this is not the case when new stable NESSs arise as a consequence of the increase of the internal entropy production, such as in the case of SMSB.

Entropy Production vs. State Function Entropy: It is often overlooked that the changes of configurational entropy, for example, when comparing racemates with scalemic mixtures, belong to the energy state function, but that the entropy production term is something rather different, not only in its physical units; it belongs to the heart of thermodynamic principles, i.e., it is the dissipated energy unable to be converted into work, which distinguishes future from past and is something that the reaction coordinate model and the reaction mechanisms do not take into account.

5. Emergence of Biological Homochirality: The Boundary between Systems Chemistry and Systems Biology

Autocatalysis is considered the alpha and omega of the chemical processes supporting life [86], and it is surely significant that enantioselective autocatalysis is a necessary, although not sufficient, condition for SMSB. This link, for example, between biological replicators and chemical spontaneous mirror symmetry breaking [80] is not likely to be fortuitous.

The accepted conceptual proposals on the origin of life are based on cooperative and collective phenomena in the self-organization of autocatalytic networks [12,13,86,87]. This is a scenario of a large set of cooperating small compartmentalized open systems. The complexity in abiotic evolution leads to the emergence of chemical functionalities of supramolecular structures. In this process of complexity increase, there is a non-zero probability for the emergence of catalytic functionalities [86], the specific case of autocatalysis being one of crucial importance for further evolution [14,88,89]. These reaction networks, working in open systems, will be capable of further evolution.

The diversity of chemical compounds that originated in the first stages of chemical evolution is large [90], but the number of organic functional groups, families of organic compounds, reaction types, and reaction mechanisms is not. At the critical transition in the emergence of catalytic reaction networks, only a fraction of the many available chemical compounds belonging to specific homologous families of functional groups would be incorporated into the reaction networks. The role of chirality in the emergence of more specific and effective catalytic functionalities is mostly overlooked, in spite of the fact that many of the biological reactions are not only autocatalytic, but also enantioselective. Enzyme catalysis and the autocatalytic mechanisms of replication of genetic information, both paradigms of life’s properties, are supported in dissymmetric supramolecular structures and are enantioselective. These are formed by homochiral building blocks of isomeric diversity, which show the same chiral sign in all living organisms. This points toward a common origin of life’s evolution [91] and to its emergence as a collective phenomenon [92].

Living state processes, as well as abiotic chemical evolution on Earth, must be explained by reaction networks with nonlinear kinetics placed in systems unable to achieve equilibrium with their surroundings, such as those of life but within the framework of nonlinear thermodynamics of irreversible processes [9].

The emergence of biases from the racemic composition in chemical evolution has often been explained by appealing to the action of natural chiral forces in kinetically controlled transformations [93,94,95]. Such a speculation is quite reasonable in astrophysical scenarios, where the ee of chiral primordial organic compounds can be obtained by kinetic control and, because of the very low temperatures, the racemization process would be slow. However, this always implies a decrease with time of the initial ee value. In consequence, this cannot explain the resilience to racemization of the homochirality in the processes of life, which implies low exergonic transformations, i.e., transformations where the approximation of irreversible (one way) reactions cannot be applied and where racemization can occur. However, in more advanced stages of chemical evolution, when enantioselective autocatalytic networks appear, SMSB scenarios are possible.

On the origin of biological chirality: The characteristics of bifurcation dynamics are (a) its stochastic character and (b) its high sensitivity to forces able to act at the bifurcation point. Notice that the stochastic character of (a) changes to a deterministic one, thanks to (b). In this respect, as SMSB processes are extremely sensitive to the chiral polarizations of the surroundings, the biological common chiral sign, arising in multiple compartmentalized systems, would occur by the chiral sign selection exerted by a general chiral polarization (a natural physical force or a small ee value of some of the compounds exchanged between systems) of the surroundings. Here, the use of exchange of the compartmentalized systems of reagents, showing small ee values, coming from asymmetric induction reactions in astrophysical scenarios, would determine a common chiral sign for all systems [96]. Notice that such a chiral sign selection by the surroundings, in a stochastic SMSB process, represents a primordial Darwinian selection of the phenotype.

Is Dissymmetry an Advantage for Chemical Evolution?

An important additional question to that of the emergence of biological chirality is if homochirality has some evolutive advantage. In our opinion, it represents an evolutive advantage in two significant aspects, as discussed in the following.

Advantage of dissymmetry in catalysis and replication: Shannon’s theory of the measure of information [97,98] widened the concept that information plays a universal role in the relationships between objects. This is a basic concept that can be applied to the natural sciences [64]. Information and evolution have also been discussed from a philosophical point of view (Chapter 5 of ref [38]) and the concepts of singularity (Erstmaligkeit), confirmation (Bestätigung), and noise (Rauschen) that support the potential information of a subject, recognition, and information flows, can be translated to the chemical physics of compounds and chemical interactions and transformations. For example, a special significance is attributed to the information of the form (Gestalt), which in modern chemistry is a self-evident statement, because the geometry of the molecular structure (shape, conformational dynamics) is the description of the electronic distribution and energy that determines the chemical and physical behaviour of the compound and also the informational exchange implicit in its interactions with other molecules and physical fields. In this respect, dissymmetry implies specific informational contents and plays a role in the interaction with other species, depending on whether they are chiral or not.

The inverse relationship of Shannon’s potential information with entropy (minimum amount of information when the thermodynamic entropy is a maximum) points to a significant role of configurational entropy when comparing achiral compounds, racemates, and scalemic or enantiopure compounds. The statistical configurational entropy due to indistinguishable spatial arrangements of the molecular structure is expressed by the entropy number (σ) [64]: σ is lower when the symmetry of the molecular geometry decreases. A high symmetry implies a large number of indistinguishable space arrangements, therefore, a high thermodynamic entropy and low potential information. This suggests that an asymmetric structure (C₁; σ = 1) is the Gestalt for a maximum of potential information. It is surely significant that biological chiral structures are not only chiral, but asymmetric (C₁) (chirality also appears for other point group symmetries [30]). Notice that as biopolymers are composed by homochiral but isomeric building blocks, for example, the α-helix shape of natural L-peptides, they show a higher potential information content than that of a helix composed of a unique type of amino acid (C₂; σ = 2). Oligomeric enzymes (n-mers) show a higher σ [99], but this is not relevant with regards to achieving a maximum of potential information because the actual catalytic species formed by the interaction with one molecule of substrate (Michaelis–Menten complex) decreases the initial symmetry to C₁. Therefore, the formation of n-mers would be a strategy to increase the number of Michaelis–Menten complexes without modification of the stereospecificity/information exchange in the chemical transformation.

Information theory has been applied to estimate the bits of information contained in the nucleic acids supporting the genetic information (see, for example, ref. [100,101,102]). This concerns the potential information of the initial compounds, but the reaction path implies the dynamic recognition process between reactants and catalyst and corresponds to the actual information [85] arising from the dynamic interaction between objects (chemical counterparts), and not to Shannon’s potential information. Shannon’s theory, despite its didactic value, is unable to give quantitative descriptions of the information flows and to express actual information in terms of potential information [85]. Notice that the reaction coordinate can be considered as an expression of the information flow between the interacting subjects along the reaction path [103,104,105], suggesting prospective work to relate the inverse relationship between Shannon information and thermodynamic entropy, and also between information flows and entropy currents.

Advantage of dissymmetry in electron transport: The chiral biopolymers of metallo-enzymes and nucleic acids are able to transport electrons at large distances through their structure [106,107], from boundary sites to a metallo-prosthetic center in the case of redox enzymes and in the case of nucleic acids, to repair free radicals caused by oxidation damages. The charge transport mechanism in proteins and nucleic acids shows analogies with those of disordered metals: conductivity occurs through some delocalized paths, showing between them energy barriers that are overcome by tunneling and hopping. The emergence of this type of protein has been proposed to be through a self-organizing critical phenomenon [108,109]. The role of these proteins in the emergence of life is crucial because they allow at the interface between systems charge separation, avoiding the recombination of oxidized and reduced counterparts driving metabolic processes. In consequence, such proteins should have emerged at the evolution stage of formation of compartmentalized systems able to exchange chemical energy with their surroundings. In this respect, the group of heme proteins is significant; for example, cytochrome c shows phylogenic traces in its amino acid sequences along many organisms of the phylogenic tree and is commonly used in cladistic studies [110]. In the evolution toward protocells, the ability of electron transport with the surroundings is essential to sustain the primordial internal redox processes.

The role of chirality here was suggested by recent experimental reports on the enantiomeric discrimination between enantiomers and polarized electrons [111,112,113], which describe the chiral recognition between the helicoidal chirality of a moving electron and, perhaps, on the effect of molecular dissymmetry upon the spin superposition of states of a single electron. The magnitude of the “filtering” effect cannot be explained by the small energy value arising from the spin-orbital effect of the electron at the conducting band of a chiral species [114]. Further work is necessary to understand this dramatic chiral recognition.

An advantage for the function of electron transport in the systems chemistry of life is suggested by the consideration of the two following points:

(1)

Electron transport is necessarily a one-electron process, but the redox processes of organic compounds (closed shell) are two-electron redox reactions. The enzymatic machinery of life solves this problem using transition metal prosthetic groups of open shell configuration that receive the single electrons, and, mediated by substrates, is able to show one-electron redox transformations intermediate to achieve the two-electron processes of the redox processes of closed shell organic molecules. In the case of DNA damage, the noxious free radical at the nucleic acid simply reacts with the carried electron to a closed shell configuration.

(2)

In regard to the former point, since living systems do not involve solid state reactions, reactions are forbidden when the total electronic spin numbers of the reactants and products are not the same. Therefore, in the case of the primordial one-electron reactions, only free electrons showing the spin sign that agrees with that of prosthetic metal group or of the free radical can participate in the reaction.

Obviously, the last point (2) states that only the half of the electrons, those of the adequate spin value, participate in the reaction. The other half will be scattered and/or lead to undesirable reactions. However, when the dissymmetry information can occur before the electron insulation, or even when the electron spin superposition of states can be selected by the chirality of the biological polymer, an efficient and faster redox process will occur.

6. Concluding Remarks

At the frontier between chemistry and quantum physics, the emergence of molecular structure and enantiomers as stable compounds occurs, thanks to fundamental symmetry violations. At the boundary with biology, chemistry should be able to describe dissymmetric complex systems. From an applied point of view, chemists are beginning to fill the knowledge gap between solution chemistry and complex chemical systems. Discussions and speculations discussed in this report are reflected in Figure 7.