Discrete-Inverse Optimal Control Applied to the Ball and Beam Dynamical System: A Passivity-Based Control Approach
Abstract
1. Introduction
- ✔
- The application of the discrete-inverse optimal control to regulate all the state variables of the ball and beam system guaranteeing passivity, stability, and optimality properties.
- ✔
- The numerical validation via simulations by working the discrete equivalent nonlinear model of the system without any special assumption on the open- or closed-loop dynamics.
- ✔
- The robustness and effectiveness of the discrete-inverse optimal control design when parametric variations affect the discrete dynamical model.
2. Dynamical Model and Discretization
3. Inverse Optimal Control Design
3.1. Passivity
3.2. Stability
3.3. Optimality
3.4. General Commentaries
- ✔
- To stabilize a nonlinear discrete dynamical system with the form defined in (4) it is used the optimal control law guaranteeing passivity, stability, and optimallity properties.
- ✔
- The application of the inverse optimal control design is subject to the fact that the dynamical system be zero detectable, which can be expressed as presented in Definition 3.Definition 3.A system (4) is locally zero-state observable (locally zero-state detectable) if there is a neighborhood of such that for allwhere is the trajectory of the unforced dynamics with initial condition . If , the system is zero-state observable (respectively zero-state detectable).
4. Numerical Validation
4.1. Regulation of the State Variables
- ✔
- All the state variables are regulated when have passed 4000 samples, i.e., ~4 s, which implies that the discrete-inverse optimal control fulfill the control objective when the control input (28) is applied to the discrete equivalent system (3).
- ✔
- The ball position exhibits a smooth dynamical behavior from the initial position (like a second-order system), i.e., cm, to the origin with a minimum overpass, which implies that the selection of the control gains was appropriate. Nevertheless, this behavior can also be improved (smoothing) if an optimization procedure over gains in is made as recommended in [13].
- ✔
- The control input presented in Figure 2c reaches the zero value when all the state variables are in the origin of coordinates, which is a natural behavior as it is a nonlinear function of all these variables working as a proportional controller that reduces its amplitude when the regulated variables are near to the origin of coordinates.
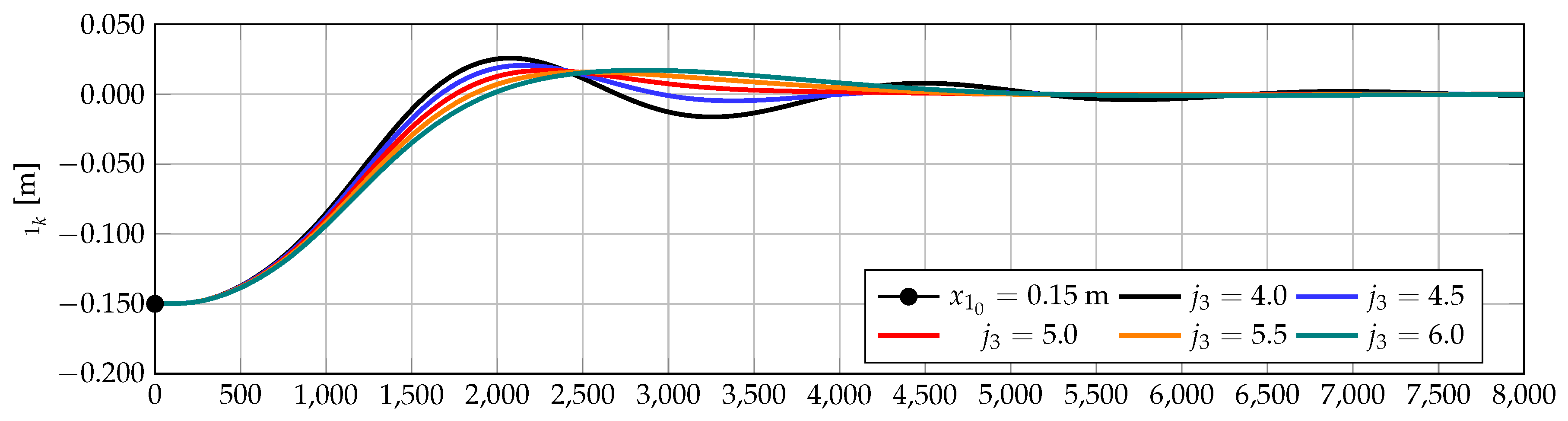
4.2. Dynamical Performance for Different Control Gains
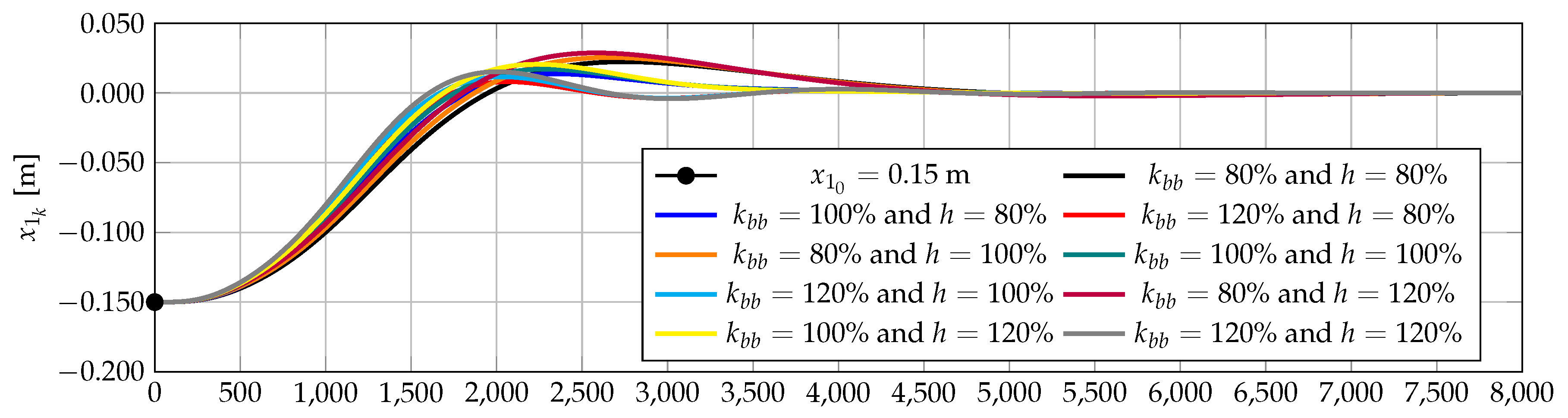
4.3. Effect of the Parameter Variations
5. Conclusions and Future Works
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kagami, R.M.; da Costa, G.K.; Uhlmann, T.S.; Mendes, L.A.; Freire, R.Z. A Generic WebLab Control Tuning Experience Using the Ball and Beam Process and Multiobjective Optimization Approach. Information 2020, 11, 132. [Google Scholar] [CrossRef]
- Koo, M.S.; Choi, H.L.; Lim, J.T. Adaptive nonlinear control of a ball and beam system using the centrifugal force term. Int. J. Innov. Comput. Inf. Control 2012, 8, 5999–6009. [Google Scholar]
- Ye, H.; Gui, W.; Yang, C. Novel Stabilization Designs for the Ball-and-Beam System. IFAC Proc. Vol. 2011, 44, 8468–8472. [Google Scholar] [CrossRef]
- Rahmat, M.F.; Wahid, H.; Wahab, N.A. Application of intelligent controller in a ball and beam control system. Int. J. Smart Sens. Intell. Syst. 2010, 3, 45–60. [Google Scholar] [CrossRef]
- Meenakshipriya, B.; Kalpana, K. Modelling and Control of Ball and Beam System using Coefficient Diagram Method (CDM) based PID controller. IFAC Proc. Vol. 2014, 47, 620–626. [Google Scholar] [CrossRef]
- Ding, M.; Liu, B.; Wang, L. Position control for ball and beam system based on active disturbance rejection control. Syst. Sci. Control. Eng. 2019, 7, 97–108. [Google Scholar] [CrossRef]
- Qi, X.; Li, J.; Xia, Y.; Wan, H. On stability for sampled-data nonlinear ADRC-based control system with application to the ball-beam problem. J. Franklin Inst. 2018, 355, 8537–8553. [Google Scholar] [CrossRef]
- Chen, C.C.; Chien, T.L.; Wei, C.L. Application of Feedback Linearization to Tracking and Almost Disturbance Decoupling Control of the AMIRA Ball and Beam System. J. Optim. Theory Appl. 2004, 121, 279–300. [Google Scholar] [CrossRef]
- Aguilar-Ibañez, C.; Suarez-Castanon, M.S.; de Jesús Rubio, J. Stabilization of the Ball on the Beam System by Means of the Inverse Lyapunov Approach. Math. Probl. Eng. 2012, 2012, 1–13. [Google Scholar] [CrossRef]
- Li, E.; Liang, Z.Z.; Hou, Z.G.; Tan, M. Energy-based balance control approach to the ball and beam system. Int. J. Control 2009, 82, 981–992. [Google Scholar] [CrossRef]
- Kelly, R.; Sandoval, J.; Santibáñez, V. A Novel Estimate of The Domain of Attraction of an IDA-PBC of a Ball and Beam System. IFAC Proc. Vol. 2011, 44, 8463–8467. [Google Scholar] [CrossRef]
- Chang, Y.H.; Chang, C.W.; Tao, C.W.; Lin, H.W.; Taur, J.S. Fuzzy sliding-mode control for ball and beam system with fuzzy ant colony optimization. Expert Syst. Appl. 2012, 39, 3624–3633. [Google Scholar] [CrossRef]
- Castillo, O.; Lizárraga, E.; Soria, J.; Melin, P.; Valdez, F. New approach using ant colony optimization with ant set partition for fuzzy control design applied to the ball and beam system. Inf. Sci. 2015, 294, 203–215. [Google Scholar] [CrossRef]
- Zavala, S.J.; Yu, W.; Li, X. Synchronization of two ball and beam systems with neural compensation. IFAC Proc. Vol. 2008, 41, 12781–12786. [Google Scholar] [CrossRef]
- Ornelas, F.; Loukianov, A.G.; Sanchez, E.N. Discrete-time Robust Inverse Optimal Control for a Class of Nonlinear Systems. IFAC Proc. Vol. 2011, 44, 8595–8600. [Google Scholar] [CrossRef]
- Atkinson, C.; Osseiran, A. Discrete-space time-fractional processes. Fract. Calc. Appl. Anal. 2011, 14. [Google Scholar] [CrossRef]
- Carrasco-Gutierrez, C.E.; Sosa, W. A discrete dynamical system and its applications. Pesqui. Oper. 2019, 39, 457–469. [Google Scholar] [CrossRef]
- Sanchez, E.N.; Ornelas-Tellez, F. Discrete-Time Inverse Optimal Control for Nonlinear Systems; CRC Press Taylor and Francis Group: Boca Raton, FL, USA, 2017. [Google Scholar]
- Galor, O. Discrete Dynamical Systems; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar] [CrossRef]
- Gil-González, W.; Serra, F.M.; Montoya, O.D.; Ramírez, C.A.; Orozco-Henao, C. Direct Power Compensation in AC Distribution Networks with SCES Systems via PI-PBC Approach. Symmetry 2020, 12, 666. [Google Scholar] [CrossRef]
- la Sen, M.D. On the Passivity and Positivity Properties in Dynamic Systems: Their Achievement under Control Laws and Their Maintenance under Parameterizations Switching. J. Math. 2018, 2018, 1–16. [Google Scholar] [CrossRef]
- Navarro-López, E.; Fossas-Colet, E. Dissipativity, passivity, and feedback passivity in the nonlinear discrete-time setting. IFAC Proc. Vol. 2002, 35, 257–262. [Google Scholar] [CrossRef]
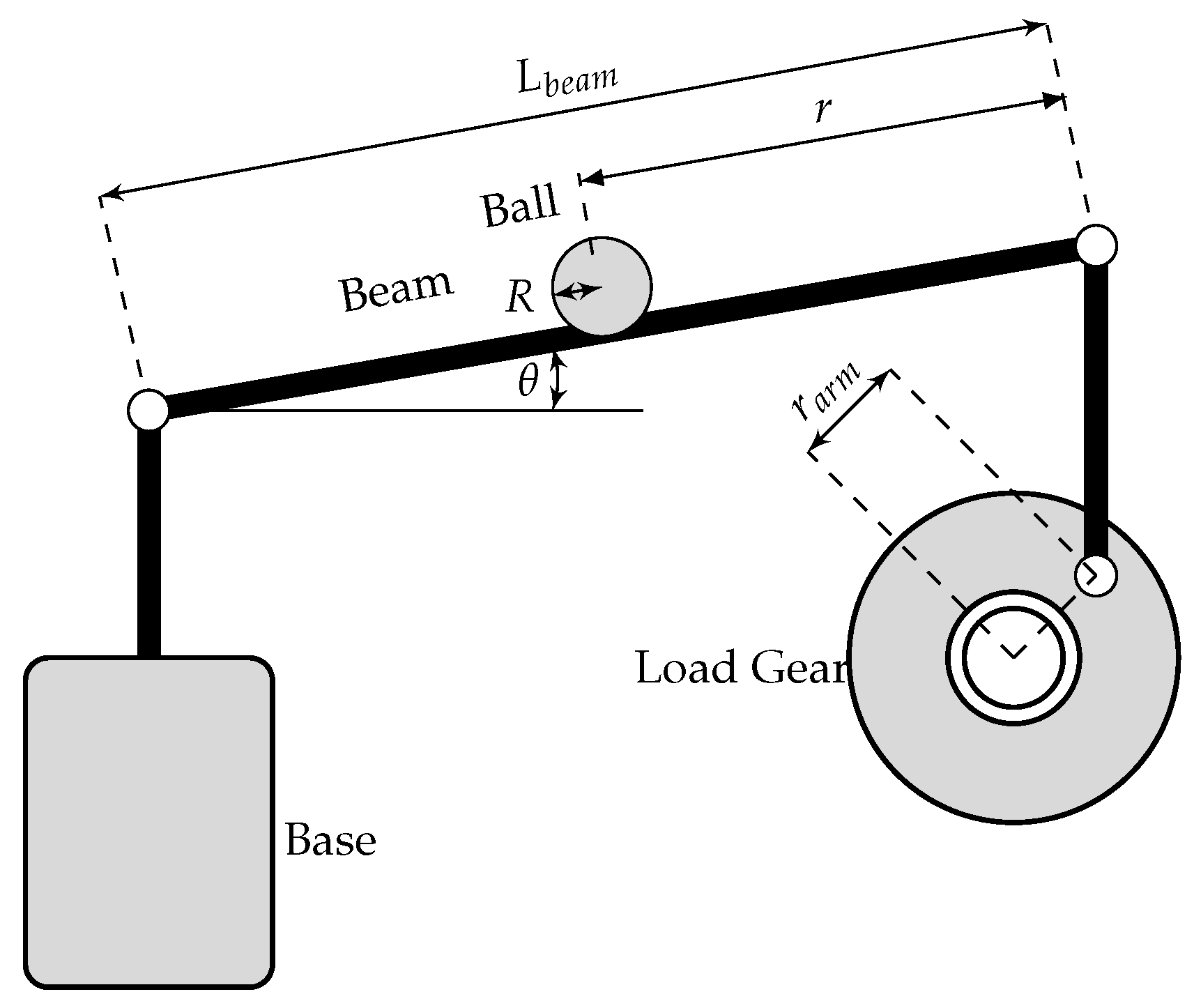


| Parameter | Value | Unity |
|---|---|---|
| 42.55 | cm | |
| 2.54 | cm | |
| R | 1.27 | cm |
| m | 64 | mg |
| g | 9.81 | m/s2 |
| 4.1290 | kgm2 | |
| 1.76 | rad/sv | |
| 28.5 | ms |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Danilo Montoya, O.; Gil-González, W.; Ramírez-Vanegas, C. Discrete-Inverse Optimal Control Applied to the Ball and Beam Dynamical System: A Passivity-Based Control Approach. Symmetry 2020, 12, 1359. https://doi.org/10.3390/sym12081359
Danilo Montoya O, Gil-González W, Ramírez-Vanegas C. Discrete-Inverse Optimal Control Applied to the Ball and Beam Dynamical System: A Passivity-Based Control Approach. Symmetry. 2020; 12(8):1359. https://doi.org/10.3390/sym12081359
Chicago/Turabian StyleDanilo Montoya, Oscar, Walter Gil-González, and Carlos Ramírez-Vanegas. 2020. "Discrete-Inverse Optimal Control Applied to the Ball and Beam Dynamical System: A Passivity-Based Control Approach" Symmetry 12, no. 8: 1359. https://doi.org/10.3390/sym12081359
APA StyleDanilo Montoya, O., Gil-González, W., & Ramírez-Vanegas, C. (2020). Discrete-Inverse Optimal Control Applied to the Ball and Beam Dynamical System: A Passivity-Based Control Approach. Symmetry, 12(8), 1359. https://doi.org/10.3390/sym12081359






