Shortest Path Solution of Trapezoidal Fuzzy Neutrosophic Graph Based on Circle-Breaking Algorithm
Abstract
1. Introduction
2. Theoretical Basis
2.1. NS
2.2. TrFNN
2.3. Ranking Function
- if
- , then
- if
- , then
- if
- , then
- ①
- if, then
- ②
- if, then
3. Neutrosophic Graph Theory
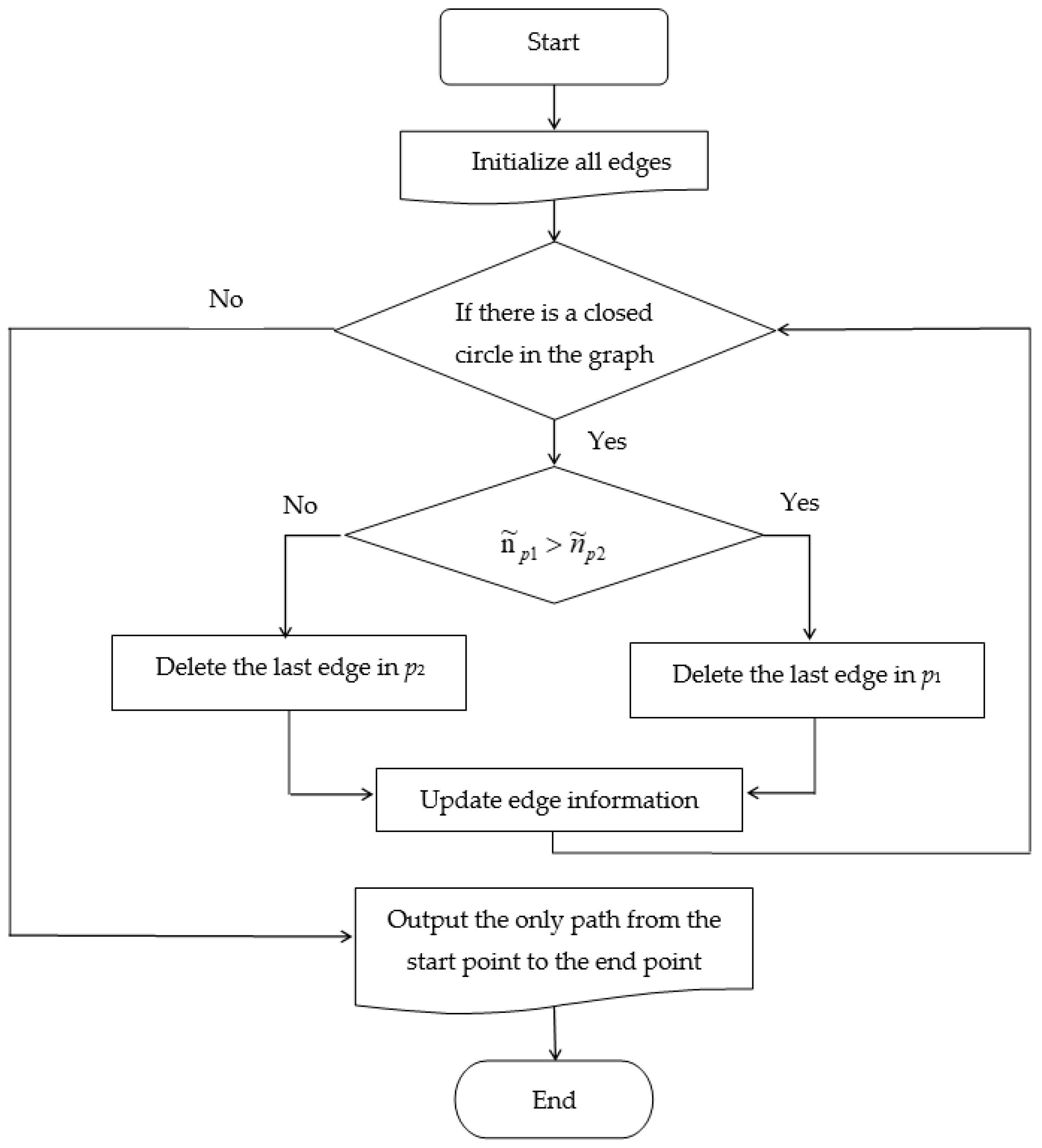
4. Method for Solving SPP of Trapezoidal Fuzzy Neutrosophic Graph Based on Circle-Breaking Algorithm
- Step 1:
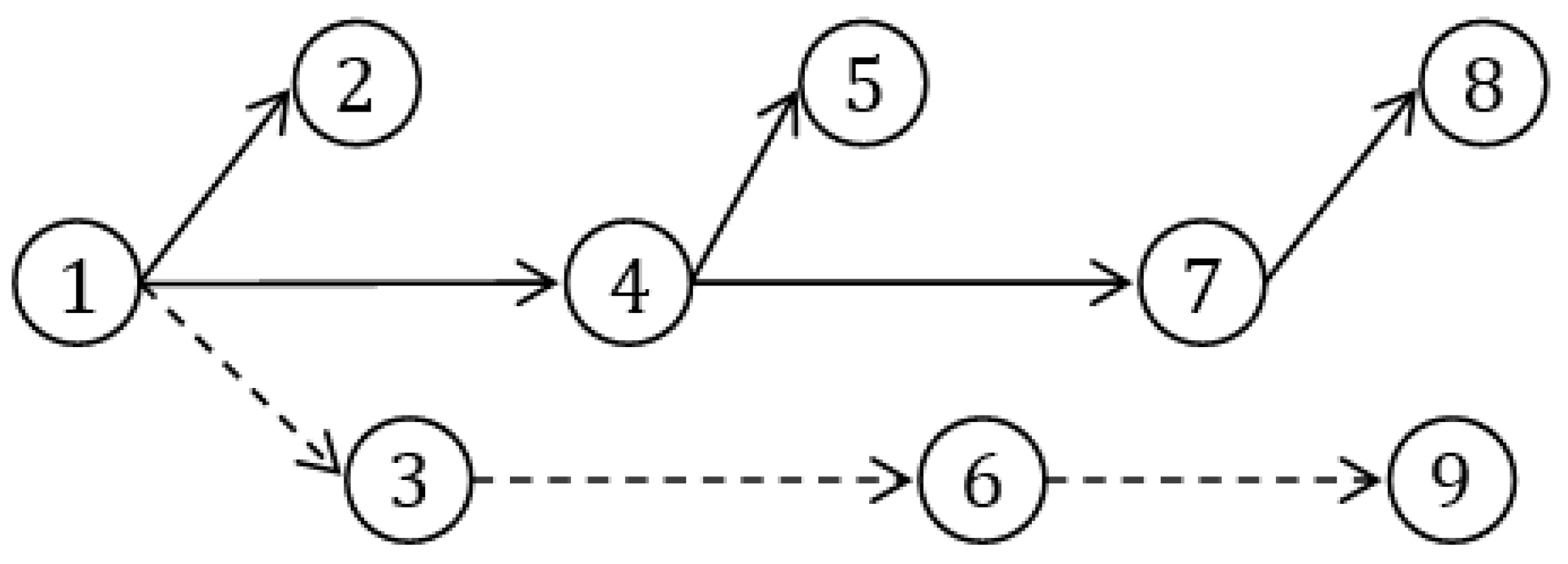
- Arbitrarily define a closed circle in the trapezoidal fuzzy neutrosophic graph, and find the two paths p1 and p2 surrounding the closed circle, whereby p1 and p2 have a common starting node recorded as N0 and a common ending node recorded as N1.
- Step 2:
- According to Equation (5), all edges of each path are summed. The trapezoidal fuzzy numbers and are then obtained, which represent the two paths.
- Step 3:
- Obtain the score function value and exact function value of , as well as the score function value and exact function value of .
- Step 4:
- Compare the sizes of and according to the ranking function, and find and delete the edge in the larger path whose vertex is N1.
- Step 5:
- Determine whether a closed circle still exists on the map. If so, go to Step 1; if not, the algorithm terminates. At this time, only one path exists from the starting node to the ending node in the neutrosophic graph, which is the shortest path.
| Algorithm 1 Circle-breaking Algorithm. |
| for i = N to 1 while(in-degree[i] > 1) if() Delete the last edge in p1 else Delete the last edge in p2 end while end for |
5. Case Study and Comparative Analysis
5.1. Case Analysis
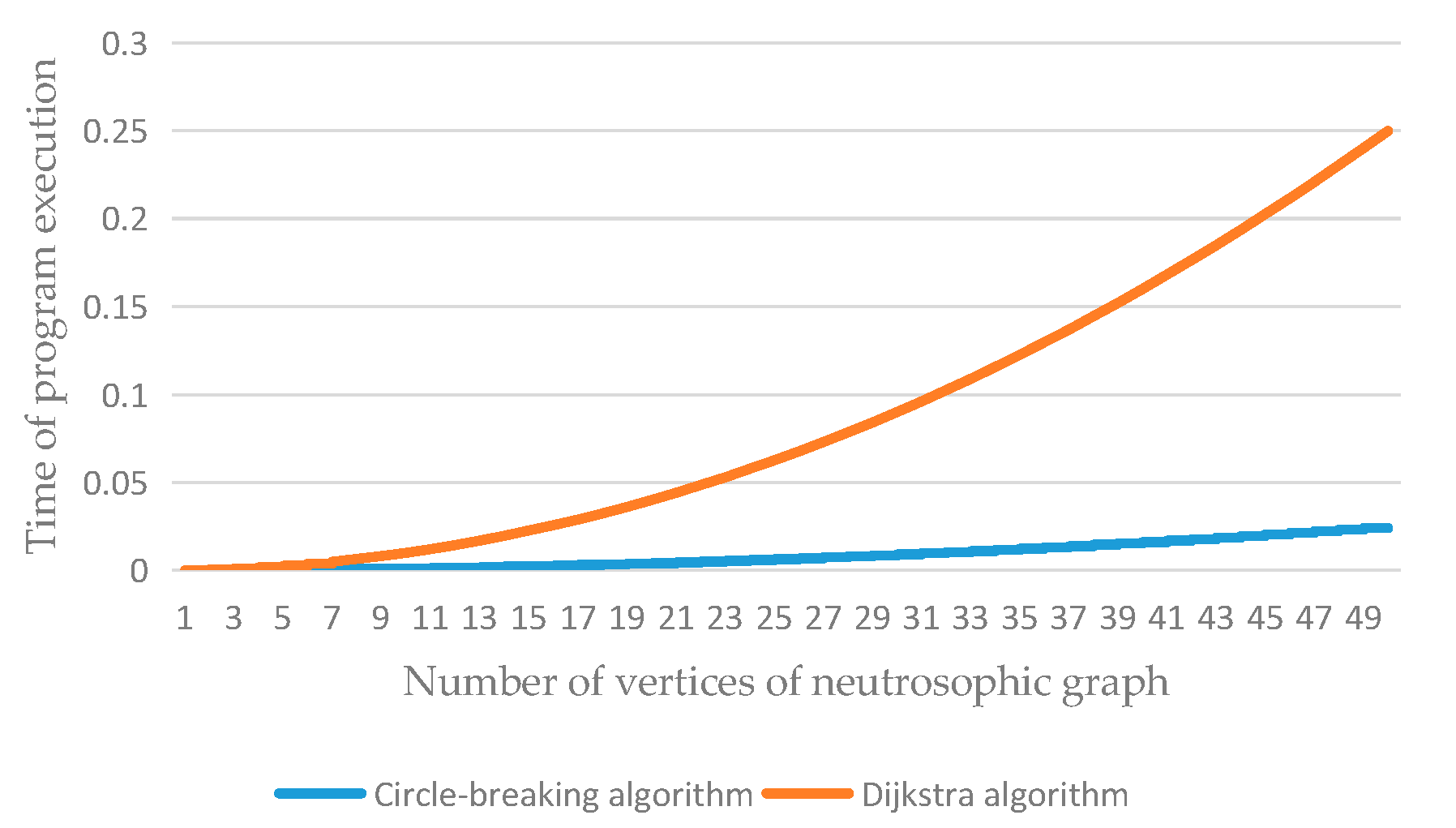
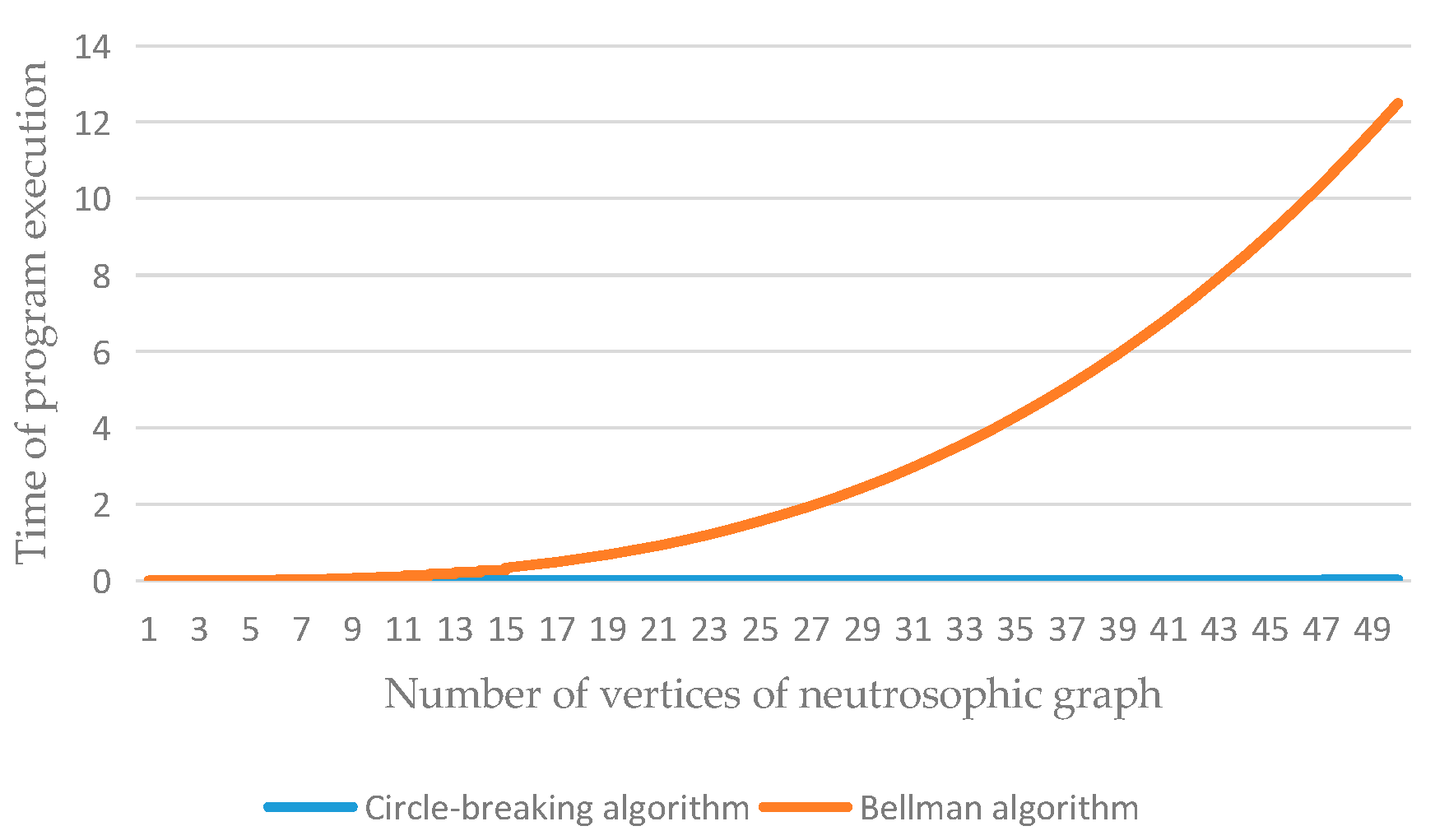
5.2. Comparative Analysis of Different Algorithms
| Algorithm 2 Multi-threaded realization of circle-breaking algorithm |
| Class Circle-breaking extends Thread{ public Circle-breaking(int k){ for(int i = (k − 1)*N/10, i < k*N/10, i++) { while(in-degree[i] > 1) { if() { Delete the last edge in p1 } else { Delete the last edge in p2 } } } } } public static void main(String[] args) { Circle-breaking[] c = new Circle-breaking [10]; for(int i = 0; i < c.length; i++) { c[i] = new Circle-breaking(i + 1); c[i].start(); } } |
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ahuja, R.K.; Mehlhorn, K.; Orlin, J.; Tarjan, R.E. Faster algorithms for the shortest path problem. J. ACM 1990, 37, 213–223. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H.; Yager, R.R. Fuzzy Information Engineering: A Guided Tour of Applications; John Wiley and Sons: New York, NY, USA, 1997. [Google Scholar]
- Biswas, S.S.; Alam, B.; Doja, M.N. Intuitionistic Fuzzy Real Time Multigraphs for Communication Networks: A Theoretical Model. In Proceedings of the 2013 AASRI Conference on Parallel and Distributed Computing and Systems, Singapore, 1–3 May 2013; pp. 114–119. [Google Scholar]
- Gabrel, V.; Murat, C.; Wu, L. New models for the robust shortest path problem: Complexity, resolution and generalization. Ann. Oper. Res. 2013, 207, 97–120. [Google Scholar] [CrossRef]
- Grigoryan, H.; Harutyunyan, H.A. The shortest path problem in the Knödel graph. J. Discret. Algorithms 2015, 31, 40–47. [Google Scholar] [CrossRef]
- Broumi, S.; Bakali, A.; Talea, M.; Smarandache, F. Isolated Single Valued Neutrosophic Graphs. Neutrosophic Sets Syst. 2016, 11, 74–78. [Google Scholar]
- Rajashi, C.; Pinaki, M.; Syamal, K.S. Interval-Valued Possibility Quadripartitioned Single Valued Neutrosophic Soft Sets and Some Uncertainty Based Measures on Them. Neutrosophic Sets Syst. 2016, 14, 35–43. [Google Scholar]
- Buckley, J.; Jowers, L.J. Fuzzy shortest path problem. Monte Carlo methods in fuzzy optimization. Stud. Fuzziness Soft Comput. 2007, 222, 191–193. [Google Scholar]
- Deng, Y.; Chen, Y.; Zhang, Y.; Mahadevan, S. Fuzzy Dijkstra algorithm for shortest path problem under uncertain environment. Appl. Soft Comput. 2012, 12, 1231–1237. [Google Scholar] [CrossRef]
- Ye, J. Multiple-attribute decision-making method under a single-valued neutrosophic hesitant fuzzy environment. J. Intell. Syst. 2014, 24, 23–36. [Google Scholar] [CrossRef]
- Peng, J.J.; Wang, J.Q. Multi-valued Neutrosophic Sets and its Application in Multi-criteria Decision-making Problems. Neutrosophic Sets Syst. 2015, 10, 3–17. [Google Scholar] [CrossRef]
- Ye, J. Trapezoidal neutrosophic set and its application to multiple attribute decision-making. Neural Comput. Appl. 2015, 26, 1157–1166. [Google Scholar] [CrossRef]
- Nancy; Harish, G. An improved score function for ranking neutrosophic sets and its application to decision making process. Int. J. Uncertain. Quantfication 2016, 6, 377–385. [Google Scholar] [CrossRef]
- Broumi, S.; Bakali, A.; Talea, M.; Smarandache, F.; Verma, R. Computing Minimum Spanning Tree in Interval Valued Bipolar Neutrosophic Environment. Int. J. Model. Optim. 2017, 7, 300–304. [Google Scholar] [CrossRef]
- Peng, X.D.; Dai, J.G. Algorithms for interval neutrosophic multiple attribute decision-making based on MABAC, similarity measure, and EDAS. Int. J. Uncertain. Quantfication 2017, 7, 395–421. [Google Scholar] [CrossRef]
- Smarandache, F. A Unifying Field in Logics: Neutrosophic Logic, Neutrosophic Set, Neutrosophic Probability and Statistics, 4th ed.; American Research Press: Rehoboth, DE, USA, 1998. [Google Scholar]
- Wang, H.B.; Smarandache, F.; Zhang, Y.Q.; Sunderraman, R. Single valued neutrosophic sets. Tech. Sci. Appl. Math. 2012, 20, 10–14. [Google Scholar]
- Deli, I.; Şubaş, Y. A ranking method of single valued neutrosophic numbers and its applications to multi-attribute decision making problems. Int. J. Mach. Learn. Cyb. 2017, 8, 1309–1322. [Google Scholar]
- Broumi, S.; Bakali, A.; Bahnasse, A. Neutrosophic sets: On overview. New Trends Neutrosophic Theor. Appl. 2018, 2, 403–434. [Google Scholar]
- Broumi, S.; Bakali, A.; Talea, M.; Smarandache, F.; Ali, M. Shortest Path Problem under Bipolar Neutrosphic Setting. Appl. Mech. Mater. 2017, 859, 59–66. [Google Scholar] [CrossRef]
- Bolturk, E.; Kahraman, C. A novel interval-valued neutrosophic AHP with cosine similarity measure. Soft Comput. 2018, 22, 4941–4958. [Google Scholar] [CrossRef]
- Biswas, P.; Pramanik, S.; Giri, B.C. Distance measure based MADM strategy with interval trapezoidal neutrosophic numbers. Neutrosophic Sets Syst. 2018, 19, 40–46. [Google Scholar]
- Deli, I. Expansions and reductions on neutrosophic classical soft set. Süleyman Demirel U. J. Nat. Appl. Sci. 2018, 22, 478–486. [Google Scholar] [CrossRef]
- Deli, I. Operators on single valued trapezoidal neutrosophic numbers and SVTN-group decision making. Neutrosophic Sets Syst. 2018, 22, 131–151. [Google Scholar]
- Deli, I.; Şubaş, Y. Some weighted geometric operators with SVTrN-numbers and their application to multi-criteria decision making problems. J. Intell. Fuzzy Syst. 2017, 32, 291–301. [Google Scholar] [CrossRef]
- Basset, M.A.; Atef, A.; Smarandache, F. A hybrid neutrosophic multiple criteria group decision making approach for project selection. Cogn. Syst. Res. 2019, 57, 216–227. [Google Scholar] [CrossRef]
- Basset, M.A.; Mohamed, M.; Sangaiah, A.K. Neutrosophic AHPDelphi Group decision making model based on trapezoidal neutrosophic numbers. J. Amb. Intel. Hum. Comp. 2017, 9, 1427–1443. [Google Scholar] [CrossRef]
- Kumar, R.; Edaltpanah, S.A.; Jha, S.; Broumi, S. Neutrosophic shortest path problem. Neutrosophic Sets Syst. 2018, 23, 5–15. [Google Scholar]
- Broumi, S.; Bakali, A.; Talea, M.; Smarandache, F.; Kishore, P.K.; Şahin, R. Shortest path problem under interval valued neutrosophic setting. Int. J. Adv. Trends Comput. Sci. Eng. 2019, 8, 216–222. [Google Scholar]
- Tan, R.P.; Zhang, W.D.; Broumi, S. Solving methods for the shortest path problem based on trapezoidal fuzzy neutrosophic numbers. Control Decis. 2019, 34, 851–860. [Google Scholar]
- Broumi, S.; Dey, A.; Talea, M.; Bakali, A.; Smarandache, F.; Nagarajan, D.; Lathamaheswari, M.; Kumar, R. Shortest path problem using Bellman algorithm under neutrosophic environment. Complex Intell. Syst. 2019, 5, 409–416. [Google Scholar] [CrossRef]
- Chakraborty, A. Application of Pentagonal Neutrosophic Number in Shortest Path Problem. Int. J. Neutrosophic Sci. 2020, 3, 21–28. [Google Scholar]
- Schweizer, P. Uncertainty: Two probabilities for the three states of neutrosophy. Int. J. Neutrosophic Sci. 2020, 2, 18–26. [Google Scholar]
- Edalatpanah, S.A. A Direct Model for Triangular Neutrosophic Linear Programming. Int. J. Neutrosophic Sci. 2020, 1, 19–28. [Google Scholar]
- Yang, L.H.; Li, D.M.; Tan, R.P. Research on the Shortest Path Solution Method of Interval Valued Neutrosophic Graphs Based on the Ant Colony Algorithm. IEEE Access 2020, 8, 88717–88728. [Google Scholar] [CrossRef]
- Guan, M.G. Algorithm of breaking circle for minimum tree. J. Math. Pract. Theory 1975, 4, 40–43. [Google Scholar]
- Zeng, J.B.; Zhang, W.; Li, X.Y. Islanding Algorithm of Distribution System with Distributed Generations based on Circle-breaking Algorithm. Power Sys. Eng. 2019, 35, 15–19. [Google Scholar]
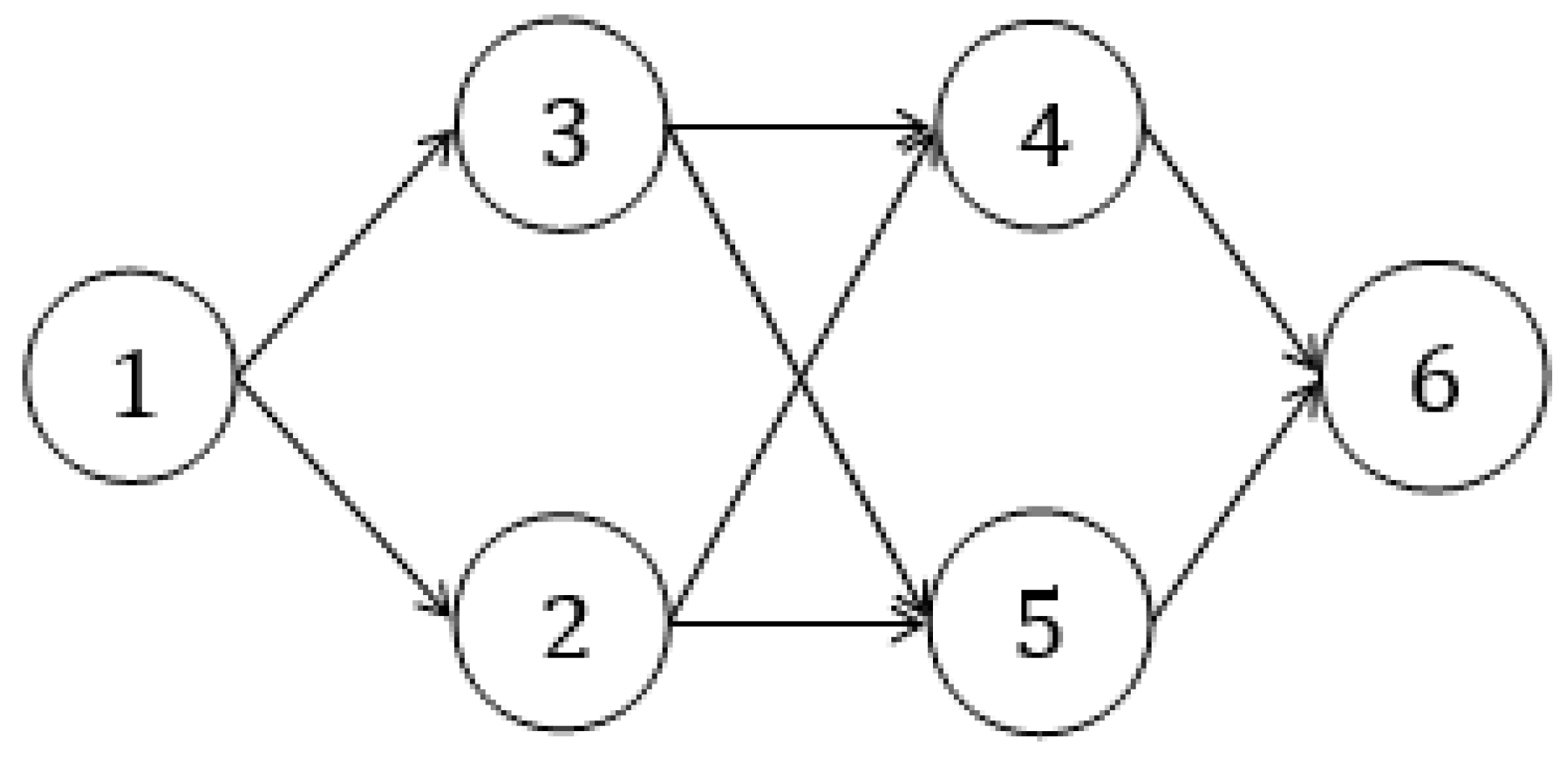

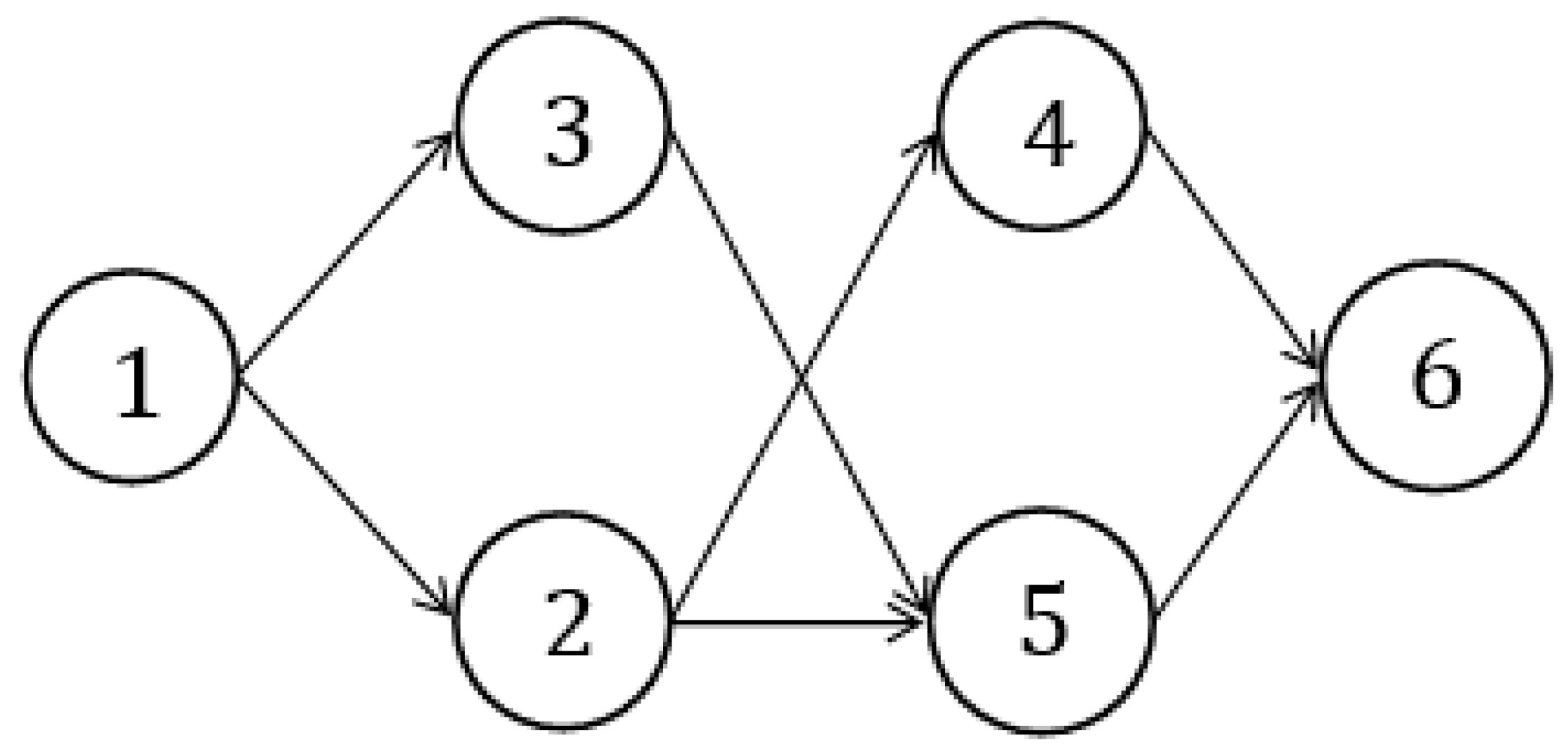
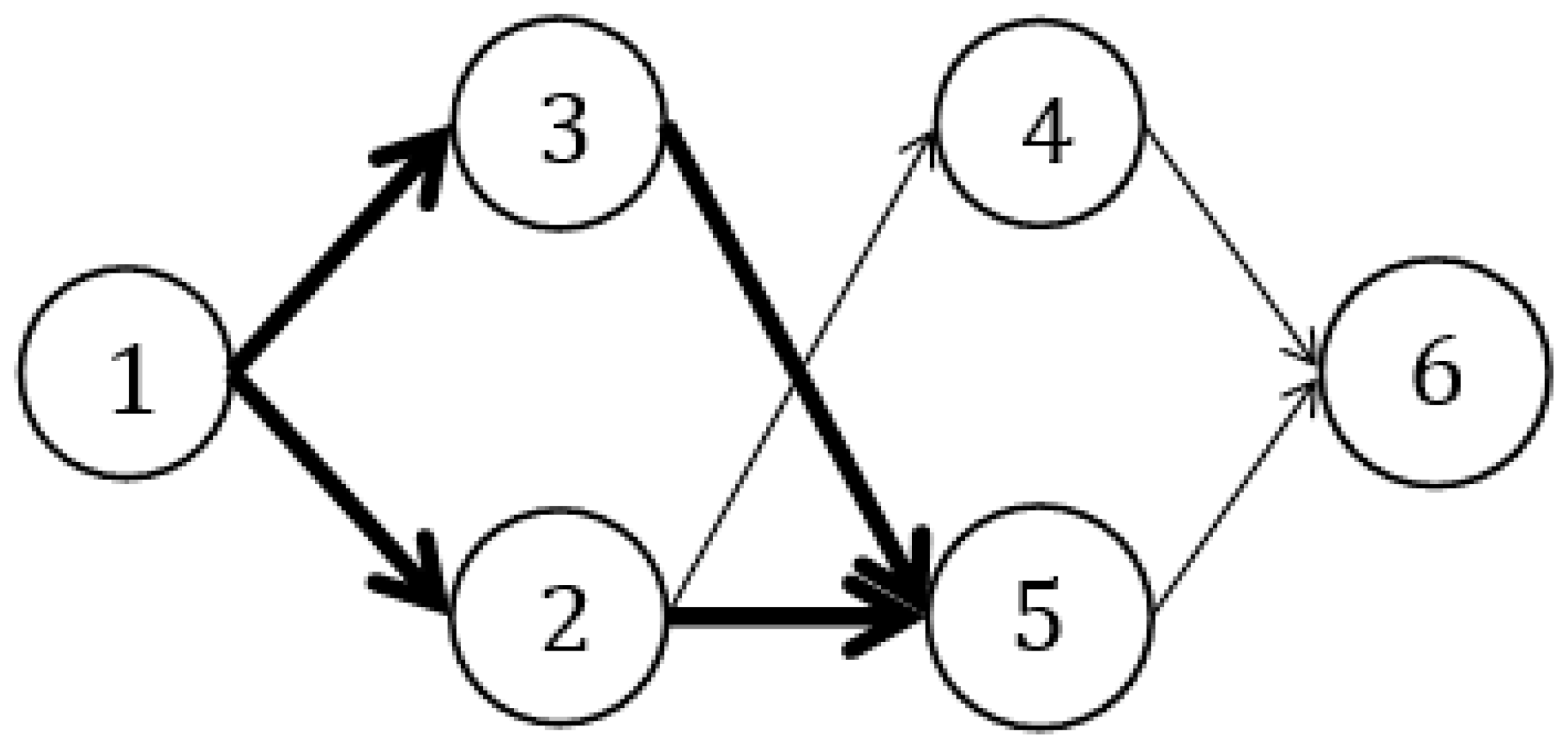
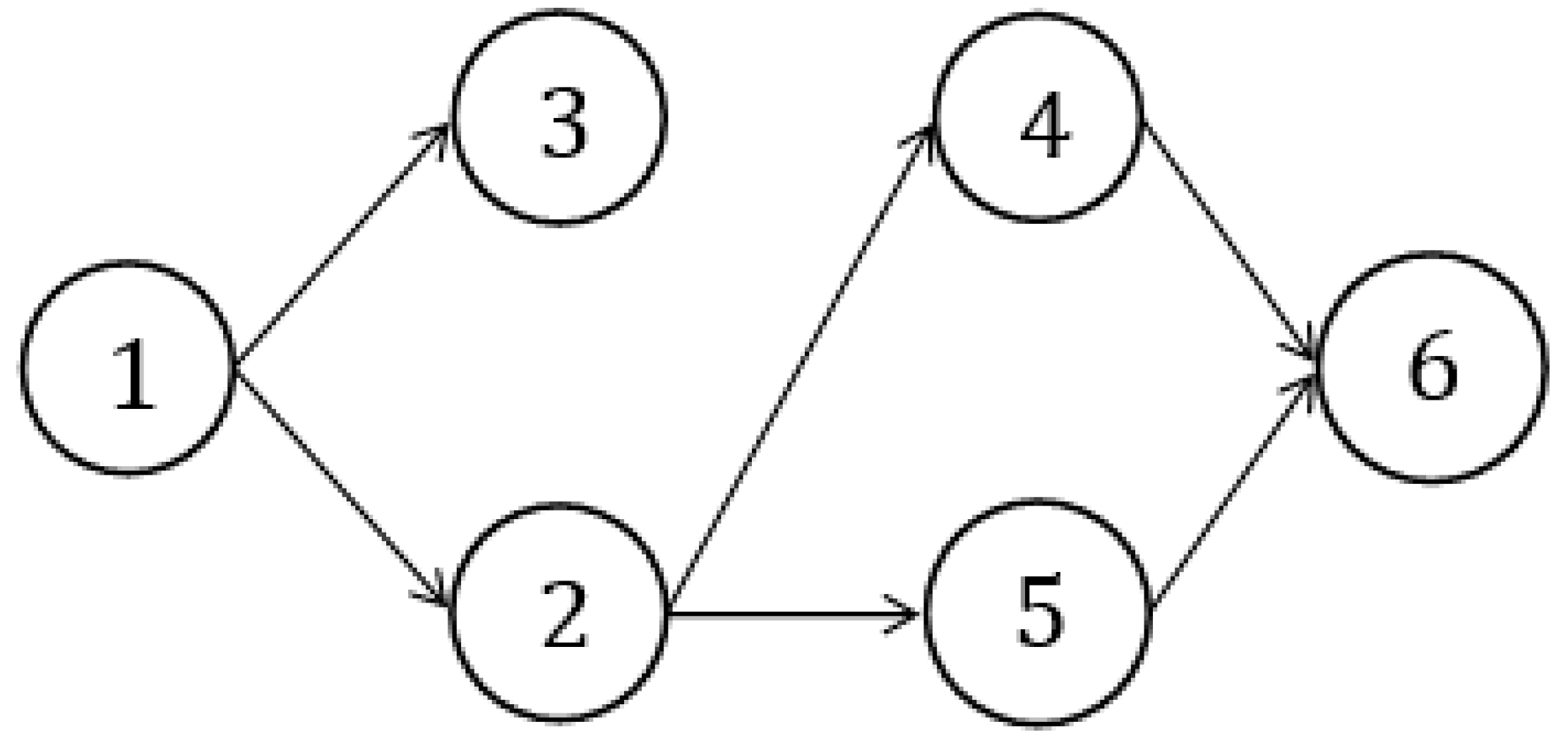
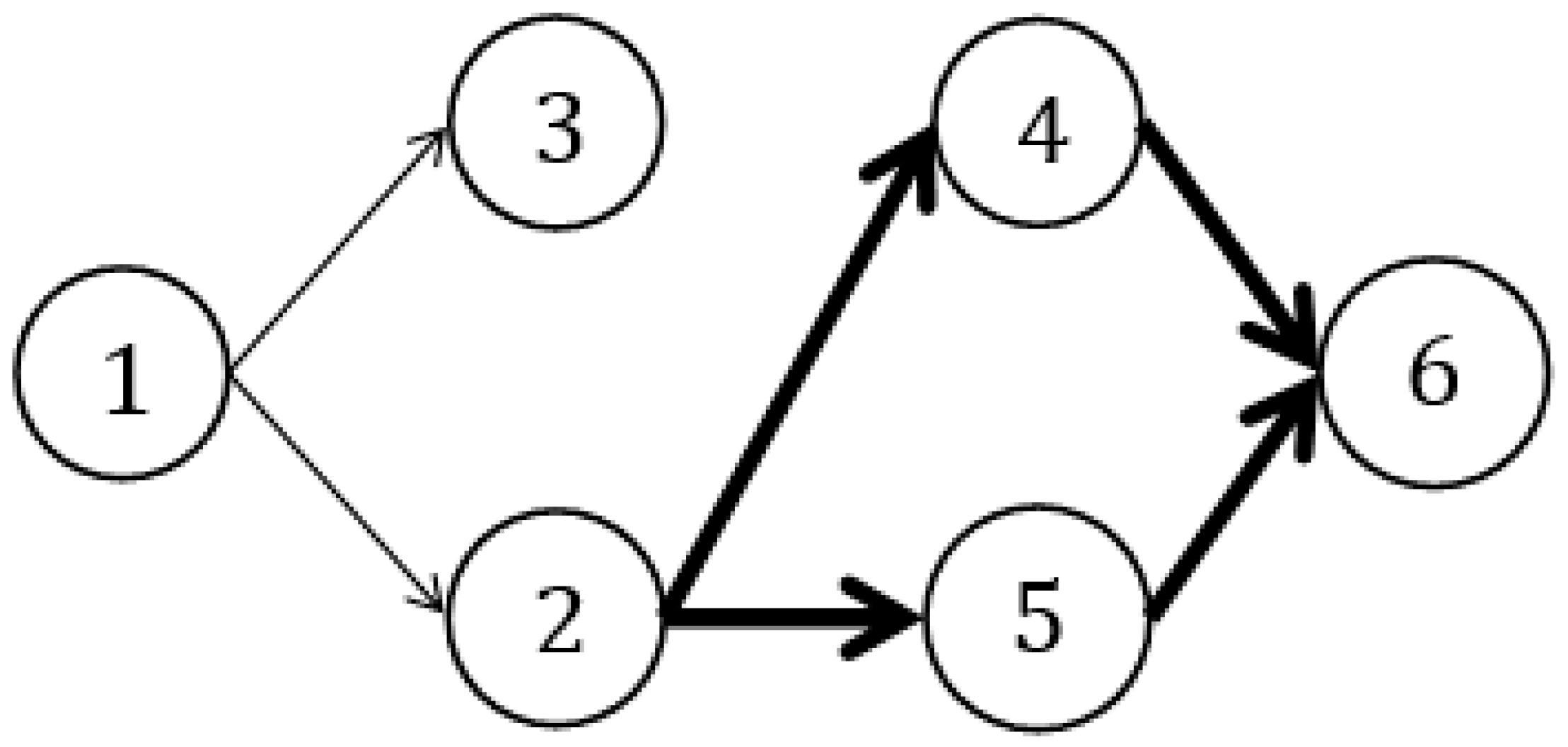
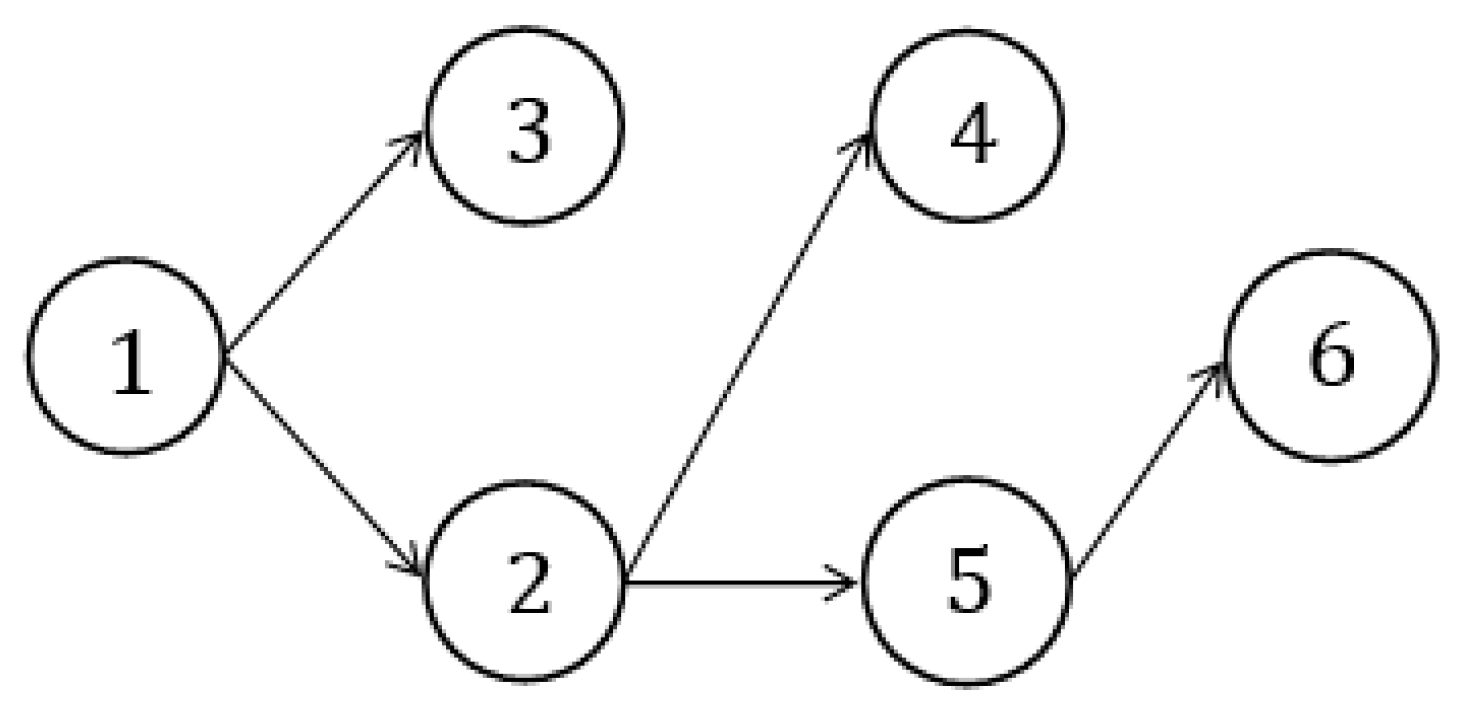
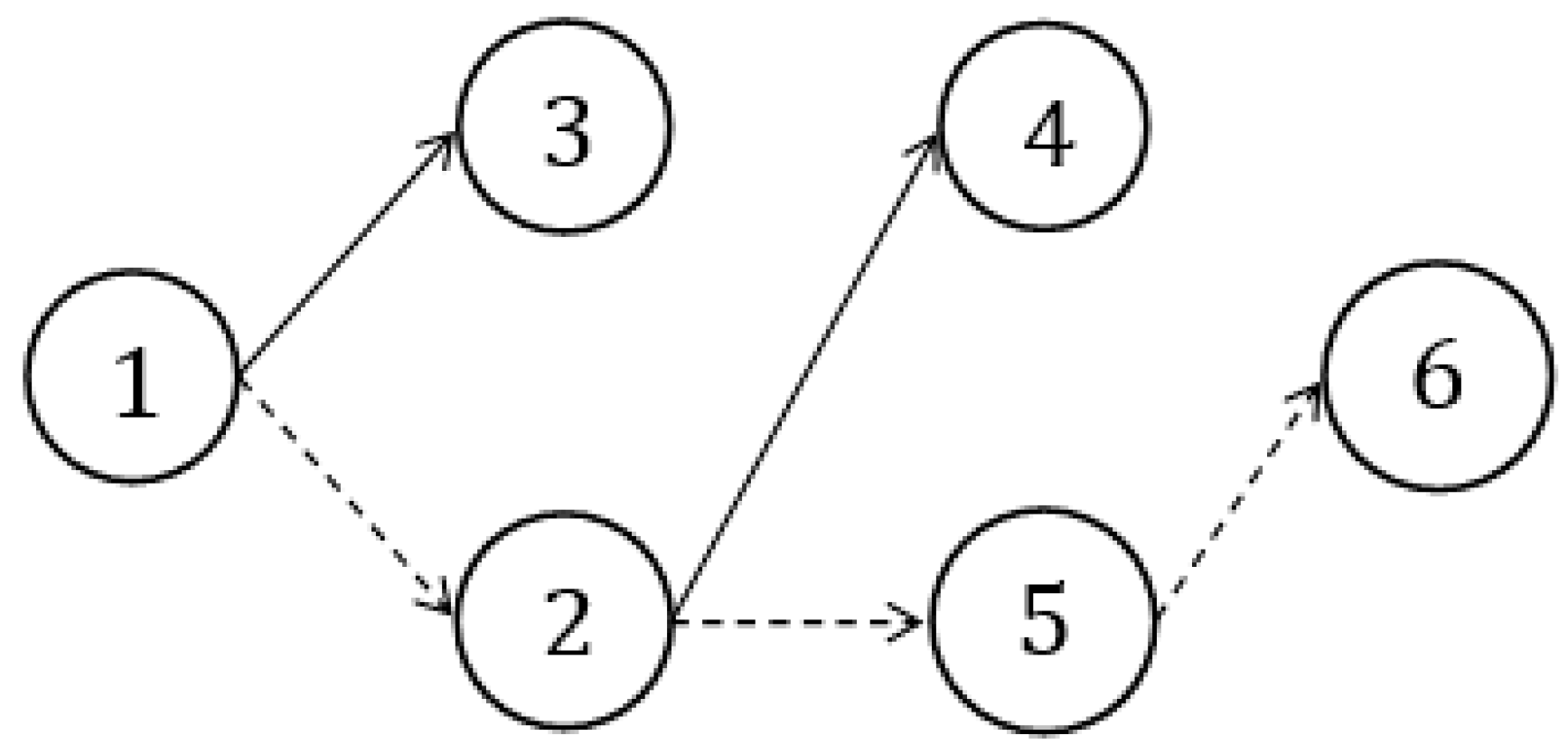

| Edges | Trapezoidal Fuzzy Neutrosophic Distances |
|---|---|
| (1, 2) | <(0.1, 0.2, 0.3, 0.5), (0.2, 0.3, 0.5, 0.6), (0.4, 0.5, 0.6, 0.8)> |
| (1, 3) | <(0.2, 0.4, 0.5, 0.7), (0.3, 0.5, 0.6, 0.9), (0.1, 0.2, 0.3, 0.4)> |
| (2, 4) | <(0.3, 0.4, 0.6, 0.7), (0.1, 0.2, 0.3, 0.5), (0.3, 0.5, 0.7, 0.9)> |
| (2, 5) | <(0.1, 0.3, 0.4, 0.5), (0.3, 0.4, 0.5, 0.7), (0.2, 0.3, 0.6, 0.7)> |
| (3, 4) | <(0.2, 0.3, 0.5, 0.6), (0.2, 0.5, 0.6, 0.7), (0.4, 0.5, 0.6, 0.8)> |
| (3, 5) | <(0.3, 0.6, 0.7, 0.8), (0.1, 0.2, 0.3, 0.4), (0.1, 0.4, 0.5, 0.6)> |
| (4, 6) | <(0.4, 0.6, 0.8, 0.9), (0.2, 0.4, 0.5, 0.6), (0.1, 0.3, 0.4, 0.5)> |
| (5, 6) | <(0.2, 0.3, 0.4, 0.5), (0.3, 0.4, 0.5, 0.6), (0.1, 0.3, 0.5, 0.6)> |
| Edges | Trapezoidal Fuzzy Neutrosophic Distance |
|---|---|
| (1, 2) | <(0.1, 0.3, 0.4, 0.5), (0.3, 0.5, 0.6, 0.7), (0.1, 0.3, 0.4, 0.6)> |
| (1, 3) | <(0.2, 0.4, 0.5, 0.7), (0.3, 0.5, 0.6, 0.9), (0.1, 0.2, 0.3, 0.4)> |
| (1, 4) | <(0.2, 0.3, 0.4, 0.6), (0.2, 0.4, 0.5, 0.6), (0.4, 0.5, 0.7, 0.8)> |
| (2, 4) | <(0.1, 0.3, 0.4, 0.5), (0.3, 0.4, 0.5, 0.7), (0.2, 0.3, 0.6, 0.7)> |
| (2, 5) | <(0.4, 0.5, 0.7, 0.8), (0.2, 0.3, 0.5, 0.6), (0.1, 0.2, 0.3, 0.5)> |
| (3, 4) | <(0.3, 0.6, 0.7, 0.8), (0.1, 0.2, 0.3, 0.4), (0.1, 0.4, 0.5, 0.6)> |
| (3, 6) | <(0.1, 0.2, 0.3, 0.4), (0.2, 0.4, 0.5, 0.6), (0.4, 0.5, 0.6, 0.7)> |
| (4, 5) | <(0.2, 0.3, 0.4, 0.5), (0.3, 0.4, 0.5, 0.6), (0.1, 0.3, 0.5, 0.6)> |
| (4, 6) | <(0.4, 0.6, 0.7, 0.9), (0.1, 0.2, 0.4, 0.5), (0.1, 0.3, 0.4, 0.6)> |
| (4, 7) | <(0.1, 0.3, 0.5, 0.6), (0.2, 0.3, 0.5, 0.7), (0.4, 0.5, 0.7, 0.8)> |
| (5, 7) | <(0.2, 0.3, 0.5, 0.6), (0.2, 0.5, 0.6, 0.7), (0.4, 0.5, 0.6, 0.8)> |
| (5, 8) | <(0.3, 0.5, 0.6, 0.7), (0.2, 0.3, 0.5, 0.6), (0.1, 0.2, 0.4, 0.5)> |
| (6, 7) | <(0.3, 0.4, 0.6, 0.7), (0.1, 0.2, 0.3, 0.5), (0.3, 0.5, 0.7, 0.9)> |
| (6, 9) | <(0.2, 0.3, 0.5, 0.6), (0.2, 0.3, 0.4, 0.5), (0.5, 0.6, 0.7, 0.9)> |
| (7, 8) | <(0.1, 0.2, 0.3, 0.5), (0.2, 0.3, 0.5, 0.6), (0.4, 0.5, 0.6, 0.8)> |
| (7, 9) | <(0.4, 0.6, 0.8, 0.9), (0.2, 0.4, 0.5, 0.6), (0.1, 0.3, 0.4, 0.5)> |
| (8, 9) | <(0.2, 0.3, 0.5, 0.6), (0.1, 0.2, 0.4, 0.5), (0.5, 0.6, 0.7, 0.8)> |
| Nodes | Distance of Shortest Path | Shortest Path |
|---|---|---|
| ② | ||
| ③ | ||
| ④ | ||
| ⑤ | ||
| ⑥ |
| Nodes | Distance of Shortest Path | Shortest Path |
|---|---|---|
| ② | ||
| ③ | ||
| ④ | ||
| ⑤ | ||
| ⑥ | ||
| ⑦ | ||
| ⑧ | ||
| ⑨ |
| Optional Path | Score Function | Exact Function |
|---|---|---|
| 0.872 | 0.686 | |
| 0.798 | 0.504 | |
| 0.871 | 0.780 | |
| 0.889 | 0.755 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Li, D.; Tan, R. Shortest Path Solution of Trapezoidal Fuzzy Neutrosophic Graph Based on Circle-Breaking Algorithm. Symmetry 2020, 12, 1360. https://doi.org/10.3390/sym12081360
Yang L, Li D, Tan R. Shortest Path Solution of Trapezoidal Fuzzy Neutrosophic Graph Based on Circle-Breaking Algorithm. Symmetry. 2020; 12(8):1360. https://doi.org/10.3390/sym12081360
Chicago/Turabian StyleYang, Lehua, Dongmei Li, and Ruipu Tan. 2020. "Shortest Path Solution of Trapezoidal Fuzzy Neutrosophic Graph Based on Circle-Breaking Algorithm" Symmetry 12, no. 8: 1360. https://doi.org/10.3390/sym12081360
APA StyleYang, L., Li, D., & Tan, R. (2020). Shortest Path Solution of Trapezoidal Fuzzy Neutrosophic Graph Based on Circle-Breaking Algorithm. Symmetry, 12(8), 1360. https://doi.org/10.3390/sym12081360




