1. Introduction
The physical phenomenon of friction between sliding bodies is a relevant topic in mechanical engineering [
1,
2]. In the case of dry friction and atomic smooth surfaces, different and complex mechanisms have been considered in the literature. In dynamic friction, the aim is to know the friction force, which is strongly dependent on the relative sliding body velocity.
Historically, the first attempt to apply Coulomb’s laws at atomic level is attributed to Tomlinson [
3] considering the atoms of one surface as uncoupled oscillators. The coupling between atoms was later considered by the Frenkel-Kontorova model [
4,
5].
The combination of the former models provides the widely used Frenkel-Kontorova-Tomlinson (FKT, hereinafter) [
6,
7] model. With regard to dynamic friction, the solutions ranging from periodic solutions or limit cycles to chaotic orbits or bound non-periodic solutions.
A short summary of the used of FKT models could start with the FKT version proposed by Elmer and Weiss (1995) [
6,
7], which was improved by Gyalog and Thomas (1997), who developed a 2-D version of this model in order to represent the motion of an atomic force microscope tip over a surface [
8]. Later, Elmer (1997) used a sticking-dependent static friction force and a velocity-dependent kinetic friction force [
9]. Hölscher and Zwörner (1998) claimed this kind of models in the analysis of this type of microscopes [
10]. Gnecco et al. (2000) analysed the friction in these devices for NaCl (100) [
11]. Sang et al. (2001) corrected the obtained relation in the former study at not very low velocities, proposing new expression for the relation between the scanning velocity and the friction force [
10,
12]. Elmer (2001) insisted on the fact that an FKT model is less expensive for simulation [
13]. Müser and Robbins (2001) studied the overdamped regime in a Tomlinson model [
10,
14]. Miura and Kamiya (2002) [
15], Prioli et al. (2003) and Fusco and Fasolino (2005) [
10] extended these researches with 2-D Tomlinson models [
11]. Alhama et al. (2011) analysed the influence of the main parameters, which define the system, with this model [
12], and Wang et al. used the Prandtl-Tomlinson model [
15].
The aim of the present work was to analyse the effect of the time step in the solutions accuracy and to check the capacity of the Lyapunov exponents [
16,
17] to assess the chaotic behaviour of the system. The network method is used as a numerical tool because its efficiency has been demonstrated in numerous science and engineering problems [
18,
19].
The design of the network model implies the following steps: the choice of the equivalence between electrical and mechanical variables and the implementation of boundary and initial conditions by suitable electric components. The software for circuit simulation Ngspice requires a relatively short computing time, thanks to the continuous adjusting of the internal time step required for the convergence.
In contrast with the numerical methods previously used for the solution of the FKT system, the network procedure does not require assumptions on the linearisation of the potential interaction function and the kind of functions (e.g., Hull function) assumed as a solution to the problem.
2. The Governing Equations
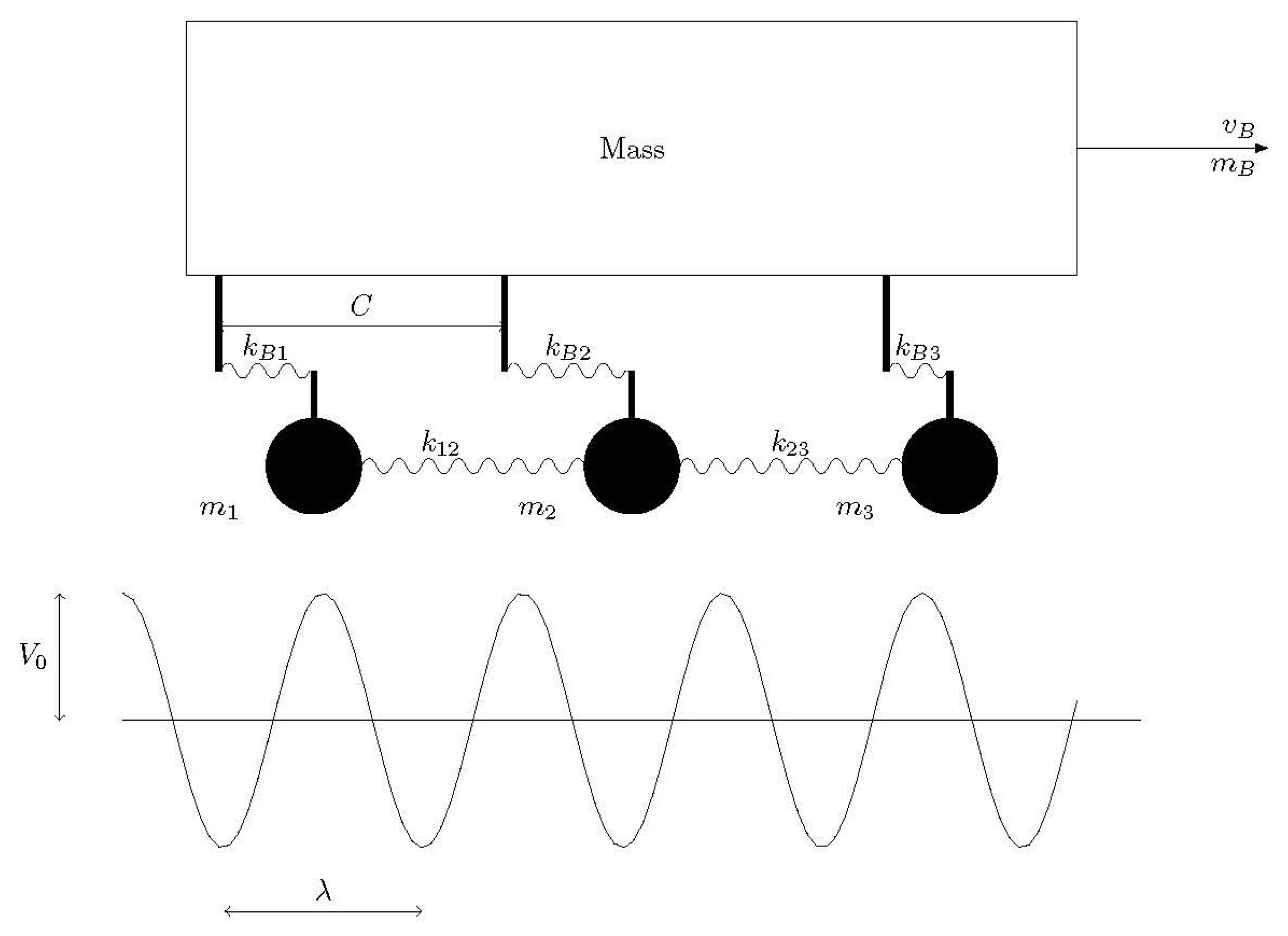
The physical scheme of the FKT model,
Figure 1, assumes two rigid sliding bodies. The interaction between the atoms of the surface layer of the upper sliding body and the neighbouring atoms and those in the bulk are represented by springs. The hypotheses currently assumed in the FKT model are summarised in the literature [
11]. One of these considers that the interaction potential between the atoms of a fixed surface and the atoms of the surface, which has a relative displacement from the other one, can be modelled as a harmonic function.
Considering an atom of the moving surface, the following equation can be written from the balance of the forces in this element [
15]
where
is the displacement of the particle
i from its equilibrium position,
m is the mass of the particle,
and
is the stiffness between neighbouring atoms on the moving surface and substrate in the moving surface, respectively,
is the body velocity,
c is the ratio between the atoms number on each surface,
is the viscous damping associated with the moving surface,
is the viscous damping associated with the still surface, and
is the potential function.
As mentioned above, the potential function is represented by:
where
b is the amplitude of potential function.
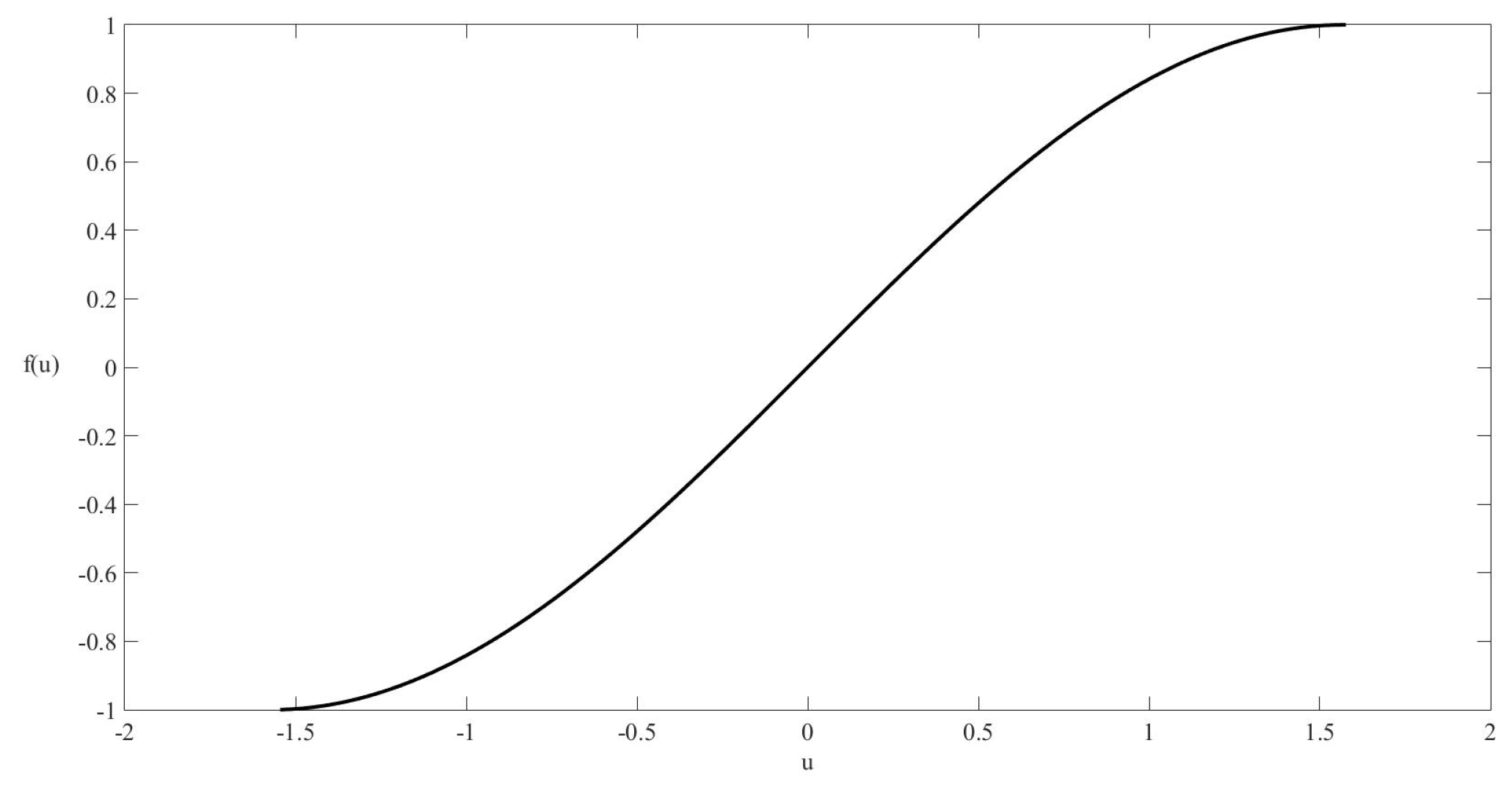
Each equation system in the FKT model is similar to the equation of an oscillatory system, which is described by
where
k represents the stiffness of the spring elements,
c is the damping coefficient,
m represents the mass, and
u represents displacement variable. The function
f can be a trigonometric function or represent the non-linear load-displacement curve of a spring,
Figure 2.
Let us assume that we have a system without energy dissipation and that the restoring force can be approximated by
Thus,
where
and
represents dissipation factor. Equation (
5) is called Duffing’s equation [
12,
15,
20,
21,
22].
Another variant of this equation is:
where
,
,
, and
represent coefficients, and
is the angular frequency in the harmonic function. Therefore, Equation (
6) will also be analysed in this work to compare the effects of the procedures that will be applied in the FKT model equations system.
3. The Convergence Criterion and the Lyapunov Exponent
As mentioned, we apply a software to the system of equations. Kirchhoff’s laws for the circuit are applying at time steps selected in order to obtain a stable convergence and that numerical approximations of integrations are sufficiently accurate [
13].
When the algorithm has reached convergence for any iteration k, we have
where
is the voltage in the node
n, and
These two parameters, RELTOL and VNTOL, which are the relative tolerance and absolute convergence, respectively, are related with the time step.
The ITL4 sets an upper limit on the number of iterations allowed to obtain a convergent solution at a timepoint.
The algorithm employed in this paper for determining Lyapunov exponents was proposed by Wolf et al. [
14]. The algorithms allow the estimation of non-negative Lyapunov exponents from an time series. In this reference, the method is tested on model systems with known Lyapunov spectra and applied to data for the Belousov-Zhabotinskii reaction and Couette-Taylor flow [
14].
The open-source free-software called Ngspice, which is used in this work, provides code models to support numerical simulation through a fast event-driven algorithm. This software is used for the simulation of large and complex circuits. In this work, we take advantage of its performance. Moreover, several tests were developed with equivalent MATLAB functions with acceptable results in case of simpler models, only with three atoms.
4. Simulation and Results
The model used in this work is based on the formal equivalence between the finite difference equations of the mathematical and network models.
Once the equivalence between electric and mechanical variables has been chosen, linear terms of the PDE are easily implemented by linear electrical devices, such as resistors, capacitors, and coils, while non-linear and coupled terms are implemented using auxiliary circuits or controlled current and voltage sources. The last are a special kind of source whose output can be defined—by software—as a function of the dependent or independent variables defined in any node or any component of the model. In addition, boundary and initial conditions—linear or not—are also immediately implemented by suitable electric components.
Once the network model has been designed, it is run with no need for other mathematical manipulations since the simulation code does this. The well-tried and powerful software for circuit simulation Ngspice, requires relatively short computing time thanks to the continuous adjusting of the internal time step required for the convergence. Solution simultaneously provides all the variables of interest: relative displacement and velocity of each atom as a function of time, phase diagrams, etc.
The Duffing equation will be solved for the following parameters: equal to , equal to 1, equal to , equal to 0.7, and equal to 1.4. The initial values are zero for the displacement and the velocity. For the calculation, the ITL4 has been set to 4000 iterations and DTMIN, the minimum internal time step, is set up in order to reduce the calculation time.
We solved the equation numerically for different convergence tolerances.
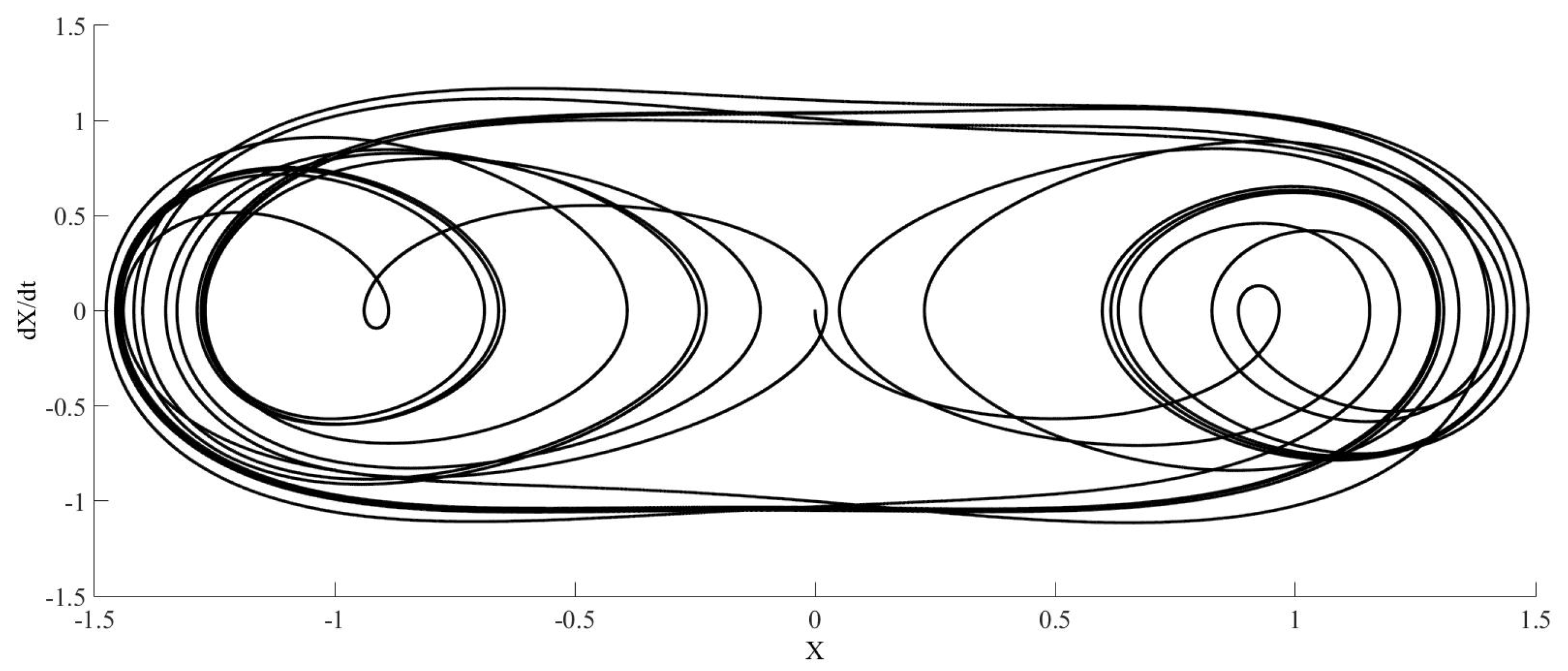
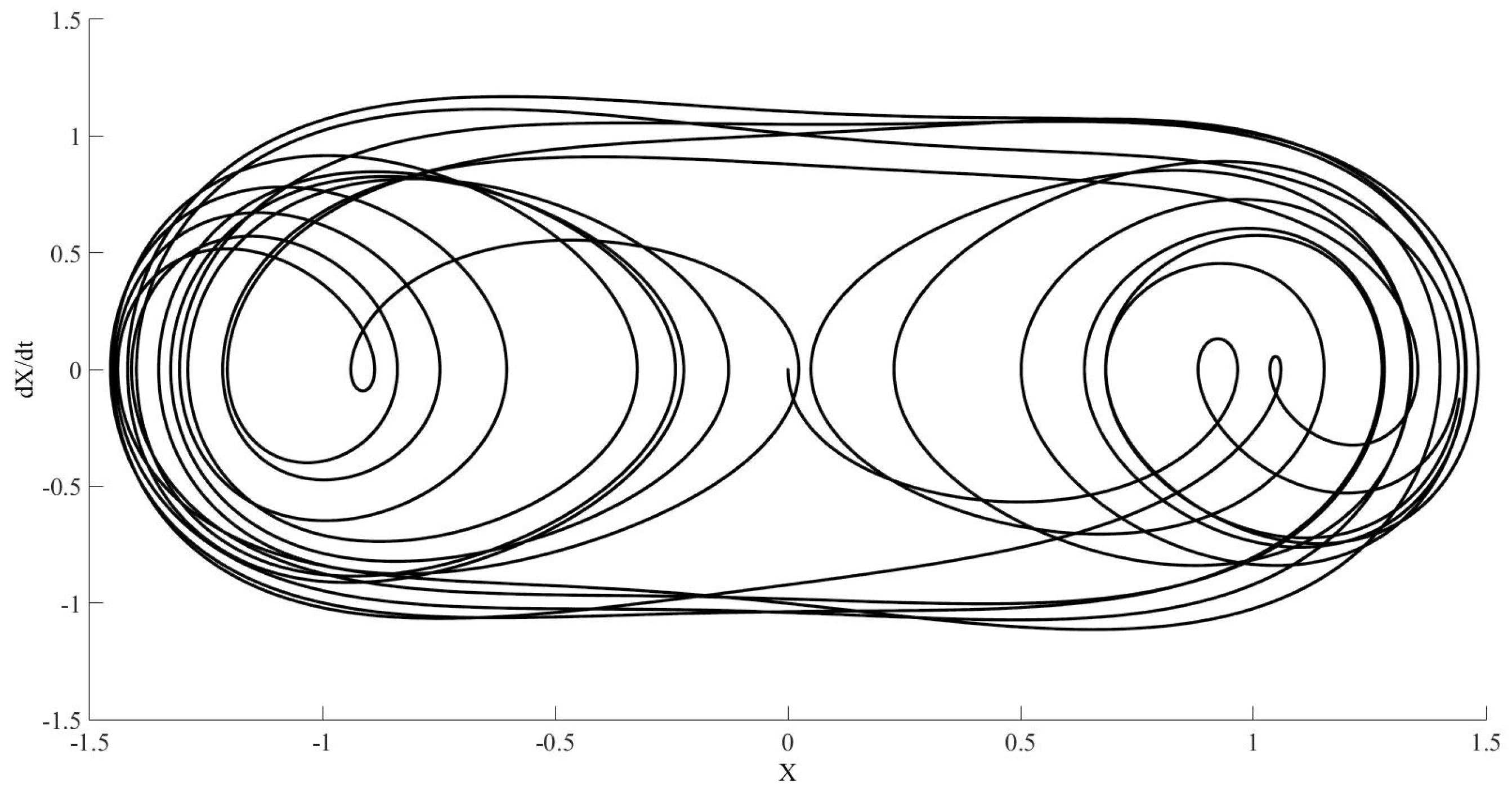
Figure 3 shows the phase diagram for RELTOL and VNTOL equal to
. The simulated time is 1000 s.
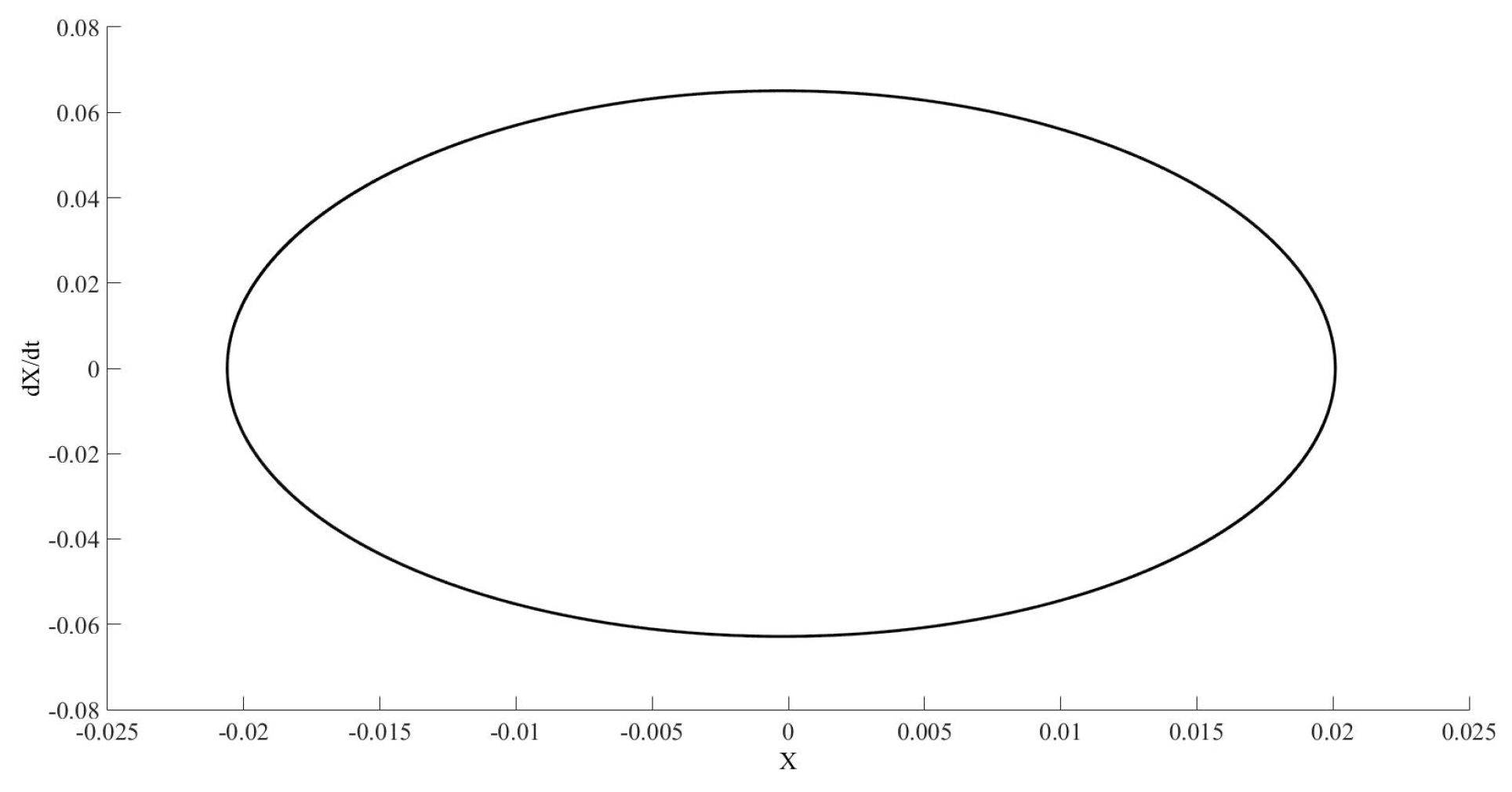
Figure 4 represents only the interval between 900 and 1000 s, while
Figure 5 represents only the interval between 0 and 100 s.
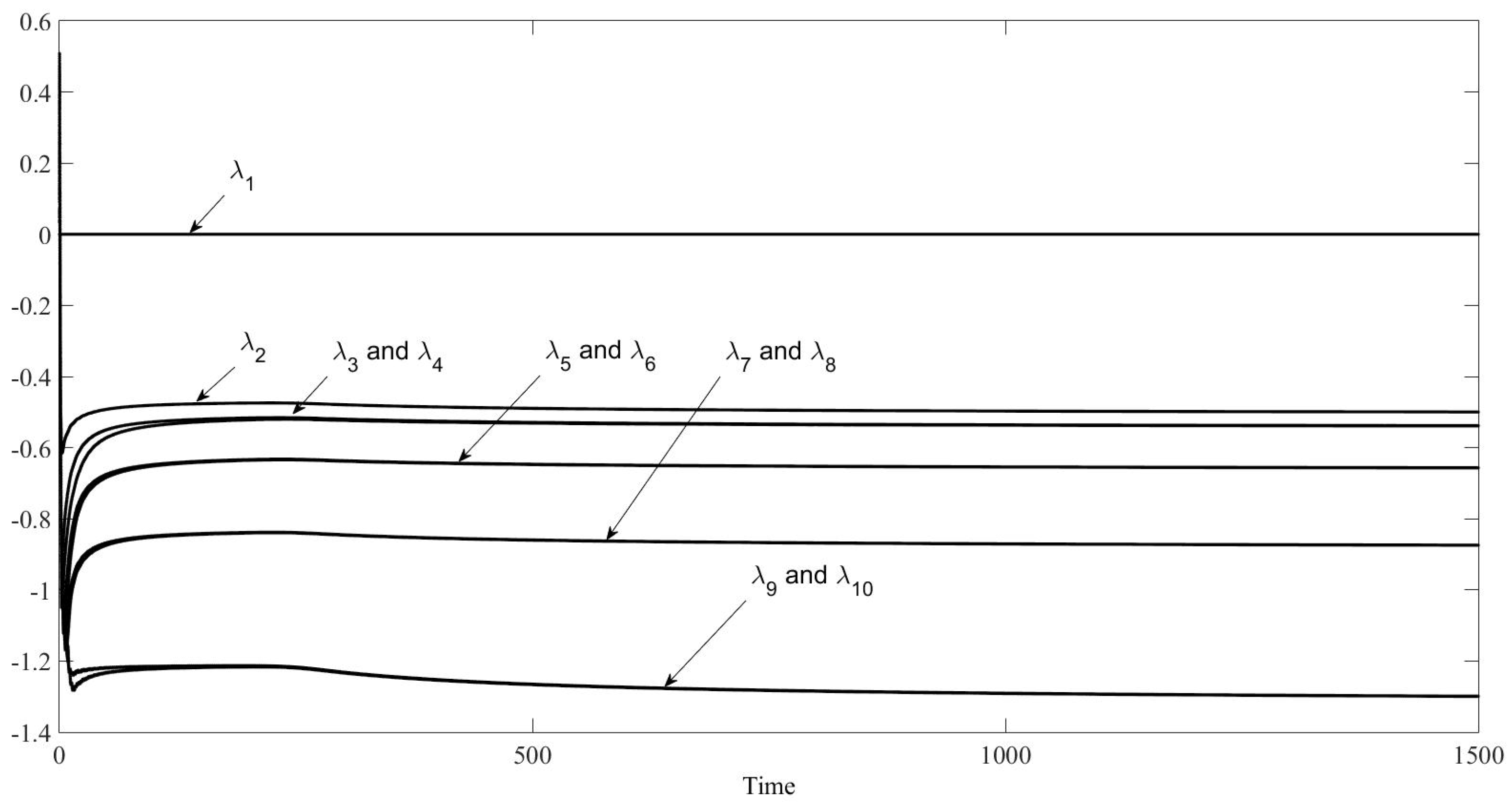
Figure 6 shows the Lyapunov exponents of this system, which are negative and therefore prove the system stability. Nevertheless, it is necessary to take care of, since it is not immediate that in physical phenomena described by differential or difference equations, the existence of a trajectory with a positive Lyapunov exponent implies the system is instable and by opposite a trajectory with negative Lyapunov exponent is stable. As Balibrea and Caballero showed [
23], the positivity or negativity are held uniformly in subsets of the phase space. In such cases positivity implies instability and negativity implies stability. A detailed analysis of Lyapunov exponents is applied to some examples in certain articles [
23,
24].
At this moment, we seek to analyse the effect of the convergence tolerance in the solution in the first seconds. Thus,
Figure 7 represents the solution for RELTOL and VNTOL equal to
. There are differences between
Figure 5 and
Figure 7 even when using these small values for tolerances. It is also possible to find differences in the case of a courser convergence tolerance as in
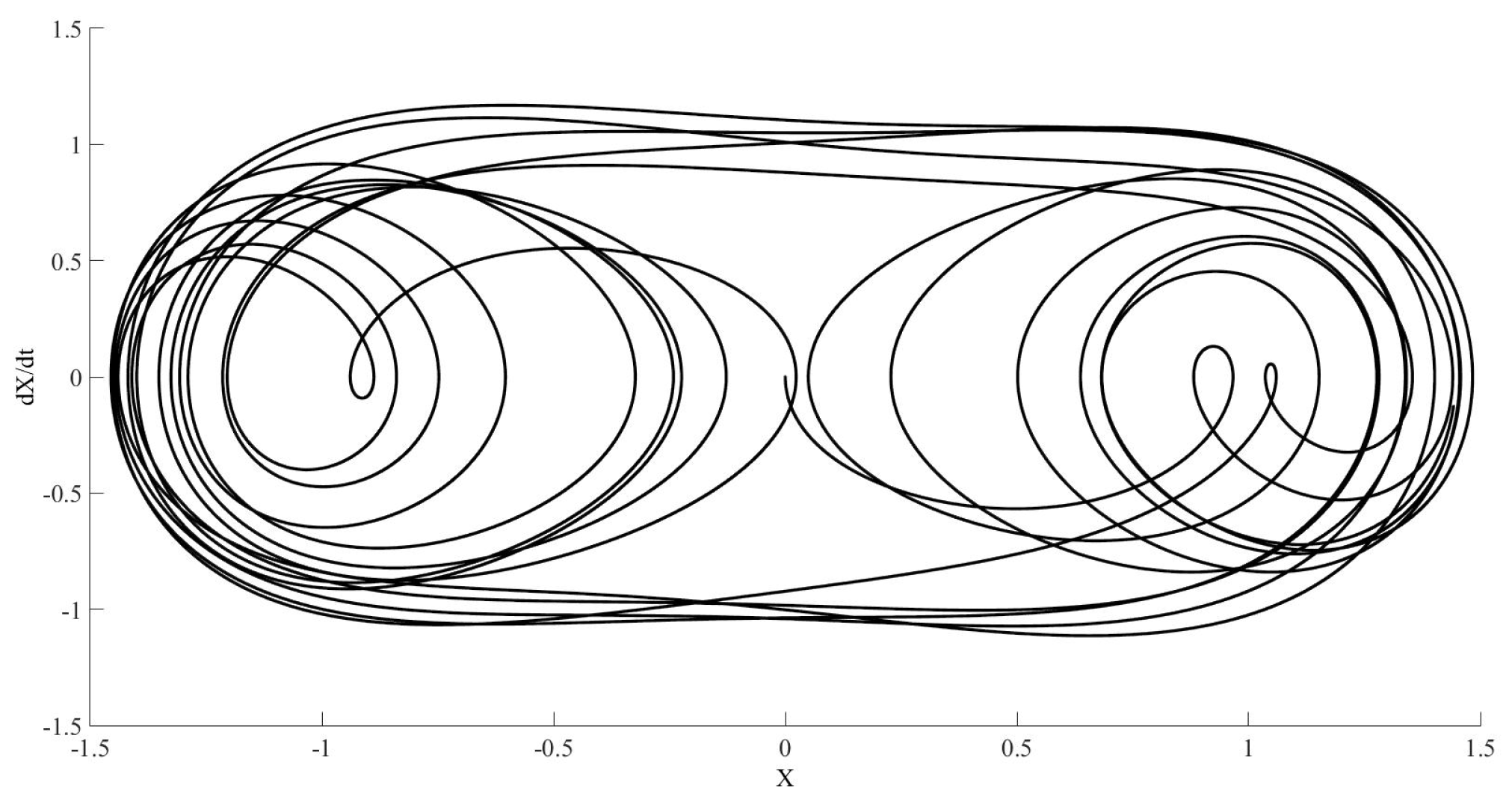
Figure 8, with RELTOL and VNTOL equal to
. Finally, with RELTOL and VNTOL equal to
,
Figure 9, we have found the same solution as in
Figure 7. Since the number of calculated points is very high with this convergence tolerance, only a selection of a few points corresponding to each second is recorded separately in order to obtain the last figure; and the calculation then starts again from zero to obtain the following second recorded.
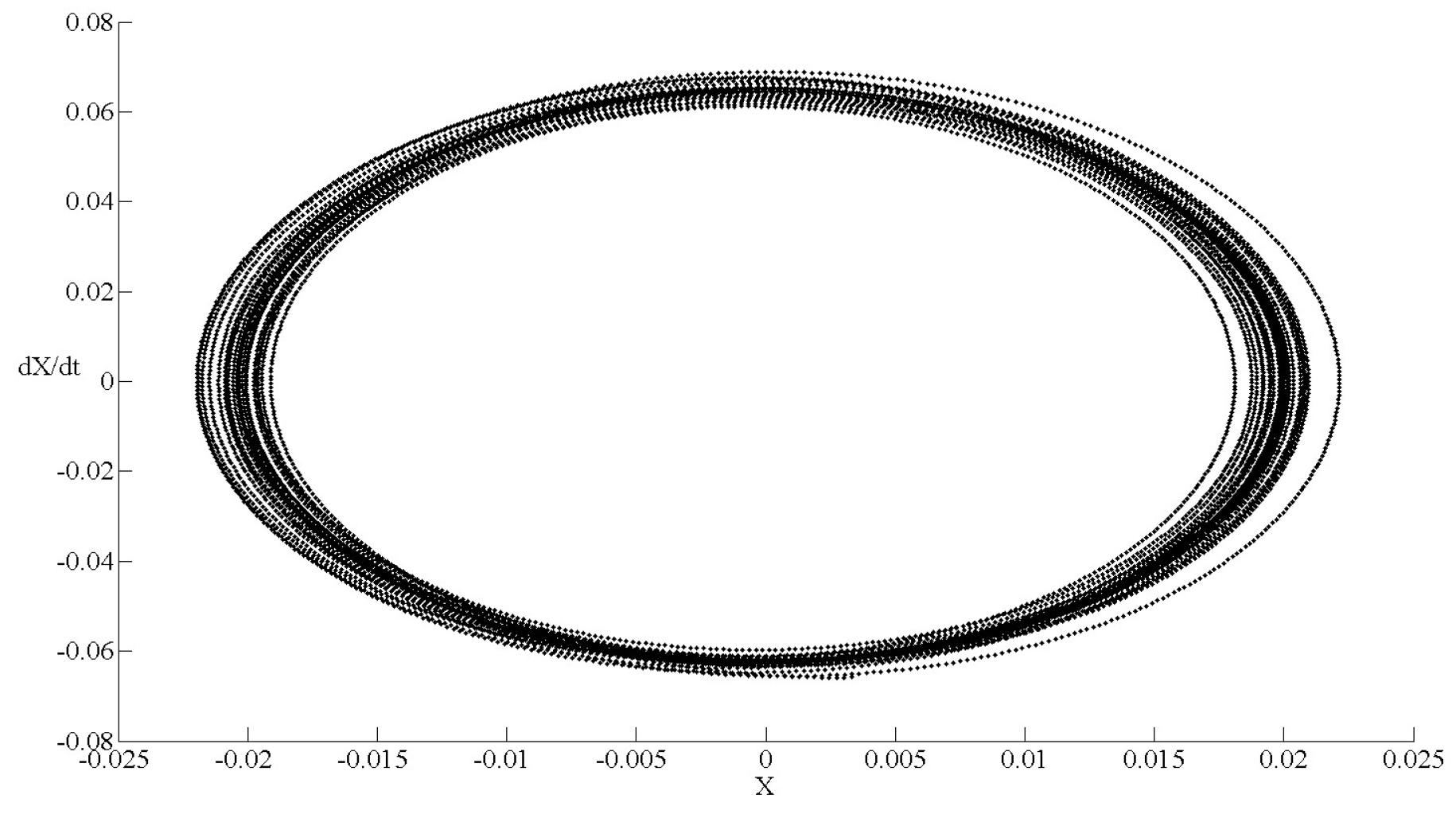
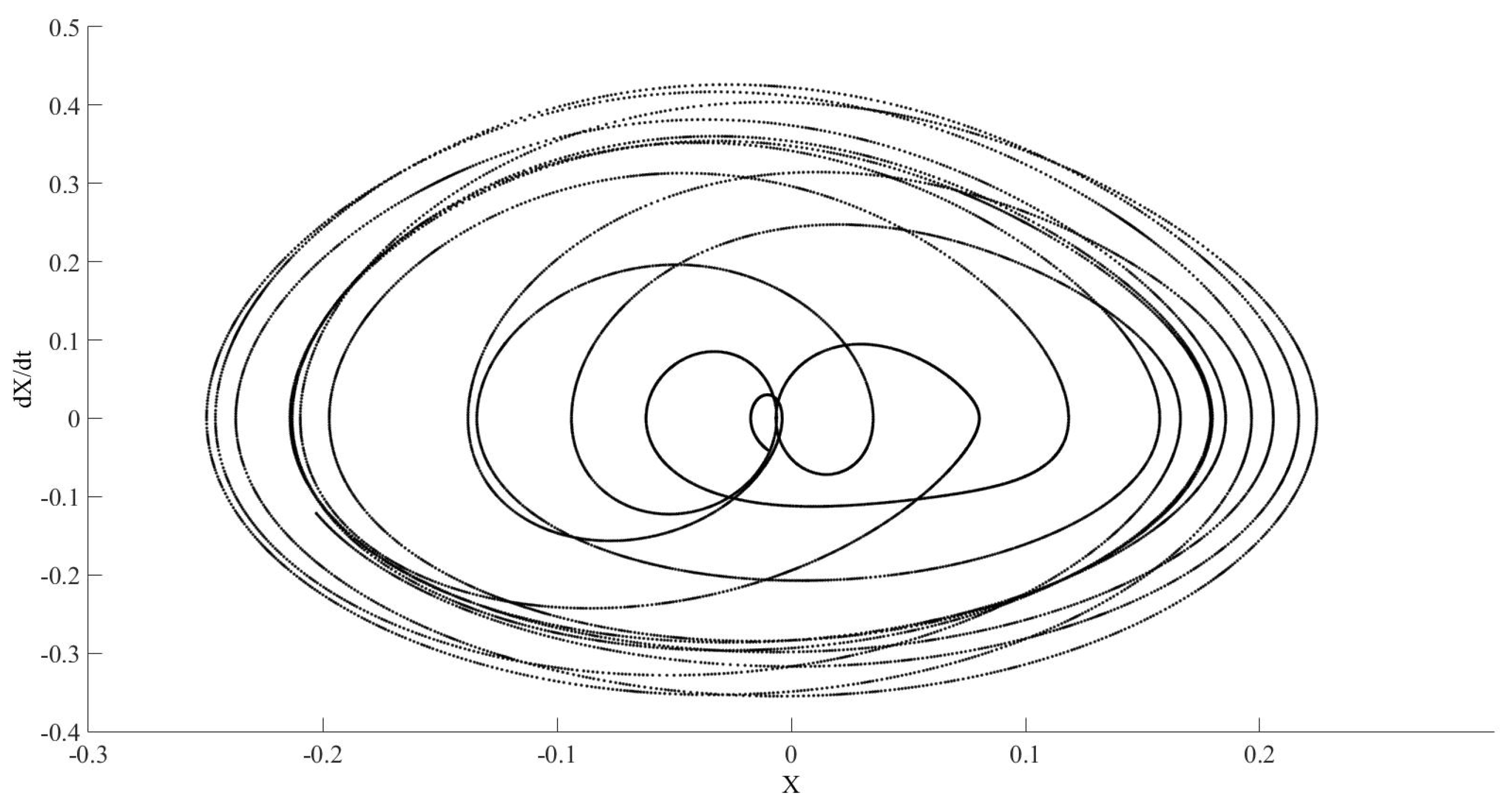
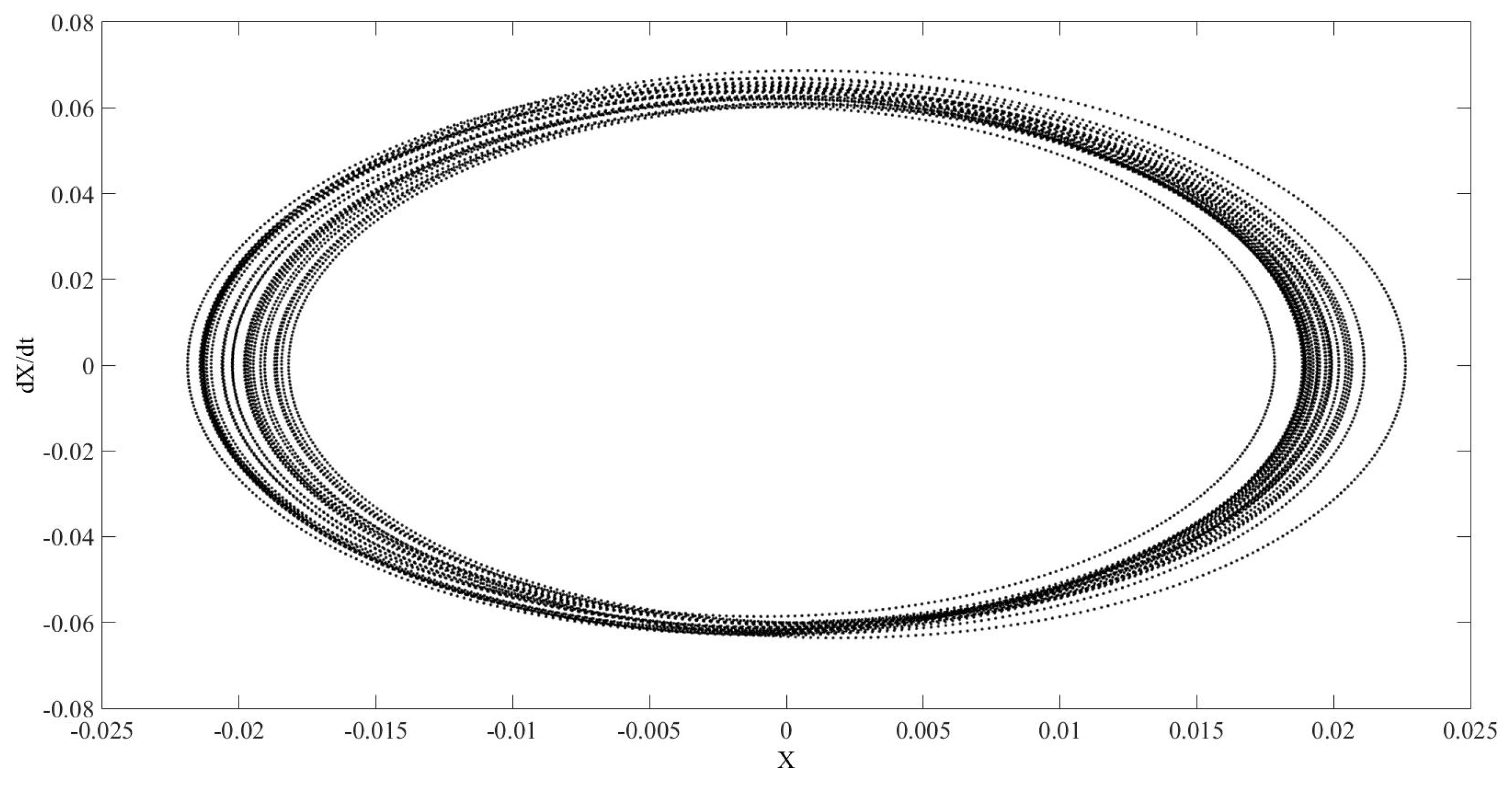
After the previous analysis, the FKT model, a more complex case, will be solved for the following parameters: equal to 0.5, c equal to 144/233, equal to 0.1, equal to 1, equal to 1.5, is equal to zero, and is equal to 0.1.
We solved the model numerically for different convergence tolerances.
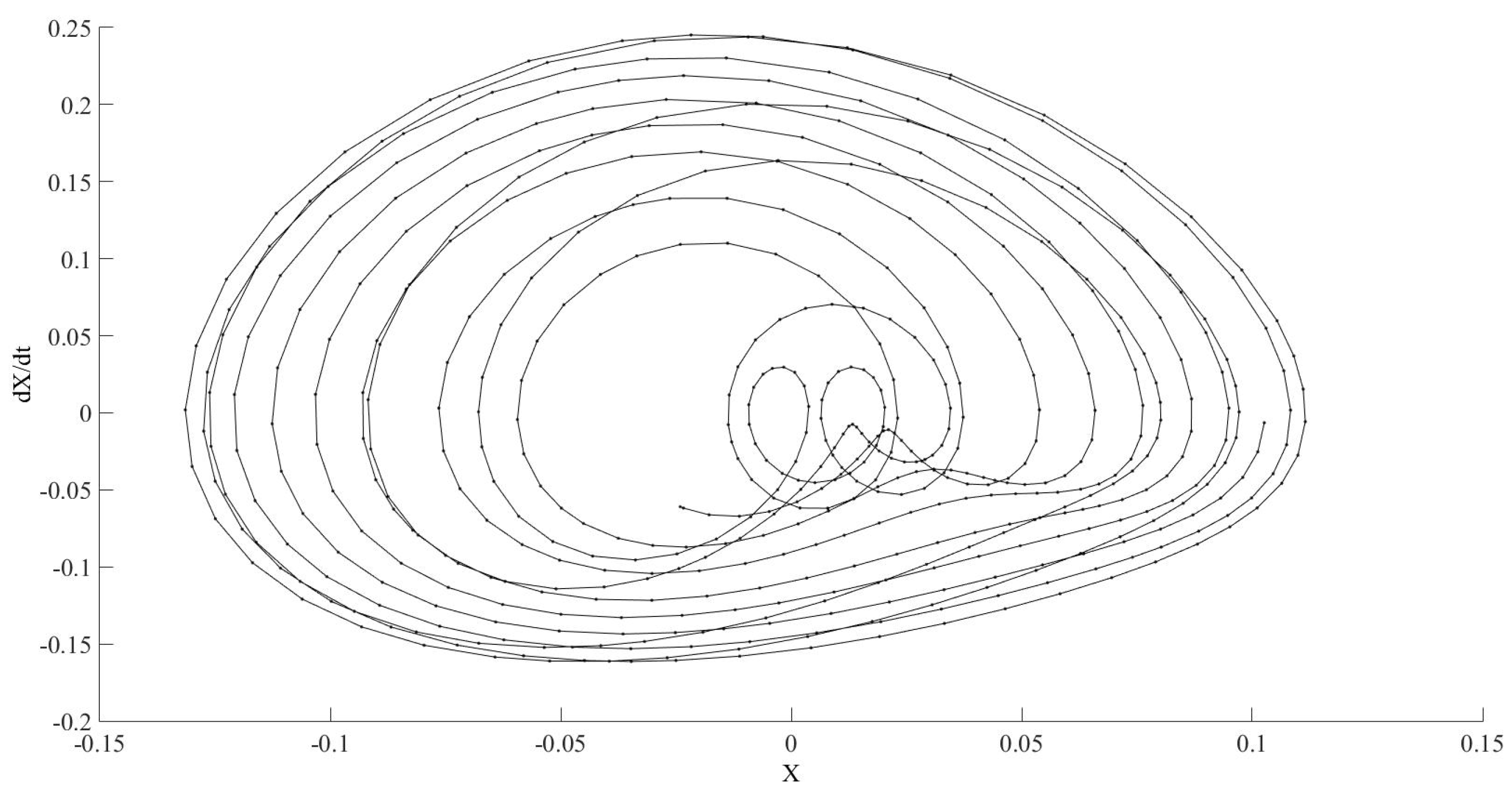
Figure 10 shows the phase diagram for RELTOL and VNTOL equal to
. The represented time is range from 1450 to 1500 s.
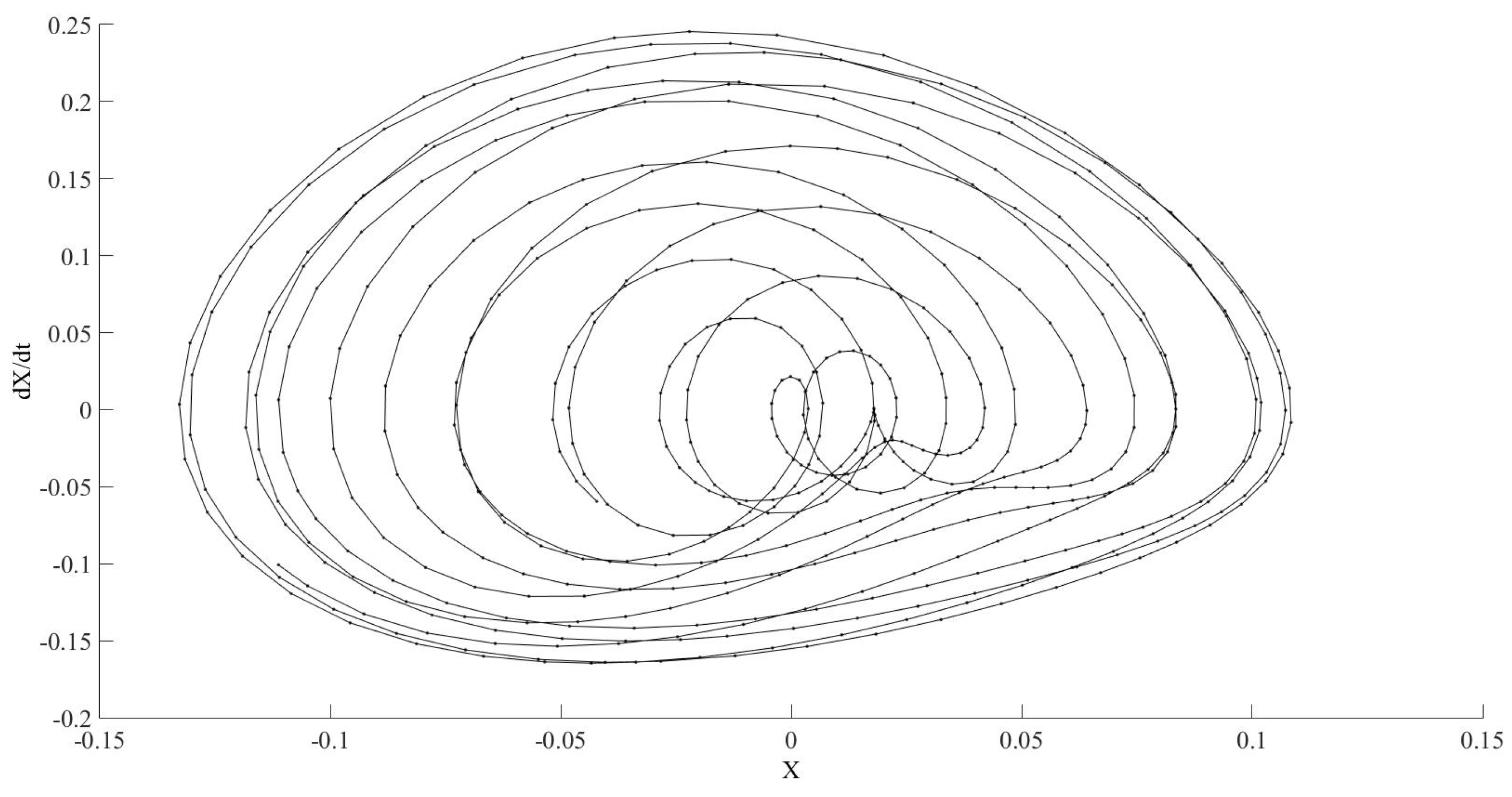
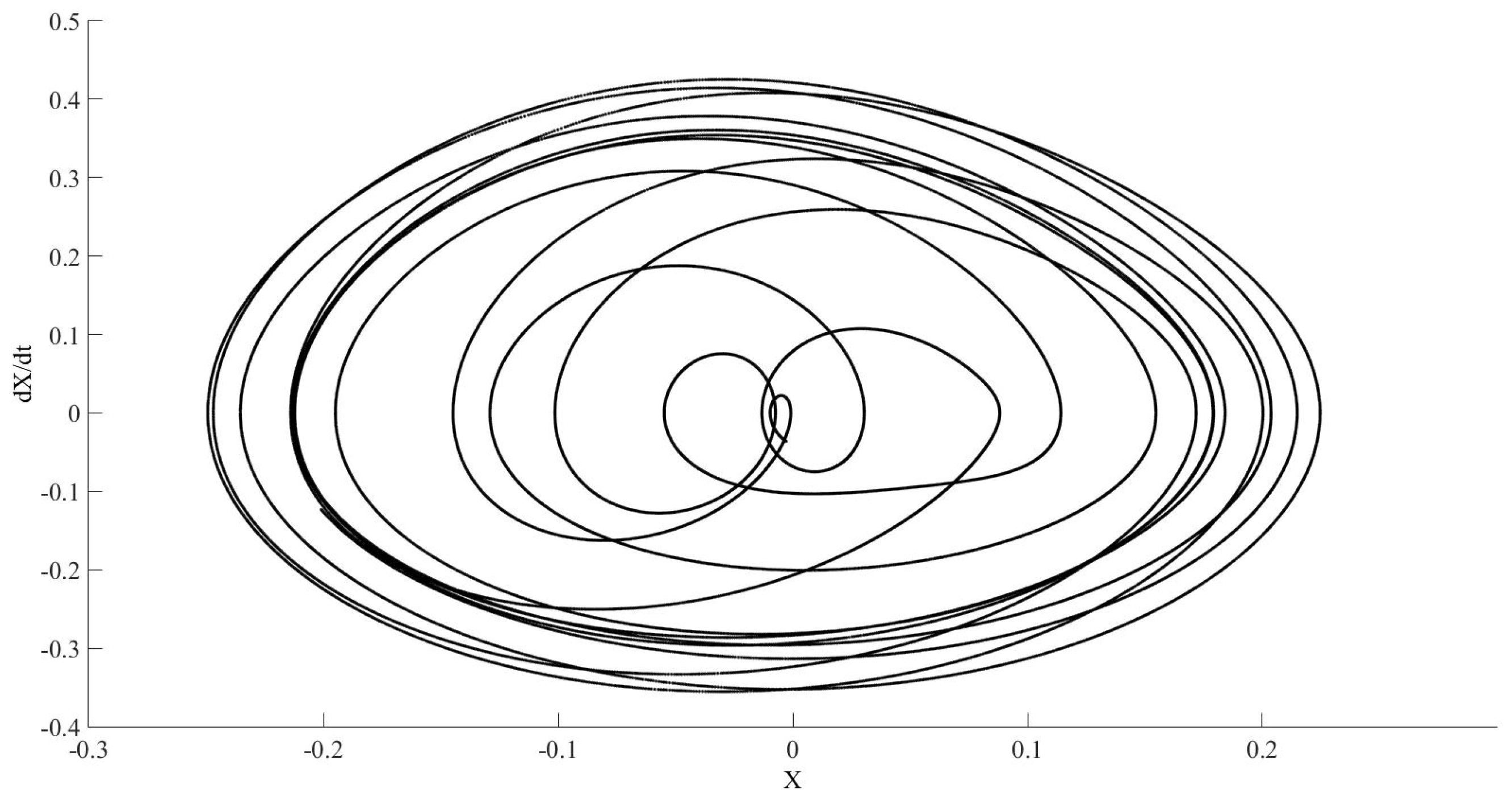
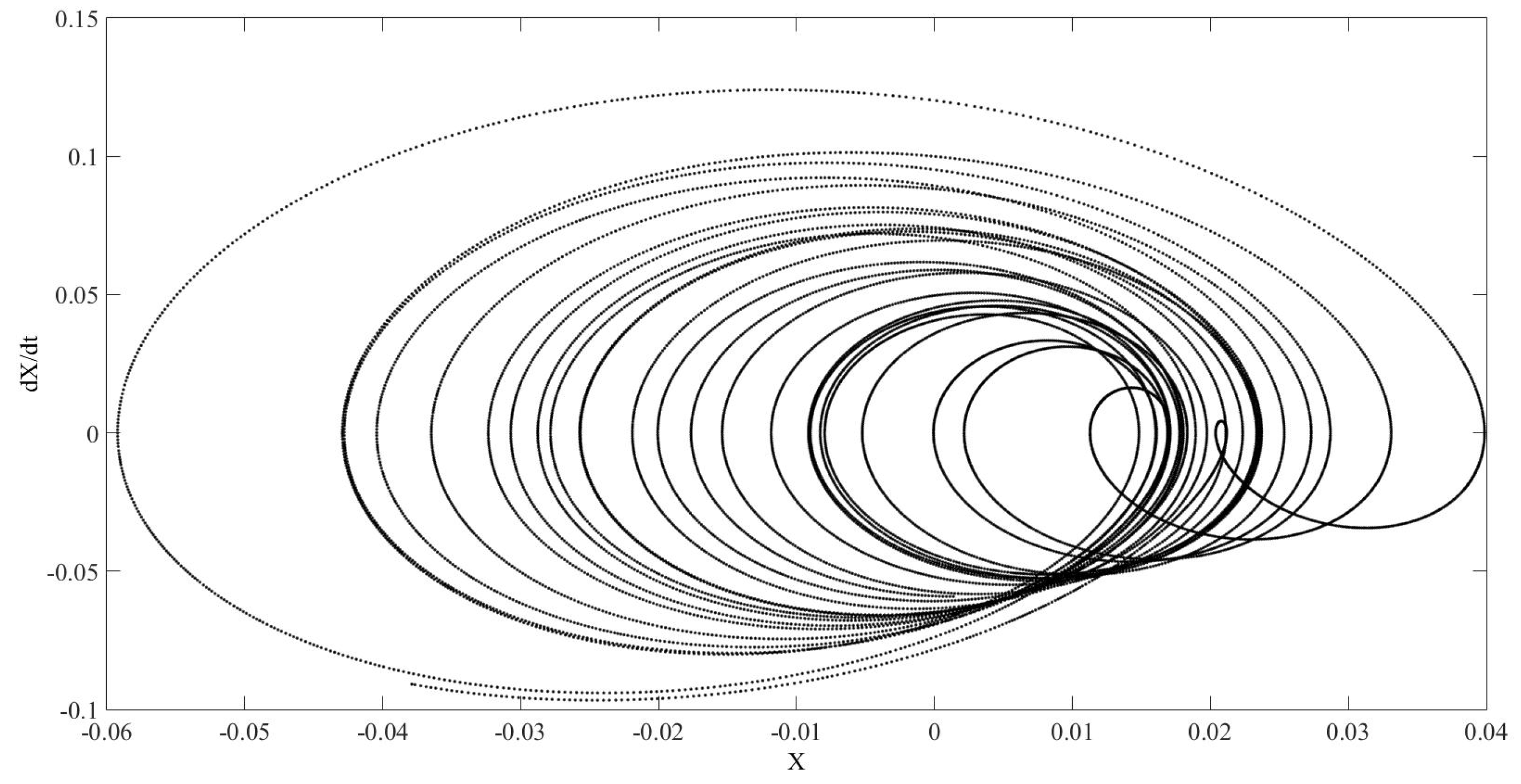
Figure 11,
Figure 12 and
Figure 13 show the effect of reducing the value of these tolerances.
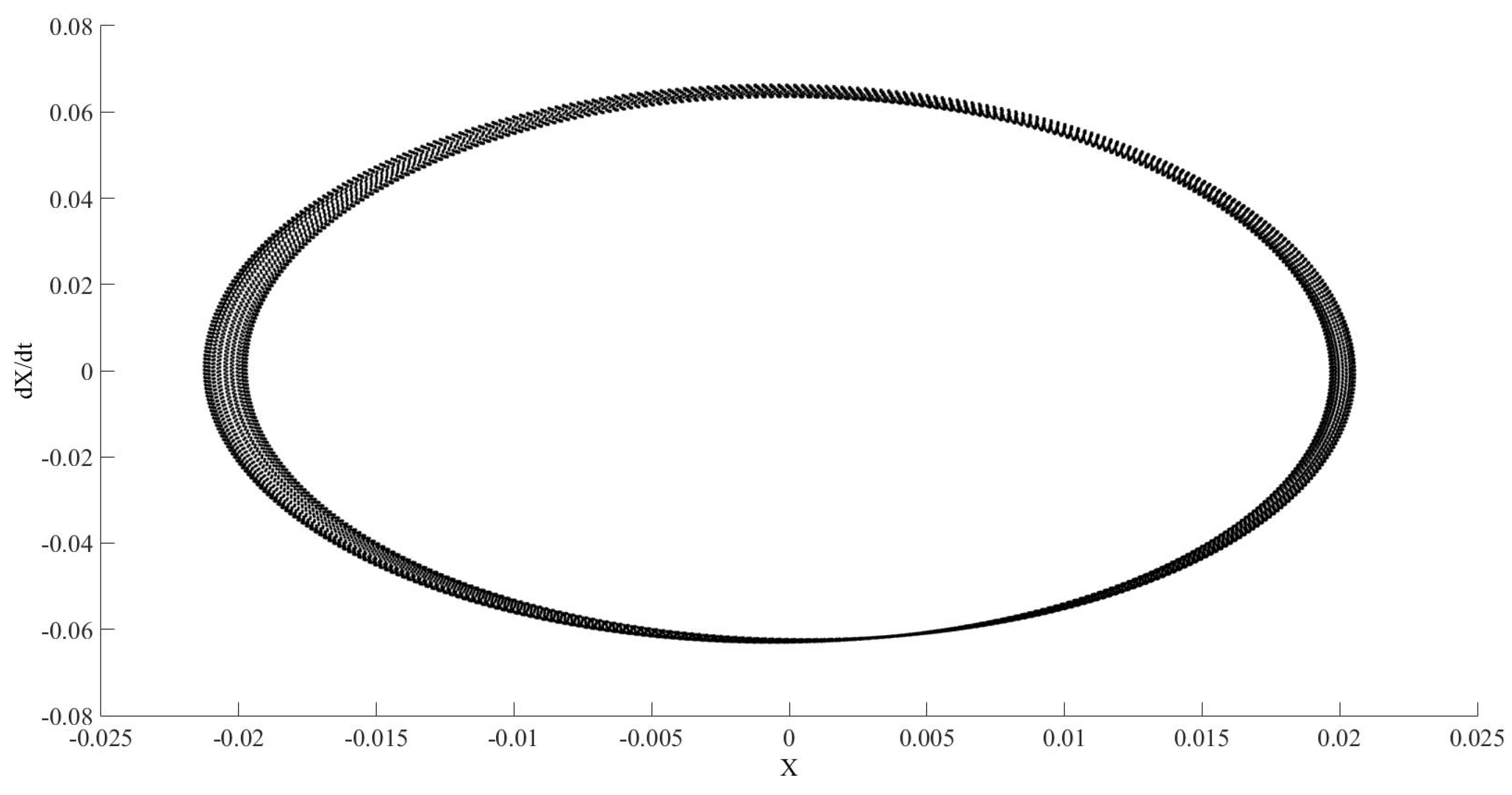
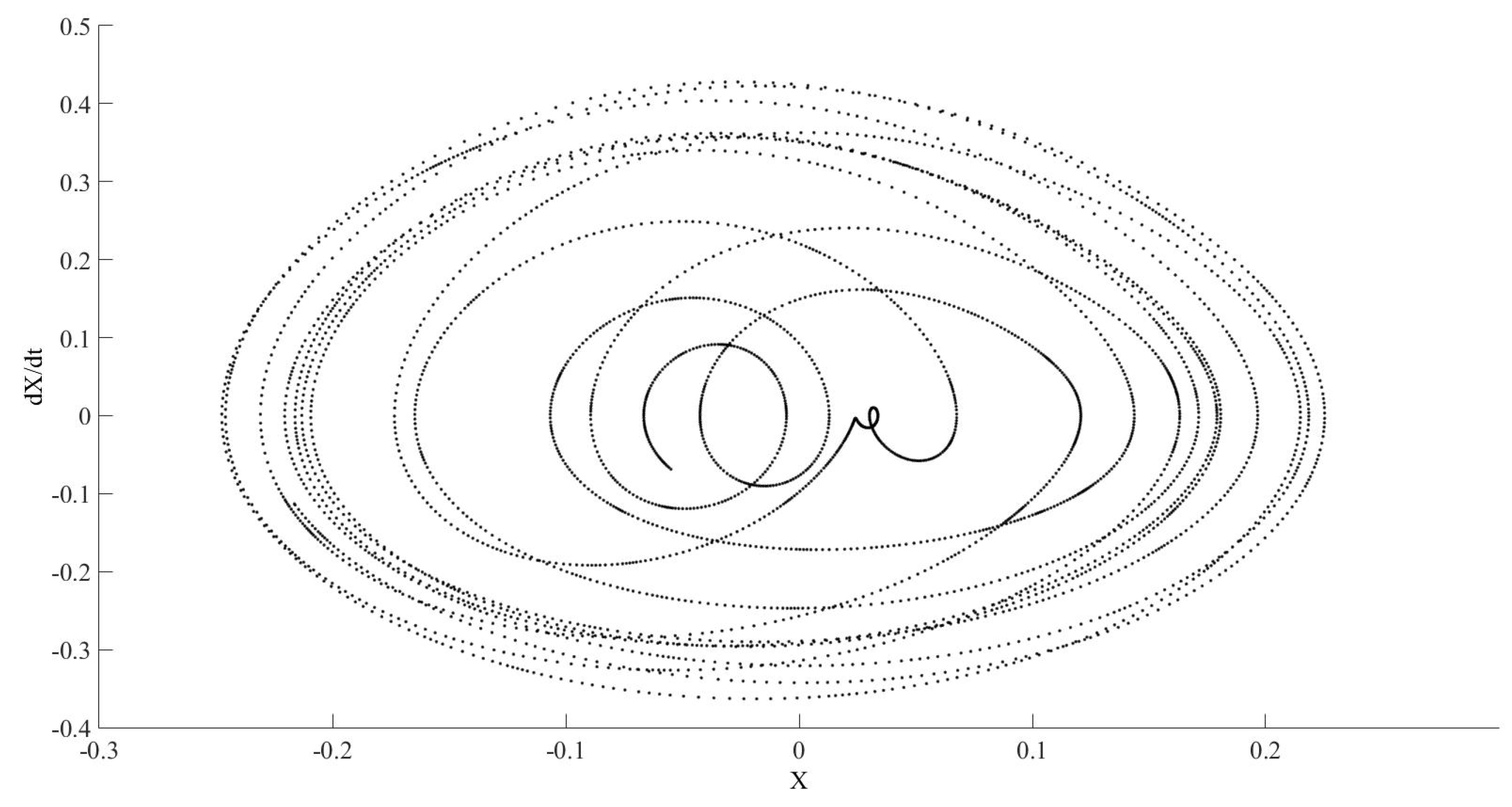
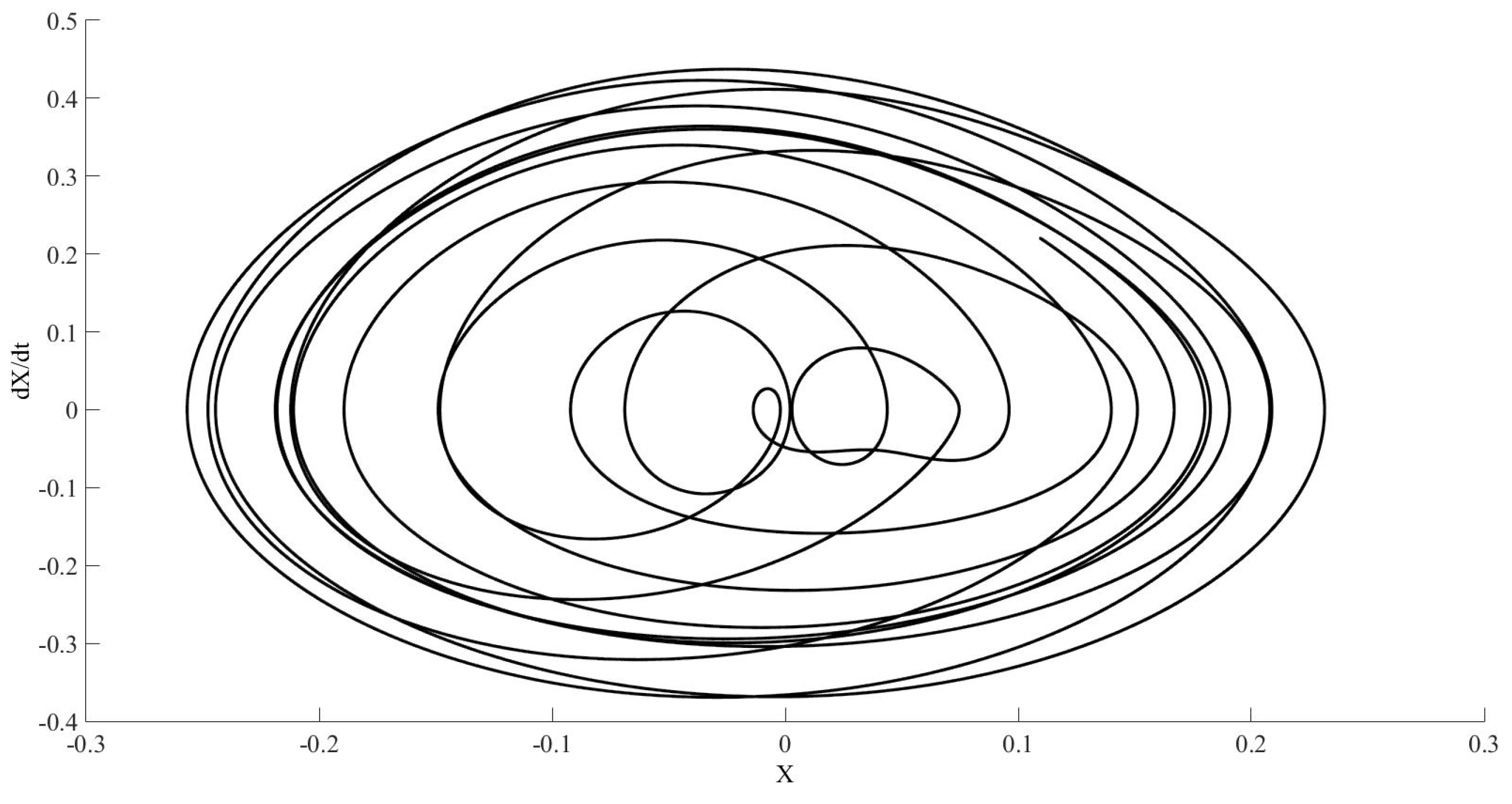
Figure 14 and
Figure 15 show the results for the same tolerances as
Figure 13 in different time intervals.
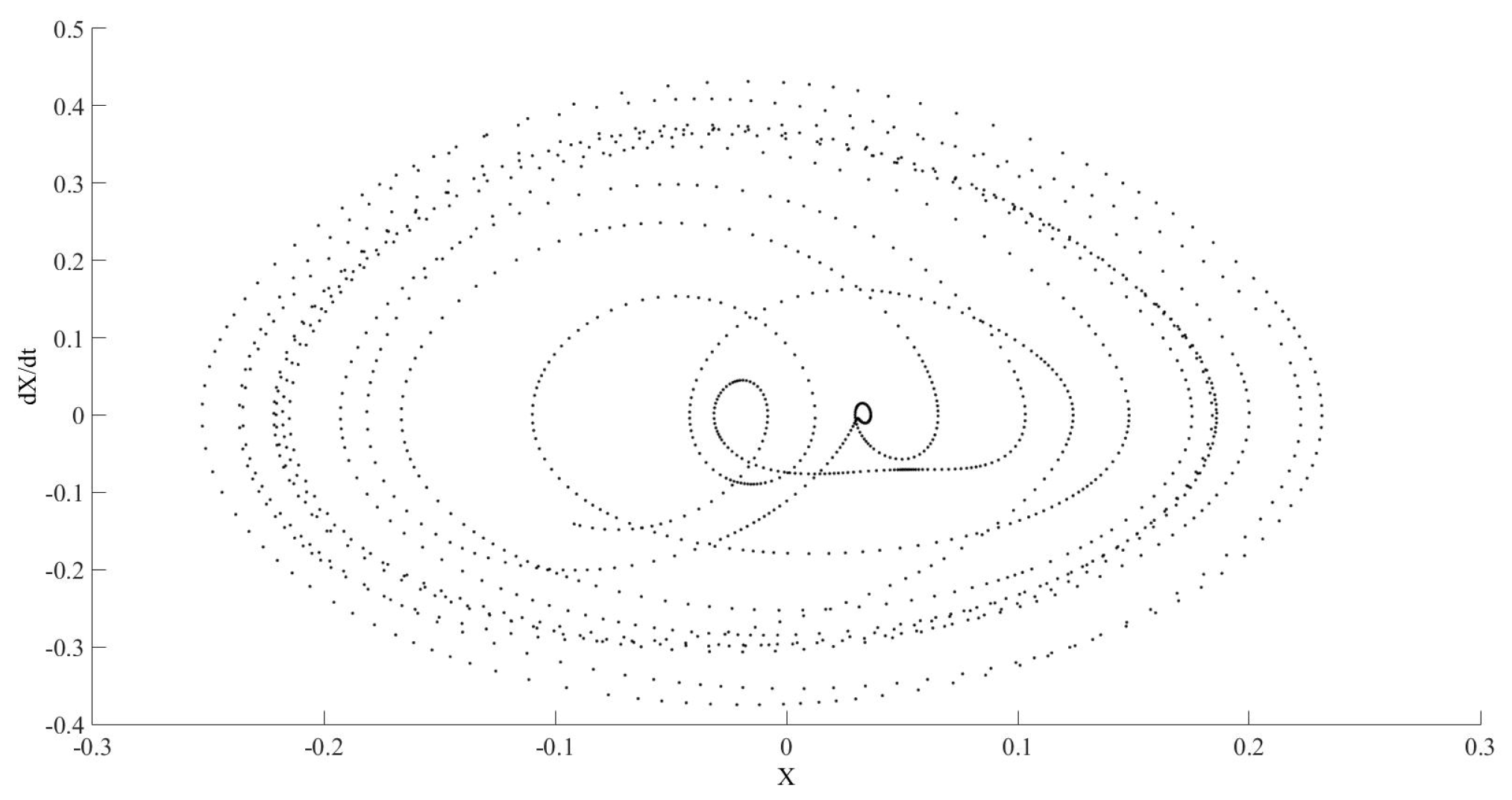
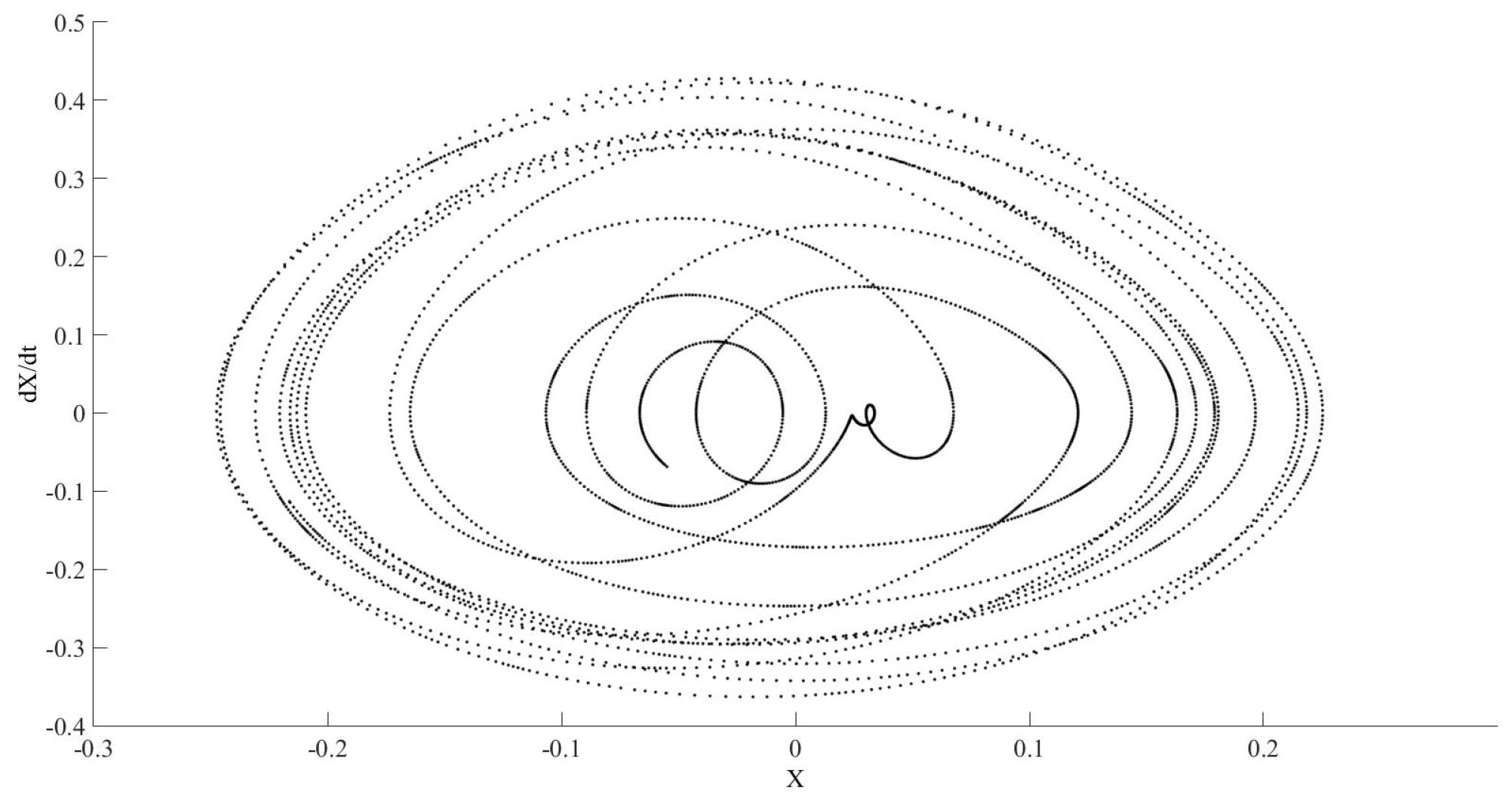
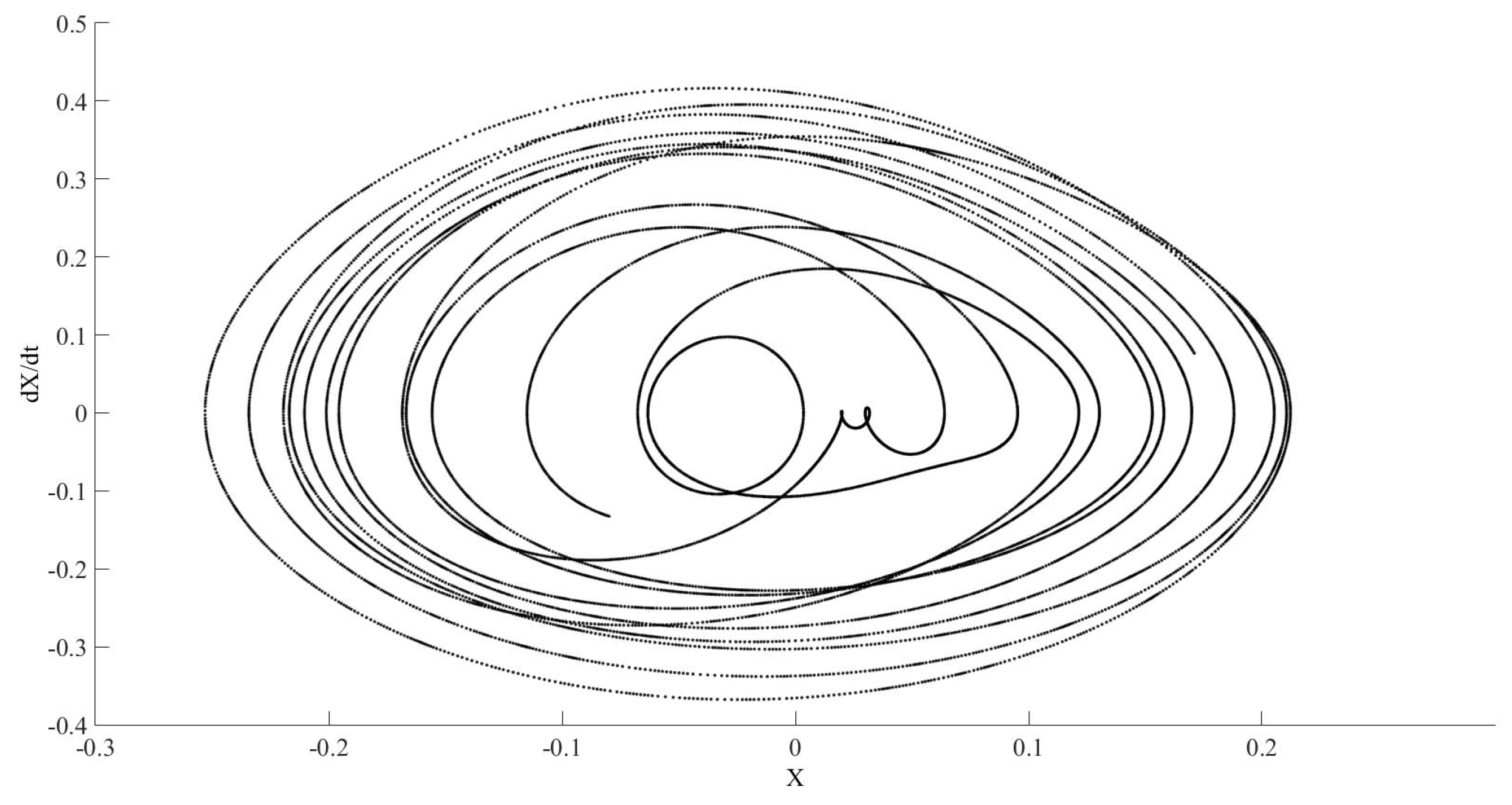
An additional calculation, represented in
Figure 18, has been developed using different characterisation parameters for the element of the network. Thus, the initial estimation for zero and infinite resistance,
and
, respectively, has been change to
and
. The differences between
Figure 10 and
Figure 18 shows the difficulty to obtain the real behaviour of this system.
It is very difficult for the hardware available to obtain the Lyapunov exponent for this equations system during at least 300 s. We try to study the phenomenon with a reduced model with 21 equations. In this case, the variable
c is 13/21.
Figure 28 and
Figure 29 show the effect of
.
Figure 29 and
Figure 30 represent the effect of the tolerance. Thus,
Figure 29, with a lower tolerance than
Figure 30, is the most accurate. The phase diagram shows that the system has no determined trajectory.
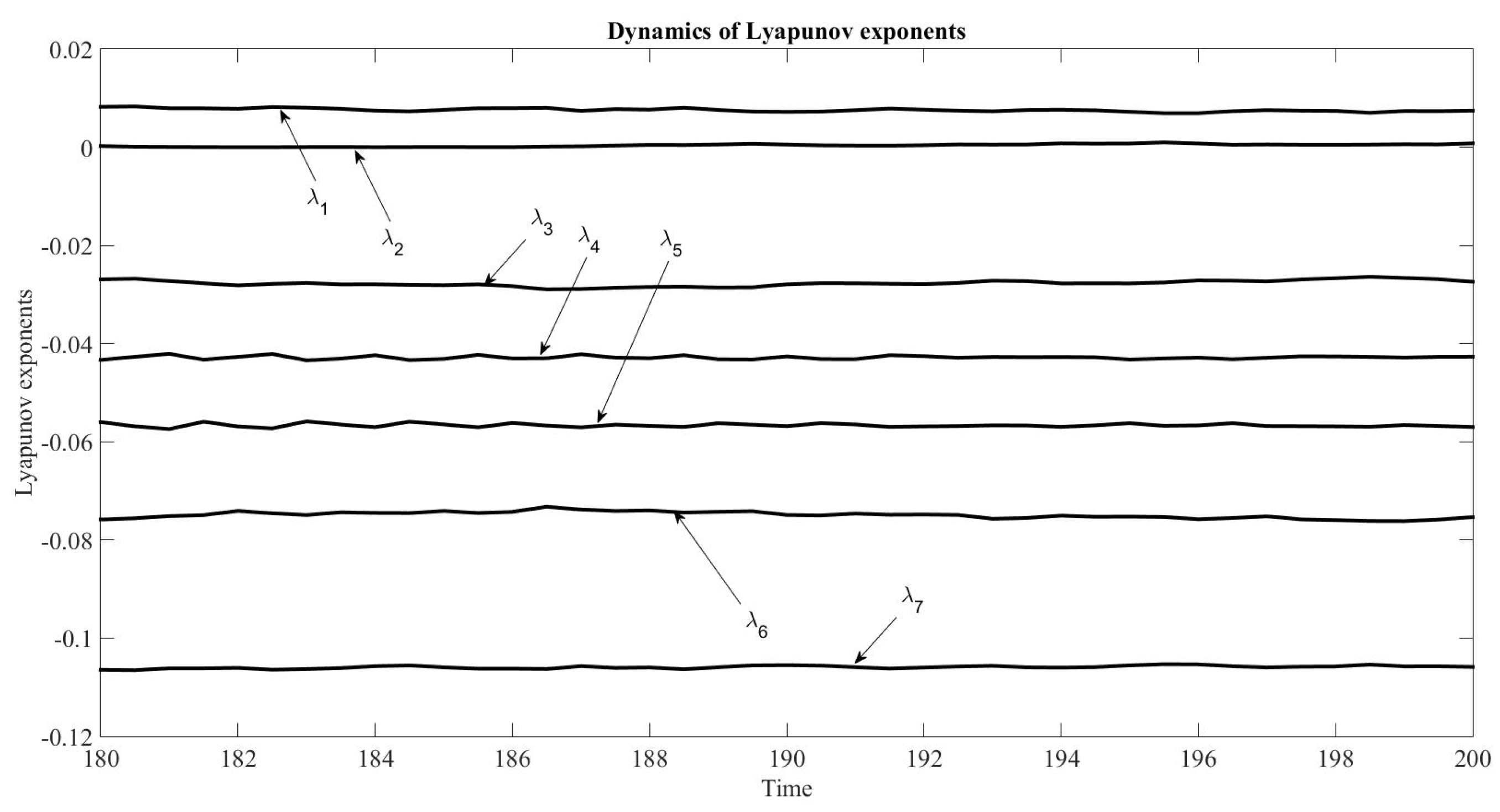
It is possible to calculate the Lyapunov exponent for this equations system,
Figure 31. There is no positive exponent; however, the system is chaotic.
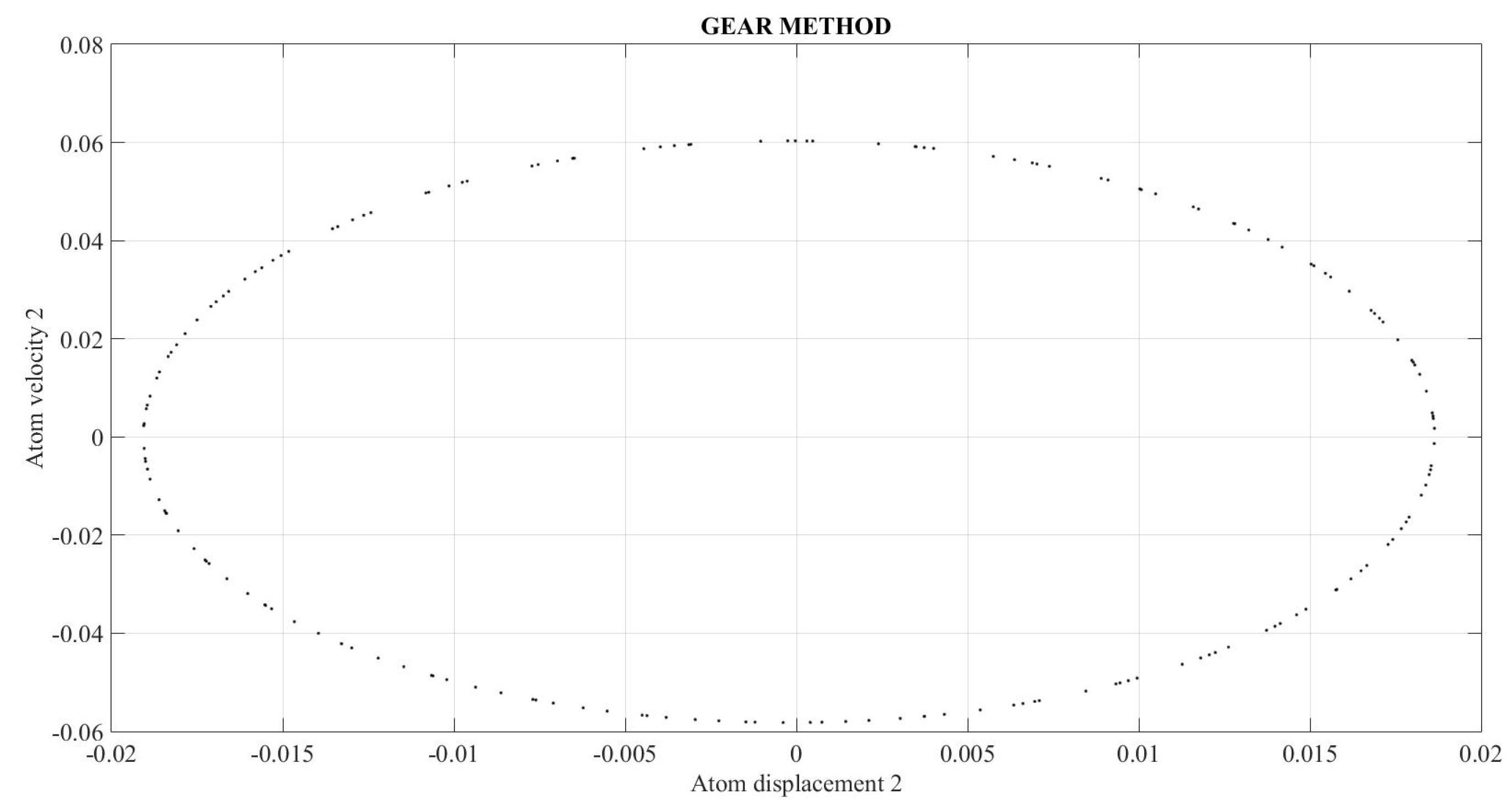
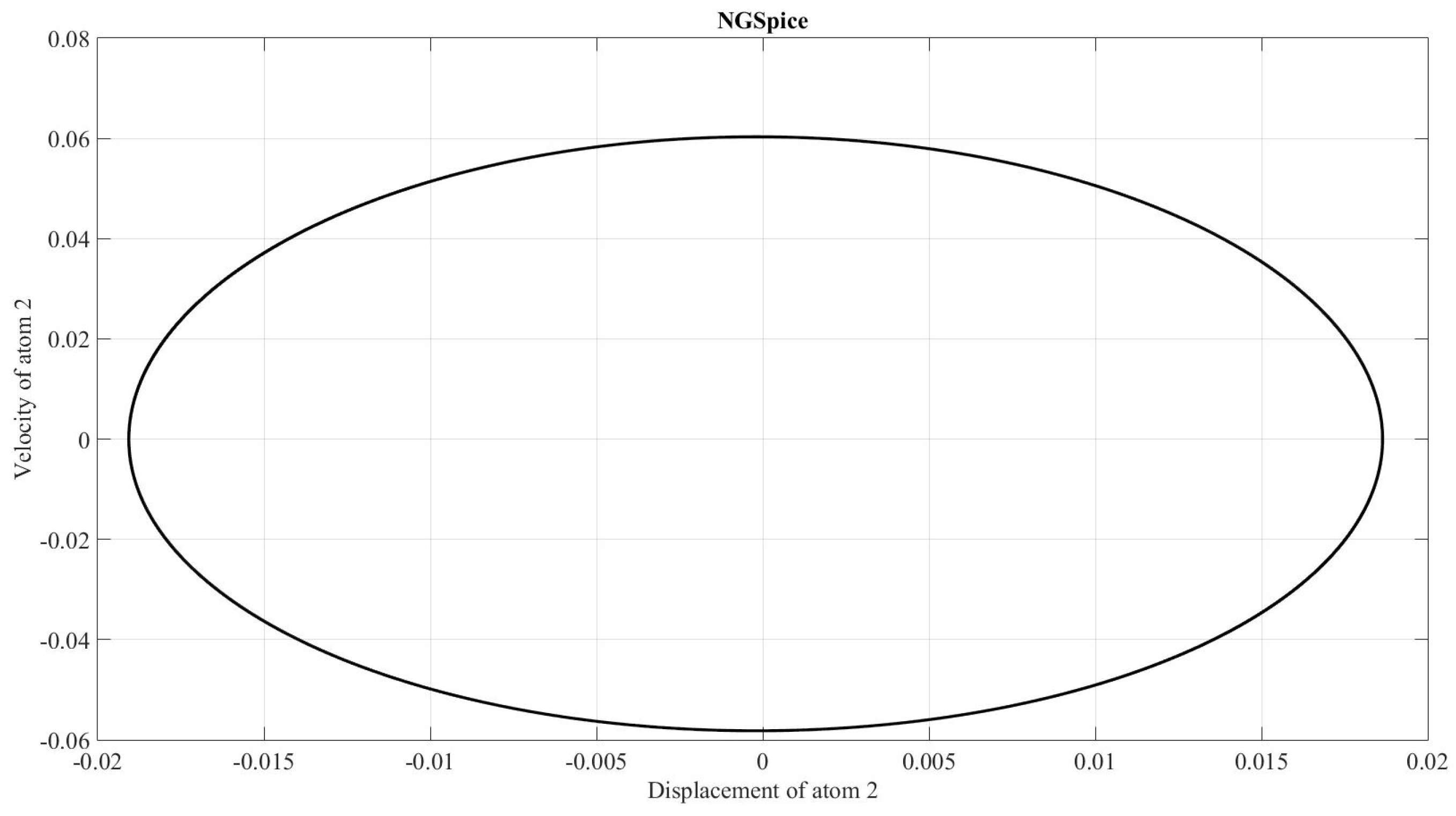
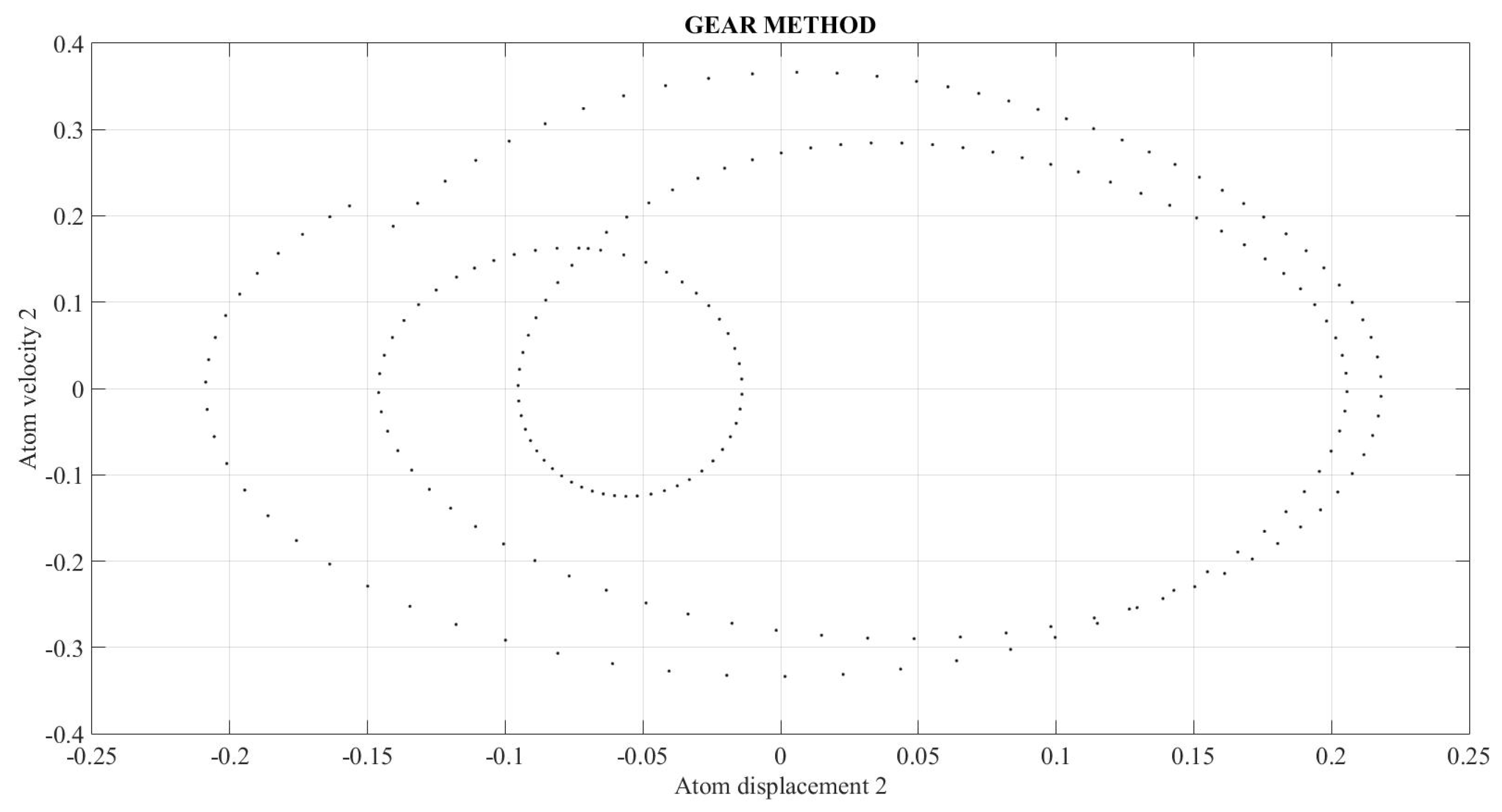
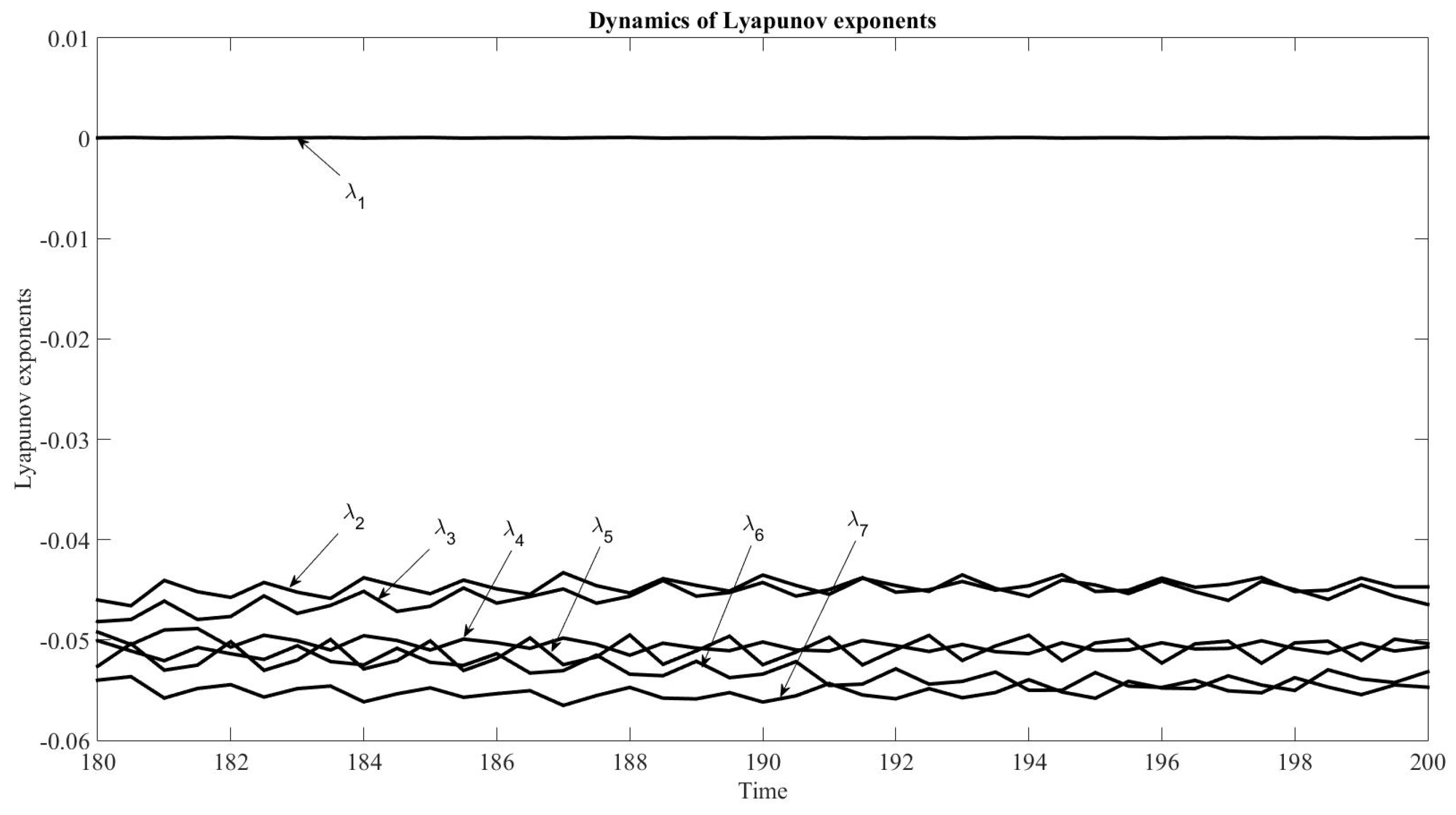
In addition to the former calculations, a comparison is made between the results using Gear Method with MATLAB and Network Simulation methods with ngspice for FKT problem with only 3 atoms,
Figure 32,
Figure 33,
Figure 34,
Figure 35,
Figure 36 and
Figure 37.
Figure 32 and
Figure 33 represent the phase diagrams with the parameter
equal to 1.6 using MATLAB and ngspice, respectively. For this parameter, the system behaviour is periodical, as both programs show. Furthermore, the results in both programs are the same.
Figure 34 and
Figure 35 represent the phase diagrams with the parameter
equal to 1.4 using MATLAB and ngspice, respectively. For this parameter, the system behaviour is chaotic, as both programs show. Furthermore, the results in both programs are similar but not equal. The Lyapunov exponents for the two values of parameter
are verified in the results shown in
Figure 36 and
Figure 37.
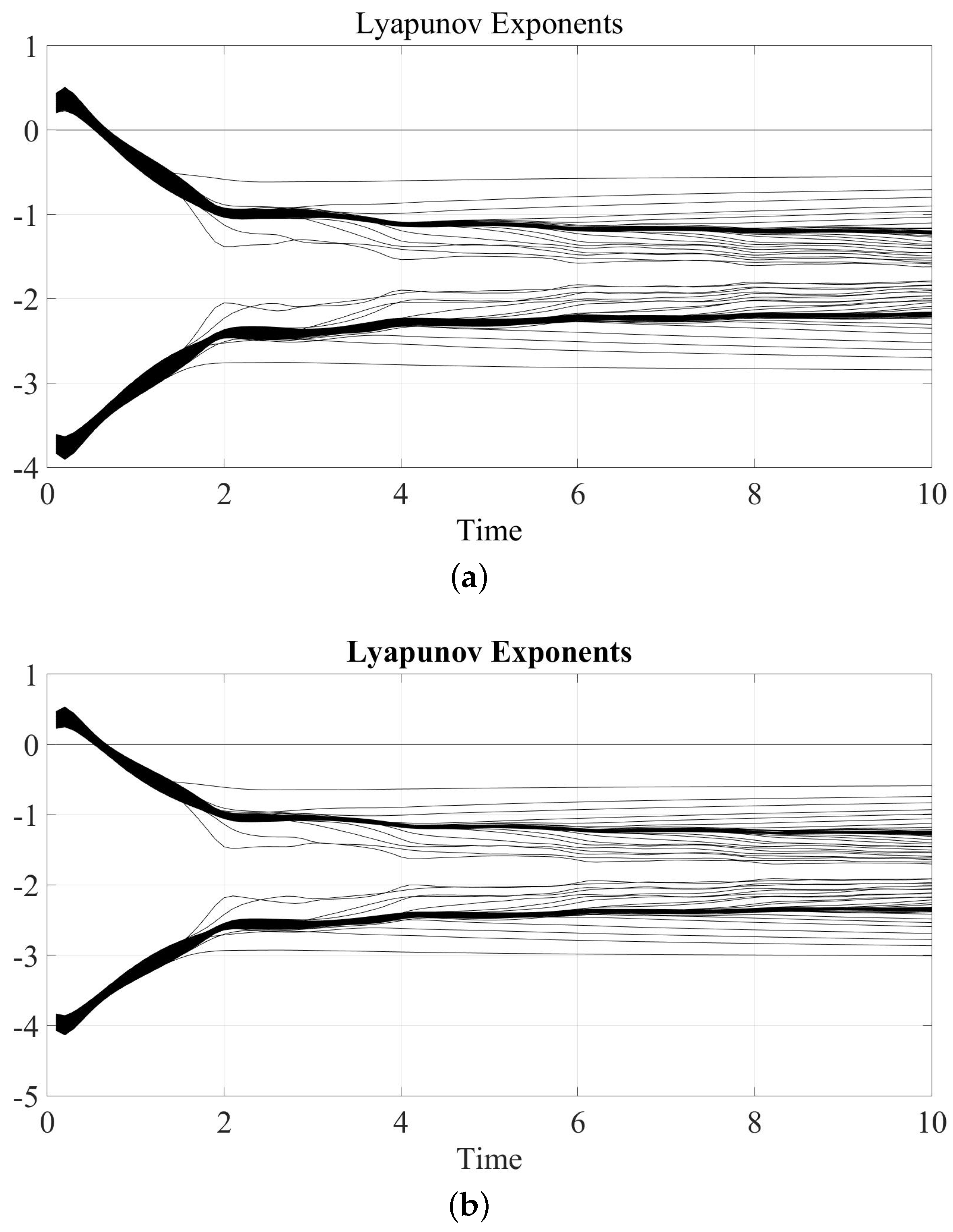
The Lyapunov exponents for two values of parameter
and 233 atoms, considering only 10 s, verify these results,
Figure 38. In this case, the Lyapunov exponents are not able to display the chaotic behaviour. Furthermore,
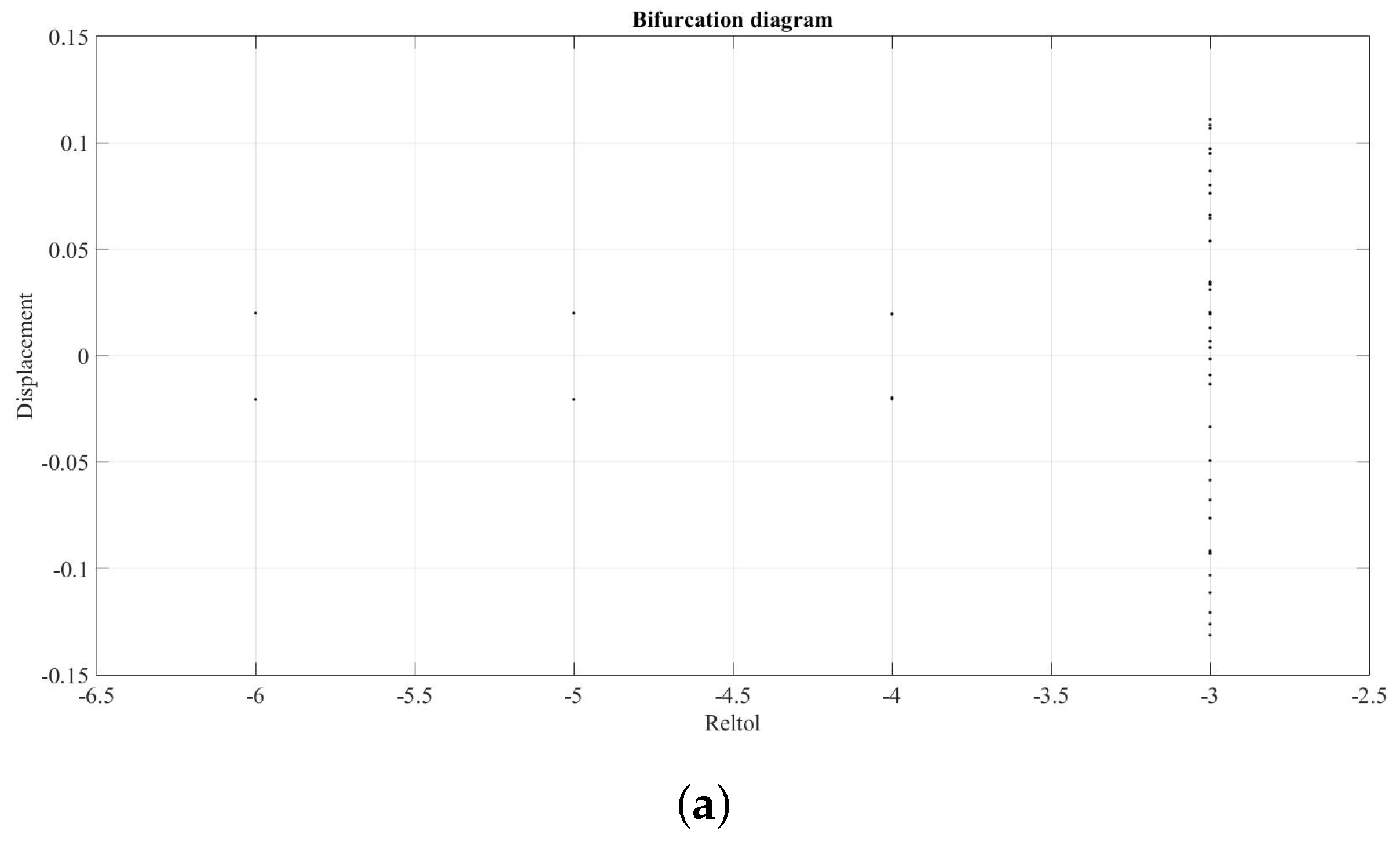
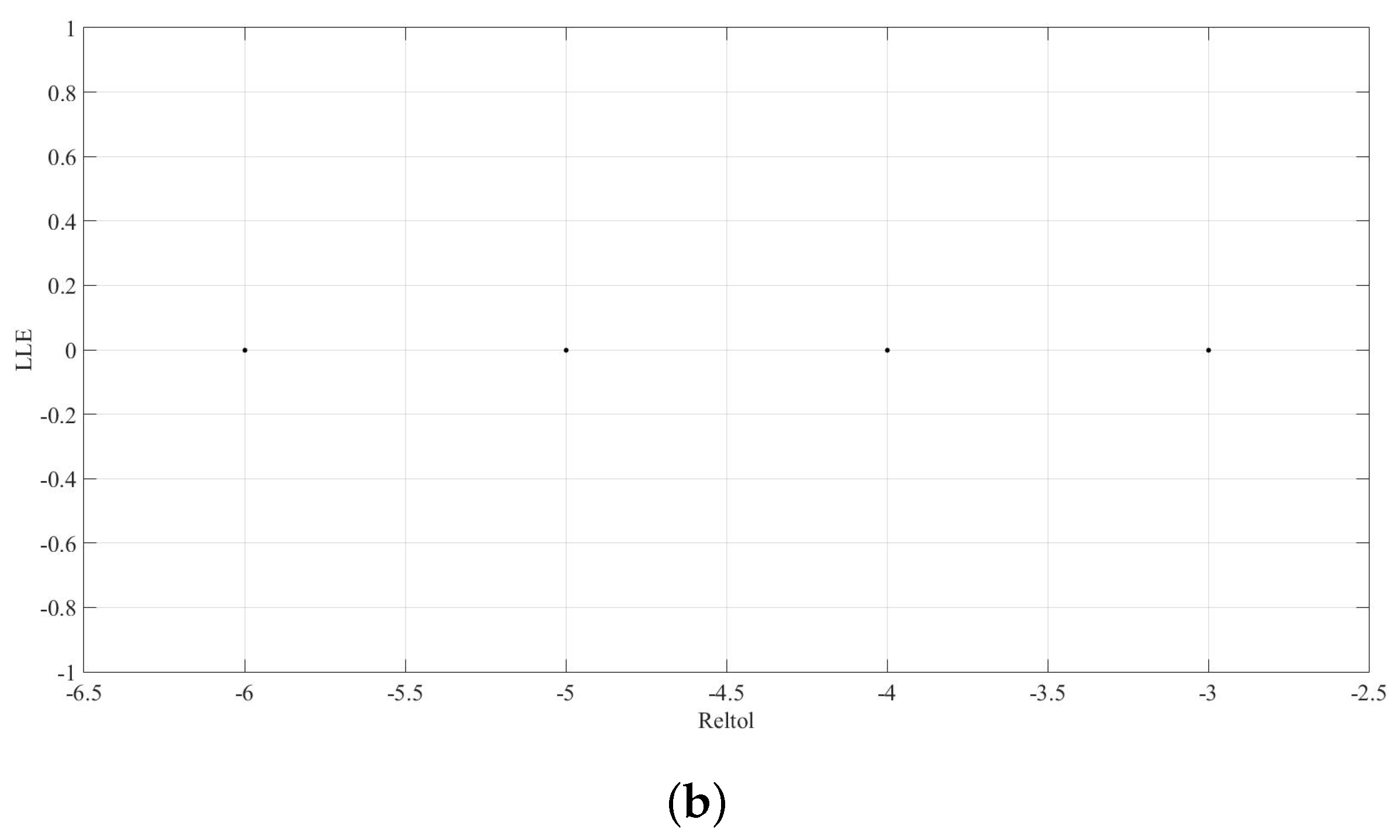
Figure 39 shows a bifurcation diagrams and graph with large Lyapunov exponent (LLE) for
[
25,
26,
27].