Non-Linear Behaviors of Transient Periodic Plasma Dynamics in a Multifractal Paradigm

Abstract

In a multifractal paradigm of motion, nonlinear behavior of transient periodic plasmas, such as Schrodinger and hydrodynamic-type regimes, at various scale resolutions are represented. In a stationary case of Schrodinger-type regimes, the functionality of “hidden symmetry” of the group SL (2R) is implied though Riccati–Gauge different “synchronization modes” among period plasmas’ structural units. These modes, expressed in the form of period doubling, damped oscillations, quasi-periodicity, intermittences, etc., mimic the various non-linear behaviors of the transient plasma dynamics similar to chaos transitions scenarios. In the hydrodynamic regime, the non-Newtonian behavior of the transient plasma dynamics can be corelated with the viscous tension tensor of the multifractal type. The predictions given by our theoretical model are confronted with experimental data depicting electronic and ionic oscillatory dynamics seen by implementing the Langmuir probe technique on transient plasmas generated by ns-laser ablation of nickel and manganese targets.

1. Introduction

Theoretical investigations of transient plasmas embody the characteristics of interdisciplinary research topics largely implemented for plasma physics coupled and based on numerical simulations and modelling. These types of systems are composed of many interacting entities that are called structural units [1]. The way in which transient period plasmas behave cannot be easily predicted only though the evolution of individual elements or by using superposition principles; rather, it is determined by the manner in which the elements relate to each other, defining the global behavior. Among the most significant properties of discharge or laser-induced plasmas are emergence, self-organization, adaptability etc. [2,3]. Classical mathematical models (hydrodynamic-type models or kinetic-type models [1,2) present the dynamics of low-temperature plasmas under the supposition that the used variables are differentiable [4,5]. The validity of these models must be understood sequentially on restricted domains where differentiability reigns true. Some differential procedures cannot be sued when tackling the analysis of complex processes that can imply non-linearity and chaos related to plasma dynamics [6,7]. If non-differentiability can be seen as a global property of the transient plasma [8,9,10], we can build a non-differentiable theoretical structure for describing the dynamics of the periodic phenomena in transient plasmas. Taking into account that the complexity of the interaction processes is completely substituted by non-differentiability, we are not confined by the use of the entirety of classical quantities from differentiable plasma physics. Consequently, when attempting to describe plasma dynamics respecting the differentiable mathematical procedures, it is essential to implement a multifractal paradigm, which introduces scale resolutions in the expression of the variables and in the fundamental equations, which govern transient plasma dynamics. Transient plasmas are described by plasmas, which have properties that evolve in both time and space and are defined by the expansion phenomena. Transient plasmas generated by laser ablation are formed in the ps temporal regime of laser–matter interaction. This transpires into a small volume of plasma defined by a high particle density, high energy, and strong optical emission (mostly continuum emission). As the time passes, the plasma expands, increasing its volume and traveling away from the target. The extreme conditions in the incipient moments of expansion make laser-produced plasma important media for fractal studies. This can also be seen as instead of “working” with a unique variable described by a non-differentiable function, it is possible to “work” only with some approximations of this mathematical function, gained by an averaging process applied at different scale resolutions. Therefore, any variable used to describe plasma dynamics will act as the limit of a series of functions, non-differentiable for null scale resolutions and differentiable otherwise [6,7].

In the present paper, considering the multifractal paradigm as being functional (in the form of the multifractal theory of motion [11,12,13]), a non-differentiable model describing the plasma dynamics is proposed. Moreover, correspondences of this theoretical model with experimental data concerning the dynamics of laser-produced plasma are presented. The empirical data contains the analysis of temporal traces of ionic and electronic current extracted using the Langmuir probe method from ns-laser-produced plasmas on Ni and Mg plasmas.

2. Mathematical Model

Short Reminder of the Multifractal Theory of Motion

The core hypothesis of the multifractal theory of motion [11,12,13], implemented for transient plasmas, implies that the evolution of any transient plasmas’ subcomponents (electrons, atoms, ions, clusters, molecules) is described by multifractal curves (continuous but non-differentiable curves). Such an assumption can be presented in a more exhaustive way when we focus on the collision processes: Between two successive collisions, the trajectory of any structural unit (plasma particle) is a straight line, and non-differentiable in the impact point. All the collision impact points establish a countless set of points, thus the trajectories of the particles become continuous and non-differentiable curves, i.e., multifractal curves. The empirical reality is understandably more complicated, considering the diversity of the particles, which constitute a transient plasma and the various types of interactions between them. Generalizing the previous reasoning for any laser-produced plasmas, it results in a reasonable approximation, and it can be assimilated to a multifractal.

This assessment implies the following consequences [11,12,13]:

(a) The multifractal curves associated to the plasma particles are explicitly scale $\delta t$ dependent. This implies, according to the Lebesgue theorem [6], that their length tends to infinity when $\delta t$ tends to zero and the space, in the Mandelbrot sense, becomes a multifractal;

(b) The evolution of the transient plasma can be assimilated to the behavior of a set of functions during the zoom in/out operation of $\delta t$, which means that $\delta t\equiv dt$ through the functionality of the substitution principle;

(c) The fractal dynamics of plasma particles are described through multifractal variables. Therefore, two derivatives of the variable field $Q\left(t,dt\right)$ are explicitly given [11,12,13]:

$$\begin{gathered} \frac{d{Q}_{+}}{dt}=\underset{\Delta t\to 0}{\lim }\frac{Q\left(t,t+\Delta t\right)-Q\left(t,\Delta t\right)}{\Delta t}, \\ \frac{d{Q}_{-}}{dt}=\underset{\Delta t\to 0}{\lim }\frac{Q\left(t,\Delta t\right)-Q\left(t-\Delta t,\Delta t\right)}{\Delta t}. \end{gathered}$$

(1)

The sign “$+$” corresponds to the forward processes, while the sign “$-$” corresponds to the backward ones with respect to the direction of the flow of the transient plasma.

(d) The differential component of the spatial coordinate field [11]:

$$d_{\pm }{X}^i\left(t, dt\right)=d_{\pm }{x}^i\left(t\right)+d_{\pm }\xi \left(t, dt\right).$$

(2)

The differentiable part $d_{\pm }{x}^i\left(t\right)$ is scale-resolution independent, while the—part $d_{\pm }\xi \left(t, dt\right)$ is scale-resolution dependent.

(e) The non-differentiable part of the spatial coordinate field satisfies the non-differentiable equation [14,15]:

$$d_{\pm }{\xi }^i\left(t, dt\right)={\lambda }_{\pm }^i{\left(dt\right)}^{\left[\frac{2}{f\left(\alpha \right)}\right]-1},$$

(3)

where ${\lambda }_{\pm }^i$ are constant coefficients associated to the differentiable–non-differentiable transition, $f\left(\alpha \right)$ is the singularity spectrum of the order $\alpha$ of the fractal dimension D_F, and $\alpha$ is the singularity index. As such, we can define various modes and furthermore a varied selection of classifications of fractal dimensions. Choosing one and implementing it for transient plasmas dynamic needs to respect the arbitrary and constant properties of the fractal dimension for the entirety of the dynamical analysis. Through (3), it is possible to categorize the transient plasmas volumes that can be described by a certain fractal dimension and the number of these volumes for which the fractal dimensions are situated in an interval of values. Moreover, the singularity spectrum $f\left(\alpha \right)$ can be used to identify classes of universality in the transient plasmas dynamics laws [13,14].

(f) The differential time reflection invariance of any variable is recovered by means of the operator:

$$\frac{\widehat{d}}{dt}=\frac{1}{2}\left(\frac{d_{+}+d_{-}}{dt}\right)-\frac{i}{2}\left(\frac{d_{+}-d_{-}}{dt}\right),$$

(4)

which is an organic result extracted from Cresson’s theorem [12]. By applying the operator (4) to the spatial coordinates field $X^i$, it yields the complex velocity fields:

$${\widehat{V}}^i=\frac{\widehat{d}{X}^i}{dt}=V_D^i-i{V}_F^i,$$

(5)

with:

$$V_D^i=\frac{1}{2}\frac{d_{+}{X}^i+d_{-}{X}^i}{dt}, V_F^i=\frac{1}{2}\frac{d_{+}{X}^i-d_{-}{X}^i}{dt}, i=1,2,3.$$

(6)

The differential velocity (real part of $V_D^i$) is scale-resolution independent, while the non-differentiable velocity (imaginary part of $V_F^i$) is scale-resolution dependent.

(g) Multifractalization of a system implies a certain stochaticization [11,14,15,16,17]; this reads as the transformation of the whole statistic toolbox (averages, variances, covariances, etc.) and becoming operational. For the average of $d_{\pm }{X}^i$, we chose the following functionality:

$$\langle d_{\pm }{X}^i\rangle \equiv d_{\pm }{x}^i,$$

(7)

$$\langle d_{\pm }{\xi }^i\rangle =0.$$

(8)

Relation (8) implies that the average of any non-differential component of the spatial coordinate field is null.

(h) By using the scale covariant derivative, given by the operator [12,13], we can describe transient plasmas dynamics:

$$\frac{\widehat{d}}{dt}={\partial }_t+{\widehat{V}}^i{\partial }_i+\frac{1}{4}{\left(dt\right)}^{\left[\frac{2}{f\left(\alpha \right)}\right]-1}{D}^{lk}{\partial }_l{\partial }_k,$$

(9)

where:

$$D^{lk}=d^{lk}-i{\overline{d}}^{lk}, d^{lk}={\lambda }_{+}^l{\lambda }_{+}^k-{\lambda }_{-}^l{\lambda }_{-}^k, {\overline{d}}^{lk}={\lambda }_{+}^l{\lambda }_{+}^k+{\lambda }_{-}^l{\lambda }_{-}^k.$$

(10)

For Markov-type stochastic processes [6,10,11], i.e.:

$${\lambda }_{+}^i{\lambda }_{+}^l={\lambda }_{-}^i{\lambda }_{-}^l=2\lambda {\delta }^{il},$$

(11)

and:

$$f\left(\alpha \right)\equiv D_F,$$

(12)

where $\lambda$ is a specific fractal–non-fractal transition coefficient and ${\delta }^{il}$ is Kronecker’s pseudo-tensor, and then the scale covariant derivative becomes:

$$\frac{\widehat{d}}{dt}={\partial }_t+{\widehat{V}}^l{\partial }_l-i\lambda {\left(dt\right)}^{\left[\frac{2}{D_F}\right]-1}{\partial }_l{\partial }^l.$$

(13)

For the particular case of dynamics on Peano-type curves, implying $D_F=2$, the scale covariant derivative (13) takes the clasicall form from the scale relativity theory (SRT) [11]:

$$\frac{\widehat{d}}{dt}={\partial }_t+{\widehat{V}}^l{\partial }_l-iD{\partial }_l{\partial }^l,$$

(14)

where $\lambda \equiv D$ is the fractal–non-fractal transition diffusion coefficient. Our approach generalizes all the results of Nottale’s theory (SRT [11]).

Now, applying the operator (9) to the transient plasmas’ fields (5), in the absence of any external constraint (free expansion regime), the geodesics equation on a multifractal space takes the following form:

$$\frac{\widehat{d}{\widehat{V}}^i}{dt}={\partial }_t{\widehat{V}}^i+{\widehat{V}}^l{\partial }_l{\widehat{V}}^i+\frac{1}{4}{\left(dt\right)}^{\left[\frac{2}{f\left(\alpha \right)}\right]-1}{D}^{lk}{\partial }_l{\partial }_k{\widehat{V}}^i=0.$$

(15)

The multifractal acceleration, ${\partial }_t{\widehat{V}}^i$, the multifractal convection, ${\widehat{V}}^l{\partial }_l{\widehat{V}}^i$, and the multifractal dissipation $D^{lk}{\partial }_l{\partial }_k{\widehat{V}}^i$ can reach a balance in any point of the multifractal curve. Particularly, for (11) and (12), the motion Equation (15) becomes:

$$\frac{\widehat{d}{\widehat{V}}^i}{dt}={\partial }_t{\widehat{V}}^i+{\widehat{V}}^l{\partial }_l{\widehat{V}}^i-i\lambda {\left(dt\right)}^{\left[\frac{2}{D_F}\right]-1}{\partial }_l{\partial }^l{\widehat{V}}^i=0.$$

(16)

Now, separating the motions on scale resolutions (the differentiable and non-differentiable scale resolutions), (15) becomes:

$$\begin{gathered} {\partial }_t{V}_D^i+V_D^l{\partial }_l{V}_D^i-V_F^l{\partial }_l{V}_F^i+\frac{1}{4}{\left(dt\right)}^{\left[\frac{2}{f\left(\alpha \right)}\right]-1}{D}^{lk}{\partial }_l{\partial }_k{V}_D^i=0, \\ {\partial }_t{V}_F^i+V_F^l{\partial }_l{V}_D^i+V_D^l{\partial }_l{V}_F^i-\frac{1}{4}{\left(dt\right)}^{\left[\frac{2}{f\left(\alpha \right)}\right]-1}{D}^{lk}{\partial }_l{\partial }_k{V}_F^i=0, \end{gathered}$$

(17)

while (16) takes the form:

$$\begin{gathered} {\partial }_t{V}_D^i+V_D^l{\partial }_l{V}_D^i-\left[V_F^l+\lambda {\left(dt\right)}^{\left[\frac{2}{f\left(\alpha \right)}\right]-1}{\partial }^l\right]{\partial }_l{V}_F^i=0, \\ {\partial }_t{V}_F^i+V_D^l{\partial }_l{V}_F^i+\left[V_F^l+\lambda {\left(dt\right)}^{\left[\frac{2}{f\left(\alpha \right)}\right]-1}{\partial }^l\right]{\partial }_l{V}_D^i=0. \end{gathered}$$

(18)

For irrotational motions of the transient plasmas’ structural units, the complex velocity fields (5) become:

$${\widehat{V}}^i=-2i\lambda {(dt)}^{\left[\frac{2}{f\left(\alpha \right)}\right]-1}{\partial }^i\ln \mathsf{\Psi },$$

(19)

where:

$$\chi =-2i\lambda {(dt)}^{\left[\frac{2}{f\left(\alpha \right)}\right]-1}\ln \mathsf{\Psi },$$

(20)

is the complex scalar potential of the complex velocity fields (5) and $\mathsf{\Psi }$ is the function of states. In these conditions, substituting (19) in (16) and using the mathematical procedures from [11,12,15], the geodesics Equation (16) takes the form of the multifractal Schrödinger-type equation:

$${\lambda }^2{(dt)}^{\left[\frac{4}{f\left(\alpha \right)}\right]-2}{\partial }^l{\partial }_l\mathsf{\Psi }+i\lambda {(dt)}^{\left[\frac{2}{f\left(\alpha \right)}\right]-1}{\partial }_t\mathsf{\Psi }=0.$$

(21)

Therefore, for the complex velocity fields (19), the dynamics of the transient plasmas’ structural units are described through Schrödinger “regimes” of the multifractal type (i.e., Schrödinger-type equations at various scale resolutions).

Moreover, if we choose $\mathsf{\Psi }$ of the form:

$$\mathsf{\Psi }=\sqrt{\rho }{e}^{is},$$

(22)

where $\sqrt{\rho }$ is the amplitude and $s$ is the phase, then the complex velocity fields (19) take the explicit form:

$${\widehat{V}}^i=2\lambda {(dt)}^{\left[\frac{2}{f\left(\alpha \right)}\right]-1}{\partial }^{i}s-i\lambda {(dt)}^{\left[\frac{2}{f\left(\alpha \right)}\right]-1}{\partial }^i\ln \rho ,$$

(23)

which enables the definition of the real velocity fields:

$$V_D^i=2\lambda {(dt)}^{\left[\frac{2}{f\left(\alpha \right)}\right]-1}{\partial }^{i}s,$$

(24)

$$V_F^i=\lambda {(dt)}^{\left[\frac{2}{f\left(\alpha \right)}\right]-1}{\partial }^i\ln \rho .$$

(25)

By (22), (24), and (25) and using the mathematical procedures from [11,12,15], the geodesics Equation (21) reduces to the multifractal hydrodynamic-type equations:

$${\partial }_t{V}_D^i+V_D^l{\partial }_l{V}_D^i=-{\partial }^{i}Q,$$

(26)

$${\partial }_t\rho +{\partial }_l\left(\rho V_D^l\right)=0,$$

(27)

with Q, the specific multifractal potential:

$$Q=-2{\lambda }^2{(dt)}^{\left[\frac{4}{f\left(\alpha \right)}\right]-2}\frac{{\partial }^l{\partial }_l\sqrt{\rho }}{\sqrt{\rho }}=-V_F^i{V}_F^i-\frac{1}{2}\lambda {(dt)}^{\left[\frac{2}{f\left(\alpha \right)}\right]-1}{\partial }_l{V}_F^l.$$

(28)

Equation (26) characterizes the multifractal-type-specific momentum conservation law, while Equation (27) to the multifractal type states the density conservation law. The multifractal-specific potential (28) infers the multifractal-specific force:

$$F^i=-{\partial }^{i}Q=-2{\lambda }^2{(dt)}^{\left[\frac{4}{f\left(\alpha \right)}\right]-2}{\partial }^i\frac{{\partial }^l{\partial }_l\sqrt{\rho }}{\sqrt{\rho }},$$

(29)

which is a measure of the multifractality of the motion curves.

Therefore, for the complex velocity fields (23), the dynamics of the transient plasmas’ structural units are described through hydrodynamic “regimes” of the multifractal type (i.e., hydrodynamic equations at various scale resolutions). In such a context, the following consequences result:

(i) Any transient plasmas’ structural units are in a permanent interaction with a multifractal medium through the specific multifractal force (29);

(ii) Any transient plasmas can be identified with a multifractal fluid, the dynamics of which is described by the multifractal hydrodynamic model (see Equations (26)–(28));

(iii) The velocity field $V_F^i$ contributes to the multifractal-type-specific momentum transfer and to the multifractal energy without explicitly contributing to the measurable velocity. The aspect seen more evidently from its role in the variational principles of the multifractal type and its absence from the multifractal type states the density conservation law;

(iv) For any interpretation of the multifractal-specific potential, one should be aware of the “self” nature of the multifractal-specific momentum transfer. The energy of the multifractal type is generally encompassed in the potential energy of the multifractal type and the mass motion of the multifractal type. The conservation of the energy and the momentum of the multifractal type ensure the existence of the eigenstates and the reversibility of the multifractal type and simultaneously denies a Lévy motion multifractal force of interaction with the external medium;

(v) If a tensor of the multifractal type is taken:

$${\widehat{\tau }}^{il}=2{\lambda }^2{\left(dt\right)}^{\left[\frac{4}{f\left(\alpha \right)}\right]-2}\rho {\partial }^i{\partial }^l\ln \rho ,$$

the equation defining the “forces” of the multifractal type that derive from the “potential” of the multifractal type $Q$ can be written in the form of an equilibrium equation of the multifractal type, physically characterizing the multifractal medium-multifractal fluid, by tensions of the multifractal type incorporated in the tensor of the multifractal type, and acted upon by “volume forces” of the multifractal type included in the gradient of the entire potential of the multifractal type, ${\partial }^{i}Q$:

$$\rho {\partial }^{i}Q={\partial }_l{\widehat{\tau }}^{il}.$$

This proves the previous statement. Part of the complications is then brought about by this very observation, because in every plasma fluid model, a constitutive law should be in effect, relating the acting stress to the overall deformation plasma. Besides, the multifractal fluid representation of the plasma can be taken, indeed, as a complex fluid as, in fact, one can define a velocity field by the variation of states of the density of the multifractal type, see (25), so that the tensor of the multifractal type ${\widehat{\tau }}^{il}$ can be written in the form:

$${\widehat{\tau }}^{il}=\eta \left({\partial }_l{V}_F^i+{\partial }_i{V}_F^l\right),$$

$$\eta =\lambda {\left(dt\right)}^{\left[\frac{2}{f\left(\alpha \right)}\right]-1}\rho .$$

This is, indeed, a linear constitutive equation of the multifractal type for a “viscous fluid” of the multifractal type, and gives the reason for an original interpretation of the coefficient $\eta$ as a dynamic viscosity of the multifractal type of the multifractal fluid representation of the plasma. The previous relations can give a non-Newtonian character to the transient plasma [18,19];

(vi) For plasma entities’ dynamics on continued but non-differentiable curves of the Peano type and at diffusion-type scale resolution (i.e., for monofractal curves with D_F = 2 at $\mathsf{\lambda }\equiv D$, where D is the plasma diffusion coefficient [20]).

3. Complex Fluid Dynamics through Schrödinger “Regimes” of Multifractal Type

3.1. “Hidden Symmetry” in Transient Plasma Dynamics

By applying the variable separation method in Equation (21), the one-dimensional stationary part of this Equation (21) takes the form (for details on the mathematical procedures, see [11,12,13]):

$$\frac{d^2\mathsf{\Psi }}{d{x}^2}+k_0^2\mathsf{\Psi }=0,$$

(30)

with

$$k_0^2=\frac{E}{2m_0{\lambda }^2{\left(dt\right)}^{\left[\frac{4}{f\left(\alpha \right)}\right]-2}}.$$

(31)

In (31), $E$ is the multifractal energy of the transient plasmas’ structural unit and $m_0$ is the rest mass of the transient plasmas’ structural unit.

The solution of (30) can be written in the form:

$$\mathsf{\Psi }\left(x\right)=h{e}^{i\left(k_{0}x+\theta \right)}+\overline{h}{e}^{-i\left(k_{0}x+\theta \right)},$$

(32)

where $h$ is the complex amplitude, $\overline{h}$ is the complex conjugate of $h$, and $\theta$ is a phase. Thus, $h$, $\overline{h}$, and $\theta$ label each structural unit from transient plasmas that have as a “fundamental property” the same $k_0$.

Equation (30) by means of a homographic group of the multifractal type presents a type of “hidden” symmetry. The ratio $\epsilon$ of two independent linear solutions from (30) is the equivalent of the solution of Schwarz’s differential equation of the multifractal type (for the classical case, see [17]):

$$\left\{\epsilon ,x\right\}=\frac{d}{dx}\left(\frac{\ddot{\epsilon }}{\dot{\epsilon }}\right)-\frac{1}{2}{\left(\frac{\ddot{\epsilon }}{\dot{\epsilon }}\right)}^2=2k_0^2,$$

(33)

$$\dot{\epsilon }=\frac{d\epsilon }{dx}, \ddot{\epsilon }=\frac{d^2\epsilon }{d{x}^2}.$$

(34)

The left part of (33) is invariant with respect to the homographic transformations of the multifractal type:

$$\epsilon \leftrightarrow {\epsilon }^{\prime }=\frac{a\epsilon +b}{c\epsilon +d^{\prime }}$$

(35)

where $a$, $b$, $c$, and $d$ are real parameters (of the multifractal type). The relation (35) corresponding to all possible values of these parameters defines the group SL (2R) of the multifractal type [21,22].

Thus, the complete density of plasma particles having the same $k_0$ are in biunivocal correspondence with the SL (2R) group transformations of the multifractal type. This permits the development of a special parameter of the multifractal type, $\epsilon$, for each individual plasma particle (structural unit). This parameter is chosen from the general form of the solution of (33), which is written as:

$${\epsilon }^{\prime }=l+m\tan \left(k_{0}x+\theta \right).$$

(36)

Thus, through $l$, $m$, and $\theta$, it is possible to characterize any transient plasmas’ structural unit. In such a conjecture, identifying the phase from (36) with the one from (32), the “personal” parameter of the multifractal type [23,24,25,26] becomes:

$${\epsilon }^{\prime }=\frac{h+\overline{h}\epsilon }{1+h}, h=l+im, \overline{h}=l-im, \epsilon \equiv e^{2i\left(k_{0}x+\theta \right)}.$$

(37)

The fact that (36) is also a solution of (33), which implies, by explaining (35), the group of SL (2R) of the multifractal type [18,19,20]:

$$h^{\prime }=\frac{ah+b}{ch+d}, \overline{h}=\frac{a\overline{h}+b}{c\overline{h}+d}, k^{\prime }=\frac{c\overline{h}+d}{ch+d}k.$$

(38)

Therefore, the group (38) acts as special “synchronization modes” of the transient plasma classes of particles (electron, ions, atoms), a process in which the amplitudes and phases of each of them obviously connected. Through the group (38), the phase of $k$ is only affected by a quantity depending on the amplitude of the plasma particle dynamics. The amplitude of the structural unit dynamic can also be controlled from a homographic perspective. The “synchronization” demonstrated through the delay of the amplitudes and phases of the plasma particles therefore represent a particular case.

The structure of group (38) is typical of SL (2R), which will be taken in the standard form:

$$\left[A_1,A_2\right]=A_1, \left[A_2,A_3\right]=A_3, \left[A_3,A_1\right]=-2A_2,$$

(39)

where $A_k,$ $k=1, 2, 3$ are the infinitesimal generators of the group. Because the group is a simple transitive, these generators can be easily found as the components of the Cartan conframe of the multifractal type from the relation [27,28,29]:

$$d\left(f\right)=\sum \frac{\partial f}{\partial x^k}d{x}^k=\left\{{\omega }^1\left[h^2\frac{\partial }{\partial h}+{\overline{h}}^2\frac{\partial }{\partial \overline{h}}+\left(h-\overline{h}\right)k\frac{\partial }{\partial k}\right]+2{\omega }^2\left(h\frac{\partial }{\partial h}+\overline{h}\frac{\partial }{\partial \overline{h}}\right)+{\omega }^3\left(\frac{\partial }{\partial h}+\frac{\partial }{\partial \overline{h}}\right)\right\}\left(f\right),$$

(40)

where ${\omega }^k$ are the components of the Cartan coframe of the multifractal type to be found from the system:

$$dh={\omega }^1{h}^2+2{\omega }^{2}h+{\omega }^3, d\overline{h}={\omega }^1{\overline{h}}^2+2{\omega }^2\overline{h}+{\omega }^3, dk={\omega }^{1}k\left(h-\overline{h}\right).$$

(41)

Thus, both the infinitesimal generators and the coframe of the multifractal types are obtained by identifying the right-hand side of (40), with the standard dot product of SL (2R) algebra of the multifractal type:

$${\omega }^1{A}_3+{\omega }^3{A}_1-2{\omega }^2{A}_2,$$

(42)

so that:

$$A_1=\frac{\partial }{\partial h}+\frac{\partial }{\partial \overline{h}}, A_2=h\frac{\partial }{\partial h}+\overline{h}\frac{\partial }{\partial \overline{h}}, A_3=h^2\frac{\partial }{\partial h}+{\overline{h}}^2\frac{\partial }{\partial \overline{h}}+\left(h-\overline{h}\right)k\frac{\partial }{\partial k},$$

(43)

and

$${\omega }^1=\frac{dk}{\left(h-\overline{h}\right)k}, 2{\omega }^2=\frac{dh-d\overline{h}}{h-\overline{h}}-\frac{h+\overline{h}}{h-\overline{h}}\frac{dk}{k}, {\omega }^3=\frac{hdh-\overline{h}dh}{h-\overline{h}}+\frac{h\overline{h}dk}{\left(h-\overline{h}\right)k}.$$

(44)

It is worth mentioning that, in [23,24,25,26], it does not work with the previous differential forms, but with the absolute invariant differentials:

$${\omega }^1=\frac{dh}{\left(h-\overline{h}\right)k}, {\omega }^2=-i\left(\frac{dk}{k}-\frac{dh+d\overline{h}}{h-\overline{h}}\right), {\omega }^3=\frac{kd\overline{h}}{h-\overline{h}}.$$

(45)

The advantage of this representation is that it makes the connection with the Poincaré representation of the Lobachevsky plane obvious. Indeed, the metric here is:

$$\frac{d{s}^2}{g}={\left({\omega }^2\right)}^2-4{\omega }^1{\omega }^2={\left(\frac{dk}{k}-\frac{dh+d\overline{h}}{h-\overline{h}}\right)}^2+4\frac{dhd\overline{h}}{{\left(h-\overline{h}\right)}^2},$$

(46)

where $g$ is a constant.

These metrics reduce to that of Poincaré in the case when ${\omega }^2=0$, which defines the variable $\theta$ as the “angle of parallelism” (in the Levi–Civita sense) of the hyperbolic plane of the multifractal type (the connection of the multifractal type (for details, see [22,23,24,25,26]).

3.2. “Synchronization Modes” through Riccati-Type Gauge in Transient Plasma Dynamics

Returning to the homographic transformation of the multifractal type (35), according to the previous presented implications of this transformation, each structural unit of any transient plasmas can be located either for homogenous coordinates $\left(a–d\right)$ or three non-homogenous coordinates when a parallelism of direction in the Levi–Civita sense becomes functional on the manifold induced by the SL (2R) group of the multifractal type (for details, see [11,13,15]). Now, the simultaneity condition of the free structural units of any transient plasmas can be differently characterized from a Riccati equation of the multifractal type in pure differentials of the multifractal type (this shall be named the Riccati gauge of the multifractal type):

$$d\frac{a\epsilon +b}{c\epsilon +d}=0,$$

(47)

which implies:

$$d\epsilon ={\omega }^1{\epsilon }^2+{\omega }^2\epsilon +{\omega }^3,$$

(48)

where ${\omega }^1$, ${\omega }^2$, and ${\omega }^3$ are the components of the Cartan coframe of the multifractal type given through the relation (44). Therefore, for the description of any transient plasmas dynamics as a succession of states of an ensemble of simultaneous structural units, as it were, it suffices to have three differentiable 1-forms, representing a coframe of SL (2R) algebra of the multifractal type. Consequently, a state of a transient plasma in given dynamics can be organized as a metric plane space, i.e., a Riemannian three-dimensional space of the multifractal type. Accordingly, the geodesics of a Riemannian space of the multifractal type are given by some conservations of equations of the multifractal type:

$${\omega }^1=a^{1}d\tau , {\omega }^2=a^{2}d\tau , {\omega }^3=a^{3}d\tau ,$$

(49)

where $a^1$, $a^2$, and $a^3$ are constant and $\tau$ is the affine parameter of the geodesics, so that along these geodesics of the differential equation, (48) is an ordinary differential of the Riccati type:

$$\frac{d\epsilon }{d\tau }=a^1{\epsilon }^2+2a^2\epsilon +a^3.$$

(50)

Let it be considered the following form of the previous equation:

$$A\frac{d\epsilon }{d\tau }-{\epsilon }^2+2B\epsilon +AC=0,$$

(51)

where:

$$\frac{1}{a^1}=A, -2\frac{a^2}{a^1}=B, -\frac{a^3}{a^1}=AC.$$

(52)

Since the roots of the polynomial:

$$P\left(\epsilon \right)={\epsilon }^2-2B\epsilon -AC,$$

(53)

can be written in the form:

$${\epsilon }_1=B+iA\mathsf{\Omega }, {\epsilon }_2=B-iA\mathsf{\Omega },{ \mathsf{\Omega }}^2=\frac{C}{A}-{\left(\frac{B}{A}\right)}^2,$$

(54)

the change of the variable:

$$z=\frac{\epsilon -{\epsilon }_1}{\epsilon -{\epsilon }_2},$$

(55)

transforms in:

$$\dot{z}=2i\mathsf{\Omega }z,$$

(56)

of the solution:

$$z\left(\tau \right)=z\left(0\right)e^{2i\mathsf{\Omega }\mathsf{\tau }}.$$

(57)

Therefore, if the initial condition $z\left(0\right)$ is conveniently expressed, then it is possible to construct the general solution of (50), by writing the transformation (55) in the form:

$$\epsilon =\frac{{\epsilon }_1+r{e}^{2i\mathsf{\Omega }\left(\tau -{\tau }_0\right)}{\epsilon }_2}{1+r{e}^{2i\mathsf{\Omega }\left(\tau -{\tau }_0\right)}},$$

(58)

where $r$ and ${\tau }_0$ are two integration constants. Using (54), it is possible to write this solution in real terms:

$$z=B+A\mathsf{\Omega }\left\{\frac{2r\sin \left[2\mathsf{\Omega }\left(\tau -{\tau }_0\right)\right]}{1+r^2+2r\cos \left[2\mathsf{\Omega }\left(\tau -{\tau }_0\right)\right]}+i\frac{1-r^2}{1+r^2+2r\cos \left[2\mathsf{\Omega }\left(\tau -{\tau }_0\right)\right]}\right\}.$$

(59)

Therefore, the “synchronization modes” in the phase and amplitude of the plasma structural units imply group invariances of the SL (2R) type. Then, period doubling, damped oscillations, quasi-periodicity, intermittence etc. emerge as natural behaviors in the transient plasma dynamics (see Figure 1a–p for $r=0.5$ and Real $\left[\left(z-B\right)/A\right]\equiv$ Amplitude at various scale resolutions, given by means of the maximum value of $\mathsf{\Omega }$).

As it can be observed in Figure 1a–p, the natural transition of a transient plasma is to evolve from a normal period doubling state towards damped oscillating and a strong modulated dynamic. The transient plasmas never reach a chaotic state, but it always evolves towards that state. The transient plasmas jump directly in a doubling period state and thus it follows again the same scenario presented here. We see here that the model is able to predict various dynamics for the electron and ions ejected as a result of laser–matter interaction. We do see the evolution contains simple oscillatory behavior-damped oscillation-modulated dynamics. The oscillatory regime (classical and damped) has already been reported on and was reported more intensely for laser-produced plasma in the past 10 years [8,9,10,18,19]. While the oscillating dynamics are relatively new, the modulated and the multiple structuring of the plasma has been reported as early as 1990, with initial reports engaging the plasma–gas particle interaction as the main drive for the structuring and the most recent ones considering the multiple ablation mechanism for the presence of groups of particles with different properties [10]. The evolution predicted by our model presents a transition from simple to more complex dynamics, which, for higher values of the scale resolution (Ω_max), almost reaches a chaotic state. This scenario was seen for carbon plasma where the dynamics were shown to reach a quasi-turbulent state at high background pressures.

The evolution of the transient plasmas was further studied with the increase of the control parameter. To this end, for a relatively small range of values, the response of the transient plasmas was investigated. It was observed (see Figure 1a–p) that the plasma particle dynamics starts from a double period state and transitions to a damped oscillating state and evolves through a quasi-chaotic state, which is never achieved. The transition is evidenced by the presence of supplementary oscillation frequencies. While the frequency response of the plasma charged particle is somehow periodical, the amplitude increases quasi-linearly as the values of the control parameter increase. The bifurcation map is presented (Figure 2), where again it is observed that the plasma charged particle dynamics starts from a steady state (double period state) and evolves towards a chaotic one (${\mathsf{\Omega }}_{max}=2, 2.5, 3\dots$), but it never reaches that state.

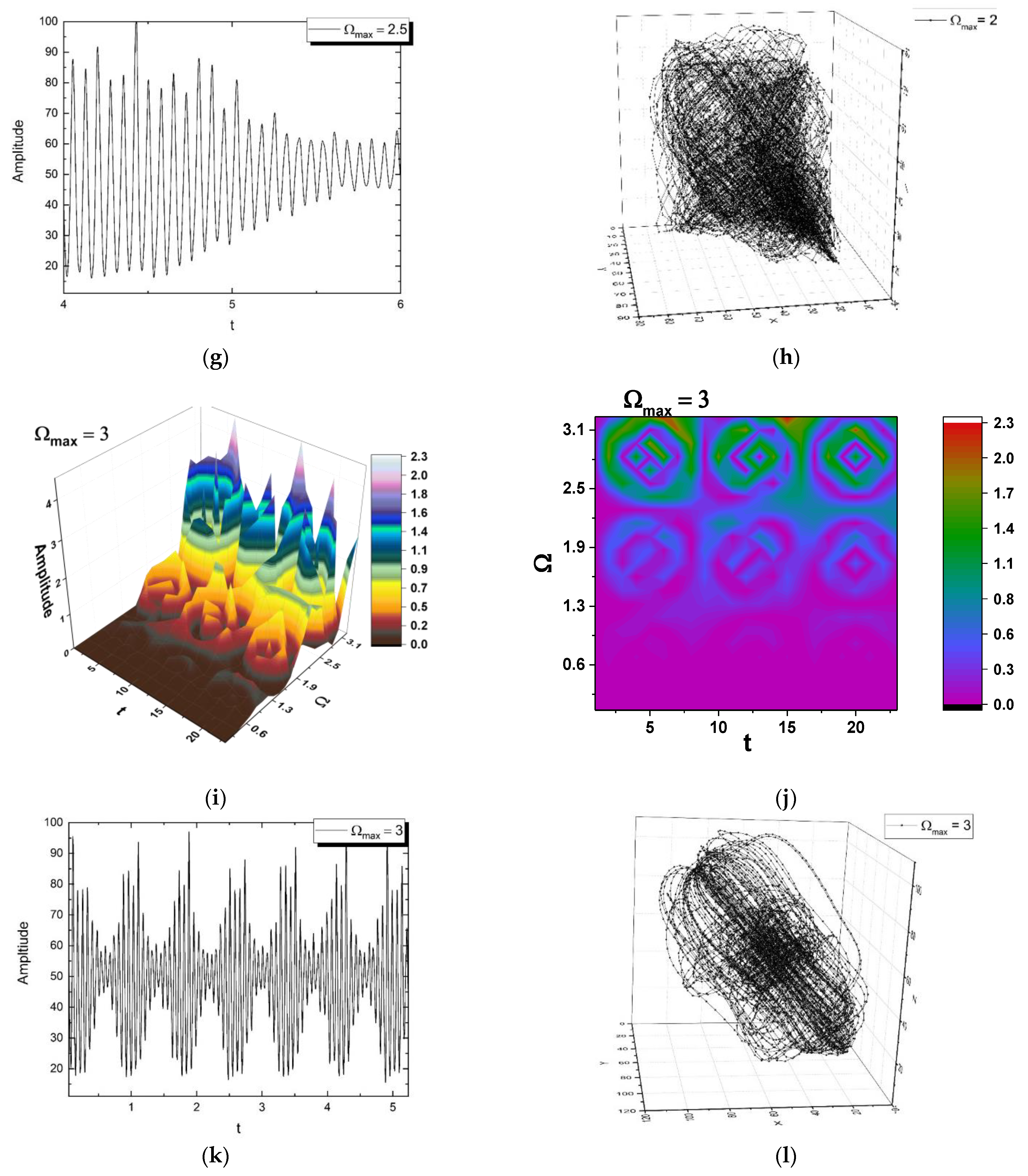
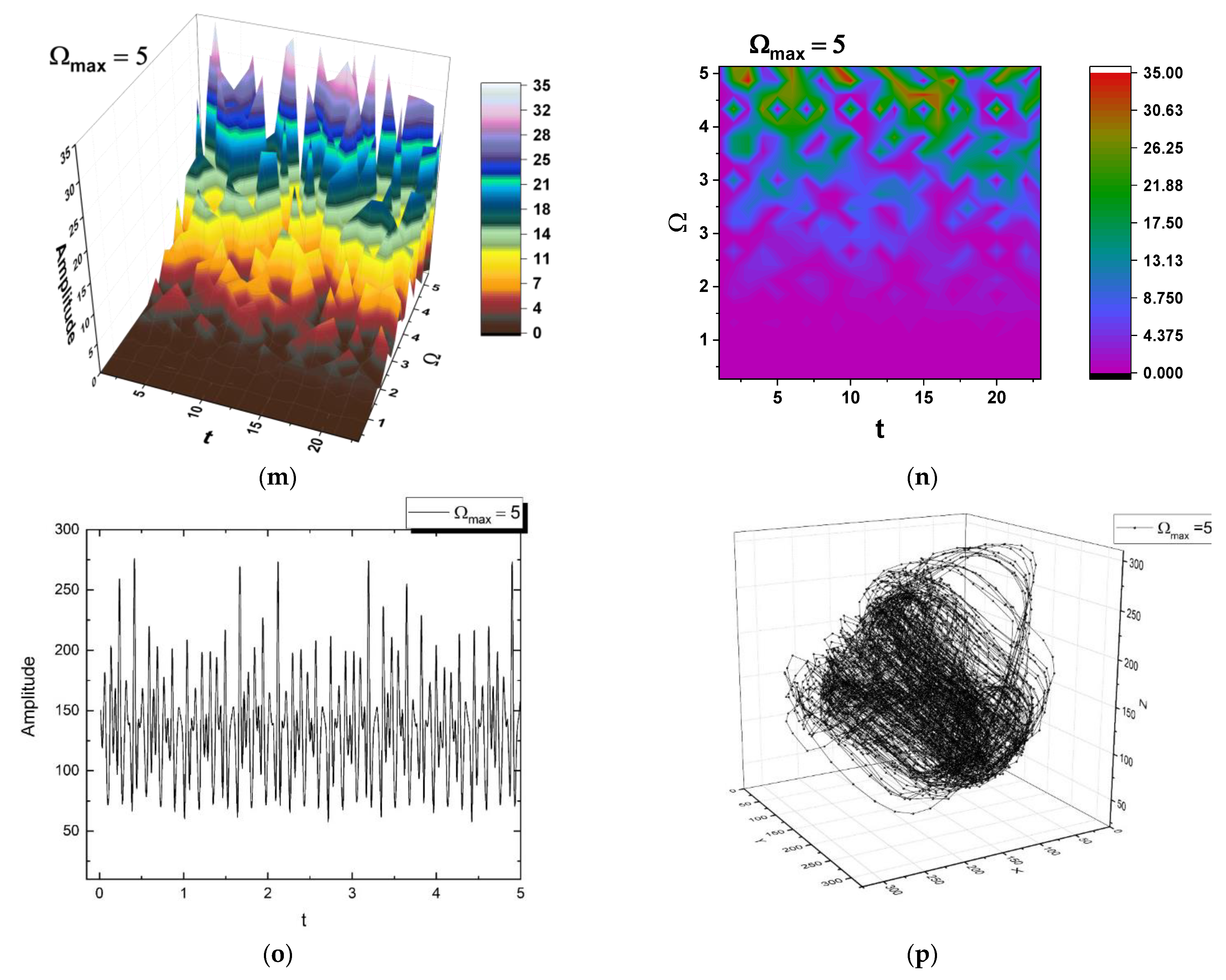
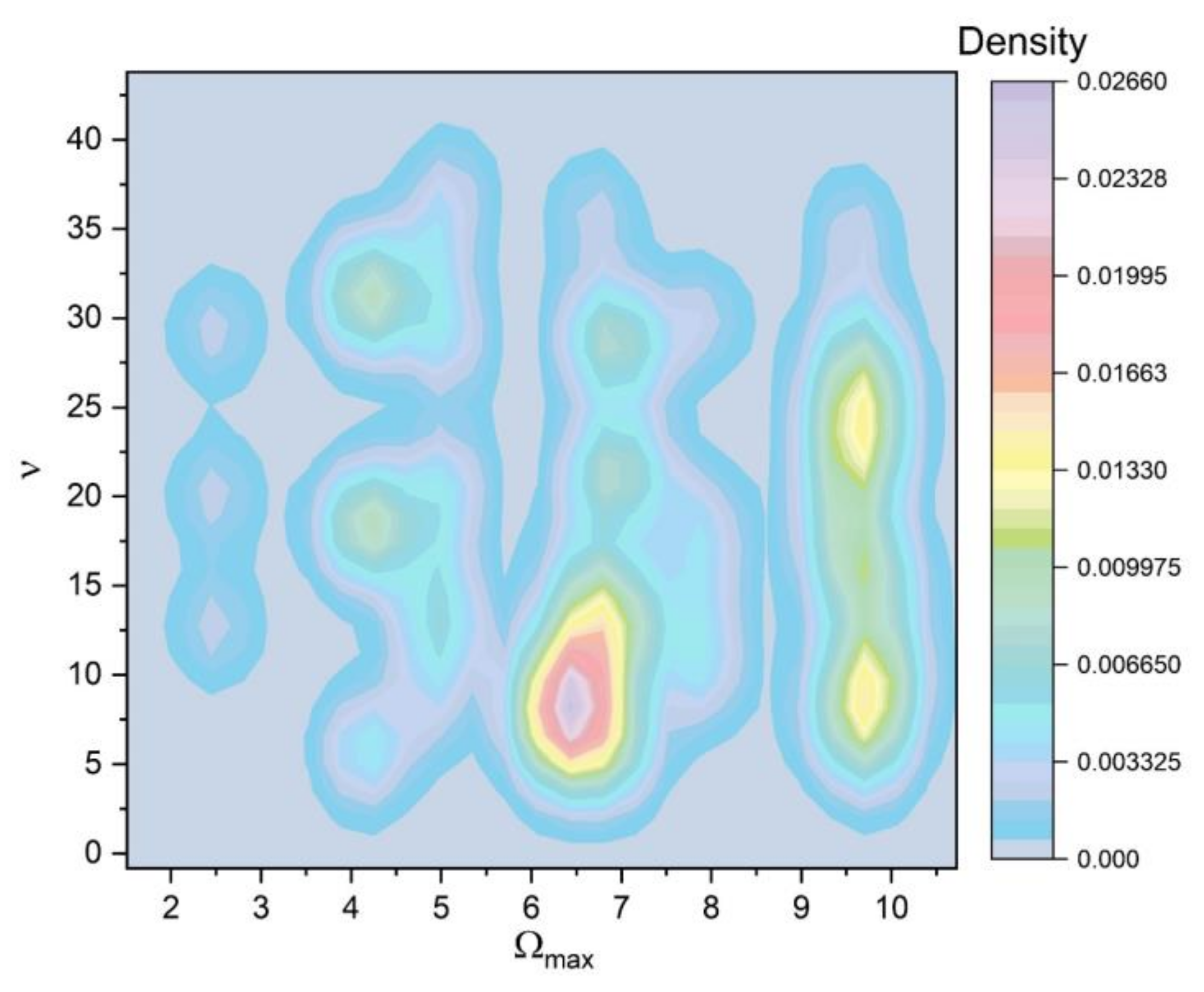
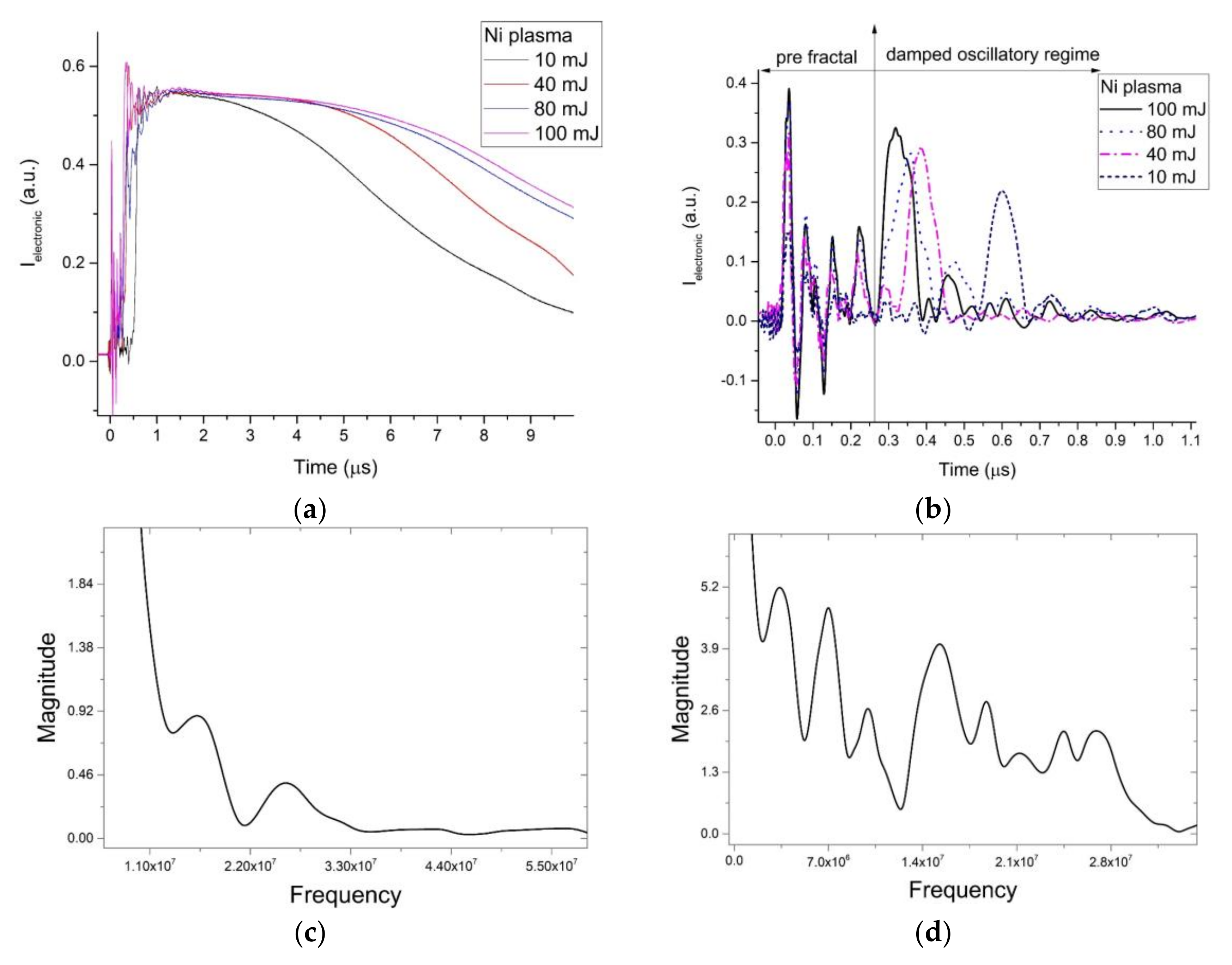
4. Application to Laser Ablation Plasma Dynamics

The use of multifractal models to describe the complex dynamics of low-temperature plasmas has been the trademark of our group in the past few years, where we either looked into nonlinear behavior of self-organized structures or into the behavior of laser-produced plasmas [30,31,32,33]. The latter problem has received more interest as there are relevant technological applications like pulsed laser deposition or material engraving, surface processing etc. The aim of the multifractal approach is to offer generalist laws that could unify different aspects of the laser–matter interactions. We previously tackled processes like plasma self-structuring, particle distribution in a single element and complex alloys, spatial-temporal evolution of certain plasma parameters, and even charge particle oscillations [30,31,32,33,34,35,36,37]. All these results were achieved by admitting that the ejected particles move on continuous but nondifferentiable curves. The multifractal approach allows an easy transition from global to local dynamics within the framework of the same mathematical model. This is the reasoning why this rather difficult theory makes the best fit in finding general laws that could even showcase the relations between the laser beam-target-plasma and thin film properties.

When analyzing the dynamics of laser-produced plasmas as a complex system in a multifractal theoretical construction, we can focus on all facets of the LPP, such as: Optical emission, global dynamics, molecular and cluster ejection, and ion or electron kinetics. Out of all the possible directions, the one that embeds more truly the multifractal behavior is the analysis on the electron dynamics. Due to their lower mass they are ejected from the target via several ablation mechanisms and suffer multiple collisions, which lead to ionization, neutralization, and excitation processes. Basically, the electrons act as the multifractal matrix of the LPP dynamics. In order to implement the theoretical consideration presented in the previous section in describing LPP dynamics, we chose to investigate transient plasma-generated UV-ns-laser ablation of Ni and Mg samples. For this experiment, we used the established experimental set-up presented in [33]. Briefly, the experiments were performed in a stainless-steel vacuum chamber (2 × 10⁻⁵ Torr residual pressure). The radiation from an Nd-YAG nanosecond laser (355 nm, = 5 ns) was focused by a f = 30 cm lens on a metallic target (Mg and Ni), and placed in the vacuumed chamber. The irradiation geometry led to an irradiation spot diameter of 0.3 mm. The metallic targets rotated during the experiments to ensure new surfaces for each pulse and were electrically grounded from the vacuum chamber. Each experiment was preceded by a surface cleaning procedure for the removal of a possible oxide layer present at the surface. The electronic current was extracted using a tungsten heated cylindrical Langmuir probe (0.25 mm diameter, 3 mm length) biased by voltages +5 V with a stabilized dc power source. The probe was heated in order to avoid deposition of the target material on the probe, thus keeping constant the collecting area of the probe during measurements.

In Figure 3, we have represented the electronic temporal traces collected on the main expansion axis at 3 cm from the target. We observe three distinct areas: The first area is a mixed ionic and electronic oscillatory regime followed by a convoluted electronic damped oscillating regime and a well-known shifted Maxwell–Boltzmann distribution of the current. In the incipient oscillating region, we can see that it does not depend on the laser energy as the only effect found was a slight increase of 10% of the overall collected electronic current. However, we found a deeper meaning of this “strange” region. This regime is different for the Mg plasma, and for the Ni plasma, it is therefore specific to the type of target used. In the paradigm of our model, this region that is constant regardless of the laser parameter but changes with the nature of the target is indeed a pre-fractal. As we can see from the FTT transform, the electrons oscillate on several frequencies; however, it is not chaotic. This region acts as a projection in the differentiable measurable dynamics of a multidimensional multifractal generated for each individual target. This projection represents the wide range of possibilities for the ejected electron that they can follow as the dynamics is “chosen”. This pre-fractal state of the plasma is different for the Mg and Ni plasma as it reflects more the properties of the targets as the plasma does not yet form, being a non-equilibrium soup of high energetic electron ions and localized optical emission [38]. For the further development of the electronic cloud, we see a damped oscillating regime being described by two frequencies. These frequencies depend on the properties of the laser, measurement angle, and distance [24] as it clearly defined the plasma state of the ablated. The recorded frequencies are part of the multitude of initial possible states from which two are selected based on the geometry and the experimental conditions. This is the first proof for the fractal theory as the selection of the dynamics can be seen empirically.

The experimental data presented here showcases an interesting scenario, through which metallic ablation plasmas transition from a quasi-chaotic state into a simple double period damped oscillation. The mathematical model predicts such a behavior as the sequence presented in Figure 2 is a cyclical one and the system always reverts to the double period. It is worth noting that the theoretical model predicts a transition from a double period state to a dapped oscillatory state, with both dynamics confirmed experimentally. In the multi-structuring, it is not clearly seen here as it occurs at a considerable later evolution times of the plasma, and it has been seen experimentally through optical emission spectroscopy [32]. Therefore, laser ablation plasmas are perfect media, which can behave according to the predictions made by our model and especially being a system that does not reach a chaotic state, at least not in high vacuum conditions where our experiments were performed. A fractal theoretical model, although admittedly complicated and heavier than other “classical” models, is suitable to investigate the dynamics of a system that presents significantly different phenomena at various temporal scales. Laser-produced plasmas are such phenomena as they present different types of interactions even for the main ablation mechanism, which act on considerable different scales fs-for the electrostatic ones and ps-ns for the thermal ones.

5. Conclusions

We implemented an analysis of transient plasma structural units in a multifractal paradigm of motion. The multifractal theory of motion is presented in the form of non-differentiability consequences, such as the multifractal curve, multifractal variables, singularity spectrum of fractal dimension, scale covariant derivative, geodesics equations, etc. For irrotational motions of the transient plasma structural units, the geodesics equation takes the form of a Schrodinger equation of the multifractal type. In the stationary case of this equation, a “hidden symmetry” of the SL (2R) type is highlighted, a situation in which various “synchronization modes” among the structural units of a complex system become functional. For a Riccati-type gauge, these “synchronization modes” were shown to be nonlinear behaviors in the form of period doubling, of damped oscillations of quasi-periodicity, of intermittencies, etc. In such a manner, possible scenarios that depict the dynamics of charged particles emitted from the metallic samples as a result of UV-ns laser–matter interactions. The simulated scenarios depict an evolution toward chaos, without concluding in chaos (nonmanifest chaos). Some correspondences of this theoretical model with experimental data concerning the dynamics of laser-produced plasma were established by implementing a Langmuir probe investigation on the electronic saturation current. The experimental data observed the presence of a damped oscillatory behavior for evolution times between 200 ns and 1 μs and a quasi-chaotic one for times below 200 ns.