Supplier Selection in the Nuclear Power Industry with an Integrated ANP-TODIM Method under Z-Number Circumstances
Abstract
1. Introduction
2. Literature Review
2.1. Supplier Selection Methods
2.2. Evaluation Criteria for Nuclear Power Equipment Supplier Selection
- (1)
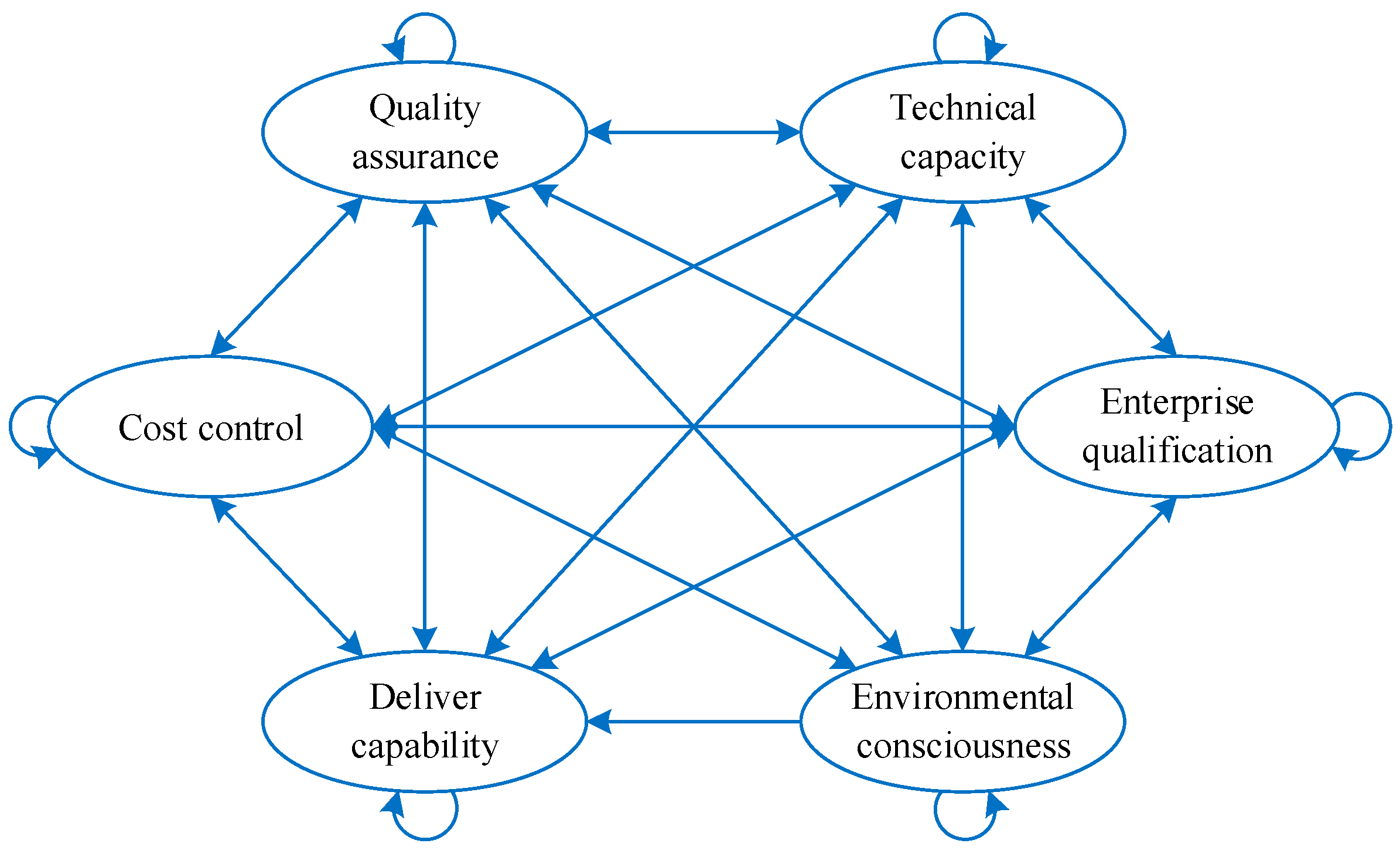
- Quality assurance (C1). The NPP usually consists of four parts: nuclear island, convention island, balance of plant, and nuclear fuel assembly [38,43]. All the nuclear power equipment of them must strictly comply with the quality standard set by IAEA, and their failure rate should be controlled at a very low level. Once a quality safety accident occurs, suppliers should have good after-sales service capabilities and provide corrective measures in the first place.
- (2)
- Cost control (C2). In previous studies [44], cost was often regarded as a key factor in supplier selection. Market surveys show that when the quality level of products or services provided by suppliers is the same, nuclear power enterprises tend to choose suppliers with lower prices so as to save the construction and operation costs of NPPs.
- (3)
- Technical capacity (C3). The nuclear power industry is a high-tech industry, and the technological level embodies the comprehensive competitiveness of nuclear power enterprises. In general, technical capacity is positively related to quality assurance capacity, but shows a negative correlation with the cost of production [39].
- (4)
- Enterprise qualification (C4). The qualification of an enterprise is closely related to its financial status, market condition, and industry influence [39,40,45]. In reality, buyers always look to strengthening cooperation with suppliers with a higher credit reputation and industry ranking. Hence, it is necessary to consider the qualification of candidates in the supplier selection process.
- (5)
- Deliver capability (C5). The delivery cycle and delivery performance are the major concerns in supplier selection [9,46]. Specifically, any delay in delivery will result in cost overruns, or even project failure. In addition, whether it can be successfully delivered in a state of emergency should also be considered in the selection of a nuclear power equipment supplier.
- (6)
- Environmental consciousness (C6). In recent years, the environmental awareness of the company and the government has gradually increased, and many nuclear power equipment suppliers increasingly focus on efficiency, energy saving, environmental protection equipment, and Research and Development (R & D). It has also become an important indicator to measure the corporate social responsibility of suppliers [7,41,47].
3. Preliminaries
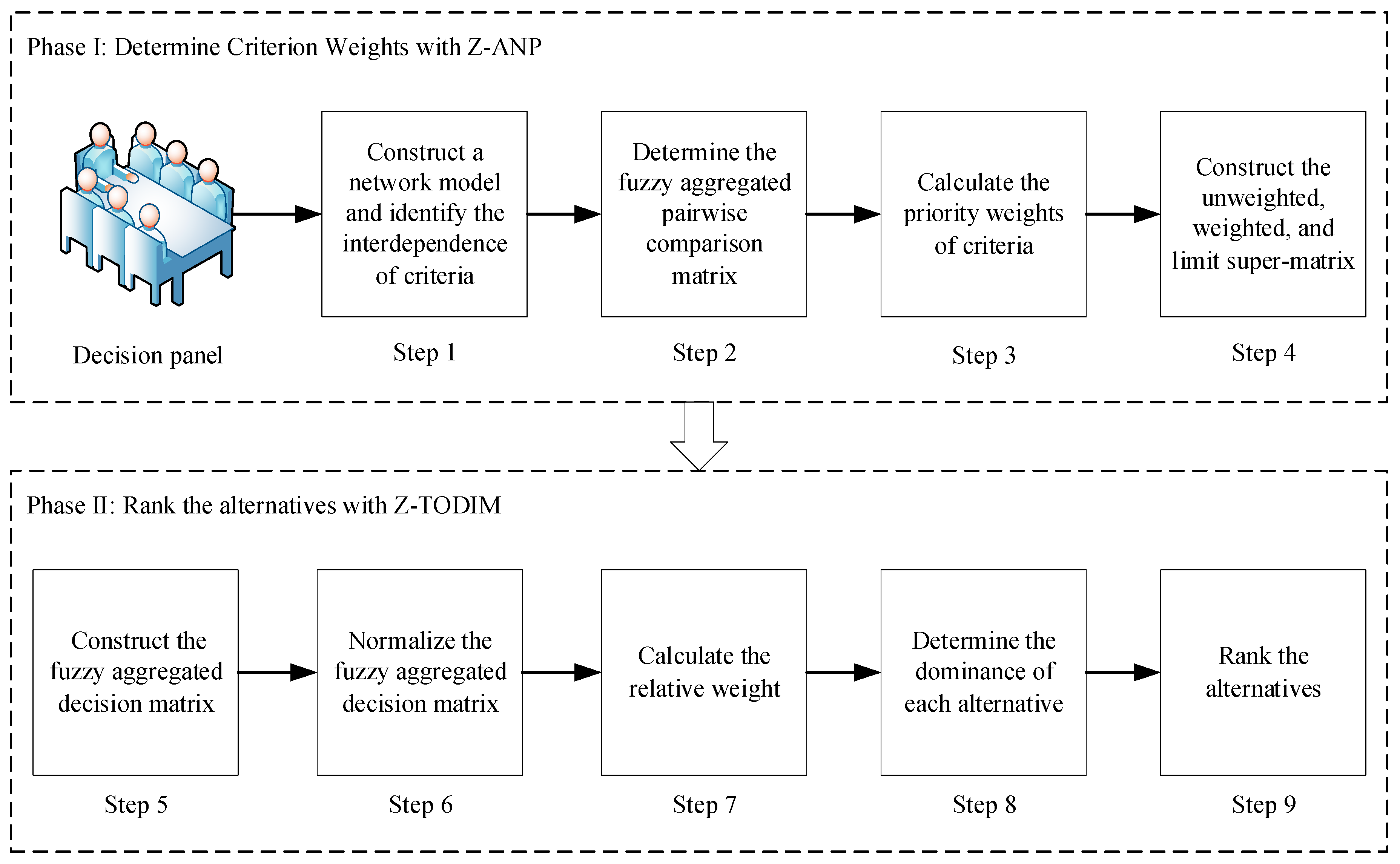
4. Methodology
4.1. Phase I Determine Criterion Weights with Z-ANP
4.2. Phase II: Rank the Alternatives with Z-TODIM
5. Case Study and Result
5.1. Phase I: Determine Criterion Weights with Z-ANP
| Algorithm 1. Calculate the limit super-matrix |
| Input: The weight matrix and the original Z-linguistic evaluation matrices for the sub-criteria with respect to each main criterion. |
| Output: The limit super-matrix . |
| (i) Generated the fuzzy aggregated pairwise comparison matrices , as in Step 2. |
| (ii) Calculate the weight matrix of each block by Step 3. |
| (iii) Construct the unweighted super-matrix . |
| (iv) Calculate the weighted super-matrix . |
| (v) Normalize the weighted super-matrix to obtain . |
| (vi) Generated the limit super-matrix . |
5.2. Phase II: Rank the Alternatives with Z-TODIM
5.3. Results and Discussion
5.3.1. Sensitivity Analysis
5.3.2. Comparison Analysis
5.3.3. Discussion
6. Conclusions, Limitation, and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Acronym | Definition |
|---|---|
| ANP | Analytic Network Process |
| TODIM | Tomada de Decisão Iterativa Multicritério |
| IAEA | International Atomic Energy Agency |
| NPPs | Nuclear Power Plants |
| SCM | Supply Chain Management |
| MCDM | Multi-criteria Decision-making |
| QUALIFLEX | Qualitative Flexible Multiple Method |
| BWM | Best-worst Method |
| VIKOR | VIsekriterijumskao ptimizacija i KOm-promisno Resenje |
| AHP | Analytic Hierarchy Process |
| DEMATEL | Decision-Making and Evaluation Laboratory |
| R & D | Research and Development |
| TFN | Triangular Fuzzy Number |
| TOPSIS | Technique for Order Performance by Similarity to Ideal Solution |
| MAIRCA | Multi-attribute Ideal Real Comparison Analysis |
Appendix B
| C11 | C12 | C13 | C14 | C21 | C22 | C23 | C31 | C32 | C33 | C41 | C42 | C43 | C51 | C52 | C53 | C61 | C62 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C11 | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | ||||||||
| C12 | √ | √ | √ | √ | √ | √ | √ | √ | ||||||||||
| C13 | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | |||||||
| C14 | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | ||||||||
| C21 | √ | √ | √ | √ | √ | √ | ||||||||||||
| C22 | √ | √ | √ | √ | ||||||||||||||
| C23 | √ | √ | √ | √ | √ | √ | √ | |||||||||||
| C31 | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | ||||||
| C32 | √ | √ | √ | √ | √ | √ | √ | √ | √ | |||||||||
| C33 | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | |||||
| C41 | √ | √ | √ | |||||||||||||||
| C42 | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | ||||||
| C43 | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | ||||||||
| C51 | √ | √ | √ | √ | √ | √ | √ | √ | √ | |||||||||
| C52 | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | ||||||||
| C53 | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | |||||||
| C61 | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | |||||||
| C62 | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ |
| Expert | Criteria | C1 | C2 | C3 | C4 | C5 | C6 |
|---|---|---|---|---|---|---|---|
| DM1 | C1 | Just equal | (MI, N) | (WI, H) | (MI, H) | (WI, H) | (MI, H) |
| C2 | (MI−1, N) | Just equal | (MI−1, N) | (WI, N) | (EI, H) | (MI, N) | |
| C3 | (WI−1, H) | (MI, N) | Just equal | (MI, H) | (WI, N) | (MI, H) | |
| C4 | (MI−1, H) | (WI−1, N) | (MI−1, H) | Just equal | (MI−1, H) | (WI, H) | |
| C5 | (WI−1, H) | (EI−1, H) | (WI−1, N) | (MI, H) | Just equal | (MI, N) | |
| C6 | (MI−1, H) | (MI−1, N) | (MI−1, H) | (WI−1, H) | (MI−1, N) | Just equal | |
| DM2 | C1 | Just equal | (EI, H) | (EI, H) | (WI, N) | (WI, H) | (WI, N) |
| C2 | (EI−1, H) | Just equal | (WI, N) | (WI, VH) | (WI, H) | (MI, N) | |
| C3 | (EI−1, H) | (WI−1, N) | Just equal | (MI, N) | (WI, VH) | (WI, VH) | |
| C4 | (WI−1, N) | (WI−1, VH) | (MI−1, N) | Just equal | (WI−1, H) | (EI, H) | |
| C5 | (WI−1, H) | (WI−1, H) | (WI−1, VH) | (WI, H) | Just equal | (MI, N) | |
| C6 | (WI−1, N) | (MI−1, N) | (WI−1, VH) | (EI−1, H) | (MI−1, N) | Just equal | |
| DM3 | C1 | Just equal | (WI−1, N) | (EI, H) | (MI, N) | (WI, H) | (MI, N) |
| C2 | (WI, N) | Just equal | (WI, H) | (MI, N) | (WI, VH) | (MI, H) | |
| C3 | (EI−1, H) | (WI−1, H) | Just equal | (WI, VH) | (WI, N) | (MI, N) | |
| C4 | (MI−1, N) | (MI−1, N) | (WI−1, VH) | Just equal | (WI−1, H) | (WI, N) | |
| C5 | (WI−1, H) | (WI−1, VH) | (WI−1, N) | (WI, H) | Just equal | (WI, VH) | |
| C6 | (MI−1, N) | (MI−1, H) | (MI−1, N) | (WI−1, N) | (WI−1, VH) | Just equal | |
| DM4 | C1 | Just equal | (EI, N) | (WI, N) | (WI, H) | (WI, N) | (WI, VH) |
| C2 | (EI−1, N) | Just equal | (WI, N) | (WI, H) | (WI, N) | (WI, H) | |
| C3 | (WI−1, N) | (WI−1, N) | Just equal | (WI, N) | (WI, H) | (WI, VH) | |
| C4 | (WI−1, H) | (WI−1, H) | (WI−1, N) | Just equal | (WI−1, N) | (EI, H) | |
| C5 | (WI−1, N) | (WI−1, N) | (WI−1, H) | (WI, N) | Just equal | (WI, N) | |
| C6 | (WI−1, VH) | (WI−1, H) | (WI−1, VH) | (EI−1, H) | (WI−1, N) | Just equal |
| C11 | C12 | C13 | C14 | C21 | C22 | C23 | C31 | C32 | C33 | C41 | C42 | C43 | C51 | C52 | C53 | C61 | C62 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C11 | 0.000 | 0.667 | 0.375 | 0.636 | 0.217 | 0.000 | 0.000 | 0.000 | 0.000 | 0.393 | 1.000 | 0.324 | 0.374 | 0.334 | 1.000 | 0.000 | 0.000 | 0.000 |
| C12 | 0.345 | 0.000 | 0.364 | 0.000 | 0.363 | 0.000 | 0.000 | 0.384 | 0.398 | 0.000 | 0.000 | 0.262 | 0.401 | 0.000 | 0.000 | 0.000 | 0.667 | 0.000 |
| C13 | 0.362 | 0.000 | 0.000 | 0.364 | 0.216 | 0.000 | 0.000 | 0.311 | 0.386 | 0.341 | 0.000 | 0.241 | 0.225 | 0.333 | 0.000 | 0.000 | 0.333 | 0.435 |
| C14 | 0.293 | 0.333 | 0.261 | 0.000 | 0.204 | 0.000 | 0.000 | 0.305 | 0.216 | 0.266 | 0.000 | 0.173 | 0.000 | 0.333 | 0.000 | 0.000 | 0.000 | 0.565 |
| C21 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.622 | 0.487 | 1.000 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 |
| C22 | 0.000 | 0.000 | 0.000 | 0.433 | 0.500 | 0.000 | 0.513 | 0.000 | 0.000 | 0.000 | 0.000 | 0.500 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| C23 | 0.000 | 0.000 | 0.000 | 0.567 | 0.500 | 0.378 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.500 | 0.000 | 1.000 | 1.000 | 1.000 | 0.000 | 0.000 |
| C31 | 0.000 | 0.361 | 0.614 | 0.500 | 0.343 | 0.000 | 0.000 | 0.000 | 0.717 | 0.691 | 0.000 | 0.334 | 0.464 | 0.000 | 0.502 | 0.575 | 0.321 | 0.520 |
| C32 | 1.000 | 0.345 | 0.000 | 0.000 | 0.333 | 0.000 | 0.000 | 0.663 | 0.000 | 0.309 | 0.000 | 0.333 | 0.425 | 0.000 | 0.000 | 0.000 | 0.317 | 0.480 |
| C33 | 0.000 | 0.294 | 0.386 | 0.500 | 0.324 | 0.000 | 0.000 | 0.337 | 0.283 | 0.000 | 1.000 | 0.333 | 0.111 | 1.000 | 0.498 | 0.425 | 0.362 | 0.000 |
| C41 | 0.312 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.500 | 0.511 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| C42 | 0.333 | 0.528 | 0.500 | 0.000 | 0.458 | 0.000 | 0.000 | 0.348 | 1.000 | 0.000 | 0.534 | 0.000 | 0.489 | 0.000 | 0.484 | 1.000 | 0.651 | 1.000 |
| C43 | 0.355 | 0.472 | 0.500 | 1.000 | 0.542 | 0.000 | 0.000 | 0.652 | 0.000 | 0.000 | 0.466 | 0.500 | 0.000 | 0.000 | 0.516 | 0.000 | 0.349 | 0.000 |
| C51 | 1.000 | 0.000 | 0.000 | 0.362 | 0.334 | 0.000 | 0.335 | 0.442 | 0.000 | 0.227 | 0.000 | 0.303 | 0.349 | 0.000 | 0.000 | 0.555 | 0.000 | 0.000 |
| C52 | 0.000 | 0.000 | 1.000 | 0.342 | 0.314 | 0.000 | 0.323 | 0.264 | 0.000 | 0.232 | 0.765 | 0.355 | 0.316 | 0.000 | 0.000 | 0.445 | 0.000 | 0.000 |
| C53 | 0.000 | 0.000 | 0.000 | 0.296 | 0.352 | 0.000 | 0.342 | 0.294 | 1.000 | 0.541 | 0.235 | 0.342 | 0.335 | 1.000 | 1.000 | 0.000 | 0.000 | 0.000 |
| C61 | 0.000 | 0.555 | 0.000 | 0.513 | 0.501 | 0.000 | 0.000 | 0.564 | 0.621 | 0.532 | 1.000 | 0.422 | 0.000 | 0.500 | 0.000 | 1.000 | 0.000 | 1.000 |
| C62 | 0.000 | 0.445 | 1.000 | 0.487 | 0.499 | 0.000 | 0.000 | 0.436 | 0.379 | 0.468 | 0.000 | 0.578 | 1.000 | 0.500 | 0.000 | 0.000 | 1.000 | 0.000 |
| C11 | C12 | C13 | C14 | C21 | C22 | C23 | C31 | C32 | C33 | C41 | C42 | C43 | C51 | C52 | C53 | C61 | C62 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C11 | 0.000 | 0.168 | 0.099 | 0.134 | 0.068 | 0.000 | 0.000 | 0.000 | 0.000 | 0.153 | 0.279 | 0.090 | 0.127 | 0.077 | 0.228 | 0.000 | 0.000 | 0.000 |
| C12 | 0.103 | 0.000 | 0.096 | 0.000 | 0.114 | 0.000 | 0.000 | 0.101 | 0.130 | 0.000 | 0.000 | 0.073 | 0.136 | 0.000 | 0.000 | 0.000 | 0.217 | 0.000 |
| C13 | 0.108 | 0.000 | 0.000 | 0.076 | 0.068 | 0.000 | 0.000 | 0.082 | 0.126 | 0.133 | 0.000 | 0.067 | 0.076 | 0.076 | 0.000 | 0.000 | 0.108 | 0.116 |
| C14 | 0.088 | 0.084 | 0.069 | 0.000 | 0.064 | 0.000 | 0.000 | 0.080 | 0.070 | 0.103 | 0.000 | 0.048 | 0.000 | 0.076 | 0.000 | 0.000 | 0.000 | 0.150 |
| C21 | 0.000 | 0.244 | 0.000 | 0.000 | 0.000 | 0.622 | 0.289 | 0.193 | 0.000 | 0.000 | 0.176 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.183 |
| C22 | 0.000 | 0.000 | 0.000 | 0.088 | 0.091 | 0.000 | 0.304 | 0.000 | 0.000 | 0.000 | 0.000 | 0.088 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| C23 | 0.000 | 0.000 | 0.000 | 0.115 | 0.091 | 0.378 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.088 | 0.000 | 0.201 | 0.200 | 0.225 | 0.000 | 0.000 |
| C31 | 0.000 | 0.091 | 0.161 | 0.105 | 0.068 | 0.000 | 0.000 | 0.000 | 0.198 | 0.228 | 0.000 | 0.071 | 0.121 | 0.000 | 0.124 | 0.159 | 0.093 | 0.123 |
| C32 | 0.298 | 0.087 | 0.000 | 0.000 | 0.066 | 0.000 | 0.000 | 0.148 | 0.000 | 0.102 | 0.000 | 0.071 | 0.110 | 0.000 | 0.000 | 0.000 | 0.092 | 0.114 |
| C33 | 0.000 | 0.074 | 0.101 | 0.105 | 0.064 | 0.000 | 0.000 | 0.075 | 0.078 | 0.000 | 0.214 | 0.071 | 0.029 | 0.247 | 0.123 | 0.117 | 0.105 | 0.000 |
| C41 | 0.052 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.062 | 0.077 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| C42 | 0.055 | 0.074 | 0.073 | 0.000 | 0.048 | 0.000 | 0.000 | 0.046 | 0.162 | 0.000 | 0.066 | 0.000 | 0.074 | 0.000 | 0.060 | 0.139 | 0.129 | 0.162 |
| C43 | 0.059 | 0.066 | 0.073 | 0.116 | 0.056 | 0.000 | 0.000 | 0.085 | 0.000 | 0.000 | 0.058 | 0.062 | 0.000 | 0.000 | 0.064 | 0.000 | 0.069 | 0.000 |
| C51 | 0.238 | 0.000 | 0.000 | 0.060 | 0.041 | 0.000 | 0.136 | 0.056 | 0.000 | 0.042 | 0.000 | 0.042 | 0.058 | 0.000 | 0.000 | 0.126 | 0.000 | 0.000 |
| C52 | 0.000 | 0.000 | 0.210 | 0.057 | 0.039 | 0.000 | 0.131 | 0.033 | 0.000 | 0.043 | 0.105 | 0.049 | 0.053 | 0.000 | 0.000 | 0.101 | 0.000 | 0.000 |
| C53 | 0.000 | 0.000 | 0.000 | 0.049 | 0.044 | 0.000 | 0.139 | 0.037 | 0.156 | 0.101 | 0.032 | 0.047 | 0.056 | 0.202 | 0.201 | 0.000 | 0.000 | 0.000 |
| C61 | 0.000 | 0.063 | 0.000 | 0.049 | 0.040 | 0.000 | 0.000 | 0.036 | 0.049 | 0.050 | 0.070 | 0.030 | 0.000 | 0.060 | 0.000 | 0.133 | 0.000 | 0.152 |
| C62 | 0.000 | 0.051 | 0.119 | 0.046 | 0.039 | 0.000 | 0.000 | 0.028 | 0.030 | 0.044 | 0.000 | 0.040 | 0.085 | 0.060 | 0.000 | 0.000 | 0.186 | 0.000 |
| C11 | C12 | C13 | C14 | C21 | C22 | C23 | C31 | C32 | C33 | C41 | C42 | C43 | C51 | C52 | C53 | C61 | C62 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C11 | 0.067 | 0.067 | 0.067 | 0.067 | 0.067 | 0.067 | 0.067 | 0.067 | 0.067 | 0.067 | 0.067 | 0.067 | 0.067 | 0.067 | 0.067 | 0.067 | 0.067 | 0.067 |
| C12 | 0.058 | 0.058 | 0.058 | 0.058 | 0.058 | 0.058 | 0.058 | 0.058 | 0.058 | 0.058 | 0.058 | 0.058 | 0.058 | 0.058 | 0.058 | 0.058 | 0.058 | 0.058 |
| C13 | 0.062 | 0.062 | 0.062 | 0.062 | 0.062 | 0.062 | 0.062 | 0.062 | 0.062 | 0.062 | 0.062 | 0.062 | 0.062 | 0.062 | 0.062 | 0.062 | 0.062 | 0.062 |
| C14 | 0.052 | 0.052 | 0.052 | 0.052 | 0.052 | 0.052 | 0.052 | 0.052 | 0.052 | 0.052 | 0.052 | 0.052 | 0.052 | 0.052 | 0.052 | 0.052 | 0.052 | 0.052 |
| C21 | 0.083 | 0.083 | 0.083 | 0.083 | 0.083 | 0.083 | 0.083 | 0.083 | 0.083 | 0.083 | 0.083 | 0.083 | 0.083 | 0.083 | 0.083 | 0.083 | 0.083 | 0.083 |
| C22 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 | 0.037 |
| C23 | 0.066 | 0.066 | 0.066 | 0.066 | 0.066 | 0.066 | 0.066 | 0.066 | 0.066 | 0.066 | 0.066 | 0.066 | 0.066 | 0.066 | 0.066 | 0.066 | 0.066 | 0.066 |
| C31 | 0.089 | 0.089 | 0.089 | 0.089 | 0.089 | 0.089 | 0.089 | 0.089 | 0.089 | 0.089 | 0.089 | 0.089 | 0.089 | 0.089 | 0.089 | 0.089 | 0.089 | 0.089 |
| C32 | 0.068 | 0.068 | 0.068 | 0.068 | 0.068 | 0.068 | 0.068 | 0.068 | 0.068 | 0.068 | 0.068 | 0.068 | 0.068 | 0.068 | 0.068 | 0.068 | 0.068 | 0.068 |
| C33 | 0.071 | 0.071 | 0.071 | 0.071 | 0.071 | 0.071 | 0.071 | 0.071 | 0.071 | 0.071 | 0.071 | 0.071 | 0.071 | 0.071 | 0.071 | 0.071 | 0.071 | 0.071 |
| C41 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 |
| C42 | 0.058 | 0.058 | 0.058 | 0.058 | 0.058 | 0.058 | 0.058 | 0.058 | 0.058 | 0.058 | 0.058 | 0.058 | 0.058 | 0.058 | 0.058 | 0.058 | 0.058 | 0.058 |
| C43 | 0.040 | 0.040 | 0.040 | 0.040 | 0.040 | 0.040 | 0.040 | 0.040 | 0.040 | 0.040 | 0.040 | 0.040 | 0.040 | 0.040 | 0.040 | 0.040 | 0.040 | 0.040 |
| C51 | 0.052 | 0.052 | 0.052 | 0.052 | 0.052 | 0.052 | 0.052 | 0.052 | 0.052 | 0.052 | 0.052 | 0.052 | 0.052 | 0.052 | 0.052 | 0.052 | 0.052 | 0.052 |
| C52 | 0.046 | 0.046 | 0.046 | 0.046 | 0.046 | 0.046 | 0.046 | 0.046 | 0.046 | 0.046 | 0.046 | 0.046 | 0.046 | 0.046 | 0.046 | 0.046 | 0.046 | 0.046 |
| C53 | 0.062 | 0.062 | 0.062 | 0.062 | 0.062 | 0.062 | 0.062 | 0.062 | 0.062 | 0.062 | 0.062 | 0.062 | 0.062 | 0.062 | 0.062 | 0.062 | 0.062 | 0.062 |
| C61 | 0.039 | 0.039 | 0.039 | 0.039 | 0.039 | 0.039 | 0.039 | 0.039 | 0.039 | 0.039 | 0.039 | 0.039 | 0.039 | 0.039 | 0.039 | 0.039 | 0.039 | 0.039 |
| C62 | 0.040 | 0.040 | 0.040 | 0.040 | 0.040 | 0.040 | 0.040 | 0.040 | 0.040 | 0.040 | 0.040 | 0.040 | 0.040 | 0.040 | 0.040 | 0.040 | 0.040 | 0.040 |
| P1 | P2 | P3 | P4 | P5 | P1 | P2 | P3 | P4 | P5 | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DM1 | C11 | (G, VH) | (G, VH) | (VG, H) | (G, H) | (G, VH) | DM2 | (G, H) | (G, H) | (G, VH) | (G, VH) | (G, H) |
| C12 | (VG, N) | (G, VH) | (G, VH) | (VG, N) | (VG, N) | (G, VH) | (G, H) | (VG, N) | (G, H) | (G, VH) | ||
| C13 | (G, H) | (G, H) | (G, H) | (G, VH) | (G, VH) | (G, VH) | (G, H) | (G, VH) | (G, H) | (G, H) | ||
| C14 | (G, VH) | (G, VH) | (VG, H) | (G, VH) | (VG, N) | (G, VH) | (G, VH) | (G, H) | (VG, H) | (VG, H) | ||
| C21 | (G, H) | (G, N) | (G, H) | (G, VH) | (G, H) | (G, VH) | (G, H) | (G, VH) | (G, H) | (G, H) | ||
| C22 | (G, VH) | (G, VH) | (G, H) | (G, H) | (G, VH) | (G, H) | (G, N) | (G, H) | (G, VH) | (VG, N) | ||
| C23 | (G, H) | (G, N) | (G, H) | (G, VH) | (F, VH) | (G, VH) | (G, H) | (G, VH) | (G, H) | (G, VH) | ||
| C31 | (G, VH) | (G, H) | (G, VH) | (G, VH) | (G, H) | (G, VH) | (G, H) | (G, VH) | (G, VH) | (VG, H) | ||
| C32 | (VG, H) | (VG, H) | (G, VH) | (F, VH) | (G, H) | (VG, H) | (VG, H) | (VG, VH) | (G, VH) | (G, VH) | ||
| C33 | (G, H) | (G, VH) | (G, H) | (G, H) | (G, N) | (G, H) | (G, H) | (G, H) | (G, N) | (G, H) | ||
| C41 | (G, VH) | (G, VH) | (G, H) | (VG, N) | (G, VH) | (G, VH) | (G, VH) | (VG, N) | (G, VH) | (G, H) | ||
| C42 | (VG, H) | (VG, H) | (VG, H) | (G, VH) | (G, H) | (VG, H) | (VG, H) | (G, VH) | (VG, N) | (VG, H) | ||
| C43 | (VG, H) | (G, VH) | (G, VH) | (G, H) | (G, H) | (G, VH) | (G, H) | (G, H) | (G, N) | (G, VH) | ||
| C51 | (G, H) | (G, VH) | (G, H) | (G, N) | (F, VH) | (G, VH) | (G, H) | (G, VH) | (G, VH) | (G, VH) | ||
| C52 | (G, VH) | (F, VH) | (VG, N) | (G, H) | (G, N) | (VG, N) | (G, H) | (G, H) | (G, N) | (G, VH) | ||
| C53 | (G, VH) | (G, H) | (VG, H) | (G, VH) | (VG, N) | (G, VH) | (G, H) | (VG, N) | (F, N) | (G, VH) | ||
| C61 | (G, H) | (G, H) | (G, VH) | (VG, N) | (G, H) | (G, H) | (G, H) | (G, VH) | (G, N) | (VG, H) | ||
| C62 | (VG, N) | (G, VH) | (G, H) | (G, H) | (G, H) | (G, VH) | (G, VH) | (G, H) | (F, N) | (G, H) | ||
| DM3 | C11 | (G, H) | (G, H) | (G, H) | (G, H) | (G, N) | DM4 | (G, VH) | (G, H) | (G, VH) | (VG, N) | (G, VH) |
| C12 | (G, H) | (G, N) | (G, N) | (F, VH) | (F, VH) | (G, VH) | (G, VH) | (VG, N) | (G, VH) | (G, H) | ||
| C13 | (F, VH) | (F, H) | (F, H) | (F, H) | (F, H) | (VG, H) | (VG, N) | (G, VH) | (VG, N) | (G, H) | ||
| C14 | (G, N) | (G, H) | (G, N) | (G, H) | (G, N) | (G, H) | (G, VH) | (G, H) | (G, VH) | (G, H) | ||
| C21 | (G, N) | (G, H) | (G, N) | (G, VH) | (G, N) | (G, H) | (F, VH) | (G, VH) | (F, VH) | (G, H) | ||
| C22 | (G, H) | (G, H) | (G, H) | (G, N) | (G, N) | (G, H) | (G, VH) | (G, H) | (G, VH) | (G, VH) | ||
| C23 | (F, H) | (F, VH) | (F, H) | (F, H) | (G, H) | (G, N) | (F, VH) | (G, VH) | (G, H) | (G, N) | ||
| C31 | (G, H) | (G, H) | (G, N) | (G, N) | (G, H) | (G, VH) | (VG, N) | (G, H) | (G, VH) | (VG, N) | ||
| C32 | (G, N) | (F, VH) | (G, N) | (F, H) | (G, VH) | (G, H) | (G, H) | (G, VH) | (G, VH) | (G, H) | ||
| C33 | (G, N) | (F, H) | (G, H) | (F, H) | (G, N) | (G, VH) | (VG, N) | (G, H) | (G, VH) | (G, H) | ||
| C41 | (G, H) | (G, N) | (G, H) | (G, N) | (G, N) | (VG, H) | (G, VH) | (G, VH) | (VG, N) | (G, VH) | ||
| C42 | (F, VH) | (G, N) | (F, H) | (G, H) | (F, VH) | (G, VH) | (G, VH) | (G, H) | (G, VH) | (G, H) | ||
| C43 | (G, N) | (G, N) | (G, H) | (G, H) | (G, N) | (G, H) | (VG, N) | (G, VH) | (G, H) | (G, VH) | ||
| C51 | (F, H) | (G, H) | (F, VH) | (G, N) | (F, VH) | (G, H) | (G, VH) | (G, N) | (G, VH) | (G, H) | ||
| C52 | (G, N) | (G, H) | (G, VH) | (G, VH) | (G, N) | (G, VH) | (G, H) | (G, VH) | (VG, N) | (G, VH) | ||
| C53 | (G, N) | (F, VH) | (F, VH) | (F, H) | (F, H) | (G, H) | (F, VH) | (G, H) | (G, VH) | (G, H) | ||
| C61 | (F, VH) | (F, VH) | (F, H) | (F, H) | (G, N) | (G, VH) | (G, H) | (G, N) | (VG, N) | (G, VH) | ||
| C62 | (G, H) | (G, N) | (G, H) | (F, VH) | (F, VH) | (G, H) | (G, VH) | (G, H) | (G, H) | (G, H) |
References
- Peng, H.; Wang, X.; Wang, T.; Liu, Y.; Wang, J. A Multi-Criteria Decision Support Framework for Inland Nuclear Power Plant Site Selection under Z-Information: A Case Study in Hunan Province of China. Mathematics 2020, 8, 252. [Google Scholar] [CrossRef]
- Power Reactor Information System (PRIS). Available online: https://pris.iaea.org/pris/ (accessed on 6 August 2020).
- Guo, Y.; Wei, Y. Government communication effectiveness on local acceptance of nuclear power: Evidence from China. J. Clean. Prod. 2019, 218, 38–50. [Google Scholar] [CrossRef]
- Grover, R.B. The Civil Liability for Nuclear Damage Act of India: An engineering perspective regarding Supplier’s liability. Prog. Nucl. Energy 2017, 101, 168–175. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Y.; Wang, J.; Cheng, P.; Li, L. A TODIM-PROMETHEE II Based Multi-Criteria Group Decision Making Method for Risk Evaluation of Water Resource Carrying Capacity under Probabilistic Linguistic Z-Number Circumstances. Mathematics 2020, 8, 1190. [Google Scholar] [CrossRef]
- Tian, Z.; Nie, R.; Wang, J. Social network analysis-based consensus-supporting framework for large-scale group decision-making with incomplete interval type-2 fuzzy information. Inf. Sci. 2019, 502, 446–471. [Google Scholar] [CrossRef]
- Tian, Z.; Zhang, H.; Wang, J.; Wang, T. Green Supplier Selection Using Improved TOPSIS and Best-Worst Method Under Intuitionistic Fuzzy Environment. Informatica 2018, 29, 773–800. (In Lithuan) [Google Scholar] [CrossRef]
- Li, J.; Wang, J. An Extended QUALIFLEX Method Under Probability Hesitant Fuzzy Environment for Selecting Green Suppliers. Int. J. Fuzzy Syst. 2017, 19, 1866–1879. [Google Scholar] [CrossRef]
- Chen, T.; He, S.; Wang, J.; Li, L.; Luo, H. Novel operations for linguistic neutrosophic sets on the basis of Archimedean copulas and co-copulas and their application in multi-criteria decision-making problems. J. Intell. Fuzzy Syst. 2019, 37, 2887–2912. [Google Scholar] [CrossRef]
- Kannan, D.; Mina, H.; Nosrati-Abarghooee, S.; Khosrojerdi, G. Sustainable circular supplier selection: A novel hybrid approach. Sci. Total Environ. 2020, 722, 137936. [Google Scholar] [CrossRef]
- Shen, K.; Wang, J. Z-VIKOR Method Based on a New Comprehensive Weighted Distance Measure of Z-Number and Its Application. IEEE Trans. Fuzzy Syst. 2018, 26, 3232–3245. [Google Scholar] [CrossRef]
- Tian, C.; Peng, J.J.; Zhang, Z.Q.; Goh, M.; Wang, J.Q. A Multi-Criteria Decision-Making Method Based on Single-Valued Neutrosophic Partitioned Heronian Mean Operator. Mathematics 2020, 8, 1189. [Google Scholar] [CrossRef]
- Xiao, F.; Wang, J. Multistage decision support framework for sites selection of solar power plants with probabilistic linguistic information. J. Clean. Prod. 2019, 230, 1396–1409. [Google Scholar] [CrossRef]
- Peng, H.; Wang, J. Multi-criteria sorting decision making based on dominance and opposition relations with probabilistic linguistic information. Fuzzy Optim. Decis. Mak. 2020, in press. [Google Scholar] [CrossRef]
- Peng, J.; Tian, C.; Zhang, W.; Zhang, S.; Wang, J. An integrated multi-criteria decision-making framework for sustainable supplier selection under picture fuzzy environment. Technol. Econ. Dev. Econ. 2020, 26, 573–598. [Google Scholar] [CrossRef]
- Gore, R.; Reynolds, P.F.J.; Kamensky, D.; Diallo, S.; Padilla, J. Statistical Debugging for Simulations. Acm. Trans. Model. Comput. Simul. 2015, 25, 1–26. [Google Scholar] [CrossRef]
- Kacprzyk, J.; Fedrizzi, M.; Nurmi, H. Group decision making and consensus under fuzzy preferences and fuzzy majority. Fuzzy Set. Syst. 1992, 49, 21–31. [Google Scholar] [CrossRef]
- Bates, J.H.T.; Young, M.P. Applying Fuzzy Logic to Medical Decision Making in the Intensive Care Unit. Am. J. Respir. Crit. Care Med. 2003, 167, 948–952. [Google Scholar] [CrossRef]
- Peng, H.; Zhang, H.; Wang, J.; Li, L. An uncertain Z-number multicriteria group decision-making method with cloud models. Inf. Sci. 2019, 501, 136–154. [Google Scholar] [CrossRef]
- Qiao, D.; Shen, K.; Wang, J.; Wang, T. Multi-criteria PROMETHEE method based on possibility degree with Z-numbers under uncertain linguistic environment. J. Ambient Intell. Humaniz. Comput. 2020, 11, 2187–2201. [Google Scholar] [CrossRef]
- Zadeh, L.A. A Note on Z-numbers. Inf. Sci. 2011, 181, 2923–2932. [Google Scholar] [CrossRef]
- Song, C.; Wang, J.; Li, J. New Framework for Quality Function Deployment Using Linguistic Z-Numbers. Mathematics 2020, 8, 224. [Google Scholar] [CrossRef]
- Shen, K.; Wang, X.; Qiao, D.; Wang, J. Extended Z-MABAC method based on regret theory and directed distance for regional circular economy development program selection with Z-information. IEEE Trans. Fuzzy Syst. 2019, 28, 1851–1863. [Google Scholar] [CrossRef]
- Jiang, S.; Shi, H.; Lin, W.; Liu, H. A large group linguistic Z-DEMATEL approach for identifying key performance indicators in hospital performance management. Appl. Soft Comput. 2020, 86, 105900. [Google Scholar] [CrossRef]
- Saaty, T.L. Decision Making with Dependence and Feedback: The Analytic Network Process; RWS Publications: Pittsburgh, PA, USA, 1996; Volume 95, pp. 129–157. [Google Scholar]
- Wu, Y.; Zhang, B.; Xu, C.; Li, L. Site selection decision framework using fuzzy ANP-VIKOR for large commercial rooftop PV system based on sustainability perspective. Sustain. Cities Soc. 2018, 40, 454–470. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, J.Q.; Wang, T.L. Multi-criteria group decision-making method based on TODIM with probabilistic interval-valued hesitant fuzzy information. Expert Syst. 2019, 36, e12424. [Google Scholar] [CrossRef]
- Kiani Mavi, R.; Standing, C. Critical success factors of sustainable project management in construction: A fuzzy DEMATEL-ANP approach. J. Clean. Prod. 2018, 194, 751–765. [Google Scholar] [CrossRef]
- Tian, C.; Peng, J. An integrated picture fuzzy anp-todim multi-criteria decision-making approach for tourism attraction recommendation. Technol. Econ. Dev. Econ. 2020, 26, 331–354. [Google Scholar] [CrossRef]
- Mistarihi, M.Z.; Okour, R.A.; Mumani, A.A. An integration of a QFD model with Fuzzy-ANP approach for determining the importance weights for engineering characteristics of the proposed wheelchair design. Appl. Soft Comput. 2020, 90, 106136. [Google Scholar] [CrossRef]
- Gomes, L.F.A.M.; Rangel, L.A.D.; Maranhão, F.J.C. Multicriteria analysis of natural gas destination in Brazil: An application of the TODIM method. Math. Comput. Model. 2009, 50, 92–100. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Y.; Martínez, L. Fuzzy TODIM method based on alpha-level sets. Expert Syst. Appl. 2020, 140, 112899. [Google Scholar] [CrossRef]
- Yu, S.; Wang, J.; Wang, J. An extended TODIM approach with intuitionistic linguistic numbers. Int. Trans. Oper. Res. 2018, 25, 781–805. [Google Scholar] [CrossRef]
- Zhu, J.; Shuai, B.; Wang, R.; Chin, K. Risk Assessment for Failure Mode and Effects Analysis Using the Bonferroni Mean and TODIM Method. Mathematics 2019, 7, 536. [Google Scholar] [CrossRef]
- Alali, F.; Tolga, A.C. Portfolio allocation with the TODIM method. Expert Syst. Appl. 2019, 124, 341–348. [Google Scholar] [CrossRef]
- Krohling, R.A.; de Souza, T.T.M. Combining prospect theory and fuzzy numbers to multi-criteria decision making. Expert Syst. Appl. 2012, 39, 11487–11493. [Google Scholar] [CrossRef]
- Krohling, R.A.; Santos, A.D.; Pacheco, A.G.C. TODIM and TOPSIS with Z-numbers. Front. Inf. Tech. Electron. Eng. 2019, 20, 283–291. [Google Scholar] [CrossRef]
- Yang, G.; Huang, W.J.; Lei, L.L. Using AHP and TOPSIS Approaches in Nuclear Power Plant Equipment Supplier Selection. Key Eng. Mater. 2010, 419–420, 761–764. [Google Scholar] [CrossRef]
- Wu, Y.; Chen, K.; Zeng, B.; Xu, H.; Yang, Y. Supplier selection in nuclear power industry with extended VIKOR method under linguistic information. Appl. Soft Comput. 2016, 48, 444–457. [Google Scholar] [CrossRef]
- Phochanikorn, P.; Tan, C. A New Extension to a Multi-Criteria Decision-Making Model for Sustainable Supplier Selection under an Intuitionistic Fuzzy Environment. Sustainability 2019, 11, 5413. [Google Scholar] [CrossRef]
- Liu, P.C.Y.; Lo, H.; Liou, J.J.H. A Combination of DEMATEL and BWM-Based ANP Methods for Exploring the Green Building Rating System in Taiwan. Sustainability 2020, 12, 3216. [Google Scholar] [CrossRef]
- Giannakis, M.; Dubey, R.; Vlachos, I.; Ju, Y. Supplier sustainability performance evaluation using the analytic network process. J. Clean. Prod. 2020, 247, 119439. [Google Scholar] [CrossRef]
- Guang, Y.; Wenjie, H. Application of the TOPSIS Based on Entropy-AHP Weight in Nuclear Power Plant Nuclear-Grade Equipment Supplier Selection. In Proceedings of the International Conference on Environmental Science and Information Application Technology, Wuhan, China, 4–5 July 2009; pp. 633–636. [Google Scholar]
- Wu, X.; Wang, J.; Peng, J.; Chen, X. Cross-Entropy and Prioritized Aggregation Operator with Simplified Neutrosophic Sets and Their Application in Multi-Criteria Decision-Making Problems. Int. J. Fuzzy Syst. 2016, 18, 1104–1116. [Google Scholar] [CrossRef]
- Nie, R.; Tian, Z.; Wang, J.; Chin, K.S. Hotel selection driven by online textual reviews: Applying a semantic partitioned sentiment dictionary and evidence theory. Int. J. Hosp. Manag. 2020, 88, 102495. [Google Scholar] [CrossRef]
- Liang, R.; Wang, J.; Zhang, H. A multi-criteria decision-making method based on single-valued trapezoidal neutrosophic preference relations with complete weight information. Neural Comput. Appl. 2018, 30, 3383–3398. [Google Scholar] [CrossRef]
- Shen, K.; Li, L.; Wang, J. Circular economy model for recycling waste resources under government participation: A case study in industrial waste water circulation in china. Technol. Econ. Dev. Econ. 2020, 26, 21–47. [Google Scholar] [CrossRef]
- Deng, X.; Hu, Y.; Deng, Y.; Mahadevan, S. Supplier selection using AHP methodology extended by D numbers. Expert Syst. Appl. 2014, 41, 156–167. [Google Scholar] [CrossRef]
- Forghani, A.; Sadjadi, S.J.; Farhang Moghadam, B. A supplier selection model in pharmaceutical supply chain using PCA, Z-TOPSIS and MILP: A case study. PLoS ONE 2018, 13, 201604. [Google Scholar] [CrossRef]
- Rezaei, J.; Nispeling, T.; Sarkis, J.; Tavasszy, L. A supplier selection life cycle approach integrating traditional and environmental criteria using the best worst method. J. Clean. Prod. 2016, 135, 577–588. [Google Scholar] [CrossRef]
- Lootsma Freerk, A. Fuzzy Logic for Planning and Decision Making; Springer Science & Business Media: Boston, MA, USA, 1997. [Google Scholar]
- Kang, B.; Wei, D.; Li, Y.; Deng, Y. A method of converting Z-number to classical fuzzy number. J. Inf. Comput. Sci. 2012, 9, 703–709. [Google Scholar]
- Kahraman, C.; Ertay, T.; Büyüközkan, G. A fuzzy optimization model for QFD planning process using analytic network approach. Eur. J. Oper. Res. 2006, 171, 390–411. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Wang, X.K.; Peng, J.J.; Zhang, H.Y.; Wang, J.Q. An integrated probabilistic linguistic projection method for MCGDM based on ELECTRE III and the weighted convex median voting rule. Expert Syst. 2020, in press. [Google Scholar] [CrossRef]
- Kahneman, D.; Tversky, A. Prospect Theory: An Analysis of Decision under Risk. Econometrica 1979, 47, 263–291. [Google Scholar] [CrossRef]
- Wang, B.; Xie, H.; Ren, H.; Li, X.; Chen, L.; Wu, B. Application of AHP, TOPSIS, and TFNs to plant selection for phytoremediation of petroleum-contaminated soils in shale gas and oil fields. J. Clean. Prod. 2019, 233, 13–22. [Google Scholar] [CrossRef]
- Pamučar, D.; Gigović, L.; Bajić, Z.; Janošević, M. Location Selection for Wind Farms Using GIS Multi-Criteria Hybrid Model: An Approach Based on Fuzzy and Rough Numbers. Sustainability 2017, 9, 1315. [Google Scholar] [CrossRef]
| Criteria | Sub-Criteria | Category | Related Literature |
|---|---|---|---|
| Quality assurance | Quality management capacity C11 | B | [38,43] |
| Quality certification level C12 | B | ||
| Acceptance rate C13 | B | ||
| Feedback and improvement C14 | B | ||
| Cost control | Product price C21 | C | [44,48] |
| Quantity discount C22 | B | ||
| Transportation and installation cost C23 | C | ||
| Technical capacity | Technical advancement C31 | B | [4,39,49] |
| R&D capability C32 | B | ||
| Technical equipment level C33 | B | ||
| Enterprise qualification | Business credit status C41 | B | [39,40] |
| Market reputation C42 | B | ||
| Industry ranking C43 | B | ||
| Deliver capability | Delivery cycle C51 | C | [9,46] |
| Rate of delivery in time C52 | B | ||
| Emergency delivery capability C53 | B | ||
| Environmental consciousness | Energy utilization ratio C61 | B | [7,41,50] |
| Energy-saving measures C62 | B |
| Linguistic Term | Triangular Fuzzy Scale | Triangular Fuzzy Reciprocal Scale |
|---|---|---|
| Just equal | (1,1,1) | (1,1,1) |
| Equal importance (EI) | (1/2,1,3/2) | (2/3,1,2) |
| Weakly importance (WI) | (1,3/2,2) | (1/2,2/3,1) |
| Moderate importance (MI) | (3/2,2,5/2) | (2/5,1/2,2/3) |
| Very importance (VI) | (2,5/2,3) | (1/3,2/5,1/2) |
| Absolutely importance (AI) | (5/2,3,7/2) | (2/7,1/3,2/5) |
| Constraint | Reliability | ||
|---|---|---|---|
| Linguistic Term | Fuzzy Scale | Linguistic Term | Fuzzy Scale |
| Very poor (VP) | (0,0,0.25) | Very low (VL) | (0,0,0.3) |
| Poor (P) | (0,0.25,0.5) | Low (L) | (0.1,0.3,0.5) |
| Fairly (F) | (0.25,0.5,0.75) | Neutral (N) | (0.3,0.5,0.7) |
| Good (G) | (0.5,0.75,1.0) | High (H) | (0.5,0.7,0.9) |
| Very good (VG) | (0.75,1.0,1.0) | Very high (VH) | (0.7,1.0,1.0) |
| C1 | C2 | C3 | C4 | C5 | C6 | |
|---|---|---|---|---|---|---|
| C1 | (1.00,1.00,1.00) | (0.55,0.86,1.20) | (0.60,1.00,1.40) | (0.97,1.35,1.74) | (0.81,1.20,1.61) | (0.99,1.39,1.79) |
| C2 | (0.51,0.74,1.24) | (1.00,1.00,1.00) | (0.64,0.93,1.24) | (0.89,1.29,1.69) | (0.73,1.14,1.56) | (1.05,1.44,1.83) |
| C3 | (0.47,0.68,1.22) | (0.55,0.73,1.01) | (1.00,1.00,1.00) | (0.99,1.39,1.79) | (0.80,1.20,1.60) | (1.05,1.48,1.92) |
| C4 | (0.35,0.45,0.65) | (0.38,0.50,0.74) | (0.36,0.47,0.67) | (1.00,1.00,1.00) | (0.38,0.50,0.74) | (0.60,1.00,1.40) |
| C5 | (0.40,0.54,0.81) | (0.45,0.63,1.04) | (0.40,0.53,0.80) | (0.91,1.31,1.71) | (1.00,1.00,1.00) | (0.95,1.33,1.71) |
| C6 | (0.36,0.47,0.67) | (0.33,0.42,0.59) | (0.39,0.51,0.73) | (0.47,0.68,1.22) | (0.35,0.45,0.65) | (1.00,1.00,1.00) |
| Criteria | Sub-Criteria | Criteria Weight |
|---|---|---|
| Quality assurance | Quality management capacity C11 | 0.067 |
| Quality certification level C12 | 0.058 | |
| Acceptance rate C13 | 0.062 | |
| Feedback and improvement C14 | 0.052 | |
| Cost control | Products price C21 | 0.083 |
| Quantity discount C22 | 0.037 | |
| Transportation and installation cost C23 | 0.066 | |
| Technical capacity | Technical advancement C31 | 0.089 |
| R&D capability C32 | 0.068 | |
| Technical equipment level C33 | 0.071 | |
| Enterprise qualification | Business credit status C41 | 0.010 |
| Market reputation C42 | 0.058 | |
| Industry ranking C43 | 0.040 | |
| Deliver capability | Delivery cycle C51 | 0.052 |
| Rate of delivery in time C52 | 0.046 | |
| Emergency delivery capability C53 | 0.062 | |
| Environmental consciousness | Energy utilization ratio C61 | 0.039 |
| Energy-saving measures C62 | 0.040 |
| P1 | P2 | P3 | P4 | P5 | |
|---|---|---|---|---|---|
| C11 | (0.036,0.517,1.000) | (0.010,0.474,0.939) | (0.149,0.629,1.000) | (0.068,0.517,0.870) | (0.000,0.464,0.928) |
| C12 | (0.128,0.614,1.000) | (0.028,0.513,1.000) | (0.123,0.558,0.792) | (0.000,0.480,0.865) | (0.000,0.480,0.865) |
| C13 | (0.130,0.610,0.983) | (0.032,0.470,0.810) | (0.027,0.513,1.000) | (0.059,0.513,0.869) | (0.000,0.470,0.940) |
| C14 | (0.000,0.439,0.879) | (0.060,0.529,1.000) | (0.055,0.464,0.767) | (0.140,0.595,0.943) | (0.110,0.504,0.701) |
| C21 | (0.055,0.471,0.887) | (0.174,0.590,1.000) | (0.000,0.432,0.862) | (0.000,0.461,0.917) | (0.110,0.511,0.912) |
| C22 | (0.028,0.513,1.000) | (0.017,0.502,0.988) | (0.000,0.469,0.938) | (0.017,0.502,0.988) | (0.078,0.547,0.915) |
| C23 | (0.114,0.510,0.907) | (0.190,0.600,1.000) | (0.000,0.425,0.850) | (0.053,0.463,0.874) | (0.076,0.487,0.892) |
| C31 | (0.060,0.529,1.000) | (0.039,0.448,0.767) | (0.000,0.438,0.878) | (0.024,0.479,0.933) | (0.145,0.555,0.767) |
| C32 | (0.291,0.661,0.839) | (0.241,0.633,0.839) | (0.277,0.688,0.989) | (0.000,0.419,0.843) | (0.177,0.588,1.000) |
| C33 | (0.109,0.548,0.987) | (0.093,0.532,0.878) | (0.119,0.559,1.000) | (0.000,0.438,0.878) | (0.046,0.454,0.862) |
| C41 | (0.149,0.629,1.000) | (0.026,0.506,0.987) | (0.068,0.517,0.870) | (0.090,0.506,0.731) | (0.000,0.464,0.928) |
| C42 | (0.148,0.660,0.936) | (0.211,0.694,0.936) | (0.010,0.510,0.890) | (0.102,0.602,1.000) | (0.000,0.493,0.872) |
| C43 | (0.131,0.557,0.876) | (0.080,0.491,0.810) | (0.085,0.542,1.000) | (0.000,0.410,0.820) | (0.050,0.491,0.932) |
| C51 | (0.145,0.538,0.931) | (0.000,0.407,0.814) | (0.167,0.561,0.949) | (0.118,0.497,0.877) | (0.167,0.588,1.000) |
| C52 | (0.164,0.594,0.932) | (0.000,0.441,0.886) | (0.200,0.645,1.000) | (0.138,0.553,0.876) | (0.072,0.502,0.932) |
| C53 | (0.183,0.591,1.000) | (0.000,0.413,0.835) | (0.235,0.624,0.835) | (0.005,0.408,0.816) | (0.145,0.539,0.849) |
| C61 | (0.027,0.511,1.000) | (0.000,0.467,0.940) | (0.000,0.473,0.946) | (0.065,0.473,0.685) | (0.201,0.658,1.000) |
| C62 | (0.252,0.617,0.904) | (0.217,0.609,1.000) | (0.183,0.548,0.913) | (0.000,0.357,0.722) | (0.104,0.478,0.857) |
| Ranking | Ranking | Ranking | Ranking | |||||
|---|---|---|---|---|---|---|---|---|
| 1.000 | 1 | 1.000 | 1 | 1.000 | 1 | 1.000 | 1 | |
| 0.485 | 3 | 0.485 | 3 | 0.485 | 3 | 0.484 | 3 | |
| 0.695 | 2 | 0.695 | 2 | 0.696 | 2 | 0.696 | 2 | |
| 0.000 | 5 | 0.000 | 5 | 0.000 | 5 | 0.000 | 5 | |
| 0.385 | 4 | 0.385 | 4 | 0.385 | 4 | 0.385 | 4 | |
| Methods | Ranking Orders |
|---|---|
| Fuzzy AHP-TOPSIS | |
| Rough BWM-MAIRCA | |
| The proposed ranking |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.-H.; Peng, H.-M.; Wang, T.-L.; Wang, X.-K.; Wang, J.-Q. Supplier Selection in the Nuclear Power Industry with an Integrated ANP-TODIM Method under Z-Number Circumstances. Symmetry 2020, 12, 1357. https://doi.org/10.3390/sym12081357
Liu Y-H, Peng H-M, Wang T-L, Wang X-K, Wang J-Q. Supplier Selection in the Nuclear Power Industry with an Integrated ANP-TODIM Method under Z-Number Circumstances. Symmetry. 2020; 12(8):1357. https://doi.org/10.3390/sym12081357
Chicago/Turabian StyleLiu, Ya-Hua, Heng-Ming Peng, Tie-Li Wang, Xiao-Kang Wang, and Jian-Qiang Wang. 2020. "Supplier Selection in the Nuclear Power Industry with an Integrated ANP-TODIM Method under Z-Number Circumstances" Symmetry 12, no. 8: 1357. https://doi.org/10.3390/sym12081357
APA StyleLiu, Y.-H., Peng, H.-M., Wang, T.-L., Wang, X.-K., & Wang, J.-Q. (2020). Supplier Selection in the Nuclear Power Industry with an Integrated ANP-TODIM Method under Z-Number Circumstances. Symmetry, 12(8), 1357. https://doi.org/10.3390/sym12081357





