Non-Linear Behaviors of Transient Periodic Plasma Dynamics in a Multifractal Paradigm
Abstract
1. Introduction
2. Mathematical Model
Short Reminder of the Multifractal Theory of Motion
3. Complex Fluid Dynamics through Schrödinger “Regimes” of Multifractal Type
3.1. “Hidden Symmetry” in Transient Plasma Dynamics
3.2. “Synchronization Modes” through Riccati-Type Gauge in Transient Plasma Dynamics
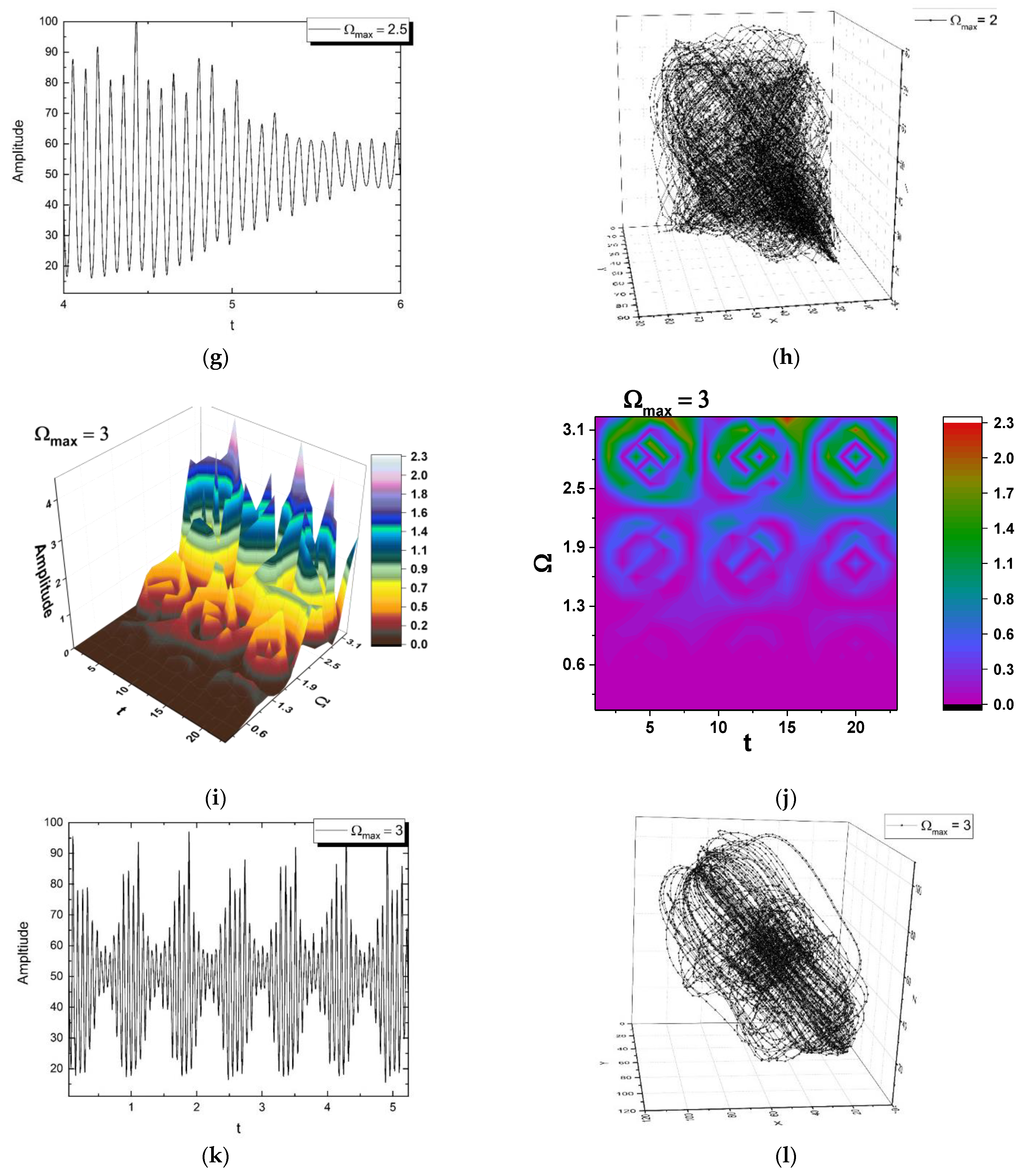
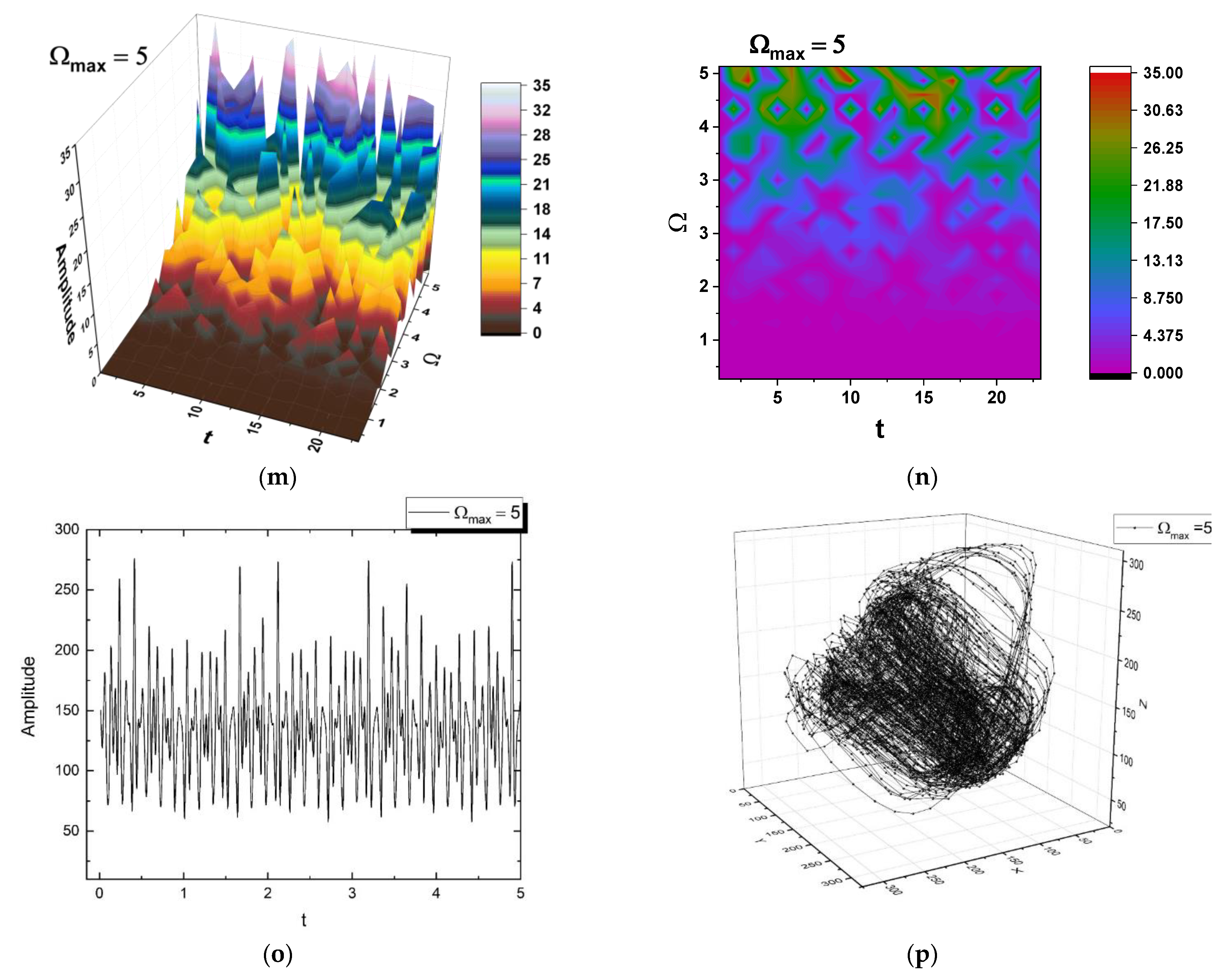
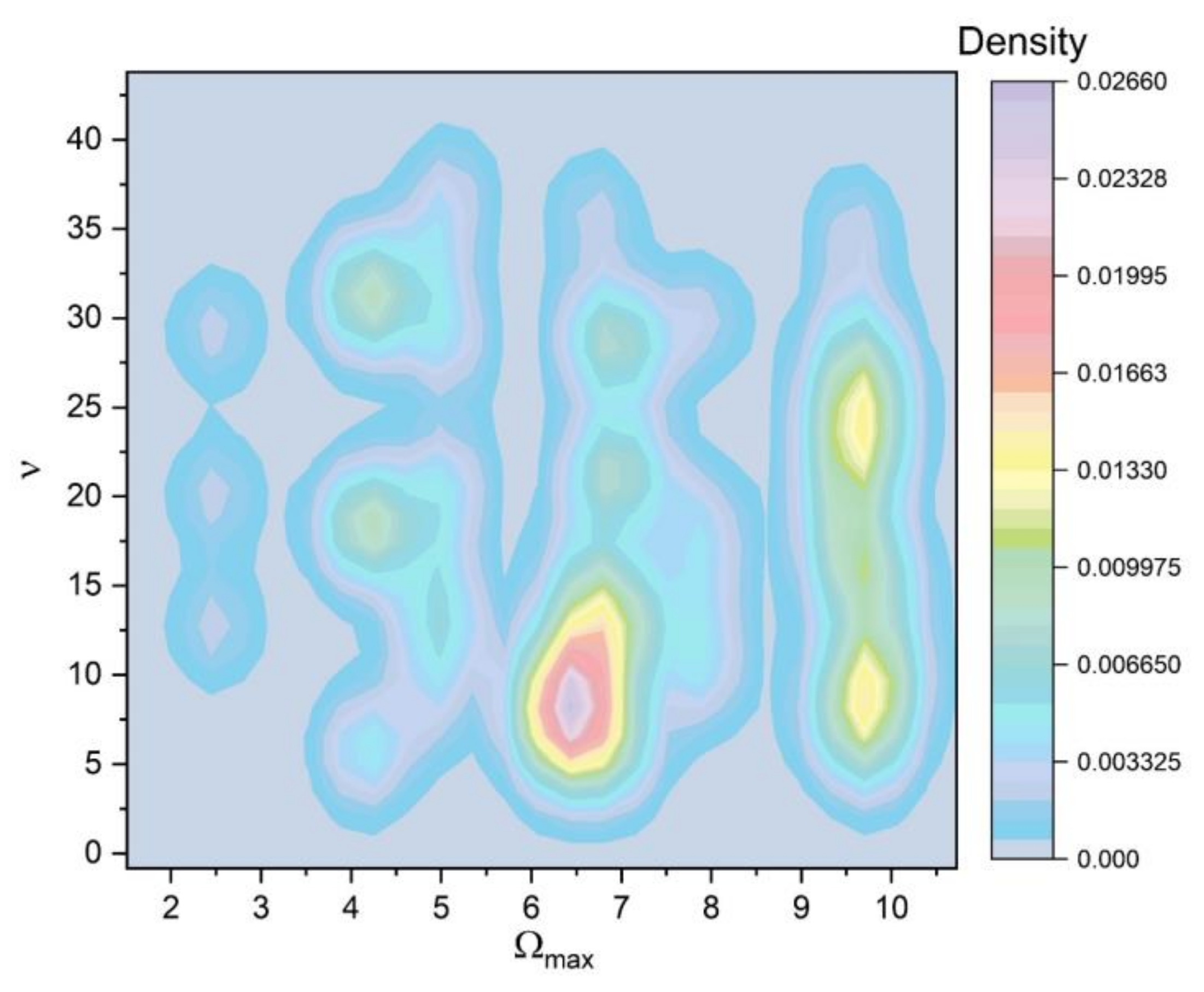
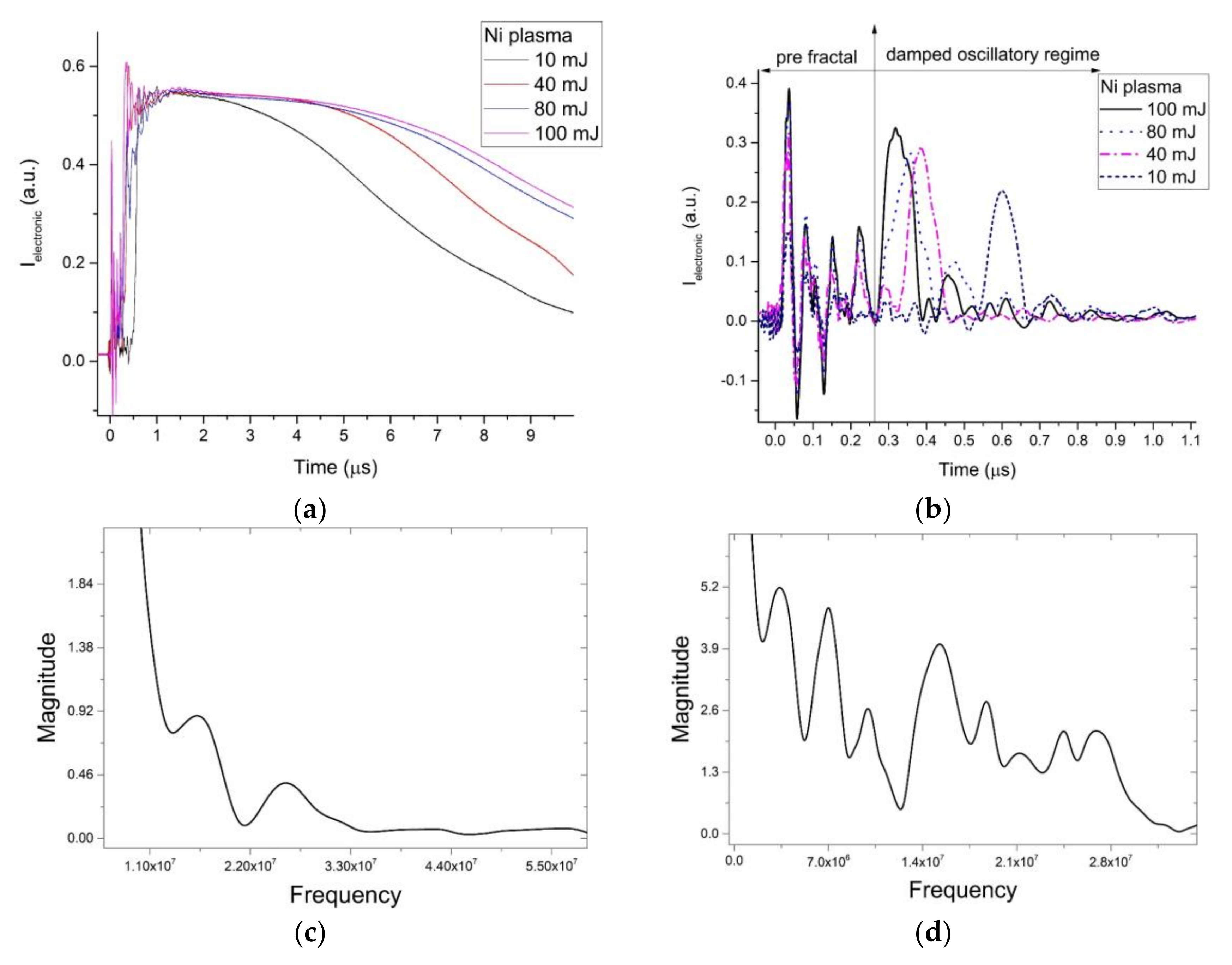
4. Application to Laser Ablation Plasma Dynamics
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Luis, G. Complex Fluids; Springer: Barcelona, Spain, 1993. [Google Scholar]
- Badii, R. Complexity: Hierarchical Structures and Scaling in Physics; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Mitchell, M. Complexity: A Guided Tour; Oxford University Press: New York, NY, USA, 2009. [Google Scholar]
- Baryam, Y. Dynamics of Complex Systems; Taylor and Francis: New York, NY, USA, 1999. [Google Scholar]
- Deville, M.; Gatski, B.T. Mathematical Modeling for Complex Fluids and Flows; Springer: Berlin, Germany, 2012. [Google Scholar]
- Skiadas, C.H.; Skiadas, C. Handbook of Application of Chaos Theory; CRC Press: New York, NY, USA, 2017. [Google Scholar]
- Horton, W.; Ichikawa, Y.H. Chaos Structures in Nonlinear Plasmas; World Scientific: Hackensack, NJ, USA, 1996. [Google Scholar]
- Kumar, A.; Singh, R.K.; Thomas, J.; Sunil, S. Parametric study of expanding plasma plume formed by laser-blow-off of thin film using triple Lanmguir Probe. J. Appl. Phys. 2009, 106, 043306. [Google Scholar] [CrossRef]
- Agop, M.; Mihaila, I.; Nedeff, F.; Irimiciuc, S.A. Charged Particle Oscillations in Transient Plasmas Generated by Nanosecond Laser Ablation on Mg Target. Symmetry 2020, 12, 292. [Google Scholar] [CrossRef]
- Geohegan, D.B. Dynamics of laser ablation plasma plume penetration through low pressure gases. Appl. Phys. Lett. 1995, 65, 197. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W. H. Freeman and Co.: San Fracisco, CA, USA, 1982. [Google Scholar]
- Nottale, L. Scale Relativity and Fractal Space-Time: A New Approach to Unifying Relativity and Quantum Mechanics; Imperial College Press: London, UK, 2011. [Google Scholar]
- Merches, I.; Agop, M. Differentiability and Fractality in Dynamics of Physical Systems; World Scientific: Hackensack, NJ, USA, 2016. [Google Scholar]
- Agop, M.; Paun, V.P. On the New Perspectives of Fractal Theory. Fundaments and Applications; Romanian Academy Publishing House: Bucharest, Romania, 2017. [Google Scholar]
- Jackson, E.A. Perspectives of Nonlinear Dynamics; Cambridge University Press: New York, NY, USA, 1993. [Google Scholar]
- Cristescu, C.P. Nonlinear Dynamics and Chaos. Theoretical Fundaments and Applications; Romanian Academy Publishing House: Bucharest, Romania, 2008. [Google Scholar]
- Cresson, J.; Adda, F.B. Quantum Derivations and Schrödinger Equations. Chaos Solitons Fract. 2004, 19, 1323–1334. [Google Scholar]
- Irimiciuc, S.; Bulai, G.; Agop, M.; Gurlui, S. Influence of laser-produced plasma parameters on the deposition process: In situ space- and time-resolved optical emission spectroscopy and fractal modeling approach. Appl. Phys. A Mater. 2018, 124, 615. [Google Scholar] [CrossRef]
- Irimiciuc, S.A.; Bulai, G.; Gurlui, S.; Agop, M. On the separation of particle flow during pulse laser deposition of heterogeneous materials-A multi-fractal approach. Powder Technol. 2018, 339, 273–280. [Google Scholar] [CrossRef]
- Chen, F.F. Introduction to Plasma Physics and Controlled Fusion: Volume 1: Plasma Physics; Springer: New York, NY, USA, 2010. [Google Scholar]
- Mihăileanu, N. Complements of Projective and Differential Analytical Geometry; Didactical and Pedagogical Publishing House: Bucharest, Romania, 1971. [Google Scholar]
- Postnikov, I. Groupes et Algèbres de Lie; Édition Mir: Moscow, Russia, 1985. [Google Scholar]
- Simon, B. Representations of Finite and Compact Groups; American Mathematical Society: Providence, RI, USA, 1996. [Google Scholar]
- Mazilu, N.; Agop, M. At the Crossroads of Theories. Between Newton and Einstein—The Barbilian Universe; ArsLonga Publishing House: Iasi, Romania, 2010. [Google Scholar]
- Mazilu, N.; Agop, M. Skyrmions. A Great Finishing Touch to Classical Newtonian Philosophy, World Philosophy Series; Nova Science Publishers: New York, NY, USA, 2012. [Google Scholar]
- Agop, M.; Merches, I. Operational Procedures Describing Physical Systems; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2019. [Google Scholar]
- Cartan, E. La Théorie des Groupes Finis et Continus et la Géométrie Différentielle Traitées par la Méthode du Repère Mobile; Gauthier–Villars: Paris, France, 1951. [Google Scholar]
- Fels, M.; Olver, P.J. Moving Coframes: I. A practical Algorithm. Acta Appl. Math. 1998, 51, 161–213. [Google Scholar] [CrossRef]
- Fels, M.; Olver, P.J. Moving Coframes: II. Regularization and Theoretical Foundations. Acta Appl. Math. 1999, 55, 127–208. [Google Scholar] [CrossRef]
- Irimiciuc, S.A.; Mihaila, I.; Agop, M. Experimental and theoretical aspects of a laser produced plasma. Phys. Plasmas 2014, 21, 93509. [Google Scholar] [CrossRef]
- Irimiciuc, S.A.; Gurlui, S.; Agop, M. Particle distribution in transient plasmas generated by ns-laser ablation on ternary metallic alloys. Appl. Phys. B 2019, 125, 190. [Google Scholar] [CrossRef]
- Ojedagp, A.; Schneider, C.W.; Döbeli, M.; Lippert, T.; Wokaun, A. Plasma plume dynamics, rebound, and recoating of the ablation target in pulsed laser deposition. J. Appl. Phys. 2017, 121, 135306. [Google Scholar] [CrossRef]
- Amoruso, S.; Tofmann, B.; Schou, J.; Velotta, R.; Wang, X. Diagnostics of laser ablated plasma plumes. Thin Solid Films 2004, 453–454, 562–572. [Google Scholar] [CrossRef]
- Garner, A.L.; Loveless, A.M.; Dahal, J.N.; Venkattraman, A. A Tutorial on Theoretical and Computational Techniques for Gas Breakdown in Microscale Gaps. IEEE Trans. Plasma Sci. 2020, 48, 808–824. [Google Scholar] [CrossRef]
- Ursu, C.; Pompilian, O.G.; Gurlui, S.; Nica, P.; Agop, M.; Dudeck, M.; Focsa, C. Al2O3 ceramics under high-fluence irradiation: Plasma plume dynamics through space- and time-resolved optical emission spectroscopy. Appl. Phys. A Mater. 2010, 101, 153–159. [Google Scholar] [CrossRef]
- Singh, S.C.; Fallon, C.; Hayden, P.; Mujawar, M.; Yeates, P.; Costello, J.T. Ion flux enhancements and oscillations in spatially confined laser produced aluminum plasmas. Phys. Plasmas 2014, 21, 093113. [Google Scholar] [CrossRef]
- Irimiciuc, S.; Enescu, F.; Agop, A.; Agop, M. Lorenz Type Behaviors in the Dynamics of Laser Produced Plasma. Symmetry 2019, 11, 1135. [Google Scholar] [CrossRef]
- Harilal, S.S.; Bindhu, C.V.; Nampoori, V.P.N.; Vallabhan, C.P.G. Influence of ambient gas on the temperature and density of laser produced carbon plasma. Appl. Phys. Lett. 1998, 72, 167–169. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Irimiciuc, S.-A.; Saviuc, A.; Tudose-Sandu-Ville, F.; Toma, S.; Nedeff, F.; Rusu, C.M.; Agop, M. Non-Linear Behaviors of Transient Periodic Plasma Dynamics in a Multifractal Paradigm. Symmetry 2020, 12, 1356. https://doi.org/10.3390/sym12081356
Irimiciuc S-A, Saviuc A, Tudose-Sandu-Ville F, Toma S, Nedeff F, Rusu CM, Agop M. Non-Linear Behaviors of Transient Periodic Plasma Dynamics in a Multifractal Paradigm. Symmetry. 2020; 12(8):1356. https://doi.org/10.3390/sym12081356
Chicago/Turabian StyleIrimiciuc, Stefan-Andrei, Alexandra Saviuc, Florin Tudose-Sandu-Ville, Stefan Toma, Florin Nedeff, Cristina Marcela Rusu, and Maricel Agop. 2020. "Non-Linear Behaviors of Transient Periodic Plasma Dynamics in a Multifractal Paradigm" Symmetry 12, no. 8: 1356. https://doi.org/10.3390/sym12081356
APA StyleIrimiciuc, S.-A., Saviuc, A., Tudose-Sandu-Ville, F., Toma, S., Nedeff, F., Rusu, C. M., & Agop, M. (2020). Non-Linear Behaviors of Transient Periodic Plasma Dynamics in a Multifractal Paradigm. Symmetry, 12(8), 1356. https://doi.org/10.3390/sym12081356







