Abstract
In this study, the problem of axisymmetric deformation of peripherally fixed and uniformly laterally loaded circular membranes with arbitrary initial stress is solved analytically. This problem could be called the generalized Föppl–Hencky membrane problem as the case where the initial stress in the membrane is equal to zero is the well-known Föppl–Hencky membrane problem. The problem can be mathematically modeled only in terms of radial coordinate owing to its axial symmetry, and in the present work, it is reformulated by considering an arbitrary initial stress (tensile, compressive, or zero) and by simultaneously improving the out-of-plane equilibrium equation and geometric equation, while the formulation was previously considered to fail to improve the geometric equation. The power-series method is used to solve the reformulated boundary value problem, and a new and more refined analytic solution of the problem is presented. This solution is actually observed to be able to regress into the well-known Hencky solution of zero initial stress, allowing the considered initial stress to be zero. Moreover, the numerical example conducted shows that the obtained power-series solutions for stress and deflection converge very well, and have higher computational accuracy in comparison with the existing solutions.
1. Introduction
Thin films as structural components or structures are essential in many applications [1,2,3,4]. The so-called circular membrane problem usually refers to the problem of axially symmetric deformation of an initially flat, peripherally fixed, laterally uniformly loaded, linearly elastic, circular isotropic membrane with or without tensile or compressive initial stress. It is actually the mechanical model abstract from practical structural problems. This problem could be called the generalized Föppl–Hencky membrane problem as the case where the initial stress in the membrane is equal to zero is the well-known Föppl–Hencky membrane problem [5]. The term “membrane” here should be understood as the so-called fully stretched plate in mechanics whose upper and lower surfaces, regardless of its thickness, are simultaneously stretched under lateral loads owing to being “peripherally fixed”. The so-called initial stress refers to the stress before uniformly laterally loading, which is produced by stretching or compressing the initially flat circular elastic membrane in the direction of the plane in which the initially flat circular elastic membrane locates. Obviously, the initial stress before uniformly laterally loading will have an influence on the mechanical behaviour of the circular membrane under uniform lateral loads, and in comparison with the stress resultant under laterally loading, the greater the initial stress, the greater the influence.
The initial stress can very easily be present in practical issues. For instance, the residual stress is the stress in the film/substrate systems or thin film devices after fabrication, which can be either tensile or compressive, and is usually an important parameter affecting the reliability or performance of film/substrate systems or thin film devices [6,7,8,9,10,11]. Therefore, the residual stress will be the so-called initial stress if the film in the film/substrate systems or thin film devices is further subjected to lateral loads. The initially flat circular elastic membrane attached to a stiff ring at its perimeter is often used to make diaphragm devices [4,12], while the membrane could be so inappropriately stressed that the stress in the attached initially flat circular membrane deviates from that expected, resulting in the so-called residual stress. In fact, the change in temperature or humidity could relax or tighten the initially flat circular membrane attached to the stiff ring, as long as the temperature or humidity at this time is different from that at attaching [13]. Such a relaxing or tightening is actually also a residual stress. The residual stress in thin film devices, as an initial stress of the thin film working under lateral loading, will result in the deviation of the performance of devices from that expected. Moreover, the variations in the processing conditions such as method of etching, humidity, temperature, or the order of fabrication procedures could give rise to a compressive or tensile residual stress in the film/substrate systems fabricated [7,9,11]. Such a residual stress could result in the delamination between a substrate and its coating [10], thus losing the reliability of film/substrate systems. To increase the reliability and ensure expected performance, the measurement of the residual stress in film/substrate systems and thin film devices is often found to be necessary after fabrication. To this end, a variety of ways have been developed to measure the residual stress, such as the peeling method [14], diffraction technique [15,16], diffraction topography technique [17], two beam laser reflection technique [18], and vibrational technique [19,20]. Among these ways, the so-called pressurized blister or bulge test technique [21,22,23,24,25,26,27] could be modelled as a circular membrane problem with or without initial tensile or compressive stress. There would be no need for an advanced experimental setup to simultaneously monitor the change in pressure and in blister dimension, if the analytical solution of the circular membrane problem, that is, the relation between pressure and blister dimension, can be available. Therefore, the analytical solutions of the circular membrane problems often play an important role in the design of thin film devices and the characterization of mechanical properties such as the residual stress, Poisson’s ratio, modulus of elasticity, and adhesion strength for film/substrate systems or thin film devices [28].
Hencky, the recognized German scientist, originally dealt with the circular membrane problems without arbitrary initial stress, and a power-series solution of the problem was presented with the bending related terms in the Föppl–von Kármán equations of large deflection of thin plates ignored [5]. Chien [29] and Alekseev [30] corrected a computational error in [5]. This problem is the so-called Föppl–Hencky membrane problem (well-known Hencky problem for short), and its solution is usually referred to as the well-known Hencky solution, which is often cited in some studies of related issues [31,32,33,34,35,36,37]. Sun et al. reformulated the well-known Hencky problem by giving up the so-called small rotation angle assumption of membranes and by improving the out-of-plane equilibrium equation, and presented a new closed-form solution of the problem [38]. Further, Sun et al. [39] reformulated the well-known Hencky problem with the out-of-plane equilibrium equation, geometric equation simultaneously improved, and presented a new refined closed-form solution. As for the case of circular membranes with initial compressive or tensile stress, based on the modification of elastic equations, Ku [40] presented an analysis of large deflection of circular elastic membranes with initial tension under uniformly distributed loads, and He et al. [41] presented an analytic solution of axisymmetrical deformation of prestressed circular membranes under uniformly laterally loading. However, Sun et al. pointed out that it is unreasonable to modify the elastic equations because the initial stress before uniformly laterally loading should not give rise to a change in the constitutive relationship of membrane materials. Therefore, Sun et al. resolved the problem with initial stress under uniformly laterally loading and presented a new power-series solution of the problem, that is, the so-called extended Hencky solution [42]. The closed-form solution that is presented in [42] can be regressed to the well-known Hencky solution, allowing the initial stress to be zero, while the solutions presented in [40,41] cannot. Moreover, the closed-form solution without the initial stress and small rotation angle assumption, which is presented in [38], was extended further to suit the more general cases with initial tensile or compressive stress, achieving the synchronous characterization for the interface and surface of film/substrate systems with residual stress [43]. Owing to improving the out-of-plane equilibrium equation and considering the initial tensile or compressive stress, this solution should be the prestressed solution with the best computational accuracy at present, and it has been incorporated into the study on the contact problem between Föppl–Hencky membranes and rigid surfaces [44].
In this study, the computational accuracy of the solution was further improved by simultaneously improving the geometric equation, out-of-plane equilibrium equation, and by considering an arbitrary initial stress. In the following section, the problem of axisymmetric deformation of the circular elastic membrane with an arbitrary initial stress is reformulated, the resulting boundary value problem is solved using the power-series method, and a new refined closed-form power-series solution is finally presented. In Section 3, on the basis of the numerical examples conducted, some important issues are discussed, such as the regression, convergence, effectiveness of the improved solution, and the effect of the initial stress on the obtained solution. Concluding remarks are presented in Section 4.
2. Membrane Equations and Closed-Form Solution
2.1. Reformulation of the Generalized Föppl–Hencky Membrane Problem
Suppose that, an initially flat, rotationally symmetric, linearly elastic unstretched circular membrane with Poisson’s ratio , Young’s modulus of elasticity , radius , and thickness is extended or shrunk a radial plane displacement at the periphery of radius , and is then fixed at the radius . A structure of the circular elastic membrane with an initial tensile or compressive stress is thus modelled. A uniformly-distributed transverse load is applied quasi-statically onto the membrane surface, as depicted in Figure 1, where and denote the radial and transverse coordinates in the cylindrical coordinate system ( also denotes the transverse displacement of the deflected membrane), and the polar coordinate plane is arranged in the plane in which the geometric middle plane of the initially flat circular elastic membrane is located.
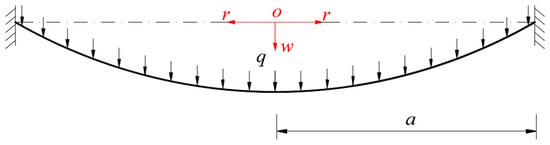
Figure 1.
Geometry of the deformed circular membrane along a diameter 2a under load q.
Take a free body with radius from the central portion of the deformed circular membrane, in order to study the static equilibrium problem of this free body under the joint actions of the uniformly-distributed loads within and the total force , which is produced by the membrane force acting on the boundary , as depicted in Figure 2, where is the radial stress and is the slope angle of the deformed circular membrane.
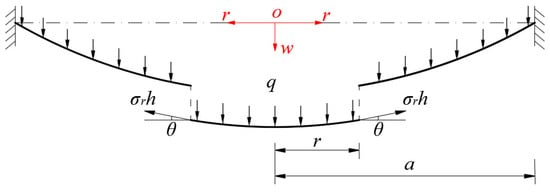
Figure 2.
The free body diagram of the deformed circular membrane with radius .
Obviously, there are two forces in the vertical direction, that is, (the total force of the uniformly-distributed loads ) and (the total vertical membrane force which is produced by the membrane force ). So, the so-called out-of-plane equation of equilibrium [31,36,38,42] is
where
Substituting Equation (2) into Equation (1), one has
There are also two forces in the horizontal direction, the circumferential membrane force and the horizontal component of the membrane force , where is the circumferential stress. So, the so-called in-plane equation of equilibrium may be written as
Equation (4) can be found in any general theory of plates and shells, so it is not necessary to discuss its detailed derivation here. Suppose that the radial strain is denoted as , the circumferential strain is denoted as , the radial displacement is denoted as , and the transversal displacement is denoted as , then the so-called geometric equations [39] are
and
Moreover, the stress and strain are still assumed to satisfy the linear elasticity relationship, so the so-called physical equations are
and
Eliminating and from Equations (5)–(8) yields
and
From Equations (4), (9) and (10), one has
After eliminating u from Equations (9) and (11), the usual so-called consistency equation can be written as
The boundary conditions to solve Equations (3), (4) and (12) can be determined based on the following solution to the plane stretching or compressing problem of the initially flat circular elastic membrane. In the problem of plane stretching or compressing (i.e., the initially flat circular elastic membrane is extended or shrunk to a radial plane displacement at ), . So, from Equations (5) and (6), one has
and
Eliminating and from Equations (7), (8), (13) and (14) yields
and
From Equations (4), (15) and (16), one has
The boundary conditions to solve Equation (17) are
and
So, under the conditions of Equations (18) and (19), the solution of Equation (17) can be written as
From Equations (13)–(16) and (20), it is found that
and
in which denotes the so-called initial stress and denotes the initial strain. Equations (21) and (22) indicate that, for the problem of plane stretching or compressing, both stress and strain are two-axis equal at every point on the flat circular membrane. This result is in accord with the fact that the residual stress is always uniform in film/substrate systems [9]. Therefore, the boundary conditions to solve Equations (3), (4) and (12) can finally be written as
and
2.2. Power Series Solution
The following dimensionless variables are used
Transform Equations (3), (4), (12), (23)–(25) into
and
Eliminating and from Equations (27)–(29), a nonlinear differential equation containing only variable can be obtained
Given that the value of stress is finite at , then can be expanded into the power-series of the
After plugging Equation (34) into Equation (33), we obtain (i = 1,3,5,…), and (i = 2,4,6,…) can be expressed in the polynomial about the undetermined constant (see Appendix A). While can be determined by the boundary condition at x = 1. From Equations (28) and (34), the condition of Equation (31) gives
After substituting all expressions of into Equation (35), an equation containing only can be obtained. So can be determined by solving this single variable equation, and the expression of can thus be determined. As for , with the known expression of , it can easily be obtained from Equation (28), so it is not necessary to derive it here. Moreover, can be expanded into the power-series of the
Hence, after plugging Equations (34) and (36) into Equation (27), it is found that (i = 1,3,5,…), and (i = 2,4,6,…) can be expressed into the polynomial about (see Appendix B). The first coefficient is another undetermined constant, which can be determined by Equation (32). From Equation (36), Equation (32) gives
After substituting all expressions of into Equation (37), the undetermined constant can be determined and, consequently, the expression of W can also be determined.
3. Results and Discussions
So far, the boundary condition Equation (23) or (30) has not been used yet. The following is the proof of whether the closed-form solution presented in Section 2 meets this boundary condition. The dimensional form of the deflection can be written as, from Equations (26) and (36),
The first derivative of Equation (38) is
So, at . Meanwhile, from the derivation in Section 2, it is already known that . Thus, at because . This indicates that the boundary condition Equation (23) or (30) can be satisfied automatically, or in other words, the closed-form solution presented in Section 2 agrees with the physical characteristic of axially symmetric deformation of the circular membrane.
3.1. Regression of the Solution Presented in Second Section
The following is the proof of whether the analytic solution presented in Section 2 is able to be regressed to the well-known Hencky solution.
From Equation (26), it can be seen that when is equal to zero, is also equal to zero. Hence, Equation (26) in [39] can easily be obtained by allowing in Equation (35) to be zero. This means that the analytic solution presented in Section 2, which applies to the case with initial stress, can be regressed to the solution presented in [39], which applies to the case without initial stress, because all the expressions for displacements and stresses obtained here have the same forms as those obtained in [39].
On the other hand, if the improved geometry equation (Equation (5) in [39] and this paper) is replaced by the classic geometric equation (Equation (5) in [38]), then the solution presented in [39] can be regressed to the solution presented in [38], which gives up the small rotation angle assumption and uses the classic geometric equation, but considers no initial stress.
Furthermore, if the small rotation angle assumption of membrane is still adopted, that is, replace Equation (2) in [38] by Equation (2) in [36], then the solution in [38] can be regressed into the well-known Hencky solution (which can be found in [5] or [36]).
Therefore, the analytic solution presented in Section 2 is able to be regressed into the well-known Hencky solution [5,36].
3.2. Comparison with Existing Solutions
For showing the difference between the existing solutions and the solution presented here, a numerical example was conducted, where four solutions were used, that is, the well-known Hencky solution that considers zero initial stress [5,36] and three solutions considering initial stress: the solution presented in this paper, the solution in [43], and the so-called extended Hencky solution in [42]. Suppose that a circular rubber thin film with Poisson’s ratio v = 0.47, Young’s modulus of elasticity E = 7.84 MPa, initial stress , and thickness h = 0.2 mm is fixed at radius a = 20 mm, and is then subjected to the transversely uniformly-distributed loads q = 0.0001 MPa, 0.003 MPa, and 0.01 MPa, respectively. Figure 3 shows the variations of the deflection with the radial coordinate r and Figure 4 shows the variations of the radial stress with the radial coordinate r, where the solid lines represent the results calculated by the solution presented in this paper, which is denoted here as Solution 1; the dotted lines represent the results calculated by the solution in [43], which is denoted as Solution 2; the dotted-dashed lines represent the results calculated by the extended Hencky solution [42], which is denoted as Solution 3; and the dashed lines represent the results calculated by the well-known Hencky solution [5,36], which is denoted as Solution 4. The values of the maximum deflection and maximum stress at r = 0 are listed in Table 1.
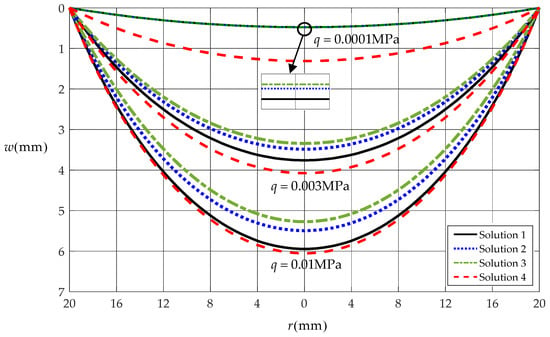
Figure 3.
Variations of deflection w with r when takes 0.1 MPa.
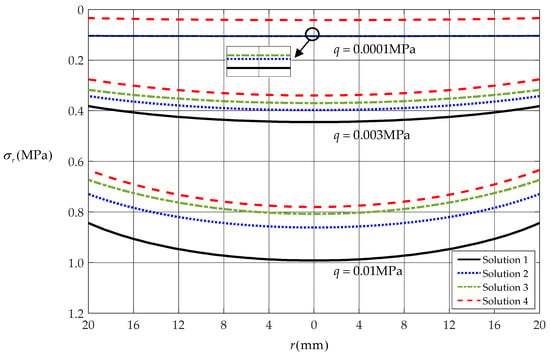
Figure 4.
Variations of radial stress with r when takes 0.1 MPa.

Table 1.
The concrete values of and when takes 0.1 MPa.
From Figure 3 and Figure 4, it can be seen that the three solutions of considering initial stress (i.e., Solution 3, Solution 2, and Solution 1) agree quite closely for the loads q = 0.0001 MPa and diverge slowly as the loads intensify. This means that the improvements implemented in this paper have had an impact on the calculating precision of the solution, because Solution 3 is obtained using the classic geometric equation and classic out-of-plane equilibrium equation, Solution 2 is obtained using the classic geometric equation and improved out-of-plane equilibrium equation, while Solution 1 (i.e., the improved solution in this paper) is obtained using the improved geometric equation and improved out-of-plane equilibrium equation. The establishment of the classic out-of-plane equilibrium equation and geometric equation is based on the small rotation angle assumption of membrane, while the so-called “improved” here actually refers to giving up the small rotation angle assumption, resulting in a better adaptability of the solution to the rotation angle of membrane. From Figure 3, it can clearly be seen that, when the load q = 0.0001 MPa, the deflection calculated by Solution 4 (i.e., the well-known Hencky solution of considering zero initial stress) is far greater than the deflections calculated by Solution 3, Solution 2, and Solution 1, and when the load q = 0.003 MPa and 0.01 MPa, the deflection curve by Solution 4 slowly approaches the one by Solution 1 (the improved solution in this paper), and at the same time, it also slowly moves a little closer to the ones by Solution 3 and Solution 2, which may be seen from the data of Table 1. This is because the initial stress is considered by Solution 3, Solution 2, and Solution 1, while the initial stress is considered by Solution 4. Therefore, when the load q = 0.0001 MPa, the deflection calculated by Solution 4 is far greater than that by the three solutions considering , in other words, when the load q is relatively small, the initial stress of plays a main role in the deflection calculations by Solution 3, Solution 2, and Solution 1. Meanwhile, when the load q = 0.003 MPa and 0.01 MPa, the small rotation angle assumption, which is adopted in the classic out-of-plane equilibrium equation and geometric equation of the Solution 4, has relatively great influence on the deflection calculation by Solution 4, and the greater the load, the greater the influence. During the establishments of the out-of-plane equilibrium equation and geometric equation of the Solution 1, however, the small rotation angle assumption has been given up and thus has no influence on the deflection calculation by Solution 1. In other words, when the load q = 0.003 MPa and 0.01 MPa, the influence of the small rotation angle assumption on the deflection calculation by Solution 4 (the well-known Hencky solution) is far greater than the influence of the initial stress of on the deflection calculation by Solution 1 (the improved solution in this paper).
On the other hand, Figure 3 and Figure 4 also show that the applicable conditions or preconditions subject to compliance must be understood before using the solutions, or the used solution would not perform as well as expected, which could cause an unacceptable calculation error. For instance, from Table 1, it can be calculated that, when q takes 0.01 MPa and in comparison with Solution 1 (i.e., the improved solution in this paper), the error of the maximum deflection is about 7.61% for Solution 2 and about 11.34% for Solution 3, while the error of the maximum stress is about 13.14% for Solution 2 and about 18.56% for Solution 3. Such a large relative error is usually unacceptable in many practical technical problems, especially in the field of precision measurements such as the characterization of the mechanical properties of thin film/substrate systems [6,7,8,9,10,11]. Note that the allowable error for the precision measurement is usually less than 1%, for the instrument design is usually less than 3%, and for the civil engineering is usually less than 15%. In addition, it is conceivable that the relative error between the solution presented in this paper and the existing solutions will increase with the increase of the membrane deflection or applied loads. Therefore, in this sense, the improvement effect of this study on the analytical solution of the so-called generalized Föppl–Hencky membrane problem is obvious.
3.3. Convergence of the Power Series Solution Obtained in Second Section
The following is the proof of whether the power series solutions for and presented in Section 2 are convergent. However, only the special solutions for and , rather than their general solutions, can be discussed, owing to the fact that the expressions of the coefficients and (i = 2,4,6,…), which are expressed as the polynomial about the undetermined constants and (see Appendix A and Appendix B), are so intractable that the expressions of the remained terms of power-series solutions and cannot be obtained. It is already known, from the derivation in Section 2, that the general solutions for and are the power-series of x (see Equations (34) and (36)), where ; and (i = 2,4,6,…) are expressed as the polynomial about the coefficients and ; and for i = 1,3,5,…, and . It seems as if the special solutions for and can easily be obtained as long as the undetermined constants and can be determined by Equations (35) and (37). However, when solving a specific problem, only the partial sum of former n terms of Equations (34) and (36), rather than Equations (34) and (36), is substituted into Equations (31) and (32); otherwise, the resulting Equations (35) and (37) would contain two infinite series and are thus difficult to solve. Therefore, it may be seen that the determined values of and by Equations (35) and (37) depend on the value of terms n, and a different value of n will determine different values of and . Hence, from this, it may be known that the special solution for and can be proved to be convergent by examining the variation of and with i for every value of terms n, especially examining the variation of and with terms n.
To this end, the numerical computations of and were started from , that is, started from the partial sum of former four terms for Equations (34) and (36), and the case of q = 0.01 MPa of the numerical example above was recalculated. Table 2 shows the obtained different numerical values of and and the obtained values of and are listed in Table 3. The variation of and with terms n is plotted in Figure 5 and Figure 6, respectively, and the variation of and with i is, only for , shown in Figure 7 and Figure 8, respectively. From Table 2 and Table 3 or Figure 5 and Figure 6, it is seen that the undetermined constants and converge reasonably well. From Table 2 and Table 3 or Figure 7 and Figure 8, it is seen that the coefficients and also converge reasonably well. Because , it may thus be concluded that the special solutions for and are convergent. Furthermore, from Figure 5 and Figure 6, it is also seen that, when , the undetermined constants and are already very close to their exact values. So, only the coefficients and (i = 2,4,6,…,20), which are expressed as the polynomial about and , are shown in Appendix A and Appendix B, respectively.

Table 2.
Values of b0–b6, b8–b14, b16–b22, and b24–b26.

Table 3.
Values of c0–c6, c8–c14, c16–c22, and c24–c26.
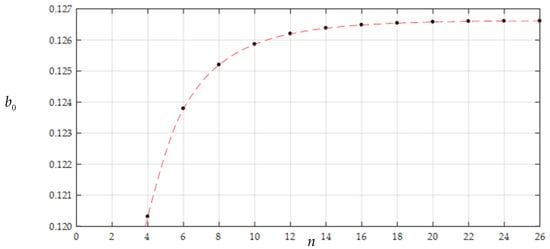
Figure 5.
The variation of with .
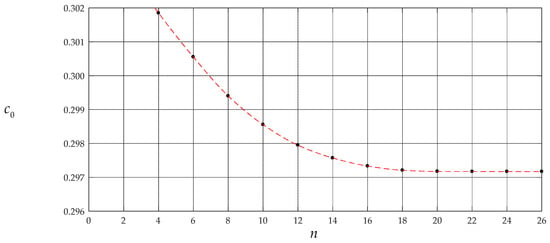
Figure 6.
The variation of with .
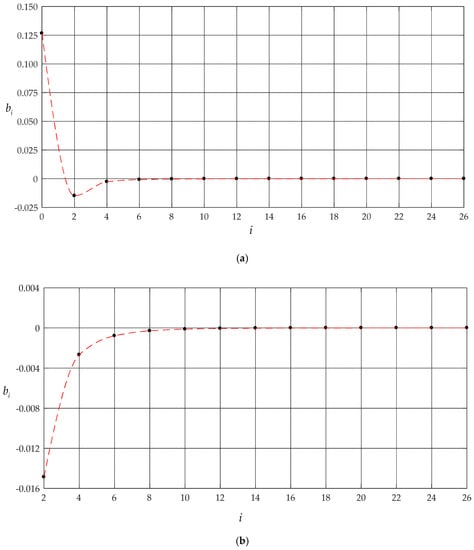
Figure 7.
Distribution of with i when n = 26: (a) and (b) .
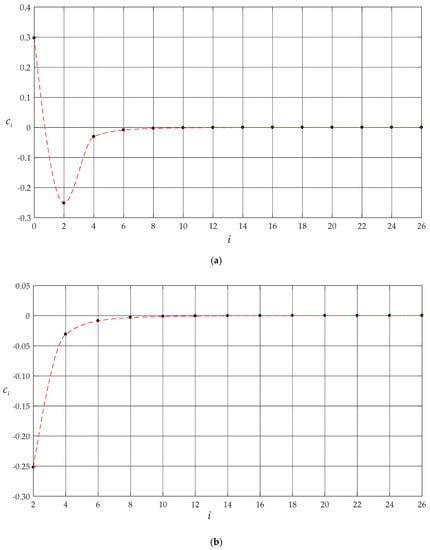
Figure 8.
Distribution of with i when n = 26: (a) and (b) .
4. Concluding Remarks
In this study, the well-known Hencky problem is generalized to include the case of an arbitrary initial compressive or tensile stress, where the classic geometric equation and out-of-plane equilibrium equation are simultaneously improved. The following conclusions can, from this study, be drawn.
In comparison with the existing solutions, which consider initial stress, the closed-form solution presented in this paper has a higher computational accuracy. The use of existing solutions does not bring too much computational error for the case of relatively small deflection of membranes, but for the relatively large deflection, the closed-form solution presented in this paper should be given priority. Otherwise, an unacceptable calculation error could be caused, which has, in the conducted numerical example, been shown to be 11.34% deflection error and 18.56% stress error. Meanwhile, the allowable error for the precision measurement, instrument design, and civil engineering is usually less than 1%, 3%, and 15%, respectively.
The proof of convergence of the power series solutions for and must be conducted, but only to their special solutions, rather than their general solutions, owing to the somewhat intractable forms of expression of the coefficients and (i = 2,4,6,…), that is, the polynomial functions with regard to the undetermined constants and (see Appendix A and Appendix B). Therefore, for the convergence proof of the special solutions for and , the following two aspects should be given full attention. First, the numerical computation of the undetermined constants and has to be started from a smallest partial sum of the former n terms of the power series, usually n = 3 or 4. Then, with the help of a scatter plot, the saturation degree for the computed obtained numerical values of and can be examined. The saturation degree for the coefficients and is not examined until a satisfactory saturation degree for the computed obtained numerical values of and has been observed. A demonstrated example and the detailed operating steps may be found in Section 3.
The large deflection phenomenon of the membrane with initial compressive or tensile stress appears very easily, especially in the mechanical properties’ characterization using the thin-film/substrate delamination by pressurized blister or bulge tests, where the maximum deflection of the blistering thin-film could reach half the radius of the circular blistering thin film, or even larger. The solutions in the existing literature are not suitable for such a large deflection owing to the approximations adopted in the classic out-of-plane equilibrium equation and geometric equation, while the solution presented in this paper has given up these approximations and can thus be used to calculate such a large deflection. Therefore, in this sense, the work presented in this paper should have a positive significance for these technical application fields.
Author Contributions
Conceptualization, J.-Y.S. and X.-T.H.; methodology, J.-Y.S. and X.L.; validation, X.-T.H.; writing—original draft preparation, Z.-H.Z. and X.L.; writing—review and editing, X.L. and X.-T.H.; visualization, X.L.; funding acquisition, J.-Y.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No. 11772072).
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Radius of the circular membrane | |
| Thickness of the circular membrane | |
| Young’s modulus of elasticity | |
| Poisson’s ratio | |
| Uniformly distributed transverse loads | |
| Radial coordinate | |
| Circumferential coordinate | |
| Transverse coordinate and transverse displacement of the deflected membrane | |
| Radial displacement of the deflected membrane | |
| Radial plane displacement | |
| Radial stress | |
| Circumferential stress | |
| Radial strain | |
| Circumferential strain | |
| Initial stress | |
| Initial strain | |
| Slope angle of the deflected membrane | |
| Pi (ratio of circumference to diameter) | |
| Dimensionless loads | |
| Dimensionless transverse displacement | |
| Dimensionless radial stress | |
| Dimensionless circumferential stress | |
| Dimensionless initial stress | |
| Dimensionless radial coordinate | |
| Coefficients of the power-series for | |
| Coefficients of the power-series for |
Appendix A
Appendix B
References
- Le, N.T.; Wang, J.-W.; Wang, C.-C.; Nguyen, T.N. Automatic defect inspection for coated eyeglass based on symmetrized energy analysis of color channels. Symmetry 2019, 11, 1518. [Google Scholar] [CrossRef]
- Li, J.; Wang, R.; Tian, H.; Wang, Y.; Qi, D. Research on the gradual process of the metallization structures and mechanical properties of wood veneer. Symmetry 2018, 10, 550. [Google Scholar] [CrossRef]
- Rehman, A.; Salleh, Z.; Gul, T.; Zaheer, Z. The impact of viscous dissipation on the thin film unsteady flow of GO-EG/GO-W nanofluids. Mathematics 2019, 7, 653. [Google Scholar] [CrossRef]
- Barba, P.D.; Fattorusso, L.; Versaci, M. A 2D non-linear second-order differential model for electrostatic circular membrane MEMS devices: A result of existence and uniqueness. Mathematics 2019, 7, 1193. [Google Scholar] [CrossRef]
- Hencky, H. On the stress state in circular plates with vanishing bending stiffness. Z. Für Math. Und Phys. 1915, 63, 311–317. (In German) [Google Scholar]
- Fernando, M.; Kinloch, A.J. Use of the inverted-blister test to study the adhesion of photopolymers. Int. J. Adhes. Adhes. 1990, 10, 69–76. [Google Scholar] [CrossRef]
- Jensen, H.M.; Thouless, M.D. Effects of residual-stresses in the blister test. Int. J. Solids Struct. 1993, 30, 779–795. [Google Scholar] [CrossRef]
- Lai, Y.H.; Dillard, D.A. A study of the fracture efficiency parameter of blister tests for films and coatings. J. Adhes. Sci. Technol. 1994, 8, 663–678. [Google Scholar] [CrossRef]
- Wan, K.T.; Guo, S.; Dillard, D.A. A theoretical and numerical study of a thin clamped circular film under an external load in the presence of a tensile residual stress. Thin Solid Film. 2003, 425, 150–162. [Google Scholar] [CrossRef]
- Sun, Z.; Wan, K.T.; Dillard, D.A. A theoretical and numerical study of thin film delamination using the pull-off test. Int. J. Solids Struct. 2004, 41, 717–730. [Google Scholar] [CrossRef]
- Guo, S.; Wan, K.T.; Dillard, D.A. A bending-to-stretching analysis of the blister test in the presence of tensile residual stress. Int. J. Solids Struct. 2005, 42, 2771–2784. [Google Scholar] [CrossRef]
- Fichter, W.B. Some solutions for the large deflections of uniformly loaded circular membranes. NASA Technical Paper No. 3658 1997. [Google Scholar]
- Jenkins, C.H.; Faisal, S.M. Thermal load effects on precision membranes. J. Spacecr. Rocket. 2001, 38, 207–211. [Google Scholar] [CrossRef]
- Williams, J.G. Energy release rates for the peeling of flexible membranes and the analysis of blister tests. Int. J. Fract. 1997, 87, 265–288. [Google Scholar] [CrossRef]
- Noyan, I.C.; Cohen, J.B. Residual Stress Measurement by Diffraction and Interpretation; Springer: New York, NY, USA, 1987. [Google Scholar]
- Malhotra, S.G.; Rek, Z.U.; Yalisove, S.M.; Bilello, J.C. Strain gradients and normal stresses in textured Mo thin films. J. Vac. Sci. Technol. A Vac. Surf. Film. 1997, 15, 345–352. [Google Scholar] [CrossRef]
- Tao, J.; Lee, L.H.; Bilello, J.C. Non-destructive evaluation of residual stresses in thin films via x-ray diffraction topography methods. J. Electron. Mater. 1991, 20, 819–825. [Google Scholar] [CrossRef]
- Geisz, J.F.; Kuech, T.F.; Lagally, M.G.; Cardone, F.; Potemski, R.M. Film stress of sputtered W/C multilayers and strain relaxation upon annealing. J. Appl. Phys. 1994, 75, 1530–1533. [Google Scholar] [CrossRef]
- Maden, M.A.; Jagota, A.; Mazur, S.; Farris, R.J. Vibrational technique for stress measurement in films: I, Ideal membrane behavior. J. Am. Ceram. Soc. 1994, 77, 625–635. [Google Scholar] [CrossRef]
- Tong, Q.K.; Maden, M.A.; Jagota, A.; Farris, R.J. Vibrational technique for stress measurement in films: II, Extensions and complicating effects. J. Am. Ceram. Soc. 1994, 77, 636–648. [Google Scholar] [CrossRef]
- Dannenberg, H. Measurement of adhesion by a blister method. J. Appl. Polym. Sci. 1961, 5, 125–134. [Google Scholar] [CrossRef]
- Williams, M.L. Relation of continuum mechanics to adhesive fracture. J. Adhes. 1972, 4, 307–332. [Google Scholar] [CrossRef]
- Beams, J.W. Mechnical properties of thin films of gold and silver. In Structure and Properties of Thin Films; proceedings; Neugebauer, C.A., Ed.; Wiley: New York, NY, USA, 1959. [Google Scholar]
- Zheng, D.; Xu, Y.; Tsai, Y.P.; Tu, K.N.; Patterson, P.; Zhao, B.; Liu, Q.Z.; Brongo, M. Mechanical property measurement of thin polymeric-low dielectric-constant films using bulge testing method. Appl. Phys. Lett. 2000, 76, 2008–2010. [Google Scholar] [CrossRef]
- Xu, D.; Liechti, K.M. Bulge testing transparent thin films with moiré deflectometry. Exp. Mech. 2010, 50, 217–225. [Google Scholar] [CrossRef]
- Sun, J.Y.; Hu, J.L.; Zheng, Z.L.; He, X.T.; Geng, H.H. A practical method for simultaneous determination of Poisson’s ratio and Young’s modulus of elasticity of thin films. J. Mech. Sci. Technol. 2011, 25, 3165–3171. [Google Scholar] [CrossRef]
- Sun, J.Y.; Qian, S.H.; Li, Y.M.; He, X.T.; Zheng, Z.L. Theoretical study of adhesion energy measurement for film/substrate interface using pressurized blister test: Energy release rate. Measurement 2013, 46, 2278–2287. [Google Scholar] [CrossRef]
- Xu, D.; Liechti, K.M. Analytical and experimental study of a circular membrane in Hertzian contact with a rigid substrate. Int. J. Solids Struct. 2010, 47, 207–214. [Google Scholar] [CrossRef]
- Chien, W.Z. Asymptotic behavior of a thin clamped circular plate under uniform normal pressure at very large deflection. Sci. Rep. Natl. Tsinghua Univ. 1948, 5, 193–208. [Google Scholar]
- Alekseev, S.A. Elastic circular membranes under the uniformly distributed loads. Eng. Corpus. 1953, 14, 196–198. (In Russian) [Google Scholar]
- Chien, W.Z.; Wang, Z.Z.; Xu, Y.G.; Chen, S.L. The symmetrical deformation of circular membrane under the action of uniformly distributed loads in its portion. Appl. Math. Mech. (Engl. Ed.) 1981, 2, 653–668. [Google Scholar]
- Chien, W.Z.; Chen, S.L. The solution of large deflection problem of thin circular plate by the method of composite expansion. Appl. Math. Mech. (Engl. Ed.) 1985, 6, 103–118. [Google Scholar]
- Arthurs, A.M.; Clegg, J. On the solution of a boundary value problem for the nonlinear Föppl-Hencky equation. Z. Angew. Math. Mech. 1994, 74, 281–284. [Google Scholar] [CrossRef]
- Plaut, R.H. Linearly elastic annular and circular membranes under radial, transverse, and torsional loading. Part I: Large unwrinkled axisymmetric deformations. Acta Mech. 2009, 202, 79–99. [Google Scholar] [CrossRef]
- Lian, Y.S.; He, X.T.; Liu, G.H.; Sun, J.Y.; Zheng, Z.L. Application of perturbation idea to well-known Hencky problem: A perturbation solution without small-rotation-angle assumption. Mech. Res. Commun. 2017, 83, 32–46. [Google Scholar] [CrossRef]
- Sun, J.Y.; Rong, Y.; He, X.T.; Gao, X.W.; Zheng, Z.L. Power series solution of circular membrane under uniformly distributed loads: Investigation into Hencky transformation. Struct. Eng. Mech. 2013, 45, 631–641. [Google Scholar] [CrossRef]
- Yang, Z.X.; Sun, J.Y.; Ran, G.M.; He, X.T. A new solution to Föppl-Hencky membrane equation. J. Mech. 2017, 33, N7–N11. [Google Scholar] [CrossRef]
- Lian, Y.S.; Sun, J.Y.; Yang, Z.X.; He, X.T.; Zheng, Z.L. Closed-form solution of well-known Hencky problem without small-rotation-angle assumption. Z. Angew. Math. Mech. 2016, 96, 1434–1441. [Google Scholar] [CrossRef]
- Lian, Y.S.; Sun, J.Y.; Zhao, Z.H.; He, X.T.; Zheng, Z.L. A revisit of the boundary value problem for Föppl–Hencky membranes: Improvement of geometric equations. Mathematics 2020, 8, 631. [Google Scholar] [CrossRef]
- Ku, C.L. On the large deflection of elastic circular membrane with initial tension under uniformly distributed load. Chin. J. Phys. 1956, 12, 319–338. (In Chinese) [Google Scholar]
- He, X.T.; Wu, J.L.; Zheng, Z.L.; Chen, S.L. Axisymmetrical deformation of prestressed circular membrane under uniformly distributed loads. J. Chongqing Univ. 2010, 33, 109–112. (In Chinese) [Google Scholar]
- Sun, J.Y.; Lian, Y.S.; Li, Y.M.; He, X.T.; Zheng, Z.L. Closed-form solution of elastic circular membrane with initial stress under uniformly-distributed loads: Extended Hencky solution. Z. Angew. Math. Mech. 2015, 95, 1335–1341. [Google Scholar] [CrossRef]
- Yang, Z.X.; Sun, J.Y.; Li, K.; Lian, Y.S.; He, X.T.; Zheng, Z.L. Theoretical study on synchronous characterization of surface and interfacial mechanical properties of thin-film/substrate systems with residual stress based on pressure blister test technique. Polymers 2018, 10, 49. [Google Scholar] [CrossRef] [PubMed]
- Lian, Y.S.; Sun, J.Y.; Dong, J.; Zheng, Z.L.; Yang, Z.X. Closed-form solution of axisymmetric deformation of prestressed Föppl-Hencky membrane under constrained deflecting. Struct. Eng. Mech. 2019, 69, 693–698. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).