Bivariate Power-Skew-Elliptical Distribution
Abstract
1. Introduction
1.1. Elliptical Distributions
1.2. Skew-Elliptical Distribution
1.2.1. Skew-Normal Distribution
1.2.2. Skew-Student-t Distribution
1.2.3. Skew-Cauchy Distribution
1.2.4. Skew-Logistic Distribution
1.2.5. Skew-Laplace Distribution
1.3. Power-Skew-Elliptical Distribution
2. Bivariate Power-Skew-Elliptical Distribution
Statistical Inference for the Bpse Model
3. Bivariate Power-Skew-Normal Model
3.1. Statistical Inference
3.2. Reparameterization for the Bpsn Model
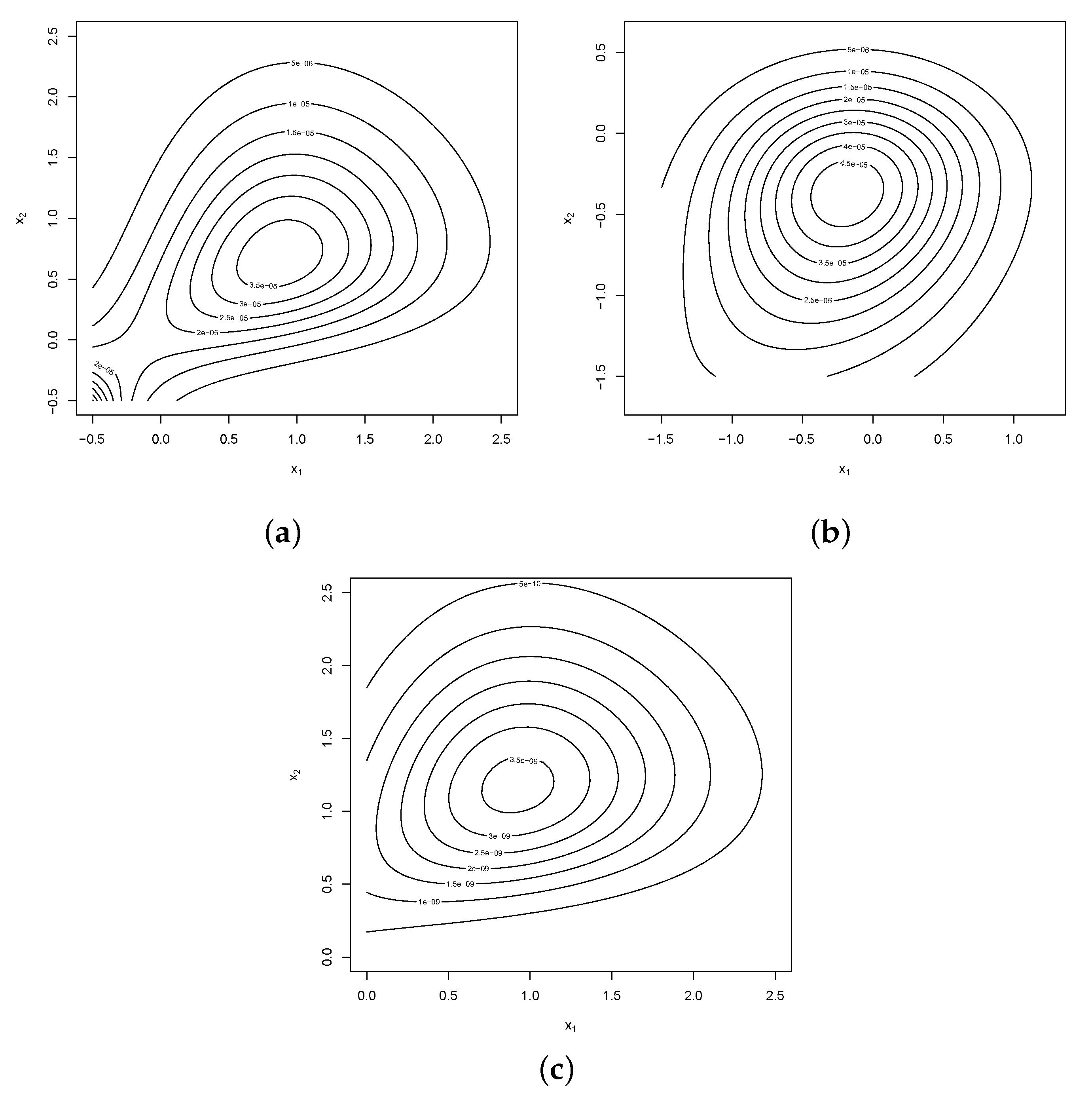
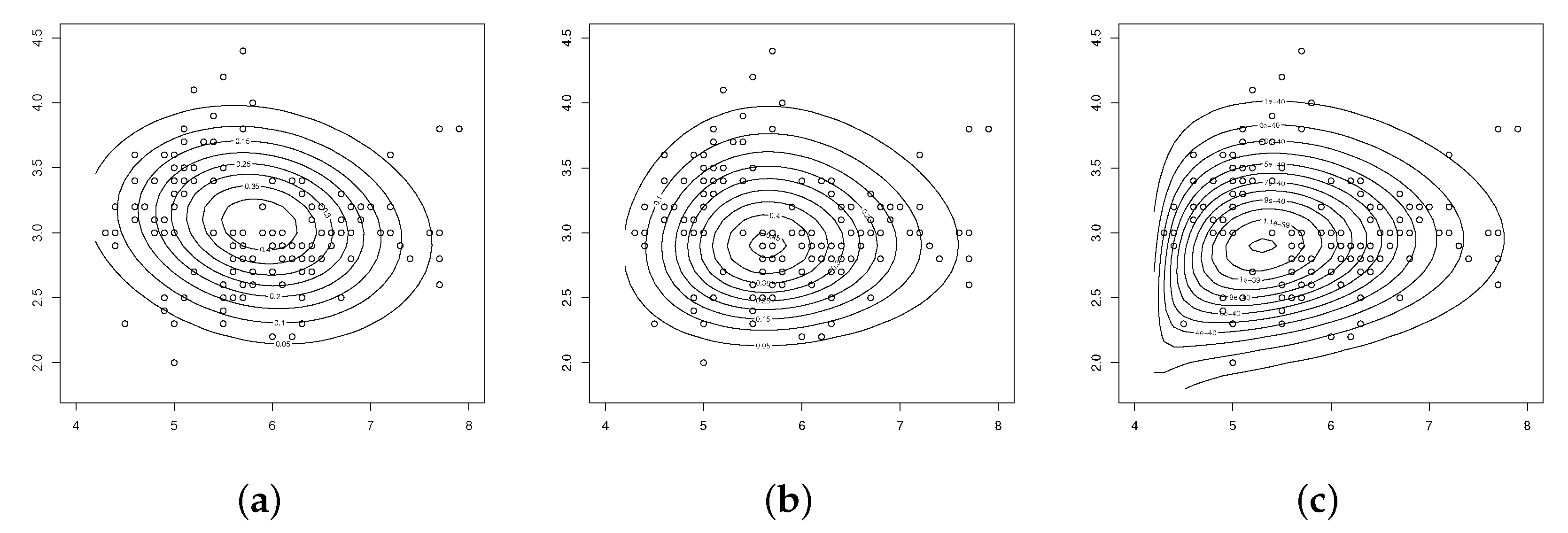
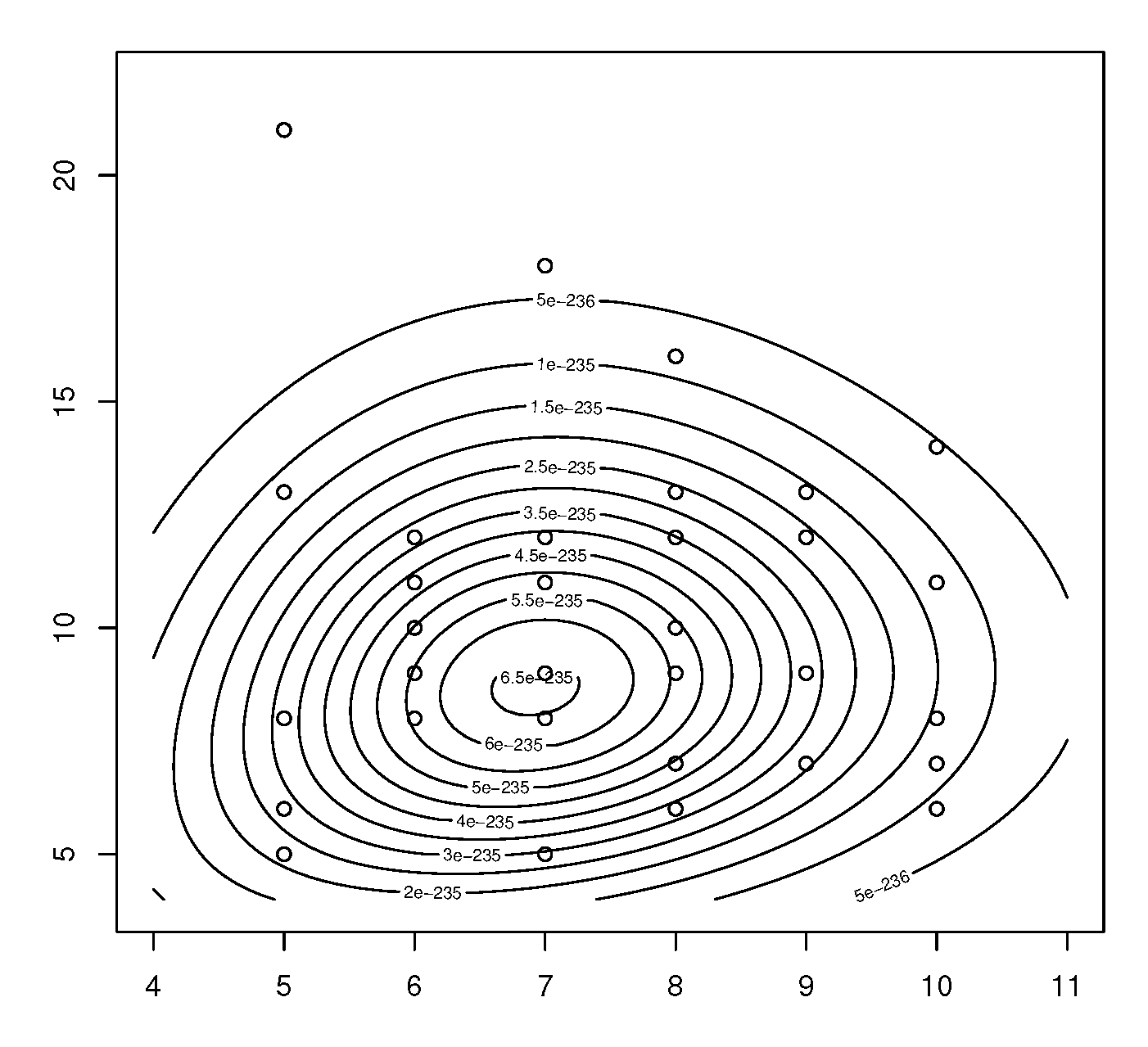
4. Numerical Illustrations
4.1. Illustration 1
4.2. Illustration 2
5. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Azzalini, A. A class of distributions which includes the normal ones. Scand. J. Stat. 1985, 12, 171–178. [Google Scholar]
- Durrans, S.R. Distributions of fractional order statistics in hydrology. Water Resour. Res. 1992, 28, 1649–1655. [Google Scholar] [CrossRef]
- Martínez-Flórez, G.; Bolfarine, H.; Gómez, H.W. Skew-normal alpha-power model. Statistics 2014, 48, 1414–1428. [Google Scholar] [CrossRef]
- Martínez-Flórez, G.; Bolfarine, H.; Gómez, Y.M.; Gómez, H.W. An Unification of Families of Birnbaum-Saunders Distributions with Applications. Rev. Stat. Stat. J. 2020. Available online: https://www.ine.pt/revstat/pdf/ANUNIFICATIONOFFAMILIESOFBIRNBAUM-SAUNDERS.pdf (accessed on 8 August 2020).
- Azzalini, A.; Dalla-Valle, A. The multivariate skew-normal distribution. Biometrika 1996, 83, 715–726. [Google Scholar] [CrossRef]
- Arnold, B.C.; Castillo, E.; Sarabia, J.M. Conditionally specified multivariate skewed distributions. Sankhya Indian J. Stat. Ser. A 2002, 64, 206–226. [Google Scholar]
- Arellano-Valle, R.; Bolfarine, H. On some characterizations of the T-Distribution. Stat. Probab. Lett. 1995, 25, 79–85. [Google Scholar] [CrossRef]
- Cambanis, S.; Huang, S.; Simons, G. On the theory of elliptically contoured distributions. J. Multivar. Anal. 1981, 11, 368–385. [Google Scholar] [CrossRef]
- Fang, K.T.; Kotz, S.; Ng, K.W. Symmetric Multivariate and Related Distributions, 3rd ed.; Chapman & Hall: London, UK, 1990. [Google Scholar]
- Gupta, A.K.; Varga, T. Elliptically Contoured Models in Statistics; Kluwer Academic Publishers: Boston, MA, USA, 1993. [Google Scholar]
- Kelker, D. Distribution theory of spherical distributions and location scale parameters generalization. Sankhya Indian J. Stat. Ser. A 1970, 32, 419–430. [Google Scholar]
- Azzalini, A.; Capitanio, A. Statistical applications of the multivariate skew normal distribution. J. R. Stat. Soc. Ser. B 1999, 61, 579–602. [Google Scholar] [CrossRef]
- Branco, M.D.; Dey, D.K. A general class of multivariate skew-elliptical distributions. J. Multivar. Anal. 2001, 79, 99–113. [Google Scholar] [CrossRef]
- Genton, M.G.; Loperfido, N.M. Generalized skew-elliptical distributions and their quadratic forms. Ann. Inst. Stat. Math. 2005, 57, 389–401. [Google Scholar] [CrossRef]
- Shushi, T. Generalized skew-elliptical distributions are closed under affine transformations. Stat. Probab. Lett. 2018, 134, 1–4. [Google Scholar] [CrossRef]
- Adcock, C.; Azzalini, A. A Selective Overview of Skew-Elliptical and Related Distributions and of Their Applications. Symmetry 2020, 12, 118. [Google Scholar] [CrossRef]
- Owen, D.B. Tables for computing bivariate normal probabilities. Ann. Math. Stat. 1956, 27, 1075–1090. [Google Scholar] [CrossRef]
- Johnson, N.L.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions, 2nd ed.; Wiley-Blackwell; John Wiley & Sons: Hoboken, NJ, USA, 1995; Volume 2. [Google Scholar]
- Martínez-Flórez, G.; Pacheco, M.; Giraldo, R. Inference in log-alpha-power and log-skew-normal multivariate models. Commun. Stat. Theory Methods 2016, 45, 4397–4415. [Google Scholar] [CrossRef]
- Martínez-Flórez, G.; Farias, R.B.A.; Moreno-Arenas, G. Multivariate log-Birnbaum-Saunders regression models. Commun. Stat. Theory Methods 2017, 46, 10166–10178. [Google Scholar] [CrossRef]
- Martínez-Flórez, G.; Lemonte, A.J.; Salinas, H.S. Multivariate Skew-Power-Normal Distributions: Properties and Associated Inference. Symmetry 2019, 11, 1509. [Google Scholar] [CrossRef]
- Lemonte, A.J.; Martínez-Flórez, G.; Moreno-Arenas, G. Multivariate Birnbaum-Saunders distribution: Properties and associated inference. J. Stat. Comput. Simul. 2016, 85, 374–392. [Google Scholar] [CrossRef]
- Pljonkin, A.P. Features of the Photon Pulse Detection Algorithm in the Quantum Key Distribution System. In Proceedings of the 2017 International Conference on Cryptography, Security and Privacy, Goa, India, 15–17 December 2017; pp. 81–84. [Google Scholar]
- Pljonkin, A.P. Vulnerability of the Synchronization Process in the Quantum Key Distribution System. Int. J. Cloud Appl. Comput. 2019, 9, 50–58. [Google Scholar] [CrossRef]
- Arnold, B.C.; Castillo, E.; Sarabia, J.M. Conditionally specified distributions. In Lecture Notes in Statistics; Berger, J., Fienberg, J., Gani, J., Krickeberg, I., Singer, B., Eds.; Springer: New York, NY, USA, 1992; Volume 73. [Google Scholar]
- Martínez-Flórez, G.; Arnold, B.C.; Bolfarine, H.; Gómez, H.W. The multivariate alpha-power model. J. Stat. Plan. Inference 2013, 143, 1244–1255. [Google Scholar] [CrossRef]
- Arnold, B.C.; Strauss, D. Bivariate distributions with conditionals in prescribed exponential families. J. Roy. Stat. Soc. Ser. B 1991, 53, 365–375. [Google Scholar] [CrossRef]
- Arnold, B.C.; Castillo, E.; Sarabia, J.M. Conditionally Specification of Statistical Models; Springer Series in Statistics; Springer: New York, NY, USA, 1999. [Google Scholar]
- Besag, J. Statistical analysis of non-lattice data. J. Roy. Stat. Soc. Ser. D 1975, 24, 179–195. [Google Scholar] [CrossRef]
- Arnold, B.C.; Strauss, D. Pseudolikelihood Estimation: Some Examples. Sankhya Indian J. Stat. Ser. B 1991, 53, 233–2435. [Google Scholar]
- Cheng, C.; Riu, J. On Estimating Linear Relationships When Both Variables Are Subject to Heteroscedastic Measurement Errors. Technometrics 2006, 48, 511–519. [Google Scholar] [CrossRef]
- Rotnitziky, A.; Cox, D.R.; Bottai, M.; Robins, J. Likelihood-based inference with singular information matrix. Bernoulli 2000, 6, 243–284. [Google Scholar] [CrossRef]
- Salinas, H.S.; Gómez, H.W.; Martínez-Flórez, G.; Bolfarine, H. Skew-normal alpha-power model [Statistics 48(2014) 1414–1428]. Statistics 2018, 52, 950–953. [Google Scholar] [CrossRef]
- Azzalini, A.; Capitanio, A. The Skew-Normal and Related Families, 1st ed.; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Fisher, R.A. The use of multiple measurements in taxonomic problems. Ann. Eugen. 1936, 7, 179–188. [Google Scholar] [CrossRef]
- Anderson, T.W.; Darling, D.A. A test of goodness of fit. J. Am. Stat. Assoc. 1954, 49, 765–769. [Google Scholar] [CrossRef]
- Doornik, J.A.; Hansen, H. An Omnibus Test for Univariate and Multivariate Normality. Oxf. Bull. Econ. Stat. 2008, 70, 927–939. [Google Scholar] [CrossRef]
- Henze, N.; Zirkler, B. A Class of Invariant Consistent Tests for Multivariate Normality. Commun. Stat. Theory Methods 1990, 19, 3595–3617. [Google Scholar] [CrossRef]
- Royston, J.P. Some Techniques for Assessing Multivarate Normality Based on the Shapiro-Wilk W. J. Roy. Stat. Soc. Ser. C 1983, 32, 121–133. [Google Scholar] [CrossRef]
- Royston, J.P. Remark AS R94: A Remark on Algorithm AS 181: The W-test for Normality. J. Roy. Stat. Soc. Ser. C 1995, 44, 547–551. [Google Scholar] [CrossRef]
- Akaike, H. A new look at statistical model identification. IEEE Trans. Autom. Contr. 1974, 19, 716–722. [Google Scholar] [CrossRef]
- Cavanaugh, J.E. Unifying the derivations for the Akaike and corrected Akaike information criteria. Stat. Probab. Lett. 1997, 33, 201–208. [Google Scholar] [CrossRef]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019; Available online: http://www.R-project.org (accessed on 10 January 2020).
- Pewsey, A. Problems of inference for Azzalini’s skew-normal distribution. J. Appl. Stat. 2000, 27, 859–870. [Google Scholar] [CrossRef]
- Justel, A.; Peña, D.; Zamar, Z. A multivariate Kolmogorov-Smirnov test of goodness of fit. Stat. Probab. Lett. 1997, 35, 251–259. [Google Scholar] [CrossRef]
- Johnson, R.A.; Wichern, D.W. Applied Multivariate Statistical Analysis, 6th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2007. [Google Scholar]
- Gokhale, S.; Khare, M. Statistical behavior of carbon monoxide from vehicular exhausts in urban environments. Environ. Model. Softw. 2007, 22, 526–535. [Google Scholar] [CrossRef]
| −1.5 | −1.0 | −0.5 | 0 | 0.5 | 1.0 | 1.5 | 2.0 | |
|---|---|---|---|---|---|---|---|---|
| −2.5 | 0.8033 | 0.3730 | −0.2686 | −0.6699 | −0.8444 | −0.9252 | −0.9680 | −0.9933 |
| −2.0 | 0.7518 | 0.3559 | −0.2385 | −0.6124 | −0.7759 | −0.8519 | −0.8924 | −0.9164 |
| −1.5 | 0.6025 | 0.2984 | −0.1661 | −0.4625 | −0.5938 | −0.6556 | −0.6888 | −0.7087 |
| −1.0 | 0.2105 | 0.1324 | −0.0046 | −0.1014 | −0.1479 | −0.1713 | −0.1845 | −0.1927 |
| −0.5 | −0.2853 | −0.0921 | 0.1722 | 0.3245 | 0.3855 | 0.4117 | 0.4246 | 0.4317 |
| 0 | −0.5511 | −0.2190 | 0.2543 | 0.5385 | 0.6573 | 0.7105 | 0.7377 | 0.7534 |
| 0.5 | −0.6643 | −0.2756 | 0.2846 | 0.6244 | 0.7679 | 0.8327 | 0.8662 | 0.8856 |
| 1.0 | −0.7183 | −0.3035 | 0.2971 | 0.6631 | 0.8185 | 0.8888 | 0.9254 | 0.9467 |
| 1.5 | −0.7478 | −0.3193 | 0.3031 | 0.6834 | 0.8451 | 0.9186 | 0.9569 | 0.9791 |
| 2.0 | −0.7657 | −0.3291 | 0.3062 | 0.6951 | 0.8609 | 0.9362 | 0.9755 | 0.9985 |
| 2.5 | −0.7776 | −0.3358 | 0.3081 | 0.7026 | 0.8709 | 0.9476 | 0.9876 | 1.0000 |
| Variable | ||||
|---|---|---|---|---|
| 5.843 | 0.828 | 0.308 | −0.605 | |
| 3.057 | 0.435 | 0.312 | 0.138 |
| Estimate | BCSN | BPN | BPSN |
|---|---|---|---|
| 5.867 (0.055) | 3.746 (0.136) | 4.119 (0.163) | |
| 3.055 (0.035) | 1.655 (0.082) | 2.572 (0.159) | |
| 0.794 (0.043) | 1.384 (0.058) | 1.417 (0.204) | |
| 0.438 (0.026) | 0.808 (0.055) | 2.146 (0.390) | |
| −0.224 (0.110) | 11.147 (3.685) | ||
| −3.200 (0.504) | |||
| 9.358 (0.613) | 2.127 (0.192) | ||
| 14.746 (0.374) | 18.260 (3.158) | ||
| 2.671 (0.715) | 5.016 (1.473) | ||
| AIC | 555.10 | 551.71 | 549.00 |
| CAIC | 557.68 | 554.73 | 552.59 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martínez-Flórez, G.; Tovar-Falón, R.; Gómez, H.W. Bivariate Power-Skew-Elliptical Distribution. Symmetry 2020, 12, 1327. https://doi.org/10.3390/sym12081327
Martínez-Flórez G, Tovar-Falón R, Gómez HW. Bivariate Power-Skew-Elliptical Distribution. Symmetry. 2020; 12(8):1327. https://doi.org/10.3390/sym12081327
Chicago/Turabian StyleMartínez-Flórez, Guillermo, Roger Tovar-Falón, and Héctor W. Gómez. 2020. "Bivariate Power-Skew-Elliptical Distribution" Symmetry 12, no. 8: 1327. https://doi.org/10.3390/sym12081327
APA StyleMartínez-Flórez, G., Tovar-Falón, R., & Gómez, H. W. (2020). Bivariate Power-Skew-Elliptical Distribution. Symmetry, 12(8), 1327. https://doi.org/10.3390/sym12081327






