A Family of Skew-Normal Distributions for Modeling Proportions and Rates with Zeros/Ones Excess
Abstract
1. Introduction
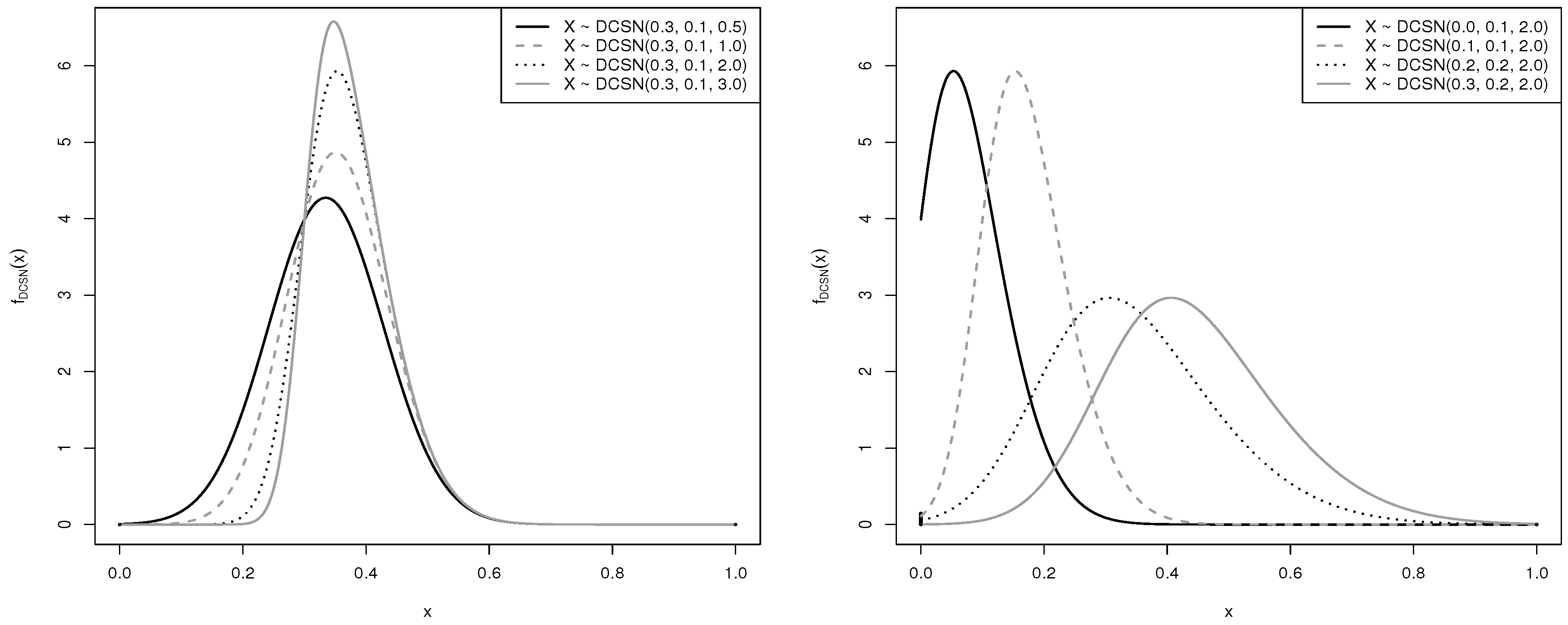
2. Doubly-Censored SN Distribution
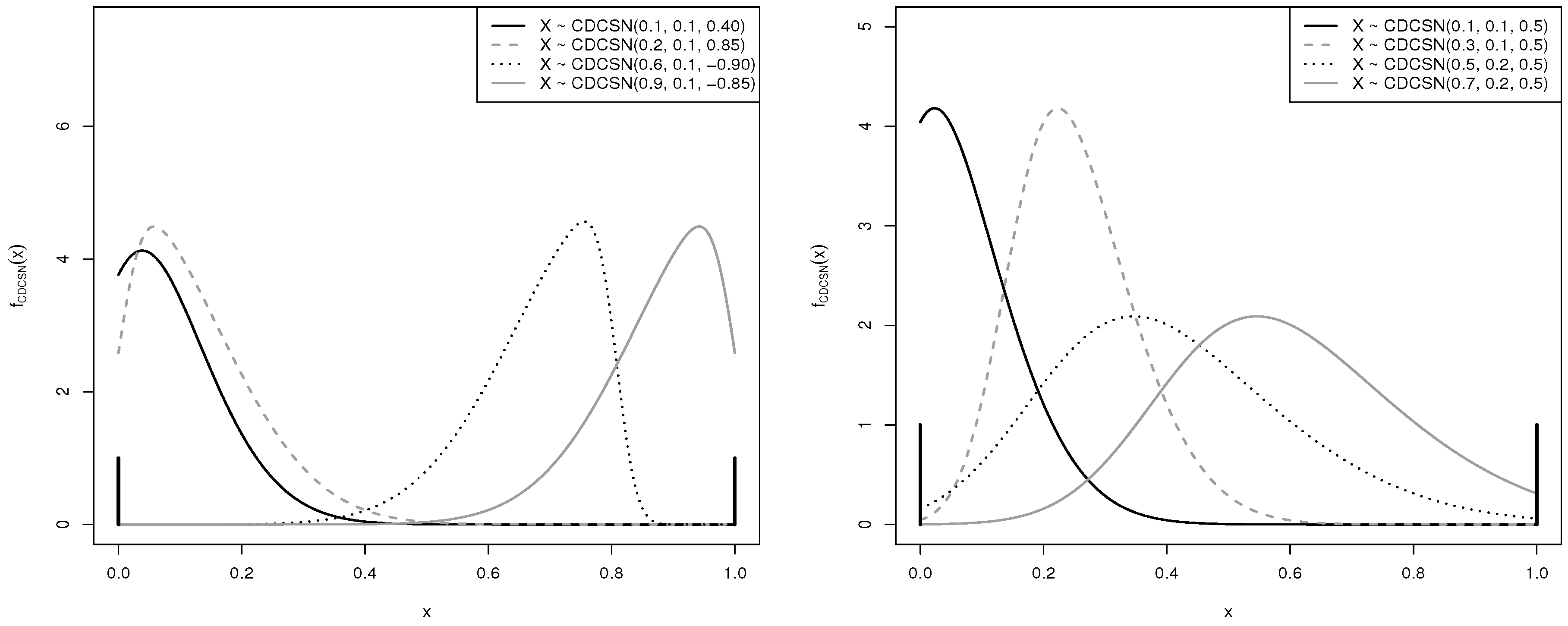
3. Doubly-Censored Log-SN and Centered SN Distributions
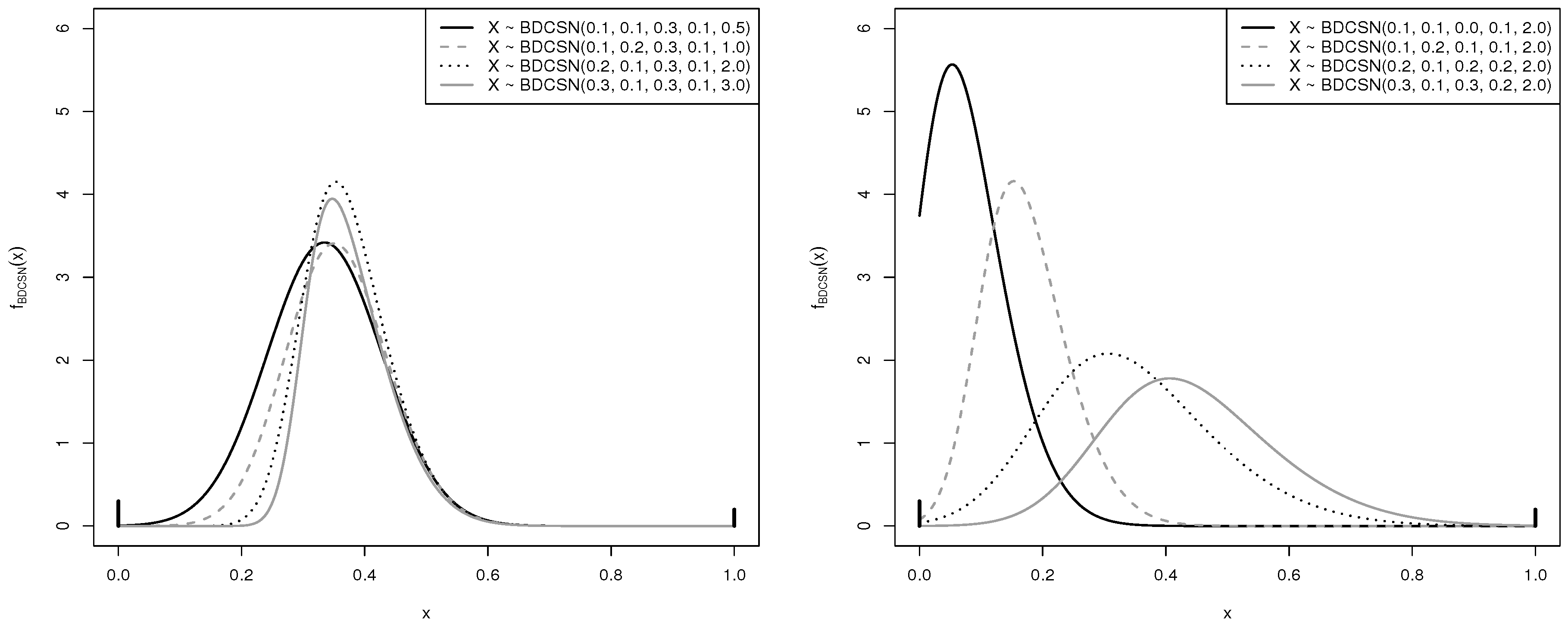
4. The Bernoulli/Doubly-Censored SN Mixture Distribution
5. Monte Carlo Simulation Study
| Algorithm 1 Generation of random numbers from the BDCSN distribution. |
| 1: Fix values for , , , , and . |
| 2: Generate values for u from . |
| 3: Compute values for x from
|
| 4: Repeat steps 2–3 until the required numbers of data (n) is completed. |
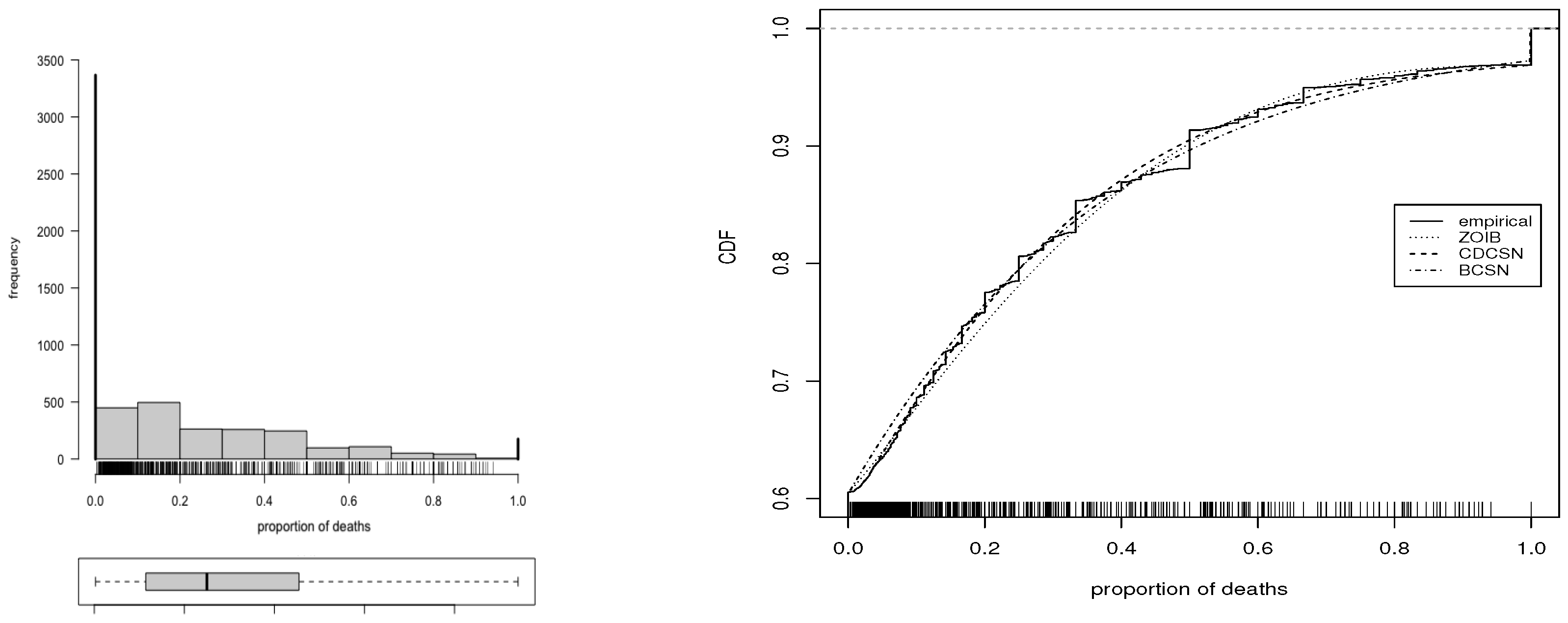
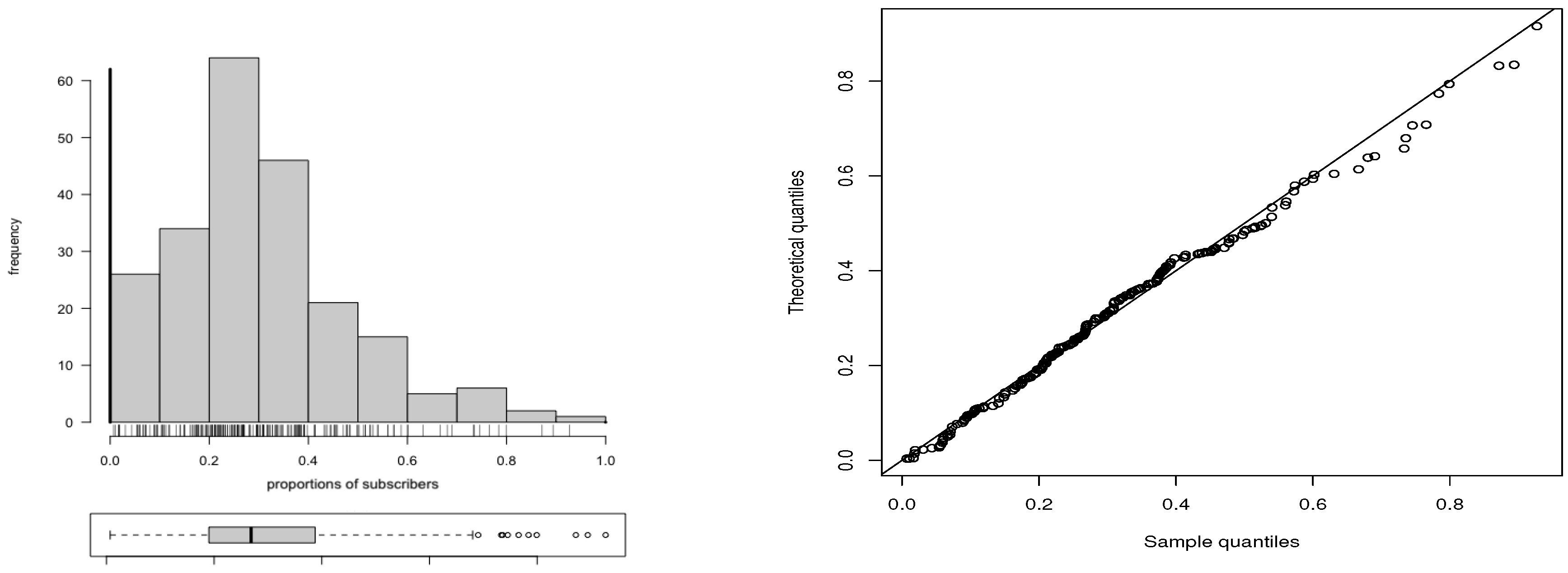
6. Real Data Application 1
7. Real Data Application 2
8. Conclusions and Future Research
- (i)
- By using skew-normal distributions, we have proposed a new family of distributions which are an alternative to the beta distribution when an excess zeros and/or one inflation is present.
- (ii)
- The parameters of the distributions were estimated by the maximum likelihood method.
- (iii)
- The expected and observed Fisher information matrices associated with the new family of distributions were derived, and an parameterization was proposed to circumvent a singularity problem in these matrices, which is inherited from the classical skew-normal distribution.
- (iv)
- The Fisher information matrix related to the new mixture distribution obtained in this study resulted to be block ortogonal, facilitating the estimation of parameters and doing it separately in two groups with respect to the discrete and continuous parts of this mixture, respectively.
- (v)
- An algorithm to generate random numbers from the new family of distributions derived in this study was proposed and implemented.
- (vi)
- Monte Carlo simulations based on the new family of distributions proposed in this research were provided to detect performance of the maximum likelihood estimators of their parameters.
- (vii)
- Examples with two real data sets were performed to illustrate the potential applications with the new family of distributions based on the skew-normal distribution proposed in the paper. In addition, we compare the new distributions to their natural competitors, corresponding to the beta and normal distributions, showing their convenience.
- (i)
- Parameter estimates of censored distributions are more efficient than when censorship is not considered. Indeed, if censored cases are present and a non-censored distribution is used, evidently it is not possible to estimate the variance of the censored part. However, if censored distributions are utilized in this case, such a variance may be estimated from the data. For more details, see page 199 in [47]. Subsequently, the study of asymptotic efficiency bounds in the new family of distributions proposed in the present investigation is an issue of interest; see details in [48]. In addition, asymptotic behavior and performance of maximum likelihood estimators in more complex statistical models can be studied in [49,50].
- (ii)
- The use of covariates when modeling a doubly-censored response with support in [0, 1] following the new family of distributions is of interest. In this case, type Tobit models can be considered as benchmark to compare the new regression models. Specifically, when studying a doubly-censored response in [0, 1] through a linear predictor which includes covariates, the number of observations below and/or above can be modeled by a Bernoulli distribution with a logit link function and polychotomous response. Given the possible orthogonality in the information matrix, the parameters of this model of two parts can be estimated separately. Refs. [30,36] discussed estimation methods for the regression parameters in a similar context under a mixture structure.
- (iii)
- (iv)
- (v)
- (vi)
- Robust estimation methods when outliers are present into the data set can be used [63].
- (vii)
- Applications of the new methodology derived here can be of interest in diverse areas [64].
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Doubly-Censored SN Distribution
Appendix A.2. The Bernoulli/Doubly-Censored SN Mixture Distribution
References
- Azzalini, A. A class of distributions which includes the normal ones. Scand. J. Stat. 1985, 12, 171–178. [Google Scholar]
- Azzalini, A. Further results on a class of distributions which includes the normal ones. Statistica 1986, 46, 199–208. [Google Scholar]
- Henze, N. A probabilistic representation of the skew-normal distribution. Scand. J. Stat. 1986, 13, 271–275. [Google Scholar]
- Chiogna, M. Notes on Estimation Problems with Scalar Skew-Normal Distributions; Technical Report 11997.15; Department of Statistical Science: Padova, Italy, 1997. [Google Scholar]
- Pewsey, A. Problems of inference for Azzalini’s skew-normal distribution. J. Appl. Stat. 2000, 27, 859–870. [Google Scholar] [CrossRef]
- Gómez, H.W.; Venegas, O.; Bolfarine, H. Skew-symmetric distributions generated by the distribution function of the normal distribution. Environmetrics 2007, 18, 395–407. [Google Scholar] [CrossRef]
- Liu, Y.; Mao, G.; Leiva, V.; Liu, S.; Tapia, A. Diagnostic analytics for an autoregressive model under the skew-normal distribution. Mathematics 2020, 8, 693. [Google Scholar] [CrossRef]
- Seijas-Macias, A.; Oliveira, A.; Oliveira, T.; Leiva, V. Approximating the distribution of the product of two normally distributed random variables. Symmetry 2020, 12, 1201. [Google Scholar] [CrossRef]
- Kotz, S.; Van Dorp, J.R. Beyond Beta: Other Continuous Families of Distributions with Bounded Support and Applications; World Scientific: New York, NY, USA, 2004. [Google Scholar]
- Paolino, P. Maximum likelihood estimation of models with beta-distributed dependent variables. Polit. Anal. 2001, 9, 325–346. [Google Scholar] [CrossRef]
- Cribari-Neto, F.; Vasconcellos, K.L.P. Nearly unbiased maximum likelihood estimation for the beta distribution. J. Stat. Comput. Simul. 2002, 72, 107–118. [Google Scholar] [CrossRef]
- Kieschnick, R.; McCullough, B.D. Regression analysis of variates observed on (0, 1): Percentages, proportions and fractions. Stat. Model. 2003, 3, 193–213. [Google Scholar] [CrossRef]
- Ferrari, S.; Cribari-Neto, F. Beta regression for modeling rates and proportions. J. Appl. Stat. 2004, 31, 799–815. [Google Scholar] [CrossRef]
- Gómez–Déniz, E.; Sordo, M.A.; Calderín-Ojeda, E. The log-Lindley distribution as an alternative to the beta regression model with applications consurance. Insur. Math. Econ. 2013, 54, 49–57. [Google Scholar] [CrossRef]
- Vasconcellos, K.L.P.; Cribari-Neto, F. Improved maximum likelihood estimation in a new class of beta regression models. Braz. J. Probab. Stat. 2005, 19, 13–31. [Google Scholar]
- Brascum, A.D.; Johnson, W.O.; Thurmond, M.C. Bayesian beta regression: Applications to household expenditure data and genetic distance between foot-and-mouth disease viruses. Aust. N. Z. J. Stat. 2007, 49, 287–301. [Google Scholar] [CrossRef]
- Bayes, C.; Bazán, J.; García, C. A new robust regression model for proportions. Bayesian Anal. 2012, 7, 841–866. [Google Scholar] [CrossRef]
- Mazucheli, J.; Menezes, A.F.B.; Dey, S. The unit-Birnbaum-Saunders distribution with applications. Chilean J. Stat. 2018, 9, 47–57. [Google Scholar]
- Mazucheli, J.; Menezes, A.F.B.; Ghitany, M.E. The unit-Weibull distribution and associated inference. J. Appl. Probab. Stat. 2018, 13, 1–22. [Google Scholar]
- Dasilva, A.; Dias, R.; Leiva, V.; Marchant, C.; Saulo, H. Birnbaum-Saunders regression models: A comparative evaluation of three approaches. J. Stat. Comput. Simul. 2020. [Google Scholar] [CrossRef]
- Cohen, A.C. Truncated and Censored Samples: Theory and Applications; Marcel Dekker: New York, NY, USA, 1991. [Google Scholar]
- Klein, J.P.; Moeschberger, M.L. Survival Analysis: Techniques for Censored and Truncated Data; Springer: New York, NY, USA, 1997. [Google Scholar]
- Schneider, H. Truncated and Censored Samples from Normal Populations; Marcel Dekker: New York, NY, USA, 1986. [Google Scholar]
- Barros, M.; Galea, M.; Gonzalez, M.; Leiva, V. Influence diagnostics in the Tobit censored response model. Stat. Methods Appl. 2010, 19, 379–397. [Google Scholar] [CrossRef]
- Barros, M.; Galea, M.; Leiva, V.; Santos-Neto, M. Generalized Tobit models: Diagnostics and application in econometrics. J. Appl. Stat. 2018, 45, 145–167. [Google Scholar] [CrossRef]
- Desousa, M.; Saulo, H.; Leiva, V.; Scalco, P. On a Tobit-Birnbaum-Saunders model with an application to medical data. J. Appl. Stat. 2018, 45, 932–955. [Google Scholar] [CrossRef]
- Papke, L.E.; Wooldridge, J.M. Econometric methods for fractional response variables with an application to 401(k) plan participation rates. J. Appl. Econ. 1996, 11, 619–632. [Google Scholar] [CrossRef]
- Ospina, R.; Ferrari, S. Inflated beta distributions. Stat. Pap. 2010, 51, 111–126. [Google Scholar] [CrossRef]
- Ospina, R.; Ferrari, S. A general class of zero-or-one inflated beta regression models. Comput. Stat. Data Anal. 2012, 56, 1609–1620. [Google Scholar] [CrossRef]
- Desousa, M.; Saulo, H.; Leiva, V.; Santos-Neto, M. On a new mixture-based regression model: Simulation and application to data with high censoring. J. Stat. Comput. Simul. 2020. [Google Scholar] [CrossRef]
- Leiva, V.; Santos-Neto, M.; Cysneiros, F.J.A.; Barros, M. A methodology for stochastic inventory models based on a zero-adjusted Birnbaum-Saunders distribution. Appl. Stoch. Model. Bus. Ind. 2016, 32, 74–89. [Google Scholar] [CrossRef]
- Moulton, L.; Halsey, N.A. A mixture model with detection limits for regression analyses of antibody response to vaccine. Biometrics 1995, 51, 1570–1578. [Google Scholar] [CrossRef]
- Chai, H.; Bailey, K. Use of log-skew normal distribution in analysis of continuous data with a discrete component at zero. Stat. Med. 2008, 27, 3643–3655. [Google Scholar] [CrossRef]
- Lin, G.D.; Stoyanov, J. The logarithmic skew-normal distribution are moment-indeterminate. J. Appl. Probab. 2009, 46, 909–916. [Google Scholar] [CrossRef]
- Mateu-Figueras, G.; Pawlowsky-Glahn, V.; Barceló-Vidal, C. The natural law in geochemistry: Log-normal or log-skew-normal? In Proceedings of the 32th International Geological Congress, Firenze, Italy, 20–28 August 2004; Volume 2, pp. 233–236. [Google Scholar]
- Farias, R.; Moreno-Arenas, G.; Patriota, A. Reduction of models in the presence of nuisance parameters. Rev. Colomb. Estadíst. 2009, 32, 99–121. [Google Scholar]
- Arellano-Valle, R.B.; Azzalini, A. The centered parametrization for the multivariate skew-normal distribution. J. Multivar. Anal. 2008, 99, 1362–1382. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Lange, K. Numerical Analysis for Statisticians; Springer: New York, NY, USA, 2010. [Google Scholar]
- Cox, D.R.; Hinkley, D.V. Theoretical Statistics; Chapman and Hall: London, UK, 1974. [Google Scholar]
- Azzalini, A. Package ‘sn’. 2017. Available online: http://azzalini.stat.unipd.it/SN/sn-manual.pdf (accessed on 21 July 2020).
- Ventura, M.; Saulo, H.; Leiva, V.; Monsueto, S. Log-symmetric regression models: Information criteria, application to movie business and industry data with economic implications. Appl. Stoch. Model. Bus. Ind. 2019, 34, 963–977. [Google Scholar] [CrossRef]
- Ferreira, M.; Gomes, M.I.; Leiva, V. On an extreme value version of the Birnbaum-Saunders distribution. Revstat 2012, 10, 181–210. [Google Scholar]
- Vuong, Q. Likelihood ratio tests for model selection and non-tested hypotheses. Econometrica 1989, 57, 307–333. [Google Scholar] [CrossRef]
- Kullback, S.; Leiber, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Federal Communication Commission. FCC 93-177, Report and Order and Further Notice of Proposed Rulemaking; Government Printing Office: Washington, DC, USA, 1994.
- Scott, J.L. Regression Models of Categorical and Limited Dependent Variables; Sage: Thousand Oaks, CA, USA, 1997. [Google Scholar]
- Inkmann, J. Asymptotic Efficiency Bounds. In Conditional Moment Estimation of Nonlinear Equation Systems; Springer: Berlin/Heidelberg, Germany, 2001; pp. 36–54. [Google Scholar]
- Genton, M.G.; Zhang, H. Identifiability problems in some non-Gaussian spatial random fields. Chilean J. Stat. 2012, 3, 171–179. [Google Scholar]
- Sánchez, L.; Leiva, V.; Galea, M.; Saulo, H. Birnbaum-Saunders quantile regression models with application to spatial data. Mathematics 2020, 8, 1000. [Google Scholar] [CrossRef]
- Aykroyd, R.G.; Leiva, V.; Marchant, C. Multivariate Birnbaum-Saunders distributions: Modelling and applications. Risks 2018, 6, 21. [Google Scholar] [CrossRef]
- Marchant, C.; Leiva, V.; Christakos, G.; Cavieres, M.F. Monitoring urban environmental pollution by bivariate control charts: New methodology and case study in Santiago, Chile. Environmetrics 2019, 30, e2551. [Google Scholar] [CrossRef]
- Leiva, V.; Sánchez, L.; Galea, M.; Saulo, H. Global and local diagnostic analytics for a geostatistical model based on a new approach to quantile regression. Stoch. Environ. Res. Risk Assess. 2020. [Google Scholar] [CrossRef]
- Leiva, V.; Saulo, H.; Souza, R.; Aykroyd, R.G.; Vila, R. A new BISARMA time series model for forecasting mortality using weather and particulate matter data. J. Forecast. 2020. [Google Scholar] [CrossRef]
- Huerta, M.; Leiva, V.; Rodriguez, M.; Villegas, D. On a partial least squares regression model for asymmetric data with a chemical application in mining. Chem. Intell. Lab. Syst. 2019, 190, 55–68. [Google Scholar] [CrossRef]
- Garcia-Papani, F.; Uribe-Opazo, M.A.; Leiva, V.; Aykroyd, R.G. Birnbaum-Saunders spatial modelling and diagnostics applied to agricultural engineering data. Stoch. Environ. Res. Risk Assess. 2017, 31, 105–124. [Google Scholar] [CrossRef]
- Saulo, H.; Leão, J.; Leiva, V.; Aykroyd, R.G. Birnbaum-Saunders autoregressive conditional duration models applied to high-frequency financial data. Stat. Pap. 2019, 60, 1605–1629. [Google Scholar] [CrossRef]
- Carrasco, J.M.F.; Figueroa-Zuniga, J.I.; Leiva, V.; Riquelme, M.; Aykroyd, R.G. An errors-in-variables model based on the Birnbaum-Saunders and its diagnostics with an application to earthquake data. Stoch. Environ. Res. Risk Assess. 2020, 34, 369–380. [Google Scholar] [CrossRef]
- Sánchez, L.; Leiva, V.; Galea, M.; Saulo, H. Birnbaum-Saunders quantile regression and its diagnostics with application to economic data. Appl. Stoch. Model. Bus. Ind. 2020. [Google Scholar] [CrossRef]
- Martinez, S.; Giraldo, R.; Leiva, V. Birnbaum-Saunders functional regression models for spatial data. Stoch. Environ. Res. Risk Assess. 2019, 33, 1765–1780. [Google Scholar] [CrossRef]
- Giraldo, R.; Herrera, L.; Leiva, V. Cokriging prediction using as secondary variable a functional random field with application in environmental pollution. Mathematics 2020, 8, 1305. [Google Scholar] [CrossRef]
- Garcia-Papani, F.; Leiva, V.; Uribe-Opazo, M.A.; Aykroyd, R.G. Birnbaum-Saunders spatial regression models: Diagnostics and application to chemical data. Chem. Intell. Lab. Syst. 2018, 177, 114–128. [Google Scholar] [CrossRef]
- Velasco, H.; Laniado, H.; Toro, M.; Leiva, V.; Lio, Y. Robust three-step regression based on comedian and its performance in cell-wise and case-wise outliers. Mathematics 2020, 8, 1259. [Google Scholar] [CrossRef]
- Kotz, S.; Leiva, V.; Sanhueza, A. Two new mixture models related to the inverse Gaussian distribution. Methodol. Comput. Appl. Probab. 2010, 12, 199–212. [Google Scholar] [CrossRef]
| True Value | Mean | Variance | Bias | RMSE | Mean | Variance | Bias | RMSE | Mean | Variance | Bias | RMSE | Mean | Variance | Bias | RMSE | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.1 | = 0.2 | 0.21148 | 0.00110 | 0.01148 | 0.03513 | 0.20632 | 0.00137 | 0.00632 | 0.03755 | 0.20642 | 0.00124 | 0.00642 | 0.03578 | 0.20976 | 0.00035 | 0.00976 | 0.02109 |
| 0.1 | 0.1 | 0.18965 | 0.00057 | 0.01034 | 0.02597 | 0.19227 | 0.00054 | 0.00773 | 0.02459 | 0.19269 | 0.00053 | 0.00730 | 0.02419 | 0.19235 | 0.00018 | 0.00765 | 0.01554 | |
| 0.1 | 0.1 | = 0.3 | 0.31774 | 0.01593 | 0.01774 | 0.12746 | 0.35869 | 0.06063 | 0.05869 | 0.25314 | 0.35355 | 0.05694 | 0.05355 | 0.24457 | 0.31103 | 0.00205 | 0.01103 | 0.04661 |
| 0.1 | 0.2 | = 0.2 | 0.21323 | 0.00123 | 0.01323 | 0.03752 | 0.20943 | 0.00126 | 0.00943 | 0.03669 | 0.20649 | 0.00142 | 0.00649 | 0.03830 | 0.21034 | 0.00044 | 0.01033 | 0.02345 |
| 0.1 | 0.2 | 0.18861 | 0.00065 | 0.01138 | 0.02796 | 0.19103 | 0.00052 | 0.00896 | 0.02458 | 0.19247 | 0.00056 | 0.00752 | 0.02489 | 0.19218 | 0.00021 | 0.00781 | 0.01654 | |
| 0.1 | 0.2 | = 0.3 | 0.30536 | 0.01117 | 0.00536 | 0.10581 | 0.33359 | 0.04294 | 0.03359 | 0.20994 | 0.36002 | 0.06839 | 0.06002 | 0.26833 | 0.30800 | 0.00443 | 0.00800 | 0.06709 |
| 0.2 | 0.1 | = 0.2 | 0.21216 | 0.00120 | 0.01216 | 0.03678 | 0.20810 | 0.00126 | 0.00810 | 0.03650 | 0.20556 | 0.00137 | 0.00556 | 0.03754 | 0.21035 | 0.00044 | 0.01035 | 0.02345 |
| 0.2 | 0.1 | 0.18884 | 0.00066 | 0.01115 | 0.02812 | 0.19139 | 0.00053 | 0.00860 | 0.02460 | 0.19262 | 0.00055 | 0.00737 | 0.02474 | 0.19217 | 0.00021 | 0.00782 | 0.01653 | |
| 0.2 | 0.1 | = 0.3 | 0.31271 | 0.01290 | 0.01271 | 0.11430 | 0.34589 | 0.05113 | 0.04589 | 0.23075 | 0.36530 | 0.06428 | 0.06530 | 0.26181 | 0.30776 | 0.00416 | 0.00776 | 0.06501 |
| 0.2 | 0.2 | = 0.2 | 0.21338 | 0.00143 | 0.01338 | 0.04013 | 0.21185 | 0.00118 | 0.01185 | 0.03633 | 0.20870 | 0.00132 | 0.00870 | 0.03749 | 0.21051 | 0.00049 | 0.01051 | 0.02453 |
| 0.2 | 0.2 | 0.18768 | 0.00076 | 0.01231 | 0.03026 | 0.18964 | 0.00056 | 0.01035 | 0.02601 | 0.19139 | 0.00052 | 0.00860 | 0.02448 | 0.19200 | 0.00024 | 0.00799 | 0.01732 | |
| 0.2 | 0.2 | = 0.3 | 0.30392 | 0.00752 | 0.00392 | 0.08681 | 0.31181 | 0.01922 | 0.01181 | 0.13914 | 0.34616 | 0.06196 | 0.04616 | 0.25316 | 0.30677 | 0.00369 | 0.00677 | 0.06119 |
| 0.3 | 0.1 | = 0.2 | 0.21337 | 0.00143 | 0.01337 | 0.04018 | 0.21184 | 0.00116 | 0.01184 | 0.03608 | 0.20867 | 0.00134 | 0.00867 | 0.03767 | 0.21049 | 0.00049 | 0.01049 | 0.02467 |
| 0.3 | 0.1 | 0.18769 | 0.00076 | 0.01230 | 0.03026 | 0.18963 | 0.00056 | 0.01036 | 0.02602 | 0.19141 | 0.00052 | 0.00859 | 0.02447 | 0.19201 | 0.00024 | 0.00798 | 0.01734 | |
| 0.3 | 0.1 | = 0.3 | 0.30449 | 0.00951 | 0.00449 | 0.09766 | 0.31186 | 0.01993 | 0.01186 | 0.14167 | 0.34602 | 0.05773 | 0.04602 | 0.24464 | 0.30712 | 0.00439 | 0.00712 | 0.06670 |
| 0.3 | 0.2 | = 0.2 | 0.21357 | 0.00172 | 0.01357 | 0.04367 | 0.21245 | 0.00135 | 0.01245 | 0.03886 | 0.21158 | 0.00115 | 0.01158 | 0.03577 | 0.21117 | 0.00057 | 0.01117 | 0.02648 |
| 0.3 | 0.2 | 0.18669 | 0.00090 | 0.01330 | 0.03296 | 0.18889 | 0.00069 | 0.01110 | 0.02851 | 0.18981 | 0.00055 | 0.01019 | 0.02555 | 0.19163 | 0.00029 | 0.00836 | 0.01902 | |
| 0.3 | 0.2 | = 0.3 | 0.30823 | 0.00996 | 0.00824 | 0.10013 | 0.30489 | 0.00961 | 0.00489 | 0.09818 | 0.31686 | 0.02287 | 0.01687 | 0.15217 | 0.30325 | 0.00537 | 0.00325 | 0.07338 |
| Minimum | Median | Mean | SD | CV | CS | CK | Maximum |
|---|---|---|---|---|---|---|---|
| 0.003 | 0.250 | 0.292 | 0.216 | 73.892 | 0.811 | −0.206 | 0.941 |
| Estimate | ZOIB | CDCSN | BDCSN |
|---|---|---|---|
| 0.2974 (0.0043) | −0.0691 (0.0217) | 0.1965 (0.0039) | |
| 0.4562 (0.0050) | 0.4448 (0.0248) | 0.1818 (0.0040) | |
| – | 0.6374 (0.1900) | 0.9905 (0.0023) | |
| 0.6055 (0.0066) | – | 0.6055 (0.0066) | |
| 0.0313 (0.0023) | – | 0.0313 (0.0023) | |
| AIC | 7464.2 | 7615.6 | 7455.7 |
| BIC | 7498.7 | 7635.5 | 7488.8 |
| CAIC | 7466.2 | 7617.6 | 7457.7 |
| −3728.1 | −3804.8 | −3722.9 |
| Minimum | Median | Mean | SD | CV | CS | CK | Maximum |
|---|---|---|---|---|---|---|---|
| 0.007 | 0.269 | 0.305 | 0.18 | 59.034 | 0.918 | 0.969 | 0.927 |
| Estimate | ZOIB | Normal | CSN | BDCSN |
|---|---|---|---|---|
| 0.3080 (0.0140) | 0.2069 (0.0153) | 0.2110 (0.0153) | 0.2952 (0.0156) | |
| 5.3239 (0.0004) | 0.2487 (0.0125) | 0.2455 (0.0129) | 0.1873 (0.0121) | |
| – | – | 0.4046 (0.1937) | 0.5750 (0.1644) | |
| 0.2198 (0.0006) | – | – | 0.2198 (0.0006) | |
| AIC | 144.748 | 142.258 | 150.278 | 135.197 |
| BIC | 155.674 | 149.542 | 161.205 | 149.765 |
| CAIC | 146.893 | 144.344 | 152.423 | 137.415 |
| −69.374 | −69.127 | −72.139 | −63.599 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martínez-Flórez, G.; Leiva, V.; Gómez-Déniz, E.; Marchant, C. A Family of Skew-Normal Distributions for Modeling Proportions and Rates with Zeros/Ones Excess. Symmetry 2020, 12, 1439. https://doi.org/10.3390/sym12091439
Martínez-Flórez G, Leiva V, Gómez-Déniz E, Marchant C. A Family of Skew-Normal Distributions for Modeling Proportions and Rates with Zeros/Ones Excess. Symmetry. 2020; 12(9):1439. https://doi.org/10.3390/sym12091439
Chicago/Turabian StyleMartínez-Flórez, Guillermo, Víctor Leiva, Emilio Gómez-Déniz, and Carolina Marchant. 2020. "A Family of Skew-Normal Distributions for Modeling Proportions and Rates with Zeros/Ones Excess" Symmetry 12, no. 9: 1439. https://doi.org/10.3390/sym12091439
APA StyleMartínez-Flórez, G., Leiva, V., Gómez-Déniz, E., & Marchant, C. (2020). A Family of Skew-Normal Distributions for Modeling Proportions and Rates with Zeros/Ones Excess. Symmetry, 12(9), 1439. https://doi.org/10.3390/sym12091439






