Abstract
In this paper, the prediction of compressive cement strength using the fuzzy linear regression (FLR) and adaptive neuro-fuzzy inference system (ANFIS) methods was studied. Specifically, an accurate prediction method is needed as the modeling of cement strength is a difficult task, which is based on its composite nature. However, many approaches are widely implemented in strength-predicting problems, such as the artificial neural network (ANN), Mamdani fuzzy rules in MATLAB, FLR and ANFIS models. Applying these methods and comparing the results with the corresponding observed ones, we concluded that the ANFIS method successfully decreased the level of uncertainty in predicting cement strength, as the average percentage error level was extremely low. Although the FLR method had the highest average percentage error level compared with the other methods, it provides a standard equation to estimate the output values by using symmetric triangular fuzzy numbers and determines the most important factor in increasing compressive strength, in contrast to ANFIS and ANN, which are black box models, and to the fuzzy method, which uses rules without providing the specific way by which the results come out. Thus, ANFIS and FLR are appropriate methods for dealing with engineering mathematical models by using fuzzy logic.
1. Introduction
Concrete is recognized as the most broadly used material in the construction of buildings, subway projects and other civil structures, which consists of cement, water and aggregates. Sometimes, powdered or liquid additives are also included in the mixture in order to improve its specific properties, such as the durability of the concrete, or to control setting or hardening. Concrete is widely used, as its raw materials are available worldwide. Concrete’s properties depend on the quality of its materials. One of the most important properties that it has is the high compressive strength at 28 days after casting. Therefore, it is necessary to test the concrete’s compressive strength, so as to define the quality and also the strength of the construction.
Cement is a material consisting of a binder within, widely used in the production of construction essentials as it acquires strong stability and durability after hardening. In this research, CEM I 42.5R European standard EN197-1 [1] was used as the type of cement, containing 95–100% clinker composition and 0–5% other additional constituents. Cement hydration is a complex process resulting from water’s reaction with cement. There are many physical and chemical parameters that affect cement hydration and, therefore, its compressive strength. One of them is the Portland cement clinker composition [2], as it mainly consists of tricalcium silicate (C3S), which is responsible for the early strength and early characteristics of cement, dicalcium silicate (C2S), which contributes to cement’s long-term compressive strength, tricalcium aluminate (C3A), which in a low amount provides resistance to sulfates, tetracalcium aluminoferrite (C4AF) that works as a flux material and sometimes trioxide sulfate (SO3) [3], which is a gypsum that is added to the clinker after its cooling for minimizing the amount of grinding energy needed. Depending on its application, cement contains over 50–70% C3S, 15–30% C2S, 5–10% C3A, 5–15% C4AF [4] and less than 4% SO3 [3]. Cement hydration also depends on the Blaine fineness of the cement particles, which ranges in value between 2000 and 5000 cm2/g, and by the alkali content in the cement composition.
Portland cement production is not an environmentally friendly process as it releases a massive amount of carbon dioxide (CO2) into the atmosphere, causing climate change and greenhouse gas emissions. On the other hand, non-conventional cementitious materials [5,6,7,8,9] are being developed in order to reduce environmental pollution and replace ordinary Portland cement with sustainable materials like self-healing concretes or alternative geopolymer-based concretes, which seem to be promising in concrete construction. Non-conventional cementitious materials also improve the characteristics of the cement and increase its compressive strength. Τhe ordinary cement compressive strength can also be improved by incorporating nanoparticles [10] in its composition to increase the density of the concrete. The prediction of the compressive strength of these types of concrete is a very important process, as it provides an option to modify the mix proportion in circumstances where the mandatory design strength is not attained, in order to avoid construction failures and substitute successfully the stability offered by Portland cement. As indicated, analytical models that include the effects of each of these factors on the compressive strength may be very complicated. Consequently, the use of fuzzy regression models, adaptive neuro-fuzzy inference systems (ANFISes) [11,12,13], as well as artificial neural networks (ANNs) [11,14,15] and fuzzy logic, seems to be a promising approach to the strength prediction problem, providing useful tools in the concrete industry.
In a previous study [16], the 28-day compressive strength was predicted with the use of ANNs and Mamdani fuzzy rules in MATLAB. The ANN method [17] was based on the structure of an artificial neural network with three levels. The first layer (input), as well as the second layer (hidden), had four neurons, and there was one output parameter, the compressive strength, in the last layer. The inputs, which were C3S, SO3, Blaine fineness and alkali, were first normalized to ranges from 0.1 to 0.9, using the equation
where α and b are the lowest and highest values of the range of normalization, respectively, Xmini and Xmaxi are the lowest and highest values of each input, respectively, and Xi is the value of each input of the ith node.
Then, those values were multiplied by the weight factors in order to train the model, with the use of the equation
where xi is the input parameter from the ith neuron and vij is the weight from the previous level i in the next level j. Afterwards, the aforementioned values were transferred to the hidden layer. For determining the activation level, the sigmoid transfer function was used with the following form:
Furthermore, a backpropagation algorithm [18] was used to minimize the error level between the output value data and the calculated values, optimizing the weight vector with the following form:
in which yi is the vector of the calculated output value, ti is the target output, P is the number of training patterns and p is the number of output neurons. The modification of the network weights was accomplished by using the following equation:
where δ, the learning rate, was equal to 0.01. The model was trained for 20,000 epochs. More details on the ANN method can be retrieved from [19].
The fuzzy logic algorithm was based on Mamdani rules and consisted of four components. Fuzzification was the first one, where each variable was represented by degrees of membership between the values 0 and 1. The variables were characterized as very low, low, medium and high. Then, rules were defined in order to comprise all possible fuzzy combinations between the processing parameters. Those rules were expressed in an If-Then conditional statement. In the fuzzy inference engine, all the fuzzy rules were taken into account and the inputs were converted to the corresponding outputs. The product method (prod) was used as an inference operator. Finally, in the last component, defuzzification [20], outputs from the previous step were converted into a number using the centroid method
where xi is the value of the output and μ(xi) is its membership value in the membership function.
In this study, the same inputs were applied in order to develop more effective fuzzy models to predict the compressive strength of cement at 28 days. Fuzzy linear regression and ANFIS methods were used to predict 50 sets of cement strength and the results of them were compared with those of the ANN and fuzzy logic algorithm methods.
2. Fuzzy Linear Regression (FLR)
Linear regression [21] provides a crisp approach between a dependent output Y and independent inputs X, using the following form:
where u includes the deviations between the observed and the predicted parameters, known as the disturbance term.
Fuzzy linear regression is an alternative process of probabilistic specification, expressed as
where Ai are symmetric fuzzy numbers, which includes the inability to determine an exact association between the dependent and independent parameters. They are expressed as A = (ri,ci)L, where ri is the center in which the membership function is equal to 1 and c is the range of values. Thus, the membership function [22] is defined as
where L(x) is the symmetric reference function of a fuzzy number that satisfies the constraints below:
L(x) = L(−x),
L(0) = 1,
L(x) is decreasing in [0, ꚙ).
Therefore, the membership function for the linear possibility Equation (8) is formed as
where i is the number of inputs and j is the number of sets. Then, the degree h is determined in order to include the data in the estimated output Y, which is
In this study, the reference function L(x) had the following form:
where L(x) is decreasing in (0,1). As a result, the coefficients of the system (8) were symmetric triangular fuzzy numbers and the following linear programming problem was turned out:
where the relations (17)–(19) were used to minimize the objective function in (16).
Furthermore, the simplex method was used to solve the linear programming problem by combining the relations (16)–(19). The results of the fuzzy triangular numbers are represented in Table 1.

Table 1.
The results of the fuzzy triangular numbers.
The equation of fuzzy linear regression was formed as follows:
With regard to the membership function, it depends on the distance of the observed output values from the center of regression. In particular, the closer the 28-day compressive strength is to the center of the regression, the higher the increase of the membership function is. The values of the root mean square error (RMSE) and the mean absolute percentage error (MAPE) were calculated as
where At and Ft are the observed and computed values, respectively, and n is the number of sets.
Theil’s inequality coefficient is a measure of the accuracy of regression and was equal to
which indicated that the fuzzy linear regression had a successful predictive capacity. The degree of the fuzziness [21] of this model was formed as
where ci contributes to the fuzziness of the system. In order to find the effect of independent inputs on the calculation of the dependent variable Y, the degree of fuzziness was calculated separately for four different models. Each model was comprised of three input variables instead of four and each time a different variable was subtracted. The results are summarized in Table 2.

Table 2.
The results of the degree of fuzziness.
Taking those results into account, it was concluded that C3S was the most important factor in increasing the compressive strength at 28 days, as it had the highest effect on the system’s degree of fuzziness. It also constitutes 50–70% of cement’s composition, which defines it as the main component in the cement. However, all variables were important for developing a successful fuzzy model to predict the 28-day compressive strength of cement. More details on the fuzzy linear regression method can be retrieved from [23,24].
3. Adaptive Neuro-Fuzzy Modeling (ANFIS)
ANFIS is a fuzzy model used as a method of constructing rule systems, by entering the data of the prediction model to derive more efficient membership functions. The membership function parameters are tuned with the use of methods based on ANNs, as ANFIS is a type of adaptive network that functions as a fuzzy system. The structure of this model is shown in Figure 1 and it is composed of four inputs, hidden layers and one output datum. The nodes of each level were connected to each other through links that indicated the direction of the information of the neural network.
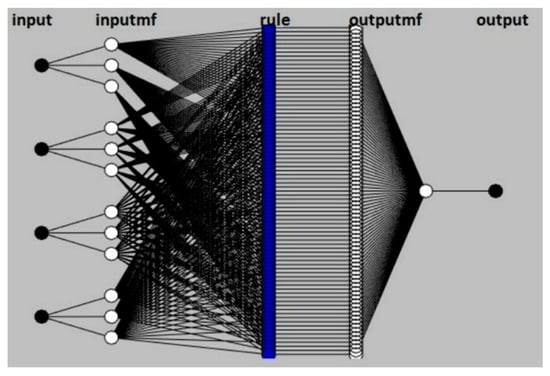
Figure 1.
The structure of the artificial neural network method.
In the first level, membership grades were generated for each input with the following form:
where μAi(x1), μBi(x2), μCi(x3) and μDi(x4) were the trapezoidal membership functions in this study and i = 1,2,3. At each node, the incoming signals were multiplied and this information was sent to the output, using the min or prod operator. The prod method was used in this study with the following form:
where wi is the weight parameter from the ith neuron. In the third layer, the degree of membership function of a rule from each node resulted, using the equation
where ) is the total weights extracted from the previous level. Then, in the fourth layer, each node was defined as
where is the parameter from the previous layer and {} are the consequent parameters for each rule. Thus, every node layer was specified as an adaptive node. In the final layer, all of the inputs were used to calculate the output by using
The ANFIS algorithm used Takagi–Sugeno–Kang rules and the output membership function was a linear function derived from the input values, in contrast to the Mamdani system, where the output of every rule was a fuzzy set.
The adjustment of the weights of each parameter provided minimization of the error level between the observed and predicted values of the output. A hybrid learning algorithm that associates the least squares method and the backpropagation gradient descent method was used in order to train Sugeno-type parameters and calculate input and output membership function parameters.
The model was trained for 20,000 epochs. The predicted and the observed outputs for testing data are presented in Figure 2. The checkpoints coincided with the data, as the error level was extremely low (MAPE = 0.0270%). Thus, the model responded satisfactorily to the observed data.
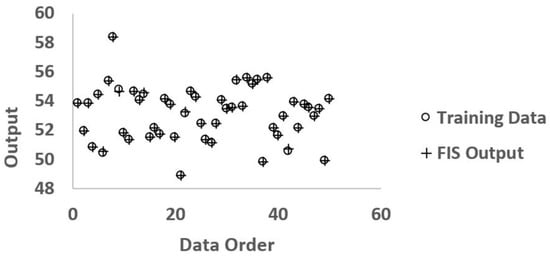
Figure 2.
The testing data of the adaptive neuro-fuzzy modeling (ANFIS) method.
4. Model Application
The estimation of 50 sets of the 28-day compressive strength of cement was analyzed by using two fuzzy methods: fuzzy linear regression and ANFIS. The results of these methods are reported in Table 3 in order to compare the two fuzzy models. According to the results, the fuzzy linear regression and ANFIS methods successfully predicted the compressive strength of cement with small deviations. The data, which were obtained from a previous study [16], had a limited range of values and led to reliable predictions of the observed cement strength just within the aforementioned range. However, the purpose of the model is to apply and control input parameters in more favorable experimental conditions in order to provide the cement compressive strength with higher accuracy.

Table 3.
Comprehensive strength of cement at 28 days as determined by the fuzzy linear regression (FLR) and ANFIS methods across 50 sets.
The values of C3S, SO3, Blaine fineness and alkali are the inputs, strength is the output, FLR (left), FLR (center) and FLR (right) are the values of the fuzzy linear regression in the boundaries and in the center of regression, μA(yi) is the membership grade of the FLR method and ANFIS presents the results obtained from the ANFIS algorithm.
For a better classification, the root mean square error (RMSE) and the mean absolute percentage error (MAPE) were determined for every method and are presented in Table 4, where the values of the ANN and fuzzy model methods were calculated in a previous study [16].

Table 4.
The root mean square error (RMSE) and mean absolute percentage error (MAPE) results of all of the methods.
In Figure 3, the fuzzy linear regression is shown, where the boundaries and the center of the regression, as well as the observed values, are represented.
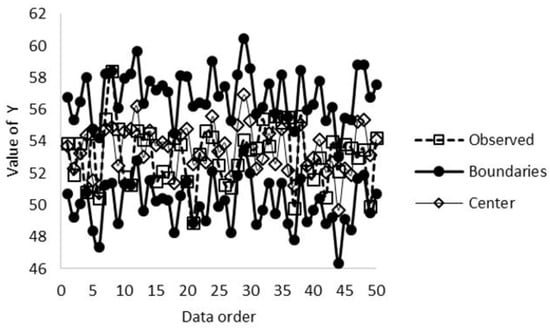
Figure 3.
The values of the fuzzy linear regression method.
As indicated, all methods had satisfactory results, with small deviations from the observed values of strength. Although the fuzzy linear regression method had a higher RMSE factor than the ANN, ANFIS and fuzzy models, it provided a reliable way to estimate the compressive strength of cement. This method uses a specific equation to compute the predicted values in order to define the coefficients on which the input variables depend for obtaining the result. In addition, the FLR method is an effective way to define the degree of fuzziness in order to calculate the effect of independent inputs on the dependent variable and determine the major factor in increasing the compressive strength of cement at 28 days.
However, the ANFIS algorithm provided the most accurate approach to calculating the compressive strength. The value of the mean square error (0.04) was lower compared with that of all of the other methods, which made the results of the ANFIS method quite satisfactory. The MAPE was computed as 0.0270%, which proved that the values of the observed and calculated outputs were very close. Although ANFIS is a black box model, as there is no access to the rules that have been created, the valid combination of verbal rules, as well as the successful choice of membership function, make it a successful fuzzy model.
5. Conclusions
The estimation of the best compressive strength of cement data is not an easy process, as it contains highly complex factors. In this study, fuzzy linear regression and ANFIS methods were developed in order to create more effective fuzzy models to estimate the 28-day compressive strength of cement. In particular, four inputs were applied in order to determine the output, which was the compressive strength of the cement. After comparing these methods with ANN and fuzzy logic models, which were both studied in a previous publication [16], and evaluating the results, we concluded that the ANFIS algorithm provided the most accurate values of the cement’s compressive strength, as the value of the mean square error was extremely low (0.04).
It was also demonstrated that fuzzy linear regression was a more valid method as it provided a standard equation to estimate the output values, although it yielded higher error values than the other fuzzy models. This is in contrast to the black box methods of the ANFIS algorithm and the ANN model, as well as fuzzy logic, which used rules without providing the specific way by which the results come out. Another advantage of the FLR method was the determination of the degree of fuzziness, which specified the consequence of the independent variables for the compressive strength of cement.
In conclusion, all methods led to reliable results with relatively small deviations. Even though the ANFIS algorithm provided the smallest deviations from the observed values, the most valid method for predicting the compressive strength of cement was the fuzzy linear regression method, which gave the most reliable estimation of the cement’s strength by providing a standard equation. This proves its capability of dealing with the perceptual uncertainties that are involved in strength prediction problems and leads to successful predictions of the predicted cement strength values, improving the design and providing a useful modeling tool in the field of engineering.
Author Contributions
The present paper was written by the PhD Candidate F.G. under the supervision of. B.P., Professor at the Democritus University of Thrace, Department of Civil Engineering. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors would like to thank Maria S. Konsta-Gdoutos for her valuable advice and corrections and the referees for their constructive comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- European Committee for Standardization (CEN). Cement Part 1: Composition, specifications and conformity criteria for common cements. Br. Stand. Inst. 2000, BS EN 197-1:2000, 12–15. [Google Scholar]
- Klieger, P.; Lamond, J.F. Significance of Tests and Properties of Concrete and Concrete-Making Materials, 4rd ed.; ASTM International: Philadelphia, PA, USA, 1994; pp. 464–465. [Google Scholar]
- Mohammed, S.; Safiullah, O. Optimization of the SO3 content of an Algerian Portland cement: Study on the effect of various amounts of gypsum on cement properties. Constr. Build. Mater. 2018, 164, 362–370. [Google Scholar] [CrossRef]
- Taylor, H.F.W. Cement Chemistry, 2nd ed.; Thomas Telford: London, UK, 1997; pp. 1–2. [Google Scholar]
- Gliozzi, A.S.; Scalerandi, M.; Anglani, G.; Antonaci, P.; Salini, L. Correlation of elastic and mechanical properties of consolidated granular media during microstructure evolution induced by damage and repair. Phys. Rev. Mater. 2018, 2, 013601. [Google Scholar] [CrossRef]
- Ouarabi, M.A.; Antonaci, P.; Boubenider, F.; Gliozzi, A.S.; Scalerandi, M. Ultrasonic monitoring of the interaction between cement matrix and alkaline silicate solution in self-healing systems. Materials 2017, 10, 46. [Google Scholar] [CrossRef] [PubMed]
- Palmero, P.; Formia, A.; Tulliani, J.M.; Antonaci, P. Valorisation of alumino-silicate stone muds: From wastes to source materials for innovative alkali-activated materials. Cem. Concr. Compos. 2017, 83, 251–262. [Google Scholar] [CrossRef]
- Humad, A.M.; Habermehl-Cwirzen, K.; Cwirzen, A. Effects of Fineness and Chemical Composition of Blast Furnace Slag on Properties of Alkali-Activated Binder. Materials 2019, 12, 3447. [Google Scholar] [CrossRef]
- Cui, Y.; Gao, K.; Zhang, P. Experimental and Statistical Study on Mechanical Characteristics of Geopolymer Concrete. Materials 2020, 13, 1651. [Google Scholar] [CrossRef]
- Sheikh, N.A.; Ching, D.L.C.; Khan, I.; Ahmad, A.; Ammad, S. Concrete Based Jeffrey Nanofluid Containing Zinc Oxide Nanostructures: Application in Cement Industry. Symmetry 2020, 12, 1037. [Google Scholar] [CrossRef]
- Khademi, F.; Akbari, M.; Jamal, S.M.; Nikoo, Μ. Multiple linear regression, artificial neural network, and fuzzy logic prediction of 28 days compressive strength of concrete. Front. Struct. Civ. Eng. 2017, 1, 90–99. [Google Scholar] [CrossRef]
- Ahmad, S.S.S.; Othman, Z.; Kasmin, F.; Borah, S. Modeling of Concrete Strength Prediction using Fuzzy Type-2 Techniques. J. Theor. Appl. Inf. Technol. 2018, 96, 7973–7983. [Google Scholar]
- Behfarnia, Κ.; Khademi, F. A comprehensive study on the concrete compressive strength estimation using artificial neural network and adaptive neuro-fuzzy inference system. Int. J. Optim. Civ. Eng. 2017, 7, 71–80. [Google Scholar]
- Asteris, P.G.; Kolovos, K.G.; Douvika, M.G.; Roinos, K. Prediction of self-compacting concrete strength using artificial neural networks. Eur. J. Environ. Civil Eng. 2016, 20, 102–122. [Google Scholar] [CrossRef]
- Naderpour, H.; Kheyroddin, A.; Godrati-Amiri, G. Prediction of FRP-confined compressive strength of concrete using artificial neural networks. Compos. Struct. 2010, 92, 2817–2829. [Google Scholar] [CrossRef]
- Akkurt, S.; Tayfur, G.; Can, S. Fuzzy logic model for the prediction of cement compressive strength. Cem. Concr. Res. 2004, 34, 1429–1433. [Google Scholar] [CrossRef]
- Akkurt, S.; Ozdemir, S.; Tayfur, G.; Akyol, B. The use of GA-ANNs in the modelling of compressive strength of cement mortar. Cem. Concr. Res. 2003, 33, 973–979. [Google Scholar] [CrossRef]
- Asteris, P.G.; Armaghani, D.J.; Hatzigeorgiou, G.D.; Karayannis, C.G.; Pilakoutas, K. Predicting the shear strength of reinforced concrete beams using Artificial Neural Networks. Comput. Concr. 2019, 24, 469–488. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks A Comprehensive Foundation, 3rd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 2007. [Google Scholar]
- Jantzen, J. Design of Fuzzy Controllers; Technical Report (98-E864); Department of Automation. Technical University of Denmark: Lyngby, Denmark, 1998. [Google Scholar]
- Papadopoulos, B.K.; Sirpi, M.A. Similarities in Fuzzy Regression Models. J. Optim. Theory Appl. 1999, 102, 373–383. [Google Scholar] [CrossRef]
- Tanaka, H.; Uejima, S.; Asai, Κ. Linear Regression Analysis with Fuzzy Model. IEEE Trans. Syst. Man Cybern. 1982, 12, 903–907. [Google Scholar]
- Terano, Τ.; Asai, Κ.; Sugeno, Ν. Fuzzy Systems Theory and Its Applications; Academic Press: London, UK, 1992; pp. 69–80. [Google Scholar]
- Klir, G.; Yuan, B. Fuzzy Sets and Fuzzy Logic: Theory and Applications; Prentice-Hall: Upper Saddle River, NJ, USA, 1995; pp. 454–459. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).