Abstract
A group of Urban Search and Rescue (USAR) Unmanned Ground Vehicles (UGVs) works in the city’s dangerous places that are caused by natural disasters or the decommissioning of nuclear facilities such as the nuclear power plant. Consider the multi sensor platform that the USAR UGV is equipped with, protecting the sensors from the danger that dwells in the working environments is highly related to the success of the USAR mission. The radioactive working environments due to the diffusion of the radioactive materials during the decommissioning of the nuclear facilities are proposed in this work. Radiation shielding boards are used to protect the sensors by installing them on the UGV. Generally, the more shielding boards installed on the UGV, the lower the probability of the sensor malfunctioning. With a large number of UGVs that are used in missions, a large number of shielding boards are needed. Considering the cost of the boards, a conflict between the finite budget and the best protection for the UGV swarm occurs. Due to differences in environments and working times, an asymmetric allocation of shielding boards might protect the UGV swarm better than that by allocating evenly. To minimize the absorption radiation doses, two methods including competitive equilibrium analysis and integer linear programming are proposed. The performances that result from the allocation of the shielding boards by two methods with different budgets are studied.
1. Introduction
Urban Search and Rescue (USAR) is defined as “the strategy, tactics, and operations for locating, providing medical treatment, and extrication of entrapped victims.” [1] The robots, which are adopted by the USAR team, are a group of autonomous mobile robots equipped with sensors [2]. The USAR robots work in the dangerous environments that are caused by natural disasters [1,3] or the decommissioning of the nuclear facilities. Such as floods [4], fires [5], earthquakes [6], nuclear accidents and the decommissioning of the nuclear facilities [7,8,9,10,11,12]. Their duties include monitoring, information sharing, searching and rescuing [13,14].
On March 11, 2011, a massive earthquake and accompanying tsunami hit Japan. The Fukushima Daiichi Nuclear Power Plants sustained extensive damage in this disaster [8]. Three buildings that housed the reactors were seriously damaged. High radiation exposure environments were highly considered to be generated both inside and outside the buildings. Instead of humans, the USAR robots were delivered to the radiation sites for disaster response missions.
In order to study the performance of the USAR robots, test fields that simulate the complex environment in the Fukushima Daiichi Nuclear Power Plants are built in Naraha Center for Remote Control Technology Development, which is used to support the development of remote control technology and operational training [12,15]. Gathering information from the radioactive environments is a concerning topic for the remote operation of the robot [12]. Simultaneous Localization and Mapping (SLAM) is a key technology that enables the robot to build 3D point cloud of components such as buildings, roads and concrete debris in working environment [16,17,18,19,20,21]. The 3D point cloud that indicates the 3D structure of the environment can help the robot navigate itself automatically, avoid obstacles, support robot operators [12]. The optical cameras and the laser range sensors are basic components of the SLAM device. Due to the serious environment, a mockup field was built to study the performance of the SLAM robot [22].
In order to perform coordinated tasks, operate remotely and share information, a communication network in the robot swarm has to be built [9,10,15,23,24]. Communication malfunctions might occur due to damages of communication devices when working in a radioactive environment. The communication malfunction in the robot swarm affects properties of the remaining robots [25], reliability of the robot system [26,27] and the cascade of failures in the robot networks [28].
After the Fukushima Daiichi Nuclear Power Plant accident, the importance of the USAR robots working in the radioactive environments is noticed again [7,8,29,30]. Robot conventional electronic components are vulnerable to radiation. Such as main controllers, motor driver boards, thermal cameras, laser range sensors, Charge-Coupled Device (CCD) image sensors and Complementary Metal-Oxide-Semiconductor (CMOS) image sensors. In which, a difference between CCD and CMOS sensors is the way they capture each frame. A CCD uses what is called a “Global Shutter” while CMOS sensors use a “Rolling Shutter”. Global Shutter means that the entire frame is captured at the exact same time, whereas a CMOS sensor captures light though capturing each pixel one-by-one. Malfunctions on CCD image sensors and laser range sensors in radiation environments are observed [7,8]. Degradations on the functionalities of CMOS image sensors in radioactive environments are analyzed in [23,31,32,33].
Delivery supplies and retrieving dangerous samples such as radioactive debris are feasible works for USAR robots [10,30]. Robot logistics including automated storage and retrieval system [34], which is inside the warehouse, and drone-assisted parcel delivery service, which is outside the warehouse, is of great concern and is a valuable technology for the USAR robot. The generality of the use of robots including vehicles and drones in logistics of dangerous goods is studied in [34,35].
High energy particles in the radioactive environments are the cause of the malfunction of the robot and the sensor. Due to the low mean free path of the charged particle in the air, the neutral particles that consist of photons (X-rays and -rays) and neutrons are the targets which should be shielded. The material with high effective atomic number and high density are used to shield photons. For instance, the alloys containing and [36], the ceramic tiles doped with lead oxide [37] and the borosilicate glasses doped with heavy metal oxides [38] are candidates for the photon shields. Materials containing H, C, , or are used in neutron shielding. For instance, the Epoxy/Clay/ nanocomposite [39], the PE--concrete [40] and the /Al [41,42] are studied.
Shields installed on an Unmanned Ground Vehicle (UGV) would increase the UGV weight and reduce mobility [43]. A robot named RICA robot for radiological characterization in nuclear fields has been developed. The RICA robot with only the stainless shield carried out 20 missions averaging 3 h each from 2012 to 2014. The reason why no shield with specific materials was used in the RICA robot is that the working time of the robot depends on the maximum dose that the weakest component could withstand. The robot has been retrieved before its components malfunction. Thus, a shield with specific materials is not needed. If the shield is used, the working time might decrease due to the increase in the payload. In addition, the working time would be decreased if more shields were installed. Generally, the RICA robot without hardening by shielding is a result of operations research considering that the working time is less than the minimum time the components could tolerate that. Although no specific shield was used when carrying out the 20 missions, the research group [43] considers a robot shield that can be used in more irradiation environments.
Shields not only protect robots from malfunctioning, but also decrease detector noises that arise from the irradiation background [44,45,46]. Lead is used to shield the photomultiplier tube (PMT)) mounted on the UGV that is used to detect the energy and the direction of gamma sources [47]. A tracked-wheel robot that incorporates stair-climbing capability is developed for nuclear power plant operations [48,49]. In this robot, cadmium selenium radiation resistant material shell is used to protect the camera and tungsten/silicone resin shielding strap is used to protect the internal electric components of the body.
Payload changes in different works due to different components that are equipped by the UGV, different missions that the UGV carries out and different budgets for the UGV. To carry tools for emergency stop valve manipulation in a nuclear power plant, a robot that could withstand a 100 kg payload is developed [50]. In response to the needs of the Chernobyl accident, a robot that is able to walk and climb could drag loads of 100 kg horizontally [51]. A robot for intervention, sampling and situation awareness in chemical, biological, radiological and nuclear (CBRN) missions is developed [52]. It is able to carry up to 40 kg of additional payload.
Considering the shield drawbacks including being a payload, increasing UGV weight, reducing mobility and the shield advantages including protecting electric components from damage, decreasing detector noises, operations research problems such as “should shields be used” and “how many shields would be used” are generated.
In this work, we build a digital city filled with radioactive materials which generate radioactive environments. We propose a USAR mission that is located in the digital city, covers a small area of 500 × 500 m and is carried out by a small team of UGVs. There are in total 314 deployment points, which are allocated to 3 deployment zones. Due to a small area covered by the mission, the point that is not located in the area would not be covered by UGVs. The team consists of 6 UGVs. Each UGV is equipped with sensors [12,22,30], such as optical cameras, binoculars, laser range sensors and radiation detectors. Radiation shields are installed on the UGV to protect sensors and UGV itself. Due to the finite budget, we cannot allow every UGV to equip radiation shields as much as possible. We must balance the finite budget and the radioactive damage to all UGVs. Thus, we propose an assumption that the budget to purchase shields for all UGVs is finite and shields cannot satisfy every UGV. Our goal in this work is to find an allocation with which the the UGV swarm could reach a feasible average radiation damage and could survive in the environment. Due to differences in working environments and working times, allocating evenly is not the best method. On the contrary, an asymmetric allocation method might enable the UGV swarm to reach a lower average damage than allocating evenly. Thus, we propose two asymmetric allocation methods, each of which considers assumptions including a finite budget to purchase shielding boards that cannot satisfy every UGV, different radioactive environments that damage the UGVs and different working times of the UGVs.
Allocation of shielding boards is a subdomain of resource allocation. Similar works are studied, such as robot deployment in disaster city [4], the roadside healthcare facility location problem [53], the ambulance redeployment [54], the electric vehicle charging problem [55], the flow control in wireless sensor networks [56,57], the rate control for conmmunication [58], allocation for access channel [59], the charging and rate control in traffic [60]. Methods for the allocation include the mixed integer linear programming [4,53,54], the nonlinear programming and the competitive analysis [59]. Notice that competitive analysis is a method transferred from microeconomics. It belongs to nonlinear programming. Due to the concavity of the utility function, competitive analysis does not ask for numerical methods. Thus, the calculation for the competitive analysis is much quicker than that for other methods. The integer constraint does not fit well with competitive analysis. The integer constraint is that the number of shielding boards is integer. The allocation does not allow a non-integer number, such as 2.6 shielding boards for the UGV. This generates a need for integer linear programming, in which mixed integer linear programming is a subdomain. Although the calculation could last for a much longer time, a better result could be found with integer linear programming. Thus, we propose two allocation methods including competitive analysis and integer linear programming (ILP). In addition to the number of shielding boards, the installation sequence of shielding boards also has impacts on radiation protection. Additionally, the installation sequence affects the weight balance of the UGV. To focus the study on radiation protection, we propose an installation sequence with at most 8 boards and we assume that this is the only one installation sequence that exists in our study.
In this paper, we face the radioactive damage from the electric devices of the UGV, as a serious problem for USAR UGVs that works in the radioactive environments. We propose a radiation protection method that is installing the radiation shielding boards on the UGV. -ray attenuations of shielding boards are simulated in the Monte-Carlo particle simulation toolkit “Geant4”. According to the attenuation, we propose the Radiation Damage Minimization Problem. To solve the problem, we propose two methods, which are competitive equilibrium analysis from the microeconomics theory and integer linear programming. Assumptions that we consider in this work are listed as follows,
- a finite budget to purchase shielding boards that cannot satisfy every UGV;
- different radioactive environments that damage the UGVs;
- different working times of the UGVs;
- only -rays that would be shielded;
- at most 8 shielding boards that each UGV could carry;
- only one installation sequence of the boards that exists in our work;
- a simple diffusion process that radioactivities of the wall and the ground are same;
- the urban area only contains concrete walls and concrete grounds.
Due to the conflict between the finite budget and the best protection for the UGV swarm, we discuss the performance of the two methods. Works are listed below.
- We propose a UGV structure and installation of the shielding board;
- we evaluate the radiation damage on the UGV with different number of the shielding board;
- we propose two methods to minimize the radiation damage for the UGV swarm;
- we discuss the performance of the two methods and compare the malfunction ratios that result from the two methods in different budget.
The UGV structure, the installation of the shielding board, two radioactive environments, the radiation damage and the radiation protection are discussed in Section 2. The allocation methods including the competitive equilibrium analysis and the integer linear programming are proposed in Section 3. The simulation and analysis of the radiation damage to the UGV, the radiation protection of the shielding board and allocation results with the two methods are described in Section 4. Conclusions are drawn in Section 5.
2. Radiation Protection
USAR UGVs are the object that we should protect from radiation. We propose a radiation shielding board that is capable of absorbing radiation. In this study, we propose a shielding board of which the installation is shown in Figure 1. Each shielding board is 500-mm long, 50-mm wide and 3-mm thick. The more shielding boards installed, the lighter the radiation damage would be. Each UGV is able to equip 8 boards at most. Notice that the size of the board is an example to study the problem of shield allocation. Considering the payload of the UGV that is used in different purpose, shielding board should be altered in to a proper size. So dose the material. These also belong to the allocation problem, in which, shielding boards with different sizes and different materials are commodities. Similar methods that use equilibrium analysis or integer linear programming are feasible.

Figure 1.
Installation of the radiation shielding boards on the Unmanned Ground Vehicle (UGV). In this example, 8 shielding boards are installed.
The units are divided into 3 deployment zones. Each deployment zone manages a recharging site which is located at the perimeter of the radioactive environment. As a result of the finite battery capacity of the USAR robot, shift works of UGVs is used to realize sustainable working, such as the 3D reconstruction of the environment, the mapping of the radiation doses and the localization of the radioactive sources. Due to different working times, the radiation doses that UGVs absorb are different. This generates a problem of shielding board allocation to the UGV team. At a finite budget, the number of shielding boards is finite. If the number is not large enough to satisfy every UGV, we must find an allocation to minimize the average radiation damage. Thus, in this work, we study the allocation of shielding boards from both the perspective of a single UGV and the whole UGV team.
2.1. Damage Evaluation for the UGVs
The radiation dose is used to evaluate the radiation damage on the component of the UGV [7,8,29,30]. The studies show that the electric devices are vulnerable to the radiation. For instance, a laser scanner, a CCD camera, an inertial navigation system, a CAN-USB converter, a DC-DC converter, a matin controller, a wireless router and a wireless AP are found malfunctioning in the radiation tests. The absorption doses vary from 50 Gy to 300 Gy. The highest radiation doses could be up to Gy/h [61]. If a UGV is working in this environment, it would malfunction within an hour.
Due to radiation protection methods include redundancy design [62,63] and radiation shielding, a malfunction of an electric device might not disable the UGV. In this work, we focus on radiation shielding. We propose a malfunction dose that might disables the UGV, denoted by = 50 Gy. The parameters used in this work are listed in Table 1.

Table 1.
Table of notations.
Due to the complexity of the four-level dominance hierarchy, we propose a two-element vector to index the USAR UGVs. It is denoted by . The first element is denoted by . It represents the index of the deployment zone that the robot belongs to. The second element is denoted by , in which, is the number of the UGVs in the deployment zone . It represents the index of the UGV in its deployment zone.
The absorption dose of all the electric devices in a UGV is denoted by . Noticing that the unit of dose is that 1 Gy = 1 J/kg, the radiation dose is not a function of mass. In this work, we consider silicon is the only part that is vulnerable to the radiation in the electric devices. Thus, the absorption dose of all electric devices is not the function of the devices’ mass. The absorption dose is a function of the geometrical parameters of the devices. For instance, the size, the orientation and the arrangement of the devices. The effects of these geometrical parameters on the absorption dose are not discussed in this work. Thus, we propose a pure-silicon box representing all devices in a UGV. We study absorption doses of this box in the simulation toolkit Geant4.
2.2. Radiation Protection of UGVs
The radiation shielding board is able to share a small portion of the radiation doses that are affected by the incident particles. This portion is denoted by . The more shielding boards, the lighter the radiation damage. To describe the damage on the UGV, we propose the malfunction ratio, denoted by . It is a function of the absorption dose and the malfunction dose, as shown below,
in which, . The higher the malfunction ratio, the worse the UGV. When the ratio is higher than 1, the UGV malfunctions.
The radiation shielding boards protect the UGV. The number of the boards and the installation of the boards have effects on the absorption dose. In this work, we propose an installation of the shielding boards, as shown in Figure 2.
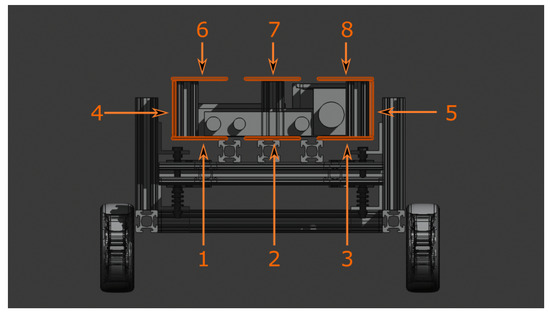
Figure 2.
The installation of the shielding boards. The numbers refer to the sequence during the installation. For instance, the board with number 1 is the first shielding board that should be installed.
Thus, the number of the boards, which is denoted by , is the only parameter that affects the absorption dose, denoted by . We propose that the debris of the reactor fuel are the radioactive sources that disperses into the ground and the buildings. The UGV is irradiated when it passes by the contaminated ground or the buildings.
To study the relation of the absorption dose and the number of the boards, we simulate the irradiation from the radioactive contaminated material to the UGV in Geant4, which is a particle simulation toolkit [38]. Two environments are simulated. The first environment is that the UGV is located on the contaminated ground. The second environment is that the UGV sits beside a contaminated wall while the ground is also contaminated. A schematic view of these environments is shown in Figure 3. Due to a typical enrichment of the nuclear fuel that is used in the reactor is 3%, we propose a radioactive material that contains radioactive isotopes (3%) and .
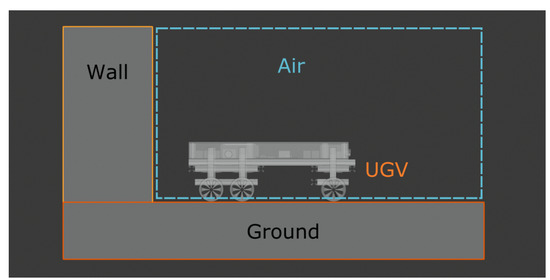
Figure 3.
Schematic view of the irradiation simulation.
2.3. Absorption Doses in Different Working Environments
The absorption dose of the UGV is affected by the working environments. We propose two environments in this work. The ground is radioactive in the first environment. Both the ground and the wall are radioactive in the second environment. The distributions of the absorption dose and the number of the shielding boards are different in two environments.
Each UGV has a specific working area. The environment where the working UGV is depends on the distance from the working area to the nearest building, denoted by . We propose a threshold, denoted by , to decide which environment that the UGV in. The index of the radioactive environment is denoted by .
We use the integer linear programming to allocate the shielding boards to the UGV. In which, the absorption dose is the object that should be minimized. According to the distribution of the absorption dose and the number of the shielding boards, the linear relation is fitted. We denote the linear relation for the UGV individual by,
in which, the parameter refers to the absorption dose when the UGV is not shielded. The parameter is the deceasing ratio of the dose. As a result that is negative, the more shields, the less radiation dose is received.
We simulate the radiation absorption in the Monte-Carlo particle simulation toolkit Geant4. In which, -rays, which belong to photons, are emitted out from the concrete ground in the first environment or a combination of the concrete ground and the concrete wall in the second environment . -rays would react with these concretes and deposit their kinetic energy to the concretes, as is noted radiation attenuation or self absorption if we consider the concrete as a part of the source. After the -ray flying out of the concrete in which it is emitted, it would react with objects in the atmosphere before hitting a UGV. The object includes air and other concrete walls if these walls lie exactly in its way to a UGV. This is an attenuation of the atmosphere. Due to a small cross-section, i.e., probability, of reactions between -ray and air, energy that is deposited by the -ray and is transferred to the air is relatively smaller than that occurring in the concrete. Then, the -ray hits a UGV and deposit its energy to the UGV. If the shielding board lied between the -ray and electric devices, energy of the -ray would be transferred firstly to the shield. Thus, electric devices are protected. In addition, due to reactions such as Compton scattering, the direction of the -ray would be altered after the -ray flying out of the shield. Thus, the -ray deviates from its original way that would hit and damage devices. Due to these processes that are simulated in Geant4, a UGV with two nearby radiation sources generally is more affected than if it is above one. If an electric device is hit by a -ray, reactions between a photon and silicon would be considered in Geant4. After the simulation, we retrieve energy depositions to the device. The energy depositions are used to estimate parameters, such as the absorption doses when the UGV is not shielded and the deceasing ratio .
3. Allocation of the Shielding Boards
3.1. The Competitive Equilibrium Analysis
We use the partial competitive equilibrium analysis in this work. It belongs to the competitive equilibrium analysis. The shielding boards equipped by the UGV are the commodities. Notice that the shielding board of each UGV is regarded as a unique commodity. Thus, the shielding boards in different UGVs belong to different commodities.
The working time and the working environment are the two parameters of the absorption dose. Due to the different delivering distances, the residual battery capacities of the UGVs while they are arriving are different. In order to prevent the UGV from running out of its battery, the longer the delivering distance, the shorter the working time. In the view of the radiation protection, the shorter the working time, the lighter the radiation damage. Thus, the allocation of the shielding boards should tend to the UGV with a long working time.
Two working environments are considered in this work. Due to the additional contaminated wall, the radioactive activity in the second environment is higher. Thus, the UGV working in the second environment would absorb more radiation dose than the UGV working in the first environment. In addition to the activity, an additional absorption dose may be caused by the photons emitted from the wall. This is the result of the Compton scattering of the photon with the shielding board. This phenomenon would be observed in the second environment. Thus, the second environment is more dangerous than the first environment.
To describe the two parameters, we propose the Cobb–Douglas utility function, denoted by,
in which, the parameter t is the index of the UGV. The UGV in 3 deployment zones are included. The parameter is the commodity vector that consists of the number of the shielding boards of all UGVs, denoted by,
The parameter considers the working time and the working environment of the UGV. To keep the constraint on , we introduce the parameter , denoted by,
in which, the parameter refers to the working time.
in which, is the working time of the UGV t through the whole monitoring mission. is the time of the monitoring mission. In this work, the monitoring mission lasts for 6 h. The parameter represents the working environment.
Thus, the parameter is denoted by,
The allocation of the shielding boards maximizes the utility function that we propose. The utility maximization problem (UMP) is as follows.
in which, the parameter p is the price of the shielding board. The parameter W is the budget of the expenditure on the shielding boards for all UGVs.
If is a solution to the UMP, then there exists a Lagrange multiplier such that,
in which, is the price vector of the boards, denoted by . The number of the elements in the price vector is . denotes the gradien vector of at ,
The allocation of the shielding boards is denoeted by,
3.2. The Integer Linear Programming
We propose the integer linear programming for the shielding board allocation. The object is minimizing the total absorption dose that is the sum of the doses of all UGVs. We refer to the minimization problem as the Radiation Damage Minimization Problem, which is shown below.
In the Radiation Damage Minimization Problem, the first constraint specifies the available number of shielding boards on the UGV. Each UGV is allowed to equip 8 shielding boards at most, denoted by . The UGV is also allowed to work without shielding, denoted by . In addition to the minimum and the maximum of the number of the shielding boards, the number must be an integer. The shielding board is a product of the manufacture. If the board were cut into pieces, the properties such as the radiation attenuation would change. The function of the absorption dose would be invalid. In the view of the mechanical property, the shielding board with specific compounds is too hard. It can only be cut with specific tools, of which the preparing are not feasible in the safe zone. Thus, we do not want to cut any shielding board. The second constraint specifies the limitation for the budget. If the budget were not limited, the allocation would be easy. As a result, we would equip every UGV with 8 shielding boards.
The parameter is not a function of the number of the shielding boards , therefore the Radiation Damage Minimization Problem is equivalently defined as follows.
in which, is the price vector, denoted by . is the vector of the decreasing ratio , denoted by,
4. Simulation and Analysis
4.1. Simulation of Radiation Damages and Shielding
Recall that we simulate radiation shielding for the UGV in two environments. In the first environment, only the ground exists. The ground is made of concrete. We propose that the ground is contaminated by the radioactive isotopes and . The enrichment of is 3%. Distributions of the gamma radiation of the two isotopes are shown in Figure 4. The distribution of the gamma radiation from the mixture of the both isotopes is also shown in the figure. In the second environment, there exist the ground and the wall. Both of them are made of concrete and both of them are contaminated. The enrichment is also 3%. Due to the real diffusion process of the radioactive material is complex and random, we assume a simple diffusion process that the radioactivity of the wall and the ground are the same.
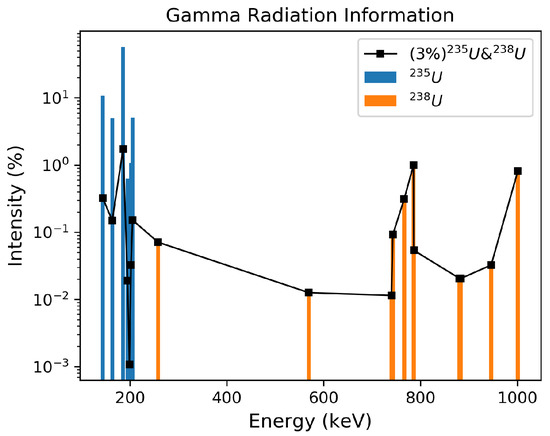
Figure 4.
Distributions of the gamma radiation of , and their mixture.
Relations between the absorption dose and the number of the shielding boards are shown in Figure 5. In the first environment, only the ground is contaminated. It means that the ground is the only radiation source that emits photons. Shielding boards that are located between the electric devices and the ground are the first 3 boards in the installation method that we propose. Thus, an obvious decreasing of the absorption dose is shown when the number of shielding boards increase from 1 to 3. In addition to the first 3 boards, the shielding boards are not located in the path of the radiation that is going to hit the electric devices. Generally they are useless. Thus, the absorption doses just vibrate in a small range, when the number of the installed boards increase from 4 to 8. A fitting result is shown in Figure 5. Decreasing ratio is −3.6 Gy.
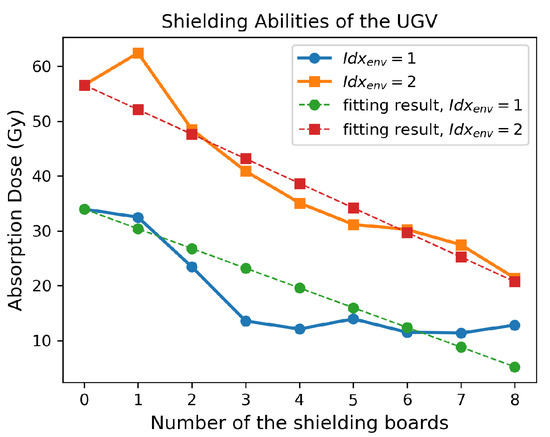
Figure 5.
Shielding abilities in two environments.
In the second environment, both the ground and the wall are contaminated. An anomaly occurs when the first shielding board is installed. The absorption dose of the devices is larger than the dose with no shielding board installed. The cause of the anomaly is the scattered photon. Due to the Compton scattering, the incident photon that is emitted from the wall reacts with the first shielding board that is located under the electric device. The reaction is the Compton scattering. The scattered photon, which is one of the products of the reaction, is emitted out of the board and flies toward the electric device. After the photon gets into the device, it would transfer its energy to the device. Thus, the absorption dose increases. A fitting result is also shown in Figure 5. Decreasing ratio is −4.5 Gy.
The absorption dose rates are 5.7 Gy/h in the first environment and 9.4 Gy/h in the second environment. Recall that the malfunction dose is 50 Gy. If the UGV was not shielded, it would keep working for about 9 h in the first environment until it is disabled. The UGV would keep working for about 5 h in the second environment. The monitoring work that is proposed in this work lasts for 6 h. The total working time of each UGV in this work is less than 5 h in both environments. The distributions of the working time of the UGV in three deployment zones are shown in Figure 6. The mean working times of the UGVs are h in , h in and h in . If the UGVs work in the first environment, the averaged absorption doses would be 10.7 Gy in , 10.6 Gy in and 11.1 Gy in . The malfunction ratio would be 21% in , 21% in and 22% in . The radiation damages on the UGVs in the second working environment are listed in Table 2.
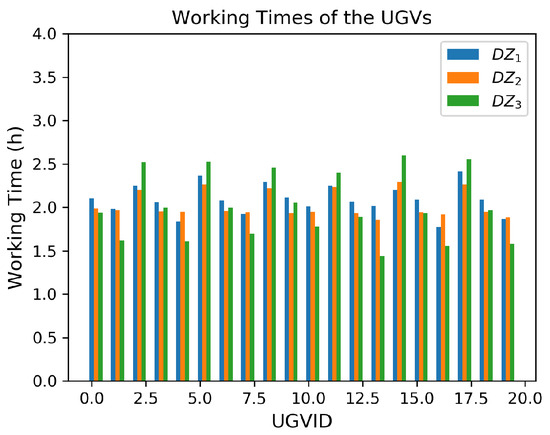
Figure 6.
Distributions of the working time of the UGV in 3 deployment zones. Working times of the first 20 UGVs in each zone are shown.

Table 2.
Averaged damages on the UGVs without shielding.
4.2. Radiation Damages on the UGV without Shielding
In this work, we propose two working environments where the UGV works. The working environment of a UGV depends on the distance from the UGV to the nearest wall. Considering that the UGV works in the urban area where concrete walls and concrete grounds are dominant components in urban areas, we make an assumption that the urban area only contains concrete walls and concrete grounds. This assumption avoids discussion about radioactive effects on other components such as trees, soils and lakes. Based on this assumption, we provide a simple structure of urban areas. A map of the buildings and the UGVs from 3 deployment zones is shown in Figure 7.
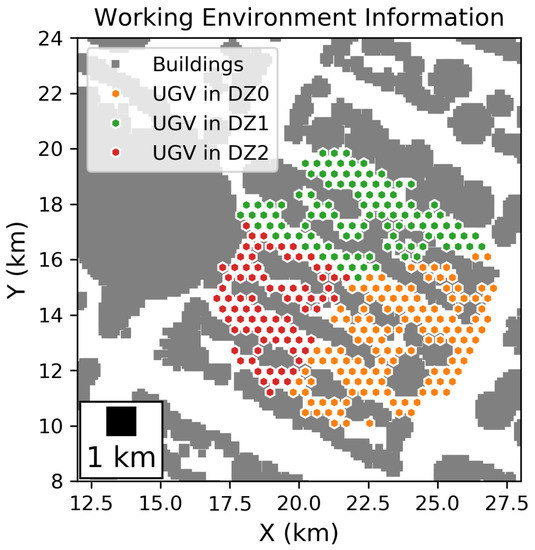
Figure 7.
The map of the buildings and the UGVs from 3 deployment zones.
By setting the threshold of the distance = 200 m, working environments in the whole digital city are shown in Figure 8. 208 deployment points are in the first environment and 106 deployment points are in the second environment. If all deployment points were covered, we would use 1032 UGVs. In which, 678 UGVs work in the first environment and 354 UGVs work in the second environments. Numbers of the UGVs that work in different environments are listed in Table 3. Recall that the USAR mission just covers a small area of 500 × 500 m and is carried out by a team of 6 UGVs. Only the mean value and the standard deviation in Table 3 are used.
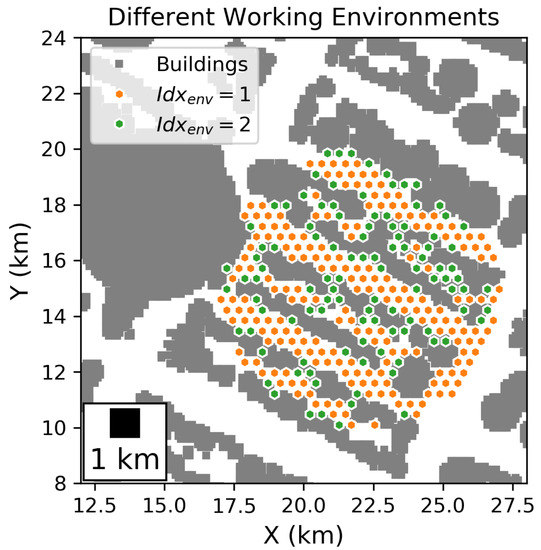
Figure 8.
Schematic view of the working environment. Each dot represents a deployment point. Different colors refer to different working environments. An orange dot refers to the first working environment . A blue dot refers to the second working environment .

Table 3.
The UGVs working in different environments.
Considering the absorption dose rates, the working times and the malfunction dose , distributions of the malfunction ratio for the UGV without shielding are shown in Figure 9. In the circumstances of no shielding, all UGVs function well when finishing the 6-h monitoring work, because all the malfunction ratios are less than 100%. Most of the malfunction ratio lies in the range of . Specifically, the average malfunction ratios, denoted by , are 25.5% ± 7.9% in , 26.5% ± 8.3% in and 27.0% ± 8.5% in .
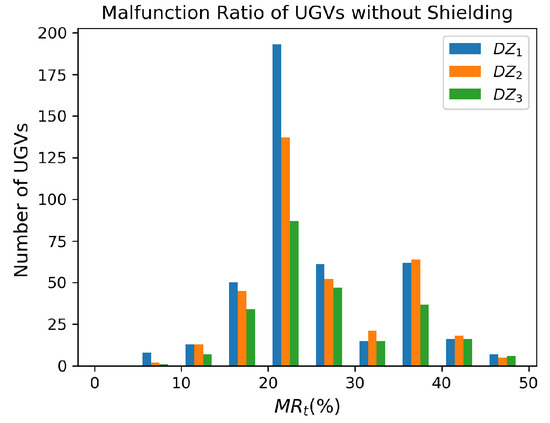
Figure 9.
The malfunction ratio of the UGVs without shielding.
Notice that the absorption dose for the UGV with only 1 shielding board decreases slightly than that without shielding in the first environment. Even worse, the dose increases in the second environment. We evaluate the malfunction ratio for the UGV that is equipped with only one shielding board. The evaluation results, which are listed in Table 3, show that the average malfunction ratio for the UGV with only one shielding board is larger than that without shielding board. We conclude that the UGV equipped with only 1 shielding board is useless or harmful to the UGV itself. Thus, we remove the installation of only one shielding board from the candidates of the shielding board installation.
4.3. Allocation of the Shielding Board
Before the allocating, we determine the parameters including , , and . The parameter is the absorption dose when the UGV is not shielded. According to the absorption doses that are simulated in this work, as shown in Figure 5, the absorption dose of the UGV without shielding is 34.0 Gy and is 56.6 Gy. Fitting results shows that the decreasing ratio is −3.6 Gy and is −4.5 Gy. A distribution of the is shown in Figure 6. A schematic view of the working environment is shown in Figure 8. In which, each dot represents a deployment point. Different color refer to different working environment. We suppose that the price of each shielding board p is 100.
Two allocation methods are proposed in this work. They behave quite differently in shielding board allocation. We take an example of shielding board allocation to 6 UGVs. The allocations of the shielding board under different budgets are shown in Figure 10. With the partial competitive equilibrium analysis, which is the first method in this paper, the ratio of the number of the shielding boards between the UGVs is fixed, denoted by . The integer linear programming method considers the UGV as the most vulnerable UGV in the field, the shielding boards are allocated to the UGV since the budget is 600. It is the only UGV to which the equipment of the shielding boards is completed.
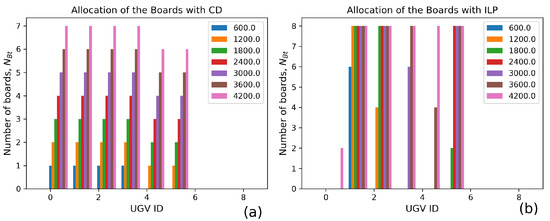
Figure 10.
Allocation of the shielding boards. The swarm consists of 6 UGVs. Figure (a) represents the allocation with the competitive equilibrium analysis. The term “CD” refers to the Cobb–Douglas function. Figure (b) represents the allocation with the integer linear programming method (ILP).
Recall that the equipping of only one shielding board just negligibly decrease the absorption dose of the UGV in the first environment, or even worse, it increases the dose in the second environment. We eliminate the installation of only 1 shielding board from the candidate set of the shielding board installation. Due to the eliminating of the installation candidate, the allocation methods need to be adjusted. The allocations are shown in Figure 11.
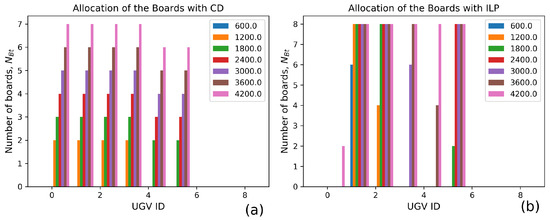
Figure 11.
Allocation of the shielding boards. The situation allocating only 1 shielding board to the UGV is eliminated. The swarm consists of 6 UGVs. Figure (a) represents the allocation with the competitive equilibrium analysis. The term CD refers to the Cobb–Douglas function. Figure (b) represents the allocation with the integer linear programming method (ILP).
The malfunction ratios are shown in Figure 12. The absorption dose for the UGV decreasing significantly along the increasing of the budget. Due to the fixed ratio of the number of the shielding boards between the UGVs, this phenomenon could be easily recognized from the result of the competitive equilibrium analysis.
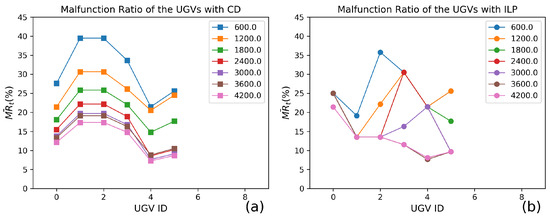
Figure 12.
Distributions of the malfunction ratio of each UGV. The situation allocating only 1 shielding board to the UGV is eliminated. The swarm consists of 6 UGVs. Figure (a) represents the allocation with the competitive equilibrium analysis. The term CD refers to the Cobb–Douglas function. Figure (b) represents the allocation with the integer linear programming method (ILP).
The result of the integer linear programming shows that the UGVs are protected better at the lower budget than the shielding allocation with the competitive equilibrium analysis. Specifically, the average malfunction ratios at the smallest budget are 31.2% ± 6.9% with the competitive equilibrium analysis and 26.2% ± 5.5% with the integer linear programming. The effects of the radiation protection are inverted at the largest budget. The average malfunction ratios at the smallest budget are 12.9% ± 3.9% with the competitive equilibrium analysis and 13.0% ± 4.3% with the integer linear programming.
Distributions of the average malfunction ratio are shown in Figure 13. Horizontal axis represents an average budget on each robot. Consider the UGV team, total budget ranges from 600 to 4200 and the average budget ranges from 100 to 700. Specifically, the budget is studied. Each wealth lies in a budget interval, of which the upper limit satisfies that each UGV could be equipped with a same number of the shielding board. Recall that the total number of the UGVs is 6. The upper limit that every UGV is equipped with l boards is . The budget interval is denoted by . The set of the budget interval is denoted by .
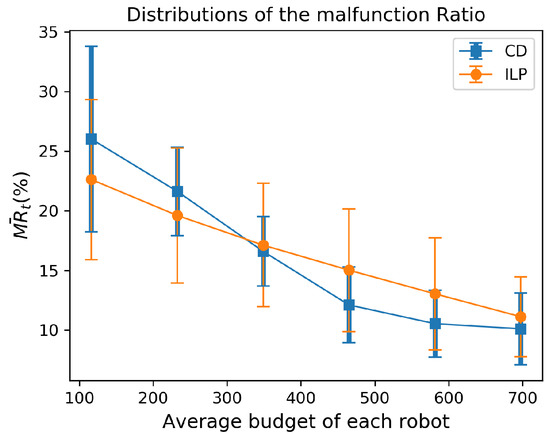
Figure 13.
Distributions of the average malfunction ratio. Horizontal axis represents an average budget on each robot. The error bar refers to the standard deviation of the malfunction ratio. The situation allocating only 1 shielding board to the UGV is eliminated. The team consists of 6 UGVs. The term CD refers to the competitive equilibrium analysis and the term ILP refers to the integer linear programming.
Allocation results, as shown in Figure 13, indicate that the allocation of the shielding boards with the competitive equilibrium analysis has a better performance in radiation protection than that with the integer linear programming when the average budget is larger than 350. In addition to expectations of the ratio, the maximum malfunction ratio that results from the competitive equilibrium analysis is also lower. For instance, the maximum malfunction ratio that results from the competitive equilibrium analysis is 18.6% for the average budget of 580, while the maximum malfunction ratio that results from the integer linear programming is 29.5%. On the contrary, the result with the integer linear programming is better when the average budget is no more than 350. This phenomenon indicates that the average malfunction ratios resulting from competitive equilibrium analysis converge faster than that resulting from integer linear programming.
5. Conclusions
In this work, we face radioactive damage to the electric devices in the UGV. This is a serious problem for the Urban Search and Rescue robot that works in a radioactive environment. For instance, the UGVs that work for the decommissioning of the nuclear power plant suffer from radioactive damage. We study radiation protection methods by installing radiation shielding boards on USAR UGVs. Considering the cost of the shielding board, a conflict between the finite budget and the best protection for a UGV swarm occurs. This is a problem of operations research. To allocate the shielding boards, we propose the Radiation Damage Minimization Problem. To solve the problem, we propose two methods, which are competitive equilibrium analysis from microeconomics theory and integer linear programming. The finite budget is considered by the constraint of both methods.
To evaluate the radioactive damage, we simulate the -ray attenuation in the Monte-Carlo particle simulation toolkit Geant4. Two radioactive environments are considered. One simulates field work with the ground which is radioactive contaminated. The other one simulates field work with contaminated ground and contaminated walls. We propose that each UGV could be equipped with 8 shielding boards. There are 6 UGVs to be protected in our work.
Results of the shielding board allocation indicate that the competitive equilibrium analysis shows better performances when the budget is larger than 350, and the integer linear programming is better when the budget is no more than 350. The performance consists of the average malfunction ratio and the maximum malfunction ratio of the UGV swarm. In addition to the performance, we find that the average malfunction ratios resulting from the competitive equilibrium analysis converge faster than that resulting from the integer linear programming.
A future research direction is inter-temporal resource allocation. Consider the fact that a UGV does not need radiation protection while it is recharging in a recharge site where there is no threat of radiation damage. A smaller number of shielding boards would satisfy UGVs, if the shielding board on the recharging UGV is retrieved and reallocated to the UGV which is going to work. This allocation concerning times is denoted by inter-temporal resource allocation. We would need an inventory to retrieve, store and reallocate shielding boards. When the inventory is considered, it is feasible to study the depreciation of the boards. Thus, we are going to study how many shielding boards would be saved, how much budget would be saved and what the depreciation would be, if we were using inter-temporal resource allocation.
Author Contributions
Conceptualization Y.Z. (Yuxian Zhang) and Y.Z. (Yingjie Zhao); formal analysis Y.Z. (Yingjie Zhao) and Z.X.; software Y.Z. (Yingjie Zhao) and Z.X.; writing—original draft preparation Y.Z. (Yingjie Zhao); writing—review and editing, Z.X. and Y.Z. (Yuxian Zhang); supervision Y.Z. (Yuxian Zhang). All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
This work has supported by the research project funded by the Zhejiang Province Basic Public Welfare Research Program (LGG18E050003) and 2019 college students in Zhejiang Province Science and technology innovation activity plan and” Xinmiao Talents Program” project (2019R475001).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Messina, E. Performance standards for urban search and rescue robots. In Proceedings of the Defense and Security Symposium, 2006, Orlando, FL, USA, 17–21 April 2006; Proc. SPIE: Bellingham, WA, USA, 2006; Volume 6230, p. 62301V. [Google Scholar] [CrossRef]
- Liu, Y.; Nejat, G. Robotic Urban Search and Rescue: A Survey from the Control Perspective. J. Intell. Robot. Syst. 2013, 72, 147–165. [Google Scholar] [CrossRef]
- Sugiyama, H.; Tsujioka, T.; Murata, M. Real-time exploration of a multi-robot rescue system in disaster areas. Adv. Robot. 2013, 27. [Google Scholar] [CrossRef]
- Malandrino, F.; Chiasserini, C.F.; Casetti, C.; Chiaraviglio, L.; Senacheribbe, A. Planning UAV Activities for Efficient User Coverage in Disaster Areas. Ad Hoc Networks 2018, 89. [Google Scholar] [CrossRef]
- Innocente, M.; Grasso, P. Self-organising swarms of firefighting drones: Harnessing the power of collective intelligence in decentralised multi-robot systems. J. Comput. Sci. 2019, 34, 80–101. [Google Scholar] [CrossRef]
- Mavroulis, S.; Emmanuel, A.; Spyrou, N.I.; Antoniou, V.; Skourtsos, E.; Papadimitriou, P.; Kassaras, I.; Kaviris, G.; Tselentis, A.; Voulgaris, N.; et al. UAV and GIS based rapid earthquake-induced building damage assessment and methodology for EMS-98 isoseismal map drawing: The June 12, 2017 Mw 6.3 Lesvos (Northeastern Aegean, Greece) earthquake. Int. J. Disaster Risk Reduct. 2019, 37, 101169. [Google Scholar] [CrossRef]
- Igarashi, H.; Kon, K.; Matsuno, F. Evaluation of sensors for mobile robots based on irradiation experiment. In Proceedings of the 2012 IEEE/SICE International Symposium on System Integration (SII), Fukuoka, Japan, 16–18 December 2012; pp. 517–522. [Google Scholar]
- Nagatani, K.; Kiribayashi, S.; Okada, Y.; Otake, K.; Yoshida, K.; Tadokoro, S.; Nishimura, T.; Yoshida, T.; Koyanagi, E.; Fukushima, M.; et al. Emergency response to the nuclear accident at the Fukushima Daiichi Nuclear Power Plants using mobile rescue robots. J. Field Robot. 2013, 30, 44–63. [Google Scholar] [CrossRef]
- Sanada, Y.; Orita, T.; Torii, T. Temporal variation of dose rate distribution around the Fukushima Daiichi nuclear power station using unmanned helicopter. Appl. Radiat. Isot. 2016, 118. [Google Scholar] [CrossRef] [PubMed]
- Takemori, T.; Miyake, M.; Hirai, T.; Wang, X.; Fukao, Y.; Adachi, M.; Yamaguchi, K.; Tanishige, S.; Nomura, Y.; Matsuno, F.; et al. Development of the multifunctional rescue robot FUHGA2 and evaluation at the world robot summit 2018. Adv. Robot. 2020, 34, 119–131. [Google Scholar] [CrossRef]
- Lee, C.; Kim, H.R. Optimizing UAV-based radiation sensor systems for aerial surveys. J. Environ. Radioact. 2019, 204, 76–85. [Google Scholar] [CrossRef]
- Kawabata, K. Toward technological contributions to remote operations in the decommissioning of the Fukushima Daiichi Nuclear Power Station. Jpn. J. Appl. Phys. 2020, 59, 050501. [Google Scholar] [CrossRef]
- Erdelj, M.; Król, M.; Natalizio, E. Wireless Sensor Networks and Multi-UAV Systems for Natural Disaster Management. Comput. Networks 2017, 124. [Google Scholar] [CrossRef]
- Erdelj, M.; Natalizio, E.; Chowdhury, K.; Akyildiz, I. Help from the Sky: Leveraging UAVs for Disaster Management. IEEE Pervasive Comput. 2017, 16, 24–32. [Google Scholar] [CrossRef]
- Kawabata, K.; Yamada, T.; Shirasaki, N.; Ishiyama, H. Designing Test Methods for Running Capabilities of Ground Robots for Nuclear Disaster Response *. In Proceedings of the 2019 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Hong Kong, China, 8–12 July 2019; pp. 559–564. [Google Scholar] [CrossRef]
- Bresson, G.; Alsayed, Z.; Yu, L.; Glaser, S. Simultaneous Localization and Mapping: A Survey of Current Trends in Autonomous Driving. IEEE Trans. Intell. Veh. 2017, 2, 194–220. [Google Scholar] [CrossRef]
- Vidal, A.R.; Rebecq, H.; Horstschaefer, T.; Scaramuzza, D. Ultimate SLAM? Combining Events, Images, and IMU for Robust Visual SLAM in HDR and High-Speed Scenarios. IEEE Robot. Autom. Lett. 2018, 3, 994–1001. [Google Scholar] [CrossRef]
- Pierzchała, M.; Giguère, P.; Astrup, R. Mapping forests using an unmanned ground vehicle with 3D LiDAR and graph-SLAM. Comput. Electron. Agric. 2018, 145, 217–225. [Google Scholar] [CrossRef]
- Deschaud, J. IMLS-SLAM: Scan-to-Model Matching Based on 3D Data. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 2480–2485. [Google Scholar]
- Ye, X.; Ji, X.; Sun, B.; Chen, S.; Wang, Z.; Li, H. DRM-SLAM: Towards dense reconstruction of monocular SLAM with scene depth fusion. Neurocomputing 2020, 396, 76–91. [Google Scholar] [CrossRef]
- Ji, S.; Qin, Z.; Shan, J.; Lu, M. Panoramic SLAM from a multiple fisheye camera rig. ISPRS J. Photogramm. Remote. Sens. 2020, 159, 169–183. [Google Scholar] [CrossRef]
- Yamada, T.; Kawabata, K. Development of a Dataset to Evaluate SLAM for Fukushima Daiichi Nuclear Power Plant Decommissioning. In Proceedings of the 2020 IEEE/SICE International Symposium on System Integration (SII), Honolulu, HI, USA, 12–15 January 2020; pp. 7–11. [Google Scholar]
- Goiffon, V.; Rolando, S.; Corbiere, F.; Rizzolo, S.; Chabane, A.; Girard, S.; Baer, J.; Estribeau, M.; Magnan, P.; Paillet, P.; et al. Radiation Hardening of Digital Color CMOS Camera-on-a-Chip Building Blocks for Multi-MGy Total Ionizing Dose Environments. IEEE Trans. Nucl. Sci. 2016, 64, 45–53. [Google Scholar] [CrossRef]
- Kantaros, Y.; Zavlanos, M.M. Distributed Intermittent Connectivity Control of Mobile Robot Networks. IEEE Trans. Autom. Control 2017, 62, 3109–3121. [Google Scholar] [CrossRef]
- Crucitti, P.; Latora, V.; Marchiori, M.; Rapisarda, A. Error and attack tolerance of complex networks. Phys. A Stat. Mech. Its Appl. 2004, 340, 388–394. [Google Scholar] [CrossRef]
- Heidari Kapourchali, M.; Sepehry, M.; Aravinthan, V. Fault Detector and Switch Placement in Cyber-Enabled Power Distribution Network. IEEE Trans. Smart Grid 2018, 9, 980–992. [Google Scholar] [CrossRef]
- Duan, Y.; Li, W.; Fu, X.; Luo, Y.; Yang, L. A methodology for reliability of WSN based on software defined network in adaptive industrial environment. IEEE/CAA J. Autom. Sin. 2018, 5, 74–82. [Google Scholar] [CrossRef]
- Buldyrev, S.V.; Parshani, R.; Paul, G.; Stanley, H.E.; Havlin, S. Catastrophic cascade of failures in interdependent networks. Nature 2010, 464, 1025–1028. [Google Scholar] [CrossRef]
- Nagatani, K.; Kiribayashi, S.; Okada, Y.; Otake, K.; Yoshida, K.; Tadokoro, S.; Nishimura, T.; Yoshida, T.; Koyanagi, E.; Fukushima, M.; et al. Gamma-ray irradiation test of electric components of rescue mobile robot Quince. In Proceedings of the 2011 IEEE International Symposium on Safety, Security, and Rescue Robotics, Kyoto, Japan, 1–5 November 2011; pp. 56–60. [Google Scholar]
- Pu, H.; Yu, B.; Luo, J.; Yang, Y.; Sun, Y.; Xie, S. Irradiation test of the control system of a tracked robot for nuclear disaster response. In Proceedings of the IECON 2017-43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 5843–5848. [Google Scholar]
- Goiffon, V.; Estribeau, M.; Cervantes, P.; Molina, R.; Gaillardin, M.; Magnan, P. Influence of Transfer Gate Design and Bias on the Radiation Hardness of Pinned Photodiode CMOS Image Sensors. IEEE Trans. Nucl. Sci. 2014, 61, 3290–3301. [Google Scholar] [CrossRef]
- Wang, Z.; Xue, Y.; Chen, W.; He, B.; Yao, Z.; Ma, W.; Sheng, J. Fixed Pattern Noise and Temporal Noise Degradation Induced by Radiation Effects in Pinned Photodiode CMOS Image Sensors. IEEE Trans. Nucl. Sci. 2018, 65, 1264–1270. [Google Scholar] [CrossRef]
- Ciarpi, G.; Magazzù, G.; Palla, F.; Saponara, S. Design, Implementation, and Experimental Verification of 5 Gbps, 800 Mrad TID and SEU-Tolerant Optical Modulators Drivers. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 829–838. [Google Scholar] [CrossRef]
- Baniasadi, P.; Foumani, M.; Smith-Miles, K.; Ejov, V. A transformation technique for the clustered generalized traveling salesman problem with applications to logistics. Eur. J. Oper. Res. 2020, 285, 444–457. [Google Scholar] [CrossRef]
- Foumani, M.; Moeini, A.; Haythorpe, M.; Smith-Miles, K. A cross-entropy method for optimising robotic automated storage and retrieval systems. Int. J. Prod. Res. 2018, 56, 6450–6472. [Google Scholar] [CrossRef]
- Singh, J.; Singh, H.; Sharma, J.; Singh, T.; Singh, P.S. Fusible alloys: A potential candidate for gamma rays shield design. Prog. Nucl. Energy 2018, 106, 387–395. [Google Scholar] [CrossRef]
- Mahmoud, M.E.; El-Khatib, A.M.; Halbas, A.M.; El-Sharkawy, R.M. Investigation of physical, mechanical and gamma-ray shielding properties using ceramic tiles incorporated with powdered lead oxide. Ceram. Int. 2020, 46, 15686–15694. [Google Scholar] [CrossRef]
- Al-Hadeethi, Y.; Sayyed, M. Analysis of borosilicate glasses doped with heavy metal oxides for gamma radiation shielding application using Geant4 simulation code. Ceram. Int. 2019, 45, 24858–24864. [Google Scholar] [CrossRef]
- Kiani, M.A.; Ahmadi, S.J.; Outokesh, M.; Adeli, R.; Mohammadi, A. Preparation and characteristics of epoxy/clay/B4C nanocomposite at high concentration of boron carbide for neutron shielding application. Radiat. Phys. Chem. 2017, 141, 223–228. [Google Scholar] [CrossRef]
- Dian, E.; Klinkby, E.; Cooper-Jensen, C.; Párkányi, D.; Hajdú, D.; Osan, J.; Patriskov, G.; Filges, U.; Bentley, P. Preparation for activation measurements of concrete and PE-B4C-concrete to be applied for shielding at the European Spallation Source. J. Physics: Conf. Ser. 2018, 1021, 012050. [Google Scholar] [CrossRef]
- Xu, Z.; Jiang, L.; Zhang, Q.; Qiao, J.; Gong, D.; Wu, G. The design of a novel neutron shielding B4C/Al composite containing Gd. Mater. Des. 2016, 111. [Google Scholar] [CrossRef]
- Pang, X.; Xian, Y.; Wang, W.; Zhang, P. Tensile properties and strengthening effects of 6061Al/12 wtcomposites reinforced with nano-Al2O3 particles. J. Alloy. Compd. 2018, 768, 476–484. [Google Scholar] [CrossRef]
- Ducros, C.; Hauser, G.; Mahjoubi, N.; Girones, P.; Boisset, L.; Sorin, A.; Jonquet, E.; Falciola, J.M.; Benhamou, A. RICA: A Tracked Robot for Sampling and Radiological Characterization in the Nuclear Field. J. Field Robot. 2017, 34, 583–599. [Google Scholar] [CrossRef]
- Taniguchi, R.; Sasaki, R.; Okuda, S.; Okamoto, K.I.; Ogawa, Y.; Tsujimoto, T. Noise characteristics of neutron images obtained by cooled CCD device. Nucl. Instruments Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2009, 605, 85–90. [Google Scholar] [CrossRef]
- Wang, Z.; Xue, Y.; Zhang, F.; Bian, J.; Ma, W.; Yao, Z.; He, B.; Sheng, J.; Dong, G. Radiation damage evaluation of the CCD detector induced by high energy protons. Nucl. Instruments Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2019, 924, 219–224. [Google Scholar] [CrossRef]
- Zhao, C.; Yan, Y.; Li, H.; Zhang, T.; Qiao, S. An effective gamma white spots removal method for CCD-based neutron images denoising. Fusion Eng. Des. 2020, 150, 111375. [Google Scholar] [CrossRef]
- Miller, A.; Machrafi, R.; Mohany, A. Development of a semi-autonomous directional and spectroscopic radiation detection mobile platform. Radiat. Meas. 2015, 72, 53–59. [Google Scholar] [CrossRef]
- Dong, P.; Wang, X.; Xing, H.; Liu, Y.; Zhang, M. Design and control of a tracked robot for search and rescue in nuclear power plant. In Proceedings of the 2016 International Conference on Advanced Robotics and Mechatronics (ICARM), Macau, China, 18–20 August 2016; pp. 330–335. [Google Scholar]
- Tsitsimpelis, I.; Taylor, C.J.; Lennox, B.; Joyce, M.J. A review of ground-based robotic systems for the characterization of nuclear environments. Prog. Nucl. Energy 2019, 111, 109–124. [Google Scholar] [CrossRef]
- Kim, S.; Jung, S.H.; Lee, S.U.; Kim, C.H.; Shin, H.C.; Seo, Y.C.; Lee, N.H.; Jung, K.M. Application of robotics for the nuclear power plants in Korea. In Proceedings of the 2010 1st International Conference on Applied Robotics for the Power Industry, Montreal, QC, Canada, 5–7 October 2010; pp. 1–5. [Google Scholar]
- Galt, S.; Luk, B.L.; Cooke, D.S.; Collie, A.A. A tele-operated semi-intelligent climbing robot for nuclear applications. In Proceedings of the Proceedings Fourth Annual Conference on Mechatronics and Machine Vision in Practice, Toowoomba, Queensland, Australia, 23–25 September 1997; pp. 118–123. [Google Scholar]
- Guzman, R.; Navarro, R.; Ferre, J.; Moreno, M. RESCUER: Development of a Modular Chemical, Biological, Radiological, and Nuclear Robot for Intervention, Sampling, and Situation Awareness*. J. Field Robot. 2016, 33, 931–945. [Google Scholar] [CrossRef]
- De Vries, H.; van de Klundert, J.; Wagelmans, A.P. The Roadside Healthcare Facility Location Problem A Managerial Network Design Challenge. Prod. Oper. Manag. 2020, 29, 1165–1187. [Google Scholar] [CrossRef]
- Maxwell, M.; Ni, E.; Tong, C.; Henderson, S.; Topaloglu, H.; Hunter, S. A Bound on the Performance of an Optimal Ambulance Redeployment Policy. Oper. Res. 2014, 62, 1014–1027. [Google Scholar] [CrossRef]
- Valogianni, K.; Ketter, W.; Collins, J.; Zhdanov, D. Sustainable Electric Vehicle Charging using Adaptive Pricing. Prod. Oper. Manag. 2020, 29, 1550–1572. [Google Scholar] [CrossRef]
- Chen, J.; He, S.; Sun, Y.; Thulasiraman, P.; Shen, X. Optimal Flow Control for Utility-Lifetime Tradeoff in Wireless Sensor Networks. Comput. Netw. 2009, 53, 3031–3041. [Google Scholar] [CrossRef]
- Chen, J.; Xu, W.; He, S.; Sun, Y.; Thulasiraman, P.; Shen, X. Utility-Based Asynchronous Flow Control Algorithm for Wireless Sensor Networks. IEEE J. Sel. Areas Commun. 2010, 28, 1116–1126. [Google Scholar] [CrossRef]
- Kelly, F.; Maulloo, A.; Tan, D. Rate Control for Communication Networks:Shadow Prices, Proportional Fairness and Stability. J. Oper. Res. Soc. 1998, 49. [Google Scholar] [CrossRef]
- Zhao, D.; Huang, C.; Chen, Y.; Alsaadi, F.; Cui, S. Resource Allocation for Multiple Access Channel with Conferencing Links and Shared Renewable Energy Sources. IEEE J. Sel. Areas Commun. 2015, 33, 423–437. [Google Scholar] [CrossRef]
- Kelly, F. Charging and Rate Control for Elastic Traffic. Eur. Trans. Telecommun. 1997, 8. [Google Scholar] [CrossRef]
- Sari, A.; Thiam, C.; Boudergui, K.; Carrel, F.; Coulon, R.; Dumazert, J.; Frangville, C.; Hamrita, H.; Lainé, F.; Trocmé, M.; et al. Investigation of fission chamber response in the frame of fuel debris localization measurements at Fukushima Daiichi. Radiat. Meas. 2019, 130, 106223. [Google Scholar] [CrossRef]
- Dolicanin, E.; Fetahovic, I. Monte Carlo optimization of redundancy of nanotechnology computer memories in the conditions of background radiation. Nucl. Technol. Radiat. Prot. 2018, 33, 208–216. [Google Scholar] [CrossRef]
- Kibar, O.O.; Mohan, P.; Rech, P.; Mai, K. Evaluating the Impact of Repetition, Redundancy, Scrubbing, and Partitioning on 28-nm FPGA Reliability Through Neutron Testing. IEEE Trans. Nucl. Sci. 2019, 66, 248–254. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).