Abstract
We define a new inversion in a cage isomerism (ic): X@C⋯Y ₪ic Y@C⋯X, (₪ is the isomerism relation) as an isomerism in the three-component system of molecules X, Y, and a cage C, in which one of the molecules is located inside and the other outside the cage. The ic isomerism is similar to the endo-exo one, which occurs only if either the interior or exterior of C is empty. By contrast, ic occurs only if neither the interior nor the exterior of C is empty. We also discuss the other closely related types of isomerisms are also discussed. Calculations of the XH⋯NH3@C60 and NH3⋯HX@C60 ic isomers were performed at the ωB97XD/Def2TZVP level. The calculated energies demonstrated that the systems with the HX acid outside (X = F, Cl) and the NH3 base inside the cage, XH⋯NH3@C60, are more stable than their ic isomers, NH3⋯HX@C60, by about 4–8 kcal/mol. This is because NH3 is more stabilized inside the cage than HX (a matter of 6.5 kcal/mol). In the studied systems and subsystems, the HX molecules are Lewis acids and the NH3 molecule is always a Lewis base. The C60 molecule with HX inside or outside the cage is also an acid for the NH3 base positioned outside or inside the cage. On the other hand, the C60 cage is truly amphoteric because it is simultaneously an acid and a base.
1. Introduction
Searching for new compounds, new materials, and their new properties are among the primary tasks of chemistry. Geometry, topology and set theory can provide a flash of inspiration for the discovery of new molecules. This is because without a name a thing does not exist in our minds, and the name for a plethora of geometric, topological and set theory relations between the objects is usually already known in mathematics. One can find new molecules through modifications of known structures, discovery of new syntheses, finding new natural products, but also through a search for new types of isomerism [1,2,3]. Isomerism is the phenomenon of the existence of molecules of identical summary formula but demonstrating different properties during the time characteristic for a given measurement.
Fullerenes form cages and exhibit quite specific types of isomerism connected to both connectivity between the atoms constituting the cage and the presence of a well-defined interior, boundary, and exterior. A cage isomerism occurs at the boundary and is due to the arrangement of the C-atoms composing the cage in polygons (mostly pentagons and hexagons) [4]. For example, there are possibly as many as 1812 C60 (non-isomorphic graphs of) fullerenes composed of only pentagons and hexagons [4]. However, in three-dimensional space, out of 1812 structures, 1508, 189, 19, 3, and 1 belong to the chiral C1, C2, D2, D3, and D5 point symmetry groups, respectively [5]. Thus 1720 of C60 fullerenes occur in two enantiomeric forms, which makes the existence of 3532 C60 fullerenes composed of 12 pentagons and 20 hexagons possible. Heterofullerenes are fullerenes with at least one C-atom replaced by a heteroatom [6]. The cage isomerism of heterofullerenes is even richer because of the combinatorial possibility of the heteroatom location at the cage. Moreover, a heterofullerene can also be chiral if it does not exhibit an orientation-reversing self-isometry. For example, there are 14 chiral out of 23 (or 28 enantiomers out of 37) different C58X2 heterofullerenes based on the buckminsterfullerene cage [7,8].
In 1991, Weiske et al. [9] and Cioslowski and Fleischmann [10] independently introduced the term endohedral fullerenes for structures containing species inside the fullerene cage. Now, the scientific community well recognizes the chemistry and physics of the endohedral fullerenes, yet they are still intensively studied e.g., [11,12,13]. The exohedral fullerenes [14] are those that interact with species outside the cage. The possibility for the existence of the same species inside and outside a fullerene gives rise to the endohedral–exohedral isomerism. However, the interaction inside and outside the cage have to be similar; otherwise, for instance, if a bond forms only on one side of the cage, the isomerism will be classified as a kind of constitutional one. The endohedral–exohedral isomerism can be, e.g., related to internal and external interaction with noble gases, alkali cations or halogen ions, or noble metal atoms with a fullerene cage [15,16,17,18,19,20].
Simmons and Park introduced the idea of in–out isomerism for macrobicyclic amines [21,22]. Dietrich, Lehn, Sauvage, and Blanzat also studied it as exo–exo, exo–endo, and endo–endo isomerisms abbreviated to xx, xn, and nn [23]. However, they pointed out the ambiguity and inconsistency of the in–out term [24] because they referred the in and out descriptors to the non-rigid cycles. In such a case, the CIP priority rules [25], generalized if needed [26], are sufficient to correctly distinguish the non-rigid macrobicyclic isomers. Nevertheless, for rigid fullerenes, the in–out terminology is intuitive and useful [27,28], even though the configuration and conformation of these isomers is again sufficient for an unequivocal distinction.
Here, we turn our attention to the possibility of the existence of yet another isomerism connected to the species present in and out of the cage: the inversion in a cage isomerism (ic). We demonstrate an example of the inversion in a cage isomerism supported by quantum-chemical DFT calculations of model through-the-cage acid-base interactions. Then we consider two situations: an acid is in and a base is out of the cage and oppositely. They are compared to the system(s) in which the acid-base interaction occurs without or outside the cage.
We have constructed the manuscript as follows. The technical issues are gathered in the Calculations section. The Results and Discussion section is divided into two independent sections—in the first, the new isomerism is defined, discussed from the point of view of the isomer classification tree, and compared with definitions of the closely related isomerisms. In the second, we give a computational example of the inversion in a cage isomer, an example of the new isomerism, which refers to the theme of a special issue—symmetry in acid-base chemistry. Although the calculations serve for the new isomerism illustration rather than for revealing meticulous details of the illustrative example, we performed a careful interaction energy consideration at the DFT level with the relatively large def2TZVP basis set, the modern ωB97XD functional accounting for dispersion forces, and calculations of the basis set superposition error for two- and three-component systems of which our example is composed. The results are summarized in the Conclusions section.
2. Calculations
The DFT calculations were done using the ωB97XD functional [29] combined with small 6-31G** [30] and large def2TZVP [31] basis sets using the Gaussian 09 suite of programs (Gaussian Inc.: Wallingford, CT, USA, see also at the Gaussian web page: https://gaussian.com/glossary/g09/) [32]. the ωB97XD functional was applied using the exact Hartree–Fock exchange in both short- and long-range, including correction for the dispersion forces, and is effective in dealing with charge-transfer states [33,34]. In comparison to many other dispersion-corrected functionals, ωB97X-D was shown to perform slightly better for non-covalent sysgtems but much better for covalent systems [35,36,37]. Here, 6-31G** is a valence double-zeta basis set with polarization functions set on both heavy and hydrogen atoms, while def2TZVP is a size-consistent basis set for all atoms and includes triple-ζ and polarization functions. The harmonic frequencies of all optimized structures were real, indicating that only true energy minima on potential energy hypersurfaces were considered. We estimated the Gibbs free energies at 298 K. To better evaluate the interaction energies, the species-cage interaction energies were corrected for basis set superposition error using the seven-point method, ΔE7 [38,39,40,41], including the Boys–Bernardi counterpoise correction, ΔECP [38]; and the cage deformation, ΔEdef. To calculate ΔE7 (Equation (1)), we further corrected the interaction energies (Equation (2)) with the Boys and Bernardi counterpoise method (Equation (3)) as well as deformation energy (Equation (4)) [39,40]. Pure BSSE is done as the difference between interaction energy and ΔE7 (Equation (5)).
where denotes the energy of dimer, , and denote the energies of dimer components optimized in their own basis sets, and denote the energies of monomers with geometries taken from dimer in basis set of dimer, and and denote the energies of monomers with geometries taken from dimer in a basis set of appropriate monomers.
In the case of ternary systems, the equations for the counterpoise and deformation energies implemented in Gaussian 09 [32] are the following:
where the indices have analogous meanning.in description of energy E and the superscript denotes the basis set in which the system indicated in the subscript is calculated.
The energetics are collected in Table 1, Table A1 and Table A2, where A denotes data gathered in Appendix C. The XYZ coordinates and pictures presenting the two- and three-components systems with the most important intermolecular distances shown after atoms in molecules analysis of bond critical points are shown in the Supplementary Information file. Notice that because the calculations are for illustrating a new type of isomerism rather than for studying details of the systems that may be compared to the real systems, we have not considered the role of environment here. Consequently, please take notice that the uncertainty of DFT calculations is ca. 2 kcal/mol.

Table 1.
Interaction energies in different HX complexes with NH3 (kcal/mol) with and without the presence of the C60 fullerene. ΔE7, ΔE, ΔECP, ΔEdef, and BSSE [38,39,40,41] denote interaction energy corrected for BSSE using the seven-point method, interaction energy calculated as a simple energy difference between products and reagents, counterpoise corrected interaction energy, deformation energy, and basis set superposition error, respectively.1 Colors in the molecular system formulae differentiate components considered in the calculation of the BSSE corrections.
3. Results and Discussion
3.1. Inversion in a Cage Isomerism
Consider an acid A and a base B forming a complex A⋯B in an equilibrium ⇌:
wherein one neglects a difference between an AB salt and an A⋯B complex.
A + B ⇌ A⋯B
Consider also a cage C. Depending on the A, B, and C size, different species can potentially be observed. In the most general case, in which one can include A + B in C, the following can be observed:
A + B + C ⇌ A⋯B + C
A@C + B ⇌ A@C⋯B
A + B@C ⇌ A⋯B@C
(A + B)@C ⇌ (A⋯B)@C
In the above, we have assumed that the interaction between A and B is much stronger than either of them is with C. Therefore, in (9), the competing interactions between A and C, between B and C, as well as both interactions (in many possible variants), were neglected for the sake of clarity. Similarly, a multitude of mutual positions of A, B, and C in Equations (10)–(12) is ignored, too. For other obvious assumptions, see Appendix A.
Formally, one can call all systems at the two sides of Equations (9)–(12) isomeric, even if the “+” symbol can also mean an infinite separation of the components. Let us denote the isomeric relation by the ₪ symbol (which commonly stands for the new Israeli shekel currency). Thus,
reads X and Y are isomers. The right superscript to the ₪ symbol, will clarify the isomerism type, e.g., ₪con and ₪R,S can denote constitutional and R,S stereo-isomerism, respectively. Notice that ₪ is the equivalence relation (Appendix B).
X ₪ Y
Taking into account the assumptions listed in Appendix A, let us focus on the isomerism between the systems at the right sides of Equations (10) and (11):
A@C⋯B₪B@C⋯A
The isomerism, ₪, of the through-the-cage C interactions between the acid A and the base B Equation (14), describes a situation when either A is in cage C and B is outside, or the opposite. One can understand it as an interchange of A with B and B with A with fixed C. Such an interchange resembles a transformation called inversion in a sphere or spherical inversion. Inversion in a sphere is a bijection of R3\{0} onto itself in which every internal point of a sphere, except the origin, is transformed on one and only one external point of the sphere, keeping the sphere fixed. As the spherical inversion is not only a reversible, but also continuous transformation, it is a homeomorphism of R3\{0} onto itself. An analogy between the isomerism demonstrated in Equation (14) and the inversion in a sphere mapping prompted us to call this kind of isomerism the inversion in a cage (ic) isomerism and use the ₪ic symbol for the relation between the ic isomers. Let us note that, while the ic isomers were already studied [19,20], the phenomenon of the ic isomerism itself, has not been the issue, yet.
Definition 1.
The inversion in a cage isomerism occurs in a three-component system of molecules X, Y, and cage C, in which one of the components is located inside and the other outside the cage.
Now, consider how the inversion in a cage isomerism between a pair of molecules X and Y bound through cage C,
can be classified [42]. To simplify the reasoning, assume that X and Y themselves are not isomers of any type.
X@C⋯Y₪icY@C⋯X
First, the ic isomerism is not a constitutional isomerism because the molecular connectivity does not change with the change of the ic isomer. This, however, requires a widely accepted though not indisputable [41,43] agreement that the intermolecular and in-the-cage interactions are not categorized as ordinary chemical bonds and do not contribute to the molecular connectivity. So X@C⋯Y and Y@C⋯X are the stereoisomers. Second, they are not mirror images of each other, hence, they are not enantiomers, but diastereoisomers. Two diastereoisomers superimposable by a rotation about a single bond, or a finite series of such rotations, are called conformational diastereoisomers; otherwise, they are configurational [42]. A single bond binds neither X with C nor Y with C nor X with Y. Consequently, the X@C⋯Y and Y@C⋯X pair of isomers must fall into the class of configurational diastereoisomers. This conclusion is counterintuitive since the considered ic isomers are placed in one class with the achiral compounds containing multiple chiral centers or with those exhibiting the (E,Z)-diastereoisomerism [44], or with rigid compounds able to be stably twisted, such as cyclododeca-octaenes [45] or some dicyclopentadienes [46].
However, if we agree that the intermolecular and in-the-cage interactions are not ordinary chemical bonds and do not change molecular connectivity, the X@C⋯Y and Y@C⋯X systems are three-component topological molecules, which were not considered in a classical isomer classification scheme [42]. Some 20 years ago, we studied model topological isomers such as knots, catenanes, Möbius strips, etc., e.g., references [47,48,49,50]. As a reflection on those structures, we modified the isomer classification scheme to include topological compounds which, unlike common molecules, can, inter alia, be as multicomponent as the catenanes and rotaxanes [51]. In the modified classification tree, as soon as two molecules are recognized as true isomers, a question about the number of independent connected components is asked [51]. Until very recently [41], we have not considered endohedral systems. Yet, just as with endohedral fullerenes and nanotubes, the number of independent connected components constituting them is crucial. Indeed, the endohedral structures may contain many species in a very convoluted manner [52,53,54,55,56,57].
The three-component ic isomers Equation (14) are similar to the two-component endo–exo isomers:
where X, C, @, and ⋯ denote the same as in Equations (8)–(12) and in the exo form X is interacting with the cage surface e.g., [19,20,58,59,60]. Indeed, if we agree that a ghost molecule Ø could be included in the set of molecules, then Equation (16) one could rewrite it as:
X@C₪ndo-exoC⋯X
X@C⋯Ø₪icØ@C⋯X
Introducing the Ø ghost molecule reveals both similarity and dissimilarity between the two isomerisms. Removing the ghost molecule from (17) makes the system two-component and thus disqualifies it from the class of the ic isomers. Then, the end–exo isomerism may occur for two- or more-, while the ic isomerism for three- or more-component systems. Thus,
Definition 2.
while Definition 1 can be reformulated as follows:The endo–exo isomerism occurs in a 2-, 3-, … n-component system if and only if either the interior or exterior of C is empty,
Definition 3.
Definition 3. The ic isomerism occurs in a 3-, 4-, … n-component system if and only if neither the interior nor the exterior of C is empty.
A more general class of isomerism, which could include both the endo–exo and ic types of isomerisms in which the same number of components is involved with respect to the same cage C, can be called the cage-host in-out isomerism. This isomerism is similar to the cage-configuration in-out isomerism, which describes, for example, the CmR2 molecules, where m is large enough and one can direct some R-groups in and the other out of the cage [28]. Notice that the designation, cage, is inevitable because the term in-out isomerism was first and foremost used to describe equilibria in the macrobicyclic molecules [21,22,23,24,25,26]. A pair of isomers composed by X, Y, and C, wherein one isomer belongs to the endo-exo isomers (e.g., (X + Y)@C) while the other, to the ic isomers (e.g., X@C⋯Y), is an example the configurational cage-in-out isomerism:
(X + Y)@C ₪chio X@C⋯Y
Definition 4.
The cage-host in–out isomerism occurs in a 2-, 3-, … n-component system with cage C, in which some of the (n-1)-components exchange their in-out positions, while the cage remains unchanged.
Definition 5.
The cage-configuration in–out isomerism occurs when configuration of cage C in two isomers is different while the cage-connectivity remains unchanged.
Let us also remember that recently, we introduced [41]
Definition 6.
The cage isomerism of the endohedral molecules is the phenomenon whereby the same internal individuum is captured in two or more cages of differing cage connectivity.
Definition 7.
The endohedral isomerism is the phenomenon whereby an internal individuum captured in a cage can occupy more than one stable position without changing the cage connectivity.
At the end of this section, one should remark that the onion-like fullerene and nanotube structures [52,53,54,55,56,57] offer a chance for the existence of a huge number of the isomerism types connected to the subsequent inclusion of cages inside the other cages and the division of the space into the three-dimensional onion-like convex (or otherwise) layers. However, here, we conclude reflections about isomerisms at one of the simplest: inversion in a cage isomerism.
3.2. Computational Example of the Inversion in a Cage Isomers
Consider a computational example of the inversion in a cage isomerism of three-component molecules composed of an acid A = HF or HCl, a base B = NH3, and a cage C = C60 (Figure 1). Encapsulation of HF and NH3 in C60 was already achieved with the molecular surgery i.e., synthesis of an open-cage fullerene and placing HF or NH3 inside and closing the cage [61,62,63,64,65]. For HCl, analogous synthesis seems to be feasible as well [66,67,68,69]. Although the XH⋯NH3 complex is likely to be stable in the C60 cage [70], here, we focus on the ic isomerism rather than on the A, B, C system in full generality.
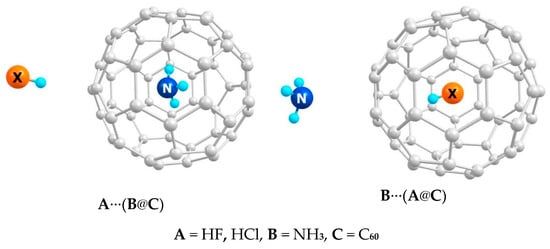
Figure 1.
Example of the inversion in a cage isomerism in the through-the-cage acid-base interaction
Look at the energetics of the studied systems (Table 1, Table A1 and Table A2). Hereafter, we will comment only on the BSSE corrected values obtained at the ωB97XD/Def2TZVP level (Table 1), while the other energy values are given for the sake of comparison only, unless stated otherwise (Table 1, Table A1 and Table A2).
We have grouped rows in Table 1 into seven Blocks numbered with Roman numbers. The first Block, I, (“the acid-base interaction”), E(HX⋯NH3)-E(HX)-E(NH3), contains interaction energies (and their components) determined for the two free XH⋯NH3 systems interacting in the vacuum. Block II (“the external interaction with the empty cage”), E(M⋯C60)-E(M)-E(C60), contains interaction energies for the XH acids or NH3 base interacting with the empty C60 cage from the outside which is denoted as M⋯C60 (where M = XH or NH3). The Block III (“the guest-cage iternal interaction”), E(M@C60)-E(M)-E(C60), shows the energies for the XH or NH3 molecules interacting from the inside with the C60 cage denoted as M@C60. The Block IV (“the ternary interaction”) presents gain in energy in the ternary systems, E(M1⋯(M2@C60))-E(M1)-E(M2)-E(C60), where M2 is inside while M1 is outside the cage in the M1⋯(M2@C60) system (M1, M2 = XH or NH3 and M1 ≠ M2; and always either M1 = NH3 or M2 = NH3). This stabilization energy contains contributions from all three components. Block V (“the external interaction with the filled cage”), E(M1⋯(M2@C60))-E(M1)-E(M2@C60) contains interaction energies for the molecule interacting from the outside with the C60 cage, which contains the partner molecule. They are similar to that in Block II, yet now C60 is not empty. Block VI (“the acid-base through-the-cage interaction”), E(M1⋯(M2@C60))-E(M1⋯M2)-E(C60) contains interaction energies between the XH and NH3 molecules where one is outside and the other is inside the C60 cage. They correspond to the energies in Block I, yet now the cage wall disturbs the interaction. The last Block, VII, (“the guest interaction with the cage and surrounding”), E(M1⋯(M2@C60))-E(M1⋯C60)-E(M2) contains interaction energies for the molecules inside the cage with the cage interacting from the outside with yet another molecule. They correspond to the energies in Block III, but now a third molecule interferes with the interaction between the guest and the cage.
First, comparison of the energy difference between A⋯B@C and B⋯A@C (Block IV, Table 1 and ΔE = E(A⋯B@C)-E(B⋯A@C), Table A2) reveals that the systems with the HX acid outside (X = F, Cl) and the NH3 base inside the cage, XH⋯NH3@C60, are more stable than their ic isomers, NH3⋯HX@C60, by about 4–8 kcal/mol. The difference depends on the acid and the kind of energy compared (Block IV, Table 1 and E, EZPE, G, total, zero-point-corrected, and Gibbs free, respectively, Table A2).
Greater stability of the ic isomers with NH3 inside is a consequence of the greater stabilization of ammonia than HX in the cage, while very similar stabilization energies occur when HX or NH3 interact from the outside of the cage. Indeed, inside the cage, the base is stabilized by about 16 kcal/mol, whereas the acid is stabalized by about 10 kcal/mol (Block III, Table 1). On the other hand, all binary systems with the molecule outside C60 are similarly stabilized by about 2.3 kcal/mol (Block II, Table 1). Both the C60 and heterofullerene cages have π-electron systems which can be donating or accepting [41,71].
However, comparison of the Li@C60 and F@C60 molecules indicates that C60 is a better π-electron acceptor than π-electron donor [71]. This explains why a free-electron-pair donor is more stabilized inside C60 than an electron acceptor. Despite the fact that NH3 and HX are both electron donors (free-electron pairs on N, F, and Cl) and electron acceptors (H atoms with a positive partial charge), ammonia is a much stronger electron donor then HX, and HX is a much stronger electron acceptor than NH3 is.
Second, notice that interaction from the outside with the filled cage is only a bit stronger (about 2.5 vs. about 2.3 kcal/mol, Block V vs. II of rows, in Block V the E(X⋯Y@C) values are separated into the (X) and (Y@C) subsystems, Table 1). On the other hand, the interaction energies of the molecule inside with the cage and a molecule outside exhibit about 6.5 ± 1.0 kcal/mol greater stabilization of NH3 than HX inside the cage (Block VII, Table 1).
Third, the energy of the acid-base interaction through-the-cage would probably be the most interesting, if it could be calculated accurately (Block VI, Table 1). But, (i) ΔECP is much more negative than ΔE, while for common binary systems it is the opposite. In the BSSE calculations, the presence of the basis functions of the interaction partner additionally stabilizes the system, its energy is decreased, and thus, the ΔECP is more positive than ΔE. (ii) The deformation energies (Equation (4)) are much higher than in the other Blocks. This is because the energies are referenced to the freely interacting XH⋯NH3 systems. Inserting the cage surface between XH and NH3 causes an enormous change in geometry of both HX and NH3 which increases the deformation contribution to the interaction energy. (iii) The BSSE correction in Block VI is also relatively large and exceeds the ΔE7 interaction energy. All these problems would be avoided if the systems could be calculated at the basis set saturation limit for which BSSE vanishes. However, for the C60 endohedral fullerenes, this is hardly possible. As a result of meticulous BSSE calculations and comparison of ΔE7 and ΔE values in Blocks I and VI, we can only say that (1) the through-the-cage acid-base interactions are weaker than the direct acid-base ones and (2), in the case of the FH⋯NH3 interaction, weakening of the interaction is quite significant whereas for the ClH⋯NH3 system, it is less evident.
However, in the light of the recent computational studies [72], conclusion (1) is not as meaningless as it seems. The analysis of the charge distribution between an endohedral species and the cage revealed that, unlike in a common lone electron pair (LP) LP-π bonding, a unique LP-π(cage) interaction pattern displays a charge-depletion in the bonding region. As a result, the HF bond inside the cage is elongated, and HF appears to be more acidic inside the cage [72]. It was shown that this effect has a significant impact on hydrogen bonding inside the cage [72], yet, the through-the-cage interaction behaves differently.
3.3. Acids and Bases in the Inversion in a Cage Isomer
Let us discuss the acid–base properties of the studied systems within the frame of the Lewis concept of acids and bases. A Lewis acid is an electron-pair acceptor, while a Lewis base is an electron-pair donor [73]. The acid and the base interact to form a Lewis adduct by sharing the electron pair furnished by the Lewis base [73]. It is clear that to call a molecule a Lewis base, the donated negative charge should not literally be an electron-pair; the Lewis base can simply supply a partial negative charge to the Lewis acid. In fact, all components of the studied systems, an acid A, a base B, and a cage C, have an amphoteric Lewis character. Actually, different parts of the HX, NH3, and C60 molecules can either accept or donate a negative charge depending on how strong a donor or an acceptor directly interacts with them.
Indeed, the gas phase deprotonation enthalpies of the studied species increase from NH3 through HF to HCl, whereas the proton affinities decrease in different order, from NH3 through HCl to HF [74,75,76,77]. These strikingly demonstrate differences between proton donating and proton accepting abilities of the studied species. In the gas phase, HCl is the strongest acid, while HF is the weakest base. On the other hand, the gas phase proton affinity of C60 is 860 kJ/mol [78], is slightly larger than that of NH3 [74,75,76,77], and makes the C60H+ cation probably the most abundant fullerene derivative in interstellar environments [79,80]. Moreover, the C60 gas phase basicity is 827.5 kJ/mol and is again a bit larger than that of NH3 [74,75]. Thus, in the studied set of compounds, C60 is located at the beginning of the two series. However, the known data for C60 refer to the properties of the fullerene outer surface of an empty molecule. The endohedral species interacts with the inner fullerene surface which has slightly other protonation and deprotonation enthalpies. Moreover, the situation varies when an additional molecule is simultaneously present inside or outside of C60. The two situations change both the inner and the outer surfaces. Although, C60 seems to be a relatively simple molecule, consideration of the gas phase basicity and proton affinity in the case of endohedral species or exohedral species, when the other molecule is present on the other side of the cage requires meticulous studies devoted exclusively to this very problem.
Taking into account the approximative sense of the acid-base terminology and the stabilization energies collected in Table 1, we can state that in both binary and ternary systems, the HX molecule can always be classified as an acid and the NH3 molecule can always be classified as a base. However, the HX interaction partner molecules are always the bases, and the NH3 interaction partner molecules are always acids. Therefore, C60 is the base in XH⋯C60 and HX@C60 interactions, while it is the acid in H3N⋯C60 and NH3@C60 interactions. Also, in the ternary systems, in the interactions with NH3 and HX (be they external or internal species) the (HX@C60) and (HX⋯C60) moieties are the acids while the (H3N@C60) and (H3N⋯C60) moieties are the bases respectively. Eventually, in the ternary systems separated into three components, C60 is amphoteric because it is simultaneously an acid and a base.
Let us finally add that heteroatoms, N or B for example, or a selected functional group introduced into the fullerene structure, can produce substantial change in the charge distribution of the internal and external surface of the parent fullerene. If there is more than one such a heteroatom or substituent, the number of possible constitutional isomers rapidly grows [8]. In consequence, a heteroatom or a substituent can stabilize more than one endohedral and exohedral position, making isomeric equilibria more complex. However, in the case of compounds exhibiting useful properties, the complexity opens a possibility for the construction of a molecular switch, a diode, or a machine. Another important modification of the studied systems could be based on the use of stronger acids or bases such as, primary, secondary, or tertiary amines. In such a case, the fullerene cage should be larger to accommodate the larger molecule. However, to do this, the art of fullerene synthesis has to be shifted to a higher level of effectiveness. Yet, this can be done quickly only if the expected usefulness of the new systems promises a breakthrough in the new applications. At the moment, computational methods are the most effective way to study the potential of the new type of isomerism.
4. Conclusions
In this paper, we have considered the possibility of the existence of the inversion in a cage isomerism (ic) which was not previously studied, although a few of its examples were computationally studied for different purposes. We define the inversion in a cage isomerism as a three-component system of molecules X, Y and a cage C, in which one of the components is located inside and the other outside the cage: X@C⋯Y ₪ic Y@C⋯X, where the ₪ symbol stands for isomerism relation and the superscript, ic, specifies the kind of isomerism. The name of the isomerism originates from the resemblance of an interchange of X with Y and Y with X with fixed C with an inversion in a sphere or spherical inversion, where R3\{0} is transformed onto itself, meaning every internal point of a sphere, except the origin, is transformed on one and only one external point of the sphere, keeping the sphere fixed. Discussion of the isomerism classification shows the similarity of the ic isomerism with the endo-exo one which occurs only if either the interior or exterior of C is empty, while ic occurs only if neither the interior nor exterior of C is empty. The other closely related types of isomerisms are also discussed. However, the possibility of the existence of a new type of isomerism can always have implications on many chemical fields. In the case of the inversion in a sphere isomerism, we suppose that, first of all, it can be important for material science chemistry wherein modifications of the inner and outer space of a cage can significantly transform the properties of the entire solid phase.
In the computational part of the study, which illustrates the new type of isomerism rather than carefully describes details of the system, we calculated the XH⋯NH3@C60 and NH3⋯HX@C60 ic isomers, and all of their components, at the ωB97XD/Def2TZVP level. Comparison of the calculated energies demonstrated that the systems with the HX acid outside (X = F, Cl) and the NH3 base inside the cage, XH⋯NH3@C60, are more stable than their ic isomers, NH3⋯HX@C60, by about 4–8 kcal/mol. This is mainly because NH3 is more stabilized inside the cage than HX (a matter of 6.5 kcal/mol), while from the outside they interact with the C60 cage with a similar strength of about 2.3 kcal/mol. As the theme of this special issue is “Symmetry in Acid-Base Chemistry,” let us only emphasize that despite the fact that different parts of the HX, NH3, and C60 molecules can either accept or donate a negative charge and are amphoteric in the sense of the Lewis acid-base concept, the HX molecules are acids and the NH3 molecule is always a base in all studied systems. The C60 molecule with HX inside or outside the cage is also an acid for the NH3 base positioned outside or inside the cage. The analogous is true for the C60 molecule with NH3 inside or outside the cage. Eventually, in the ternary systems separated into three components, the C60 cage is truly amphoteric because it is simultaneously an acid and a base.
Supplementary Materials
The following are available online at https://www.mdpi.com/2073-8994/12/8/1291/s1.
Author Contributions
J.C.D.: the project concept, project administration, part of the quantum chemical calculations, writing of the original draft; S.O.: part of the quantum chemical calculations, data analysis, writing of the original draft. All authors have read and agreed to the published version of the manuscript.
Funding
This project was supported by the Institute of Nuclear Chemistry and Technology statutory funds for 2020.
Acknowledgments
We gratefully acknowledge the computational grant from the Świerk Computing Centre (CIŚ). The authors thank hab. Joanna E. Rode from the Institute of Nuclear Chemistry and Technology, Warsaw for the discussion. The authors thank Rachel Muracka for her help in English language corrections.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
As we deal with chemical systems, we obviously assume that
A + B ⇌ B + A
A⋯B ⇌ B⋯A
C + A⋯B ⇌ A⋯B + C
A@C + B ⇌ B + A@C
B@C ⋯ A ⇌ A ⋯ B@C
A@C ≠ C@A
(A + B)@C ≠ A@C + B@C
(A⋯B)@C ≠ A@C⋯B@C
Appendix B
In this set of molecules, isomerism is an equivalence relation:
X ₪ X reflexivity
X ₪ Y then Y ₪ X symmetry
X ₪ Y and Y ₪ Z then X ₪ Z transitivity
Appendix C

Table A1.
Interaction energies in different HX complexes with NH3 (kcal/mol) with and without the presence of the C60 fullerene. ΔE7, ΔE, ΔECP, ΔEdef, and BSSE [38,39,40,41] denote interaction energy corrected for BSSE using the seven-point method, interaction energy calculated as a simple energy difference between products and reagents, counterpoise corrected interaction energy, deformation energy, and basis set superposition error, respectively.1 Colors in the molecular system formulae differentiate components considered in the calculation of the BSSE corrections.
Table A1.
Interaction energies in different HX complexes with NH3 (kcal/mol) with and without the presence of the C60 fullerene. ΔE7, ΔE, ΔECP, ΔEdef, and BSSE [38,39,40,41] denote interaction energy corrected for BSSE using the seven-point method, interaction energy calculated as a simple energy difference between products and reagents, counterpoise corrected interaction energy, deformation energy, and basis set superposition error, respectively.1 Colors in the molecular system formulae differentiate components considered in the calculation of the BSSE corrections.
| Block | System | ωB97XD/Def2TZVP | ωB97XD/6-31G** | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ΔE7 | ΔE | ΔECP | ΔEdef | BSSE | ΔE7 | ΔE | ΔECP | ΔEdef | BSSE | ||
| I | FH⋯NH3 | −13.07 | −13.92 | −13.90 | 0.83 | 0.85 | −13.40 | −14.70 | −13.96 | 0.56 | 1.30 |
| ClH⋯NH3 | −9.33 | −10.36 | −10.04 | 0.71 | 1.03 | −12.30 | −14.11 | −13.84 | 1.55 | 1.81 | |
| II | FH⋯C60 | −2.44 | −3.29 | −2.48 | 0.04 | 0.86 | −0.98 | −4.34 | −1.00 | 0.02 | 3.36 |
| ClH⋯C60 | −2.27 | −2.77 | −2.28 | 0.01 | 0.50 | −2.55 | −3.31 | −2.57 | 0.02 | 0.76 | |
| H3N⋯C60 | −2.22 | −2.92 | −2.22 | 0.00 | 0.71 | −1.86 | −3.46 | −1.86 | 0.00 | 1.60 | |
| III | HF@C60 | −10.75 | −12.57 | −10.79 | 0.04 | 1.82 | −8.13 | −13.62 | −8.19 | 0.06 | 5.49 |
| HCl@C60 | −9.29 | −10.98 | −9.33 | 0.04 | 1.69 | −10.48 | −12.91 | −10.53 | 0.05 | 2.43 | |
| NH3@C60 | −15.92 | −17.84 | −15.97 | 0.05 | 1.92 | −15.61 | −20.50 | −15.66 | 0.05 | 4.89 | |
| IV | H3N⋯(HF@C60) | −13.14 | −15.68 | −13.18 | 0.04 | 2.54 | −10.12 | −17.22 | −10.15 | 0.03 | 7.09 |
| H3N⋯(HCl@C60) | −11.68 | −14.09 | −11.70 | 0.02 | 2.41 | −12.46 | −16.52 | −12.50 | 0.04 | 4.05 | |
| FH⋯(NH3@C60) | −18.61 | −21.36 | −18.69 | 0.08 | 2.75 | −16.84 | −25.06 | −16.90 | 0.06 | 8.23 | |
| ClH⋯(NH3@C60) | −18.32 | −20.73 | −18.38 | 0.06 | 2.41 | −18.40 | −24.05 | −18.46 | 0.06 | 5.65 | |
| V | H3N⋯(HF@C60) | −2.39 | −3.11 | −2.42 | 0.03 | 0.72 | −2.02 | −3.60 | −2.03 | 0.01 | 1.58 |
| H3N⋯(HCl@C60) | −2.37 | −3.37 | −3.08 | 0.01 | 0.71 | −2.02 | −3.62 | −2.03 | 0.01 | 1.59 | |
| FH⋯(NH3@C60) | −2.69 | −3.52 | −2.74 | 0.05 | 0.83 | −1.11 | −4.57 | −1.14 | 0.03 | 3.46 | |
| ClH ⋯(NH3@C60) | −2.40 | −2.89 | −2.42 | 0.02 | 0.50 | −2.71 | −3.55 | −2.73 | 0.02 | 0.84 | |
| VI | H3N⋯(HF@C60) | 0.75 * | −1.76 * | −12.59 * | 13.34 * | 2.51 * | 4.66 | −2.51 | −9.46 | 14.12 | 7.18 |
| H3N⋯(HCl@C60) | −1.69 | −4.05 | −11.27 | 9.58 | 2.37 | 1.43 | −2.68 | −11.92 | 13.35 | 4.11 | |
| FH⋯(NH3@C60) | −4.75 | −7.44 | −18.1 | 13.35 | 2.69 | −2.13 | −10.36 | −16.56 | 14.43 | 8.19 | |
| ClH⋯(NH3@C60) | −8.33 | −10.69 | −18.02 | 9.69 | 2.36 | −4.53 | −10.20 | −17.95 | 13.42 | 5.67 | |
| VII | H3N⋯(HF@C60) | −10.93 | −12.75 | −10.99 | 0.06 | 1.83 | −8.25 | −13.77 | −8.28 | 0.03 | 5.52 |
| H3N⋯(HCl@C60) | −9.46 | −11.17 | −9.51 | 0.05 | 1.71 | −10.60 | −13.07 | −10.64 | 0.04 | 2.48 | |
| FH⋯(NH3@C60) | −16.15 | −18.06 | −16.20 | 0.05 | 1.92 | −15.78 | −20.73 | −15.83 | 0.05 | 4.94 | |
| ClH⋯(NH3@C60) | −16.04 | −17.96 | −16.10 | 0.06 | 1.92 | −15.85 | −20.74 | −15.89 | 0.04 | 4.89 | |
1 Only systems with the lowest total energy are listed. * The values are estimated based on a not fully optimized structure with one imaginary frequency.

Table A2.
Energetics of different HX complexes with NH3 (a.u.) with and without the presence of the C60 fullerene.1) The EA⋯B@C-EB⋯A@C energy difference in the last two rows refer to the systems with the HF and HCl molecules, respectively.
Table A2.
Energetics of different HX complexes with NH3 (a.u.) with and without the presence of the C60 fullerene.1) The EA⋯B@C-EB⋯A@C energy difference in the last two rows refer to the systems with the HF and HCl molecules, respectively.
| System | ωB97XD/Def2TZVP | ωB97XD/6-31G** | ||||
|---|---|---|---|---|---|---|
| Total | ZPE | Gibbs Free | Total | ZPE | Gibbs Free | |
| HF | −100.462986 | −100.453491 | −100.469888 | −100.404833 | −100.395270 | −100.411669 |
| HCl | −460.817098 | −460.810283 | −460.828159 | −460.782991 | −60.776154 | −460.794033 |
| NH3 | −56.564335 | −56.529785 | −56.548845 | −56.538783 | −56.503923 | −56.522991 |
| C60 | −2286.129284 | −2285.746652 | −2285.789339 | −2285.455680 | −2285.072455 | −2285.115257 |
| FH⋯NH3 | −157.049486 | −157.000710 | −157.025302 | −156.967034 | −156.917986 | −156.942771 |
| ClH⋯NH3 | −517.397416 | −517.352302 | −517.378181 | −517.343823 | −517.298097 | −517.323707 |
| FH⋯C60 | −2386.597516 | −2386.204068 | −2386.253997 | −2385.867420 | −2385.473283 | −2385.520938 |
| ClH⋯C60 | −2746.950794 | −2746.560299 | −2746.610222 | −2746.243940 | −2745.852699 | −2745.902481 |
| H3N⋯C60 | −2342.698277 | −2342.280249 | −2342.332021 | −2341.999973 | −2341.581128 | −2341.633465 |
| HF@C60 | −2386.612290 | −2386.216769 | −2386.261739 | −2385.882203 | −2385.486287 | −2385.532132 |
| HCl@C60 | −2746.963914 | −2746.570802 | −2746.615744 | −2746.259229 | −2745.866648 | −2745.912129 |
| NH3@C60 | −2342.722027 | −2342.299986 | −2342.344821 | −2342.027106 | −2341.604915 | −2341.649989 |
| H3N⋯(HF@C60) | −2443.181575 * | −2442.749552 * | −2442.800353 * | −2442.426715 | −2441.995066 | −2442.050334 |
| H3N⋯(HCl@C60) | −2803.533157 | −2803.104201 | −2803.157997 | −2802.803770 | −2802.375135 | −2802.429715 |
| FH⋯(NH3@C60) | −2443.190621 | −2442.756905 | −2442.808853 | −2442.439213 | −2442.006495 | −2442.056459 |
| ClH⋯(NH3@C60) | −2803.543733 | −2803.114174 | −2803.166803 | −2802.815748 | −2802.385858 | −2802.438281 |
| HF ic isomers | −5.676 * | −4.614 * | −5.334 * | −7.843 | −7.172 | −3.843 |
| HCl ic isomers | −6.637 | −6.258 | −5.526 | −7.516 | −6.729 | −5.375 |
* The estimate is based on a not fully optimized structure with one imaginary frequency.
References
- Berzelius, J.J. Ueber die Zusmmensetzung der Weinsäure und Traubensäure (John’s Säure aus den Vogesen), über das Atomengewicht das Bleioxyds, nebst allgemeinen Bemerkungen über soche Körper, die gleiche Zusammensetzung, aber ungleiche Eigenschaften besitzen. Ann. Phys. Chem. 1830, 19, 305–335. [Google Scholar] [CrossRef]
- Rouvray, D.H. Isomer Enumeration Methods. Chem. Soc. Rev. 1974, 3, 355–372. [Google Scholar] [CrossRef]
- Slanina, Z. Contemporary Theory of Chemical Isomerism; Academia: Praha, Czech Republic, 1986. [Google Scholar]
- Fowler, P.W.; Manolopoulos, D.E. An Atlas of Fullerenes; Clarendon Press: Oxford, UK, 1995. [Google Scholar]
- Babić, D.; Klein, D.J.; Sah, C.H. Symmetry of fullerenes. Chem. Phys. Lett. 1993, 211, 235–241. [Google Scholar] [CrossRef]
- Vostrowsky, O.; Hirsch, A. Heterofullerenes. Chem. Rev. 2006, 106, 5191–5207. [Google Scholar] [CrossRef]
- Hummelen, J.C.; Bellavia-Lund, C.; Wudl, F. Heterofullerenes. In Fullerenes and Related Structures; Hirsch, A., Ed.; Springer: Berlin/Heidelberg, Germany, 1999; Volume 199, pp. 93–134. [Google Scholar]
- Ashrafi, A.R.; Ghorbani, M. Enumeration of a class of IPR hetero-fullerenes. J. Serb. Chem. Soc. 2010, 75, 361–368. [Google Scholar] [CrossRef]
- Weiske, T.; Böhme, D.K.; Hrušák, J.; Krätschmer, W.; Schwarz, H. Endohedral cluster compounds—Inclusion of helium within C60·+ and C70·+ through collision experiments. Angew. Chem. Int. Ed. 1991, 30, 884–886. [Google Scholar] [CrossRef]
- Cioslowski, J.; Fleischmann, E.D. Endohedral complexes: Atoms and ions inside the C60 cage. J. Chem. Phys. 1991, 94, 730–3734. [Google Scholar] [CrossRef]
- Popov, A.A.; Yang, S.; Dunsch, L. Endohedral Fullerenes. Chem. Rev. 2013, 113, 5989–6113. [Google Scholar] [CrossRef]
- Matsuo, Y.; Okada, H.; Ueno, H. Endohedral Lithium-Containing Fullerenes; Preparation, Derivatization, and Application; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Popov, A.A. (Ed.) Endohedral Fullerenes: Electron Transfer and Spin; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Filippone, S.; Nazario, M. Exohedral Fullerenes. In Encyclopedia of Polymeric Nanomaterials; Kobayashi, S., Müllen, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 1–16. [Google Scholar]
- Ohtsuki, T.; Ohno, K.; Shiga, K.; Kawazoe, Y.; Maruyama, Y.; Masumoto, K. Insertion of Xe and Kr Atoms into C60 and C70 Fullerenes and the Formation of Dimers. Phys. Rev. Lett. 1998, 81, 967–970. [Google Scholar] [CrossRef]
- Iglesias-Groth, S.; Breton, J.; Girardet, C. Structure of the Van der Waals rare gas–C60 exohedral complexes [(C60)(RG)n; n=1, 2]. Chem. Phys. 1998, 237, 285–293. [Google Scholar] [CrossRef]
- Ichimura, K.; Imaeda, K.; Inokuchi, H. Bonding States of He, Ne and Ar in Solid C60. Chem. Lett. 2000, 29, 196–197. [Google Scholar] [CrossRef]
- Watanabe, S.; Katabuchi, T.; Ishioka, N.; Matsuhashi, S.; Muramatsu, H. Production of endohedral 133Xe-higher fullerenes by ion implantation. J. Radioanal. Nuclear Chem. 2007, 272, 467–469. [Google Scholar] [CrossRef]
- Kuganathan, N.; Arya, A.K.; Rushton, M.J.D.; Grimes, R.W. Trapping of volatile fission products by C60. Carbon 2018, 132, 477–485. [Google Scholar] [CrossRef]
- Kuganathan, N.; Ratnasothy Srikaran, R.; Chroneos, A. Stability of Coinage Metals Interacting with C60. Nanomaterials 2019, 9, 1484. [Google Scholar] [CrossRef]
- Simmons, H.E. 20th National Organic Chemistry Symposium Program Book; Division of Organic Chemistry of the American Chemical Society: Burlington, VT, USA, 1967; pp. 12–13. Available online: http://organicdivision.org/noshistory (accessed on 12 March 2017).
- Park, C.H.; Simmons, H.E.; Uyeda, R.T.; Habibi, M.F. Macrobicyclic amines. Trans. N. Y. Acad. Sci. 1970, 32, 521–534. [Google Scholar]
- Dietrich, B.; Lehn, J.M.; Sauvage, J.P.; Blanzat, J. Cryptates-X. Syntheses et Proprietes Physiques de Systemes Diaza-Polyoxa-Macrobicycliques. Tetrahedron 1973, 29, 1629–1645. [Google Scholar] [CrossRef]
- Alder, R.W.; East, S.P. In/Out Isomerism. Chem. Rev. 1996, 96, 2097–2112. [Google Scholar] [CrossRef]
- Cross, L.C.; Klyne, W. Rules for the Nomenclature of Organic Chemistry: Section E: Stereochemistry (Recommendations 1974). Pure Appl. Chem. 1976, 45, 11–30. [Google Scholar]
- Prelog, V.; Helmchen, G. Basic Principles of the CIP-System and Proposals for a Revision. Angew. Chem. Int. Ed. Engl. 1982, 21, 567–583. [Google Scholar] [CrossRef]
- Dodziuk, H.; Nowinski, K.S. ‘Horror vacui’ or topological in-out isomerism in perhydrogenated fullerenes. Part 1. C60H60 and monoalkylated perhydrogenated fullerenes. Chem. Phys. Lett. 1996, 249, 406–412. [Google Scholar] [CrossRef]
- Dodziuk, H.; Lukin, O.; Nowiński, K.S. Topological “In-Out” Isomerism in Perhydrogenated fullerenes Revisited. C60H60R1R2 with Two R Groups “In” (R1,R2=H, Me). Pol. J. Chem. 1999, 73, 299–306. [Google Scholar]
- Grimme, S. Semiempirical GGA-Type Density Functional Constructed with a Long-Range Dispersion Correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
- Ditchfield, R.; Hehre, W.J.; Pople, J.A. Self-Consistent Molecular Orbital Methods. 9. Extended Gaussian-type basis for molecular-orbital studies of organic molecules. J. Chem. Phys. 1971, 54, 724–728. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision D.01; Gaussian Inc.: Wallingford, CT, USA, 2013.
- Chai, J.-D.; Head-Gordon, M. Long-Range Corrected Double-Hybrid Density Functionals. J. Chem. Phys. 2009, 131, 174105. [Google Scholar] [CrossRef]
- Ou, Q.; Subotnik, J.E. Electronic Relaxation in Benzaldehyde Evaluated via TD-DFT and Localized Diabatization: Intersystem Crossings, Conical Intersections, and Phosphorescence. J. Phys. Chem. C 2013, 117, 19839–19849. [Google Scholar] [CrossRef]
- Chai, J.-D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef]
- Dobrowolski, J.C.; Lipiński, P.F.J.; Karpińska, G. Substituent Effect in the First Excited Singlet State of Monosubstituted Benzenes. J. Phys. Chem. A 2018, 122, 4609–4621. [Google Scholar] [CrossRef]
- Dobrowolski, J.C.; Karpińska, G. Substituent Effect in the First Excited Triplet State of Monosubstituted Benzenes. ACS Omega 2020, 5, 9477–9490. [Google Scholar] [CrossRef]
- Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Turi, L.; Dannenberg, J.J. Correcting for basis set superposition error in aggregates containing more than two molecules: Ambiguities in the calculation of the counterpoise correction. J. Phys. Chem. 1993, 97, 2488–2490. [Google Scholar] [CrossRef]
- Rode, J.E.; Dobrowolski, J.C. Theoretical studies on the Oxetane⋯HCl and Thietane⋯HCl complexes. Chem. Phys. Lett. 2002, 360, 123–132. [Google Scholar] [CrossRef]
- Ostrowski, S.; Garnuszek, P.; Dobrowolski, J.C. Endohedral Isomerism in Model Achiral and Chiral La@C58N2 Systems. Spectrochim. Acta Part A 2020, 231, 117791. [Google Scholar] [CrossRef] [PubMed]
- Dodziuk, H. The classification scheme of isomers of organic molecules. Tetrahedron 1996, 52, 12941–12946. [Google Scholar] [CrossRef]
- Ayers, P.L.; Boyd, R.J.; Bultinck, P.; Caffarel, M.; Carbó-Dorca, R.; Causá, M.; Cioslowski, J.; Contreras-Garcia, J.; Cooper, D.L.; Coppens, P.; et al. Six questions on topology in theoretical chemistry. Comput. Theor. Chem. 2015, 1053, 2–16. [Google Scholar] [CrossRef]
- Testa, B. Organic stereochemistry. Part 3: Other stereogenic elements: Axes of chirality, planes of chirality, helicity, and (E,Z)-diastereoisomerism. Helv. Chim. Acta 2013, 96, 351–374. [Google Scholar] [CrossRef]
- Nori-Shargh, D.; Soltani, B.; Deyhimi, F. Ab initio study of configurational and conformational properties of cyclododeca-1,2,4,5,7,8,10,11-octaene. J. Mol. Struct. THEOCHEM 2002, 585, 257–263. [Google Scholar] [CrossRef]
- Jamróz, M.E.; Gałka, S.; Dobrowolski, J.C. On dicyclopentadiene isomers. J. Mol. Struct. THEOCHEM 2003, 634, 225–233. [Google Scholar] [CrossRef]
- Dobrowolski, J.C.; Mazurek, A.P. On the C60 Cyclized Hook and Ladder Carbynes. Int. J. Quantum. Chem. 2000, 80, 1087–1098. [Google Scholar] [CrossRef]
- Dobrowolski, J.C. On the Belt and Moebius Isomers of the Coronene Molecule. J. Chem. Inf. Comp. Sci. 2002, 42, 490–499. [Google Scholar] [CrossRef]
- Dobrowolski, J.C.; Mazurek, A.P. Model Carbyne Knots vs. Ideal Knots. J. Chem. Inf. Comp. Sci. 2003, 43, 861–869. [Google Scholar] [CrossRef] [PubMed]
- Dobrowolski, J.C.; Mazurek, A.P. Model Carbyne vs. Ideal and DNA Catenanes. J. Chem. Inf. Model. 2005, 45, 1030–1038. [Google Scholar] [CrossRef] [PubMed]
- Dobrowolski, J.C. On the Classification of Topological Isomers: Knots, Links, Rotaxanes, etc. Croat. Chem. Acta 2003, 76, 145–152. [Google Scholar]
- Kroto, H.W. Carbon onions introduce new flavour to fullerene studies. Nature 1992, 359, 670–671. [Google Scholar] [CrossRef]
- Sloan, J.S.; Dunin-Borkowski, R.E.; Hutchison, J.L.; Coleman, K.S.; Clifford Williams, V.C.; John, B.; Claridge, J.B.; York, A.P.E.; Xu, C.; Bailey, S.R.; et al. The size distribution, imaging and obstructing properties of C60 and higher fullerenes formed within arc-grown single walled carbon nanotubes. Chem. Phys. Lett. 2000, 316, 191–198. [Google Scholar] [CrossRef]
- Kawase, T.; Tanaka, K.; Shiono, N.; Seirai, Y.; Oda, M. Onion-Type Complexation Based on Carbon Nanorings and a Buckminsterfullerene. Angew. Chem. Int. Ed. 2004, 43, 1722–1724. [Google Scholar] [CrossRef]
- Sun, B.-Y.; Sato, Y.; Suenaga, K.; Okazaki, T.; Kishi, N.; Sugai, T.; Bandow, S.; Iijima, S.; Shinohara, H. Entrapping of exohedral metallofullerenes in carbon nanotubes: (CsC60)n@SWNT nano-peapods. J. Am. Chem. Soc. 2005, 127, 17972–17973. [Google Scholar] [CrossRef]
- Yang, W.L.; Xu, Z.Y.; Wei, H.; Feng, M.; Suter, D. Quantum–information–processing architecture with endohedral fullerenes in a carbon nanotube. Phys. Rev. A 2010, 81, 032303. [Google Scholar] [CrossRef]
- Zhao, H.; Shi, Q.; Han, Z.; Gong, H.; Zhang, Z.; Wu, S.; Wu, J. Anomalous thermal stability in supergiant onion-like carbon fullerenes. Carbon 2018, 138, 243–256. [Google Scholar] [CrossRef]
- Hesselmann, A.; Korona, T. On the accuracy of DFT-SAPT, MP2, SCS-MP2, MP2C, and DFT+Disp methods for the interaction energies of endohedral complexes of the C60 fullerene with a rare gas atom. Phys. Chem. Chem. Phys. 2011, 13, 732–743. [Google Scholar] [CrossRef]
- Malani, H.; Zhang, D. Theoretical Insight for the Metal Insertion Pathway of Endohedral Alkali Metal Fullerenes. J. Phys. Chem. A 2013, 117, 3521–3528. [Google Scholar] [CrossRef] [PubMed]
- Kaiser, A.; Leidlmair, C.; Bartl, P.; Zöttl, S.; Denifl, S.; Mauracher, A.; Probst, M.; Scheier, P.; Echt, O. Adsorption of hydrogen on neutral and charged fullerene: Experiment and theory. J. Chem. Phys. 2013, 138, 074311. [Google Scholar] [CrossRef] [PubMed]
- Whitener, K.E.; Frunzi, M.; Iwamatsu, S.; Murata, S.; Cross, R.J.; Saunders, M. Putting ammonia into a chemically opened fullerene. J. Am. Chem. Soc. 2008, 130, 13996–13999. [Google Scholar] [CrossRef] [PubMed]
- Christopher, M.; Stanisky, R.; Cross, J.; Saunders, M. Putting Atoms and Molecules into Chemically Opened Fullerenes. J. Am. Chem. Soc. 2009, 131, 3392–3395. [Google Scholar]
- Lakhlifi, A.; Dahoo, P.R. Enhanced localization of tunneling of the NH3 umbrella mode in nano-cage fullerene. Chem. Phys. 2011, 386, 73–80. [Google Scholar] [CrossRef]
- Krachmalnicoff, A.; Bounds, R.; Mamone, S.; Alom, S.; Concistrè, M.; Meier, B.; Kouřil, K.; Light, M.E.; Johnson, M.R.; Rols, S.; et al. The dipolar endofullerene HF@C60. Nat. Chem. 2016, 8, 953–957. [Google Scholar] [CrossRef]
- Vidal, S.; Izquierdo, M.; Alom, S.; Garcia-Borràs, M.; Filippone, S.; Osuna, S.; Solà, M.; Whitby, R.J.; Martín, N. Effect of incarcerated HF on the exohedral chemical reactivity of HF@C60. Chem. Comm. 2017, 53, 10993–10996. [Google Scholar] [CrossRef]
- Bloodworth, S.; Gräsvik, J.; Alom, S.; Kouřil, K.; Elliott, S.J.; Wells, N.J.; Horsewill, A.J.; Mamone, S.; Jiménez-Ruiz, M.; Rols, S.; et al. Synthesis and Properties of Open Fullerenes Encapsulating Ammonia and Methane. ChemPhysChem 2018, 19, 266–276. [Google Scholar] [CrossRef]
- Bloodworth, S.; Sitinova, G.; Alom, S.; Vidal, S.; Bacanu, G.R.; Elliott, S.J.; Light, M.E.; Herniman, J.M.; Langley, G.J.; Levitt, M.H.; et al. First Synthesis and Characterization of CH4@C60. Angew. Chem. Int. Ed. Engl. 2019, 58, 5038–5043. [Google Scholar] [CrossRef]
- Ma, F.; Li, Z.R.; Xu, H.L.; Li, Z.J.; Wu, D.; Li, Z.S.; Gu, F.L. Proton transfer in the complex H3N⋯HCl catalyzed by encapsulation into a C60 cage. ChemPhysChem 2009, 10, 1112–1116. [Google Scholar] [CrossRef]
- Zhang, R.; Murata, M.; Wakamiya, A.; Shimoaka, T.; Hasegawa, T.; Murata, Y. Isolation of the simplest hydrated acid. Sci. Adv. 2017, 3, e1602833. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.-J.; Li, X.-P.; Liu, Z.-B.; Li, Z.-R.; Huang, X.-R.; Sun, C.-C. Electric Field-Driven Acid-Base Chemistry: Proton Transfer from Acid (HCl) to Base (NH3/H2O). J. Phys. Chem. A 2011, 115, 1418–1422. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, A.K.; Pandey, S.K.; Pandey, A.K.; Misra, N. C60 as Electron Acceptor and Donor: A Comparative DFT Study of Li@C60 and F@C60. Aust. J. Chem. 2018, 71, 953–956. [Google Scholar] [CrossRef]
- Jaroš, A.; Badri, Z.; Bora, P.L.; Bonab, E.F.; Marek, R.; Straka, M.; Foroutan-Nejad, C. How Does a Container Affect Acidity of its Content: Charge Depletion Bonding Inside Fullerenes. Chem. Eur. J. 2018, 24, 4245–4249. [Google Scholar] [CrossRef]
- Muller, P. Glossary of terms used in physical organic chemistry (IUPAC Recommendations 1994). Pure Appl. Chem. 1994, 66, 1077–1184. [Google Scholar] [CrossRef]
- Hunter, E.P.L.; Lias, S.G. Evaluated Gas Phase Basicities and Proton Affinities of Molecules: An Update. J. Phys. Chem. Ref. Data 1998, 27, 413–656. [Google Scholar] [CrossRef]
- Hunter, E.P.L.; Lias, S.G. Proton Affinity Evaluation. In NIST Chemistry WebBook, NIST Standard Reference Database No. 69; Linstrom, P.J., Mallard, W.G., Eds.; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2014. Available online: http://webbook.nist.gov/chemistry (accessed on 10 July 2015).
- Raczyńska, E.D.; Gal, J.-F.; Maria, P.-C. Enhanced Basicity of Push–Pull Nitrogen Bases in the Gas Phase. Chem. Rev. 2016, 116, 13454–13511. [Google Scholar] [CrossRef]
- Raczyńska, E.D.; Gal, J.-F.; Maria, P.-C.; Szeląg, M. Proton Transfer Chemistry in the Gas Phase. Is a Spontaneous ‘Neutralization’ Reaction a Myth or a Reality? Croat. Chem. Acta 2009, 82, 87–103. [Google Scholar]
- Bohme, D.K. Buckminsterfullerene cations: New dimensions in gas-phase ion chemistry. Mass Spectrom. Rev. 2009, 28, 672–693. [Google Scholar] [CrossRef]
- Kroto, H.W.; Jura, M. Circumstellar and interstellar fullerenes and their analogues. Astron. Astrophys. 1992, 263, 275–280. [Google Scholar]
- Palotás, J.; Martens, J.; Berden, G.; Oomens, J. The infrared spectrum of protonated buckminsterfullerene C60H+. Nat. Astron. 2019. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).