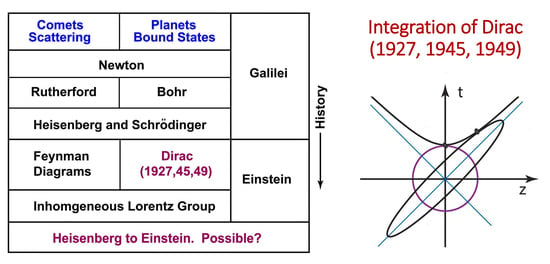
Integration of Dirac’s Efforts to Construct a Quantum Mechanics Which is Lorentz-Covariant
Abstract
1. Introduction
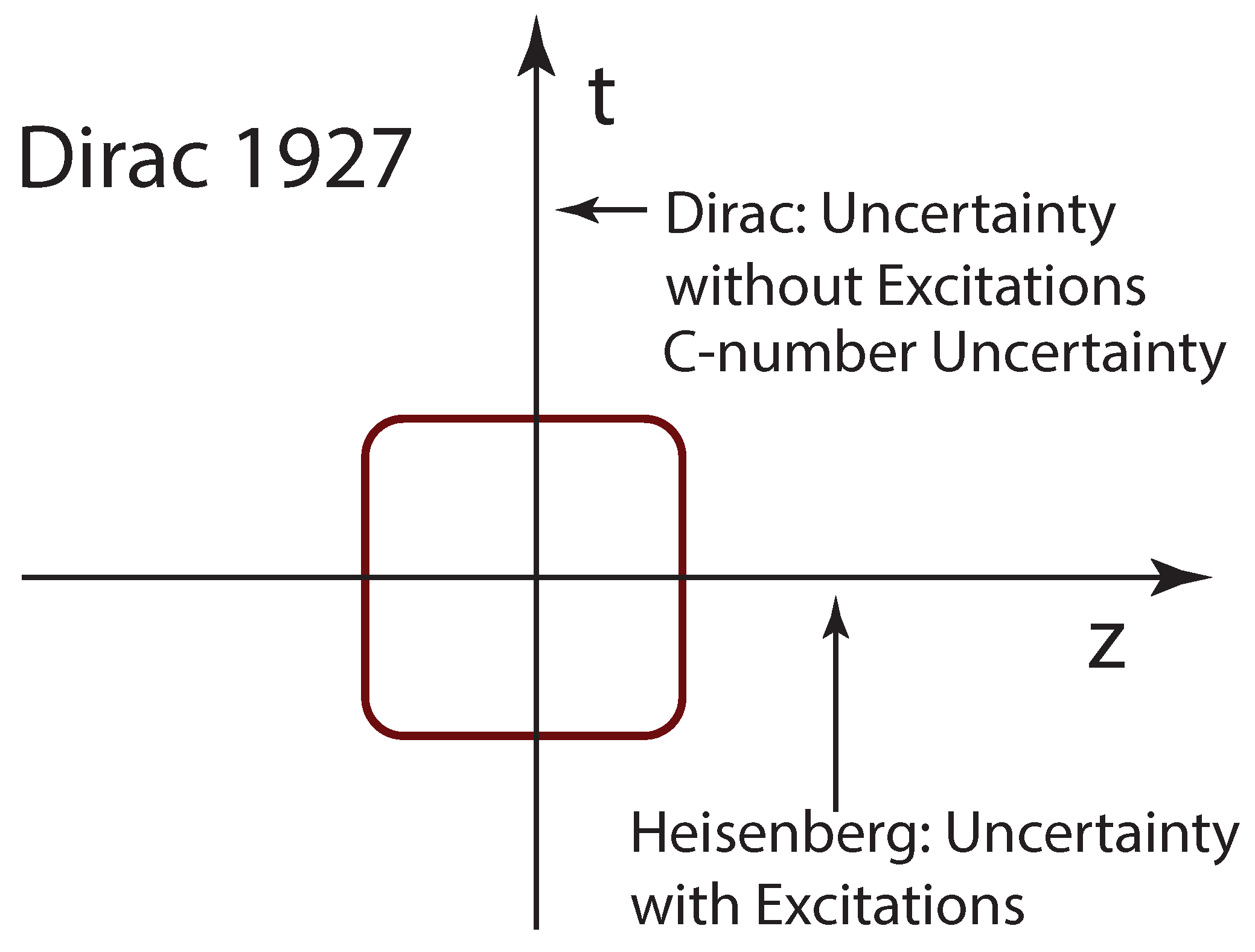
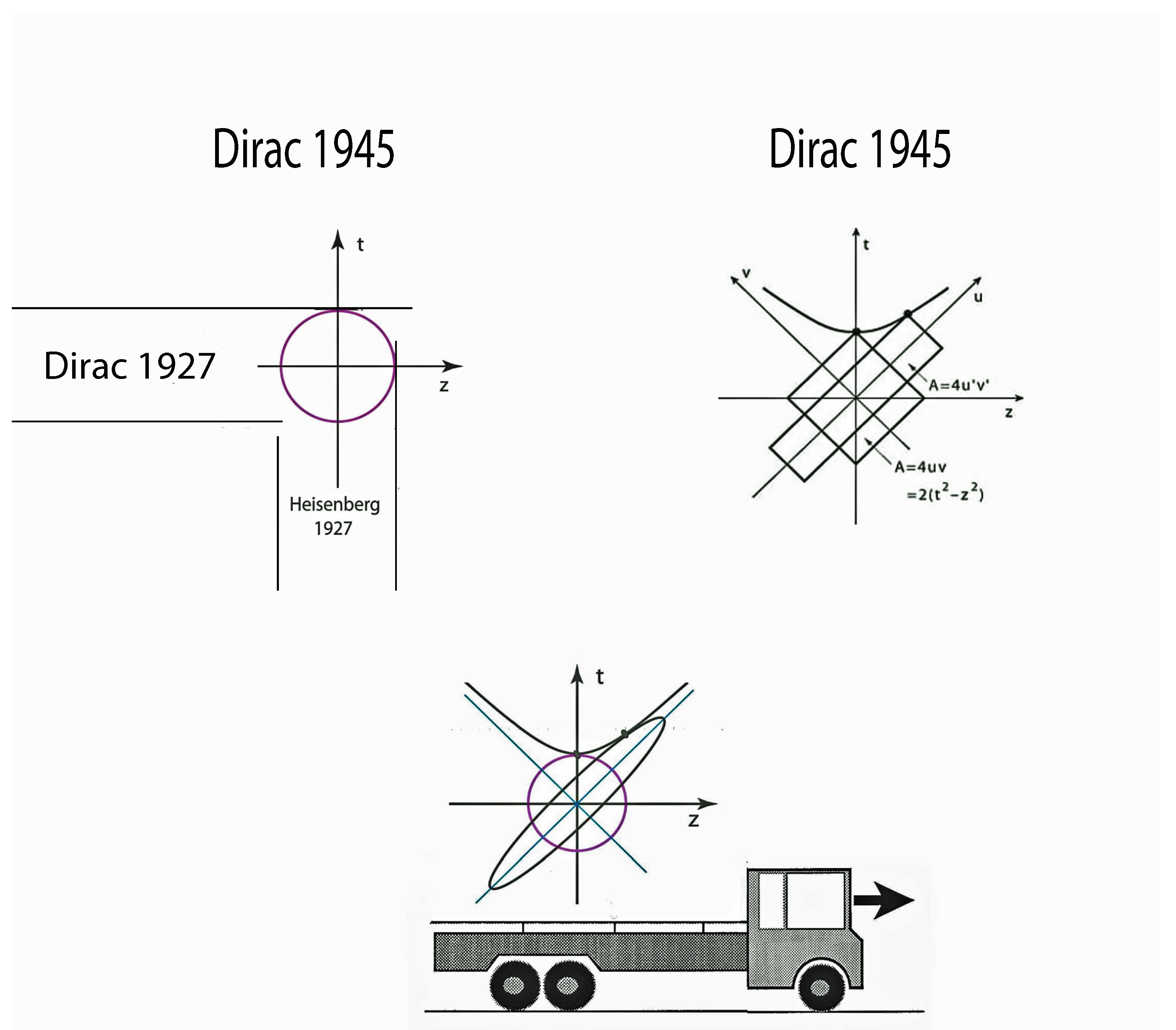
- In 1927, Dirac pointed out that the time-energy uncertainty should be considered if the system is to be Lorentz-covariant [19].
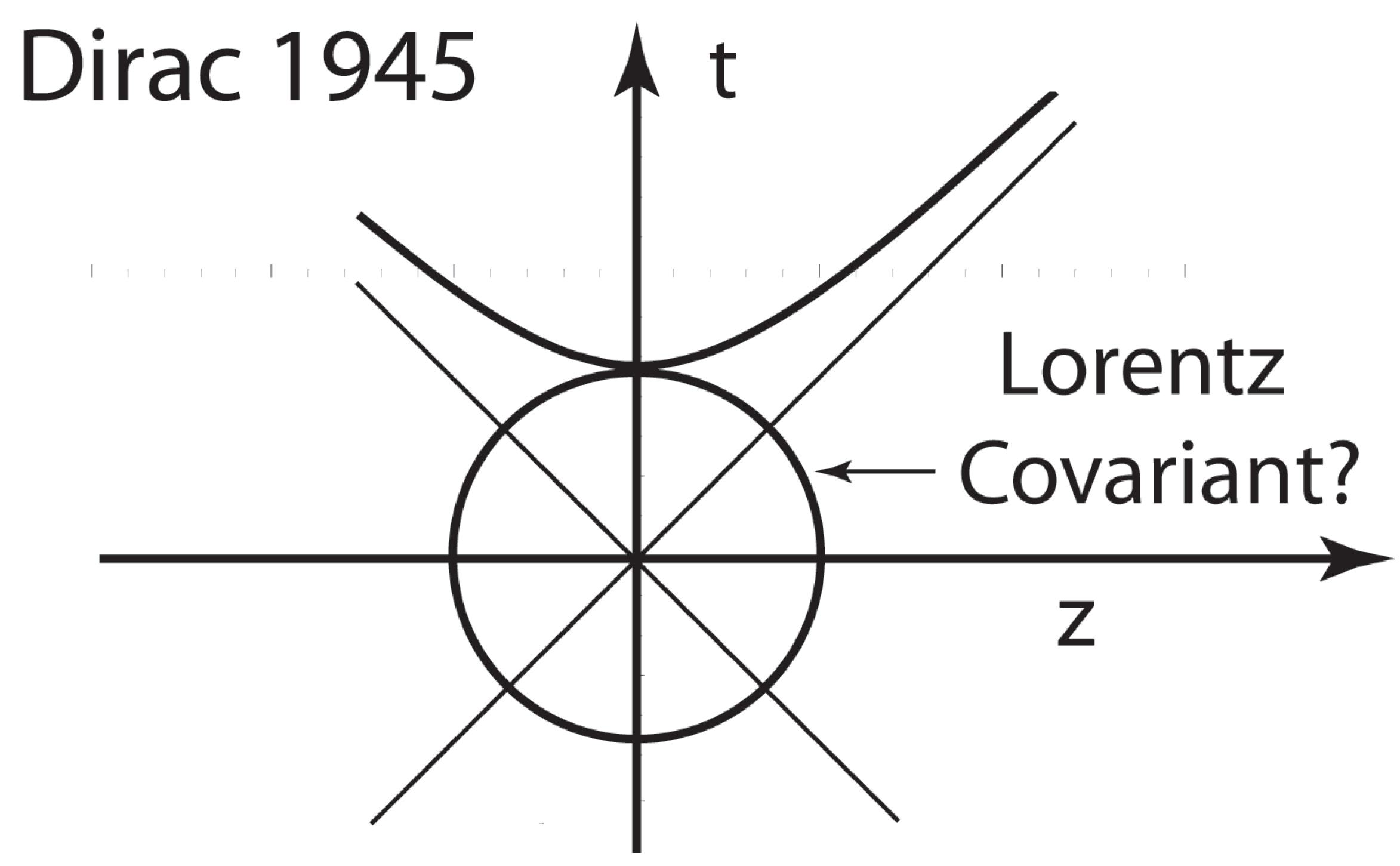
- In 1945, Dirac said the Gaussian form could serve as a representation of the Lorentz group [20].
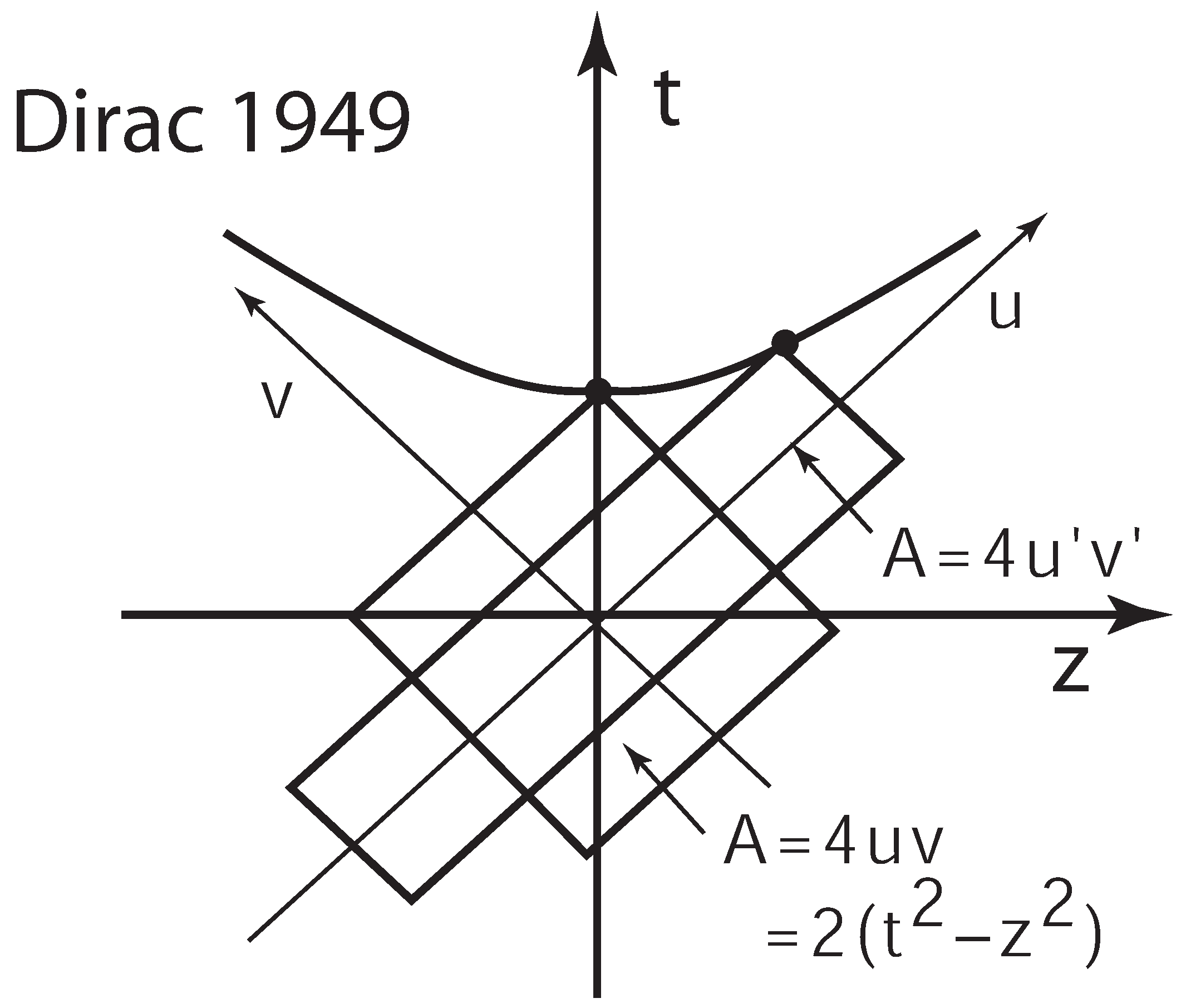
- In 1949, when Dirac introduced both his instant form of quantum mechanics and his light-cone coordinate system [21], he clearly stated that finding a representation of the inhomogeneous Lorentz group was the task of Lorentz-covariant quantum mechanics.
- In 1963, Dirac used the symmetry of two coupled oscillators to construct the group [22].
2. Dirac’s Efforts to Make Quantum Mechanics Lorentz-Covariant
2.1. Dirac’s C-Number Time-Energy Uncertainty Relation
2.2. Dirac’s Four-Dimensional Oscillators
2.3. Dirac’s Light-Cone Coordinate System
3. Scattering and Bound States
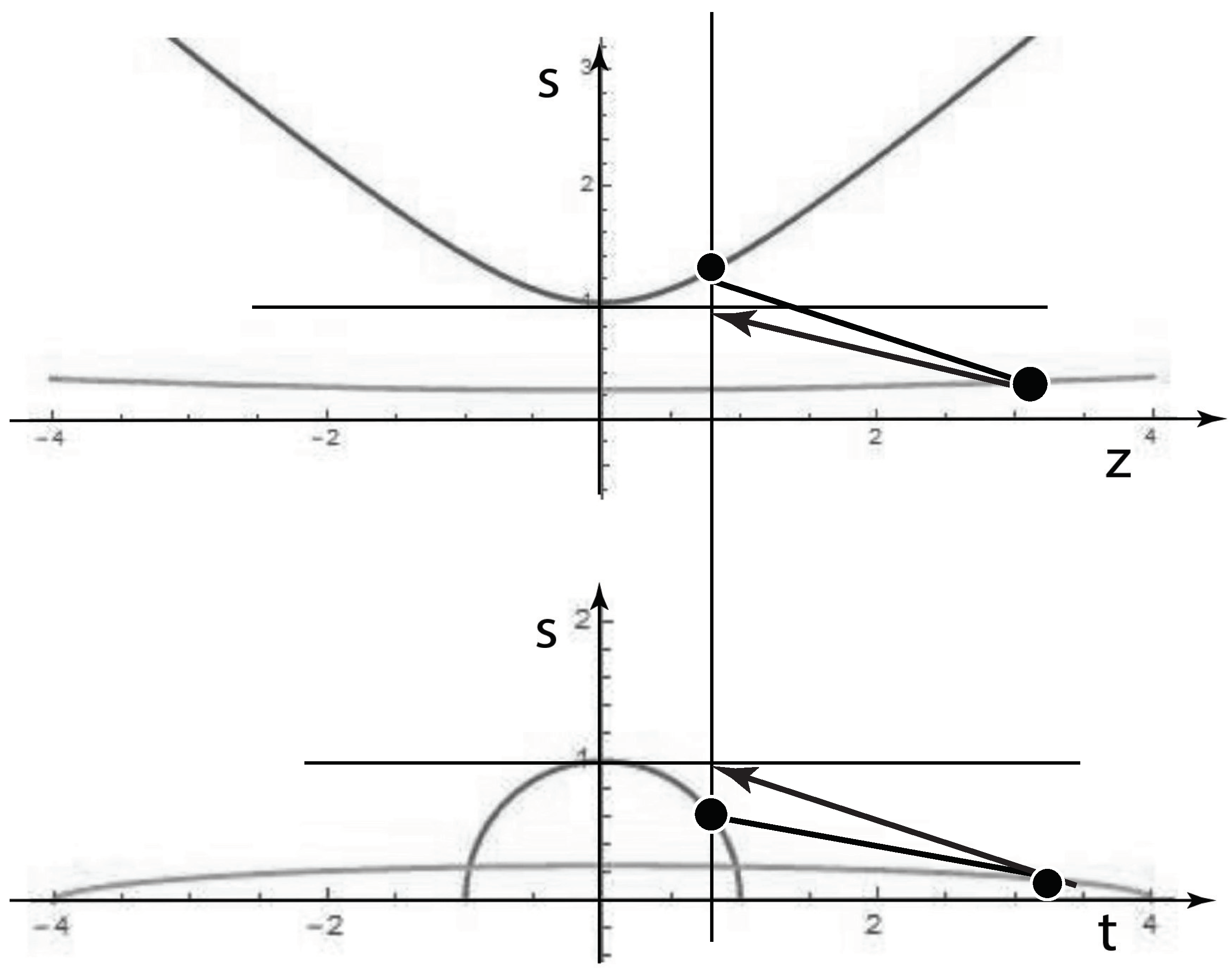
4. Lorentz-Covariant Picture of Quantum Bound States
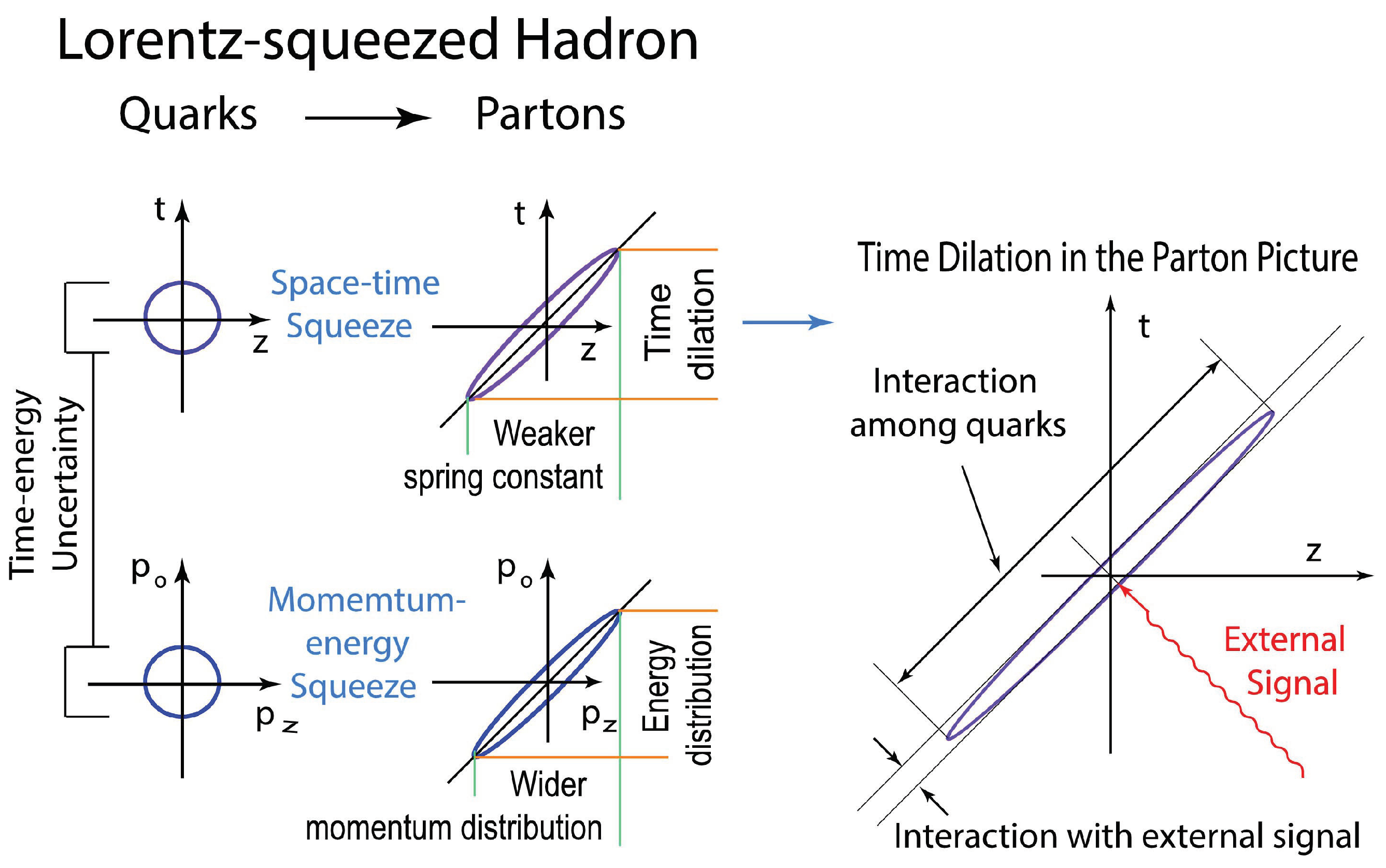
5. Lorentz-Covariant Quark Model
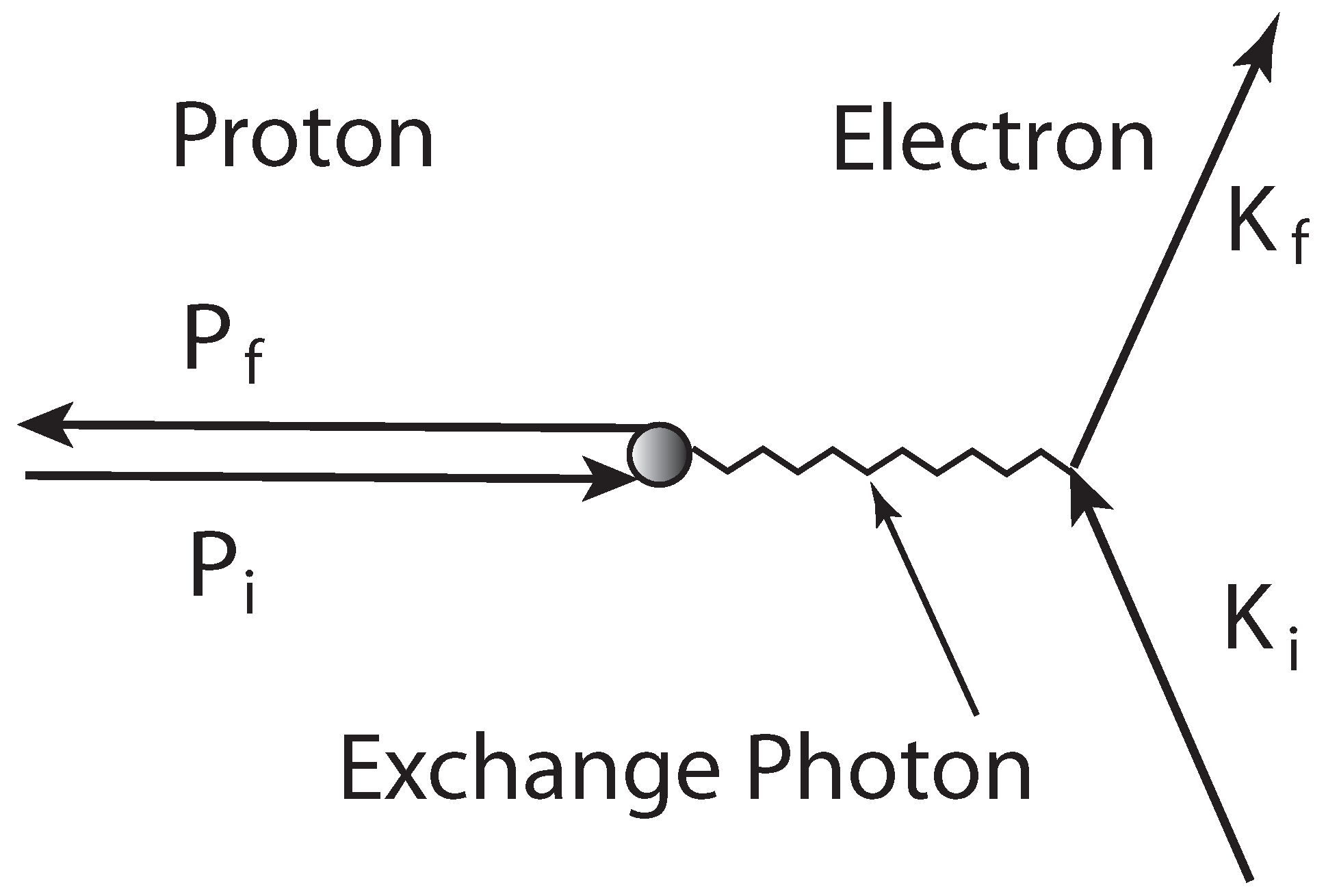
5.1. Proton Form Factor
5.2. Feynman’S Parton Picture
- When protons move with velocity close to that of light, the parton picture is valid.
- Partons behave as free independent particles when the interaction time between the quarks becomes dilated.
- Partons have a widespread distribution of momentum as the proton moves quickly.
- There seems to be an infinite number of partons or a number much larger than that of quarks.
5.3. Historical Note
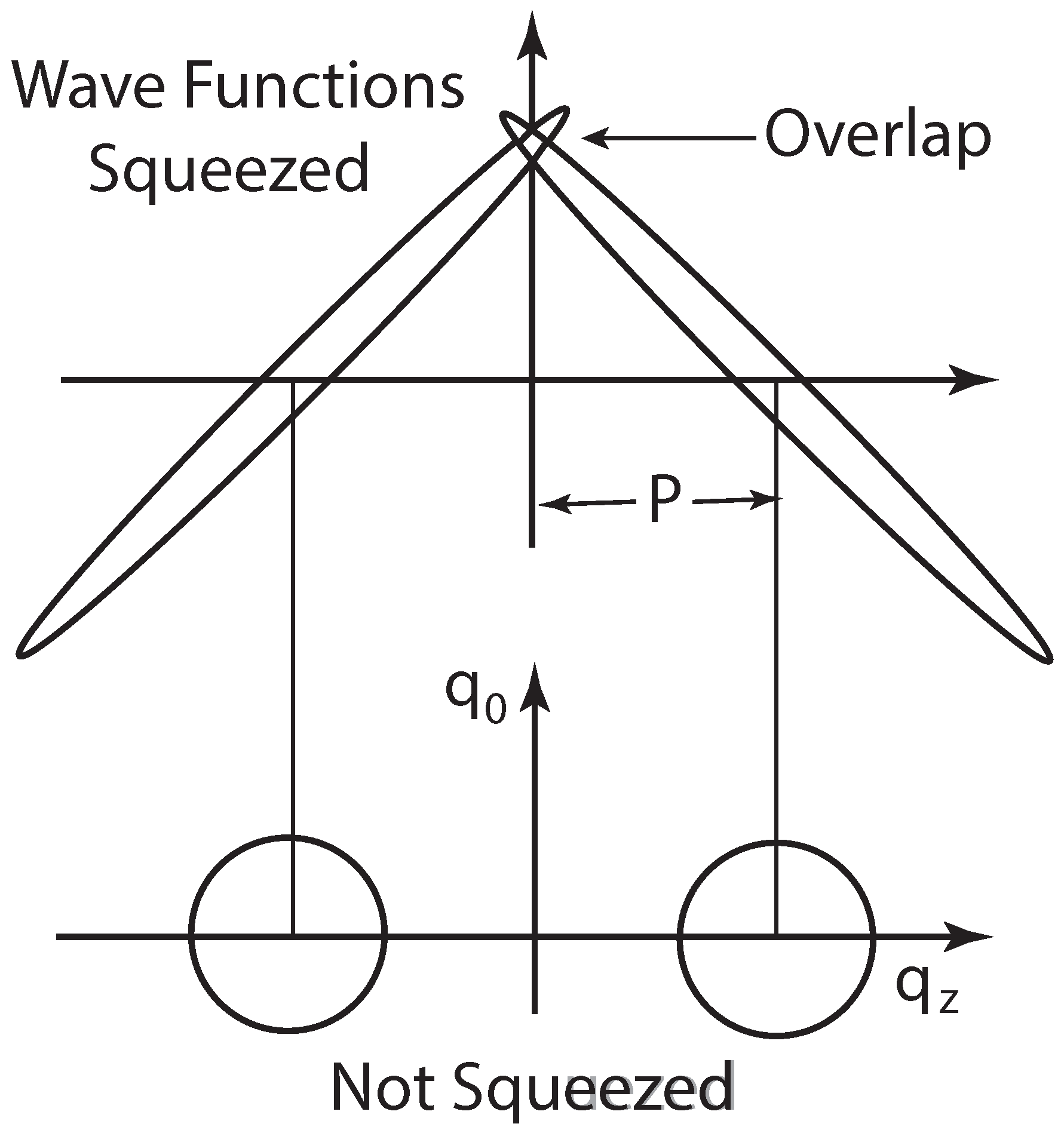
5.4. Lorentz-Invariant Uncertainty Products
6. O(3,2) Symmetry Derivable from Two-Photon States
7. Contraction of O(3, 2) to the Inhomogeneous Lorentz Group
8. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Kim, Y.S.; Noz, M.E. Covariant harmonic oscillators and the quark model. Phys. Rev. D 1973, 8, 3521–3627. [Google Scholar] [CrossRef]
- Kim, Y.S.; Noz, M.E. Theory and Applications of the Poincaré Group; Reidel: Dordrecht, The Netherlands, 1986. [Google Scholar]
- Başkal, S.; Kim, Y.S.; Noz, M.E. Physics of the Lorentz Group, IOP Concise Physics; Morgan & Claypool Publisher: San Rafael, CA, USA; IOP Publishing: Bristol, UK, 2015. [Google Scholar]
- Kim, Y.S.; Noz, M.E. New Perspectives on Einstein’s E = mc2; World Scientific: Singapore, 2018. [Google Scholar]
- Başkal, S.; Kim, Y.S.; Noz, M.E. Mathematical Devices for Optical Sciences; IOP Publishing: Bristol, UK, 2019. [Google Scholar]
- Ruiz, M.J. Orthogonality relations for covariant harmonic oscillator wave functions. Phys. Rev. D 1974, 10, 4306–4307. [Google Scholar] [CrossRef]
- Kim, Y.S.; Noz, M.E.; Oh, S.H. A simple method for illustrating the difference between the homogeneous and inhomogeneous Lorentz groups. Am. J. Phys. 1979, 47, 892–897. [Google Scholar] [CrossRef]
- Gell-Mann, M. A Schematic Model of Baryons and Mesons. Phys. Lett. 1964, 8, 214–215. [Google Scholar] [CrossRef]
- Feynman, R.P. Very High-Energy Collisions of Hadrons. Phys. Rev. Lett. 1969, 23, 1415–1417. [Google Scholar] [CrossRef]
- Kim, Y.S.; Noz, M.E. Covariant harmonic oscillators and the parton picture. Phys. Rev. D 1977, 15, 335–338. [Google Scholar] [CrossRef]
- Kim, Y.S. Observable gauge transformations in the parton picture. Phys. Rev. Lett. 1989, 63, 348–351. [Google Scholar] [CrossRef]
- Kim, Y.S.; Noz, M.E.; Oh, S.H. Representations of the Poincaré group for relativistic extended hadrons. J. Math. Phys. 1979, 20, 1341–1344. [Google Scholar] [CrossRef]
- Wigner, E. On unitary representations of the inhomogeneous Lorentz group. Ann. Math. 1939, 40, 149–204. [Google Scholar] [CrossRef]
- Yuen, H.P. Two-photon coherent states of the radiation field. Phys. Rev. A 1976, 13, 2226–2243. [Google Scholar] [CrossRef]
- Kim, Y.S.; Noz, M.E. Coupled oscillators, entangled oscillators, and Lorentz-covariant harmonic oscillators. J. Opt. B Quantum Semiclass. Opt. 2005, 7, S458–S467. [Google Scholar] [CrossRef]
- Başkal, S.; Kim, Y.S.; Noz, M.E. Harmonic Oscillators and Space Time Entanglement. Symmetry 2016, 8, 55. [Google Scholar] [CrossRef]
- Han, D.; Kim, Y.S.; Son, D. Gauge transformations as Lorentz-boosted rotations. Phys. Lett. B 1983, 131, 327–329. [Google Scholar] [CrossRef]
- Kim, Y.S.; Wigner, E.P. Space-time geometry of relativistic-particles. J. Math. Phys. 1990, 31, 55–60. [Google Scholar] [CrossRef]
- Dirac, P.A.M. The Quantum Theory of the Emission and Absorption of Radiation. Proc. R. Soc. (Lond.) 1927, A114, 243–265. [Google Scholar]
- Dirac, P.A.M. Unitary Representations of the Lorentz Group. Proc. R. Soc. (Lond.) 1945, A183, 284–295. [Google Scholar]
- Dirac, P.A.M. Forms of Relativistic Dynamics. Rev. Mod. Phys. 1949, 21, 392–399. [Google Scholar] [CrossRef]
- Dirac, P.A.M. A Remarkable Representation of the 3 + 2 de Sitter Group. J. Math. Phys. 1963, 4, 901–909. [Google Scholar] [CrossRef]
- Dirac, P.A.M. Can equations of motion be used in high energy physics? Phys. Today 1970, 23, 29–31. [Google Scholar] [CrossRef]
- Farmelo, G. The Strangest Man, the Hidden Life of Paul Dirac, Mystic of Atom; Basic Books: New York, NY, USA, 2009. [Google Scholar]
- Feynman, R.P.; Kislinger, M.; Ravndal, F. Current Matrix Elements from a Relativistic Quark Model. Phys. Rev. D 1971, 3, 2706–2732. [Google Scholar] [CrossRef]
- Frazer, W.; Fulco, J. Effect of a Pion-Pion Scattering Resonance on Nucleon Structure. Phys. Rev. Lett. 1960, 2, 365–368. [Google Scholar] [CrossRef]
- Bjorken, J.D.; Paschos, E.A. Electron-Proton and γ-Proton Scattering and the Structure of the Nucleon. Phys. Rev. 1969, 185, 1975–1982. [Google Scholar] [CrossRef]
- Başkal, S.; Kim, Y.S.; Noz, M.E. Poincaré Symmetry from Heisenberg’s Uncertainty Relations. Symmetry 2019, 11, 409. [Google Scholar] [CrossRef]
- Başkal, S.; Kim, Y.S.; Noz, M.E. Einstein’s E = mc2 derivable from Heisenberg’s Uncertainty Relations. Quantum Rep. 2019, 1, 236–251. [Google Scholar] [CrossRef]
- Wigner, E.P. On the Time-Energy Uncertainty Relation. In Aspects of Quantum Theory; Salam, A., Wigner, E.P., Eds.; Cambridge University Press: London, UK, 1972; pp. 237–247. [Google Scholar]
- Fujimura, K.; Kobayashi, T.; Namiki, M. Nucleon Electromagnetic Form Factors at High Momentum Transfers in an Extended Particle Model Based on the Quark Model. Prog. Theor. Phys. 1970, 43, 73–79. [Google Scholar] [CrossRef]
- Kim, Y.S.; Noz, M.E. The Question of Simultaneity in Relativity and Quantum Mechanics. In Quantum Theory: Reconsideration of Foundations–3; Adenier, G., Khrennikov, A., Nieuwenhuizen, T.M., Eds.; American Institute of Physics: College Park, MD, USA, 2006; Volume 810, pp. 168–178. [Google Scholar]
- Rotbart, F.C. Complete orthogonality relations for the covariant harmonic oscillator. Phys. Rev. D 1981, 23, 3078–3080. [Google Scholar] [CrossRef]
- Beg, M.A.B.; Lee, B.W.; Pais, A. SU(6) and Electromagnetic Interactions. Phys. Rev. Lett. 1964, 13, 514–517. [Google Scholar] [CrossRef]
- Greenberg, O.W.; Resnikoff, M. Symmetric Quark Model of Baryon Resonances. Phys. Rev. 1967, 163, 1844–1851. [Google Scholar] [CrossRef]
- Yukawa, H. Structure and Mass Spectrum of Elementary Particles. I. General Considerations. Phys. Rev. 1953, 91, 415–416. [Google Scholar] [CrossRef]
- Markov, M. On Dynamically Deformable Form Factors in the Theory of Particles. Suppl. Nuovo Cim. 1956, 3, 760–772. [Google Scholar] [CrossRef]
- Ginzburg, V.L.; Man’ko, V.I. Relativistic oscillator models of elementary particles. Nucl. Phys. 1965, 74, 577–588. [Google Scholar] [CrossRef]
- Hofstadter, R.; McAllister, R.W. Electron Scattering from the Proton. Phys. Rev. 1955, 98, 217–218. [Google Scholar] [CrossRef]
- Frazer, W. Elementary Particle Physics; Prentice Hall: Englewood Cliffs, NJ, USA, 1966. [Google Scholar]
- Itzykson, C.; Zuber, J.B. Quantum Field Theory; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Licht, A.L.; Pagnamenta, A. Wave Functions and Form Factors for Relativistic Composite Particles I. Phys. Rev. D 1970, 2, 1150–1156. [Google Scholar] [CrossRef]
- Lipes, R. Electromagnetic Excitations of the Nucleon in a Relativistic Quark Model. Phys. Rev. D 1972, 5, 2849–2863. [Google Scholar] [CrossRef]
- Henriques, A.B.; Keller, B.H.; Moorhouse, R.G. General three-spinor wave functions and the relativistic quark model. Ann. Phys. (NY) 1975, 93, 125–151. [Google Scholar] [CrossRef]
- Matevosyan, H.H.; Thomas, A.W.; Miller, G.A. Study of lattice QCD form factors using the extended Gari-Krumpelmann model. Phys. Rev. C 2005, 72, 065204. [Google Scholar] [CrossRef]
- Alkofer, R.; Holl, A.; Kloker, M.; Karssnigg, A.; Roberts, C.D. On Nucleon Electromagnetic Form Factors. Few-Body Syst. 2005, 37, 1–31. [Google Scholar] [CrossRef]
- Hussar, P.E. Valons and harmonic oscillators. Phys. Rev. D 1981, 23, 2781–2783. [Google Scholar] [CrossRef]
- Han, D.; Kim, Y.S.; Noz, M.E. Physical principles in quantum field theory and in covariant harmonic oscillator formalism. Found. Phys. 1981, 11, 895–905. [Google Scholar] [CrossRef]
- Strocchi, F. An Introduction to Non-Perturbative. In Foundations of Quantum Field Theory Oxford Science Publications; Oxford Science Publications: Oxford, UK, 2013. [Google Scholar]
- Park, J.W.; Kim, H.S.; Brumme, T.; Heine, T.; Yeom, H.W. Artificial relativistic molecules. Nat. Commun. 2020, 11, 815. [Google Scholar] [CrossRef]
- Grant, I. Relativistic Atomic Structure. In Springer Handbook of Atomic, Molecular, and Optical Physics; Drake, G., Ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Hartemann, F.; Toffano, Z. Relativistic electrodynamics of continuous media. Phys. Rev. A 1990, 41, 5066–5073. [Google Scholar] [CrossRef] [PubMed]
- Dodonov, V.V.; Man’ko, V.I. Theory of Nonclassical States of Light; Taylor: London, UK; Francis: New York, NY, USA, 2003. [Google Scholar]
- Saleh, B.E.A.; Teich, M.C. Fundamentals of Photonics, 2nd ed.; Wiley Series in Pure and Applied Optics; Wiley Interscience: Hoboken, NJ, USA, 2007. [Google Scholar]
- Walls, D.F.; Milburn, G.J. Quantum Optics, 2nd ed.; Springer: Berlin, Germany, 2008. [Google Scholar]
- Yurke, B.S.; McCall, S.L.; Klauder, J.R. SU(2) and SU(1,1) interferometers. Phys. Rev. A 1986, 33, 4033–4054. [Google Scholar] [CrossRef] [PubMed]
- Inönü, E.; Wigner, E.P. On the Contraction of Groups and their Representations. Proc. Natl. Acad. Sci. USA 1953, 39, 510–524. [Google Scholar] [CrossRef] [PubMed]
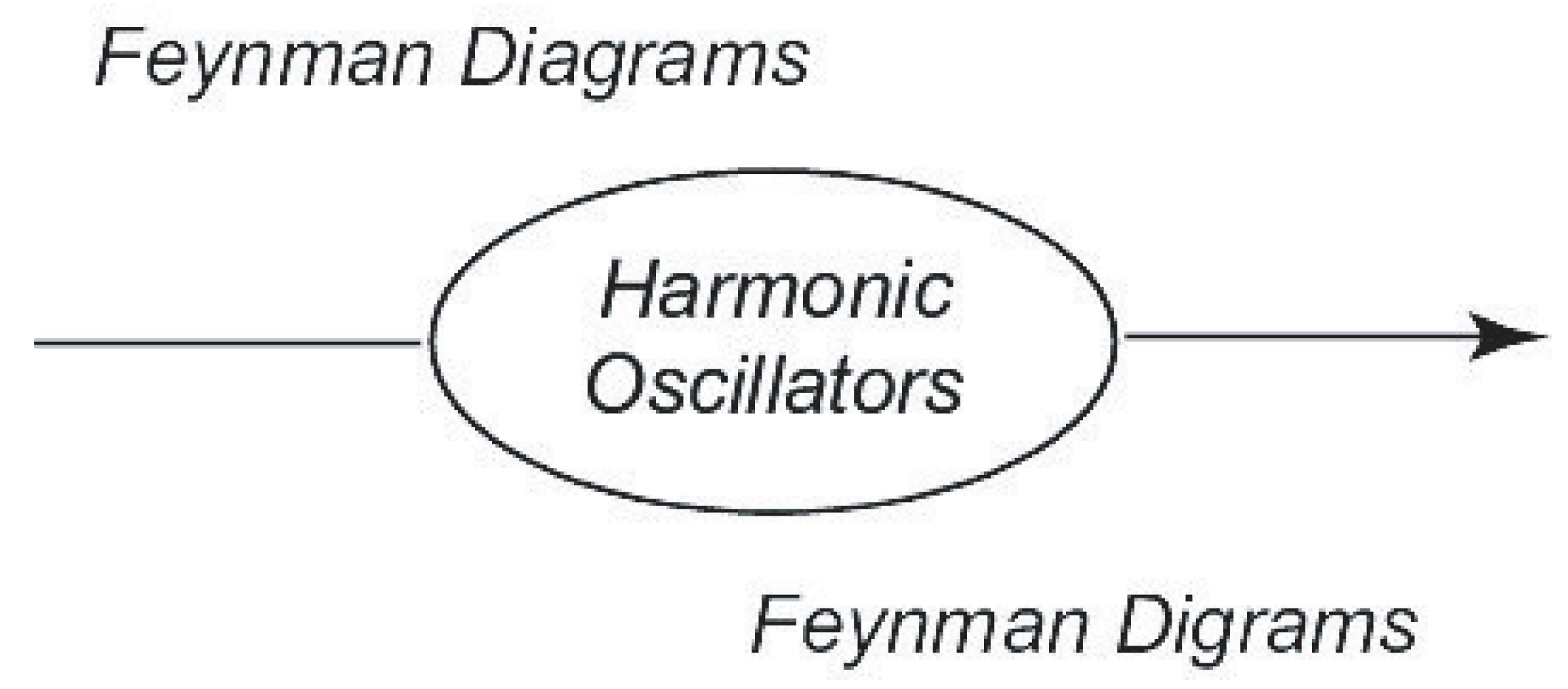


| Massive, Slow | COVARIANCE | Massless, Fast | |
|---|---|---|---|
| Energy-Momentum | Einstein’s | ||
| Internal | |||
| Space-time | Wigner’s | Gauge | |
| Symmetry | Little Groups | Transformation | |
| Relativistic | Integration | ||
| Extended | Quark Model | of Dirac’s papers | Parton Model |
| Particles | 1927, 1945, 1949 |
| Generators | Differential | Matrix | |||
|---|---|---|---|---|---|
| Generators | Differential | Matrix | |||
|---|---|---|---|---|---|
| Generators | Differential | Matrix | |||
|---|---|---|---|---|---|
| Generators | Differential | Matrix | |||
|---|---|---|---|---|---|
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, Y.S.; Noz, M.E. Integration of Dirac’s Efforts to Construct a Quantum Mechanics Which is Lorentz-Covariant. Symmetry 2020, 12, 1270. https://doi.org/10.3390/sym12081270
Kim YS, Noz ME. Integration of Dirac’s Efforts to Construct a Quantum Mechanics Which is Lorentz-Covariant. Symmetry. 2020; 12(8):1270. https://doi.org/10.3390/sym12081270
Chicago/Turabian StyleKim, Young S., and Marilyn E. Noz. 2020. "Integration of Dirac’s Efforts to Construct a Quantum Mechanics Which is Lorentz-Covariant" Symmetry 12, no. 8: 1270. https://doi.org/10.3390/sym12081270
APA StyleKim, Y. S., & Noz, M. E. (2020). Integration of Dirac’s Efforts to Construct a Quantum Mechanics Which is Lorentz-Covariant. Symmetry, 12(8), 1270. https://doi.org/10.3390/sym12081270