Abstract
Calcifying marine green algae of genus Halimeda have siphonous thalli composed of repeated segments. Their outer surface is formed by laterally appressed peripheral utricles which often form a honeycomb structure, typically with varying degrees of asymmetry in the individual polygons. This study is focused on a morphometric analysis of the size and symmetry of these polygons in Mediterranean H. tuna. Asymmetry of surface utricles is studied using a continuous symmetry measure quantifying the deviation of polygons from perfect symmetry. In addition, the segment shapes are also captured by geometric morphometrics and compared to the utricle parameters. The area of surface utricles is proved to be strongly related to their position on segments, where utricles near the segment bases are considerably smaller than those located near the apical and lateral margins. Interestingly, this gradient is most pronounced in relatively large reniform segments. The polygons are most symmetric in the central parts of segments, with asymmetry uniformly increasing towards the segment margins. Mean utricle asymmetry is found to be unrelated to segment shapes. Systematic differences in utricle size across different positions might be related to morphogenetic patterns of segment development, and may also indicate possible small-scale variations in CaCO3 content within segments.
1. Introduction
The green macroalgae of the genus Halimeda J.V.Lamouroux are important calcifying organisms in tropical and sub-tropical marine ecosystems. Their macroscopic thallus is composed of branched filaments (siphons) which contain multiple nuclei but are not divided by any cell walls. Thus, the entire plant represents a single giant multinucleate cell [1]. The above-ground part of the thallus consists of a serial sequence of segments that are separated by short and narrow nodes (see Figure 1a). The segments are composed of medullar filaments (located in the central part) and a cortex formed by several layers of swollen utricles. The peripheral (primary) utricles are usually laterally appressed, forming an analogy of an epidermis which separates seawater from the internal interutricular spaces, the prime location of CaCO3 precipitation.
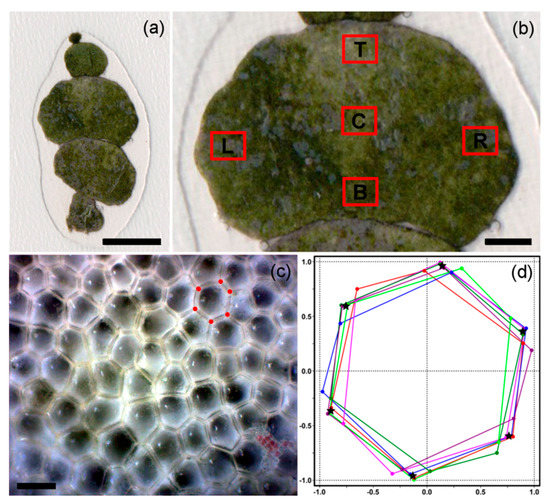
Figure 1.
Morphology of Mediterranean H. tuna and surface views of the peripheral utricles: (a) a single branch of H. tuna consisting of four mature segments and one developing protosegment in the apical position. Note that only the mature segments were used in subsequent morphometric analyses. Scale bar = 5 mm; (b) segment with five positions selected for the analyses of surface utricles, depicted as: B—bottom, C—centre, T—top, L—left, R—right. Scale bar = 1 mm; (c) microphotograph showing surface views of peripheral utricles. Vertices of a single polygon are depicted. Scale bar = 75 µm; (d) 6th-order cyclic symmetry group of the same polygon depicted in (c). The vertices of this size-normalized hexagon are sequentially rotated around the center of mass of this configuration by 2*pi*i/6 radians, where i varies from 1 to 6. The continuous symmetry measure (CSM) value is the average squared distance between the original vertices and the co-ordinates of the perfectly symmetrical hexagon (depicted by black stars).
The size and shape of the peripheral utricles vary among species, which is one of the important identification features of individual taxa [1,2]. Their size has been shown to be related to varying levels of CaCO3 tissue content among species [3,4]. It has been observed that taxa with larger primary utricles and longer lateral adhesion layer tend to be less calcified than species with smaller utricles and comparatively short lateral adhesion layer, resulting in a shorter diffusion pathway for dissolved ions between the interutricular spaces and the external environment [4].
While interspecific variation in the anatomical structure of surface utricles has been studied in detail for the purpose of discrimination among species and their genus-level taxonomy [2], the extent and patterns of infraspecific plasticity in these features are considerably less understood. The surface utricle morphology might vary among different individuals, among segments forming a developmental series of a single plant, or even among the different parts of individual segments. Therefore, we specifically focused on morphometric analyses of variation in the shape and size of the surface views of peripheral utricles in the Mediterranean Halimeda tuna (J.Ellis and Solander) J.V.Lamouroux, the type species of the section Halimeda and the genus as a whole. This species is typified by tight lateral adhesion of the peripheral utricles which form a honeycomb-like surface structure (Figure 1c and Figure 2), a pattern shared by multiple other Halimeda taxa. This pattern results from synchronous development of the peripheral utricles during segment morphogenesis. Surface utricles develop synchronously during segment morphogenesis by lateral expansion, which only ceases when they adhere with their neighbors in the peripheral cortex [1].

Figure 2.
Microphotographs showing the surface views of peripheral utricles of Mediterranean H. tuna in (a) bottom and (b) top positions of a single segment. Scale bar = 50 µm.
Interestingly, this surface structure actually corresponds to a Voronoi tessellation, which is a plane partitioned into convex polygons such that each point in a given polygon is closer to its generating point (seed) than to any other [5,6]. The position of the seed in each utricle is defined by its constricted base. In the case of ideal regular positioning of the utricle bases and their synchronized developmental timing, the resulting structure corresponds to a regular honeycomb tessellation of regular hexagons. As a regular hexagonal tiling creates a partition with minimum total perimeter of the individual parts [5], such a pattern is optimal with regards to the energy required for the construction of the segment cortex. Any deviation in position of peripheral utricles or their developmental timing necessarily leads to an increase in the asymmetry of the polygons comprising the surface layer of segments. This is also accompanied by an increase in the total perimeter of the utricles and, consequently, an increased amount of cell wall material needed for cortex development. Thus, an increase in the asymmetry of the Voronoi tessellation of peripheral utricles might result in the lower fitness of such individuals within Halimeda populations.
The segments themselves are usually also highly variable within and among individuals of the same species. This variation is related to their position on the thallus [7], which may also be caused by environmental heterogeneity [8,9,10]. Recently, it has been shown that morphological variation of H. tuna segments is tightly constrained by the allometric size-to-shape relation [11]. It is unclear whether the infraspecific variation in morphology of the peripheral utricles is related to the morphology of segments. It has been shown several times that the lateral sides of peripheral utricles in old basal segments are longer and they usually have thicker cell walls [7,12]. However, to the best of our knowledge, quantitative variation in the shape features of the surface utricles (e.g., their size and symmetry) within segments has not yet been explicitly investigated.
Thus, in this study, we attempt to respond to the following specific question regarding morphological variation in Halimeda thalli: are there any systematic differences in size or symmetry of H. tuna surface utricles in relation to size and shape of segments, or related to their different position within segments? The null hypothesis of individual analyses was complete independence between the size and symmetry of peripheral utricles, the size and shape of segments, and their position on segments. As this is the first morphometric study of the symmetry of polygons formed by the peripheral utricles of Halimeda segments, we also provide a methodological framework for the analysis of their shape and size features, which may be useful for future comparative studies of these structures among species and in different experimental settings.
2. Materials and Methods
2.1. Sampling and Microscopy of Segments
The algae were sampled on October 21, 2019, on the shore of the Ist Island, Croatia (44.2816883N, 14.7426897E), as part of the field survey for a broader study focused on the phenotypic plasticity of Mediterranean H. tuna. Thalli were taken in the upper sublittoral zone at 200 cm depth in a 30 × 30 cm square.
The branches of fresh plants consisting of fully developed segments were scanned using a Doxie Flip portable scanner (Apparent Corporation, Beaverton, Oregon, USA). Individual segments were then inspected under a Bresser BioScience Trino light microscope (Bresser GmbH, Rhede, Germany). In each segment, the surface of the cortex layer formed by tessellation of the peripheral utricles was photographed at five different locations, corresponding to bottom, center, top, left, and right positions (Figure 1b,c) under 100× magnification with a Bresser MikroCam SP 5.0 digital camera.
2.2. Morphometric Analysis of Surface Utricles
In each of the five locations on segments, 30 polygons formed by appressed peripheral utricles were randomly selected and their vertices digitized using the TpsDig software, version 2.22 [13]. Coordinates of the individual polygons are included in Table S1. It should be noted that Halimeda thalli lack any unambiguous anterior–posterior differentiation. Thus, the “left” and “right” sides of segments cannot be identified across different plants, and so the polygons sampled at these positions were treated as “lateral” in the subsequent analyses. The sizes of the polygons were assessed using two parallel measures. First, their areas were computed by the triangle method for convex polygons implemented by the function polyarea in the package geometry, version 0.4.5 [14], of the R software, version 3.5.1 [15]. Then, the centroid size (CS) of the configurations formed by the vertices of individual polygons was also used as an alternative size measure. The CS is defined as the square root of the sum of squared distances of each point composing the configuration from their centroid [16].
Symmetry of the polygon configurations was also assessed by two parallel approaches. The continuous symmetry measure (CSM) was originally developed for morphometric evaluation of symmetry in convex polygons of chemical structures [17,18]. It has mostly been used in studies evaluating the symmetry or chirality of cyclic molecules [18,19,20], but current applications include a wide array of different scientific topics, such as for the quantification of the bilateral asymmetry of leaves [21] or Paleolithic handaxes [22]. CSM indicates the magnitude of difference to perfect symmetry for each individual polygon. Based on the concept of cyclic symmetry groups, it quantifies the minimal distance that the vertices of a polygon have to undergo in order to be transformed into a perfectly symmetric polygon with the same number of vertices. In other words, the CSM value estimates by how much a distorted polygon (n-gon) deviates from perfect nth-order cyclic symmetry [18,21].
In short, the folding of n points corresponding to the Cn symmetry group of a single n-gon, with its size normalized to unitary length of the longest distance from any vertex to the center of mass [17], is created by sequential rotation of its vertices around the center of mass of this configuration by an angle corresponding to 2*pi*i/n radians, where i varies from 1 to n (Figure 1d). The points are averaged and unfolded by inverted sequential rotation to a regular n-gon. The CSM is then defined as:
where Pi represents individual vertices of each polygon and a CSM value of 0.0 corresponds to the perfectly regular n-gon; while an increase in polygon asymmetry leads to a corresponding CSM increase, approximating a value of 1.0 in extremely asymmetric configurations [21].
In addition to CSM, generalized Procrustes analysis (GPA) was also used to evaluate the asymmetry of individual polygons. GPA of the complete cyclic symmetry group Cn of each of the analyzed n-gons was carried out using the function procGPA implemented in the package shapes, version 1.2.5 [23], of the R software, version 3.5.1. This widely used procedure transforms the original coordinates of the n-gons which represented the cyclic symmetry group Cn of a single analyzed polygon to an optimal registration using translation, rotation, and scaling to a unitary centroid size. The consensus configuration representing the mean values of n vertices is necessarily a regular polygon with n vertices. The residual distances among individual elements of the symmetry group represent their shape differences. The Procrustes distances (PDs) between the original configurations of the analyzed polygons and the mean shapes produced by the GPA of their cyclic symmetry group were then used as the measure of their shape asymmetry. It should be mentioned that the evaluation of PDs among the configurations formed by the complete cyclic symmetry group is closely related to CSM [24]. Therefore, we expected these measures to yield very similar results.
Differences in the asymmetry of the Voronoi tessellation formed by the surface utricles of H. tuna may also be reflected by variation in the average number of vertices of individual polygons. A regular honeycomb tessellation is composed solely of regular hexagons; however, increasing asymmetry in the positions of seeds of individual polygons leads to a steady increase in the proportion of n-gons with n ≠ 6 within the analyzed honeycomb structure [5,25]. Thus, the average number of polygon vertices was registered for each position (Figure 1) in all analyzed segments. In addition, sample variance for the distribution of polygon vertices was also quantified for each position. The 95% confidence intervals for these values were created by bootstrapping of the original data based on 9999 bootstrap replicates.
All parameters were sampled from surface utricles of 32 segments composing 7 plants. Thus, with 30 analyzed utricles in five different positions on each segment, a total of 4800 surface utricles were used in the morphometric analyses.
2.3. Statistical Analysis of Utricle Parameters
First, the linear correlations among the evaluated morphometric parameters of the surface utricles were conducted. These analyses were intended to illustrate the eventual close relationships among different parameters, such as the two parallel measurements of utricle size (polygon area and CS) or asymmetry (CSM and PDs).
Then, variation in the utricle parameters was decomposed into different sources, such as individual plants, segments, position of utricles on segments, and their interactions. For this purpose, the utricle parameters (i.e., size, asymmetry, and number of vertices) were used separately as dependent factors in the distance-based type I analysis of variance (ANOVA) models. The main random effect of “plant” was distinguished among the 7 studied individuals. The random effect of “segment”, which evaluated the differences in utricle parameters measured on different segments, was nested within the “plant” effect. The main fixed effect of “position” accounted for the differences among utricles located at the bottom, center, top, or lateral positions on segments. Finally, the interactions among these three effects were used to evaluate the differences in utricle parameters taken from different positions among plants and among segments. The nested structure of the data was reflected in the construction of the F-values based on the ratios of the mean squares (MS) of individual factors and the MS of their appropriate nested effects. The randomized residual permutation procedure (RRPP) was used to evaluate individual factors, based on the randomization of the residual values from a reduced model with respect to the nested structure of the data. The randomized residuals were then added to the predicted values of the dependent variable of the full model, resulting in the pseudo-values yielding multiple random sets of sums of squares (SS). The percentiles of the Z-scores and the standard deviates of the random F-values were used as the p-values, depicting the probability of obtaining an SS of the same size by chance, as assumed by the null hypothesis [26,27]. The randomization analyses were based on 999 permutations. The function procD.lm of the R package geomorph, version 3.2.1 [28], was used for these analyses.
The post hoc tests following up on the above described ANOVA models included the evaluation of differences in utricle parameters among segments in different positions. The differences in the mean values of utricle parameters sampled at different positions across the entire data set of 4800 utricles were tested by permutation tests on differences in means [29]. The 999 random permutations were restricted to the level of individual segments.
2.4. Morphometric Analysis of Segments
The segment outlines were registered by a series 80 equidistant points located along their margins (Table S2). The points were digitized using the automated background curves tool of TpsDig, version 2.22 [13]. The segments were digitized twice. First, the outlines were registered clockwise. Then, in the second digitization, they were registered counter-clockwise and relabeled to match the order of the first digitization. The starting point of the outline at the basal node position was treated as the sole fixed landmark in the subsequent analysis. The remaining 79 points were considered semi-landmarks; that is, during GPA, they were slid iteratively along the tangents to the outline curve, in order to assure optimal correspondence of individual curves to the mean configuration by minimizing the bending energy between each analyzed specimen and the consensus shape [30,31]. As the shape analysis of segments only involved the variation among specimens, their symmetric halves were averaged. This involved reflecting the objects across their axis of symmetry, relabeling the paired semi-landmarks, and averaging the original and mirrored configurations in the GPA [32]. These symmetrized and averaged coordinates aligned by GPA were then subjected to principal component analysis (PCA). The resulting principal components (PCs) were used to illustrate the most important patterns of variation in the shapes of the segments in the studied sample. The sizes of the analyzed segments were captured by the CS of the outline configurations. The function procGPA of the R package geomorph, version 3.2.1 [28], was used for these analyses. The shapes characterizing the marginal occupied positions of individual PCs were visualized in TpsRelw, version 1.65 [13].
The sizes of the segments were compared with the mean utricle parameters (i.e., area, asymmetry, and number of vertices) in individual positions on segments by a series of linear correlation analyses in PAST, version 2.17c [33]. In addition, the differences in mean values of utricle parameters among the analyzed positions within the segments were also compared to the segment size. The shapes of the segments were related to mean values of utricle parameters by a series of multivariate regression analyses. Goodall’s F-ratio was used as the test statistic and the significance of these ratios were assessed by permutation tests with 999 randomizations of the data. The p-values of these analyses were adjusted for multiple comparisons using the Bonferroni correction [34]. The shapes characterizing the marginal occupied positions of the trends predicted by the multivariate regression models were visualized in TpsRegr, version 1.42 [13].
3. Results
3.1. Correlation among Utricle Parameters
The two parallel measures of utricle size (i.e., their polygon area and CS) proved to be closely related (r = 0.98; Table 1). At the same time, the CSM and PDs were closely related, as indicators of polygon asymmetry (r = 0.97). Given the fact that these measures are mathematically closely related and due to their strong mutual correlation, the subsequent analyses only focused on the polygon areas of utricles and their CSM. Among the 4800 analyzed polygons representing the surface views of peripheral utricles, n-gon shapes with n varying from 4 to 9 were observed; of which, 62.4% were hexagons, 20.6% were pentagons, 15.5% were heptagons, and 1.5% were other polygons. The number of vertices of the individual polygons was moderately positively correlated with their area (Table 1), where larger utricles tended to have more vertices than the smaller utricles. Conversely, the correlation between the number of vertices and polygon asymmetry was considerably weaker. Likewise, the measures of polygon size were only weakly positively correlated with their shape asymmetry (Table 1).

Table 1.
Results of the linear correlation analyses among the utricle parameters. Pearson’s r values are shown above the diagonal, the coefficients of determination (R2) below the diagonal. Probabilities (p-values) that individual correlations are not different from zero based on the permutation tests were 0.0001 in all comparisons.
3.2. Utricle Size
The ANOVA model showed that utricle area was most strongly controlled by their position on segments (Table 2). However, differences among segments (evaluated both at the level of individual plants and separately) were also highly significant. At the same time, utricle size also significantly differed among different segments, with regard to their position (Table 2). In total, the analyzed sources of variation in utricle size explained 48.3% of the total variation.

Table 2.
Results of three separate analysis of variance models evaluating the variation in surface utricle parameters of H. tuna.
The subsequent post hoc diagnostic test comparing the areas of utricles in different positions revealed that there was actually a pronounced gradient in utricle size within segments. The utricles sampled at the bottom of segments were, on average, 22.9% smaller than those in central positions (Figure 3a). Likewise, the centrally located utricles were approximately 12.2–15.4% smaller than those measured along the lateral margins and at the top of segments. All of these differences proved to be highly significant, on the basis of the permutation tests on differences in means between the samples (Table 3).
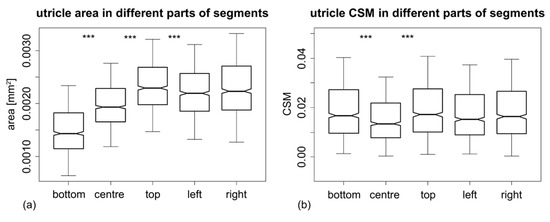
Figure 3.
Boxplots showing the differences in (a) utricle area and (b) polygon asymmetry among different positions on segments. Significant differences between adjacent positions are depicted as *** indicating the p-value = 0.001. The values of mean differences are included in Table 3.

Table 3.
Results of permutation tests evaluating differences in mean values of utricle polygon areas and asymmetry among different positions on segments. The observed differences in mean values are shown above the diagonal and the p-values based on 999 permutations are shown below the diagonal.
3.3. Utricle Symmetry
The ANOVA model evaluating the deviations from symmetry of surface polygons measured by their CSM showed a rather moderate relationship between the independent factors and the analyzed variables (Table 2). However, the symmetry of utricles was significantly different among segments, either at the level of individual plants or evaluated separately as the nested effect within plants. The position of utricles on segments also significantly affected their symmetry, which was significant also in the interaction effect with the factor of segments. Still, the overall model only accounted for 12.3% of the observed variation in the CSM levels among analyzed utricles.
Significance of the “position” effect was largely due to the lower CSM of centrally located utricles (Figure 3b). The CSM values measured in the center of segments were, on average, 15.8–19.8% lower than those sampled in other positions. This difference was significant when comparing the centrally located utricles to all other positions. Conversely, the CSM values of the three remaining positions (bottom, top, and lateral) did not differ more than could be reasonably expected, based on the random variation of their CSM values (Table 3).
3.4. Number of Polygon Vertices of Utricle Shapes
The mean number of polygon vertices proved to be largely unrelated to the analyzed factors. Thus, the ANOVA models showed that this parameter did not significantly differ among different segments or different positions of utricles (Table 2). The overall ANOVA model accounted for only 1.3% of the total variation in the number of polygon vertices in the studied data set.
However, the sample variance significantly differed among different positions on segments. Notably, sample variance of the polygons from the central parts of segments (0.364, 95% C.I.: 0.319–0.405) was significantly lower than in those from the top (0.450, 95% C.I.: 0.406–0.494) or lateral positions (0.445, 95% C.I.: 0.414–0.475). Sample variance of the n-gon distribution of the bottom polygons (0.413, 95% C.I.: 0.371–0.453) was higher than in the centrally located polygons, but the confidence intervals overlapped; thus, this difference was deemed not significant by the bootstrapping tests. These differences in sample variance were also accompanied by different proportion of the hexagons in individual tessellations. While there were 68.0% of hexagons among the centrally located polygons, this proportion was 63.1% in the basal polygons, 60.4% in the lateral polygons, and 59.9% in the top located polygons.
3.5. Morphology of Segments and Their Relation to Utricle Size and Symmetry
The PCA showed that most of the variation in shape of the segments was concentrated into two dimensions, represented by PC1 (76.8%) and PC2 (14.5%). PC1 illustrated the shape change from the segments, with inversely conic shapes possessing distinctly elongated basal parts compared to those with wide reniform shapes, while PC2 largely illustrated the difference between segments with distinctly convex basal regions and segments with concave basal portions and rounded apical outlines (see Figure 4a). The multivariate regression of the shape data on the CS of segments yielded a highly significant model which explained 51.6% of the total variation in segment shapes (F = 32.35, p = 0.001). According to this model, small segments were typically related to inversely conic shapes with relatively flat apical parts of the outline. Conversely, large segments were generally related to reniform shapes with concave basal portions (Figure 4b).
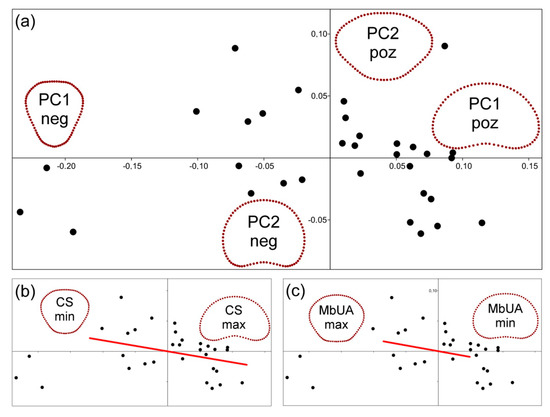
Figure 4.
Plots showing the ordination structure of segment shapes: (a) two principal components describing most of the variation in segment outlines. Shapes corresponding to marginal occupied positions on both axes are shown; (b) the ordination plot of PC1 vs. PC2 with the allometric line (which was reconstructed by the multivariate regression model) projected onto the ordination space. The signs “CSmin” and “CSmax” correspond to shapes typical of segments with minimum and maximum centroid size values; and (c) the ordination plot of PC1 vs. PC2. The line representing the multivariate regression of segment shapes on their mean utricle area in the bottom positions projected onto the ordination space. The signs “MbUAmin” and “MbUAmax” correspond to shapes typical for segments with the minimum and maximum areas of utricles in their bottom positions.
Comparison of the segment size with utricle parameters showed that utricle area in the basal parts of segments was the only parameter which was significantly related to their CS (Pearson’s r = −0.54, p = 0.0013; Table S3). Segment CS was also significantly positively related to mean differences in size among the utricles located at the bottom of segments and those in other positions. The Pearson’s r of these relationships varied from 0.51–0.73 in different comparisons (Table S4). Thus, the relatively small segments with inversely conic shapes had consistently less pronounced gradients of within-segment utricle area variation than comparatively large segments with discoid and reniform shapes (Figure 5); on the other hand, there was no significant relationship between the segment size and the extent of differences in CSM among different positions on segments (Table S4). A series of multivariate regression analyses explaining the shape variation of segments by different utricle parameters showed that the utricle area at the bottom of segments was moderately related to the outline shape (F = 3.619, R2 = 0.108, p = 0.036). Although the p-value of this relationship proved to be above the Bonferroni-corrected threshold, the area of utricles in the basal position was the single most important explanatory factor with regard to the shape of the analyzed segments (Table S5). The segments with relatively small utricles in their basal parts tended to have more reniform shapes, while these located on the opposite side of this model had relatively narrower and inversely conic shapes (Figure 4c).
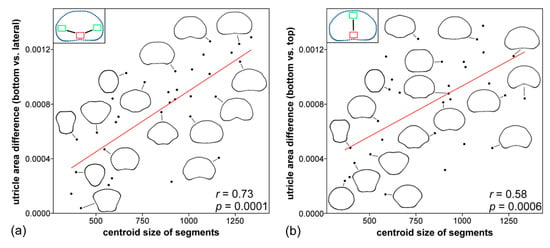
Figure 5.
Linear correlation between the segment size (CS) and the difference in means of utricle parameters sampled: (a) at the bottom and along the lateral margins of individual segments, and (b) at the bottom and in the apical parts of segments. The outline shapes of selected segments along the gradients are shown.
4. Discussion
The primary subject of this study was the quantitative evaluation of the size and symmetry of H. tuna surface utricles. The sizes of the surface polygons formed by the upper side of the primary utricles proved to be significantly related to their position on H. tuna segments. The utricles in the basal parts had, on average, about 35% smaller area than those located in the marginal position on segments. To the best of our knowledge, such systematic variation of surface utricle dimensions within segments has not been reported in the published literature and it is currently unknown whether similar gradients in surface polygon areas may also occur in other Halimeda species. On the other hand, infraspecific variation in utricle size among different segments, which is usually expressed as the diameter of the surface polygons, has been recorded many times in the taxonomic literature [1,2,35]. It has also been shown, in Mediterranean H. tuna and in tropical H. copiosa, that plants growing in deeper parts of the sublittoral with lower illumination typically have larger surface utricles [36,37]. Conversely, substantial variation in the surface diameters of the primary utricles was not correlated with any environmental factors, such as depth or illumination, in tropical H. macroloba [9]. The magnitude of the size variation in surface utricles of Mediterranean H. tuna, as observed in this study, which took place at a small scale from the base of the segments to their top and marginal parts, was broadly comparable to the above-mentioned infraspecific variability; or even to the differences among related species, at least those with a closed polygon-shaped surface layer of primary utricles [1,4,35]. It should be noted that the observed size variation of surface polygons does not necessarily mean that their volumes were different, as well. It is possible that the smaller utricles located in the basal parts of segments were more tightly packed, leading to their relatively smaller apical polygon area. In such a scenario, they should be relatively longer than the utricles in other parts of segments.
It has been repeatedly shown that species with differently sized surface utricles vary in mean CaCO3 content in their segments [3,4]. Thus, it is conceivable that different parts of H. tuna segments may also reach different calcification levels. Such a hypothesis could be tested by a detailed analysis of CaCO3 gradients within segments; preferably those with relatively large size, as our analyses showed that the within-segment utricle size gradient was considerably more pronounced in relatively large segments. These segments usually have discoid to reniform shapes, which are considered “typical” for Mediterranean H. tuna [1,2,38]. Conversely, the analyses showed that smaller segments with shapes considered deviant from the species-specific template that more often occur in lower portions of Halimeda thalli [7] had a considerably less pronounced gradient in surface utricle area. However, it should be noted that this might have also been related to the fact that the actual spatial distance among the bottom, center, and marginal locations was smaller in these segments, rather than to their shape differences from the considerably larger reniform segments.
The overall size of the surface views of peripheral utricles was largely independent of the segment size. The only significant relationship between utricle and segment size was a negative correlation between polygon area of the utricles located in the basal positions and CS of segments. However, this relationship was due to the above-mentioned and more pronounced differentiation in utricle size within large reniform segments; otherwise, it can be stated that utricle size was not significantly related to segment size. This means that the surface of the small segments was composed of fewer peripheral utricles than in comparatively large segments, but their species-specific size was retained within and among individuals. This finding is largely analogous to the overall lack of correlation between mesophyll cell size and leaf area in vascular plants [39]. In this respect, the Halimeda segments, which are composed of a multinucleate syncytium, are constructed in a similar way as the multicellular tissue of plant leaves. The final segment size depends on the number of surface utricles and, hence, on the number of branchlets formed by the secondary filaments in the early stages of segment morphogenesis [40], which is somewhat analogous to the number of cell divisions determining the final leaf area of plants [39,41].
In addition to size differences, the surface utricles also differed in their symmetry. The central parts of segments proved to be composed of significantly more symmetric surface polygons than those in marginal locations. This pattern was also confirmed by the higher proportion of hexagons and overall lower variance of the n-gon distribution in the central parts of segments. All this suggests that the bases of the peripheral utricles are located more regularly in the central region of segments. The precursors of utricles in the early stages of segment morphogenesis are formed by small branchlets of the secondary filaments, produced in a perpendicular direction to the surface of the developing segment [40]. These protoutricles are packed close to each other and eventually form the closed surface layer by lateral adhesion of their cell walls. Thus, the position or developmental timing of these young utricles is probably more irregular along the margins of the developing segment, which was indicated by the higher polygon asymmetry of mature surface utricles forming the outer cortex layer. It should be noted that this pattern is probably independent of the within-segment size variation among the peripheral utricles. While the bottom surface polygons were significantly smaller than those located in the lateral and top positions, their asymmetry was approximately equal. Thus, the only factor leading to an increase in overall symmetry of the surface tessellation seems to be the distance from the segment margins. In addition, this seemed to apply equally to different segments, regardless of their size, as lower asymmetry of centrally located surface polygons held evenly across the size gradient of segments.
While mean area and asymmetry of the surface utricles differed among segments, they were not closely related to their size and shape. In fact, mean utricle size in the basal parts of segments proved to be the only marginally significant relationship among the utricle size and shape features of segments. This relationship indicated that smaller segments with inversely conic shapes usually had relatively larger utricles in their basal parts. Of course, this analysis concurs well with the relatively tight relationship between the utricle and segment size, since the segments with inversely conic shapes and smaller size values had less pronounced gradients of within-segment utricle area variation than comparatively large segments with discoid and reniform shapes.
The CSM values were not larger in the smaller segments with non-reniform shapes. Based on our analyses, deviation from an ideally symmetric hexagonal tessellation, as evaluated by an increase in mean CSM of individual polygons, did not depend on the size of segments or their position in the morphospace. Therefore, the differences among segments in overall polygon symmetry of their surface layer may have been related to specific environmental or physiological conditions during their morphogenesis, but they could not be easily judged based on their morphology.
Lateral fusion of the surface utricles has been observed in some taxa belonging to the same section of the genus Halimeda as the studied species [42,43,44]. In such cases, two or more adjacent utricles were fused, which, in the surface view, can be recognized by occurrence of a large and usually distinctly elongated polygon [1]. Thus, the presence of such laterally fused utricles could obviously lead to an increase in mean CSM of the analyzed configurations. However, Kooistra et al. reported that lateral fusion of peripheral utricles does not occur in H. tuna [45], and we did not detect any obvious example of this phenomenon in our photographs either. While the occasional occurrence of lateral fusion of peripheral utricles in Mediterranean H. tuna cannot be completely ruled out, there were no indications that these fused utricles should be more frequent in any particular position on segments. Therefore, it is deemed unlikely that this phenomenon might have influenced the presented analyses.
Shape variation of segments was largely concentrated in the two dimensions recovered by PCA. These dimensions were remarkably similar to the two most important axes of symmetric shape variation, as illustrated in a previous study of shape variation in H. tuna segments [11]. Given the fact that the present study was conducted on a completely different population of this species, it can be assumed that these axes represent the genetically fixed segment variation patterns of Mediterranean H. tuna. The same applies to the allometric shape change between small and large segments, which was very similar to the regression model illustrated in the previous study of this species [11]. These stable variation patterns may represent deeply fixed features of the entire family-level lineage, or they may vary across different sections or species of the genus Halimeda. However, this remains to be investigated in the future, by comparison of the morphospace structure and allometric trajectories of multiple taxa across the phylogenetic diversity of the genus.
The methodology of this study was based on the registration of individual utricles. However, current algorithms of pattern recognition of mesh-like structures [46] might represent a promising way towards automated registration of larger portions of the polygon tessellation formed by the Halimeda surface utricles. This might then facilitate rapid analyses of large datasets that could be suitable for evaluating a wide range of hypotheses concerning the biology and ecology of Halimeda populations.
Supplementary Materials
The following are available online at https://www.mdpi.com/2073-8994/12/8/1271/s1, Table S1: Landmark coordinates of the vertices of individual utricles used in the morphometric analyses, Table S2: Landmark coordinates of segment outlines of Halimeda tuna used in the geometric morphometric analyses, Table S3: Results of the linear correlation analyses between the size of segments (CS) and the mean values of utricle parameters, Table S4: Results of the linear correlation analyses between the segment size (CS) and the difference in means of utricle parameters sampled at two different positions on individual segments, Table S5: Results of the multivariate regression analyses evaluating the relationships between the variation in shape of individual segments and the mean values of utricle parameters.
Author Contributions
J.N. and Y.N. conceived and designed the research; J.N. performed the experiments and analyzed the data; and both J.N. and Y.N. wrote the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Charles University in Prague; project number “Progres no. 43”.
Acknowledgments
The algae were sampled based on the field research permit awarded to the authors by the Ministry of the Sea, Transport, and Infrastructure of the Republic of Croatia (no. 6422/2019/JLJ). The authors thank MDPI Author Services for English language editing and style corrections.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Hillis-Colinvaux, L. Ecology and Taxonomy of Halimeda: Primary Producer of Coral Reefs; Academic Press: London, UK, 1980; p. 327. [Google Scholar]
- Verbruggen, K.; Kooistra, W.H.C.F. Morphological characterization of lineages within the calcified tropical seaweed genus Halimeda (Bryopsidales, Chlorophyta). Eur. J. Phycol. 2004, 39, 213–228. [Google Scholar] [CrossRef]
- Borowitzka, M.A.; Larkum, A.W.D. Calcification in the green alga Halimeda. III. The sources of inorganic carbon for photosynthesis and calcification and a model of the mechanism of calcification. J. Exp. Bot. 1976, 27, 879–893. [Google Scholar] [CrossRef]
- Peach, K.E.; Koch, M.S.; Blackwelder, P.L.; Guerrero-Given, D.; Kamasawa, N. Primary utricle structure of six Halimeda species and potential relevance for ocean acidification tolerance. Bot. Mar. 2017, 60, 1–11. [Google Scholar] [CrossRef]
- Phillips, D. Tessellation. WIRES Comput. Stat. 2014, 6, 202–209. [Google Scholar] [CrossRef]
- Caër, G.L.; Ho, J.S. The Voronoi tessellation generated from eigenvalues of complex random matrices. J. Phys. A Math. Gen. 1990, 23, 3279–3295. [Google Scholar] [CrossRef]
- Verbruggen, H.; De Clerck, O.; Coppejans, E. Deviant segments hamper a morphometric approach towards Halimeda taxonomy. Crypt. Algol. 2005, 26, 259–274. [Google Scholar]
- Vroom, P.S.; Smith, C.M.; Coyer, J.A.; Walters, L.J.; Hunter, C.L.; Beach, K.S.; Smith, J.E. Field biology of Halimeda tuna (Bryopsidales, Chlorophyta) across a depth gradient: Comparative growth, survivorship, recruitment, and reproduction. Hydrobiologia 2003, 501, 149–166. [Google Scholar] [CrossRef]
- Pongparadon, S.; Zuccarello, G.C.; Prathep, A. High morpho-anatomical variability in Halimeda macroloba (Bryopsidales, Chlorophyta) in Thai waters. Phycol. Res. 2017, 65, 136–145. [Google Scholar] [CrossRef]
- Pongparadon, S.; Nooek, S.; Prathep, A. Phenotypic plasticity and morphological adaptation of Halimeda opuntia (Bryopsidales, Chlorophyta) to light intensity. Phycol. Res. 2020, 68, 115–125. [Google Scholar] [CrossRef]
- Neustupa, J.; Nemcova, Y. Morphological allometry constrains symmetric shape variation, but not asymmetry, of Halimeda tuna (Bryopsidales, Ulvophyceae) segments. PLoS ONE 2018, 13, e0206492. [Google Scholar] [CrossRef]
- Noble, J.M. Halimeda magnidisca (Caulerpales, Chlorophyta), a new species from the Great Barrier Reef, Australia. Phycologia 1986, 25, 331–339. [Google Scholar] [CrossRef]
- Rohlf, F.J. The tps series of software. Hystrix Ital. J. Mammal. 2015, 26, 9–12. [Google Scholar]
- Barber, C.B.; Dobkin, D.P.; Huhdanpaa, H.T. The Quickhull algorithm for convex hulls. ACM Trans. Math. Softw. 1996, 22, 469–483. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing. 2018. Available online: https://www.r-project.org/ (accessed on 8 June 2020).
- Klingenberg, C.P. Size, shape, and form: Concepts of allometry in geometric morphometrics. Dev. Genes Evol. 2016, 226, 113–137. [Google Scholar] [CrossRef] [PubMed]
- Zabrodsky, H.; Peleg, S.; Avnir, D. Continuous symmetry measures. J. Am. Chem. Soc. 1992, 114, 7843–7851. [Google Scholar] [CrossRef]
- Zabrodsky, H.; Peleg, S.; Avnir, D. Symmetry as a continuous feature. IEEE Trans. Pattern Anal. Mach. Intell. 1995, 17, 1154–1166. [Google Scholar] [CrossRef]
- Zabrodsky, H.; Avnir, D. Continuous symmetry measures. 4. Chirality. J. Am. Chem. Soc. 1995, 117, 462–473. [Google Scholar] [CrossRef]
- Zahrt, A.F.; Denmark, S.E. Evaluating continuous chirality measure as a 3D descriptor in chemoinformatics applied to asymmetric catalysis. Tetrahedron 2019, 75, 1841–1851. [Google Scholar] [CrossRef]
- Graham, J.H.; Whitesell, M.J.; Fleming, M., II.; Hel-Or, H.; Nevo, E.; Raz, S. Fluctuating asymmetry of plant leaves: Batch processing with LAMINA and continuous symmetry measures. Symmetry 2015, 7, 255–268. [Google Scholar] [CrossRef]
- Iovita, R.; Tuvi-Arad, I.; Moncel, M.H.; Despriée, J.; Voinchet, P.; Bahain, J.J. High handaxe symmetry at the beginning of the European Acheulian: The data from la Noira (France) in context. PLoS ONE 2017, 12, e0177063. [Google Scholar] [CrossRef]
- Dryden, I.L. Shapes: Statistical Shape Analysis. R Package Version 1.2.5. 2019. Available online: https://CRAN.R-project.org/package=shapes (accessed on 8 June 2020).
- Klingenberg, C.P. Analyzing fluctuating asymmetry with geometric morphometrics: Concepts, methods, and applications. Symmetry 2015, 7, 843–934. [Google Scholar] [CrossRef]
- Li, K.; Gao, X.L.; Wang, J. Dynamic crushing behavior of honeycomb structures with irregular cell shapes and non-uniform cell wall thickness. Int. J. Sol. Struct. 2007, 44, 5003–5026. [Google Scholar] [CrossRef]
- Anderson, M.J.; Ter Braak, C.J.F. Permutation tests for multi-factorial analysis of variance. J. Stat. Comp. Sim. 2003, 73, 85–113. [Google Scholar] [CrossRef]
- Collyer, M.L.; Sekora, D.J.; Adams, D.C. A method for analysis of phenotypic change for phenotypes described by high-dimensional data. Heredity 2015, 115, 357–365. [Google Scholar] [CrossRef] [PubMed]
- Adams, D.C.; Otárola-Castillo, E. Geomorph: An R package for the collection and analysis of geometric morphometric shape data. Meth. Ecol. Evol. 2013, 4, 393–399. [Google Scholar] [CrossRef]
- Good, P.I. Permutation, Parametric, and Bootstrap Tests of Hypotheses, 3rd ed.; Springer: New York, NY, USA, 2005; p. 316. [Google Scholar]
- Bookstein, F.L. Landmark methods for forms without landmarks: Morphometrics of group differences in outline shape. Med. Image Anal. 1997, 1, 225–243. [Google Scholar] [CrossRef]
- Perez, S.I.; Bernal, V.; Gonzales, P.N. Differences between sliding semi-landmark methods in geometric morphometrics, with an application to human craniofacial and dental variation. J. Anat. 2006, 208, 769–784. [Google Scholar] [CrossRef]
- Klingenberg, C.P.; Barluenga, M.; Meyer, A. Shape analysis of symmetric structures: Quantifying variation among individuals and asymmetry. Evolution 2002, 56, 1909–1920. [Google Scholar] [CrossRef]
- Hammer, Ø.; Harper, D.A.T.; Ryan, P.D. PAST: Paleontological statistics software package for education and data analysis. Palaeont. Electron. 2001, 4, 1–9. [Google Scholar]
- Perrett, J.J.; Mundfrom, D.J. Bonferroni procedure. In Encyclopedia of Research Design; Salkind, N.J., Ed.; Sage Publ.: Thousand Oaks, CA, USA, 2010; Volume 1, pp. 98–101. [Google Scholar]
- Pongparadon, S.; Zuccarello, G.C.; Phang, S.M.; Kawai, H.; Hanyuda, T.; Prathep, A. Diversity of Halimeda (Chlorophyta) from the Thai–Malay Peninsula. Phycologia 2015, 54, 349–366. [Google Scholar] [CrossRef]
- Mariani Colombo, P.; Orsenigo, M. Sea depth effects on the algal photosynthetic apparatus II. An electron microscopic study of the photosynthetic apparatus of Halimeda tuna (Chlorophyta, Siphonales) at—0–5 m and—6–0 m sea depths. Phycologia 1977, 16, 9–17. [Google Scholar] [CrossRef]
- Blair, S.M.; Norris, J.N. The deep-water species of Halimeda Lamouroux (Halimedaceae, Chlorophyta) from San Salvador Island, Bahamas: Species composition, distribution and depth records. Coral Reefs 1988, 6, 227–236. [Google Scholar] [CrossRef]
- Verbruggen, H.; De Clerck, O.; Schils, T.; Kooistra, W.H.C.F.; Coppejans, E. Evolution and phylogeography of Halimeda section Halimeda (Bryopsidales, Chlorophyta). Mol. Phyl. Evol. 2005, 37, 789–803. [Google Scholar] [CrossRef] [PubMed]
- John, G.P.; Scoffoni, C.; Sack, L. Allometry of cells and tissues within leaves. Am. J. Bot. 2013, 100, 1936–1948. [Google Scholar] [CrossRef]
- Larkum, A.W.D.; Salih, A.; Kühl, M. Rapid mass movement of chloroplasts during segment formation of the calcifying siphonalean green alga, Halimeda macroloba. PLoS ONE 2011, 6, e20841. [Google Scholar] [CrossRef][Green Version]
- Pérez-Pérez, J.M.; Rubio-Díaz, S.; Dhondt, S.; Hernández-Romero, D.; Sánchez-Soriano, J.; Beemster, G.T.S.; Rosa Ponce, M.; Micol, J.L. Whole organ, venation and epidermal cell morphological variations are correlated in the leaves of Arabidopsis mutants. Plant Cell Environ. 2011, 34, 2200–2211. [Google Scholar] [CrossRef]
- Kojima, R.; Hanyuda, T.; Kawai, H. Taxonomic re-examination of Japanese Halimeda species using genetic markers, and proposal of a new species Halimeda ryukyuensis (Bryopsidales, Chlorophyta). Phycol. Res. 2015, 63, 178–188. [Google Scholar] [CrossRef]
- Cremen, M.C.M.; Huisman, J.M.; Marcelino, V.R.; Verbruggen, H. Taxonomic revision of Halimeda (Bryopsidales, Chlorophyta) in south-western Australia. Aust. Syst. Bot. 2016, 29, 41–54. [Google Scholar] [CrossRef]
- Ximenes, C.F.; Cassano, V.; Oliveira-Carvalho, M.F.; Bandeira-Pedrosa, M.E.; Gurgel, C.F.D.; Verbruggen, H.; Barreto Pereira, S.M. Systematics of the genus Halimeda (Bryopsidales, Chlorophyta) in Brazil including the description of Halimeda jolyana sp. nov. Phycologia 2017, 56, 369–381. [Google Scholar] [CrossRef]
- Kooistra, W.H.C.F.; Coppejans, E.G.G.; Payri, C. Molecular systematics, historical ecology, and phylogeography of Halimeda (Bryopsidales). Mol. Phyl. Evol. 2002, 24, 121–138. [Google Scholar] [CrossRef]
- Lin, W.C.; Liu, Y. A lattice-based MRF model for dynamic near-regular texture tracking. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 777–792. [Google Scholar] [CrossRef] [PubMed]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).