Ambit Field Modelling of Isotropic, Homogeneous, Divergence-Free and Skewed Vector Fields in Two Dimensions
Abstract
1. Introduction
2. Background
2.1. Two-Dimensional Turbulence
2.2. Lévy Bases
- (a)
- is infinitely divisible for all ;
- (b)
- are independent for disjoint subsets ;
- (c)
- For disjoint subsets with we have
2.3. Ambit Fields
3. Modeling Framework
3.1. Stream Function
3.2. Vector Field
4. Skewness
4.1. Decomposition
4.2. Triads
5. Key Example
6. Discussion
Funding
Conflicts of Interest
Appendix A
References
- Barndorff-Nielsen, O.; Schmiegel, J. Ambit processes; with applications to turbulence and cancer growth. In Stochastic Analysis and Applications: The Abel Symposium 2005; Benth, F., Di Nunno, G., Linstrøm, T., Øksendal, B., Zhang, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 93–124. [Google Scholar]
- Schmiegel, J. Ambit fields: A stochastic modelling approach. Math. Comput. Model. Dyn. Syst. 2018, 24, 383–400. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O.; Benth, F.; Veraart, A. Ambit Stochastics; Springer Nature: Cham, Switzerland, 2018. [Google Scholar]
- Veraart, A. Modelling, simulation and inference for multivariate time series of counts using trawl pocesses. J. Multivar. Anal. 2019, 169, 110–129. [Google Scholar] [CrossRef]
- Bennedsen, M.; Lunde, A.; Pakkanen, M. Hybrid scheme for Brownian semistationary processes. Financ. Stoch. 2017, 21, 931–965. [Google Scholar] [CrossRef]
- Hedevang, E.; Schmiegel, J. A Lévy based approach to random vector fields: With a view towards turbulence. Int. J. Nonlinear Sci. Numer. Simul. 2014, 15, 411–435. [Google Scholar] [CrossRef]
- Frisch, U. Turbulence; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Kraichnan, R.; Montgomery, D. Two-dimensional turbulence. Rep. Prog. Phys. 1980, 43, 547–620. [Google Scholar] [CrossRef]
- Chevillard, L.; Garban, C.; Rhodes, R.; Vargas, V. On a skewed and multifractal unidimensional random field, as a probabilistic representation of Kolmogorov’s views on turbulence. Ann. Henri Poincaré 2019, 20, 3693–3741. [Google Scholar] [CrossRef]
- Muzy, J.F. Continuous cascades in the wavelet space as models for synthetic turbulence. Phys. Rev. E 2019, 99, 042113. [Google Scholar] [CrossRef] [PubMed]
- Pereira, M.; Garban, C.; Chevillard, L. A dissipative random velocity field for fully developed fluid turbulence. J. Fluid Mech. 2016, 794, 369–408. [Google Scholar] [CrossRef]
- Tabeling, P. Two-dimensional turbulence: A physicist approach. Phys. Rep. 2002, 362, 1–62. [Google Scholar] [CrossRef]
- Rajput, B.; Rosinski, J. Spectral representation of infinitely divisible distributions. Probab. Theory Relat. Fields 1989, 82, 451–487. [Google Scholar] [CrossRef]
- Sauri, O. On the divergence and vorticity of vector ambit fields. Stoch. Process. Their Appl. 2020, in press. [Google Scholar] [CrossRef]
- Rivera, M.; Wu, X. Homogeneity and the inertial range in driven two-dimensional turbulence. Phys. Fluids 2002, 14, 3098. [Google Scholar] [CrossRef]
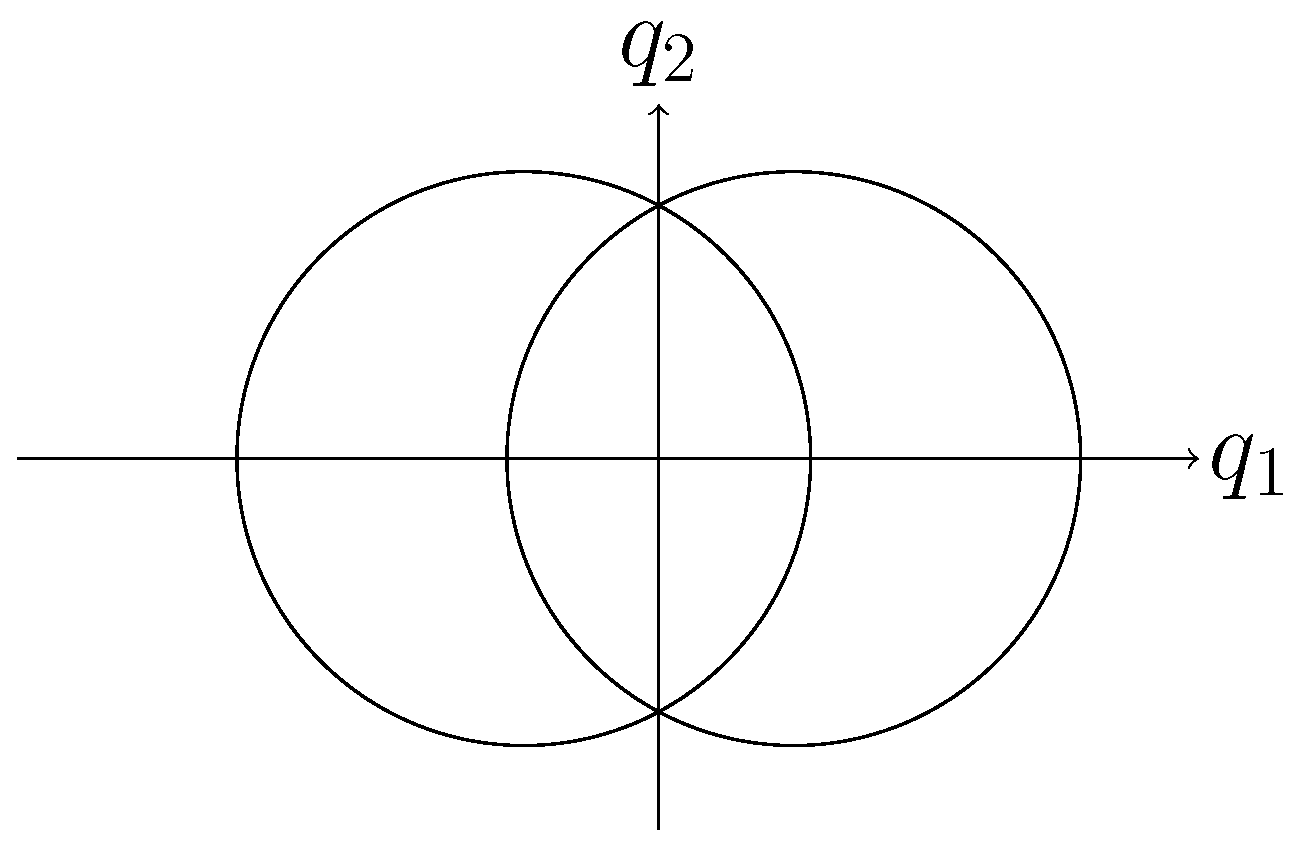
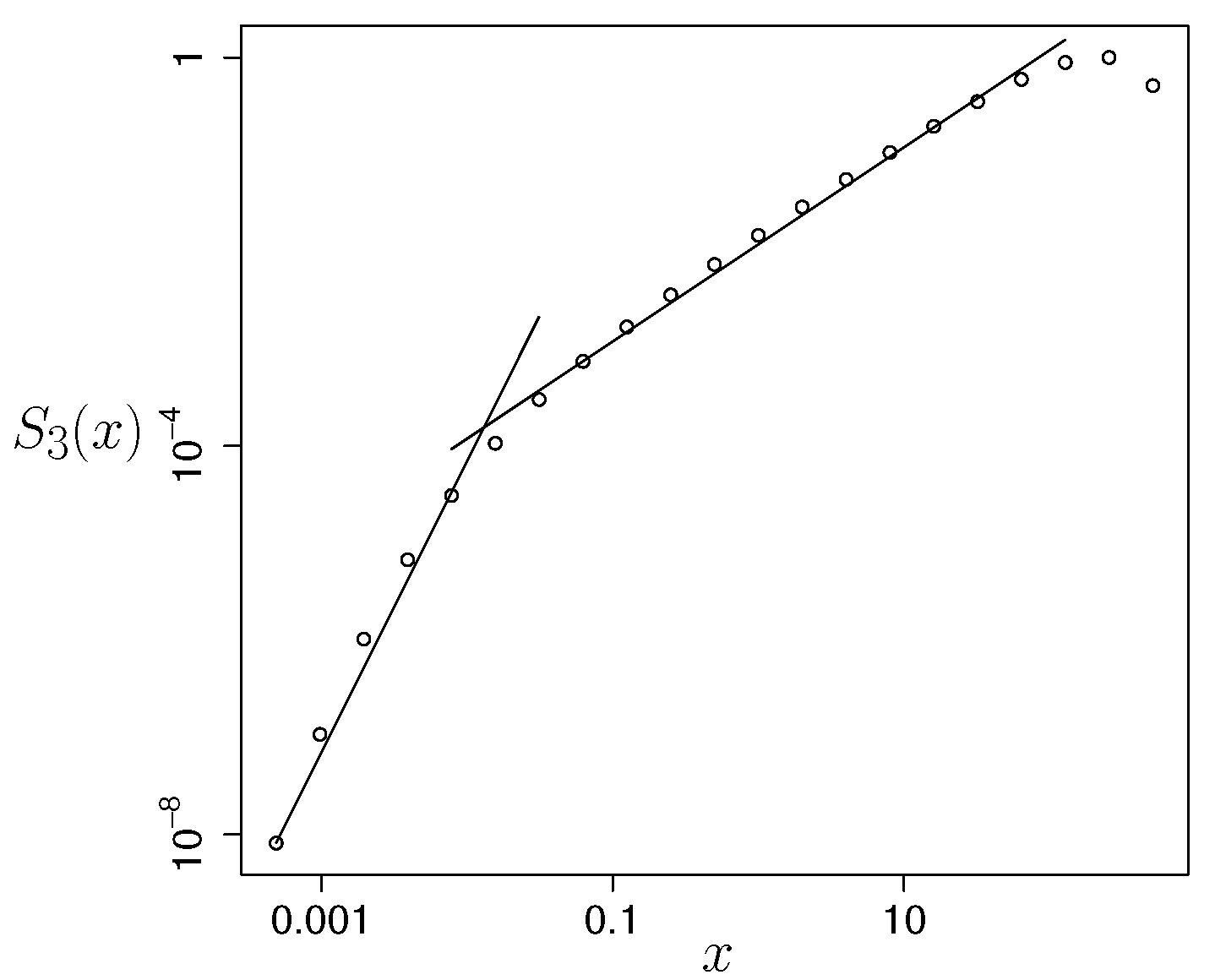
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schmiegel, J. Ambit Field Modelling of Isotropic, Homogeneous, Divergence-Free and Skewed Vector Fields in Two Dimensions. Symmetry 2020, 12, 1265. https://doi.org/10.3390/sym12081265
Schmiegel J. Ambit Field Modelling of Isotropic, Homogeneous, Divergence-Free and Skewed Vector Fields in Two Dimensions. Symmetry. 2020; 12(8):1265. https://doi.org/10.3390/sym12081265
Chicago/Turabian StyleSchmiegel, Jürgen. 2020. "Ambit Field Modelling of Isotropic, Homogeneous, Divergence-Free and Skewed Vector Fields in Two Dimensions" Symmetry 12, no. 8: 1265. https://doi.org/10.3390/sym12081265
APA StyleSchmiegel, J. (2020). Ambit Field Modelling of Isotropic, Homogeneous, Divergence-Free and Skewed Vector Fields in Two Dimensions. Symmetry, 12(8), 1265. https://doi.org/10.3390/sym12081265



