Numerical Picard Iteration Methods for Simulation of Non-Lipschitz Stochastic Differential Equations
Abstract
1. Introduction
2. Numerical Analysis of the Splitting Approaches
- Homogeneous equation:where we have the solution , where m are the iterative steps of the Picard iterations, see the Section 2.1.
- Inhomogeneous equation:where we have the solution , where m are the iterative steps of the Picard iterations, see the Section 2.1.
- Approximate the diffusion process,
- Picard iterations with Doléans-Dade solutions of the SDE,
- Discretisation of the Picard iterations in time.
- Discretisation of the Picard iterations in time for the inhomogeneous part,
- Approximation of the integral-formulation of the inhomogeneous part.
2.1. Homogeneous Equation
2.1.1. Approximate the Diffusion Process
2.1.2. Picard Iterations with Doléans-Dade Solutions of the SDE
2.1.3. Discretisation of the Picard Iterations in Time
2.2. Inhomogeneous Equation
2.2.1. Discretisation of the Picard Iterations in Time for the Inhomogeneous Part
2.2.2. Approximation of the Integral-Formulation of the Inhomogeneous Part
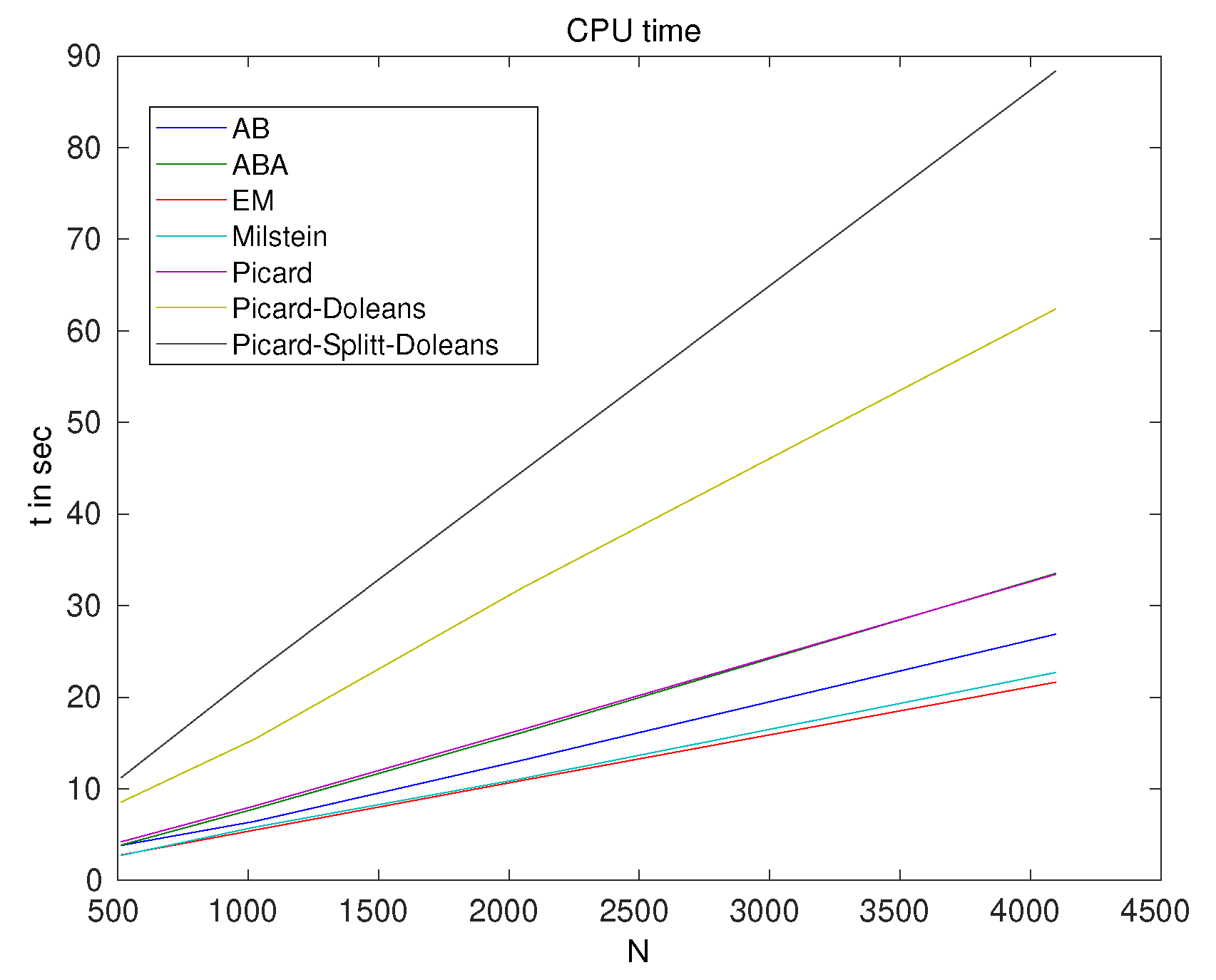
3. Numerical Examples
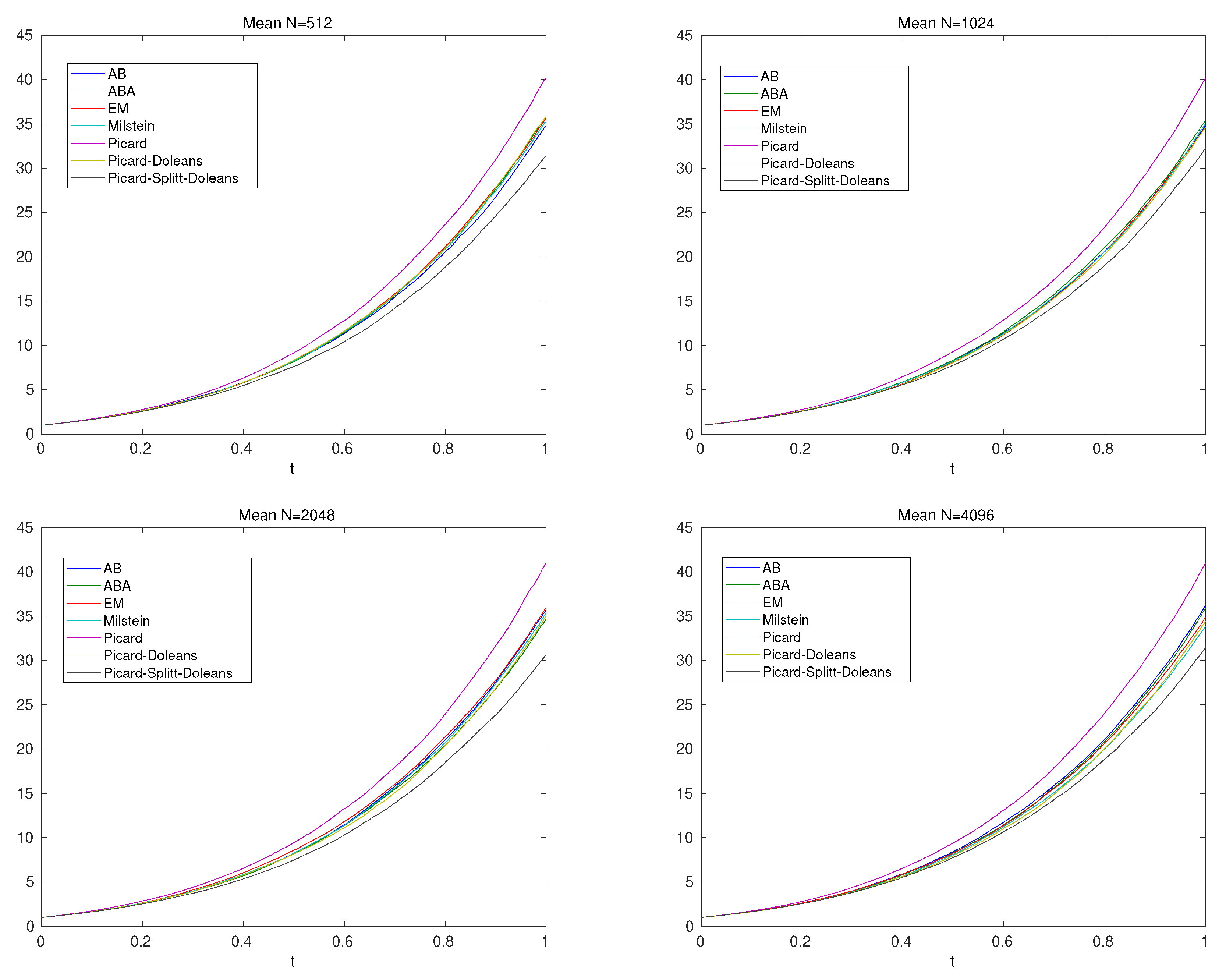
- AB-splitting approaches (AB), see [26],
- Iterative Picard-splitting with Doléans-Dade exponential approach (Picard-Splitt-Doleans), see Section 2.
3.1. First Example: Nonlinear SDE With Root-Function or Irrational Function
- Euler-Maruyama-Schemewhere , and obeys the Gaussian normal distribution with and .We have with .
- Milstein-Schemewhere , and obeys the Gaussian normal distribution with and .We have with .
- AB-splitting approach:We initialize with , while and we have is the initial condition.We deal with the 2 steps:
- A-step:
- B-part:where we have the solution and we go to the next time-step till .
- ABA-splitting approach:We initialize with , while and we have is the initial condition.We deal with the 2 steps:
- A-step ():
- B-part ():
- A-step ():where we have the solution and we go to the next time-step till .
- Iterative Picard approach:we apply an Picard-Iterationwhere , while we apply the implicit method in the drift term and the explicit method in the diffusion term.The algorithm is given as: We initialize with , while and we have is the initial condition.We deal with the 2 loops (loop 1 is the computation over the full time-domain and loop 2 is the computation with ):
- :
- :
- Computation
- , if then we are done, else we go to Step (c)
- , if then we are done, else we go to Step (b)
- Iterative Picard with Doléans-Dade exponential approach:we apply an Picard with Doléans-Dade exponential approachwhere , while we apply the implicit method in the drift term and the explicit method in the diffusion term.The algorithm is given as: We initialize with , while and we have is the initial condition.We deal with the 2 loops (loop 1 is the computation over the full time-domain and loop 2 is the computation with ):
- :
- :
- Computation
- , if then we are done, else we go to Step (c)
- , if then we are done, else we go to Step (b)
- Iterative Picard-Splitting with Doléans-Dade exponential approach:we apply the following splitting approach:where .We apply the Picard-iterations with Doléans-Dade exponential approach and the splitting approach:where , while we apply the implicit method in the drift term and the explicit method in the diffusion term.The algorithm is given as: We initialize with , while and we have is the initial condition.We deal with the 2 loops (loop 1 is the computation over the full time-domain and loop 2 is the computation with ):
- :
- :
- Computation (we apply the full exp):
- , if then we are done, else we go to Step (c)
- , if then we are done, else we go to Step (b)
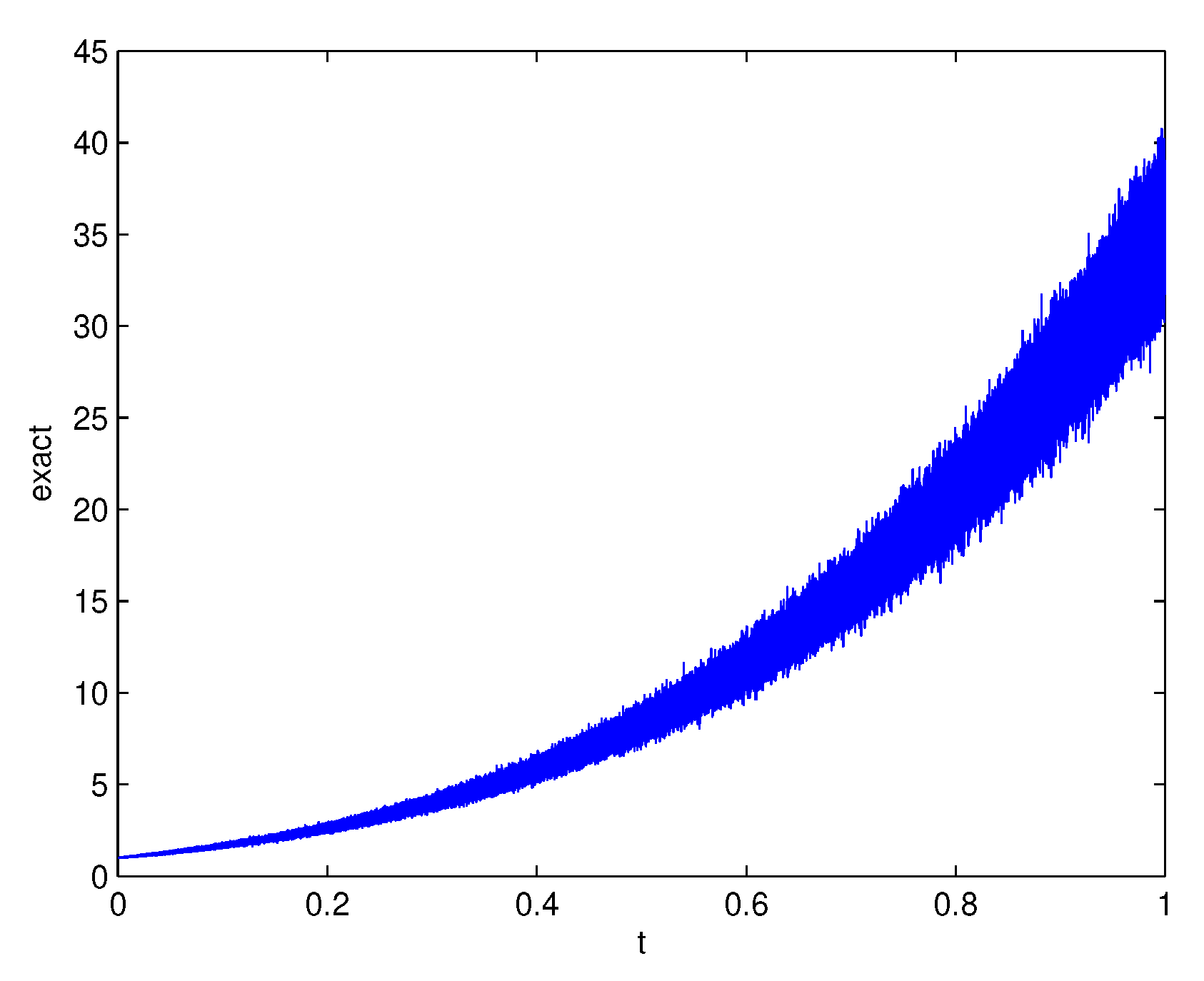
- Mean value at and J-sample paths:we deal with time-step with and the time-points are , with end-time-point . For the sample paths, we apply or and for the methods, we have .
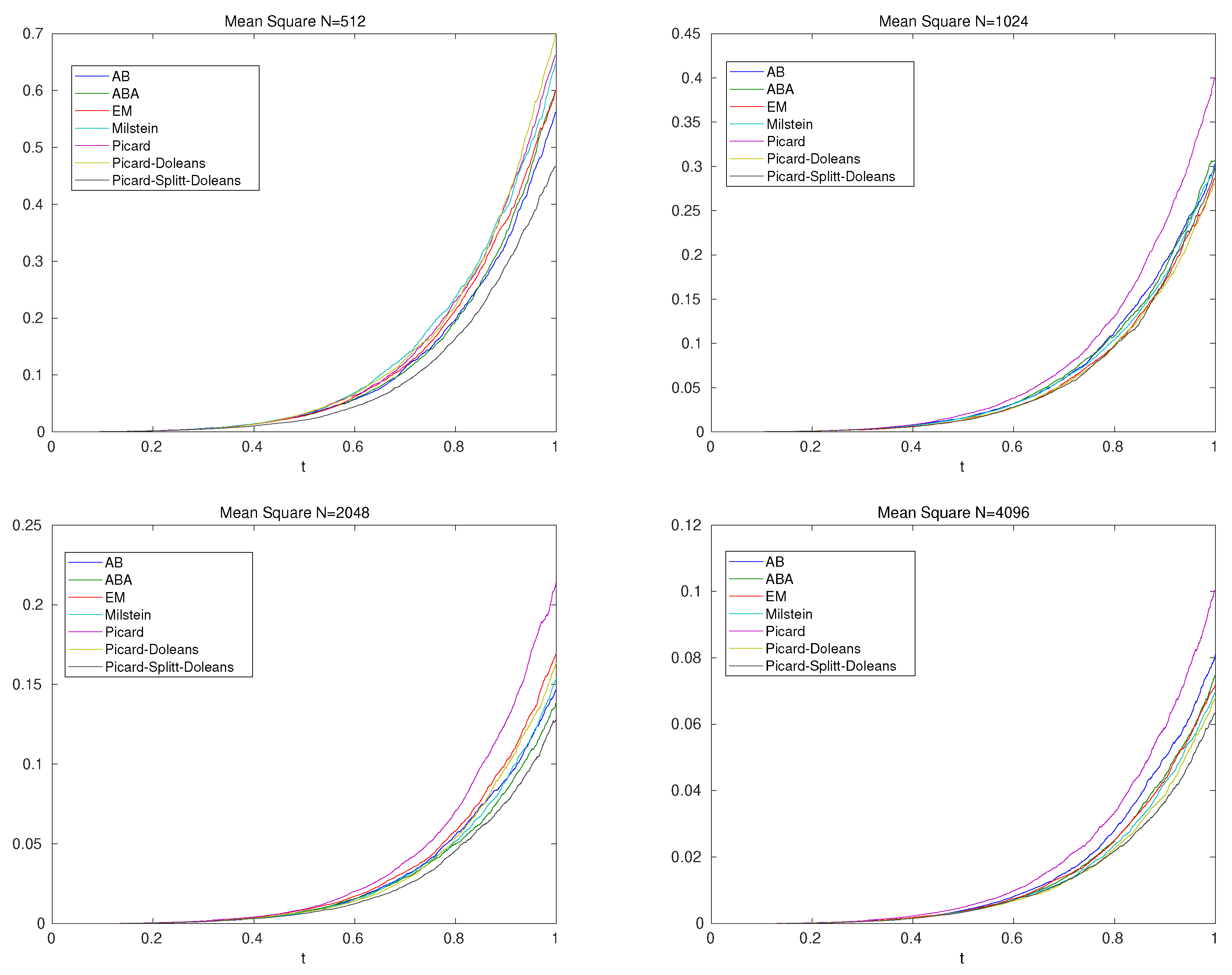
- Local mean square error value at and J-sample paths:we deal with time-step with and the time-points are , with end-time-point . For the sample paths, we apply or and for the methods, we have .
- Global means square error over the full time-scale with different time-steps and J-sample path:where we apply the Equation (30) for the local means square error. Further, we deal with with . For the sample paths, we apply or and for the methods, we have .
3.2. Second Example: Linear/Nonlinear SDE with Potential Function
- Euler-Maruyama-Schemewhere , and obeys the Gaussian normal distribution with and .We have with .
- Milstein-Schemewhere , and obeys the Gaussian normal distribution with and .We have with .
- AB-splitting approach:We initialize with , while and we have is the initial condition.We deal with the 2 steps:
- A-step:
- B-part:where we have the solution and we go to the next time-step till .
- ABA-splitting approach:We initialize with , while and we have is the initial condition.We deal with the 2 steps:
- A-step ():
- B-part ():
- A-step ():where we have the solution and we go to the next time-step till .
- Iterative Picard approach:we apply an Picard-Iterationwhere , while we apply the implicit method for the drift term and the explicit method for the diffusion term.The algorithm is given as:We initialize with , while and we have is the initial condition.We deal with the 2 loops (loop 1 is the computation over the full time-domain and loop 2 is the computation with ):
- :
- :
- Computationwhere , and obeys the Gaussian normal distribution with and .
- , if then we are done, else we go to Step (c)
- , if then we are done, else we go to Step (b)
- Iterative Picard-splitting with Doléans-Dade exponential approach:we apply the following splitting approach:where .We apply an Picard with Doléans-Dade exponential approach and right hand sidewhere , while we apply the implicit method in the drift term and the explicit method in the diffusion term.The algorithm is given as: We initialize with , while and we have is the initial condition.We deal with the 2 loops (loop 1 is the computation over the full time-domain and loop 2 is the computation with ):
- :
- :
- Computation (we apply Version 1 or Version 2)
- Computation (we apply the full exp and integration of the RHS)
- , if then we are done, else we go to Step (c)
- , if then we are done, else we go to Step (b)
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Additional Proofs
Appendix A.2. Approximated exp-Functions
References
- Zhang, Z.; Karniadakis, G.E. Numerical Methods for Stochastic Partial Differential Equations with White Noise; Applied Mathematical Sciences, No. 196; Springer International Publishing: Heidelberg/Berlin, Germany; New York, NY, USA, 2017. [Google Scholar]
- Duran-Olivencia, M.A.; Gvalani, R.S.; Kalliadasis, S.; Pavliotis, G.A. Instability, Rupture and Fluctuations in Thin Liquid Films: Theory and Computations. arXiv 2017, arXiv:1707.08811. [Google Scholar] [CrossRef] [PubMed]
- Grün, G.; Mecke, K.; Rauscher, M. Thin-film flow influenced by thermal noise. J. Stat. Phys. 2006, 122, 1261–1291. [Google Scholar] [CrossRef]
- Diez, J.A.; González, A.G.; Fernández, R. Metallic-thin-film instability with spatially correlated thermal noise. Phys. Rev. E Am. Phys. Soc. 2016, 93, 013120. [Google Scholar] [CrossRef] [PubMed]
- Baptiste, J.; Grepat, J.; Lepinette, E. Approximation of Non-Lipschitz SDEs by Picard Iterations. J. Appl. Math. Financ. 2018, 25, 148–179. [Google Scholar] [CrossRef]
- Geiser, J. Multicomponent and Multiscale Systems: Theory, Methods, and Applications in Engineering; Springer: Heidelberg, Germany, 2016. [Google Scholar]
- Moler, C.B.; Loan, C.F.V. Nineteen dubious ways to compute the exponential of a matrix, twenty-five years later. SIAM Rev. 2003, 45, 3–49. [Google Scholar] [CrossRef]
- Bader, P.; Blanes, S.; Fernando, F.C. Computing the Matrix Exponential with an Optimized Taylor Polynomial Approximation. Mathematics 2019, 7, 1174. [Google Scholar] [CrossRef]
- Najfeld, I.; Havel, T.F. Derivatives of the matrix exponential and their computation. Adv. Appl. Math. 1995, 16, 321–375. [Google Scholar] [CrossRef]
- Geiser, J. Iterative semi-implicit splitting methods for stochastic chemical kinetics. In Proceedings of the Seventh International Conference, FDM:T&A 2018, Lozenetz, Bulgaria, 11–26 June 2018; Lecture Notes in Computer Science No. 11386: 32-43. Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Geiser, J.; Bartecki, K. Iterative and Non-iterative Splitting approach of the stochastic inviscid Burgers’ equation. In Proceedings of the AIP Conference Proceedings Paper, ICNAAM 2019, Rhodes, Greece, 23–28 September 2019. [Google Scholar]
- Geiser, J. Iterative Splitting Methods for Differential Equations; Numerical Analysis and Scientific Computing Series; Taylor & Francis Group: Boca Raton, FL, USA; London, UK; New York, NY, USA, 2011. [Google Scholar]
- Geiser, J. Additive via Iterative Splitting Schemes: Algorithms and Applications in Heat-Transfer Problems. In Proceedings of the Ninth International Conference on Engineering Computational Technology, Naples, Italy, 2–5 September 2014; Ivanyi, P., Topping, B.H.V., Eds.; Civil-Comp Press: Stirlingshire, UK, 2014. [Google Scholar] [CrossRef]
- Vandewalle, S. Parallel Multigrid Waveform Relaxation for Parabolic Problems; Teubner Skripten zur Numerik, B.G. Teubner Stuttgart: Leipzig, Germany, 1993. [Google Scholar]
- Gyöngy, I.; Krylov, N. On the Splitting-up Method and Stochastic Partial Differential Equations. Ann. Probab. 2003, 31, 564–591. [Google Scholar] [CrossRef]
- Duan, J.; Yan, J. General matrix-valued inhomogeneous linear stochastic differential equations and applications. Stat. Probab. Lett. 2008, 78, 2361–2365. [Google Scholar] [CrossRef]
- Bonaccorsi, S. Stochastic variation of constants formula for infinite dimensional equations. Stoch. Anal. Appl. 1999, 17, 509–528. [Google Scholar] [CrossRef]
- Reiss, M.; Riedle, M.; van Gaans, O. On Emery’s Inequality and a Variation-of-Constants Formula. Stoch. Anal. Appl. 2007, 25, 353–379. [Google Scholar] [CrossRef]
- Scheutzow, M. Stochastic Partial Differential Equations; Lecture Notes, BMS Advanced Course; Technische Universität Berlin: Berlin, Germany, 2019; Available online: http://page.math.tu-berlin.de/~scheutzow/SPDEmain.pdf (accessed on 20 February 2020).
- Prato, G.D.; Jentzen, A.; Röckner, M. A mild Ito formula for SPDEs. Trans. Am. Math. Soc. 2019, 372, 3755–3807. [Google Scholar] [CrossRef]
- Deck, T. Der Ito-Kalkül: Einführung und Anwendung; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Teschl, G. Ordinary Differential Equations and Dynamical Systems; American Mathematical Society, Graduate Studies in Mathematics: Providence, RI, USA, 2012; Volume 140. [Google Scholar]
- Oksendal, B. Stochastic Differential Equations: An Introduction with Applications; Springer: Heidelberg/Berlin, Germany, 2003. [Google Scholar]
- Stoer, J.; Bulirsch, R. Introduction to Numerical Analysis; Springer: Heidelberg/Berlin, Germany; New York, NY, USA, 1980. [Google Scholar]
- Kloeden, P.E.; Platen, E. The Numerical Solution of Stochastic Differential Equations; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Karlsen, K.H.; Storrosten, E.B. On stochastic conservation laws and Malliavin calculus. J. Funct. Anal. 2017, 272, 421–497. [Google Scholar] [CrossRef]
- Ninomiya, S.; Victoir, N. Weak approximation of stochastic differential equations and application to derivative pricing. Appl. Math. Financ. 2008, 15, 107–121. [Google Scholar] [CrossRef][Green Version]
- Ninomiya, M.; Ninomiya, S. A new higher-order weak approximation scheme for stochastic differential equations and the Runge–Kutta method. Financ. Stoch. 2009, 13, 415–443. [Google Scholar] [CrossRef]
- Bayram, M.; Partal, T.; Buyukoz, G.O. Numerical methods for simulation of stochastic differential equations. Adv. Differ. Equ. 2018, 2018. [Google Scholar] [CrossRef]
- Geiser, J. Multicomponent and Multiscale Systems—Theory, Methods, and Applications in Engineering; Springer International Publishing AG: Heiderberg/Berlin, Germany; New York, NY, USA, 2016. [Google Scholar]
- Geiser, J. Computing Exponential for Iterative Splitting Methods: Algorithms and Applications. Math. Numer. Model. Flow Transp. 2011, 2011, 193781. [Google Scholar] [CrossRef]
- Fouque, J.-P.; Papanicolaou, G.; Sircar, R. Multiscale Stochastic Volatility Asymptotics. SIAM J. Multiscale Model. Simul. 2003, 2, 22–42. [Google Scholar] [CrossRef]
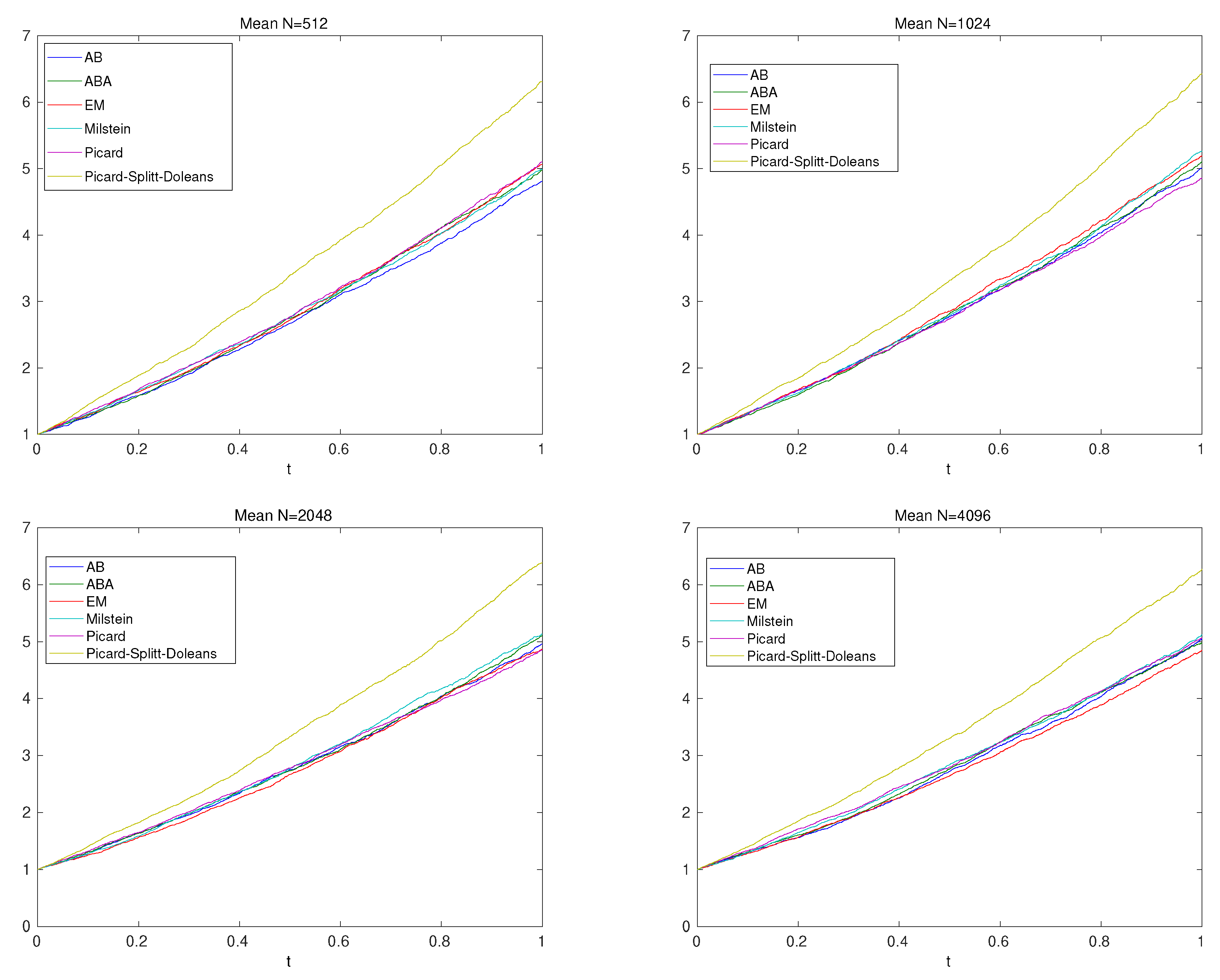

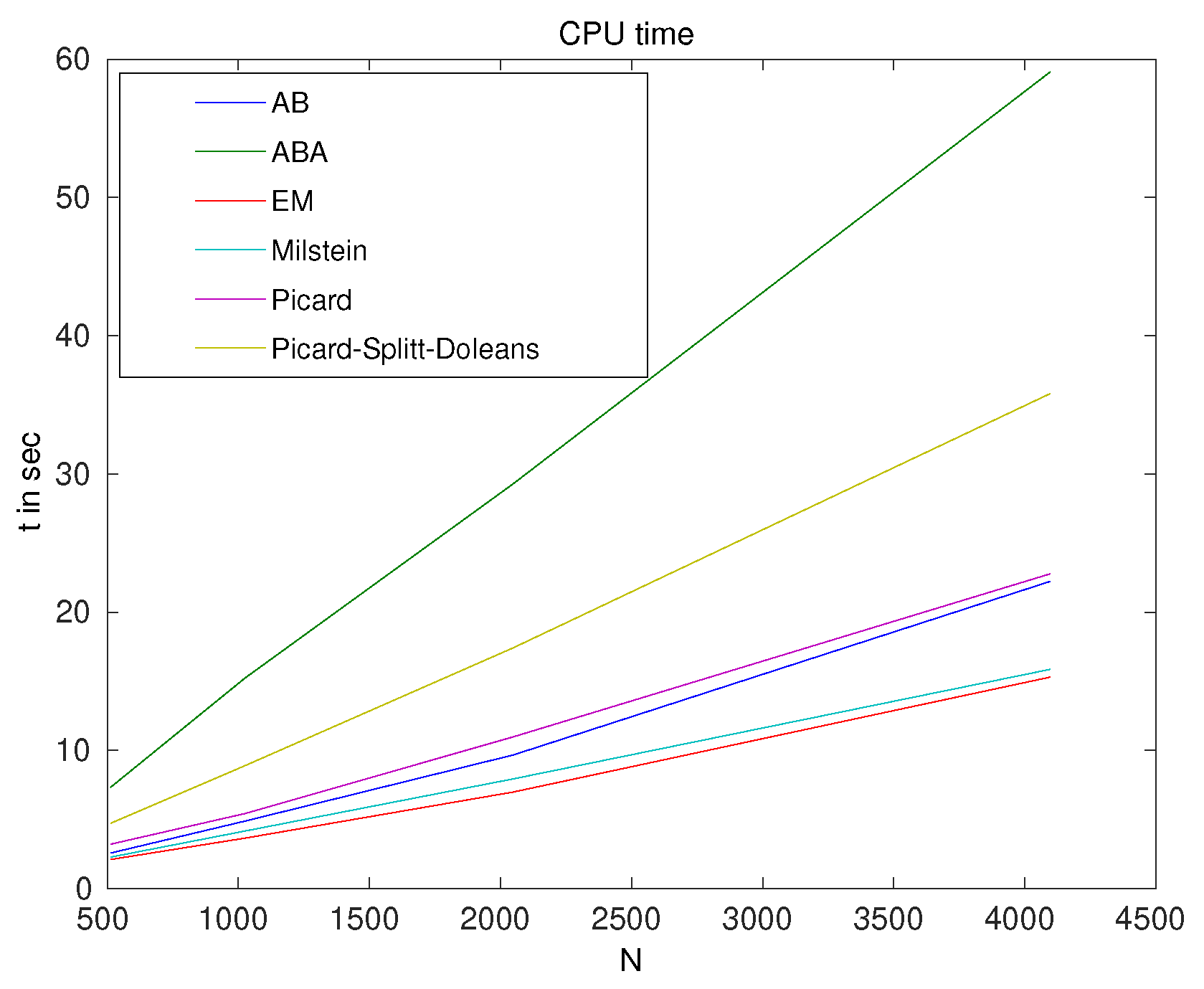
| N | EM- | Milstein | AB | ABA | Picard | Picard- | Picard-Splitt- |
|---|---|---|---|---|---|---|---|
| Doleans | Doleans | ||||||
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geiser, J. Numerical Picard Iteration Methods for Simulation of Non-Lipschitz Stochastic Differential Equations. Symmetry 2020, 12, 383. https://doi.org/10.3390/sym12030383
Geiser J. Numerical Picard Iteration Methods for Simulation of Non-Lipschitz Stochastic Differential Equations. Symmetry. 2020; 12(3):383. https://doi.org/10.3390/sym12030383
Chicago/Turabian StyleGeiser, Jürgen. 2020. "Numerical Picard Iteration Methods for Simulation of Non-Lipschitz Stochastic Differential Equations" Symmetry 12, no. 3: 383. https://doi.org/10.3390/sym12030383
APA StyleGeiser, J. (2020). Numerical Picard Iteration Methods for Simulation of Non-Lipschitz Stochastic Differential Equations. Symmetry, 12(3), 383. https://doi.org/10.3390/sym12030383




