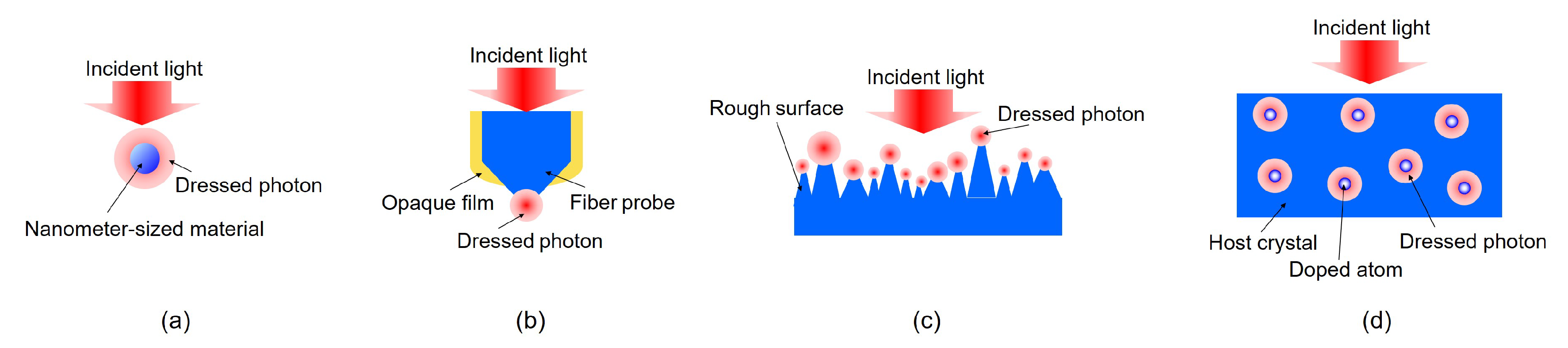
3. Quantization of the Clebsch Dual Field and DP Model
Using the plane wave form mentioned above,
derived from (
4) satisfies
which shows that “momentum-like vector”
lies in a submanifold of the Lorentzian manifold called de Sitter space in cosmology, which is a pseudo-hypersphere with radius
embedded in
. The importance of this space in the context of spacetime quantization was first noted by Snyder [
30], who proposed a quantization scheme with Planck length and the built-in Lorentz invariance based on the assumption that hypothetical momentum 5-vector
in
is constrained to lie on de Sitter space,
i.e.,. The similarity between (
13) and the de Sitter space structure of
seems to imply that the isomorphism (
9) between
and
derived for the classical field equation is valid also for quantized fields, which is surely an important issue to be investigated.
A particularly interesting point concerning this similarity is the following contrast: in Snyder’s quantization scheme, the parameter
does not explicitly appear although a Planck scale is introduced independently. On the contrary,
plays a key role in the Clebsch dual field. This observation suggests that conformal symmetry breaking related to (
4) may be closely related to the dynamic origin of the cosmological constant
, which Snyder did not discuss. In this section, firstly, we will show that the introduction of
can be justified only when we consider the quantization of the Clebsch dual field. In addition, its physical implication for cosmology will be discussed in
Section 4 from the viewpoint of simultaneous conformal symmetry breaking of electromagnetic and gravitational fields.
Note that
in (
8) is isomorphic to the EM tensor of freely moving fluid particles, so the kinetic theory of molecules suggests that the
field can be quantized. Since the physical dimensions of
and
are the same as those of
and
, respectively, using
given in (
8), we see that
has the dimension of length. Therefore, the quantization of
means that there exists a certain quantized length of which the inverse is
. Now, let us consider the Dirac equation of the form
which can be regarded as the “square root”of the time-like KG equation:
. Therefore, the Dirac equation for
must be
. On the other hand, an electrically neutral Majorana representation exists for (
14), in which all the values of the
matrix become purely imaginary numbers such that this matrix has the form of
, which is identical to the Dirac equation for the above space-like KG equation. The reason why we have introduced the Clebsch dual field as the space-like extension of the electrically neutral electromagnetic wave field is because the Greenberg and Robinson theorem mentioned in in
Section 2.1 requires such a field for quantum field interactions, so that the above arguments suggest that Majorana field must be such a quantum field.
The Majorana field is fermionic with a half-integer spin 1/2, so the same state cannot be occupied by two fields according to Pauli’s exclusion principle. A possible configuration of a couple of Majorana fields corresponding to the Clebsch dual field that behaves like a boson with spin 1 can be identified with the help of Pauli–Lubanski vector
describing the spin states of moving particles.
has the form of
, where
and
are the angular and linear momenta of the Majorana field, respectively. Note that the two fields
and
can share the same
such that
when their linear momenta
and
are orthogonal, i.e.,
. Two Majorana fields satisfying this orthogonality condition can be combined, as in the case of a Cooper pair in the superconducting phenomenon, to form a vector boson with spin 1, which can be identified as the quantized Clebsch dual field satisfying the orthogonality condition in (
5).
Now, we are ready to consider the mechanism through which a DP emerges. As a mathematically simple situation, let us consider the case in which the space-like KG Equation (
4) is perturbed by the interaction with a point source
, where
r denotes the radial coordinate of a spherical coordinate system. The essential causal aspects of this problem were already investigated by Aharonov et al. [
31], who showed that the resulting time-dependent behavior of the solution can be expressed by the superposition of a superluminal (space-like) stable oscillatory mode and a time-like linearly unstable mode whose combined amplitude spreads with a speed slower than the light velocity. A time-like unstable mode of the solution to (
4) expressed in a polar coordinate system with spherical symmetry has the form of
, where
satisfies
whose solution becomes the Yukawa potential:
, which rapidly falls off as
r increases. The nonzero component of the
deformed Clebsch dual bivector field
derived by the combined use of (
16) and (
7) is
, namely,
and
, which are, in the classical interpretation, growing and damping solutions. However, quantum mechanically, these two can be interpreted as follows. The transmutation from a space-like mode to a pair of these two time-like modes through the interaction with a point source can be regarded as a pair creation of Majorana particles: one going forward in time and the other antiparticle going backward in time. This pair creation is possible because the Clebsch dual field consists of a pair of Majorana fields. Since these modes are non-propagating, they are superimposed to yield a non-propagating light field called a DP that can be regarded as a pair annihilation. The energy density of the DP generated by these processes is given by
. If we use a natural unit system, then
possessing the dimension of
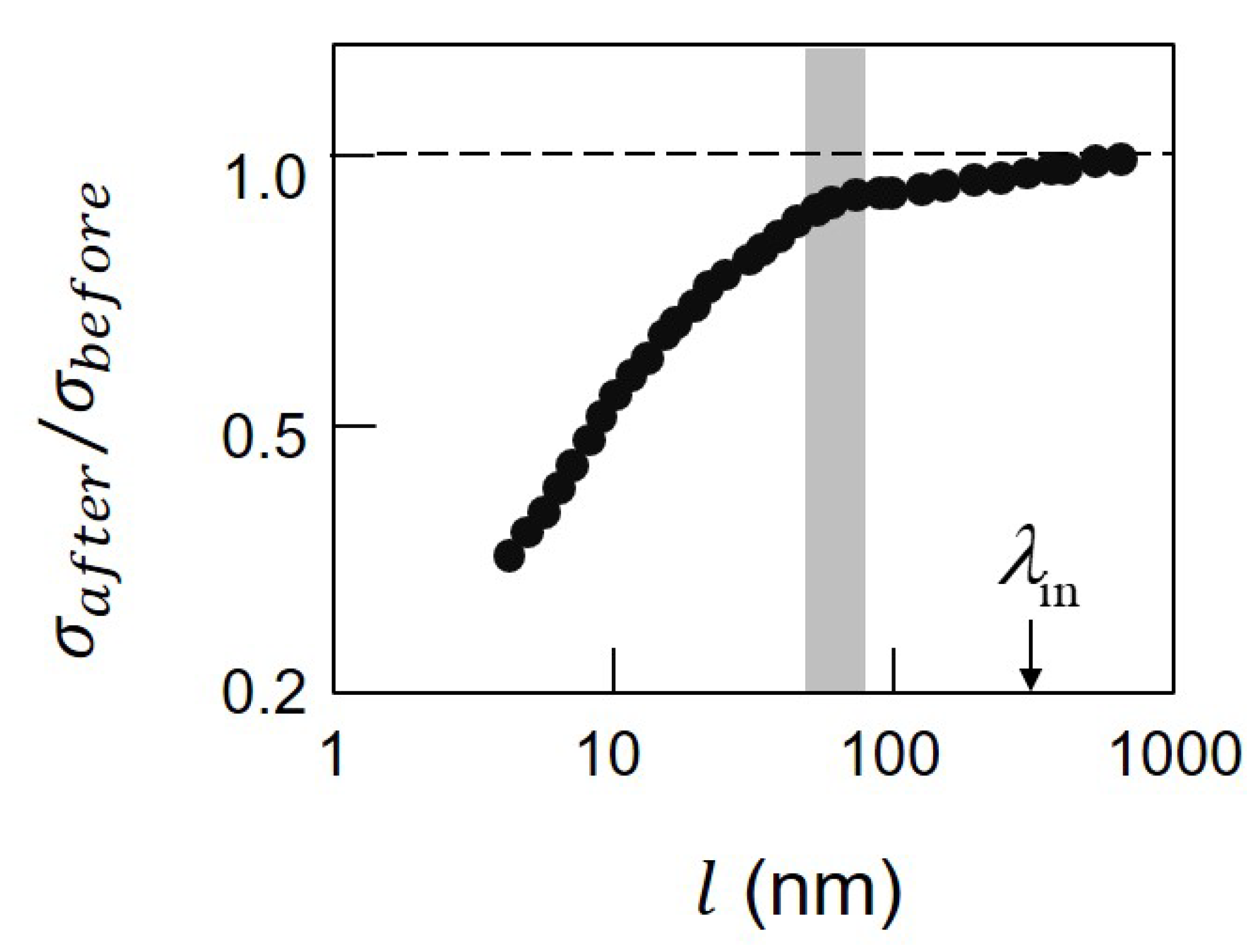
may be regarded as an elemental block of DP energy. In subsection 1.2, we have observed that the maximum size of a DP is approximately 50 nm. Since this size can naturally be assumed to correspond to the minimum energy of the DP, we have Min
using (
16).
4. Connection with Cosmology
Since the spatial dimension of our physical spacetime is three, the maximum number of momentum vectors satisfying the orthogonality condition (
15) is also three, that is,
, which indicates the existence of a compound state of Majorana fermions with spin
denoted by
. Note that this state can play the role of “the ground state”of the Clebsch dual field in the sense that Clebsch dual fields as extended virtual photons can be excited from any of the three different configurations of the “Clebsch dual structure” (
15) embedded in
. Electromagnetic interactions are ubiquitous phenomena such that incessant occurrence of excitation–deexcitation cycles between “the ground”and non-ground states makes the former a fully occupied state from the viewpoint of a macroscopic time scale. In such a situation,
would exist not as an extremely ephemeral virtual state but as a stable unseen off-shell state.
In order to apply our new idea on the Clebsch dual field to cosmological problems, we first point out that the formulation of it derived for Minkowski space in
Section 2 and
Section 3 is readily generalized to cover the case of a curved spacetime for which the partial derivative
of a given field defined on the former must be replaced by the covariant derivative
of the field defined on the latter. At the end of
Section 2, we have shown the isomorphsm between the energy-momentum tensor of Clebsch dual field and Einstein’s field equation by utilizing
. It is clear that a curved spacetime does not create any problem for defining the skew-symmetric simple bivector field
and hence
. One of the notable problems we have in the case of dealing with a curved spacetime is that differential operators do not commute in general. For a given vector field
on Minkowski space, we have
. On a curved spacetime, however, we have
where
denotes Riemann curvature tensor, so that the order of differentiation matters. The sole exception for this non-commuting rule is the case where a vector field
is replaced by a scalar field
S, for which we have
and
because the affin connection
is symmetric with respect to the subscripts
and
. Notice again that the skew-symmetric Clebsch dual field
given in (
7) is a bivector field represented in terms of the exterior product of a couple of gradient vector
and
. Therefore, while
only contains the first derivatives of scalar fields
and
, the entire formulation of the Clebsch dual field covering, for instance,
involves the first and second derivatives of them, for the latter of which the order of differentiation does not matter. We mentioned already that the simple bivector property of
is a crucial element for deriving the first equation in (
11). In reference [
5], we show that, not only for (
11) but also for the other parts of the Clebsch dual formulation, the simple bivector property of
and the commutativity of the second derivatives of scalar fields
and
are essential elements. By using those properties, we can prove
since, as far as the mathematical manipulations are concerned, those in a curved spacetime are essentially similar to those in Minkowsky space. Thus, we show that the isomorphism (
9) can be extended to that in a curved spacetime.
Having stated this, we now move on to the well-known isotropic spacetime structure employed in cosmological arguments:
where
denotes the curvature parameter taking one of the triadic values of (0, +1, −1) and the other notations are conventional. The coordinate system employed in (
17) is a unique co-moving (co-moving with matter) one singled out by Weyl’s hypothesis on the cosmological principle with which the energy-momentum tensor
of the universe becomes identical in form to the following one of the hydrodynamics:
In addition, corresponding to (
18), the components of metric tensor
can be chosen in such that off-diagonal elements of Einstein tensor
are also zeros. A caveat in using this coordinate system for our Clebsch dual field is that, due to its space-like property, the energy-momentum tensor
of the Clebsch dual field to be given by (
23) cannot be diagonalized as in the case of (
18) since the field resides outside the familiar time-like universe. In spite of that, the above coordinates system introduced by Weyl is a quite informative one from the viewpoint of cosmological observations, so that we think one of the meaningful approaches to estimate the impact of
on our time-like universe would be to focus solely on its diagonal components, especially the trace
as the sum of them whose justification will be given shortly, projected on the four-dimensional “screen”spanned by the set of basis vectors of the Weyl coordinates.
In what follows, we are going to derive the energy-momentum tensor ((
23) or (
27)) directly related to a compound state of Majorana fermions
referred to at the beginning of this section. To avoid misunderstanding of the characters of this tensor, the following remark on fermionic fields is important to be made in advance: in quantum theory, the time change of a state is described by the dynamics acting on the (C
-)algebra of observables. The non-commutativity inherent to quantum theory requires the notions of quantum “observables”and “states”of a given system to be distinguished more clearly than in the classical case. Even in the classical Einstein field equation, it is true that “observables”or “physical quantities”(represented typically by the energy-momentum) and “states”(represented by the curvature of spacetime) are seen to occupy different places in a way that the former and the latter appear in the right and the left hand sides of the equation, respectively. In regard to fermionic fields, we can say that, though state changes of fermionic fields are visible, the physical quantities satisfying Fermi statistics with anti-commutation relations cannot be visible. In the conventional quantum field theory, such invisible entities as fermionic fields were introduced as an ad hoc fashion and it is not until the advent of Doplicher-Haag-Roberts theory [
32] that their existence was justified through a process of reconstructing all the members of a standard formulation of the theory involving fermionic entities, just starting from the formalism consisting of only observable data structure in the context of Galois theory.
According to these arguments, the physical quantities associated with ((
23) or (
27)) derived from the spacelike Majorana fermionic field explained in
Section 3 should be invisible in nature. The reason is as follows: the Clebsch dual field can be manipulated mathematically as if it is a classical field, similarly to the case of Schroedinger’s wave equation. As far as the invisible nature of a spacelike 4 momentum vector is concerned, however, we have to take the above-mentioned property of Fermi statistics into consideration. (The close relation between the quantization of spacelike 4 momentum and Fermi statistics was pointed out first by Feinberg [
33].) The key question in our analysis on dark energy is, therefore, whether we can find observable quantities or not. Since the relevant criterion for singling out such quantities may change depending on the choices of situations and aspects, however, we have no choice but to make a good guess. The fact which seems to work as “the guiding principle”is that, within the framework of relativistic quantum field theory, any observable without exception associated with the given internal symmetry is the invariant under the action of transformation group materializing the symmetry under consideration. By extending this knowledge on the internal symmetry to the external (spacetime) one, we assume that the trace
as the invariant of general coordinate transformation is observable since it is directly related to the actual observable quantity of the expansion rate of the universe through the isomorphism (
9) which has been shown to be valid for a curved spacetime through the arguments in the second paragraph in this section.
To implement our analyses on dark energy, for the sake of simplicity, we take two-stage approach I and II. In the first stage I, we confine the scope of our argument to sub-Hubble scales in which the spacetime of the isotropic universe can be regarded as Minkowski space in an approximate sense. Then, in the second stage II, we smoothly extend our argument beyond those limits to cover the entire curved spacetime.
Stage I analyses
Firstly, to incorporate the fundamental quantum condition of
into the Clebsch dual field, let us consider the light-like case given by (
8), where we have
. Using plane wave expressions of
where
i,
and
denote the imaginary unit, the quantized elemental amplitude and the number of such an elemental mode, we obtain
In deriving the second equation of (
20),
has been used since the dimension of
is length squared. Now, we introduce Cartesian coordinates
and
such that the
k vector for
is parallel to the
direction and consider a rectangular parallelepiped
V spanned by the length vector
. Using (
20) and
where
c denotes the light velocity, the volume integration of
over
V as the energy per quantum becomes
from which the condition corresponding to
is identified as the second equation in (
21), where
denotes a unit square meter. For the non-light-like case of
, using (
12), since we have
,
defined as that for
becomes
Since the Clebsch dual wave field, as in the case of an electromagnetic wave, has a propagating direction, to have isotropic radiation, we need three fields, any pair of which is mutually orthogonal. Such three fields are given, for instance, by (
), (
) and (
).
derived by the superposition of these fields with
and
turns out to be
which is the energy-momentum tensor of the anti dark energy (dark energy with negative energy density, that is,
) we propose in this paper. As we will see shortly, the dark energy (with positive energy density)
given by (
27)
having exactly the same trace as that of the anti dark energy(
23) can be introduced accordingly. Here, a remark must be made to clear the following point concerning different types of dark energy. Although the cosmological term
with
is well-known and presumably the simplest candidate model of the dark energy, the up-to-date notion of dark energy includes presently-unknown entities other than
. The present model
now we are considering belongs to the latter type.
Stage II analyses
The above analyses in I shows that
. As we already pointed out, the isomorphism between
and
in (
9) can be extended to the one in a curved space-time. Using this relation, we can say that the existence of
induces a constant negative scalar curvature in the universe. The configuration of such a universe is described as a four-dimensional hyper pseudo-sphere with a certain “radius”
embedded in a fifth dimensional Minkowski space. This universe is known as de Sitter space whose metric invariant
can be rewritten with polar coordinates
as
where
denotes a constant initial radius of the universe. By comparing (
24) with (
17), we see that the curvatue parameter
of de Sitter space is zero, which shows that the analyses in the first stage I can be extended smoothly to the second stage II. Since de Sitter space is a unique solution of the Einstein field equation for the cosmological term of
, we see that the impact of
can be observed in a form of cosmological constant.
To the best of authors’knowledge, the observational data available to us on our expanding universe is the cosmological constant
derived on the assumption that the dark energy may be modeled by the cosmological term
. If the dark energy is modeled by
, then the Einstein field equation with the sign convention of
becomes the first equation in (
25), and if it is modeled by
, then the Einstein field equation becomes the second one in (
25):
which suggests that one of the meaningful observational validations of our dark energy candidate model
would be to compare the traces of
and
. Since the trace of
is the same as that of
, we see that, using (
22), the magnitude of
corresponding to the above-mentioned isotropic radiation is evaluated as
, whose numerical value can be derived by the use of (
21), and the experimentally determined value of
. Using
nm, we get
, which may be regarded as the “reduced cosmological constant”of
, while the value of
derived by Planck satellite observations [
34] is
. Thus, we can say that
is a promising candidate for dark energy.
Note that the energy density
in (
23) is negative. In order to figure out the meaning of
, let us consider a simple case of the on-shell condition of a real-valued 4-momentum vector
. Without the loss of generality, we can choose a coordinate system in which
and
vanish, so that we have
Clearly,
satisfies (
26) when
is a solution to it. Since energy and time are canonically conjugate variables, the time evolution of a given dynamical system with negative energy (Hamiltonian) can be reinterpreted as the backward time evolution of the counterpart system with positive energy. We often encounter such reinterpretations in Feynman diagrams to distinguish the anti-particle arising from a pair creation, so that, at the microscopic quantum level, the emergence of negative energy does not create any fundamental problem, as we already referred to the two-sided energy spectra of the Tomita–Takesaki extension of the thermal equilibrium. At the macroscopic classical level, however, there is no hint of the existence of anti-matter in abundance. To explain it, the idea of a twin universe as the cosmic version of a pair creation was proposed by Petit [
35], though the issue remains unsettled yet. Whatever the reason may be, the weak energy condition (positivity of the energy) in the classical general theory of relativity related to the stability of a given dynamical system under consideration must be tied to the matter (with positive energy) dominated property of our universe.
The simple argument on (
26) suggests that the classically unfavorable negative property of
can be circumvented as follows. In (
26), if we formally replace
by
and
by
, then we readily see that (
26) remains the same. This procedure can be applied to transform (
23) into the following trace invariant (
27). Notice that, with the Hodge dual exchanging between (
) and (
) in (
23), which corresponds qualitatively to the above exchange between (
) and (
) because electric and magnetic fields respectively bear temporal and spatial attributes from the Lorentz group theoretical viewpoint,
turns into the following
in which the transformed 4-momentum vector density in the first row (in comparison to that in (
23)), which changes the sign while the trace of it remains exactly the same as that of
in (
23). The sign change for the spatial components in the first row occurs in exactly the same manner as the one in (
26), though the sign change for the temporal component differs from it. This is because, as we already pointed out, electric and magnetic field respectively bear temporal and spatial attributes, so that the appearance of
in (
27) is a consistent change in this respect. Thus, the physical meaning of the dual existence of (
23) and (
27) is that the notion of matter-antimatter duality can be extended to the dark energy model based on the Clebsch dual field. Notice that the diagonal components of
resemble the artificial partition of the diagonal components of
into
and
(
cf.(
18)) already employed as the hypothetical equation of state of dark energy in the conventional cosmology.
In considering the problem of dark matter from the viewpoint of conformal symmetry breaking mentioned at the beginning of
Section 3, we cast a spotlight on the Bel–Robinson tensor [
36]
satisfying
, where
denotes the covariant derivative. We can readily show that
where
denotes the Weyl tensor. A lengthy but straightforward calculation [
37] shows that
vanishes identically, which indicates that
Since the magnitude of
in the well-known Schwarzschild outer solution of a given star decreases monotonously along radius direction, for discussions on cosmological phenomena for which mass distributions can be approximated as that of continuous medium, we would have no need to worry about the singular point of
. Notice that (
29) shows an intriguing possibility that we can figure out the physical meaning of the cosmological term
which remains a unsettled issue ever since the time of Einstein, though it is tentatively used as a dark energy model. The unique property of (
29) that should be distinguished from the one of usual
as a metric tensor is the fact that the former can be defined in the spacetime whose dimension is larger than or equal to 4 because the Weyl tensor does not exist in the lower dimension and that it is directly related to gravitational field. Such being the case, we introduce a new notation
to represent the right-hand side of (
29).
In our preceding arguments on dark energy, we have shown a possibility that dark energy may be explained by a new model different from the cosmological term
. If that is the case, then
must represent another phenomenon. Note that the magnitude
measures the deviation of spacetime from the conformally flat FRW metric for the isotropic universe. Thus, a field whose energy-momentum tensor
having the following form:
would behave like a field with an attractive nature of gravity, that is to say, that it must work as the seed of galaxy formations, which suggests us to look into a possibility that
is one of the candidates of the dark matter model. One of the intriguing properties of
is that its form remains the same irrespective of the magnitude of
. Considering its attractive nature of gravity, the initial quite small magnitude
which seems to be relating to the observed slight density variations in the early universe identified by COBE mission would grow monotonously. Thus,
is a parameter playing a similar role as
in (
24) and the existence of
may be regarded as a major dynamical cause for monotonously increasing
field.
The important question in fixing the dark matter model
is the determination of
. For this problem, we think that the isomorphism between conformally broken space-like electromagnetic field (Clebsch dual field) and gravitational one (
9) must play a key role. At the end of
Section 2, we show that
in (
12) is an elemental contribution of the former to the scalar curvature of spacetime. As we have already shown, the magnitude of this elemental contribution corresponds in the converted unit of cosmological constant to
where
is the reduced cosmological constant of our dark energy model defined in the 6th line from Equation (
25). Since (
9) is the isomorphism between Clebsch dual field and Ricci part of gravitational field, it would be natural to assume that
in
as a conformally broken scale parameter associated with Weyl part is equal to
, which we call simultaneous conformal symmetry breaking of electromagnetic and gravitational fields. As a partial justification of this hypothesis, we point out that the consensus ranges of the estimated percentage of dark energy and matter are (
) and (
), so that the coefficient
of
is consistent with the mean values of these ranges. In the limit of
, where
,
asymptotically approaches to the anti-de Sitter space extensively studied in the Maldacena duality [
38]. Thus, if
actually exists, then we can say that the anti-de Sitter space existed in the early universe.
5. Methods: Formulation of the Clebsch Dual Field
The quantization of the electromagnetic field cannot be performed without gauge fixing of some sort, which suggests that
can be specified in a physically meaningful fashion. We next discuss that the Feynman gauge first introduced by Fermi in the Lagrangian density
, containing a gauge fixing term
whose variation with respect to
is the second equation in (
31),
which is exactly such a gauge specification. Combining (
1) and (
31) with the well-documented equation
on the divergence of the EM tensor
given by (
3), we obtain
of which the second equation shows that the EM conservation
holds well, even in the case of
, as long as the vector
is perpendicular to
. In addition, directly from the second equation in (
31), using the antisymmetry of
, we have
Using Nakanishi–Lautrup (NL)
B-field formalism mentioned in
Section 2.2, we can show that (
33) is the gauge-fixing condition we want to obtain. NL formalism realizes manifestly-covariant quantization of electromagnetic field in which the Lorentz gauge condition (
) can be
generalized to the covariant linear gauges of the form:
where
,
B and
respectively denote a gauge-fixing Lagrangian density to be added to the gauge- invariant Lagrangian density
, NL
B-field to be defined below and a real parameter. The gauge-fixing condition and
B-field are given by
In particular, the gauge-fixing condition with
is known as the Feynman gauge and we readily show that the total Lagrangian density
with this gauge becomes equal to the first equation in (
31). The second equation in (
35) is called a subsidiary condition necessary to identify the physically meaningful sector in which quantized transverse modes reside. Quantum mechanically,
B-field is shown to be a physical quantity in the sense that it is “non-ghost”field though it is invisible.
Notice that the subsidiary condition on
B given in (
35) is identical to (
33) on
defined in (
32) and the Feynman gauge shows that
. Since the classical physicality of
in the sense of
is assured by the orthogonality condition of
, we are going to look into this condition further. Using (
2), the first equation in (
32) can be regarded as a partial differential equation on
given the above result of (
33) specifying
, namely,
where
and
denote homogeneous and inhomogeneous solutions, respectively.
obviously represents a transverse mode, and the second equation gives, in hydrodynamic terms, a balance between rotational and irrotational modes. The existence of such a balance is well documented in the hydrodynamic literature explaining the mathematical description of irrotational motion of a two-dimensional incompressible fluid. Due to the irrotationality of the motion, the velocity vector (
) is expressed in terms of the gradient of the vector potential
, namely, (
); on the other hand, the incompressibility of the fluid makes its motion non-divergent such that (
) is alternatively expressed as (
), where
denotes a streamfunction. Equating these two, we obtain
, showing that
and
satisfy the Cauchy–Riemann relation in complex analysis. This example serves as a useful reference in proving that
a null vector current propagating along the axis perpendicular to can be reinterpreted as the current of the longitudinal (-directed) electric field, of which a detailed explanation is given in reference [
21] and the existence of such longitudinally propagating electric field was actually reported by [
39]. Thus, based on the above arguments on
and
B, we can say that they are physically meaningful key quantities in formulating the Clebsch dual field.
The orthogonality condition
derived by (
32) is mathematically equivalent to the relativistic hydrodynamic equation of motion of a barotropic (isentropic) fluid [
40]:
, where
,
and
w are the vorticity tensor, 4-velocity, and proper enthalpy density of the fluid, respectively. This observation suggests that we look into the unknown form of 4-vector potential
relating to a longitudinal virtual photon that may have space-like momentum by the method of Clebsch parametrisation [
41]:
where the two scalars
and
become canonically conjugate variables in the parametrized Hamiltonian isentropic vortex dynamics. Now, let us determine the
field by referring to the following structures of electromagnetic waves: (1)
and (2)
is advected along a longitudinal null Poynting 4-vector. Corresponding to these structures, we introduce, with a constant
to be determined, a space-like KG equation
(the middle equation of (
4)) with the directional constraint
, where
and
. Multiplying this constraint by
and
yields
which shows that
and
are advected along
. In particular, if
and
are perpendicular at the initial time, then they remain so after that. Thus, as an important constraint, we can introduce
The main results of the Clebsch dual formulation can be summarized as follows by classifying this formulation into two categories:
i.e., [I] the light-like (
) case possessing “gauge symmetry (GS)”in the sense of (
33) and [II] the space-like (
) case with broken GS.
Category I.
(1) The field strength
corresponding to
is given by a simple bivector with the important orthogonality condition that cannot be satisfied when
is a time-like vector:
(2)
is a tangential vector along a null geodesic satisfying the following wave equation:
(3) The EM tensor corresponding to (
3) with the opposite sign can be defined together with its conservation law. In references [
5,
20,
21,
22] referred to at the beginning of subsection 4, this sign change is not properly accounted for, which should be fixed as a typo. The sign change is necessary because we are dealing with the negative energy that can be clearly seen in the
field in (
41),
The first equation in (
41) clearly shows that the Clebsch wave field has the dual representation of a wave,
, and longitudinally moving particles,
with negative “density”
(
because
is a space-like vector), which corresponds to an unphysical longitudinal mode in QED. Equation (
40) proves (
6) in subsection 2.2. Thus, we have shown that
the Clebsch dual field given in (6) possessing space-like momentum characteristics carries a longitudinally propagating electric field satisfying “gauge invariant”condition (33), which implies that the quantization of the Clebsch dual field gives an alternative representation of a gauge boson that emerges in the perturbative calculations in QED.Category II.
(1)
that is advected by
along a geodesic is redefined.
The form of
given in (
39) remains unchanged by (
42).
(2) The EM tensor satisfying the conservation law of
is redefined.
defined above has the same antisymmetric properties as the Riemann tensor
including the first Bianchi identity,
, which holds well since
is a bivector field given by (
39). Thus,
given in (
44) becomes isomorphic to Einstein tensor
, where the Ricci tensor
is defined as
.