1. Introduction
Architectured materials are those that possess an inner geometry [
1]. This multi-scale spatial arrangement of the constitutive materials allows for achieving mechanical properties that are not present in bulk material itself [
2]. Although this appears to be an engineering-based approach to materials design, it should be noted that this strategy is, in fact, central in nature where biomaterials must perform many functions from a small and limited set of elementary chemical elements [
3,
4]. Therefore, to enhance some target properties, regular patterns often emerge. The best-known example is the honeycomb, where bees need to maximize the volume of the cells while minimizing the quantity of matter (wax) used [
5]. Another example is the iridescent color of the wings of some butterflies. This phenomenon is due to the non-centrosymmetric mesostructure of the material constituting the wings, which acts a photonic crystal [
6,
7].
The study of elastic waves propagating in architectured materials is of particular interest since unconventional effects due to the local organization of the matter can emerge on a macroscale. In order to study these phenomena adequately, two points of view can be adopted. Either to describe all the details of the architecture or to consider an effective continuum as replacement. The first option is very general since no particular modeling assumptions are involved. However, since the inner geometry of the material has to be explicitly described and meshed, the numerical cost is often prohibitive for actual applications. Moreover, the computed solution often contains many unnecessary details for practical use. The second option, which is based on elastodynamic homogenization [
8,
9,
10] amounts to substitute the initial heterogeneous material by an equivalent homogeneous continuum. This equivalence is only valid under specific assumptions on the range of variation of some intrinsic parameters, and hence more restrictive than the first approach. However, within the validity domain of the method, the physics, up to a certain order is correctly described. Indeed, an effective theory is a reduced model obtained by filtering the actual physics so as to retain, in the continuum formulation, only the most prominent effects. Depending on the targeted applications, the effective model can be of different degrees of richness. This results in a fairly important reduction in the computational cost, which is very interesting for optimizing an architectured material, since in that case the numerical model has to be computed many times along the process.
For infinite Periodic Architectured Materials (PAM), which are the subject of this paper, the condition under which the complete wave problem can be substituted by an effective one relies on the ratio (
) between the size of the periodic unit cell (
L) and the wavelength (
) of the mechanical field. When this ratio approaches zero, the classical Long-Wavelength (LW) approximation is obtained and, provided that the frequency
is also low (Low-Frequency (LF) approximation), the heterogeneous material can be replaced by a classical effective continuum. This situation, which has been well investigated, is completely contained in what is called LF-LW elastodynamics homogenization [
8,
9,
10]. When the equivalent medium is a classical continuum (Cauchy continuum), the effective behavior is non-sensitive to certain features of the inner geometry such as noncentrosymmetry, chirality, or a
-fold axis of rotational anisotropy [
11,
12,
13].
Now, when the scale separation ratio
is small, but not vanishingly small, elastic waves propagating through the matter interact with the inner architecture. In this situation, several propagation quantities, such as the phase and group velocities, become frequency dependent and the wave propagation is dispersive [
14]. Non-standard dependencies on the architecture, that were left over in LF-LW approximation, may thus appear. These situations, which are outside the frame of standard elastodynamic homogenization, can nevertheless be modeled if the Cauchy equivalent continuum is replaced by a generalized continuum [
15,
16,
17]. In this work we focus on bulk propagation, however it is important to notice that effects near boundaries, such as surface waves [
18,
19], are also of particular interest.
Wave propagation in non-centrosymmetric or chiral materials, the two concepts being distinct (see
Appendix A for a dictionary of point groups and their associated properties), has been a subject of interest among physicists for centuries, mainly in the field of optics and electromagnetism. The first experiments showing the interaction of light with chiral molecules like sugar goes back to the beginning of the 19th century [
20]. The effect which is associated to electromagnetic waves propagating in non-centrosymmetric crystals is the rotation of the plane of polarization when the wave propagates along an optical axis, i.e., an axis of rotational symmetry. The rotation is due to the decomposition of the linearly polarized transverse wave into two circularly polarized waves with opposite handedness and different phase velocities [
21]. This phenomenon is known under the name of “optical activity”. The analogue of this effect can be observed for elastic waves and is known as “acoustical activity” [
21]. It is interesting to remark that optically-active crystals are also found to be acoustically active and that, as it will be shown in this paper, this effect can occur also in the LF-LW regime.
Recently, the interest in investigating the properties of materials based on chiral and non-centrosymmetric architectures has grown. To this end it is important to point out that chirality and noncentrosymmetry are not equivalent, and that their impact on the physics of the problem can be different.
The set of transformations that let the unit cell of an architectured material invariant constitutes its symmetry group. The material is said chiral if its symmetry group contains only rotations and it is said to be centrosymmetric when it contains the inversion [
22]. It is important to observe that in a 2D space the inversion is a rotation (preserving the material orientation) while in 3D, it is a transformation reversing the material orientation. Since the nature of the inversion depends on the dimension of the space, the implication between chirality and centrosymmetry are not the same in 2D and 3D. In 2D, the chirality and centrosymmetry are independent [
15], while in 3D chiral materials are necessarily non-centrosymmetric [
23].
Several works can be found in the literature that investigate 2D chiral elasticity and focus on their unusual mechanical properties such as negative Poisson ratio [
24,
25]. Concerning wave propagation, these architectures have been extensively studied [
26,
27,
28] and the need for a generalized continuum theory in order to capture the onset of dispersion and anisotropy at higher frequencies has been pointed out [
15,
16]. In all these cases, the unit cells under investigation are chiral and centrosymmetric. Again, it is worth noting that such a combination is possible pnly in 2D. When moving to 3D, the picture becomes more complex and due to habits coming from the 2D situation, an ambiguity between the two definitions can be usually found in the literature. For instance, the well-known and studied in-plane hexachiral and tetrachiral patterns [
29,
30], are no more chiral once extruded in 3D.
Concerning wave propagation in non-centrosymmetric materials, if the phenomenon can be studied in 2D [
15], the effects become even more interesting in 3D as the polarization of waves are then richer. As a consequence, interest in 3D non-centrosymmetric metamaterials have recently emerged for their strech-twist coupling [
31] or their acoustical activity [
32]. The effects related to size-dependent properties and characteristic lengths are also exploited and investigated in [
33] and a micropolar generalized model is used to investigate acoustical activity in [
32].
The present work is focused on the features of elastic wave propagating in non-centrosymmetric architectured materials. Among them, those based on gyroid architectures are probably the most commonly used. In electromagnetics they are widely studied as metamaterials [
6], in acoustics as phononic crystals [
34], and in biomechanics as bone substitutes [
35,
36]. In this paper, we will highlight a particular situation for which the solution predicted by classic continuum mechanics is wrong even for very long wavelengths. It is important to note that the sensitivity of the mechanical behavior to the lack of centrosymmetry can also manifest in statics [
37,
38,
39].
The paper is organized as follows: In
Section 2 the gyroid lattice is described. In
Section 3 the Bloch–Floquet analysis is introduced along with some necessary definitions for polarization studies. Dispersion analysis is performed and discussed in
Section 4.
Section 5 compares the results from
Section 4 to those obtained in the LW-LF approximation. Finally, some conclusions are drawn in
Section 6.
Notations
Throughout this paper, the Euclidean space
is equipped with a rectangular Cartesian coordinate system with origin
and an orthonormal basis
. Upon the choice of a reference point
in
, the Euclidean space and its underlying vector space
can be considered as coincident. As a consequence, points will be designated by their vector positions with respect to
. For the sake of simplicity,
will, from now on, simply be denoted
. In the following,
will designate the position vector of a point
, and, with respect to
,
When needed, Einstein summation convention is used, i.e., when an index appears twice in an expression, it implies summation of that term over all the values of the index. The dot operator
stands for the scalar product, the ∧ for the cross product, and
is the Kronecker delta.
Moreover, the following convention is retained:
Blackboard fonts will denote tensor spaces: ;
Tensors of order will be denoted using uppercase Roman Bold fonts: ;
Vectors will be denoted by lowercase Roman Bold fonts: .
The orthogonal group in is defined as , in which denotes the set of invertible transformations acting on .
4. Dispersion Analysis Using Finite Elements Analysis (FEA)
In order to investigate the ultrasonic properties of the gyroid lattice, and given the periodicity of the architecture as described in the previous sections, an approach based on Bloch–Floquet analysis will be followed. For the sake of simplicity, the conventional unit cell depicted in
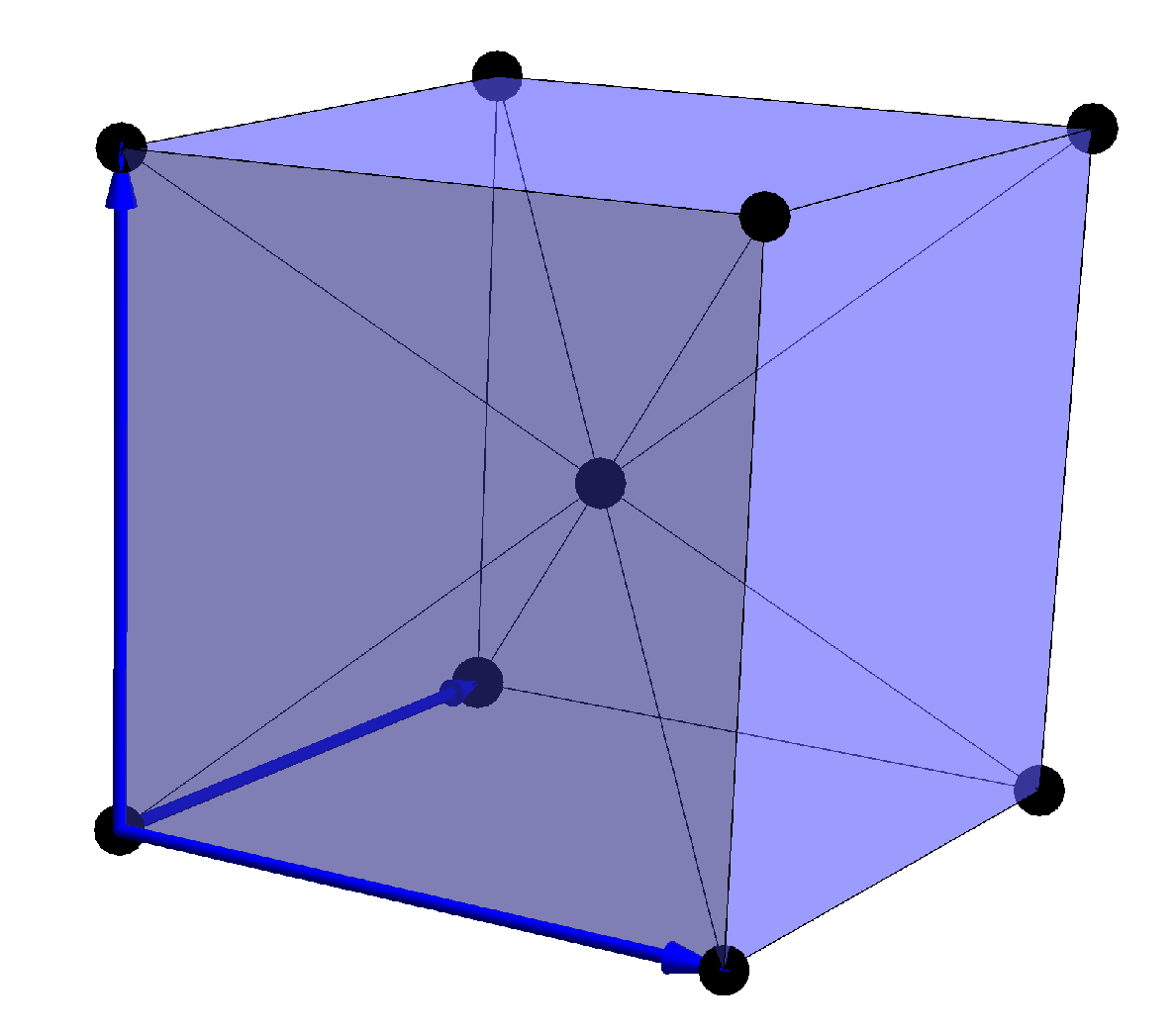
Figure 6 is used to define the numerical model. For the investigation of the elastodynamic properties of the gyroid crystal, the wavevector will be restricted to the boundaries of the Irreducible Brillouin Zone (IBZ), as depicted in red in
Figure 7a. The high symmetry points of this IBZ are defined in
Table 1. The model has been implemented using the commercial software Comsol Multiphysics and considering titanium as constitutive material, the parameters of which are displayed in
Table 3. The mesh of the unit cell is presented in
Figure 6 and consists of 66,232 tetrahedral elements. Lagrange quadratic elements are used, for a total of 329,277 degrees of freedom. Periodic Bloch–Floquet conditions are implemented by imposing them as displacement conditions at the boundaries, following Equation (
11). Then, the wavenumber in
is imposed and the corresponding frequencies are retrieved by solving the eigenvalue problem. The computation of each wavenumber took an average of 109 seconds on a workstation equipped with an Intel(R) Xeon(R) CPU E5-1650 v2 at 3.50 GHz using six cores.
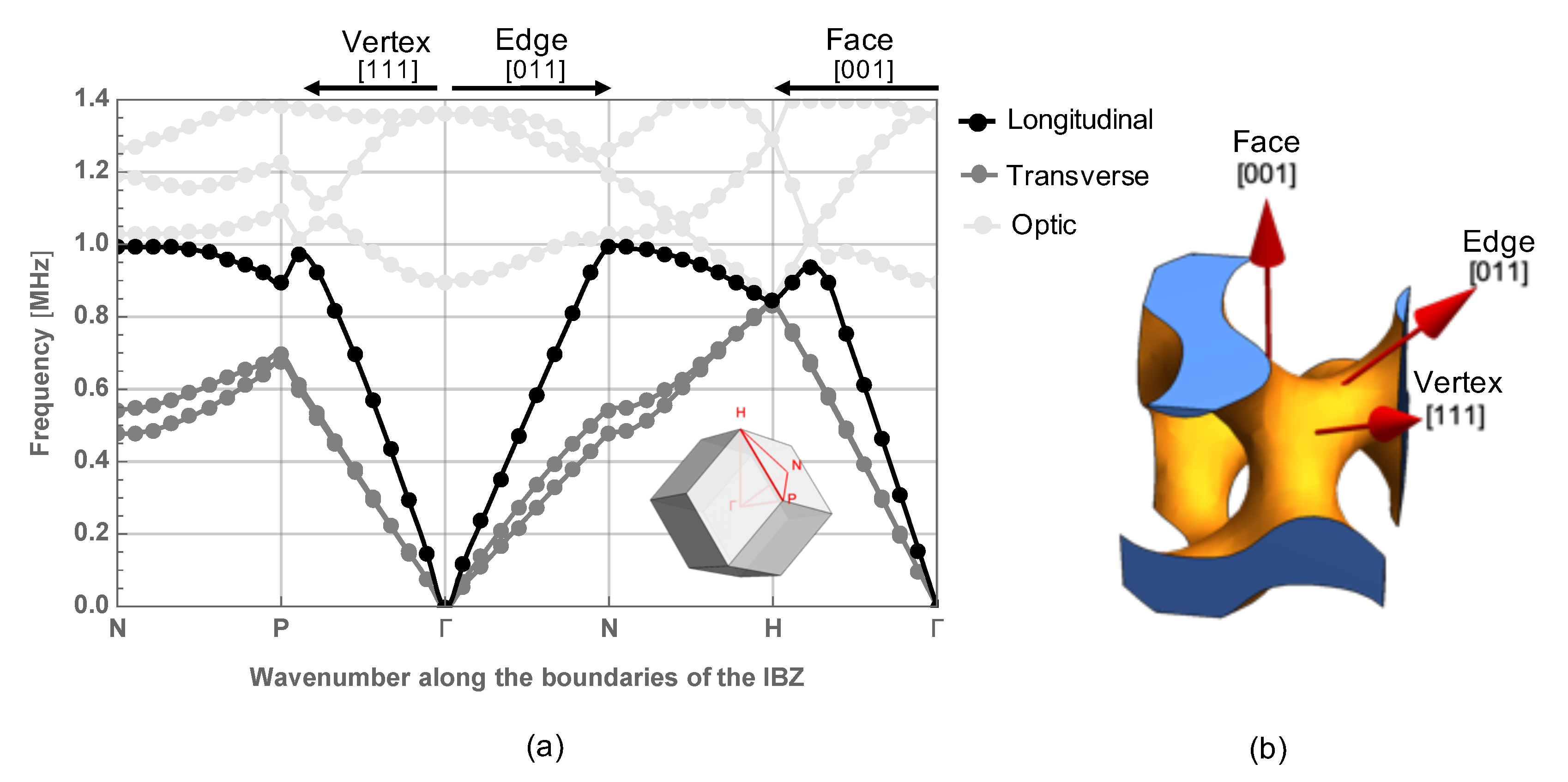
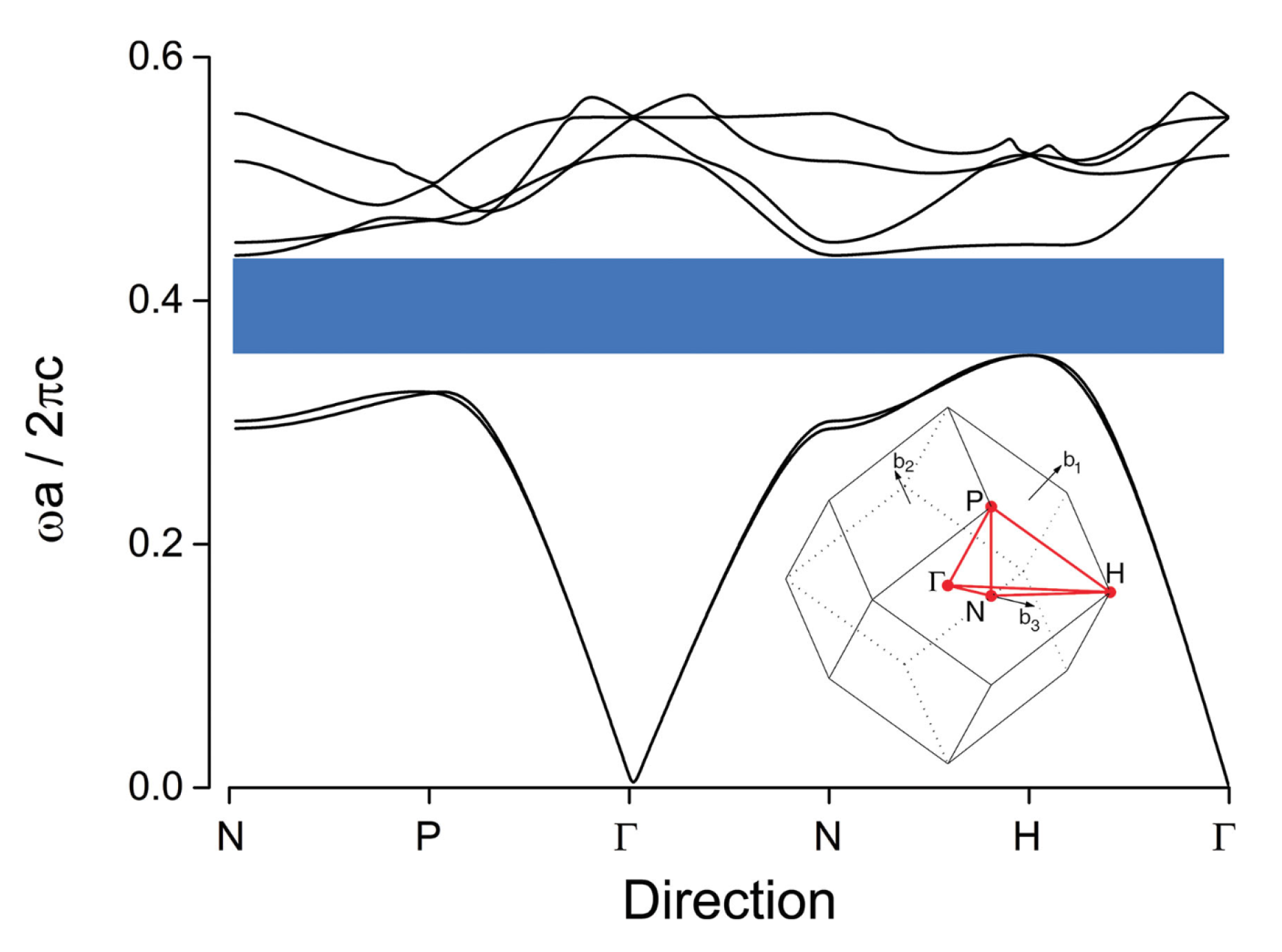
The results of the dispersion analysis are depicted in
Figure 7a. It can be observed, qualitatively, that these results are similar to those obtained for electromagnetic waves in [
6] (see
Figure 8). In particular, the behavior of the acoustic branches, i.e., those branches starting from the origin
, corresponding to transverse waves (gray lines in
Figure 7a) is remarkably similar.
Since the objective of the paper is to investigate the behavior of the lattice within the LW-LF approximation given by classic continuum mechanics, the phase velocities and polarization of waves have been computed for large values of the wavelength with respect to the size of the unit cell. In this case,
m
, which corresponds to a wavelength close to 60 times the size of the unit cell. For each mode, the polarization vector has been estimated by computing the average of the complex displacement of the eigen-mode over the unit cell, and the results are listed in
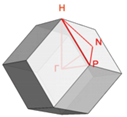
Table 4. We will now analyze the results along the following directions of propagation, also depicted in
Figure 7b:
: This direction is going from the center of the fundamental cell to the middle of a face. It corresponds to an axis of rotation of order 4 (rotations of rad);
: This direction is going from the center of the fundamental cell to the middle of an edge. It corresponds to an axis of rotation of order 2 (rotations of rad);
: This direction is going from the center of the fundamental cell to a vertex. It corresponds to an axis of rotation of order 3 (rotations of rad).
Using the conditions listed in
Table 2, we have characterized the polarization for each of the above propagation directions. The results are summarized in
Table 4.
Along the direction
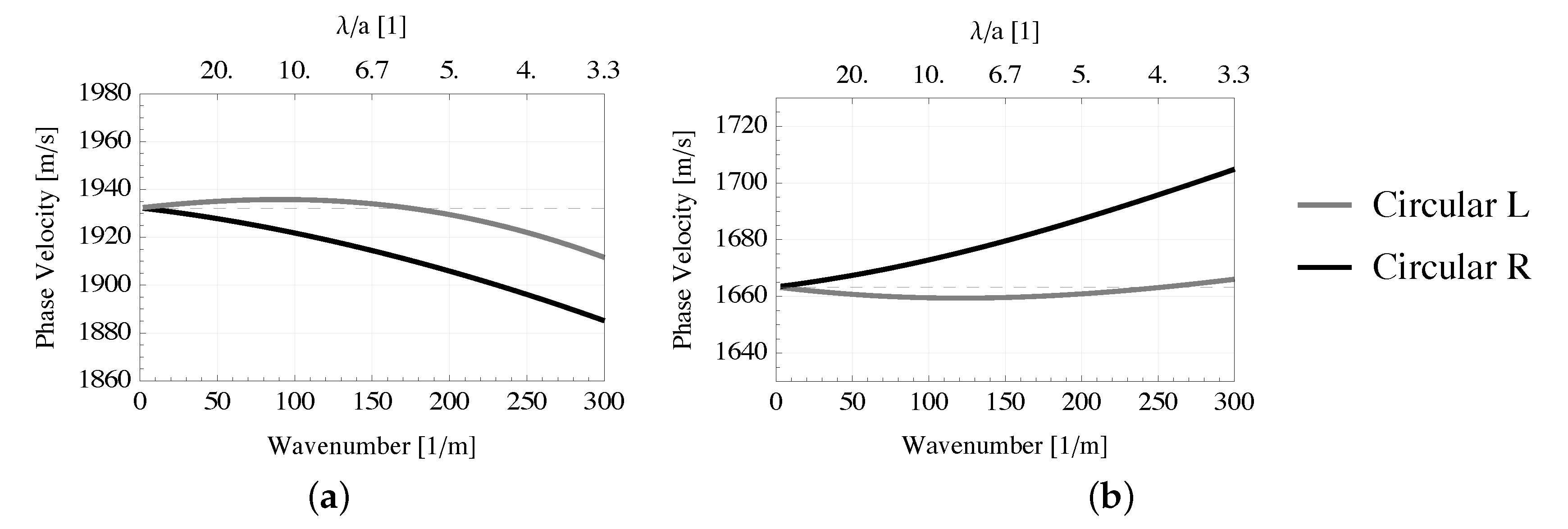
a longitudinal wave propagating at 3018.5 m/s can be observed. The two transverse waves have eigenmodes with complex amplitude and propagate with close phase velocity that tends to a common value of of 1932.2 m/s for infinite wavelengths, as it can be also observed in
Figure 9. These complex amplitudes correspond to two circularly polarized transverse waves with opposite handedness. In the direction
, a longitudinal wave propagating at 3249.8 m/s can be observed. One transverse wave is linearly polarized in direction
, and propagates with a phase velocity of 1931.7 m/s. The last solution corresponds again to a transverse wave, linearly polarized along
, with velocity 1510.9 m/s. Finally, direction
has a linearly polarized longitudinal wave at 3322.8 m/s, and two circularly polarized waves with opposite handedness and propagating with close velocity, converging to 1663.4 m/s.
In summary, circularly polarized waves exist only if the direction of propagation is along a rotation axis of symmetry of order greater than 2. Moreover, as can be seen in
Figure 9, for both
and
directions, the circularly polarized waves with opposite handedness propagate with the same phase velocity only in the infinite wavelength limit, and they start to diverge as the wavenumber increases. In particular, for direction
the right handed wave becomes slower than the left handed one, while the opposite phenomenon can be observed for direction
. This is due to the chirality of the unit cell. As one can notice, phase velocities are different even for a very large wavelength compared to the size of the unit cell, i.e.,
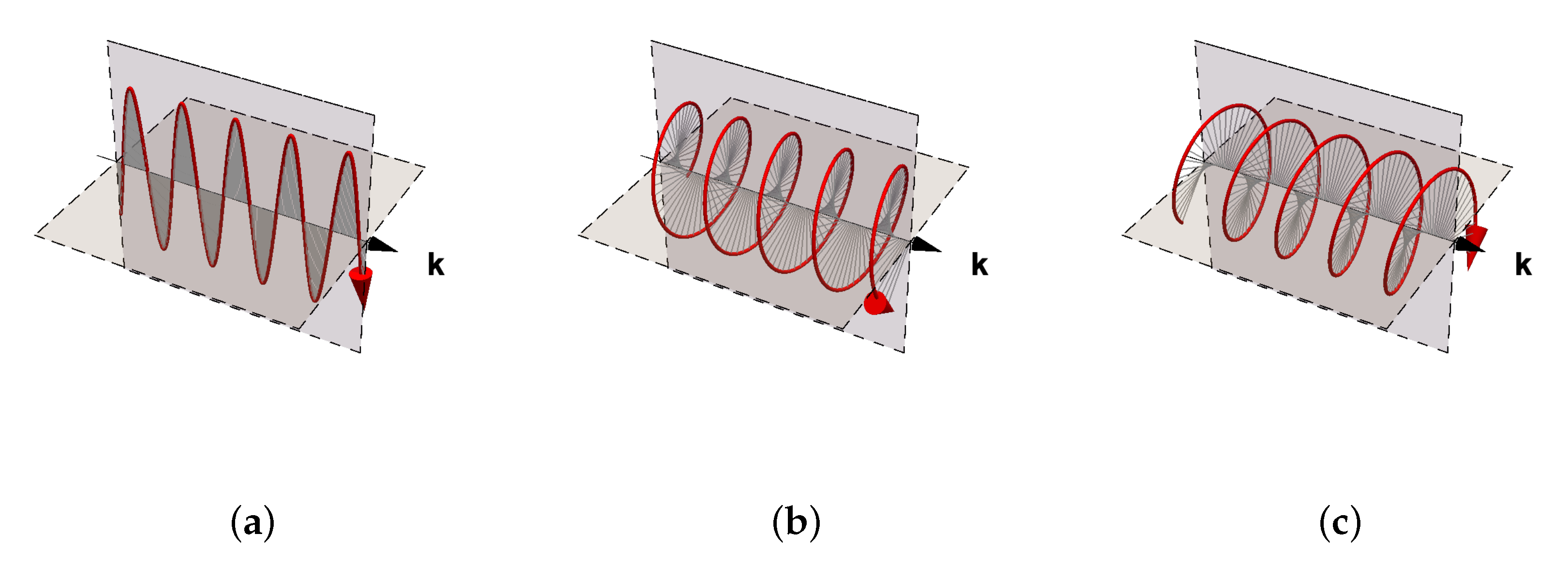
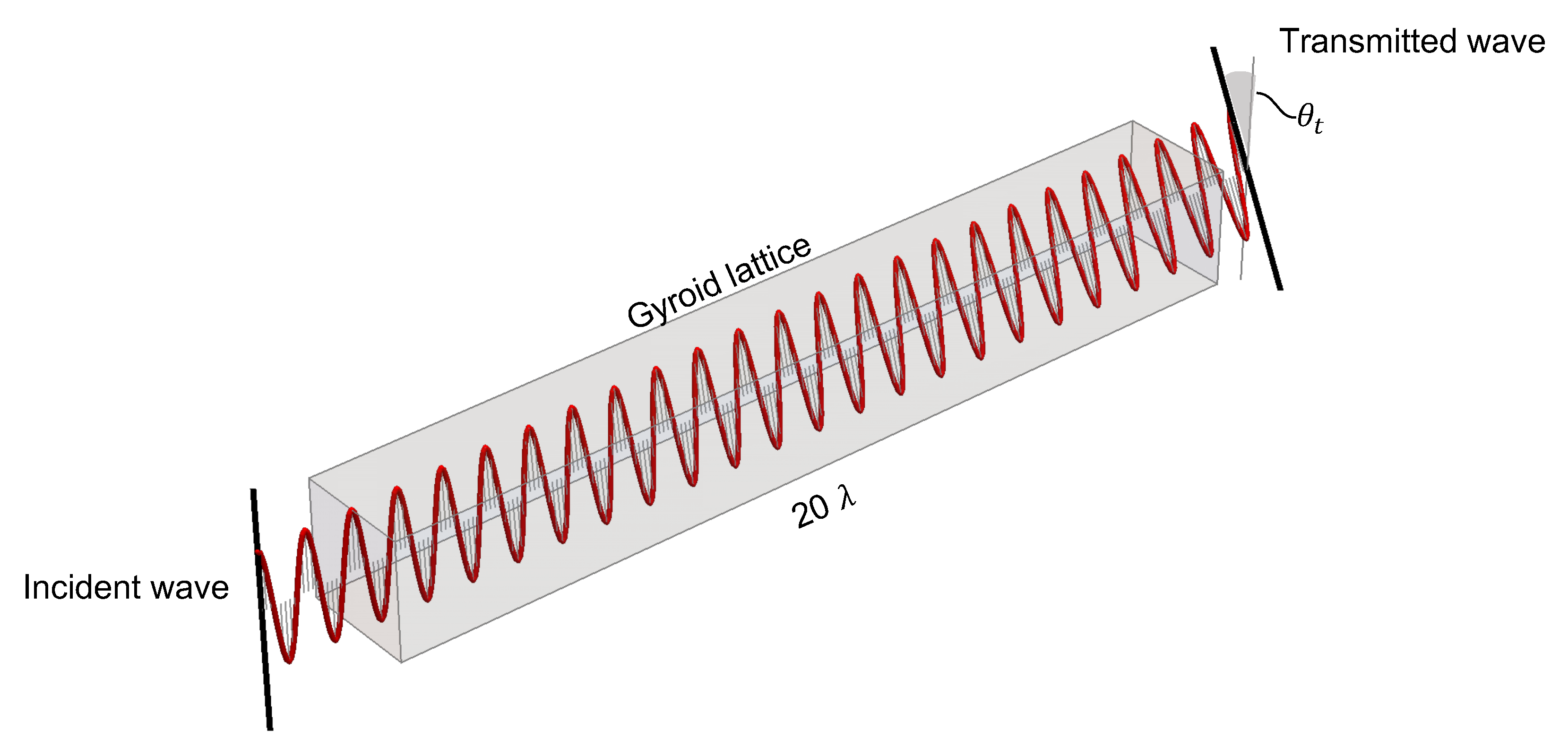
. Since only the phase velocity is affected, and not the amplitude, this effect can be interpreted as the elastic equivalent of circular birefringence in optics. This means that if a linearly polarized wave passes through a gyroid lattice, the polarization plane of the incident wave will be rotated. This is due to the phase difference (retardance) between the two circular components, which produces a rotation of the polarization plane. The concept is illustrated in
Figure 10. Moreover, since phase velocity is involved in reflection of waves at boundaries via the Snell–Descartes law, and in particular in the definition of the Brewster angle of total reflection, gyroid lattices show the potential for being used as elastic circular polarizing filters.
Furthermore, the overall dispersion is normal for direction
, i.e., phase velocity decreases when increasing the frequency, and anomalous for direction
(see [
48] for the definition). The anisotropy of the material and the dispersive properties could also have consequences on surface and guided waves propagating in presence of boundaries [
49,
50], as well as in reflection/transmission problems [
51]. These effects will be investigated in further works.
5. Long-Wavelength and Low-Frequency Approximation and Classic Elasticity
In this last section we will introduce and identify the equivalent homogenized model in the framework of classic linear elasticity. This equivalent homogenized model is characterized by a couple of effective tensors
and
in such a way that the displacement field
is solution of the following problem:
where
verifies
,
denotes the spatial average operator over
and
is the displacement field solution to the heterogeneous problem Equation (
9), as done for instance in [
10].
Since the effective continuum is homogeneous, we consider a plane wave solution with
where
c is the phase velocity of the wave and
a unitary vector. The substitution of this wave solution and of a linear elastic constitutive law into Equation (
12) leads to following equation:
where
is the Christoffel, or acoustic, tensor. The solution of the eigenvalue problem stated in Equation (
13) for a given direction
gives the phase velocities and polarizations of waves in the effective continuum.
In classical elasticity, a material with cubic symmetry is defined by three independent material constants. Using Mandel notation [
52], the corresponding elastic tensor for a material having its symmetry axis parallel to
reads:
It is worth noting that classical elasticity is insensitive to the lack of centrosymmetry [
53]. The symmetry class of the elasticity tensor in the cubic system is
meaning that even if the material symmetry group of the unit cell does not contain the inversion, the symmetry group of elasticity tensor will inherit it.
In the case of cubic materials, the solutions of Equation (
13) listed in
Table 5 are directly obtained.
Using the phase velocities computed from the Bloch–Floquet analysis, parameters
,
,
, and
can be identified and the homogeneous equivalent properties listed in
Table 6 are then deduced. It can be noticed that, as presented in
Table 5, since we considered the propagation along the rotational axes of symmetry, for each direction we observe a purely longitudinal wave and two purely transverse waves.
We now move on to comparing phase velocities and polarizations obtained from the Bloch–Floquet analysis with the ones forecast by the Long-Wavelength and Low-Frequency approximation using classical elasticity. We start with direction
. As already mentioned, this direction corresponds to a rotational axis of symmetry of order 4. In this case, as the elasticity tensor is non sensitive to chirality, the symmetry group of the physical phenomenon (the symmetry group of the physical phenomenon is the intersection of the symmetry group of the constitutive equations and the symmetry group of the mechanical solicitation) is conjugate to
. Indeed, as the acoustic tensor defined in Equation (
13) is a second-order tensor, the Hermann theorem of Crystal physics [
11] predicts its behavior as transversely isotropic, i.e.,
. As a consequence
must have an eigenspace of dimension 2. All the directions of wave propagation for which this is verified are called acoustic axis of the material. Moving to the results presented in
Table 5, we can see that the classic theory indeed predicts one faster longitudinal wave and two slower transverse waves propagating with the same phase velocity.
In the previous section we saw that Bloch–Floquet analysis identifies these waves as circularly polarized with opposite handedness, which is of course equivalent. Indeed, even for very large wavelengths, the numeric evaluation of the polarization provided by
Table 4 corresponds to the eigensystem (eigenvalues plus eigenvectors) of a Hermitian acoustic tensor. In such case, the space corresponding to the double eigenvalue (which is real due to Hermitian nature of the matrix) is two dimensional over the complex field
. However, in the case of a classic Cauchy continuum the acoustic tensor is symmetric real, and the eigen-space corresponding to the double eigenvalue is two dimensional over the real field
. Since the 2D vector space over
can be considered as a four dimensional vector space over
the span is not equivalent. Moreover, as presented in
Section 4, when the ratio between the wavelength and the size of the unit cell becomes finite, this 2D eigenspace splits into two 1D eigenspaces with different phase velocities. It is important to notice again that this effect occurs in the LF-LW regime, where the classical elastodynamic homogenization is supposed to hold, or give at least approximated results while preserving the physics of the problem. Similar results are obtained for propagation along
, which corresponds to the rotational axis of symmetry of order 3. In this case the symmetry group of the physical phenomenon is conjugate to
, and thus again transverse isotropy is imposed to the acoustic tensor. Finally, the direction of propagation
is along to a rotation axis of symmetry of order 2, the physical point group is thus conjugate to
. Here, the symmetry class of the acoustic tensor is
, and all the eigenspaces are unidimensional. In this last case, as this kind of symmetry can be seen by second order tensors, the results from FEA on the heterogeneous material and classic elasticity are in agreement in the LF-LW regime.
In this section we have shown that some discrepancies can be observed when using an overall homogeneous continuum of Cauchy type. Classical elasticity (as opposed to generalized elasticity) is not rich enough to capture certain specific physical phenomena related to the symmetries of the material. In particular, if phase velocities are correctly estimated the polarizations are incorrectly predicted. Moreover, as it is well known, the onset of dispersion when frequency or wavenumber increase cannot be described in the classic Cauchy model.
6. Conclusions
In this work it was shown that a classical continuum model could not capture the correct behavior of elastic waves propagating in gyroid lattices. This is due to the fact that the classic continuum mechanics was insensitive to the lack of centrosymmetry of the architectured material. However, it is a well-established belief that the effects of non-centrosymmetry are only related to waves having a wavelength which compares to the size of the microstructure. Here we demonstrate that the solution given by the classical theory failed to predict the correct response, even in the Long Wavelength-Low Frequency domain.
In order to capture the onset of this unconventional behavior, called acoustical activity, the elastic continuum model needs to be enriched. Different strategies of enrichment are possible. In particular, the use of strain-gradient elasticity will be investigate in a forthcoming study.
The main practical consequence of the results presented in this work was in the evidence that circularly polarized waves could be observed in gyroid lattices, and that classic models failed to describe such effect. This could have a practical interest, since devices based on manipulation of circular polarization are frequently used in optics and electromagnetism. However, if one wants to exploit the same effects in mechanics, it appears important not to rely on classical theories of elasticity. Finally, it should be noted that, in this work, we addressed bulk wave propagation in an infinite medium. The interaction of these waves with boundaries, in the case of reflection/transmission problems or in the case of guided propagation, also deserves to be investigated.