Abstract
In this paper, stationary solitary and periodic waves of a nonlinear nonintegrable lattice are numerically constructed using a two-stage approach. First, as a result of continualization, a nonintegrable generalized Boussinesq—Ostrovsky equation is obtained, for which the solitary-wave and periodic solutions are numerically found by the Petviashvili method. In the second stage, discrete analogs of the obtained solutions are used as initial conditions in the numerical simulation of the original lattice. It is shown that the initial perturbations constructed in this way propagate along the lattice without changing their shape.
1. Introduction
Nonlinear discrete mathematical models often arise in problems of the dynamics of deformable systems, in physics and biology. They appear either as a result of discretization of physically significant integrable partial differential equations (PDEs), such as the Korteweg–de Vries, the sine—Gordon, and the nonlinear Schrödinger equations, or when modeling systems that are discrete in nature. In the first case, nonlinear lattices arise that are integrated by the inverse scattering problem technique [1,2]. These lattices, the most famous representatives of which are the Ablowitz–Ladik, Toda, Volterra, and Ito–Narita–Bogoyavlensky lattices [3], have multisoliton solutions and Lax pairs, admit Bäcklund transformations, and have other distinctive features. In the second case, the problem is most often reduced to the study of a nonintegrable nonlinear differential-difference equation (DDE), the canonical example of which is the Fermi–Pasta–Ulam–Tsingou (FPUT) lattice [4].
Many nonintegrable evolutionary and quasi-hyperbolic equations have exact solitary-wave and periodic solutions [5]. In contrast to them, for nonintegrable nonlinear DDEs, exact solutions can be found only in rare cases. Thus, in [6], a discrete analogue of the Burgers-type equation was constructed using the method of generalized conditional symmetries [7]. In fact, from a linearizable (so-called C-integrable) equation, a linearizable DDE with two-kink and two-soliton solutions is obtained. In [8], a discrete version of the linearizable Eckhaus equation is introduced, which is a coupled system of two difference evolutionary equations. This system is reduced to a single nonlinear first-order difference equation that does not have exact solutions and exhibits chaotic dynamics. Therefore, the authors called the equation “quasi” integrable.
The analysis of literature sources shows that the existence of an exact solution to a nonlinear DDE, if it does not guarantee integrability, is at least a serious argument for its presence. This is obvious if the exact solutions are obtained using the inverse scattering problem [1,2], Hirota [9,10], Riemann theta functions [11,12], Casorati determinant [13], and Pfaffian [14] representations methods or on the basis of Darboux transformations of Lax pairs [15,16]. At the same time, for integrable DDEs, particular methods of constructing exact solutions also work: methods of hyperbolic tangents [17], truncated expansions [18], geometric series [19,20], etc. When studying nonintegrable DDEs, other approaches are used. As a rule, these include various versions of the quasi-continuous approximation [21], asymptotic methods of multiscale expansions [22], and Padé approximants [23]. In [24,25], the formation of solitary waves in a diatomic FPUT lattice, predicted by multiscale asymptotic analysis, was confirmed by the results of numerical simulations. Direct numerical modeling of nonlinear DDEs in the search for their solutions is rarely used. Thus, in [26], on the basis of the finite-difference approach using the Newton–Raphson method, traveling periodic waves in the FPUT lattice were investigated.
Therefore, there is a problem of constructing solitary-wave and periodic solutions of nonintegrable DDEs. The solution to this problem can be based on the use of numerical modeling methods or on the study of a continuous analogue. In the second case, there is a relatively favorable situation when the continuous limit of the DDE is an integrable PDE, for example the KdV equation for FPUT, Toda, or Volterra lattices. The problem becomes more complicated if, as a result of continualization, a nonintegrable, but exactly solvable equation arises, for example the Kawahara equation or the Korteveg–de Vries–Burgers equation. The most difficult case seems to be when a nonintegrable DDE is modeled by a nonintegrable PDE that does not have exact solutions. This article deals with just such a case.
The purpose of this study is to construct stable periodic and solitary-wave solutions of a nonintegrable DDE based on a combined approach. In the first stage, continualization (continuumization) of the initial lattice is carried out, and stationary solutions are numerically constructed. Then, a numerical simulation of the lattice is carried out, and a discrete analogue of the solution constructed earlier is used as the initial perturbation. A similar approach was used in [27] when obtaining soliton solutions of a nonintegrable generalization of a coupled Volterra system. The article is organized as follows. In the next section, the structure of the lattice and equation of motion is introduced. The lattice continualization, that is the transition from the original DDE to a PDE, is carried out in the third section. In Section 4, exact solutions of the reduced PDE are used to establish the physical consistency of the continualization process. In the next two sections, based on the Petviashvili method [28,29], steady solitary wave and periodic solutions of a full nonlinear PDE are numerically constructed. Then, using a discrete analog of the obtained solutions, a numerical simulation of the original nonlinear lattice is carried out, and the stable propagation of the disturbances is demonstrated.
2. Structure and Equation of Motion of the Lattice
Consider a one-dimensional infinite lattice of identical particles with masses m, which in the state of equilibrium are located along the horizontal axis with a step of h (Figure 1). The particles are connected both with each other by horizontal nonlinear elastic springs and with the foundation by vertical prestressed springs. Suppose that: (1) particles can move only in the horizontal direction along the axis ; (2) the potential energy of a horizontal spring is represented by a sixth degree polynomial in even powers of their absolute deformation; (3) the maximum displacement of particles during oscillations is much less than both the initial length of vertical springs and their initial absolute deformations obtained as a result of prestressing.
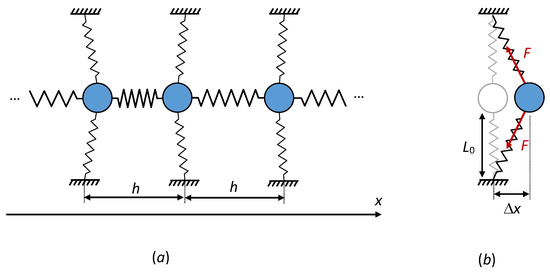
Figure 1.
(a) Lattice structure; (b) modeling the interaction of a particle with a foundation.
The latter assumption allows us to assume that the resulting force transmitted to the particle from the foundation is horizontal and directly proportional to the displacement of the particle.
Taking into account the above, the equation of motion for the particle of the lattice can be written as follows:
where denotes the displacement of the n-th particle. The first three terms in brackets on the right-hand side of Equation (1) characterize the interaction of the n-th particle with two neighboring particles; the last term describes the interaction of the n-th particle with the foundation. From physical considerations, it follows that when the vertical springs are pre-stretched and for their preliminary compression; coefficients and m are always positive. The signs of the remaining coefficients are arbitrary.
3. Transition from a Lattice Equation to a Continuous Equation
Our goal is to construct steady traveling wave solutions of Equation (1). Note that Equation (1) is a nonlinear nonintegrable DDE that does not have exact solutions.
Let us introduce the continuous coordinate x scaled in such a way that at the nodes of the lattice, coinciding with the centers of particles in a state of equilibrium. We assume that is a discrete approximation to continuous function ,
We seek a long-wave solution, whose spatial period is much larger than the distance between the particles h. Using a Maclaurin series expansion, one can write:
where x is the horizontal coordinate. Let the coefficients of Equation (1) have the following orders in variable h:
where parameters have the order of unity. Substituting expression (2) into Equation (1) and limiting ourselves to terms of order no higher than , we obtain:
This equation generalizes the combination of the Boussinesq and Klein–Gordon equations [30] and can be called the generalized Boussinesq–Ostrovsky equation. As in the case of the original Ostrovsky equation [31], Equation (4) has no exact solutions and can only be investigated numerically. Equation (4) has two important symmetry properties. First, it is invariant under the transformations , that is it has the property of reversibility, which is of fundamental importance for the search for localized solutions [32]. Secondly, it allows arbitrary shifts in independent variables, allowing further analysis in the class of stationary solutions [33].
Let us pass in Equation (4) to the traveling wave variable and replace the dependent variable with using equality :
where:
To reduce the number of coefficients of Equation (5), we scale the variables:
Denoting:
we finally obtain:
where and the plus in the left-hand side corresponds to the case of the preliminary compression of vertical springs.
4. Checking the Correctness of the Transition to a Continuous Equation
Let us check whether continuous Equation (9) can be used to model the propagation of traveling waves of the original lattice Equation (1). Assuming in Equation (1), we repeat the steps from the previous paragraph to get the simplified equation:
in which it is assumed that:
where , and the coefficients are related to the coefficients of the original Equation (1) as follows:
Equation (10), in contrast to Equation (9), does not contain in its left-hand side the term responsible for the long-wave dispersion and allows double integration over variable :
Note that a similar equation arose in [34] when simulating solitary waves in a three-layer symmetrically stratified fluid in the framework of an extended nonintegrable version of the modified Korteweg–de Vries equation.
Let us find exact solutions of Equation (13). Substitution , where p is the pole order of the sought solution, shows that the balance of the leading terms of Equation (13) is achieved at . Therefore, we will seek the solution in the form , where must be a simple pole function. The left-hand side of Equation (13) contains an even order derivative; nonlinear terms have a simple polynomial form; in this case, it is convenient to express function in terms of Jacobi elliptic functions.
In the case of , where is elliptic cosine and are arbitrary constants, we obtain two branches of exact particular solutions:
if relationships between the coefficients of Equation (13) and the parameters of the solution have the form:
and:
if:
The first branch (14) gives a real and bounded solution when ; the second branch (16) defines solution of this kind under the conditions or in the case and in the case .
If we choose , we get the following exact solution:
under conditions:
The function (18) is real and bounded in cases and , while its graph has a bell-like shape (Figure 2).
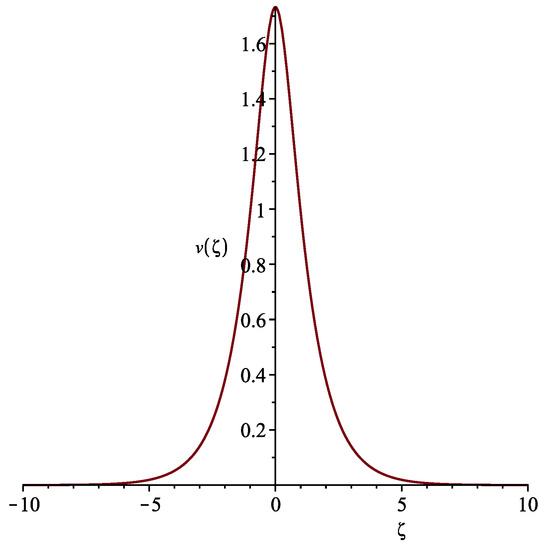
Figure 2.
Solution (18) for and .
Function (18) defines a steady traveling wave solution of Equation (4) propagating without changing the shape along axis at speed W. Replacing the DDE (1) with the PDE (4), which, in turn, reduces to the ODE (9), can be considered justified if the corresponding wave in the lattice will also propagate without distortion. To check this, we solve the corresponding initial problem for the lattice Equation (1).
Setting two parameters and does not allow unambiguously determining the values of all coefficients of Equation (1). Put , and consider two cases: small distance between particles and large distance .
For the case of small distance, from equalities (12), we determine the values of the two remaining coefficients of the lattice equation: . To observe the evolution of the wave impulse, we choose segment . This segment contains particles for ; therefore, Equation (1) can be considered as a system of second-order ordinary differential equations (ODEs) for functions , , . The first initial condition for this system is determined by the antiderivative of solution (18):
the kink-like shape of which allows us to accept as the boundary conditions. As the second initial condition, we have:
The graphs of solutions obtained by the Runge–Kutta–Fehlberg method of the fifth order of accuracy for time points and are shown in Figure 3a. In this case, the wave front propagates without changing shape.
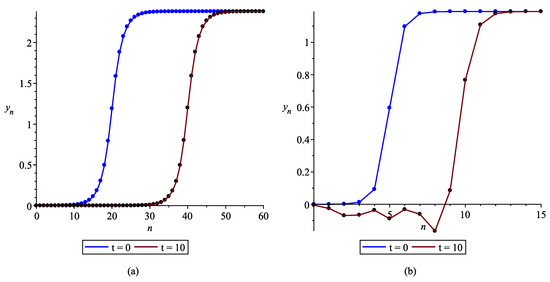
Figure 3.
Wave propagation in periodic lattice structure at for initial conditions determined by the exact solution (18). (a) ; (b) .
In the second case, for , we find . The results for the second case (Figure 3b) show that the wave impulse is significantly distorted with time. Such a distortion of the shape is associated with large errors that the Maclaurin series (2) gives when calculating the values of rapidly changing functions, if only a few first terms of the expansion are retained in it. Our modeling shows that solutions of PDE (9) can be used as initial conditions for setting a steady solitary wave of DDE (1), if the effective width of the wave pulse accounts for at least 10–12 lattice particles. It is easy to see that this condition is satisfied in the first case and not satisfied in the second case.
The kink-like form of solution Figure 3 is not very convenient for tracking its shape over long time intervals; calculations have to be stopped when the wave front approaches the boundary of the integration region. Note that due to the symmetry of Equation (13), there is a soliton-like solution with negative polarity, propagating in the same direction and with the same speed as the solution with positive polarity. Combining two identical pulses with opposite polarities, separated by a sufficient spatial interval, allows us to form an approximate bell-shaped solution of Equation (1), the motion of which can be tracked for a long enough time if we use periodic boundary conditions.
Consider solution (13) for case . At close to zero values of the parameter , the solution has a classical soliton-like form. When the value of approaches its lower boundary , the amplitude of the soliton grows, and the vertex becomes sharper. The combined approximate solution (Figure 4) of Equation (13), composed of two of its exact solutions (18) for , corresponds to a soliton-like wave of Equation (1), the simulation results for which are shown in Figure 5.
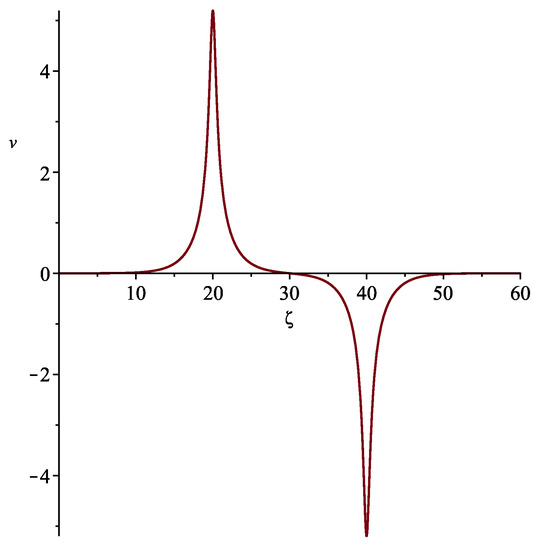
Figure 4.
Approximate solution of Equation (13), combining two exact solutions for .
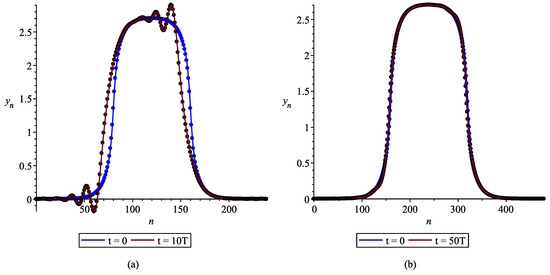
Figure 5.
Soliton-like wave in the lattice. (a) ; (b) .
Figure 5 shows the original wave profile (blue) and the same wave profile (red) after an integer number of oscillation periods T. Under periodic boundary conditions, in a time equal to the period, the steady wave runs through the integration segment and must coincide with its original profile. As in the previous case (Figure 3), with an insufficient number of particles falling on the inclined section of the profile, a distortion of the waveform is observed (Figure 5a). When the distance between the lattice particles is halved, the wave remains visually unchanged for at least 50 periods.
Exact solutions (14) and (16) allow us to simulate the propagation of periodic waves in the lattice. Note that not every real and bounded solution of Equation (13) is suitable for constructing a physically meaningful solution of the lattice Equation (1). Solitary-wave solutions must obey condition:
while the periodic solution must satisfy condition:
in which the integration is carried out over the whole period; otherwise, inverse transformation (11) leads to an unbounded function . Although periodic solutions (14) and (16) do not directly satisfy condition (23), it is possible to build a solution with the required property.
To do this, we can use, for example, solution (14), the values of which at and change continuously from a certain maximum to zero (Figure 6a).
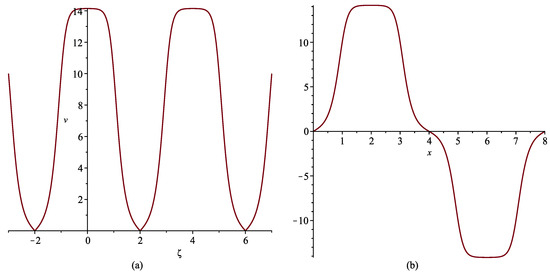
Figure 6.
(a) Solution (14) and (b) smooth combined solution at .
From the symmetry of Equation (13), it follows that is also its solution. Alternating the periods of functions and , we obtain a smooth periodic solution (Figure 6b) satisfying condition (23). To simplify the numerical simulation, the value of parameter k was chosen so that the solution period was integer; in addition, the solution was shifted by a quarter of the period to the left. Taking into account that the values of parameters are of the order of unity, we put , and for the coefficients of Equation (1), we have . The graphs of the corresponding initial disturbance for the lattice and wave profile after 50 periods are shown in Figure 7a, respectively in blue and red. The graph of the absolute error (Figure 7b) indicates a satisfactory coincidence of the two considered wave profiles.
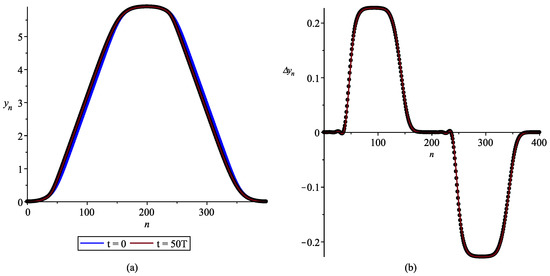
Figure 7.
(a) Initial wave profile (blue) and wave profile (red) after 50 oscillation periods; (b) absolute error .
5. Approximate Solution of the Original Lattice Equation, Case 1
Condition , adopted in the previous section, made it possible to pass to a simplified continuous Equation (10), which has an exact solitary-wave solution. Equation (9), corresponding to the original lattice equation, does not have exact solutions. However, it is possible to construct an approximate solution to Equation (9) using the Petviashvili method. Consider the case with a minus in front of the last term on the left side of the equation.
The Petviashvili method is intended for the iterative solution of nonlinear system:
where v is an matrix of unknowns, L is a nonsingular real matrix, and is a nonlinear function, which is homogeneous with respect to the components of vector v.
From a starting point , the method generates the recurrence:
where is the iteration number, is the stabilizing factor, is the notation for the Euclidean inner product, and q is a free real parameter that affects the rate of convergence. It is shown that for a homogeneous function of degree P, the rate of convergence reaches a maximum when . For the exact solution of system (24), we have . With convergence, iterative calculations continue until the value becomes sufficiently small.
To pass from differential Equation (9) to the system of algebraic Equation (25), we introduce the vector of unknowns with coordinates corresponding to the values of function on some symmetric segment :
Then, in Equation (9), rewritten in the form:
we replace the unknown function and all its derivatives with the difference expressions:
for each index k, k = 1 ... M, obtaining a system of M algebraic equations. In order for symmetric formulas (28) to be written for any k, vector gets additional coordinates , and the system is supplemented by four equations corresponding to the periodic boundary conditions:
After multiplying the right-hand side of the resulting system by a stabilizing factor m, we obtain a system ready for recurrent computations. Before starting the computations, it remains to choose the values of coefficients V, , and the width of the segment, on which the solution of the problem is built, and assign the start vector .
Substitution into the linearized Equation (27) with a zero right-hand side gives for the wave number K the equation:
among the roots of which there is a pair of real ones:
This means that for any value of the coefficient V, Equation (27) has a periodic solution in the form of an infinitesimal harmonic wave, the length of which is . Let us make sure that the Petviashvili method finds this solution if we put:
Let us choose for parameters of ratios (3) arbitrary values in the vicinity of unity: . Consider the case by setting in Equation (27). To simplify the analysis, the scaling factor of the independent variables in Equations (7) will be taken equal to one:
Under condition (33), the width of the segment should be chosen to be a multiple of the distance h between the particles in the lattice, for example . Then, from relations (31) and (32), we have , and from relations (6) and (33), we obtain . Having calculated constants from Equation (6), we substitute them into Equation (8) to get . It is easy to check that the case under consideration corresponds to the following coefficients of the original Equation (1): .
If we choose , then the computation process reaches accuracy in about 20 iterations and converges to the solution shown in Figure 8a.
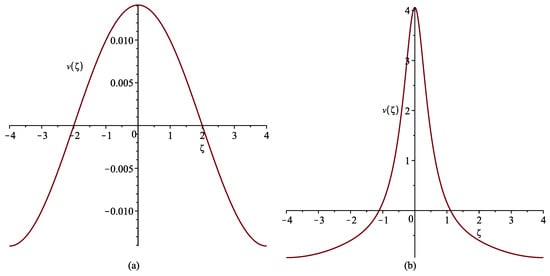
Figure 8.
Periodic solution of Equation (27) for: (a) ; (b) .
Let us verify that the approximate solution of Equation (27) obtained by the Petviashvili method defines a periodic wave of the lattice Equation (1). For this, as in the previous section, considering the lattice equation as a system of ODEs, we compose a problem for it by introducing periodic boundary conditions:
where and use solution Figure 8a and its numerical derivative to set two initial conditions.
The numerical solution of this initial problem shows that the periodic wave retains its shape unchanged. Figure 9a shows the waveform at the initial moment of time and after 100 oscillation periods; these graphs are visually indistinguishable. From Figure 9b, it follows that the ordinates of the graphs in Figure 9a differ by slightly more than 0.2%.
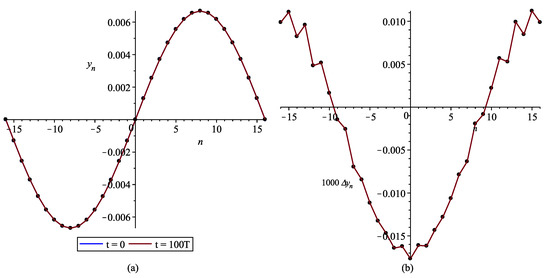
Figure 9.
Weakly nonlinear periodic wave in the lattice. (a) Coincidence of the initial wave profile and the profile after oscillation periods; (b) absolute error .
For a wave with such a small amplitude as shown in Figure 9a, the influence of the nonlinear terms in Equation (1) can be neglected. Let us get a solution for the opposite situation, when this influence is large. For this, the width of the segment , which imposes the period of the sought solution on the Petviashvili method, we choose, for example, half as large as . Let us keep the previous values for parameters and , but require that and . From equalities (6), (8), and (31)–(33), we obtain and the following coefficients of the original Equation (1): . The solution, to which the Petviashvili method converges at new values of the parameters V and , differs significantly in shape from a harmonic wave (Figure 8b). The corresponding profiles of the traveling periodic wave for the lattice and the absolute error accumulated during the wave motion for 10 periods are shown in Figure 10.
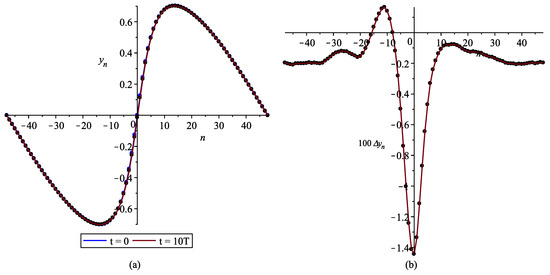
Figure 10.
Strongly nonlinear periodic lattice wave. (a) coincidence of the initial wave profile and the profile after oscillation periods; (b) absolute error .
As we can see, in the numerical simulation of a substantially nonlinear wave, the accumulation of errors is much faster. The largest error is accumulated in the center of the wave profile, in the zone of its maximum slope. At the same time, it can be argued that in this case, we also constructed an approximate solution to the lattice equation in the form of a stable periodic wave.
6. Approximate Solution of the Original Lattice Equation, Case 2
Consider now the second version of Equation (9), with a plus sign on its left-hand side, which can be written as follows:
The linear dispersion relation for this case:
has roots:
that are real under condition and complex otherwise. The linear dispersion relation for this case has roots that are real under Condition 1 and complex otherwise. Consequently, in region , in which Equation (35) has no solutions in the form of an infinitesimal harmonic wave, the existence of solitary wave solutions is possible.
Let . For such values of the parameters, taking into account condition (33), we obtain . Calculating all the coefficients using equalities (6), we substitute them in Equation (8) and find . If we put , the iterations of the Petviashvili method converge to the solution, the graph of which is shown in Figure 11a. The corresponding profiles of a solitary wave in the lattice at the initial moment and after 50 oscillation periods are shown in Figure 11b.
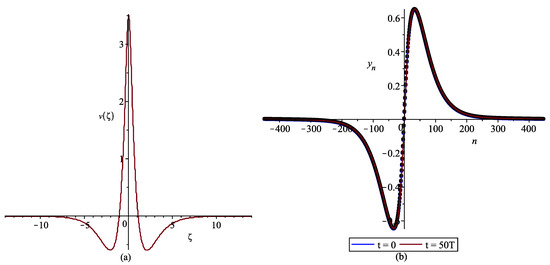
Figure 11.
(a) Solitary wave solution of Equation (35) and (b) corresponding wave in the original lattice for .
It is necessary to explain what periods of oscillations of the solitary wave are mentioned above. The point is that, both in the Petviashvili method and in the numerical simulation of the lattice, we still use periodic boundary conditions, which are convenient for observing the wave at large time intervals. Formally, we obtain, as before, periodic solutions, each period of which contains a central “burst” that rapidly decays at . Such bursts, quite distant from each other, practically do not interact and can be considered as solitary waves. The fact that we now obtain solitary wave solutions is easily verified by increasing the width of segment , at which the width of the central burst remains unchanged.
As the parameter V decreases and approaches the boundary value , beyond which the region of periodic solutions begins, the shape of the solitary wave changes, and it gradually turns into a wave packet. The corresponding solution for is shown in Figure 12.
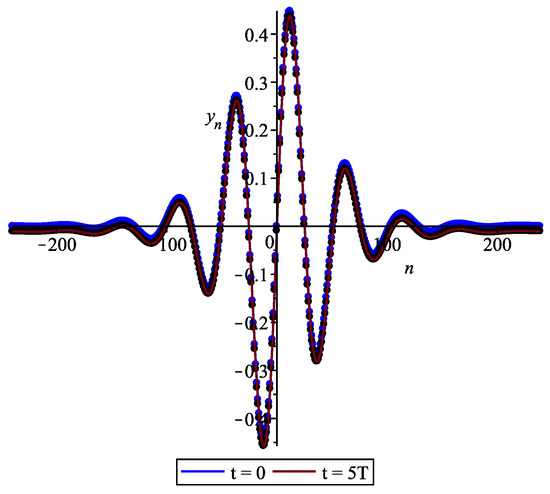
Figure 12.
Solitary wave in the original lattice for .
In Figure 12, one can notice the uniform downward shift of the solitary wave in comparison with its initial position. This is due to the instability of the zero solution for the lattice in the case under consideration, when the vertical springs are precompressed. Indeed, assuming that does not depend on n, we substitute in Equation (1) and obtain a linear equation , the solution of which at increases exponentially in absolute value over time. Thus, we are faced here with the appearance of the so-called runaway solution, which manifests itself in the appearance and exponential growth of a pedestal, on top of which a solitary wave continues to run. This effect occurs only in the case of a positive sign in front of the last term on the left-hand side of Equation (9) with insufficiently accurate determination of the initial wave profile, which was specially done when constructing Figure 12. A decrease in the step between particles in the lattice together with an increase in the dimension M of the system (24) of the Petviashvili method makes it possible to delay the onset of the effect and observe the wave profile unchanged for 20–30 periods.
7. Discussion and Conclusions
The proposed procedure makes it possible to find approximate steady solitary-wave and periodic solutions of the lattice Equation (1). Since these are only approximate solutions, then in direct numerical modeling, the waveform is inevitably distorted, sooner or later. The accuracy of approximate solutions is mainly influenced by the errors of the truncation of the Maclaurin series at the continualization stage and errors in replacing derivatives with difference formulas when compiling the system (24). The first of these errors decreases with the distance h between the particles, which limits the procedure to studying only long waves in the lattice. The second error decreases with increasing dimension M of the system (24) at the cost of a multiple increase in the computation time. In all the cases considered, the convergence rate of the Petviashvili method’s iterations was at least linear; therefore, it is not difficult to reduce the iterative error parameter by one or two orders of magnitude; the calculated time increases insignificantly. The quality of the found solution is determined by the wave lifetime before the appearance of significant distortions during the propagation of the initial disturbance over the lattice. The determination of ratio:
calculated for solution of Petviashvili’s method helps to estimate this lifetime before the launch of the most resource-intensive stage: the numerical simulation of wave propagation in the lattice. As in the case with the Ostrovsky equation [31], any smooth steady traveling wave solution of Equation (9) obeys the property:
where integration is carried out in infinite limits for the solitary wave and over the period for the periodic wave. The closer parameter is to zero, the more accurately property (39) is fulfilled. Experiments have shown that for , the wave lifetime is at least 50 periods.
The nonintegrable FPUT lattice, along with some integrable lattices, in the continuous limit transforms into the KdV equation. The integrable Ablowitz–Ladik lattice and nonintegrable generalizations close to it are transformed into the nonlinear Schrödinger equation. Thus, the analysis of nonintegrable nonlinear DDEs is carried out on the basis of their integrable continuous analogs with exact soliton solutions, an infinite set of conservation laws, and other useful properties. The peculiarity of the problem considered in the article is that the nonintegrable lattice Equation (1), which has no exact solutions, after correct continualization transforms into the nonintegrable generalized Boussinesq–Ostrovsky equation, which also has no exact solutions. Therefore, here, it was required to use a numerical procedure called the Petviashvili method to construct solitary wave and periodic solutions of the continuous analogue (4). It turned out that the initial perturbations, given in the form of the discretization of the numerical solution of the continuous model, propagates along the lattice without changing the shape at a constant speed. The answers to the questions, how the implemented approach works for other nonintegrable lattices and coupled systems of lattices and how wide classes of solitary wave and periodic solutions can be constructed can be obtained as a result of further research.
A feature of the approach proposed in the article is that the construction of a solitary wave and periodic solutions is not carried out directly, as, for example, in [26], but on the basis of a continuous analog of the lattice. The question may arise whether maybe this is an artificial complication of the problem. In our opinion, this approach is natural when analyzing long waves in nonlinear lattices. The Petviashvili method is effectively used for the numerical solution of nonlinear PDEs, and its adaptation to DDEs is an independent problem, the solution of which is beyond the scope of this article. The generalized nonintegrable Boussinesq–Ostrovsky equation obtained as a result of continualization is new, and its analytically solvable reductions model a wide range of nonlinear dynamics problems. Thus, an important side result of the study is the numerical construction of periodic and solitary wave solutions of the new nonintegrable evolutionary equation.
Author Contributions
Conceptualization, I.A.; investigation, A.Z. and A.B.; methodology, A.Z.; software, A.B.; supervision, I.A.; validation, V.E.; writing—original draft preparation, A.Z. and A.B.; writing—review and editing, I.A. and V.E. All authors have read and agreed to the published version of the manuscript.
Funding
The reported study was funded by RFBR, Project Numbers 20-38-70158, 20-01-00123, and 18-29-10073.
Acknowledgments
We thank the anonymous reviewers for the valuable comments and suggestions, which helped to improve the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ablowitz, M.J.; Ladik, J.F. Nonlinear differential-difference equations. J. Math. Phys. 1975, 16, 598. [Google Scholar] [CrossRef]
- Toda, M. Studies of a non-linear lattice. Phys. Rep. 1975, 18, 1–123. [Google Scholar] [CrossRef]
- Shabat, A.B. (Ed.) Encyclopedia of Integrable Systems; L.D. Landau Institute for Theoretical Physics: Moscow, Russia, 2010; Available online: http://home.itp.ac.ru/~adler/E/e.pdf (accessed on 23 September 2020).
- Fermi, E.; Pasta, J.; Ulam, S. Studies of Nonlinear Problems; Document LA-1940. Los Alamos National Laboratory, 1955. Available online: http://www.physics.utah.edu/~detar/phys6720/handouts/fpu/FermiCollectedPapers1965.pdf (accessed on 23 September 2020).
- Conte, R.; Musette, M. The Painlevé Handbook; Springer: New York, NY, USA, 2008. [Google Scholar]
- Common, A.K.; Musette, M. Exact solutions of nonintegrable lattice equations. J. Phys. A Math. Gen. 2001, 34, 10401–10410. [Google Scholar] [CrossRef]
- Fokas, A.S.; Liu, Q.M. Generalized conditional symmetries and exact solutions of nonintegrable equations. Math. Theor. Phys. 1994, 99, 263–277. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Ahrens, C.D.; De Lillo, S. On a “quasi” integrable discrete Eckhaus equation. J. Nonlinear Math. Phys. 2005, 12 (Suppl. 1), 1–12. [Google Scholar] [CrossRef]
- Hirota, R. Nonlinear partial difference equations. II. Discrete-time Toda equation. J. Phys. Soc. Jpn. 1977, 43, 2074–2078. [Google Scholar] [CrossRef]
- Silindir, B. Soliton solutions of q-Toda lattice by Hirota direct method. Adv. Differ. Equ. 2012, 2012, 121. [Google Scholar] [CrossRef]
- Krichever, I.; Wiegmann, P.; Zabrodin, A. Elliptic solutions to difference non-linear equations and related many-body problems. Commun. Math. Phys. 1998, 193, 373–396. [Google Scholar] [CrossRef]
- Matveev, V.B. 30 years of finite-gap integration theory. Philos. Trans. R. Soc. A 2008, 366, 837–875. [Google Scholar] [CrossRef]
- Ohta, Y.; Hirota, R. A discrete KdV equation and its Casorati determinant solution. J. Phys. Soc. Jpn. 1991, 60, 2095. [Google Scholar] [CrossRef]
- Tsujimoto, S.; Hirota, R. Pfaffian representation of solutions to the discrete BKP hierarchy in bilinear form. J. Phys. Soc. Jpn. 1996, 65, 2797–2806. [Google Scholar] [CrossRef]
- Matveev, V.B. Darboux transformation and the explicit solutions of differential-difference and difference-difference evolution equations I. Lett. Math. Phys. 1979, 3, 217–222. [Google Scholar] [CrossRef]
- Levi, D.; Ragnisco, O. The inhomogeneous Toda lattice: Its hierarchy and Darboux-Backlund transformations. J. Phys. A 1991, 24, 1729–1739. [Google Scholar] [CrossRef]
- Baldwin, D.; Goktas, U.; Hereman, W. Symbolic computation of hyperbolic tangent solutions for nonlinear differential–difference equations. Comput. Phys. Commun. 2004, 162, 203–217. [Google Scholar] [CrossRef]
- Ryabov, P.N. Exact solutions of the Kudryashov-Sinelshchikov equation. Appl. Math. Comput. 2010, 217, 3585–3590. [Google Scholar] [CrossRef]
- Zemlyanukhin, A.I.; Bochkarev, A.V. Exact solutions and numerical simulation of the discrete Sawada–Kotera equation. Symmetry 2020, 12, 131. [Google Scholar] [CrossRef]
- Bochkarev, A.V.; Zemlyanukhin, A.I. The geometric series method for constructing exact solutions to nonlinear evolution equations. Comput. Math. Math. Phys. 2017, 57, 1111–1123. [Google Scholar] [CrossRef]
- Wattis, J.A.D. Solitary waves in a diatomic lattice: Analytic approximations for a wide range of speeds by quasi-continuum methods. Phys. Lett. A 2001, 284, 16–22. [Google Scholar] [CrossRef]
- Awrejcewicz, J.; Andrianov, I.V.; Manevitch, L.I. Asymptotic Approaches in Nonlinear Dynamics: New Trends and Applications; Springer: Berlin, Germany, 1998. [Google Scholar]
- Katz, S.; Givli, S. Solitary waves in a nonintegrable chain with double-well potentials. Phys. Rev. E 2019, 100, 032209. [Google Scholar] [CrossRef]
- Vainchtein, A.; Starosvetsky, Y.; Wright, J.D.; Perline, R. Solitary waves in diatomic chains. Phys. Rev. E 2016, 93, 042210. [Google Scholar] [CrossRef]
- Starosvetsky, Y.; Vainchtein, A. Solitary waves in FPU lattices with alternating bond potentials. Mech. Res. Commun. 2018, 93, 148–153. [Google Scholar] [CrossRef]
- Rodriguez-Achach, M.; Perez, G. Periodic traveling waves in nonlinear chains. Rev. Mex. Fis. 1996, 42, 878–896. [Google Scholar]
- Bibik, Y.V.; Popov, S.P. Soliton solutions of a generalization of the coupled Volterra system. Comput. Math. Math. Phys. 2019, 59, 1806–1815. [Google Scholar] [CrossRef]
- Petviashvili, V.I. Equation of an extraordinary soliton. Sov. J. Plasma Phys. 1976, 2, 257–258. [Google Scholar]
- Pelinovsky, D.E.; Stepanyants, Y.A. Convergence of Petviashvili’s iteration method for numerical approximation of stationary solutions of nonlinear wave equations. SIAM J. Numer. Anal. 2004, 42, 1110–1127. [Google Scholar] [CrossRef]
- Khusnutdinova, K.; Tranter, M. D’Alembert-type solution of the Cauchy problem for the Boussinesq-Klein-Gordon equation. Stud. Appl. Math. 2019, 142, 551–585. [Google Scholar] [CrossRef]
- Ostrovsky, L.A. Nonlinear internal waves in a rotating ocean. Oceanology 1979, 18, 119–125. [Google Scholar]
- Hunt, G.W.; Bolt, H.M.; Thompson, J.M.T. Structural localisation phenomena and the dynamical phase-space analogy. Proc. R. Soc. Lond. 1989, 425, 245–267. [Google Scholar]
- Olver, P. Applications of Lie Groups to Differential Equations; Springer: New York, NY, USA, 1993. [Google Scholar]
- Kurkina, O.E.; Kurkin, A.A.; Ruvinskaya, E.A.; Pelinovsky, E.N.; Soomere, T. Dynamics of solitons in a nonintegrable version of the modified Korteweg-de Vries equation. JETP Lett. 2012, 95, 91–95. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).