Pinocytosis as the Biological Mechanism That Protects Pgp Function in Multidrug Resistant Cancer Cells and in Blood–Brain Barrier Endothelial Cells

Abstract

Cancer is the second leading cause of death worldwide. Chemotherapy has shown reasonable success in treating cancer. However, multidrug resistance (MDR), a phenomenon by which cancerous cells become resistant to a broad range of functionally and structurally unrelated chemotherapeutic agents, is a major drawback in the effective use of chemotherapeutic agents in the clinic. Overexpression of P-glycoprotein (Pgp) is a major cause of MDR in cancer as it actively effluxes a wide range of structurally and chemically unrelated substrates, including chemotherapeutic agents. Interestingly, Pgp is also overexpressed in the endothelial cells of blood–brain barrier (BBB) restricting the entry of 98% small molecule drugs to the brain. The efficacy of Pgp is sensitive to any impairment of the membrane structure. A small increase of 2% in the membrane surface tension, which can be caused by a very low drug concentration, is enough to block the Pgp function. We demonstrate in this work by mathematical equations that the incorporation of drugs does increase the surface tension as expected, and the mechanism of endocytosis dissipates any increase in surface tension by augmenting the internalisation of membrane per unit of time, such that an increase in the surface tension of about 2% can be dissipated within only 4.5 s.

1. Introduction

Cancer is the second leading cause of death worldwide [1]. It is a major health problem worldwide with more than 18 million patients diagnosed with cancer in 2018, and a death toll of around 9.5 million. The incidence rate of cancer is estimated to increase to 24 million new cases in 2030, with 13 million annual deaths [2]. Chemotherapy has shown reasonable success in treating cancer; for example, Hodgkin’s lymphoma and paediatric acute lymphoblastic leukaemia were considered uniformly fatal diseases few decades ago, and today, 75 to 80% of patients are cured using a course of combination chemotherapy [3]. However, multidrug resistance (MDR) is a major drawback in the effective use of chemotherapeutic agents in the clinic [4,5]. MDR is a phenomenon by which cancerous cells become resistant to a broad range of functionally and structurally unrelated chemotherapeutic agents [6]. Cancer cells can develop MDR through different mechanisms, such as decreasing drug uptake, increasing drug efflux, activation of detoxifying systems and activation of DNA repair mechanisms [7]. Overexpression of P-glycoprotein (Pgp), also known as ATP Binding Cassette Subfamily B Member 1 (ABCB1) or multidrug resistance 1 (MDR1), is a major cause of MDR in cancer. MDR cell lines exhibit a reduced intracellular accumulation of drug relative to the parental drug- sensitive cell lines [8]. Furthermore cancer aggressiveness, i.e., the metastatic potential of tumours, is related to MDR [9]. Pgp actively effluxes a wide range of structurally and chemically unrelated substrates, including chemotherapeutic agents. Extensive research has been carried out over the past few decades to reverse Pgp-mediated MDR. While Pgp inhibitors were successful in resensitising MDR cells to chemotherapeutic agents in vitro, they failed to show any significant clinical benefit [6].

In addition to its role in cancer, MDR is a significant hurdle to overcome in the development of effective drugs for central nervous system (CNS) diseases. The lack of effective pharmacological treatments for diseases of the CNS is a prominent issue within our society; with 1 in 6 people suffering from a form of CNS disease as of 2019 [10]. The difficulty in designing drugs for CNS diseases is, in part, due to MDR at the blood–brain barrier (BBB). The BBB controls the transport of critical nutrients and waste products in and out of the CNS, maintaining the carefully regulated microenvironment required for neuronal signalling. The continuous monolayer of endothelial cells that line the microvessels within the CNS forms the BBB through expression of tight junctional adhesion proteins, MDR efflux transporters and metabolic enzymes. The tight junctions at the BBB eliminates the paracellular diffusion of drug-like molecules and forces molecules through the transcellular pathway [11]. Molecules are then forced through the transcellular pathway and are subject to non-specific MDR efflux transporters. Pgp was the first MDR transporter to be identified in BBB-forming endothelial cells and has been the most extensively studied [12]. MDR transporters, including Pgp, work in conjunction with tight junctional adhesion to restrict the entry of 98% of all small molecule drugs, and 100% of all biologics, to the brain [13].

As a result of the effects on both cancer chemotherapy and CNS drug development, Pgp remains the archetypical drug transporter whose function needs to be fully elucidated to improve drug efficiency. Although Pgp has always been considered the centrepiece of MDR in cancer and at the BBB, it has become clear over the years that, on its own, Pgp cannot fully explain its function as a drug barrier element. Indeed, it has been shown that the drug-membrane interaction, including the physicochemical properties of drugs and the biophysical state of the membrane, are essential to support Pgp function [14,15,16,17,18,19].

It follows that the efficacy of Pgp should be sensitive to any impairment of the structure that supports its function. Through proteoliposome studies, it has been deduced that changes in surface tension of the cell membrane induced by the incorporation of drugs are enough to impede Pgp function [20]. Experimental results confirming this theory suggest that a small increase in the membrane surface, of about 2%, is enough to block the effect of Pgp [20]. This conclusion, in turn, means that even considerably low drug concentrations could affect Pgp function, and therefore, we hypothesise that there is a biological mechanism in place to protect Pgp efficiency against any change in the membrane surface tension.

We demonstrate here that a key element protecting Pgp function is pinocytosis, which is also known as fluid phase endocytosis [21]. Indeed, we demonstrate that the incorporation of drugs does increase the surface tension as expected, but that the mechanism of endocytosis dissipates any increase in surface tension by augmenting the internalisation of membrane per unit of time, such that an increase in the surface tension of about 2% can be dissipated within 4.5 s. We suggest that this mechanism protects Pgp function and efficiency involved in MDR in cancer chemotherapy and at the BBB.

2. Physical Impact of Drug–Lipid Monolayer Interaction

To simplify the model, let us consider a lipid monolayer of total surface area $S$ and composed $N$ identical lipids modelled as cylinder each occupying an optimal surface area $a_0$. The variable $a_0$ results from two fundamental properties of lipids linked to their amphipathic nature and we aim to determine an expression of $a_0$ as a function of basic physicochemical properties of lipids. To achieve this, we consider the hydrophobic part of the lipids and introduce a penalty energy, i.e., positive energy, linked the surface area per lipid. To visualise this penalty energy, let us imagine that the total surface area of the leaflet is increased, for example by ‘pulling’ the leaflet laterally, then as the leaflet surface area contains a constant number of lipids, expending the leaflet is only possible if the surface area available per lipid increases as well. However, when the distance between lipids increases, water molecules can penetrate the leaflet and interact with the hydrophobic part of the lipids that, in turn, is not favoured (Figure 1A). As a result, one can define this penalty energy as being proportional to the surface area of lipids under the form $~\lambda a$ where $\lambda$ is a positive constant and $a$ is the surface area per lipid (Figure 1A). The latter energy stipulates that any increase in the surface area per lipid provides a (positive) penalty energy. If this was the only energy term considered, then the membrane should shrink totally to impose $a~0$. However, this is not possible due to steric repulsions between lipids and therefore the shrinkage has limits. In this context, one introduces a second energy term stating that when $a$ tends towards zero a penalty energy occurs under the form $~\mu /a$ where $\mu$ is also a positive constant resulting from lipid–lipid repulsion (Figure 1A). 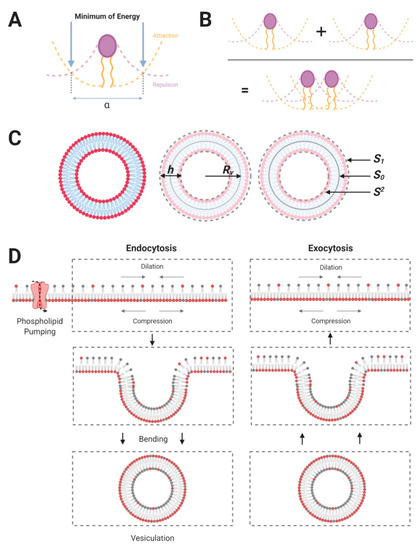As a result and by definition, as the energies balance each other when $a~a_0$ the relation that defines $a_0$ as a function of lipids fundamental physicochemical properties is then $\lambda a_0~\mu /a_0$ or equivalently: $a_0~\sqrt{\mu /\lambda }$ (Figure 1B).

To summarize, the total energy per lipid, or lipid physicochemical potential, is given by $~\lambda a+\mu /a$ and the energy of the leaflet is then the energy per lipid multiplied by the number of lipids composing the leaflet $~N\left(\lambda a+\mu /a\right)$.

Let us now assume that drugs incorporate into the leaflet and that the surface area of the leaflet is fixed. It is then expected that the incorporation of drugs will have an impact on the optimal surface area per lipids, transforming $a_0$ to $a_0+\delta a$ where $\delta a<0$ is the variation in the surface area per lipid due to the presence of drugs in the membrane. Note that $\delta a<0$ as drugs are expected to compress the lipids of the leaflet. In any case, the energy of the leaflet can be rewritten as $~N\left(\lambda \left(a_0+\delta a\right)+\mu /\left(a_0+\delta a\right)\right)$; but if one assumes that the relative compression is small, in that $\delta a/a_0\ll 1$, then the energy of the leaflet can be developed mathematically up to the second order as: $~N\lambda a_0+N\lambda a_0\frac{\delta a}{a_0}+N\frac{\mu }{a_0}-N\frac{\mu }{a_0}\frac{\delta a}{a_0}+\frac{N}{2}\frac{\mu }{a_0}{\left(\frac{\delta a}{a_0}\right)}^2$. The latter expression can then be rewritten as: $~N\left(\lambda a_0+\frac{\mu }{a_0}\right)+N\left(\lambda a_0-\frac{\mu }{a_0}\right)\frac{\delta a}{a_0}+\frac{N}{2}\frac{\mu }{a_0}{\left(\frac{\delta a}{a_0}\right)}^2$. The first term, i.e., $N\left(\lambda a_0+\frac{\mu }{a_0}\right)$, is the initial energy of the leaflet without any drugs, and the second term, i.e., $N\left(\lambda a_0-\frac{\mu }{a_0}\right)\frac{\delta a}{a_0}$, is null as $a_0$ is defined by $\lambda a_0~\mu /a_0$. As a result, the energy of the leaflet, $E$, is simply: $E~E_0+\frac{\lambda N{a}_0}{2}{\left(\frac{\delta a}{a_0}\right)}^2$; where $E_0=N\left(\lambda a_0+\frac{\mu }{a_0}\right)$ corresponds to the initial energy of the leaflet without any perturbation. To express the energy as a function of the drug concentration in the leaflet, one rewrites the term $\frac{\delta a}{a_0}$ as: $\frac{N\delta a}{N{a}_0}$. As the term $N\delta a$ corresponds to the reduction of the surface area of the leaflet, in particular the reduction of surface area due to the incorporation of drugs, let us assume that $N_D$ drugs have incorporated the membrane and that drugs have a cross section area given by $a_D$, then: $N\delta a=-N_D{a}_D$; and as a result: $E~E_0+\frac{\lambda N{a}_0}{2}{\left(\frac{N_D{a}_D}{N{a}_0}\right)}^2$. As $N{a}_0$ is the surface area of an unperturbed leaflet the term, $\frac{N_D{a}_D}{N{a}_0}$, corresponds to the surface density of drugs. It is also worth noting here that for drugs that are small enough, their volume in angstrom units, noted $V_D$, is proportional to their molecular weight: $V_D~{\left(MW\right)}_D$; the cross sectional area of a drug can be rewritten as: $a_D~\alpha {\left(MW\right)}_D{}^{2/3}$ where $\alpha$ is a geometrical factor given by $\alpha ={\left(3\sqrt{\pi }/4\right)}^{2/3}$ for a drug that is assumed to be spherical. Finally, by posing $\beta =\frac{\lambda {\alpha }^2}{2}$; and noting $C_D=\frac{N_D}{N{a}_0}$ the surface concentration of drugs, one deduces:

$$E-E_0~N{a}_0\beta {\left(MW\right)}_D{}^{4/3}{\left(C_D\right)}^2$$

(1)

Traditionally $C_D$ is determined by the octanol-water partition coefficient of the drug chemical, and therefore the energy of the leaflet is a function of two well-characterized drug parameters. Perhaps the most interesting is to note that, as far as the membrane is involved, the drug molecular weight and its affinity for the membrane are, to some extent, equivalent. Indeed, as far as the leaflet energy is concerned, and as long as the term ${\left(MW\right)}_D{}^{4/3}{\left(C_D\right)}^2$ is constant, the energy remains constant. The next question is to provide a generalization of the development above, while considering the plasma membrane as a whole and the impact of drugs on membrane vesiculation.

3. Physical Impact of Drug–Membrane Interaction

Let us go back to the leaflet’s energy, but this time considering that the parameter $\frac{\delta a}{a_0}$ results from two effects: (i) a constant lipid asymmetry linked to the flippase activity and, (ii) the accumulation of drugs. In this context, we note the inner leaflet as the subscript ‘2′ and the outer leaflet as subscript ‘1′. Finally, we shall also assume that the drug chemical is small enough to be present in both leaflets in similar proportion.

The leaflets’ energy are written as: $E_{1,2}~E_0+\frac{\lambda N{a}_0}{2}{\left(\frac{N\delta a_{1,2}}{N{a}_0}\right)}^2$, where $N\delta a_{1,2}=\delta S_{1,2}$ is the change in the surface area of either leaflet. However, the later description is valid for ‘flat’ leaflets and does not consider possible local curvatures, i.e., vesiculation or membrane budding, that are fundamentally involved in releasing the membrane energy. This is the reason why it is preferable to use a differentiated form of leaflets’ energy and consider the surface tension of leaflets, noted ${\sigma }_{1,2}$, and defined formally by: ${\sigma }_{1,2}=d{E}_{1,2}/d{S}_{1,2}$, where ‘$d$’ means difference. Thus, for either leaflet, ${\sigma }_{1,2}$ is defined as the surface energy and represents the variation of leaflets energy as function of a change in surface area of leaflet. In this context, $d{E}_{1,2}~{\sigma }_{1,2}d{S}_{1,2}$ where ${\sigma }_{1,2}=\lambda \frac{N\delta a_{1,2}}{N{a}_0}$ is the surface tension of either leaflet. The meaning of the differential form for the leaflets’ energy is slightly different from the leaflet energy described by Equation (1). Indeed, as any energy state of a physical system has to be as small as possible, if ${\sigma }_1<0$ for example, then the energetically favoured state is the one selecting $d{S}_1>0$ that is to say that a compressed leaflet (${\sigma }_1<0)$ will try to expand ($d{S}_1>0)$ such that the energy variation of the leaflet is negative ($d{E}_1<0$) to become in due course the smallest possible. Let us consider now the total energy of the membrane, namely the addition of the individual leaflets energy: $d{E}_1+d{E}_2={\sigma }_{1}d{S}_1+{\sigma }_{2}d{S}_2$, and assume that the total energy is the smallest possible; then in this case $d{E}_1+d{E}_2=0$. The latter relation mathematically explains that the membrane energy is the smallest possible and cannot decrease further. This relation also implies that ${\sigma }_{1}d{S}_1+{\sigma }_{2}d{S}_2=0$ or equivalently: $\frac{d{S}_1}{d{S}_2}=-\frac{{\sigma }_2}{{\sigma }_1}$. The latter relation is important as it states that as the bilayer membrane is composed of two sub-systems, i.e., the leaflets, then the only possibility for the bilayer membrane to optimize its energy is to find a way such as $\frac{d{S}_1}{d{S}_2}=-\frac{{\sigma }_2}{{\sigma }_1}$; and one possibility is to create membrane buds (leading to the formation of vesicles) (Figure 1C,D).

By taking a pool of lipids from the outer leaflet to place it onto the outer leaflet, the flippase activity compresses the inner leaflet and dilates the outer one to a similar extent without changing the overall number of lipids composing the bilayer membrane (Figure 1D). Let us note $\delta N$ the lipid number asymmetry; one deduces that the relative variation in surface area per lipid in the inner leaflet is $-\frac{\delta N}{N}$ due to compression and $+\frac{\delta N}{N}$ in the outer leaflet due to dilation. To further consider the presence of drug chemicals distributing equally between leaflets determines that finally: ${\sigma }_1/\lambda =-\frac{\delta N}{N}-\frac{N_D{a}_D}{N{a}_0}$ and ${\sigma }_2/\lambda =+\frac{\delta N}{N}-\frac{N_D{a}_D}{N{a}_0}$. As a result, the energy of the flat bilayer membrane written as a differential form becomes:

$$d{E}_1+d{E}_2={\sigma }_{1}d{S}_1+{\sigma }_{2}d{S}_2=\lambda \left(-\frac{\delta N}{N}-\frac{N_D{a}_D}{N{a}_0}\right)d{S}_1+\lambda \left(\frac{\delta N}{N}-\frac{N_D{a}_D}{N{a}_0}\right)d{S}_2$$

(2)

From Equation (2), one deduces that as ${\sigma }_1<0$ the inner leaflet will try to expand to verify $d{S}_1>0$. For the outer leaflet, however, nothing can be considered clear-cut, as this depends on the amount of drug that is present since ${\sigma }_2$ can be either positive or negative as a function of the surface concentration of drugs. As the two leaflets are coupled, the expansion or dilation of leaflets can be performed via the formation of membrane curvature relative to the neutral surface area that is defined as the surface at the mid-distance between leaflets, namely, the surface separating the two leaflets of the membrane bilayer (Figure 1C).

Let us consider now that the membrane bilayer starts budding locally, in this case $d{S}_1$ and $d{S}_2$ will become a function of the curvature radius of the membrane bud (Figure 1C,D). For small buds, like vesicles, it is necessary to add a further energy term linked to membrane bending that we shall note $d{E}_c$ where the subscript ‘c’ refers to cuvature. Using the differentiated form this term is written as $d{E}_c=\frac{k_c}{2h^2}{\left(\frac{h}{R_V}\right)}^{2}d{S}_0$ where ‘$k_c$’ ‘$S_0$’, ‘$h$’ and ‘$R_V$’ designate, respectively, the bending modulus of the membrane, the neutral surface (Figure 1C), the membrane thickness (Figure 1C,D) and the curvature radius of the membrane bud (Figure 1C,D). As a result, the differentiated form of the total energy, $d{E}_{tot}=d{E}_c+d{E}_1+d{E}_2$, is:

$$d{E}_{tot}=\frac{k_c}{2h^2}{\left(\frac{h}{R_V}\right)}^{2}d{S}_0+\lambda \left(-\frac{\delta N}{N}-\frac{N_D{a}_D}{N{a}_0}\right)d{S}_1+\lambda \left(\frac{\delta N}{N}-\frac{N_D{a}_D}{N{a}_0}\right)d{S}_2$$

(3)

Equation (3) is null namely the membrane bilayer system has found its equilibrium state when $d{E}_{tot}=0$. As result, the bilayer membrane and related vesicle radius must abide by:

$$\frac{k_c}{2h^2}+\lambda \left(-\frac{\delta N}{N}-\frac{N_D{a}_D}{N{a}_0}\right)\frac{d{S}_1}{d{S}_0}+\lambda \left(\frac{\delta N}{N}-\frac{N_D{a}_D}{N{a}_0}\right)\frac{d{S}_2}{d{S}_0}=0$$

(4)

Further using $\frac{d{S}_1}{d{S}_0}={\left(1+\frac{h}{2R_V}\right)}^2$ and $\frac{d{S}_2}{d{S}_0}={\left(1-\frac{h}{2R_V}\right)}^2$ (see Figure 1C) one deduces:

$$\left(\frac{2k_c}{h^2}-2\lambda \frac{N_D{a}_D}{N{a}_0}\right){\left(\frac{h}{2R_V}\right)}^2-2\lambda \frac{\delta N}{N}\left(\frac{h}{2R_V}\right)-2\lambda \frac{N_D{a}_D}{N{a}_0}=0$$

(5)

Let us solve the quadratic equation given by Equation (5) one finds:

$$\left(\frac{h}{2R_V}\right)=\frac{2\lambda \frac{\delta N}{N}+\sqrt{{\left(2\lambda \frac{\delta N}{N}\right)}^2+4\left(2\lambda \frac{N_D{a}_D}{N{a}_0}\right)\left(\frac{2k_c}{h^2}-2\lambda \frac{N_D{a}_D}{N{a}_0}\right)}}{\left(\frac{2k_c}{h^2}-2\lambda \frac{N_D{a}_D}{N{a}_0}\right)}$$

(6)

Note that quadratic equations bring two solutions, however, in our case Equation (6) is the only solution possible as when the drugs are absent, but the lipid asymmetry is present, a solution must exist. Let us note ${\left(\frac{h}{2R_V}\right)}_0$ the solution to Equation (6) when drugs are absent, i.e., for $C_D=0$, then the solution is: ${\left(\frac{h}{2R_V}\right)}_0=\left(2\lambda \frac{\delta N}{N}\right)/\left(\frac{2k_c}{h^2}\right)$ as determined elsewhere [21].

From Equation (6), one can determine the critical or maximal amount of drugs required to block or inhibit the endocytic process imposes a vesicle radius that is null. Let us note ${\left(\frac{N_D{a}_D}{N{a}_0}\right)}_M$ the critical surface density of drugs one deduces theoretically: ${\left(\frac{N_D{a}_D}{N{a}_0}\right)}_M~\frac{k_c}{\lambda h^2}$. Using $k_c~{10}^{-19}J$, $\lambda ~0.2 \mathrm{N}·{\mathrm{m}}^{-1}$ and $h~5$ nm [20] one can estimate: ${\left(\frac{N_D{a}_D}{N{a}_0}\right)}_M~0.2$. This value is 10 times higher than the amount required to impair the function of the drug transporter Pgp [22].

As a conclusion, by affecting the surface tension, the interaction of drugs with the membrane decreases the vesicle radius. This point is important as the vesicle radius is directly related to the kinetics of membrane endocytosis [20]. The next question is to determine whether the presence of drugs in the membrane perturbs the membrane recycling that, in turn, protects Pgp function and activity.

4. Physical Impact of a Change in Surface Tension on the Kinetics of Membrane Pinocytosis

There is one remark of great importance to be made before clarifying how a change in surface tension affects the kinetics of pinocytosis. We saw above that once homogenously incorporated into the membrane, drugs are able change the surface tension. If one assumes that the kinetics of pinocytosis are impacted, given that pinocytosis occurs everywhere as the membrane is not compressible, the amount of surface area leaving the plasma membrane per unit of time will not uniquely involve drugs. A different way to understand this is to say that drugs in the membrane trigger an overall response from the plasma membrane, and that the kinetics of pinocytosis, when changed, will dissipate the excess in surface tension brought initially by drugs. So in this context, instead of writing ‘$\frac{N_D{a}_D}{N{a}_0}$’ the excess of surface area of the plasma membrane, one can write it more generically under the form: ‘$\frac{\delta S}{N{a}_0}$’ and determine the variation of ‘$\frac{\delta S}{N{a}_0}$’ as a function of time with the condition that $\frac{\delta S}{N{a}_0}\left(t=0\right)=\frac{N_D{a}_D}{N{a}_0}$. In these conditions, Equation (6) can then be rewritten by replacing ‘$\frac{N_D{a}_D}{N{a}_0}$’ by ‘$\frac{\delta S}{N{a}_0}$’.

To determine ‘$\frac{\delta S}{N{a}_0}$’ as a function of time, we start by considering the steady state of membrane recycling and assume that when the membrane is not perturbed the kinetics of endocytosis is identical to the kinetics of exocytosis. This initial assumption guaranties the balance of membrane being exchanged and recycled through endocytosis and exocytosis. If there are $N_V$ endocytic vesicles, each of surface area $S_V$, being created from the plasma membrane between the times $t$ and $t+dt$, then the amount of membrane being internalized is $N_V{S}_V\mathrm{d}t/{\tau }_V$; where ${\tau }_V$ is the characteristic time for a vesicle to be created. Previous work has demonstrated that the membrane recycling between the plasma membrane and the intracellular compartments is controlled by the volume exchanged [20], and that the flow of volume endocytosed must equate the flow of volume exocytosed. A simple way to understand this principle is to consider a cell with a given volume and imagine that vesicles are forced to penetrate the cytosol. As each vesicle entering the cytosol needs a free cytosolic volume equivalent to their own volume, if a fraction of the cytosolic volume was not released by exocytosis then forcing endocytosis would increase the pressure inside the cells. However, this is not possible as the cytosol is an aqueous medium with a resulting compressibility that is almost null. Thus, in a context were cells in tissues maintain their constant volume (as otherwise tissues would swell) the volume entering the cell per unit of time must be constant, in other words $\frac{N_V{V}_V}{{\tau }_V}~cte$ where $V_V$ is the vesicular volume. Noting that $R_V$ the vesicle radius, as $V_V=\frac{S_V{R}_V}{3}$ for a spherical vesicle, this principle allows one to deduce that the kinetics of membrane endocytosis is: $\frac{N_V{S}_V}{{\tau }_V}~\frac{3}{R_V}$. Let us now compare two states, an initial one where the cellular membrane is not perturbed and generates vesicles with a radius noted ${\left(R_V\right)}_0$; and another state where the cellular membrane is perturbed by drugs and as a result the vesicle radius has changed and is now $R_V$. Then the amount of membrane being internalised in the latter case can be expressed as a function of the amount of membrane being internalised in the former case under the form: $\frac{N_V{S}_V}{{\tau }_V}~{\left(\frac{N_V{S}_V}{{\tau }_V}\right)}_0\frac{{\left(R_V\right)}_0}{R_V}$. As a result, the difference in membrane flow is: $\frac{N_V{S}_V}{{\tau }_V}-{\left(\frac{N_V{S}_V}{{\tau }_V}\right)}_0={\left(\frac{N_V{S}_V}{{\tau }_V}\right)}_0\left[\frac{{\left(R_V\right)}_0}{R_V}-1\right]$. Consequently, over a time interval ‘$dt$’ the amount of excess surface area being removed from the plasma membrane through a change in the kinetics of pinocytosis is: $\left[\frac{N_V{S}_V}{{\tau }_V}-{\left(\frac{N_V{S}_V}{{\tau }_V}\right)}_0\right]dt={\left(\frac{N_V{S}_V}{{\tau }_V}\right)}_0\left[\frac{{\left(R_V\right)}_0}{R_V}-1\right]dt$. This excess being removed from the plasma membrane will result in a drop of ‘$\delta S$’ from ‘$\delta S$’ to ‘$\delta S-d\left(\delta S\right)$’. As a result, one can deduce a temporal differential equation for ‘$\delta S$’ under the form: $-d\left(\delta S\right)~{\left(\frac{N_V{S}_V}{{\tau }_V}\right)}_0\left[\frac{{\left(R_V\right)}_0}{R_V}-1\right]dt$. Let us divide the right and left members by ‘$N{a}_0$’ and note ‘$\delta \tilde{S}=\frac{\delta S}{N{a}_0}$’ and $\delta {\tilde{S}}_M={\left(\frac{N_D{a}_D}{N{a}_0}\right)}_M~\frac{k_c}{\lambda h^2}$ to simplify notations and define, $k_0\stackrel{\mathrm{def}}{=}\frac{1}{N{a}_0}{\left(\frac{N_V{S}_V}{{\tau }_V}\right)}_0$ as the fraction of plasma membrane surface area being internalized by the process of pinocytosis per unit of time for an unperturbed membrane, one deduces:

$$\frac{\left(1-\frac{\delta \tilde{S}}{\delta {\tilde{S}}_M}\right)d\left(\frac{\delta \tilde{S}}{\delta {\tilde{S}}_M}\right)}{\left[\sqrt{1+4{\left(\frac{2{\left(R_V\right)}_0}{h}\right)}^2\frac{\delta \tilde{S}}{\delta {\tilde{S}}_M}\left(1-\frac{\delta \tilde{S}}{\delta {\tilde{S}}_M}\right)}+\frac{\delta \tilde{S}}{\delta {\tilde{S}}_M}\right]}~-\frac{k_0}{\delta {\tilde{S}}_M}dt$$

(7)

We note from Equation (7) that in the case where $\frac{\delta \tilde{S}}{\delta {\tilde{S}}_M}\ll 1$, i.e., $\left(1-\frac{\delta \tilde{S}}{\delta {\tilde{S}}_M}\right)~1$, the fraction of plasma membrane per unit of time undergoing pinocytosis is similar to the kinetics of pinocytosis if $4{\left(\frac{2{\left(R_V\right)}_0}{h}\right)}^2\frac{\delta \tilde{S}}{\delta {\tilde{S}}_M}\ll 1$. The latter inequality allows one to define the lower concentration of membrane drugs, or the lower excess in surface tension, brought about by the addition of surface area to the plasma membrane, leading to an increase in the kinetics of pinocytosis. Indeed, by defining ‘$\delta {\tilde{S}}_m$’ and writing: $4{\left(\frac{2{\left(R_V\right)}_0}{h}\right)}^2\frac{\delta {\tilde{S}}_m}{\delta {\tilde{S}}_M}~1$; ‘$\delta {\tilde{S}}_m$’ is then the lower fraction of membrane aforementioned. Let us assume that a typical vesicle radius is ${\left(R_V\right)}_0~50$ nm [21], using this radius one finds: $\frac{\delta {\tilde{S}}_m}{\delta {\tilde{S}}_M}~1.5·{10}^{-4}$, or equivalently $\delta {\tilde{S}}_m~1.5·{10}^{-4}·\delta {\tilde{S}}_M~3·{10}^{-5}$, suggesting this is a remarkably sensitive process. As a result, Equation (7) can be rewritten in the form:

$$\frac{\left(1-\frac{\delta \tilde{S}}{\delta {\tilde{S}}_M}\right)d\left(\frac{\delta \tilde{S}}{\delta {\tilde{S}}_M}\right)}{\left[\sqrt{1+\frac{\delta {\tilde{S}}_M}{\delta {\tilde{S}}_m}\times \frac{\delta \tilde{S}}{\delta {\tilde{S}}_M}\left(1-\frac{\delta \tilde{S}}{\delta {\tilde{S}}_M}\right)}+\frac{\delta \tilde{S}}{\delta {\tilde{S}}_M}\right]}~-\frac{k_0}{\delta {\tilde{S}}_M}dt$$

(8)

From Equation (8) one sees that, for a physiologically acceptable concentration of drugs when $\left(1-\frac{\delta \tilde{S}}{\delta {\tilde{S}}_M}\right)~1$, the equation can be approximated and solved as: $\sqrt{1+\frac{\delta {\tilde{S}}_M}{\delta {\tilde{S}}_m}\times \frac{\delta \tilde{S}}{\delta {\tilde{S}}_M}}~-\frac{k_0}{2\delta {\tilde{S}}_m}t+K$; where ‘$K$’ is an integration constant. To determine ‘$K$’ let us note ‘$T$’ the time needed to dissipate the excess in surface tension, which is defined by $\delta \tilde{S}\left(t=T\right)=0$, then by definition: $1~-\frac{k_0}{2\delta {\tilde{S}}_m}T+K$; and as a result: $\sqrt{1+\frac{\delta {\tilde{S}}_M}{\delta {\tilde{S}}_m}\times \frac{\delta \tilde{S}}{\delta {\tilde{S}}_M}}~1+\frac{k_0}{2\delta {\tilde{S}}_m}\left(T-t\right)$. We also recognise that by noting $\delta \tilde{S}\left(t=0\right)=\delta {\tilde{S}}_0$, the time ‘$T$’ needed to dissipate the excess in surface tension is related to ‘$\delta {\tilde{S}}_0$’ under the form: $\sqrt{1+\frac{\delta {\tilde{S}}_M}{\delta {\tilde{S}}_m}\times \frac{\delta {\tilde{S}}_0}{\delta {\tilde{S}}_M}}~1+\frac{k_0}{2\delta {\tilde{S}}_m}T$.

In this context let us assume that $\delta {\tilde{S}}_0~2\%$, which is sufficient to block Pgp function [22], then: $\frac{\delta {\tilde{S}}_M}{\delta {\tilde{S}}_m}\times \frac{\delta {\tilde{S}}_0}{\delta {\tilde{S}}_M}~\frac{\delta {\tilde{S}}_0}{\delta {\tilde{S}}_m}~666\gg 1$; using $k_0~2\% {\min }^{-1}$ typically [21] one deduces: $T~4.5$ s.

As a result, the time ‘$T$’ needed to dissipate the excess in surface tension is remarkably short amid to the sensitivity of pinocytosis and as a result Pgp function and activity is protected by the membrane.

5. Discussion and Conclusions

Much of the work around MDR in cancer chemotherapy, or CNS drug resistance at the BBB, revolves around the notion of efflux by drug transporters. Pgp is the archetypal MDR transporter, as it has been extensively studied in both physiological cases [6,13]. However, many works have determined that Pgp on its own is not sufficiently responsible for drug efflux, as the experimental data obtained seems contradictory [16,17,23]. One aspect that has attracted our attention concerns the experimental fact that a relatively small increase in the surface tension of the cell membrane (around 2%) through drug accumulation can block Pgp function [21]. This impairment of Pgp function and activity is primarily linked to the physicochemical properties of the drug, including the octanol–water partition coefficient, the drug molecular weight, and consequently, their affinity to the plasma membrane.

Therefore, the key question was to determine what biological process could be in place to maintain Pgp function, as the critical 2% increase in surface tension is largely expected to occur at relatively low physiological concentrations of drug. In turn, we have determined that the mechanism of pinocytosis (fluid-phase endocytosis) acts to dissipate the increase in surface tension induced by drugs through augmentation of the rate of internalisation of membrane, such that an increase in the surface tension of about 2% can be dissipated within 4.5 s. It is thus conclusive that pinocytosis is the biological mechanism that protects Pgp, and is required to maintain MDR in cancer chemotherapy and CNS drug impermeability at the BBB.