Color Image Quantization Based on the Artificial Bee Colony and Accelerated K-means Algorithms

Abstract

Color image quantization techniques have been widely used as an important approach in color image processing and data compression. The key to color image quantization is a good color palette. A new method for color image quantization is proposed in this study. The method consists of three stages. The first stage is to generate N colors based on 3D histogram computation, the second is to obtain the initial palette by selecting K colors from the N colors based on an artificial bee colony algorithm, and the third is to obtain the quantized images using the accelerated K-means algorithm. In order to reduce the computation time, the sampling process is employed. The closest color in the palette for each sampled color pixel in the color image is efficiently determined by the mean-distance-ordered partial codebook search algorithm. The experimental results show that the proposed method can generate high-quality quantized images with less time consumption.

1. Introduction

Color image quantization is one of the digital image processing techniques [1]. Color image quantization consists of two steps. The first step is to generate a set of representative colors in order to obtain a color palette. The second is to map each pixel in the color image to one color in the color palette. The main purpose of color image quantization is to reduce the storage requirements and the transfer time of the image.

Hsieh and Fan [2] proposed a method for color image quantization based on an adaptive clustering algorithm and a pixel-mapping algorithm. Omran et al. [3] developed a color image quantization algorithm based on particle swarm optimization and the K-means algorithm. The main disadvantage of their method is the high computational cost. Hu and Lee [4] introduced the use of stable flags for palette entries in order to accelerate the K-means algorithm for palette design. Celebi [5] implemented the fast and exact variants of K-means with several initialization schemes. Su and Hu [6] proposed a color image color quantization algorithm based on self-adaptive differential evolution. El-Said [7] proposed a fuzzy clustering algorithm, which combines the artificial fish swarm algorithm and an efficient extension of fuzzy c-means (FCM), for color image quantization. Schaefer and Nolle [8] introduced a new approach to color image quantization. In their method, the color palette is derived by the simulated annealing algorithm in order to provide good image quality according to S-CIELAB. In 2015, a color quantization method, called ATCQ, was proposed by Pérez-Delgado [9]. ATCQ adapted some of the features of the basic Ant-tree to obtain a quicker algorithm for color image quantization. Ueda et al. [10] described a modification of the median cut algorithm. In their method, a combination of linear discriminant analysis and principal analysis was used to accomplish effective partitioning of the color space. In 2019, application of the shuffled-frog leaping algorithm to perform color image quantization was proposed by Pérez-Delgado [11]. Each frog represented a quantized palette and the objective function considered is the mean square error.

Although some existing methods can obtain high-quality quantized images, these methods suffer from the drawback of high computational cost. In order to obtain the quantized images with high image quality and low computational cost, a color image quantization technique is proposed in this study. Experimental results show that the proposed method can generate high-quality quantized images with less time consumption.

The rest of this paper is organized as follows. In Section 2, some related works are reviewed. In Section 3, the color image quantization method is described. In Section 4, some experimental results are presented. Finally, some conclusions are given in Section 5.

2. Related Works

In this section, the artificial bee colony algorithm and the mean-distance-ordered partial codebook search algorithm will be reviewed.

2.1. Artificial Bee Colony (ABC) Algorithm

The artificial bee colony algorithm [12,13,14,15,16,17,18,19,20,21,22] was first proposed by Karaboga and was inspired by the foraging behaviors of bee colonies. In this study, the number of food sources is denoted by SN, and the position of a food source represents a possible solution to the optimization problem. Each solution s_i (i = 0, 1, 2, …, SN − 1) is a K-dimensional vector. Here, K is the color number of a color palette.

In the employed bee phase, a new solution v_i is produced by the i-th employed bee as follows:

$$v_{i,j}=s_{i,j}+{\phi }_{ij}(s_{i,j}-s_{t,j})$$

(1)

where s_t is a food source selected randomly, j is selected from the set {0, 1, 2, …, K − 1}, and ${\phi }_{ij}$ is a random number within the range [−1, 1]. In the onlooker bee phase, each onlooker bee selects a food source depending on prob_i which is calculated by the following expression:

$$pro{b}_i=\frac{fitness(s_i)}{{\displaystyle \sum _{j=0}^{SN-1}fitness(s_j)}}$$

(2)

where fitness(s_i) is the fitness value of the solution s_i. Then, the onlooker bees try to improve the solutions by using Equation (1).

The main steps of the ABC algorithm (Algorithm 1) are shown as follows:

Algorithm 1: ABC algorithm [12]

Step 1: Generate the initial population si, i = 0, 1, 2, …, SN − 1    triali = 0, i = 0, 1, 2, …, SN − 1. In the ABC algorithm, trial is a vector holding trial numbers    through which solutions cannot be improved    Set cycle to 1  Step 2: Evaluate the fitness fitness(si) of the population and memorize the best solution so far Repeat  Step 3: Employed bee phase  Step 4: Compute the values probi (i = 0, 1, 2, …, SN − 1) by using Equation (2)  Step 5: Onlooker bee phase  Step 6: Memorize the best solution so far  Step 7: Scout bee phase   cycle = cycle + 1 Until cycle ≤ ABC_cycle

2.2. Mean-Distance-Ordered Partial Codebook Search (MPS) Algorithm

The MPS algorithm is a fast search algorithm for vector quantization [23,24]. Here, the MPS algorithm is employed to achieve reduction in computation time for color image quantization. For each color pixel in the color image, the closest color in the palette can be efficiently determined by the MPS algorithm.

For the color pixel x and the palette color c in the palette, the squared Euclidean distance (SED) and the squared sum distance (SSD) are defined as follows.

$$SED(x,c) = {\displaystyle \sum _{j=1}^3{(x_j-c_j)}^2}$$

(3)

$$SSD(x,c) = ({\displaystyle \sum _{j=1}^3{x}_j-{\displaystyle \sum _{j=1}^3{c}_j}{)}^2}$$

(4)

The following inequality that holds true for the color pixel x and the palette color c is described as follows [23]:

$$SSD(x,c) \le 3\times SED(x,c)$$

(5)

In the MPS algorithm, the test condition was employed to reject some impossible palette colors:

$$3\times d_{\min } < SSD(x,c)$$

(6)

where d_min denotes the minimal SED between the color pixel x and the closest color c_min found so far. The inequality d_min < SED(x,c) can be derived from Equations (5) and (6), and thus the palette color c cannot be the closest color.

If the color pixel x = (100, 50, 80), the sorted palette of K colors is as depicted in Figure 1a. In this study, the initial searched palette color for the color pixel x is the palette color with the closest mean value to x. The initial searched palette color can be found by the binary search technique. In this case, the palette color with the closest mean value to x is (101, 52, 78); therefore, the searching order of colors in the palette is depicted in Figure 1b.

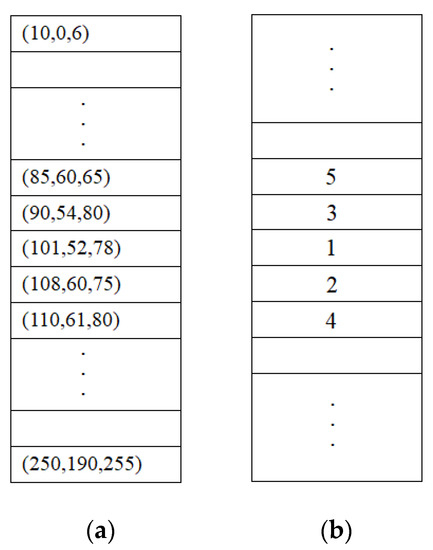
Figure 1. (a) The sorted palette of K colors; (b) the searching order of colors if the color pixel x = (100, 50, 80).

It is noted that the MPS test condition has two properties. Here, mean (c), mean (c1), and mean (x) denote the mean value of palette color c, the mean value of palette color c1, and the mean value of color pixel x, respectively. The first property is that if mean (c) is less than mean (x), when the palette color c is rejected, the palette color c1 is also rejected if mean (c1) is less than mean (c). The second property is that if mean (c) is greater than mean (x), when the palette color c is rejected, the palette color c1 is also rejected if mean (c1) is greater than mean (c).

3. Proposed Color Image Quantization Algorithm

The method consists of three stages. The system flowchart is shown in Figure 2. The three stages are described in this section.

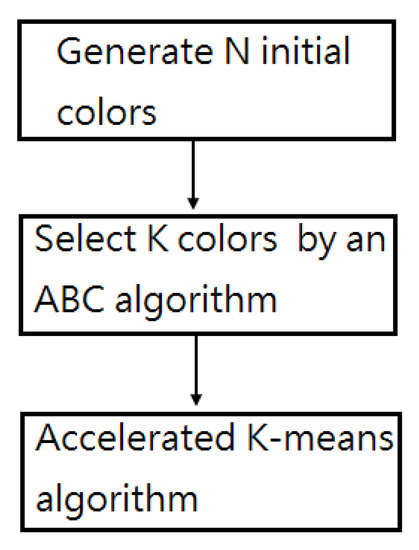
Figure 2. The system flowchart.

3.1. Generate N Initial Colors

The RGB color system is adopted in this study. The R, G and B values range from 0 to 255. For the Lake image, Figure 3 shows its 3D histogram. The RGB values of each pixel in an image correspond to a point of its 3D histogram. In the proposed scheme, the 3D RGB space is divided into non-overlapping cubes, and the size of each cube is 16 × 16 × 16. There are (256 × 256 × 256)/(16 × 16 × 16) = 4096 cubes in total. It is observed that many cubes contain no point. If the point number contained in the cube is equal to or larger than the threshold PixelThr, then the cube will be preserved. Assume that the number of the preserved cube is N. The point number contained in the i-th preserved cube is denoted by initialn[i] (i = 0, 1, 2, …, N − 1), and the center of all the points in the i-th preserved cube is denoted by initialc[i]. The colors initialc[0], initialc[1], …,initialc[N − 1] are called the N initial colors.

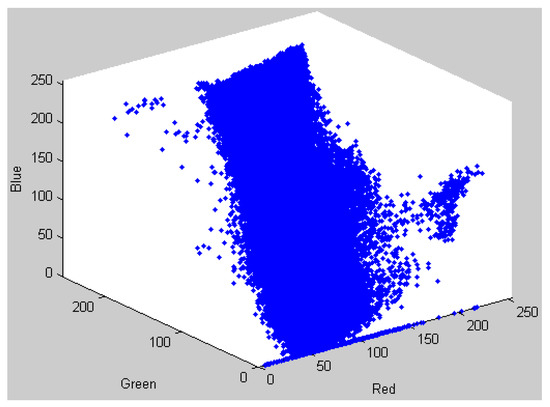
Figure 3. An example of a 3D histogram.

For example, there are 8 cubes shown in Figure 4, and they contain 0, 0, 10, 1, 0, 12, 2, and 0 points, respectively. Assume the value of PixelThr is set to 5. Cubes 2 and 5 will be preserved because the point numbers contained within them are equal to or larger than 5. Hence, the values of N, initialn[0] and initialn[1] are 2, 10 and 12, respectively. The center of the 10 points contained in cube 2 is called initialc[0]. Consequently, the center of the 12 points contained in cube 5 is called initialc[1].

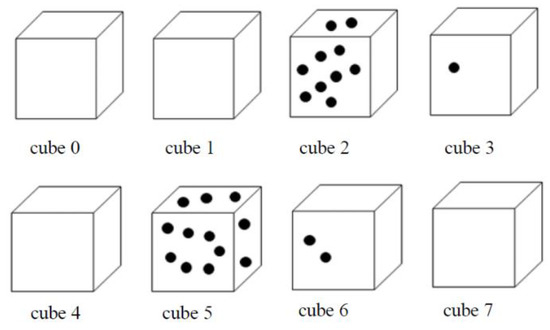
Figure 4. Cubes 0–7 contain 0, 0, 10, 1, 0, 12, 2, and 0 points, respectively.

3.2. Select K Colors by an ABC Algorithm

In this study, an ABC algorithm is employed to select K colors from the N initial colors to form the initial palette. The basic components of the artificial bee colony algorithm for solving this problem are described in the following subsections.

3.2.1. Representation of Solutions and Fitness Function

The proposed method considers the N initial colors and their corresponding point numbers in order to generate the initial palette. In the initialization phase, the SN solution s_i (i = 0, 1, 2, …, SN − 1) is generated, where s_i = (s_i,0, s_i,1, s_i,2,…, s_i,K−1), s_i,j is an integer number and the 0 ≤ s_i,j < s_i,j+1 ≤ N − 1 for j = 0, 1, 2,…, K − 2. Solution s_i indicates that the set of initial palette colors is {initialc[s_i,0], initialc[s_i,1], initialc[s_i,2], …,initialc[s_i,K−1]}. Then, the fitness, fitness(s_i), of a solution s_i is defined as

$$\begin{gathered} fitness\left(s_i\right)=\frac{1}{1+MS{E}_1} , \\ MS{E}_1=\frac{{{\displaystyle \sum }}_{j=0}^{N-1}initialn\left[j\right]\times D\left(initialc\left[j\right],s_i\right)}{{{\displaystyle \sum }}_{j=0}^{N-1}initialn\left[j\right]} , \end{gathered}$$

(7)

where D(initialc[j], s_i) = min{SED(initialc[j], initialc[s_i,0]), SED(initialc[j], initialc[s_i,1]), …, SED(initialc[j], initialc[s_i,K−1])}.

3.2.2. Generation of a New Solution v_i

As described in Section 2.1, the structure of the original ABC is suitable for continuous problems. Thus, Equation (1) needs to be modified for this specific problem. Let s_i = (s_i,0, s_i,1, s_i,2, …, s_i,K−1) be the present solution, while s_t = (s_t,0, s_t,1, s_t,2, …,s_t,K−1) is the randomly selected solution. The proposed method will generate the new solution v_i. The new solution v_i is the same as s_i except that s_i,j is replaced by v_i,j, where j is selected from the set {0, 1, 2,…, K − 1}.

The value of v_i,j (Algorithm 2) is computed by the following steps:

Algorithm 2: The steps of computing the value of vi,j

Step 1: Range1 = si,j − abs(si,j − st,j),    Range2 = si,j + abs(si,j − st,j),     If (Range1 < 0) { Range1 = 0; }     If (Range2 > (N − 1)) { Range2 = N − 1; } Step 2: SetX = {};    for (y = Range1; y ≤ Range2; y++)      { If (y is not an element of si) SetX = SetX ∪ {y}; } Step 3: If (SetX == {}) { vi,j = si,j; }     else { Assume SetX = { y0, y1, …, ym−1}, the probability of the value of vi,j is set to yr being       initialn(yr)/(initialn[y0] + initialn[y1] +… + initialn[ym−1]) for r = 0, 1, …, m − 1; }

3.2.3. The Search Process

In the employed bee phase, the i-th employed bee produces a new solution v_i by the method described in Section 3.2.2. If fitness(v_i) > fitness(s_i) then s_i is replaced by v_i and trial_i is set to 0 else trial_i = trial_i + 1. In the onlooker bee phase, each onlooker bee which selects a solution s_i depending on prob_i also produces a new solution v_i by the method described in Section 3.2.2. If fitness(v_i) > fitness(s_i) then s_i is replaced by v_i and trial_i is set to 0 else trial_i = trial_i+1. In the scout bee phase, the scout bee randomly produces the new solution to replace s_i if the trial_i of solution s_i is more than the parameter ‘limit’. In this study, the value of the parameter ‘limit’ is set to 10. The ABC algorithm is finished if the criterion cycle > ABC_cycle is satisfied. The best solution found so far is output and it represents the initial palette in this study.

In the second stage, the criterion N $\ge$ K must be satisfied. If the value of N obtained is less than the value of K, the proposed method will decrease the value of PixelThr in order to satisfy the criterion N $\ge$ K. When the value of PixelThr is set to 1 and the value of N obtained is less than the value of K, the proposed method will skip the second stage and set K = N. That is, the color number of a color palette is N.

3.3. Accelerated K-means Algorithm

The K-means algorithm is the most commonly used algorithm for data clustering. It is found that the computational cost of the K-means algorithm for color image quantization is very high. Hence, the accelerated K-means algorithm is employed for color image quantization in this study.

In order to achieve reduction in computation time, the sampling process is employed in this study. First, the color image is divided into many non-overlapping blocks. When every pixel of the color image is sampled it indicates that the sampling rate = 1, when only one pixel is sampled for a 2 × 2 block it indicates that the sampling rate = 0.25, when only two pixels are sampled for a 4 × 4 block it indicates that the sampling rate = 0.125, and when only one pixel is sampled for a 4 × 4 block it indicates that the sampling rate = 0.0625. Then, the sampled pixels and the initial palette serve as the input of the accelerated K-means algorithm. Detailed descriptions of the accelerated K-means algorithm (Algorithm 3) for color image quantization are given below.

Algorithm 3: Accelerated K-means algorithm for color image quantization

Step 1: The initial palette is generated by selecting K colors from the N initial colors based on an    ABC algorithm.    Set cycle to 1 Step 2: For each sampled color pixel in the color image, the closest color in the palette is efficiently    determined by the MPS algorithm. If the index value of its closest palette color is j, the    sampled color pixel is classified into the j-th group. Step 3: The mean values of these K groups are computed. These K values are sorted in the    ascending order of their means in order to generate the new color palette.    cycle = cycle + 1 Step 4: If the stopping criterion cycle > K_means_cycle is satisfied, then the algorithm stops.    Otherwise, go to Step 2.

4. Experimental Results

The proposed algorithm was implemented in C language and executed on a PC running under the operating system of Windows 7 with Intel Core 3.6 GHz CPU and 32 GBytes of RAM. The five color images Lena, Baboon, Lake, Peppers and Airplane with a size of 512 × 512 were used for conducting the experiments. The following parameters were used in the experiments: PixelThr = 30, SN = 20, ABC_cycle = 15 and K_means_cycle = 20.

In the experiments, the proposed algorithm was executed 20 times for each given image. Table 1 shows the experimental results. The results presented are the solutions with the average mean square error, the standard deviation (S.D.), and average computation time. The mean square error (MSE) was defined as follows:

$$MSE=\frac{1}{512\times 512}{\displaystyle \sum _{i=0}^{511}{\displaystyle \sum _{j=0}^{511}SED(f(i,j),f\prime (i,j))}},$$

(8)

where f is the original color image, and f′ is the quantized image. It was observed that when K increased, the average mean square error decreased and the average computation time increased. When the sampling rate increased, the average computation time increased for all cases, and the average mean square error decreased in most cases.

Table 1. Results of the proposed method with PixelThr = 30, SN = 20, ABC_cycle = 15 and K_means_cycle = 20. (Sr: sampling rate, MSE_a: average mean square error (MSE), T: average computation time (milliseconds)).

		K = 32			K = 64			K = 128			K = 256
Image	Sr	MSEa	S.D.	T	MSEa	S.D.	T	MSEa	S.D.	T	MSEa	S.D.	T
Lena	1.0	121.33	1.52	527	73.84	1.02	848	47.53	0.53	1460	31.31	0.12	2484
	0.25	121.36	1.67	170	74.13	0.89	252	47.66	0.43	414	31.71	0.14	644
	0.125	121.66	1.83	93	74.17	0.73	156	48.03	0.48	237	32.03	0.11	422
	0.0625	122.14	1.32	75	74.5	0.81	110	48.58	0.41	168	32.68	0.11	275
Baboon	1.0	382.57	4.7	835	242.19	1.7	1226	155.61	1.5	1962	100.16	0.8	3259
	0.25	383.01	5.0	260	242.68	2.9	413	155.95	1.9	677	100.52	0.8	1145
	0.125	383.42	4.7	193	242.76	2.5	273	157.06	1.6	461	101.85	0.8	783
	0.0625	387.06	4.3	146	244.46	1.9	218	158.06	1.4	351	103.44	0.8	606
Peppers	1.0	236.77	3.2	659	141.73	4.0	1029	86.45	3.3	1644	55.46	0.4	2876
	0.25	237.31	3.0	207	141.95	3.9	331	86.51	3.5	539	56.05	0.4	908
	0.125	237.87	4.6	129	141.72	2.7	209	87.37	3.3	318	56.81	0.3	565
	0.0625	239.28	6.9	87	143.03	3.5	137	88.34	3.2	237	58.07	0.4	408
Lake	1.0	207.73	3.2	651	134.88	1.6	1001	87.41	1.4	1538	57.09	0.5	2665
	0.25	208.38	2.6	217	135.19	1.6	343	88.58	1.1	514	57.71	0.6	818
	0.125	208.95	3.6	120	135.83	1.8	192	89.1	0.9	316	58.57	0.8	532
	0.0625	210.29	3.5	100	137.59	2.4	132	90.45	1.0	222	60.24	0.7	387
Airplane	1.0	68.56	3.8	322	41.91	2.5	380	26.52	1.1	601	18.19	0.4	1136
	0.25	68.97	2.6	105	41.62	2.0	123	27.11	1.0	224	18.46	0.4	440
	0.125	69.69	3.5	56	42.26	2.1	83	27.05	1.4	146	18.82	0.4	292
	0.0625	70.17	3.6	51	42.49	1.8	63	27.75	1.0	108	19.05	0.5	241

In the proposed method, the total computation time was the summation of computation time for initial palette generation and computation time for clustering by the accelerated K-means algorithm. Table 2 shows the computation time for color image quantization. These results were obtained by the proposed method with a sampling rate of 0.125. It was observed that the computation time for initial palette generation always increased with the increase in K. Similarly, the computation time for clustering by accelerated K-means algorithm always increased with the increase in K.

Table 2. The computation time (milliseconds) for color image quantization.

Image	K	Computation Time for Initial Palette Generation	Computation Time for Clustering by Accelerated K-means Algorithm	Total Computation Time
Lena	32	31	62	93
	64	46	110	156
	128	78	159	237
	256	141	281	422
Baboon	32	78	115	193
	64	117	156	273
	128	227	234	461
	256	409	374	783
Peppers	32	63	66	129
	64	84	125	209
	128	115	203	318
	256	222	343	565
Lake	32	52	68	120
	64	78	114	192
	128	146	170	316
	256	224	308	532
Airplane	32	26	30	56
	64	42	41	83
	128	78	68	146
	256	167	125	292

Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 illustrate the quantized images of Lena, Baboon, Lake, Peppers, and Airplane, respectively, corresponding to K = 32, 64, 128 and 256. These figures were obtained by the proposed method with a sampling rate of 0.125. It shows that the proposed method can generate high-quality quantized images. We can observe that there is no visual difference between the original and the 256 colors quantized images. In Figure 8a, there is a red tree in the middle region. However, the color of this tree is not red in Figure 8b. That is, there are some visual differences between the original and the 32 colors quantized images.

Figure 5. (a) The Lena image, (b) 32 colors quantized image, (c) 64 colors quantized image, (d) 128 colors quantized image, (e) 256 colors quantized image.

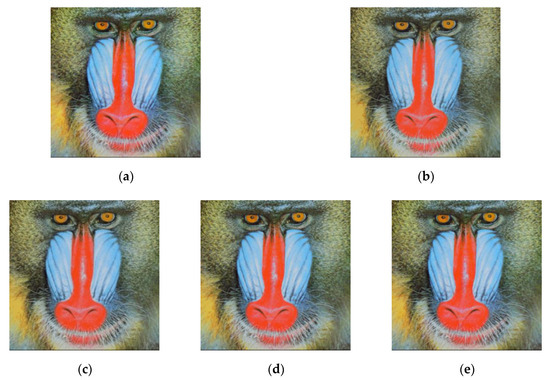
Figure 6. (a) The Baboon image, (b) 32 colors quantized image, (c) 64 colors quantized image, (d) 128 colors quantized image, (e) 256 colors quantized image.

Figure 7. (a) The Pepper image, (b) 32 colors quantized image, (c) 64 colors quantized image, (d) 128 colors quantized image, (e) 256 colors quantized image.

Figure 8. (a) The Lake image, (b) 32 colors quantized image, (c) 64 colors quantized image, (d) 128 colors quantized image, (e) 256 colors quantized image.

Figure 9. (a) The Airplane image, (b) 32 colors quantized image, (c) 64 colors quantized image, (d) 128 colors quantized image, (e) 256 colors quantized image.

4.1. The Effect of the Algorithm Parameters

This subsection analyzes the effect of the algorithm parameters on the solution. The comparison was applied to the Lena image quantized to 32 and 256 colors. The following parameters were used in the experiments: PixelThr = 30, SN = 20, ABC_cycle = 15 and K_means_cycle = 20. When a parameter was analyzed, the other parameters remained unchanged, and the average MSE and the average computation time (milliseconds) obtained will be shown in a figure for comparison.

As described in Section 3.1, the 3D RGB space was divided into non-overlapping cubes, and the size of each cube was 16 × 16 × 16. If the point number contained in the cube was equal to or larger than the threshold PixelThr, then the cube was preserved. The number of the preserved cube was N in this study. Figure 10 compares the results of PixelThr = {5, 15, 30}. This figure shows that as PixelThr increased, the computation time decreased slightly for all cases. When PixelThr increased, the MSE value decreased slightly in most cases.

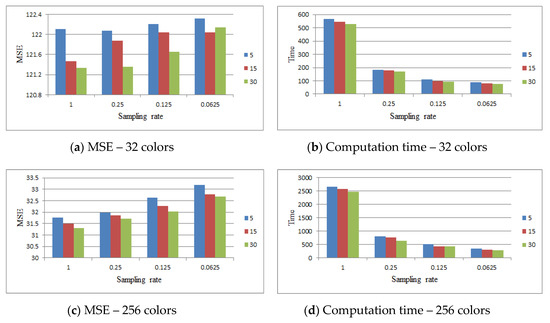
Figure 10. Comparing the results of PixelThr = {5, 15, 30} for the Lena image.

SN is the number of food sources in the ABC algorithm. The ABC algorithm was employed to select K colors from the N initial colors to form the initial palette in this study. Figure 11 compares the results of SN = {10, 20, 30}. This figure shows that as SN increased, the computation time increased slightly for all cases. It was observed that the MSE value does not always decrease with the increase in SN.

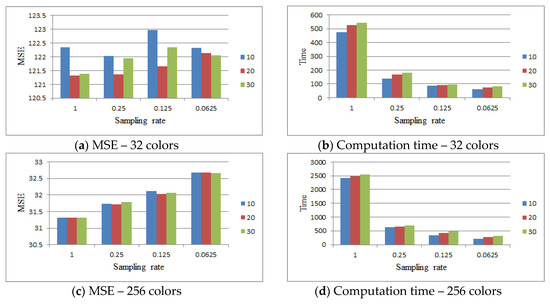
Figure 11. Comparing the results of SN = {10, 20, 30} for the Lena image.

The ABC algorithm was finished if the criterion cycle > ABC_cycle was satisfied. Figure 12 compares the results of ABC_cycle = {5, 15, 30}. This figure shows that as ABC_cycle increased, the computation time increased slightly for all cases. It was observed that the MSE value does not always decrease with the increase in ABC_cycle.

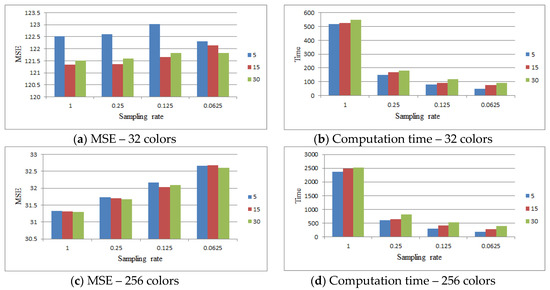
Figure 12. Comparing the results of ABC_cycle = {5, 15, 30} for the Lena image.

In the accelerated K-means algorithm, the algorithm stops if the criterion cycle > K_means_cycle is satisfied. Figure 13 compares the results of K_means_cycle = {5, 10, 20}. This figure shows that as K_means_cycle increased, the computation time increased and the average MSE decreased for all cases.

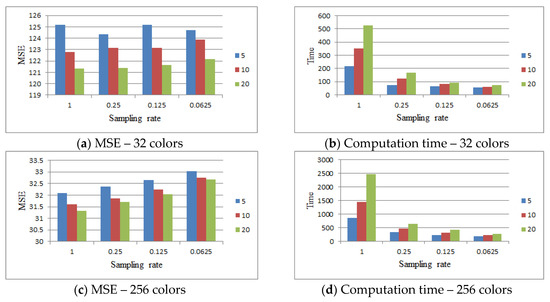
Figure 13. Comparing the results of K_means_cycle = {5, 10, 20} for the Lena image.

4.2. Comparison with the Method Proposed by Pérez-Delgado

In 2019, the application of the shuffled-frog leaping algorithm to perform color quantization was proposed by Pérez-Delgado [11], and this method is identified as SFLA-CQ. The SFLA-CQ algorithm was coded in C language and executed on a PC running under the Linux operating system with 8 GBytes of RAM and an AMD Ryzen 7 1800X Turbo processor (4.0 GHz). Table 3 shows the results obtained by SFLA-CQ.

Table 3. Results of the method proposed by Pérez-Delgado [11]. (Sr: sampling rate, MSE_a: average MSE, T: average computation time (milliseconds)).

		K = 32			K = 64			K = 128			K = 256
Image	Sr	MSEa	S.D.	T	MSEa	S.D.	T	MSEa	S.D.	T	MSEa	S.D.	T
Lena	1.0	120.37	1.21	8654	73.76	0.98	17022	47.64	0.57	35134	31.06	0.24	70477
	0.5	120.50	0.74	4579	74.32	1.52	8589	47.32	0.40	17888	31.19	0.39	35801
	0.2	121.27	1.63	1908	73.87	0.53	3548	47.74	0.75	7193	31.56	0.25	14665
	0.1	121.56	2.21	955	74.79	1.01	1865	48.23	0.76	3714	31.96	0.31	7626
Baboon	1.0	379.10	3.7	8089	238.87	1.6	15768	153.01	0.8	32843	98.05	0.4	65011
	0.5	381.48	4.2	4102	239.03	1.8	7966	153.69	1.2	16734	98.55	0.5	31460
	0.2	379.65	3.0	1688	239.69	1.6	3310	154.03	0.8	6722	99.41	0.5	12806
	0.1	382.09	3.7	892	240.77	1.2	1721	154.77	0.7	3500	100.58	0.6	6586
Peppers	1.0	233.98	2.3	7962	140.55	3.6	14767	87.20	3.4	29386	55.60	0.5	58755
	0.5	235.59	3.6	4026	141.83	3.7	7518	87.10	2.9	15149	55.89	0.6	30413
	0.2	236.74	5.2	1678	141.25	4.3	3109	89.21	4.2	6069	56.56	0.6	12313
	0.1	234.86	2.5	884	143.66	3.2	1635	88.45	3.3	3221	57.24	0.7	6323
Lake	1.0	205.86	1.8	8147	133.61	1.4	14749	88.14	1.0	29328	57.95	0.8	57507
	0.5	205.92	1.6	4181	133.94	1.4	7430	88.51	1.1	14856	58.45	0.8	28967
	0.2	206.64	1.9	1716	136.19	3.0	3075	89.40	1.1	6165	59.16	0.8	11931
	0.1	206.91	2.2	892	136.00	3.0	1580	89.37	1.1	3105	60.16	1.0	6257
Airplane	1.0	112.42	14.8	7755	59.76	8.1	15400	37.55	2.4	29939	23.39	1.2	60463
	0.5	105.41	12.2	3885	60.55	7.1	7769	35.88	1.5	15081	23.21	1.0	30198
	0.2	123.11	14.0	1672	58.61	4.4	3305	34.97	2.2	6180	23.34	1.0	12669
	0.1	111.98	11.4	854	57.47	5.3	1649	36.49	1.9	3146	23.36	0.8	6507

The performance of the proposed method with sampling rate = 0.125 was compared to SFLA-CQ with sampling rate = 0.1. For the Lena image, the average MSE obtained by the proposed method was near to that obtained by SFLA-CQ. For the Baboon image, the average MSE obtained by the proposed method was slightly higher than that obtained by SFLA-CQ. For the Pepper and Lake images, the average MSE obtained by the proposed method was slightly lower than that obtained by SFLA-CQ when K = 64, 128 and 256. For the Airplane image, the average MSE obtained by the proposed method was lower than that obtained by SFLA-CQ. These results clearly show that the computation time of SFLA-CQ is greater than that of the proposed method.

In summary, the proposed method can generate high-quality quantized images. These results reveal that the proposed method is superior to SFLA-CQ in terms of average computation time.

5. Conclusions

A new method is presented for color image quantization in this study. The method consists of three stages. The first stage is to generate N colors based on 3D histogram computation, the second is to obtain the initial palette by selecting K colors from the N colors based on an ABC algorithm, and the third is to obtain the quantized images using the accelerated K-means algorithm. In order to achieve reduction in computation time, the sampling process and the MPS algorithm are employed in this study.

Experimental results show that the proposed method can generate high-quality quantized images. When the sampling rate = 0.125, the average computation time of the proposed method is less than 1 s for all cases. The main contributions of this paper are that the proposed method can generate high-quality quantized images with less time consumption, and the experimental results reveal the feasibility of the proposed approach.