Investigating Long-Range Dependence of Emerging Asian Stock Markets Using Multifractal Detrended Fluctuation Analysis
Abstract
1. Introduction
2. Literature Review
3. Materials and Methods
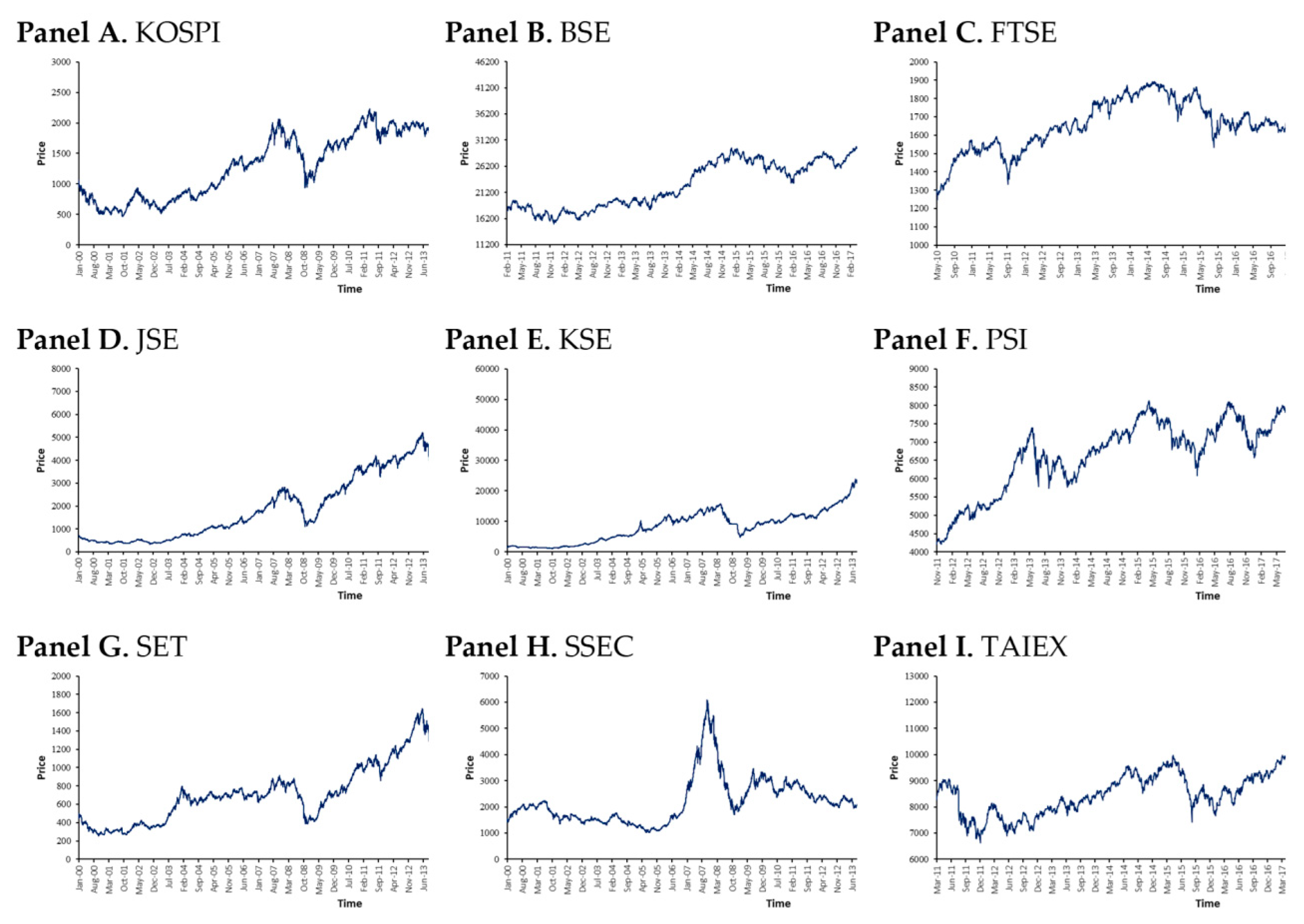
3.1. Data Description
3.2. Methodology
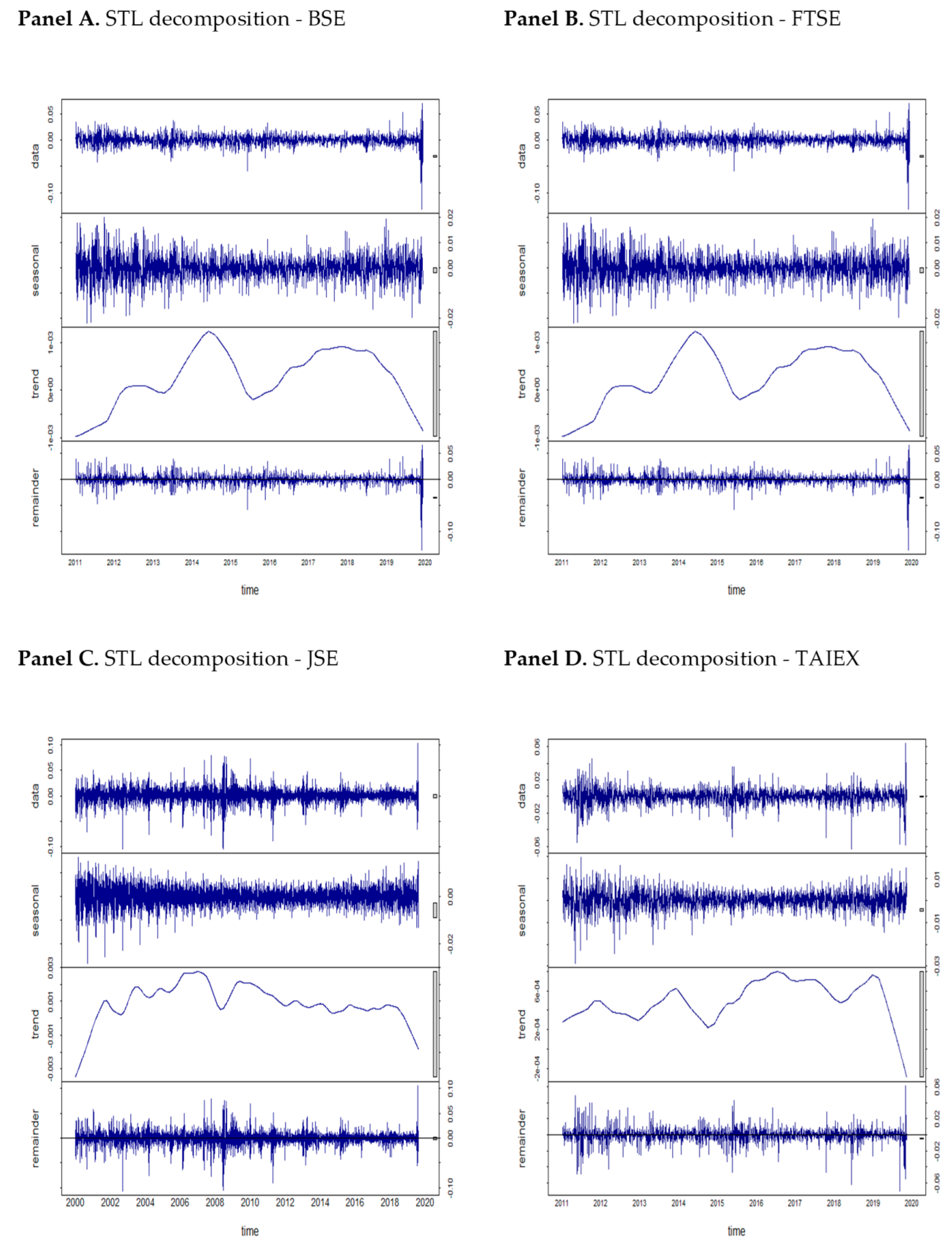
3.2.1. Seasonal and Trend Decomposition Using Loess (STL)
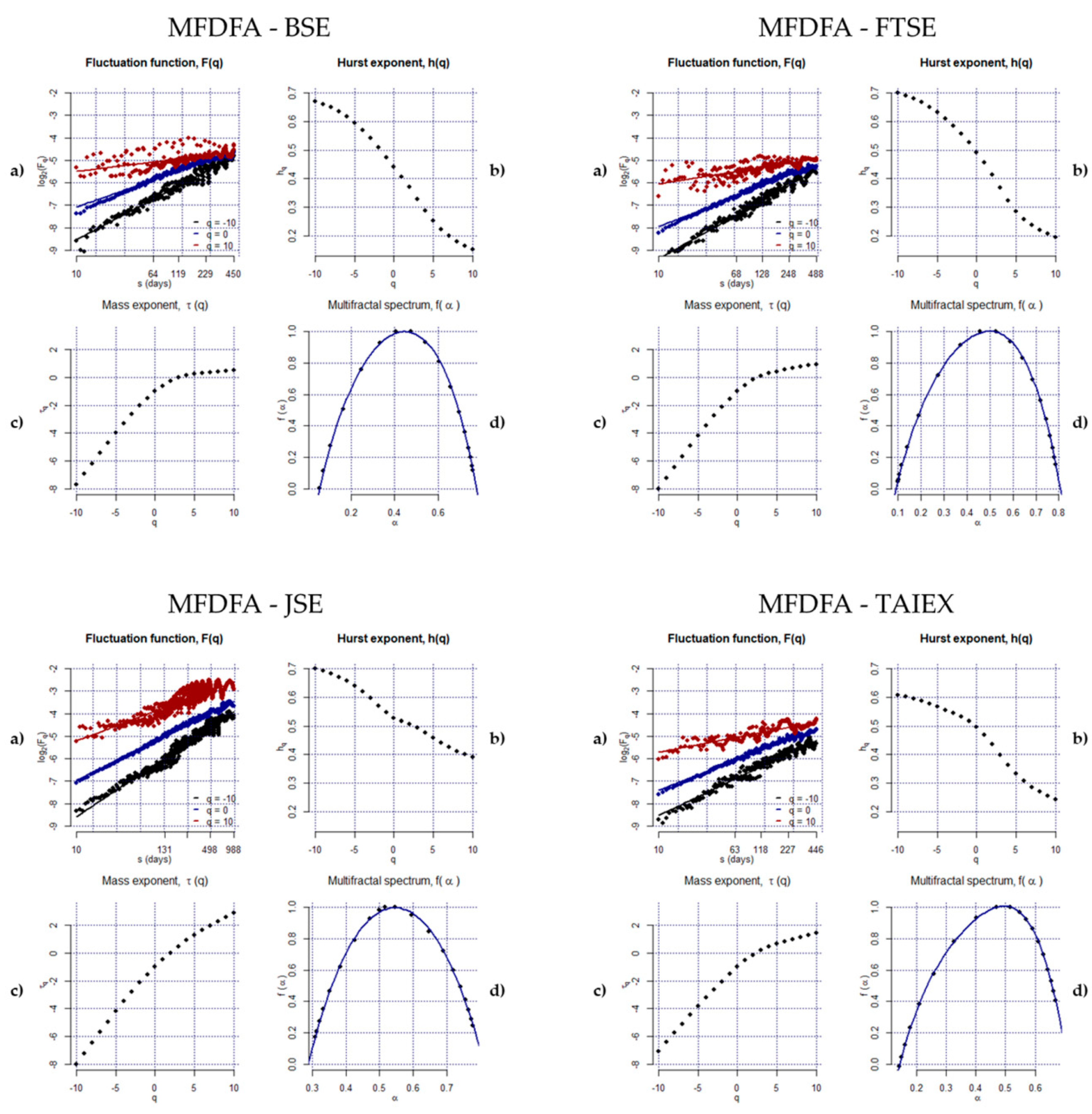
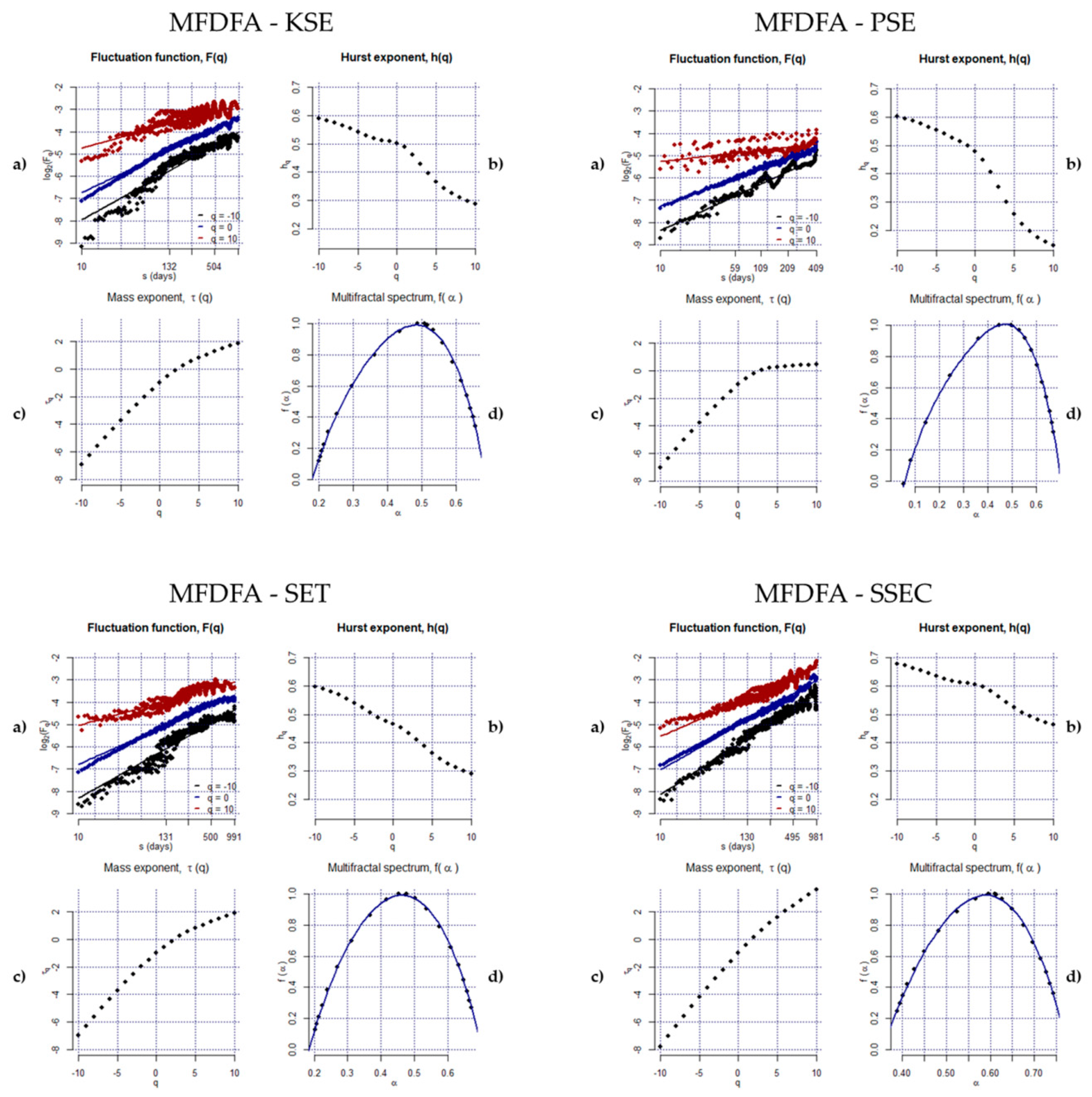
3.2.2. Multifractal Detrended Fluctuation Analysis (MFDFA)
4. Empirical Results
5. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A

Appendix B. BDS Test for Emerging Asian Stock Markets
| k | KOSPI | BSE | FTSE | JSE | KSE | PSI | SET | SSEC | TAIEX |
|---|---|---|---|---|---|---|---|---|---|
| 2 | 0.0218 ** | 0.0090 ** | 0.0231 ** | 0.0224 ** | 0.0351 ** | 0.0163 ** | 0.0217 ** | 0.0166 ** | 0.0112 ** |
| 3 | 0.0507 ** | 0.0210 ** | 0.0444 ** | 0.0445 ** | 0.0660 ** | 0.0307 ** | 0.0474 ** | 0.0375 ** | 0.0250 ** |
| 4 | 0.0735 ** | 0.0296 ** | 0.0569 ** | 0.0595 ** | 0.0869 ** | 0.0411 ** | 0.0661 ** | 0.0535 ** | 0.0355 ** |
| 5 | 0.0898 ** | 0.0354 ** | 0.0626 ** | 0.0684 ** | 0.0982 ** | 0.0452 ** | 0.0777 ** | 0.0630 ** | 0.0419 ** |
| 6 | 0.0992 ** | 0.0362 ** | 0.0636 ** | 0.0708 ** | 0.1034 ** | 0.0461 ** | 0.0845 ** | 0.0680 ** | 0.0436 ** |
References
- Bachelier, L. Theory of Speculation in the Random Character of Stock Market Prices; MIT: Cambridge, MA, USA, 1900. [Google Scholar]
- Malkiel, B.G.; Fama, E.F. Efficient capital markets: A review of theory and empirical work. J. Financ. 1970, 25, 383–417. [Google Scholar] [CrossRef]
- Mandelbrot, B. The variation of some other speculative prices. J. Bus. 1967, 40, 393–413. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. When can price be arbitraged efficiently? A limit to the validity of the random walk and martingale models. Rev. Econ. Stat. 1971, 53, 225–236. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The variation of the prices of cotton, wheat, and railroad stocks, and of some financial rates. In Fractals and Scaling in Finance; Springer: Berlin/Heidelberg, Germany, 1997; pp. 419–443. [Google Scholar]
- Gopikrishnan, P.; Plerou, V.; Gabaix, X.; Amaral, L.; Stanley, H. Price fluctuations and market activity. Phys. A Stat. Mech. Appl. 2001, 299, 137–143. [Google Scholar] [CrossRef]
- Alvarez-Ramirez, J.; Alvarez, J.; Rodriguez, E. Short-term predictability of crude oil markets: A detrended fluctuation analysis approach. Energy Econ. 2008, 30, 2645–2656. [Google Scholar] [CrossRef]
- Kim, S.; Eom, C. Long-term memory and volatility clustering in high-frequency price changes. Phys. A Stat. Mech. Appl. 2008, 387, 1247–1254. [Google Scholar]
- He, L.-Y.; Fan, Y.; Wei, Y.-M. The empirical analysis for fractal features and long-run memory mechanism in petroleum pricing systems. Int. J. Glob. Energy Issues 2007, 27, 492–502. [Google Scholar] [CrossRef]
- Adrangi, B.; Chatrath, A.; Dhanda, K.K.; Raffiee, K. Chaos in oil prices? Evidence from futures markets. Energy Econ. 2001, 23, 405–425. [Google Scholar] [CrossRef]
- Miloş, L.R.; Haţiegan, C.; Miloş, M.C.; Barna, F.M.; Boțoc, C. Multifractal Detrended Fluctuation Analysis (MF-DFA) of Stock Market Indexes. Empirical Evidence from Seven Central and Eastern European Markets. Sustainability 2020, 12, 535. [Google Scholar] [CrossRef]
- Peters, E.E. Fractal Market Analysis: Applying Chaos Theory to Investment and Economics; John Wiley & Sons: Hoboken, NJ, USA, 1994; Volume 24. [Google Scholar]
- Edgar, P.E. Chaos and Order in the Capital Markets, A New View of Cycles, Prices and Market Volatility; John Wiley Sons, Inc.: New York, NY, USA, 1991. [Google Scholar]
- Kristoufek, L. Fractal markets hypothesis and the global financial crisis: Scaling, investment horizons and liquidity. Adv. Complex Syst. 2012, 15, 1250065. [Google Scholar] [CrossRef]
- Peng, C.-K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E 1994, 49, 1685. [Google Scholar] [CrossRef] [PubMed]
- Cajueiro, D.O.; Tabak, B.M. Testing for time-varying long-range dependence in volatility for emerging markets. Phys. A Stat. Mech. Appl. 2005, 346, 577–588. [Google Scholar] [CrossRef]
- Di Matteo, T.; Aste, T.; Dacorogna, M.M. Long-term memories of developed and emerging markets: Using the scaling analysis to characterize their stage of development. J. Bank. Financ. 2005, 29, 827–851. [Google Scholar] [CrossRef]
- Barabási, A.-L.; Vicsek, T. Multifractality of self-affine fractals. Phys. Rev. A 1991, 44, 2730. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal detrended fluctuation analysis of nonstationary time series. Phys. A Stat. Mech. Appl. 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhuang, X.-T.; Jin, X. Measuring multifractality of stock price fluctuation using multifractal detrended fluctuation analysis. Phys. A Stat. Mech. Appl. 2009, 388, 2189–2197. [Google Scholar] [CrossRef]
- Telesca, L.; Lapenna, V.; Macchiato, M. Multifractal fluctuations in seismic interspike series. Phys. A Stat. Mech. Appl. 2005, 354, 629–640. [Google Scholar] [CrossRef]
- Kumar, S.; Deo, N. Multifractal properties of the Indian financial market. Phys. A Stat. Mech. Appl. 2009, 388, 1593–1602. [Google Scholar] [CrossRef]
- López-García, M.; Trinidad-Segovia, J.; Sánchez-Granero, M.; Pouchkarev, I. Extending the Fama and French model with a long term memory factor. Eur. J. Oper. Res. 2019, 15, 1–6. [Google Scholar] [CrossRef]
- Fama, E.F.; French, K.R. A five-factor asset pricing model. J. Financ. Econ. 2015, 116, 1–22. [Google Scholar] [CrossRef]
- Wawrzkiewicz-Jałowiecka, A.; Trybek, P.; Dworakowska, B.; Machura, Ł. Multifractal Properties of BK Channel Currents in Human Glioblastoma Cells. J. Phys. Chem. B 2020, 124, 2382–2391. [Google Scholar] [CrossRef] [PubMed]
- Bhoumik, G.; Deb, A.; Bhattacharyya, S.; Ghosh, D. Comparative Multifractal Detrended Fluctuation Analysis of Heavy Ion Interactions at a Few GeV to a Few Hundred GeV. Adv. High Energy Phys. 2016, 1–9. [Google Scholar] [CrossRef]
- Cuenca, D.I.; Estévez, J.; García-Marín, A.P. Multifractal Characterization of Seismic Activity in the Provinces of Esmeraldas and Manabí, Ecuador. Proceedings 2019, 24, 27. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, G.; Qiu, L.; Zhang, B.; Sun, Y.; Gui, Z.; Zhang, Q. A Modified Multifractal Detrended Fluctuation Analysis (MFDFA) Approach for Multifractal Analysis of Precipitation in Dongting Lake Basin, China. Water 2019, 11, 891. [Google Scholar] [CrossRef]
- Farjah, E. Proposing an Efficient Wind Forecasting Agent Using Adaptive MFDFA. J. Power Technol. 2019, 99, 152–162. [Google Scholar]
- Drożdż, S.; Oświȩcimka, P.; Kulig, A.; Kwapień, J.; Bazarnik, K.; Grabska-Gradzińska, I.; Rybicki, J.; Stanuszek, M. Quantifying origin and character of long-range correlations in narrative texts. Inf. Sci. 2016, 331, 32–44. [Google Scholar] [CrossRef]
- Nagy, Z.; Mukli, P.; Herman, P.; Eke, A. Decomposing multifractal crossovers. Front. Physiol. 2017, 8, 533. [Google Scholar] [CrossRef]
- Ihlen, E. Introduction to Multifractal Detrended Fluctuation Analysis in Matlab. Front. Physiol. 2012, 3. [Google Scholar] [CrossRef]
- Rizvi, S.A.R.; Dewandaru, G.; Bacha, O.I.; Masih, M. An analysis of stock market efficiency: Developed vs Islamic stock markets using MF-DFA. Phys. A Stat. Mech. Appl. 2014, 407, 86–99. [Google Scholar] [CrossRef]
- Podobnik, B.; Stanley, H.E. Detrended cross-correlation analysis: A new method for analyzing two nonstationary time series. Phys. Rev. Lett. 2008, 100, 084102. [Google Scholar] [CrossRef]
- Wang, Y.; Wei, Y.; Wu, C. Cross-correlations between Chinese A-share and B-share markets. Phys. A Stat. Mech. Appl. 2010, 389, 5468–5478. [Google Scholar] [CrossRef]
- Oh, G.; Kim, S.; Eom, C. Multifractal Analysis of Korean Stock Market. J. Korean Phys. Soc. 2010, 56, 982–985. [Google Scholar] [CrossRef]
- Jagric, T.; Podobnik, B.; Kolanovic, M. Does the efficient market hypothesis hold?: Evidence from six transition economies. East. Eur. Econ. 2005, 43, 79–103. [Google Scholar] [CrossRef]
- Domino, K. The use of the Hurst exponent to predict changes in trends on the Warsaw Stock Exchange. Phys. A Stat. Mech. Appl. 2011, 390, 98–109. [Google Scholar] [CrossRef]
- Pleşoianu, A.; Todea, A.; Căpuşan, R. The informational efficiency of the Romanian stock market: Evidence from fractal analysis. Procedia Econ. Financ. 2012, 3, 111–118. [Google Scholar] [CrossRef]
- Caraiani, P. Evidence of multifractality from emerging European stock markets. PLoS ONE 2012, 7, e40693. [Google Scholar] [CrossRef]
- Ferreira, P. Long-range dependencies of Eastern European stock markets: A dynamic detrended analysis. Phys. A Stat. Mech. Appl. 2018, 505, 454–470. [Google Scholar] [CrossRef]
- Boţoc, C. Individual and Regional Efficiency in Emerging Stock Markets: Empirical Investigations. J. Appl. Econ. Sci. 2015, 10, 70–81. [Google Scholar]
- Laib, M.; Golay, J.; Telesca, L.; Kanevski, M. Multifractal analysis of the time series of daily means of wind speed in complex regions. Chaos Solitons Fractals 2018, 109, 118–127. [Google Scholar] [CrossRef]
- Dragotă, V.; Ţilică, E.V. Market efficiency of the Post Communist East European stock markets. Central Eur. J. Oper. Res. 2014, 22, 307–337. [Google Scholar] [CrossRef]
- Mensi, W.; Lee, Y.-J.; Al-Yahyaee, K.H.; Sensoy, A.; Yoon, S.-M. Intraday downward/upward multifractality and long memory in Bitcoin and Ethereum markets: An asymmetric multifractal detrended fluctuation analysis. Financ. Res. Lett. 2019, 31, 19–25. [Google Scholar] [CrossRef]
- Aslam, F.; Mohti, W.; Ferreira, P. Evidence of Intraday Multifractality in European Stock Markets during the recent Coronavirus (COVID-19) Outbreak. Int. J. Financ. Stud. 2020, 8, 31. [Google Scholar]
- Smith, G. The changing and relative efficiency of European emerging stock markets. Eur. J. Financ. 2012, 18, 689–708. [Google Scholar] [CrossRef]
- Tokić, S.; Bolfek, B.; Peša, A.R. Testing efficient market hypothesis in developing Eastern European countries. Investig. Manag. Financ. Innov. 2018, 15, 281. [Google Scholar]
- Engle, R.F.; Russell, J.R. Autoregressive conditional duration: A new model for irregularly spaced transaction data. Econometrica 1998, 66, 1127–1162. [Google Scholar] [CrossRef]
- Engle, R.F. The econometrics of ultra-high-frequency data. Econometrica 2000, 68, 1–22. [Google Scholar] [CrossRef]
- Racicot, F.-É.; Théoret, R.; Coën, A. Forecasting uhf financial data: Realized volatility versus UHF-GARCH models. Int. Adv. Econ. Res. 2007, 13, 243–245. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O.E.; Shephard, N. Aggregation and Model Construction for Volatility Models; Economics Group, Nuffield College, University of Oxford: Oxford, UK, 1998. [Google Scholar]
- Guidi, F.; Gupta, R.; Maheshwari, S. Weak-form market efficiency and calendar anomalies for Eastern Europe equity markets. J. Emerg. Mark. Financ. 2011, 10, 337–389. [Google Scholar] [CrossRef]
- Karadagli, E.C.; Omay, N. Testing weak form market efficiency of emerging markets: A nonlinear approach. J. Appl. Econ. Sci. 2012, 7, 235–245. [Google Scholar]
- Ghazani, M.M.; Araghi, M.K. Evaluation of the adaptive market hypothesis as an evolutionary perspective on market efficiency: Evidence from the Tehran stock exchange. Res. Int. Bus. Financ. 2014, 32, 50–59. [Google Scholar] [CrossRef]
- Lingaraja, K.; Selvam, M.; Vasanth, V. The stock market efficiency of emerging markets: Evidence from Asian region. Asian Soc. Sci. 2014, 10, 158. [Google Scholar] [CrossRef]
- Zunino, L.; Tabak, B.M.; Figliola, A.; Pérez, D.; Garavaglia, M.; Rosso, O. A multifractal approach for stock market inefficiency. Phys. A Stat. Mech. Appl. 2008, 387, 6558–6566. [Google Scholar] [CrossRef]
- Ikeda, T. Multifractal structures for the Russian stock market. Phys. A Stat. Mech. Appl. 2018, 492, 2123–2128. [Google Scholar] [CrossRef]
- Mohti, W.; Dionísio, A.; Ferreira, P.; Vieira, I. Frontier markets’ efficiency: Mutual information and detrended fluctuation analyses. J. Econ. Interact. Coord. 2019, 14, 551–572. [Google Scholar] [CrossRef]
- Horta, P.; Lagoa, S.; Martins, L. The impact of the 2008 and 2010 financial crises on the Hurst exponents of international stock markets: Implications for efficiency and contagion. Int. Rev. Financ. Anal. 2014, 35, 140–153. [Google Scholar] [CrossRef]
- Aktan, C.; Sahin, E.E.; Kucukkaplan, I. Testing the Information Efficiency in Emerging Markets. In Management from an Emerging Market Perspective; Kucukkocaogky, G., Gokten, S., Eds.; IntechOpen: London, UK, 2018; pp. 49–67. [Google Scholar]
- Nurunnabi, M. Testing weak-form efficiency of emerging economies: A critical review of literature. J. Bus. Econ. Manag. 2012, 13, 167–188. [Google Scholar] [CrossRef][Green Version]
- Cleveland, R.B.; Cleveland, W.S.; McRae, J.E.; Terpenning, I. STL: A seasonal-trend decomposition. J. Off. Stat. 1990, 6, 3–73. [Google Scholar]
- Brock, W.A.; Hsieh, D.A.; LeBaron, B.D.; Brock, W.E. Nonlinear Dynamics, Chaos, and Instability: Statistical Theory and Economic Evidence; MIT Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Brock, W.A.; Scheinkman, J.A.; Dechert, W.D.; LeBaron, B. A test for independence based on the correlation dimension. J. Econom. Rev. 1996, 15, 197–235. [Google Scholar] [CrossRef]
- Racicot, F.-É. Notes on nonlinear dynamics. Aestimatio IEB Int. J. Financ. 2012, 5, 162–221. [Google Scholar]
- Laib, M.; Telesca, L.; Kanevski, M. Long-range fluctuations and multifractality in connectivity density time series of a wind speed monitoring network. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 033108. [Google Scholar] [CrossRef]
- Shiskin, J. The X-11 Variant of the Census Method II Seasonal Adjustment Program; US Government Printing Office: Washington, DC, USA, 1965.
- Feder, J. Fractals; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Kantelhardt, J.W. Fractal and Multifractal Time Series. In Mathematics of Complexity and Dynamical Systems; Meyers, R.A., Ed.; Springer: New York, NY, USA, 2011; pp. 463–487. [Google Scholar]
- De Bondt, W.F.; Thaler, R.H. Further evidence on investor overreaction and stock market seasonality. J. Financ. 1987, 42, 557–581. [Google Scholar] [CrossRef]
- Anagnostidis, P.; Varsakelis, C.; Emmanouilides, C.J. Has the 2008 financial crisis affected stock market efficiency? The case of Eurozone. Phys. A Stat. Mech. Appl. 2016, 447, 116–128. [Google Scholar] [CrossRef]
- Arshad, S.; Rizvi, S.A.R.; Haroon, O. Understanding Asian emerging stock markets. Bul. Ekon. Monet. Perbank. 2019, 21, 495–510. [Google Scholar] [CrossRef]
- Rizvi, S.A.R.; Arshad, S. Investigating the efficiency of East Asian stock markets through booms and busts. Pac. Sci. Rev. 2014, 16, 275–279. [Google Scholar] [CrossRef][Green Version]
- Samadder, S.; Ghosh, K.; Basu, T. Fractal analysis of prime Indian stock market indices. Fractals 2013, 21, 1350003. [Google Scholar] [CrossRef]
- Šonje, V.; Alajbeg, D.; Bubaš, Z. Efficient market hypothesis: Is the Croatian stock market as (in) efficient as the US market. Financ. Theory Pract. 2011, 35, 301–326. [Google Scholar] [CrossRef]
- Tabak, B.M.; Cajueiro, D.O. Are the crude oil markets becoming weakly efficient over time? A test for time-varying long-range dependence in prices and volatility. Energy Econ. 2007, 29, 28–36. [Google Scholar] [CrossRef]
- Rizvi, S.A.R.; Arshad, S.; Alam, N. A tripartite inquiry into volatility-efficiency-integration nexus-case of emerging markets. Emerg. Mark. Rev. 2018, 34, 143–161. [Google Scholar] [CrossRef]
- Grech, D.; Pamuła, G. The local Hurst exponent of the financial time series in the vicinity of crashes on the Polish stock exchange market. Phys. A Stat. Mech. Appl. 2008, 387, 4299–4308. [Google Scholar] [CrossRef]
- Wei, Y.; Huang, D. Multifractal analysis of SSEC in Chinese stock market: A different empirical result from Heng Seng index. Phys. A Stat. Mech. Appl. 2005, 355, 497–508. [Google Scholar] [CrossRef]
- Matia, K.; Ashkenazy, Y.; Stanley, H.E. Multifractal properties of price fluctuations of stocks and commodities. EPL Europhys. Lett. 2003, 61, 422. [Google Scholar] [CrossRef]
- Norouzzadeh, P.; Rahmani, B. A multifractal detrended fluctuation description of Iranian rial–US dollar exchange rate. Phys. A Stat. Mech. Appl. 2006, 367, 328–336. [Google Scholar] [CrossRef]
- Dewandaru, G.; Rizvi, S.A.R.; Bacha, O.I.; Masih, M. What factors explain stock market retardation in Islamic Countries. Emerg. Mark. Rev. 2014, 19, 106–127. [Google Scholar] [CrossRef]
- Jiang, Z.-Q.; Xie, W.-J.; Zhou, W.-X.; Sornette, D. Multifractal analysis of financial markets: A review. Rep. Prog. Phys. 2019, 82, 125901. [Google Scholar] [CrossRef] [PubMed]
- Su, Z.-Y.; Wang, Y.-T. An investigation into the multifractal characteristics of the TAIEX stock exchange index in Taiwan. J. Korean Phys. Soc. 2009, 54, 1395–1402. [Google Scholar] [CrossRef]
- Wei, Y.; Wang, P. Forecasting volatility of SSEC in Chinese stock market using multifractal analysis. Phys. A Stat. Mech. Appl. 2008, 387, 1585–1592. [Google Scholar] [CrossRef]
- Rizvi, S.A.R.; Arshad, S. How does crisis affect efficiency? An empirical study of East Asian markets. Borsa Istanb. Rev. 2016, 16, 1–8. [Google Scholar] [CrossRef]
- Ramos-Requena, J.P.; Trinidad-Segovia, J.; Sánchez-Granero, M. Introducing Hurst exponent in pair trading. Phys. A Stat. Mech. Appl. 2017, 488, 39–45. [Google Scholar] [CrossRef]
- Kobeissi, Y.H. Multifractal Financial Markets: An Alternative Approach to Asset and Risk Management; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Dacorogna, M.; Müller, U.; Olsen, R.; Pictet, O. Defining efficiency in heterogeneous markets. Quant. Financ. 2001, 1, 198–201. [Google Scholar] [CrossRef]
- Chen, H.; Wu, C. Forecasting volatility in Shanghai and Shenzhen markets based on multifractal analysis. Phys. A Stat. Mech. Appl. 2011, 390, 2926–2935. [Google Scholar] [CrossRef]
- Hodrick, R.J.; Prescott, E.C. Postwar U.S. Business Cycles: An Empirical Investigation. J. Money Credit. Bank. 1997, 29, 1–16. [Google Scholar] [CrossRef]
- Cooley, T.F.; Prescott, E.C. Economic growth and business cycles. In Frontiers of Real Business Cycle Research; Cooley, T.F., Ed.; Princeton University Press: Princeton, NJ, USA, 1995. [Google Scholar]
- Racicot, F.E.; Théoret, R.; Calmès, C. La titrisation aux États-Unis et au Canada. Rev. Sci. Gest. 2016, 280, 21–34. [Google Scholar] [CrossRef]
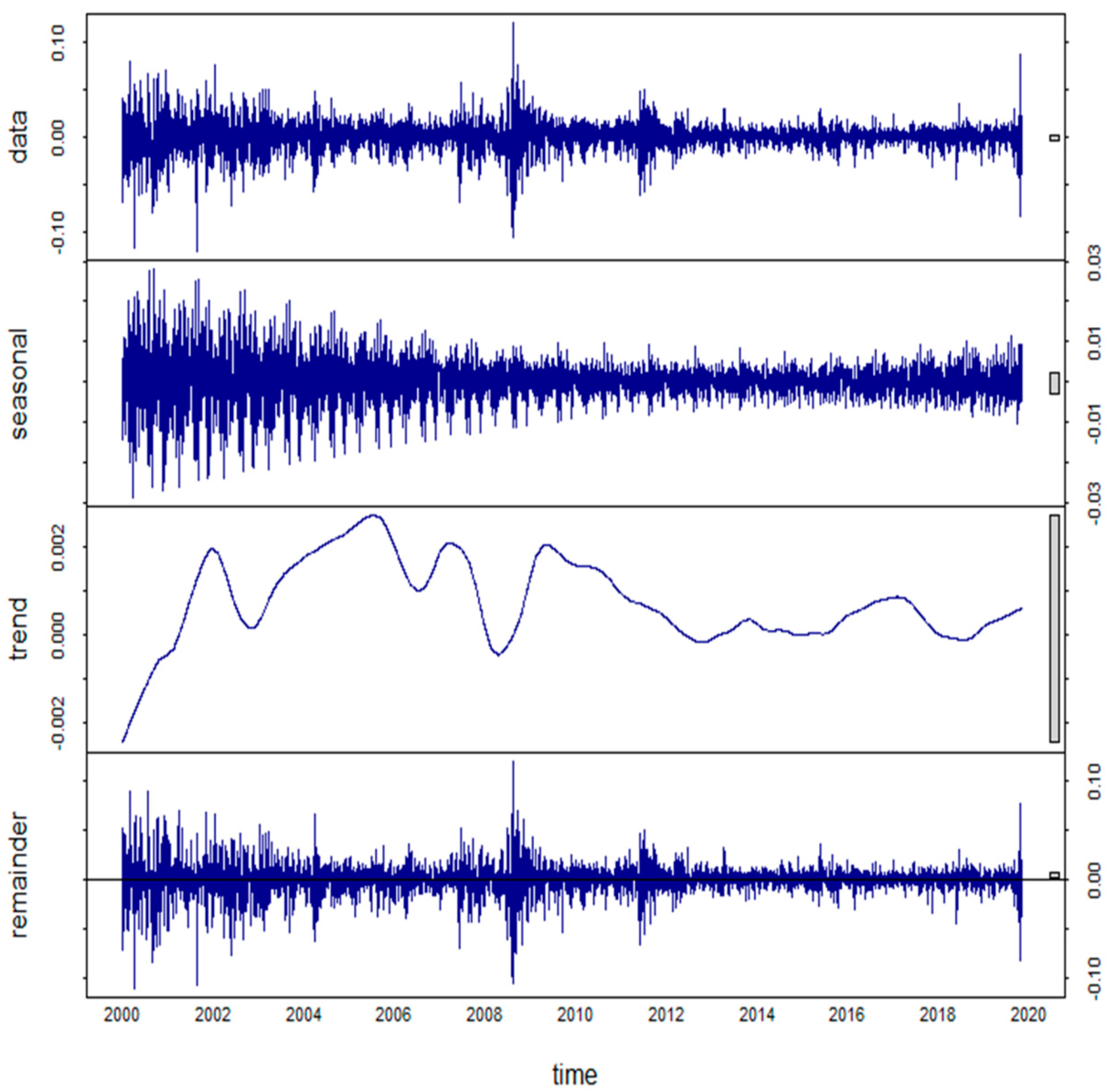
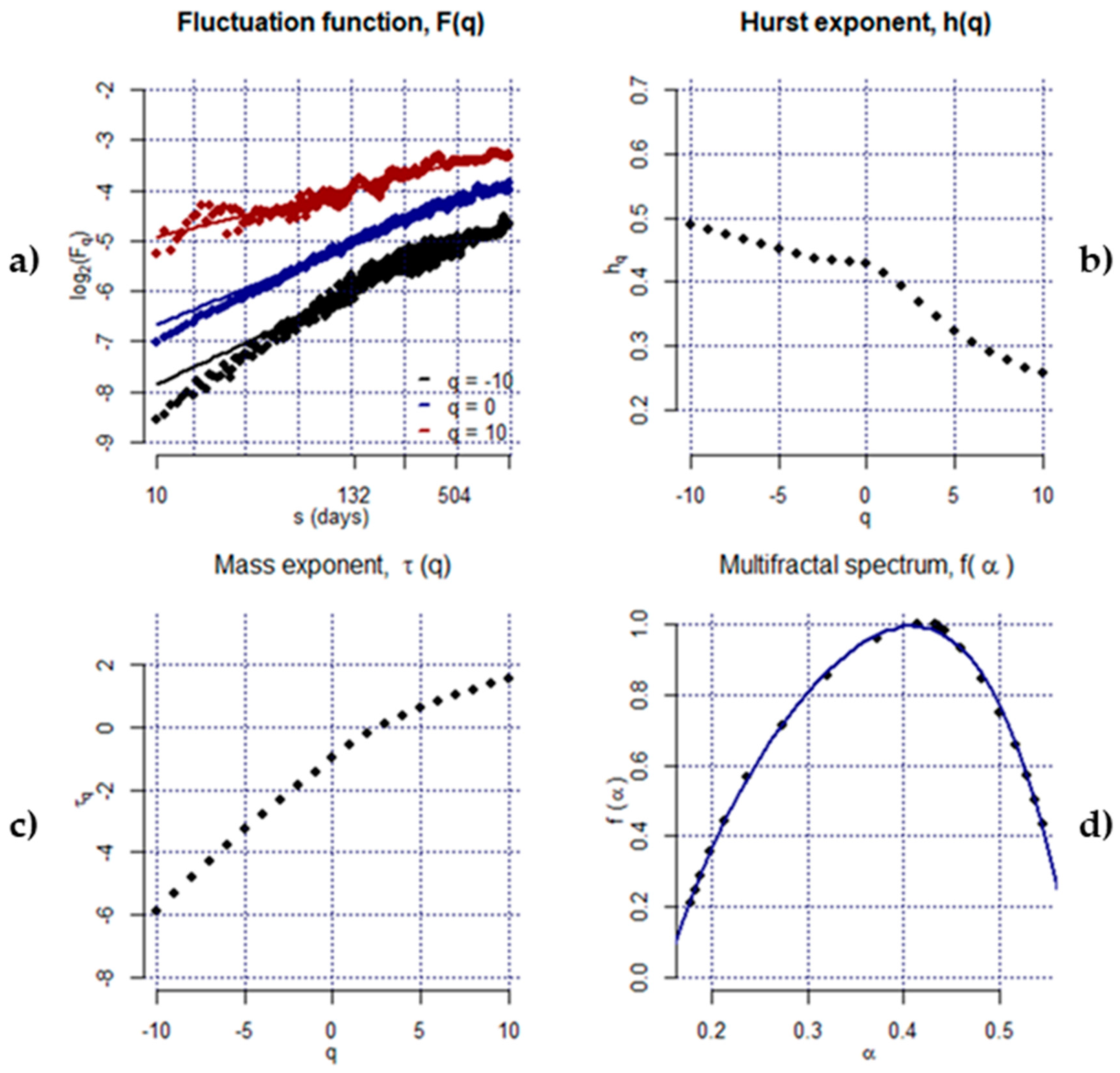
| S.No. | Country | Index Symbol | Data Range | Observation (Daily) |
|---|---|---|---|---|
| 1 | India | BSE | 24-Feb-2011 to 1-Apr-2020 | 2252 |
| 2 | Malaysia | FTSE | 20-May-2010 to 2-Apr-2020 | 2441 |
| 3 | Indonesia | JSE | 4-Jan-2000 to 2-Apr-2020 | 4941 |
| 4 | South Korea | KOSPI | 4-Jan-2000 to 1-Apr-2020 | 5000 |
| 5 | Pakistan | KSE | 3-Jan-2000 to 31-Mar-2020 | 5000 |
| 6 | Philippines | PSE | 2-Nov-2011 to 1-Apr-2020 | 2049 |
| 7 | Thailand | SET | 4-Jan-2000 to 2-Apr-2020 | 4958 |
| 8 | China | SSEC | 4-Jan-2000 to 2-Apr-2020 | 4908 |
| 9 | Taiwan | TAIEX | 17-Mar-2011 to 1-Apr-2020 | 2233 |
| Order q | BSE | FTSE | JSE | KOSPI | KSE | PSE | SET | SSEC | TAIEX |
| −10 | 0.67 | 0.70 | 0.70 | 0.49 | 0.59 | 0.60 | 0.60 | 0.68 | 0.61 |
| −8 | 0.65 | 0.68 | 0.68 | 0.47 | 0.57 | 0.59 | 0.58 | 0.66 | 0.59 |
| −6 | 0.62 | 0.65 | 0.66 | 0.46 | 0.55 | 0.57 | 0.56 | 0.65 | 0.58 |
| −4 | 0.57 | 0.61 | 0.62 | 0.44 | 0.53 | 0.54 | 0.52 | 0.62 | 0.56 |
| −2 | 0.51 | 0.56 | 0.57 | 0.43 | 0.51 | 0.51 | 0.49 | 0.61 | 0.53 |
| 0 | 0.44 | 0.49 | 0.53 | 0.43 | 0.50 | 0.48 | 0.47 | 0.61 | 0.50 |
| 2 | 0.37 | 0.41 | 0.51 | 0.39 | 0.46 | 0.41 | 0.44 | 0.58 | 0.44 |
| 4 | 0.29 | 0.32 | 0.48 | 0.34 | 0.40 | 0.30 | 0.39 | 0.54 | 0.36 |
| 6 | 0.22 | 0.26 | 0.44 | 0.30 | 0.34 | 0.22 | 0.34 | 0.51 | 0.31 |
| 8 | 0.18 | 0.22 | 0.41 | 0.28 | 0.31 | 0.18 | 0.31 | 0.48 | 0.27 |
| 10 | 0.15 | 0.20 | 0.39 | 0.26 | 0.29 | 0.15 | 0.29 | 0.46 | 0.24 |
| ∆h | 0.52 | 0.50 | 0.31 | 0.23 | 0.30 | 0.46 | 0.31 | 0.22 | 0.37 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aslam, F.; Latif, S.; Ferreira, P. Investigating Long-Range Dependence of Emerging Asian Stock Markets Using Multifractal Detrended Fluctuation Analysis. Symmetry 2020, 12, 1157. https://doi.org/10.3390/sym12071157
Aslam F, Latif S, Ferreira P. Investigating Long-Range Dependence of Emerging Asian Stock Markets Using Multifractal Detrended Fluctuation Analysis. Symmetry. 2020; 12(7):1157. https://doi.org/10.3390/sym12071157
Chicago/Turabian StyleAslam, Faheem, Saima Latif, and Paulo Ferreira. 2020. "Investigating Long-Range Dependence of Emerging Asian Stock Markets Using Multifractal Detrended Fluctuation Analysis" Symmetry 12, no. 7: 1157. https://doi.org/10.3390/sym12071157
APA StyleAslam, F., Latif, S., & Ferreira, P. (2020). Investigating Long-Range Dependence of Emerging Asian Stock Markets Using Multifractal Detrended Fluctuation Analysis. Symmetry, 12(7), 1157. https://doi.org/10.3390/sym12071157






